Trends and Persistence of Dry–Wet Conditions in Northeast Brazil
Abstract
1. Introduction
2. Material and Methods
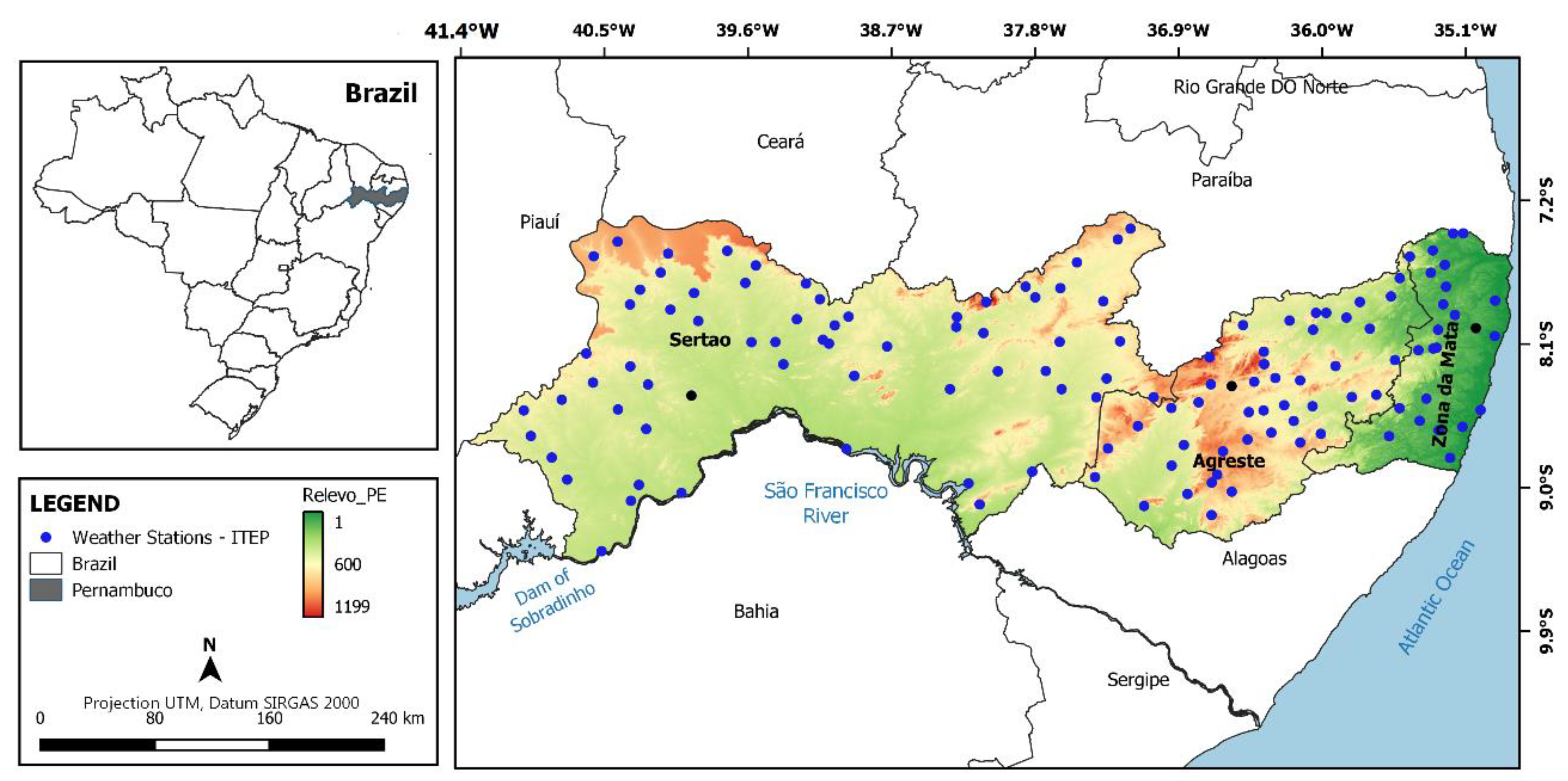
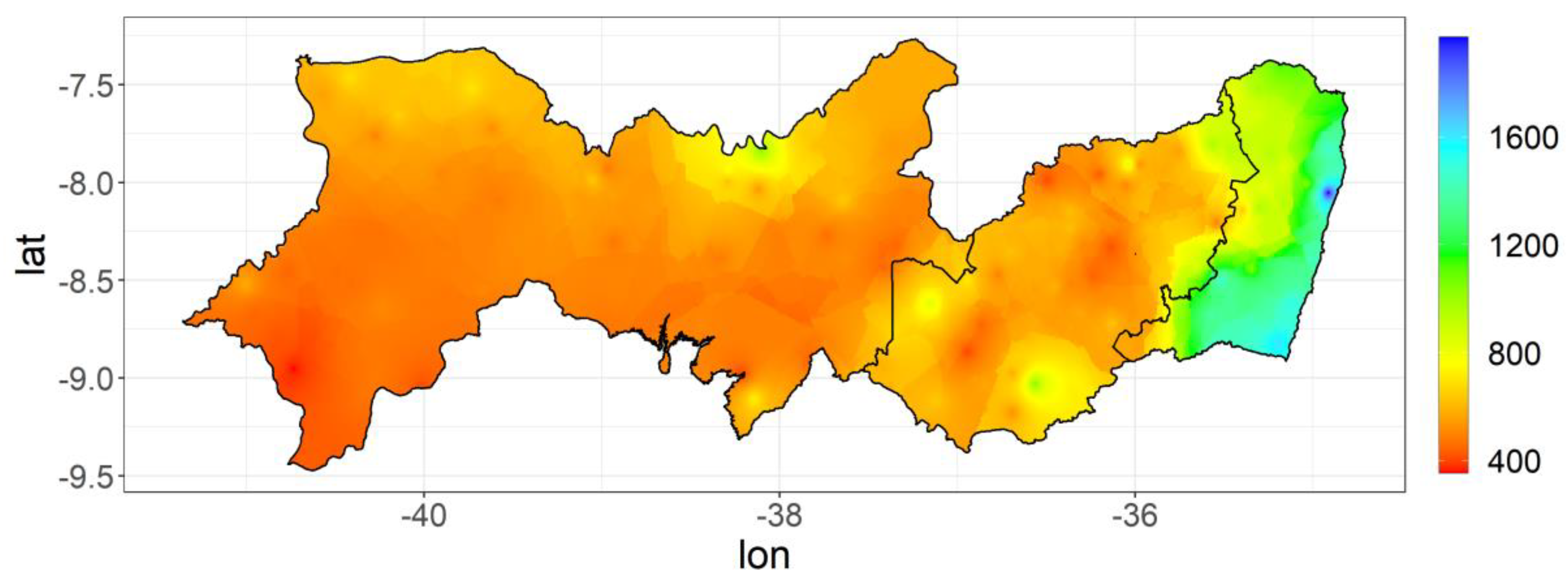
2.1. Study Area and Dataset
2.2. Standardized Precipitation Index
2.3. Mann–Kendall Test
2.4. Wilcoxon–Mann–Whitney Test
2.5. Sen’s Slope of Trend
2.6. Detrended Fluctuation Analysis
- (i)
- The original temporal series , is integrated to calculatewhere is the average.
- (ii)
- Next, the integrated series is divided into non-overlapping segments of length (here stands for the integer value of the argument), and in each segment the local trend (linear or higher order polynomial least square fit—termed DFA1, DFA2, DFA3,…, for polynomials of order 1,2, 3,…, respectively) is estimated and subtracted from . In DFAm, trends of order in the profile , and of order in the original record are eliminated.
- (iii)
- The detrended variance is now calculated as
- (iv)
- Repeating this calculation for different window sizes provides the relationship between the fluctuation function and the window size . If long-term correlations are present in original series, increases with according to a power law
3. Results and Discussion
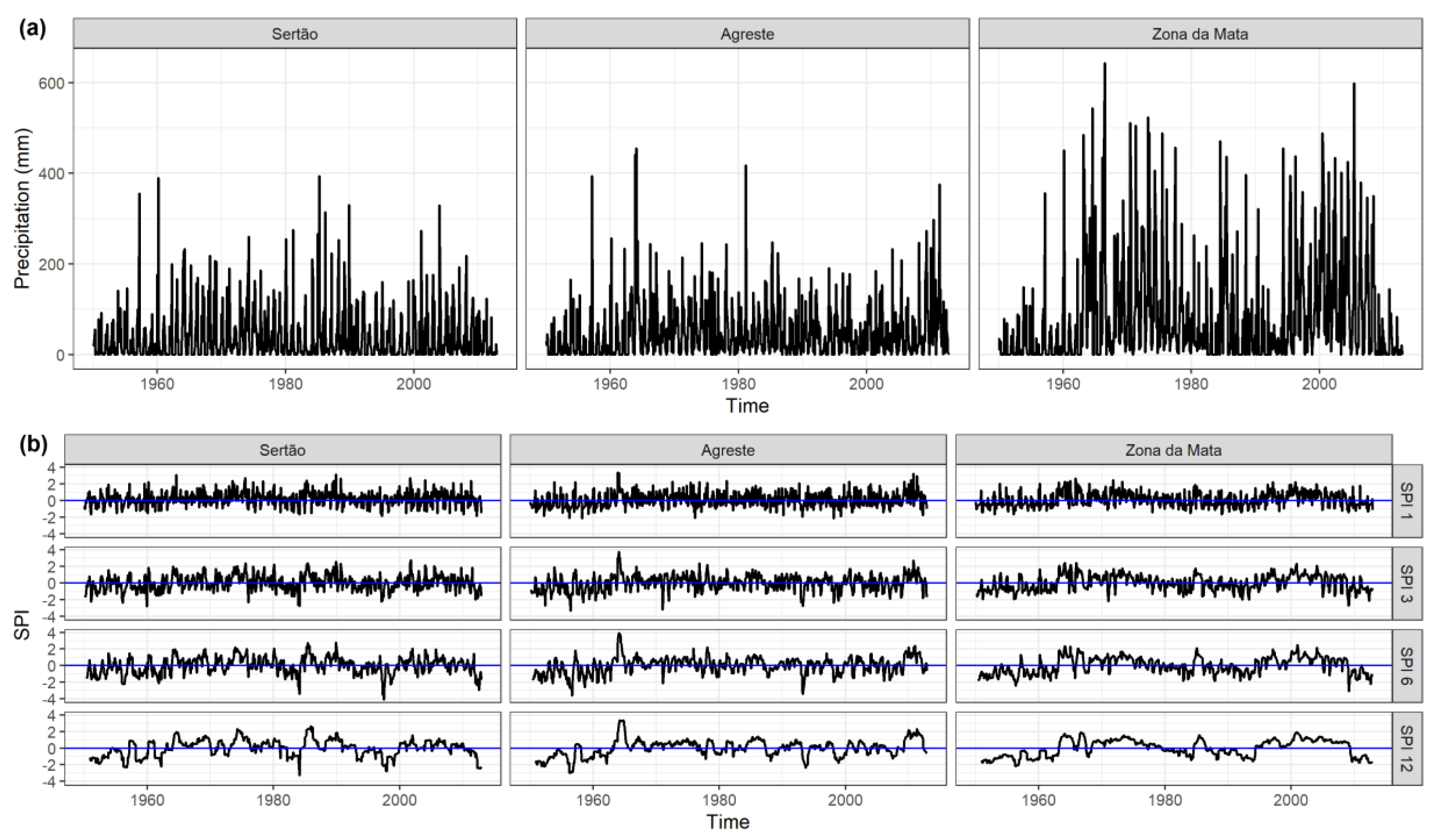
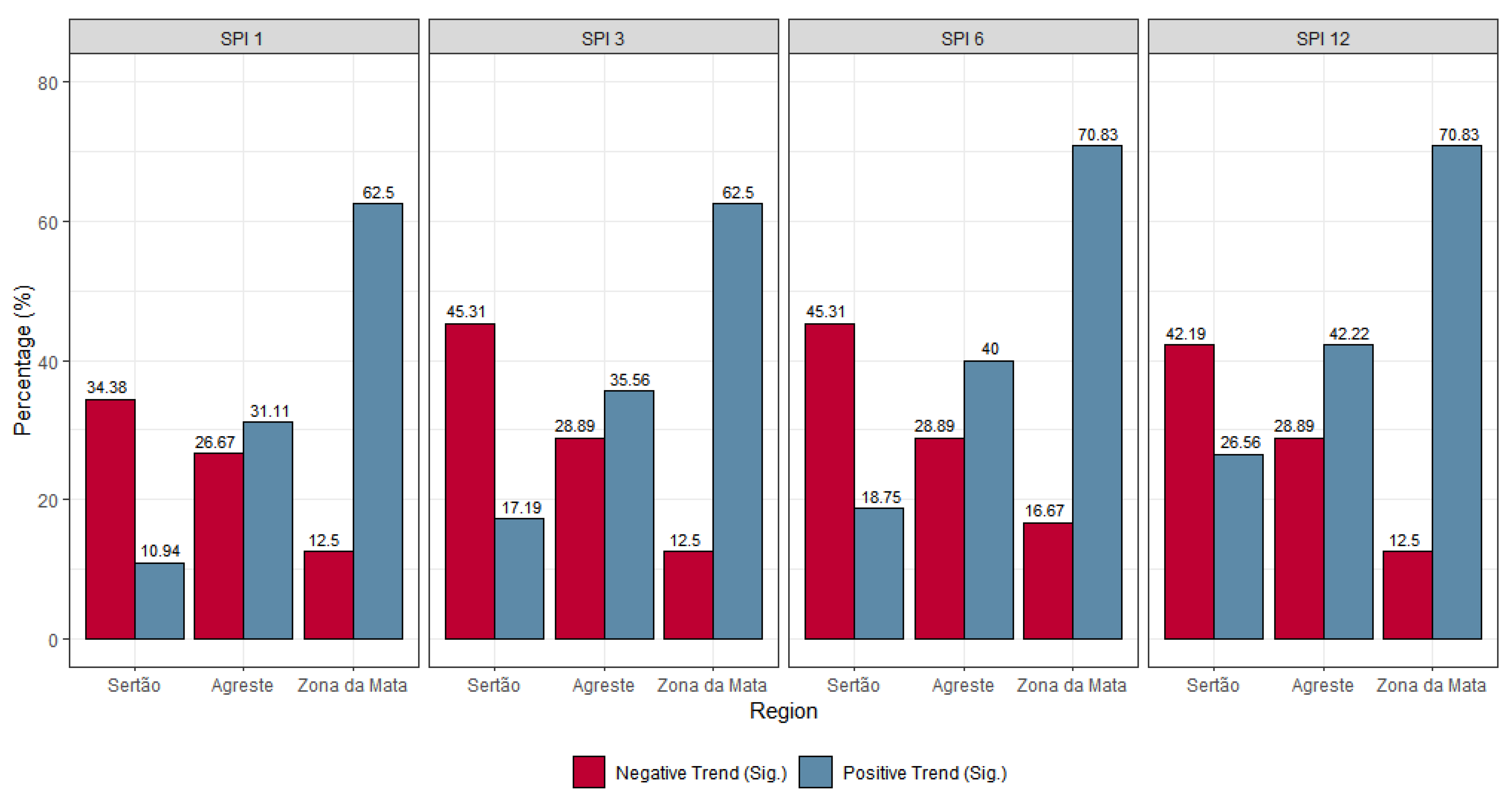
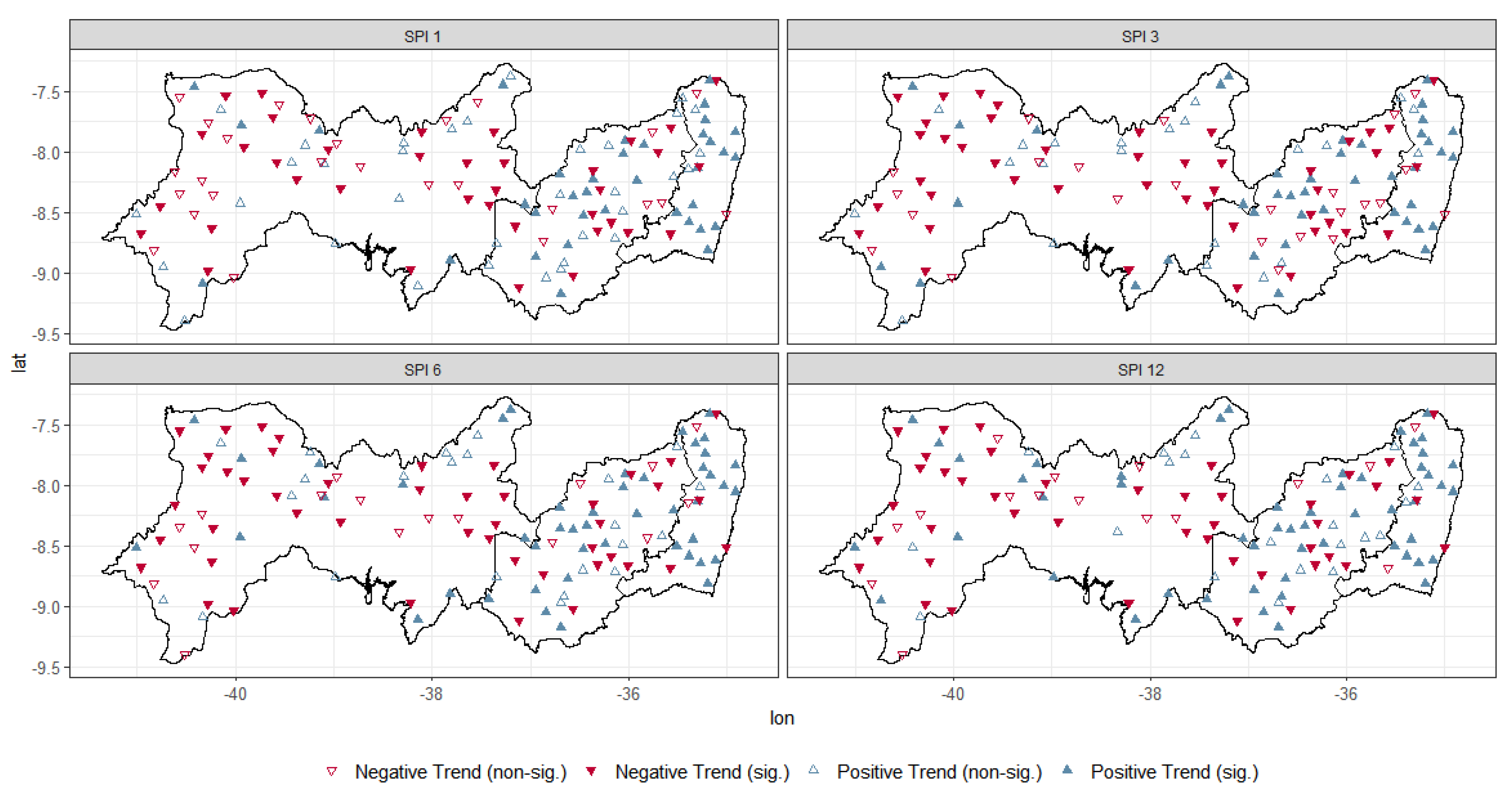
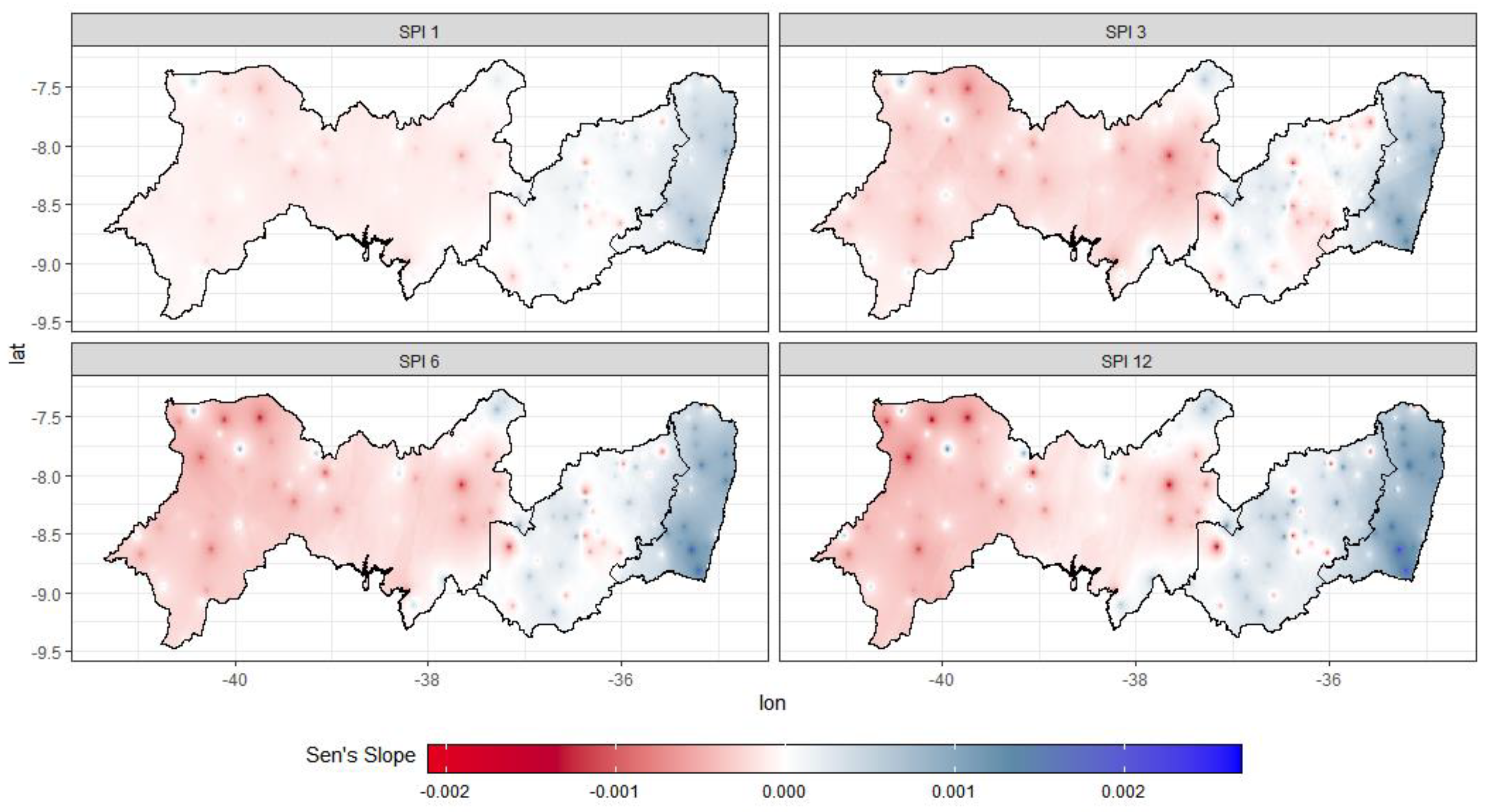
3.1. Trend Analysis
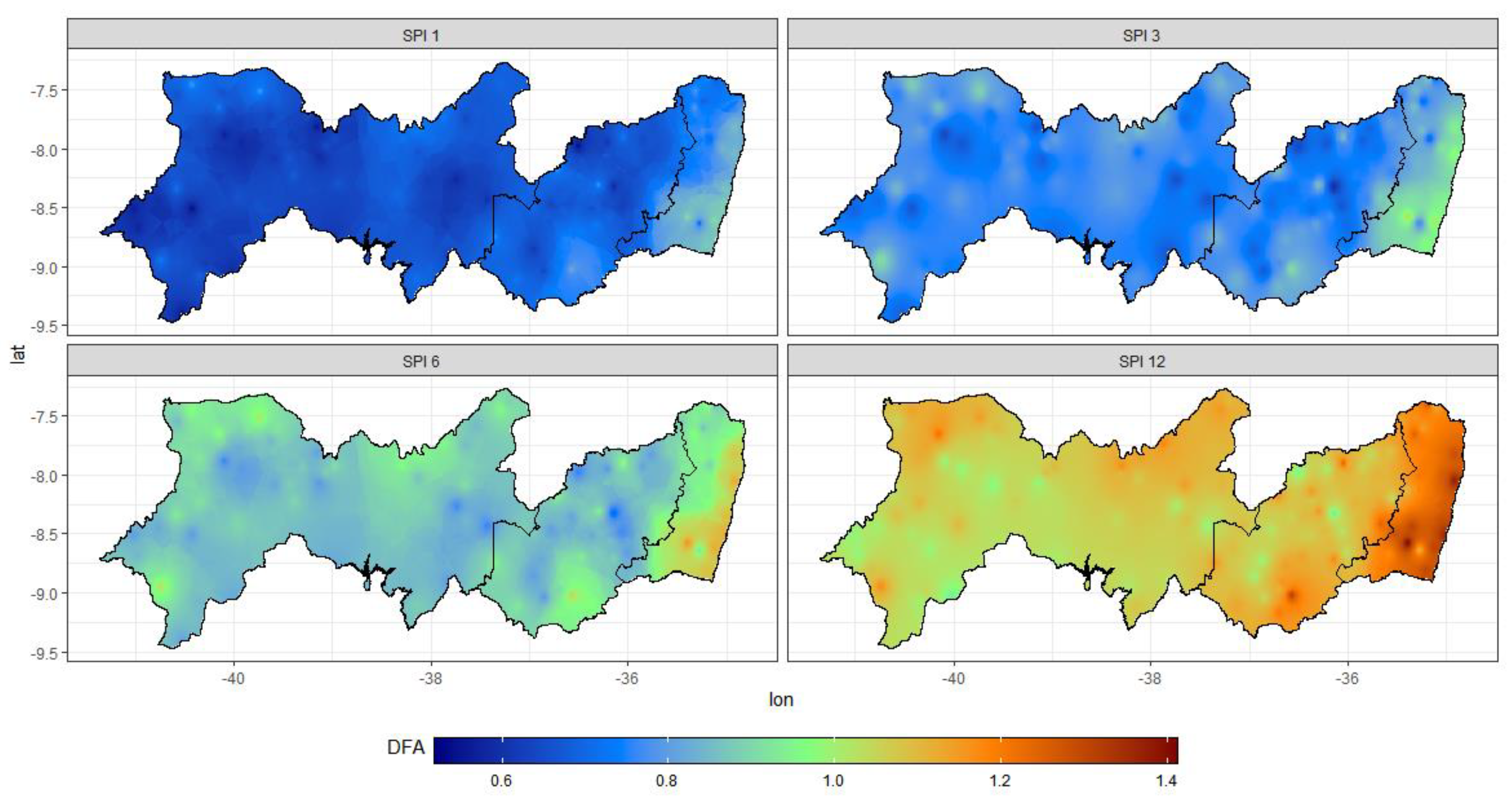
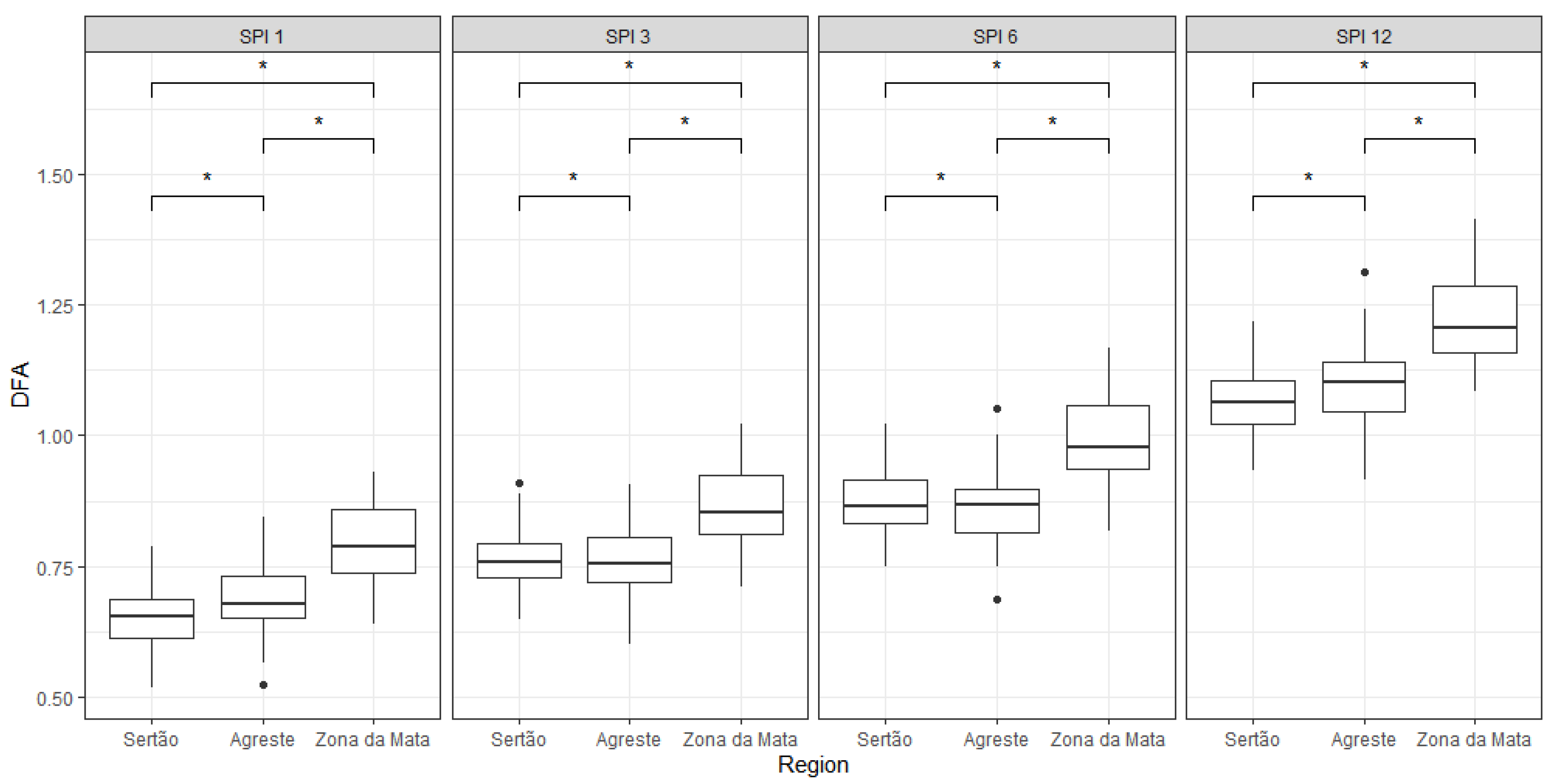
3.2. Detrended Fluctuation Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trnka, M.; Semerádová, D.; Novotný, I.; Dumbrovský, M.; Drbal, K.; Pavlík, F.; Vopravil, J.; Štěpánková, P.; Vizina, A.; Balek, J.; et al. Assessing the Combined Hazards of Drought, Soil Erosion and Local Flooding on Agricultural Land: A Czech Case Study. Clim. Res. 2016, 70, 231–249. [Google Scholar] [CrossRef]
- Kalantari, Z.; Ferreira, C.S.S.; Keesstra, S.; Destouni, G. Nature-Based Solutions for Flood-Drought Risk Mitigation in Vulnerable Urbanizing Parts of East-Africa. Curr. Opin. Environ. Sci. Health 2018, 5, 73–78. [Google Scholar] [CrossRef]
- Bond, N.R.; Lake, P.S.; Arthington, A.H. The Impacts of Drought on Freshwater Ecosystems: An Australian Perspective. Hydrobiologia 2008, 600, 3–16. [Google Scholar] [CrossRef]
- Patz, J.A. Hotspots in Climate Change and Human Health. BMJ 2002, 325, 1094–1098. [Google Scholar] [CrossRef] [PubMed]
- Chadwick, R.; Good, P.; Martin, G.; Rowell, D.P. Large Rainfall Changes Consistently Projected over Substantial Areas of Tropical Land. Nat. Clim. Chang. 2016, 6, 177–181. [Google Scholar] [CrossRef]
- Palmer, W.C. Keeping Track of Crop Moisture Conditions, Nationwide: The New Crop Moisture Index. Weatherwise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a Standardized Runoff Index for Characterizing Hydrologic Drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, American Meteorological Society, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index User Guide; (WMO-No. 1090); WMO-World Meteorological Organization: Geneva, Switzerland, 2012; Available online: www.wamis.org/agm/pubs/SPI/WMO_1090_EN.pdf (accessed on 10 August 2020).
- Du, J.; Fang, J.; Xu, W.; Shi, P. Analysis of Dry/Wet Conditions Using the Standardized Precipitation Index and Its Potential Usefulness for Drought/Flood Monitoring in Hunan Province, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 377–387. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Analyses of Drought Events in Calabria (Southern Italy) Using Standardized Precipitation Index. Water Resour. Manag. 2015, 29, 557–573. [Google Scholar] [CrossRef]
- Ashraf, M.; Routray, J.K. Spatio-Temporal Characteristics of Precipitation and Drought in Balochistan Province, Pakistan. Nat. Hazards 2015, 77, 229–254. [Google Scholar] [CrossRef]
- Caloiero, T. Drought Analysis in New Zealand Using the Standardized Precipitation Index. Environ. Earth Sci. 2017, 76, 569. [Google Scholar] [CrossRef]
- Li, W.; Fu, R.; Juárez, R.I.N.; Fernandes, K. Observed Change of the Standardized Precipitation Index, Its Potential Cause and Implications to Future Climate Change in the Amazon Region. Phil. Trans. R. Soc. B 2008, 363, 1767–1772. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Alvala, R.C.S.; Cunha, A.P.; Brito, S.; Moraes, O.L.L. Climatic Characteristics of the 2010–2016 Drought in the Semiarid Northeast Brazil Region. An. Acad. Bras. Ciênc. 2018, 90 (Suppl. 1), 1973–1985. [Google Scholar] [CrossRef] [PubMed]
- Marengo, J.A.; Torres, R.R.; Alves, L.M. Drought in Northeast Brazil—Past, Present, and Future. Theor. Appl. Climatol. 2017, 129, 1189–1200. [Google Scholar] [CrossRef]
- Cunha, A.P.M.A.; Tomasella, J.; Ribeiro-Neto, G.G.; Brown, M.; Garcia, S.R.; Brito, S.B.; Carvalho, M.A. Changes in the Spatial-Temporal Patterns of Droughts in the Brazilian Northeast. Atmos. Sci. Lett. 2018, 19, e855. [Google Scholar] [CrossRef]
- Marengo, J.A.; Bernasconi, M. Regional Differences in Aridity/Drought Conditions over Northeast Brazil: Present State and Future Projections. Clim. Chang. 2015, 129, 103–115. [Google Scholar] [CrossRef]
- Debortoli, N.S.; Camarinha, P.I.M.; Marengo, J.A.; Rodrigues, R.R. An Index of Brazil’s Vulnerability to Expected Increases in Natural Flash Flooding and Landslide Disasters in the Context of Climate Change. Nat. Hazards 2017, 86, 557–582. [Google Scholar] [CrossRef]
- Brito, S.S.B.; Cunha, A.P.M.A.; Cunningham, C.C.; Alvalá, R.C.; Marengo, J.A.; Carvalho, M.A. Frequency, Duration and Severity of Drought in the Semiarid Northeast Brazil Region. Int. J. Climatol. 2018, 38, 517–529. [Google Scholar] [CrossRef]
- Silva, B.K.N.; Lucio, P.S. Characterization of Risk/Exposure to Climate Extremes for the Brazilian Northeast—Case Study: Rio Grande Do Norte. Theor. Appl. Climatol. 2015, 122, 59–67. [Google Scholar] [CrossRef]
- Lyra, G.B.; Oliveira-Júnior, J.F.; Gois, G.; Cunha-Zeri, G.; Zeri, M. Rainfall Variability over Alagoas under the Influences of SST Anomalies. Meteorol. Atmos. Phys. 2017, 129, 157–171. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Brasil Neto, R.M.; da Silva, R.M.; dos Santos, D.C. Innovative Approach for Geospatial Drought Severity Classification: A Case Study of Paraíba State, Brazil. Stoch. Environ. Res Risk Assess. 2019, 33, 545–562. [Google Scholar] [CrossRef]
- Melo Santos, A.M.; Cavalcanti, D.R.; da Silva, J.M.C.; Tabarelli, M. Biogeographical Relationships among Tropical Forests in North-Eastern Brazil. J. Biogeogr. 2007, 34, 437–446. [Google Scholar] [CrossRef]
- Ranta, P.; Blom, T.; Niemela¨, J.; Joensuu, E.; Siitonen, M. The fragmented Atlantic rain forest of Brazil: Size, shape and distribution of forest fragments. Biodivers. Conserv. 1998, 7, 385–403. [Google Scholar] [CrossRef]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s Climate Classification Map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Da Silva, A.S.A.; Stosic, B.; Menezes, R.S.C.; Singh, V.P. Comparison of Interpolation Methods for Spatial Distribution of Monthly Precipitation in the State of Pernambuco, Brazil. J. Hydrol. Eng. 2019, 24, 04018068. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistic Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org (accessed on 10 August 2020).
- Thorsten Pohlert. Trend: Non-Parametric Trend Tests and Change-Point Detection. R Package Version 1.1.2. 2020. Available online: https://CRAN.R-project.org/package=trend (accessed on 10 August 2020).
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln Declaration on Drought Indices: Universal Meteorological Drought Index Recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef]
- Svensson, C.; Hannaford, J.; Prosdocimi, I. Statistical Distributions for Monthly Aggregations of Precipitation and Streamflow in Drought Indicator Applications. Water Resour. Res. 2017, 53, 999–1018. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Wu, H.; Svoboda, M.D.; Hayes, M.J.; Wilhite, D.A.; Wen, F. Appropriate Application of the Standardized Precipitation Index in Arid Locations and Dry Seasons. Int. J. Climatol. 2007, 27, 65–79. [Google Scholar] [CrossRef]
- Thom, H. Some Methods of Climatological Analysis; The World Meteorological Organization: Geneva, Switzerland, 1966; pp. 16–22. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Table; Courier Corporation: North Chelmsford, MA, USA, 1965; Volume 55. [Google Scholar]
- Lloyd-Hughes, B.; Saunders, M.A. A Drought Climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica. J. Econ. Soc. 1945, 13, 245–259. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Birsan, M.V.; Dumitrescu, A.; Micu, D.M.; Cheval, S. Changes in annual temperature extremes in the carpathians since AD 1961. Nat. Hazards 2014, 74, 1899–1910. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of Changes in Meteorological Variables Using Mann-Kendall and Sen’s Slope Estimator Statistical Tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Raziei, T.; Daryabari, J.; Bordi, I.; Pereira, L.S. Spatial Patterns and Temporal Trends of Precipitation in Iran. Theor. Appl. Climatol. 2014, 115, 531–540. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. Spatial distribution of unidirectional trends in climate and weather extremes in Nileriver basin. Theor. Appl. Climatol. 2019, 137, 1181–1199. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Fernandes, R.; Leblanc, S.G. Parametric (modified least squares) and non-parametric (Theil–Sen) linear regressions for predicting biophysical parameters in the presence of measurement errors. Remote Sens. Environ. 2005, 95, 303–316. [Google Scholar] [CrossRef]
- Chervenkov, H.; Slavov, K. Theil-Sen Estimator vs. Ordinary LeastSquares—Trend Analysis for Selected ETCCDI Climate Indices. Comptes Rendus Acad. Bulg. Sci. 2019, 72, 47–54. [Google Scholar] [CrossRef]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic Organization of DNA Nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Ivanov, P.C.; Chen, Z.; Carpena, P.; Stanley, H.E. Effect of Trends on Detrended Fluctuation Analysis. Phys. Rev. E 2001, 64, 011114. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Ivanov, P.C.; Hu, K.; Stanley, H.E. Effect of Nonstationarities on Detrended Fluctuation Analysis. Phys. Rev. E 2002, 65, 041107. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.N.; Hausdorff, J.M.; Ivanov, P.C.; Peng, C.-K.; Stanley, H.E. Fractal Dynamics in Physiology: Alterations with Disease and Aging. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. 1), 2466–2472. [Google Scholar] [CrossRef]
- Currenti, G.; Negro, C.; Lapenna, V.; Telesca, L. Fluctuation Analysis of the Hourly Time Variability of Volcano-Magnetic Signals Recorded at Mt. Etna Volcano, Sicily (Italy). Chaos Solitons Fractals 2005, 23, 1921–1929. [Google Scholar] [CrossRef]
- Kiraly, A.; Janosi, I.M. Detrended Fluctuation Analysis of Daily Temperature Records: Geographic Dependence over Australia. Meteorol. Atmos. Phys. 2005, 88, 119–128. [Google Scholar] [CrossRef][Green Version]
- De Oliveira Santos, M.; Stosic, T.; Stosic, B.D. Long-Term Correlations in Hourly Wind Speed Records in Pernambuco, Brazil. Phys. A Stat. Mech. Appl. 2012, 391, 1546–1552. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Lopez-Moreno, I.; Vicente-Serrano, S. Investigation of Scaling Properties in Monthly Streamflow and Standardized Streamflow Index (SSI) Time Series in the Ebro Basin (Spain). Phys. A Stat. Mech. Appl. 2012, 391, 1662–1678. [Google Scholar] [CrossRef]
- Yamasaki, K.; Muchnik, L.; Havlin, S.; Bunde, A.; Stanley, H.E. Scaling and Memory in Volatility Return Intervals in Financial Markets. Proc. Natl. Acad. Sci. USA 2005, 102, 9424–9428. [Google Scholar] [CrossRef]
- Adarsh, S.; Kumar, D.N.; Deepthi, B.; Gayathri, G.; Aswathy, S.S.; Bhagyasree, S. Multifractal Characterization of Meteorological Drought in India Using Detrended Fluctuation Analysis. Int. J. Climatol. 2019, 39, 4234–4255. [Google Scholar] [CrossRef]
- Tatli, H.; Dalfes, H.N. Long-Time Memory in Drought via Detrended Fluctuation Analysis. Water Resour. Manag. 2020, 34, 1199–1212. [Google Scholar] [CrossRef]

| SPI Classification | SPI Value |
|---|---|
| Extremely dry | |
| Severely dry | |
| Moderately dry | |
| Near Normal | |
| Moderately wet | |
| Very wet | |
| Extreme wet |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves da Silva, A.S.; Cunha Filho, M.; Simões Cezar Menezes, R.; Stosic, T.; Stosic, B. Trends and Persistence of Dry–Wet Conditions in Northeast Brazil. Atmosphere 2020, 11, 1134. https://doi.org/10.3390/atmos11101134
Alves da Silva AS, Cunha Filho M, Simões Cezar Menezes R, Stosic T, Stosic B. Trends and Persistence of Dry–Wet Conditions in Northeast Brazil. Atmosphere. 2020; 11(10):1134. https://doi.org/10.3390/atmos11101134
Chicago/Turabian StyleAlves da Silva, Antonio Samuel, Moacyr Cunha Filho, Rômulo Simões Cezar Menezes, Tatijana Stosic, and Borko Stosic. 2020. "Trends and Persistence of Dry–Wet Conditions in Northeast Brazil" Atmosphere 11, no. 10: 1134. https://doi.org/10.3390/atmos11101134
APA StyleAlves da Silva, A. S., Cunha Filho, M., Simões Cezar Menezes, R., Stosic, T., & Stosic, B. (2020). Trends and Persistence of Dry–Wet Conditions in Northeast Brazil. Atmosphere, 11(10), 1134. https://doi.org/10.3390/atmos11101134





