The Influence of Land Surface Temperature in Evapotranspiration Estimated by the S-SEBI Model
Abstract
1. Introduction
2. Materials and Methods
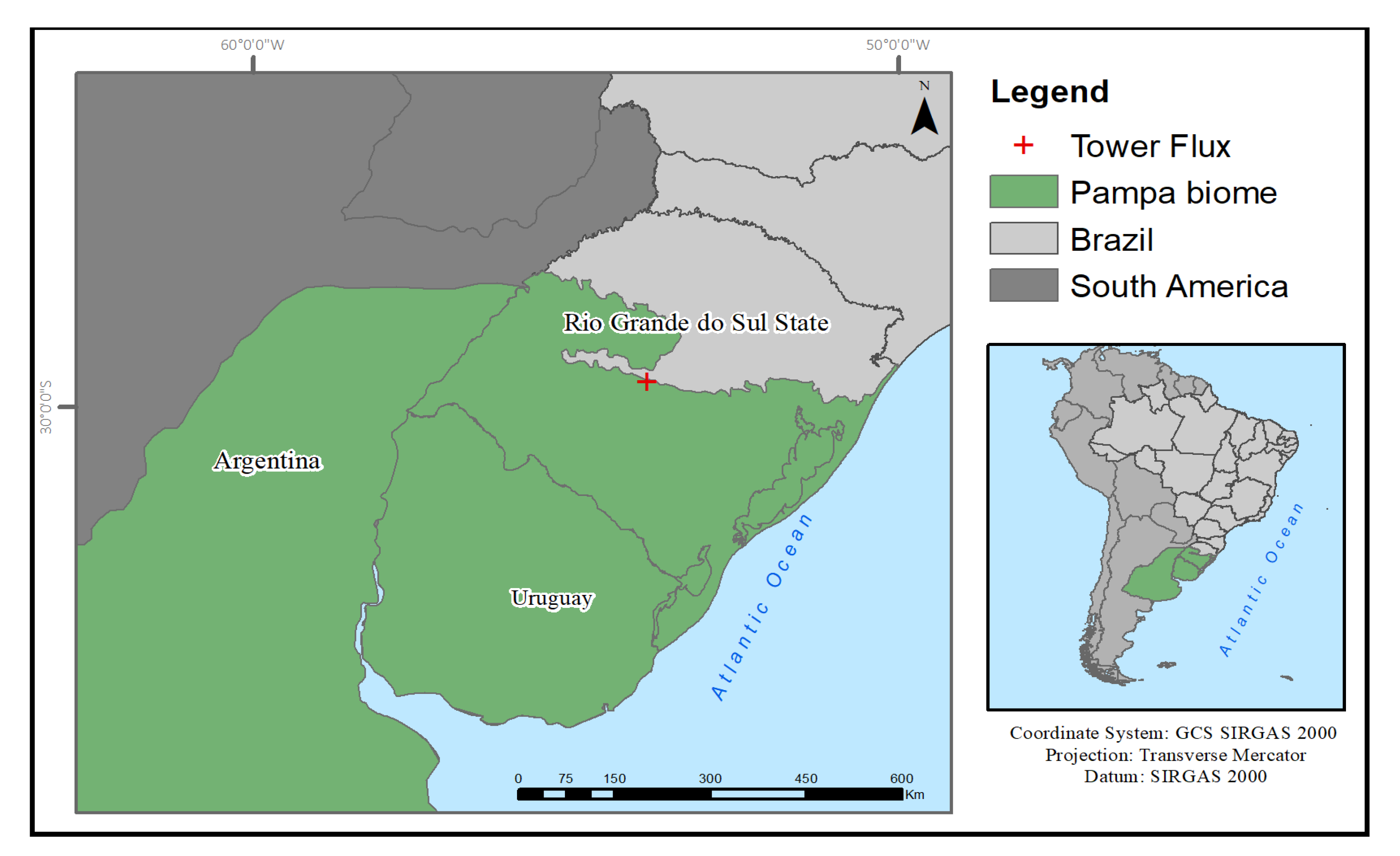
2.1. Study Area
2.2. Simplify Surface Energy Balance Index (S-SEBI)
2.3. Daily Evapotranspiration
2.4. Data Used in the Model
2.4.1. Satellite Data
2.4.2. Meteorological Data
2.5. Variables Input of S-SEBI
2.6. Land Surface Temperature of S-SEBI Model
2.7. Validation
2.7.1. Eddy-Covariance (EC) Data and Flux Tower
2.7.2. Statistical Analyses
3. Results
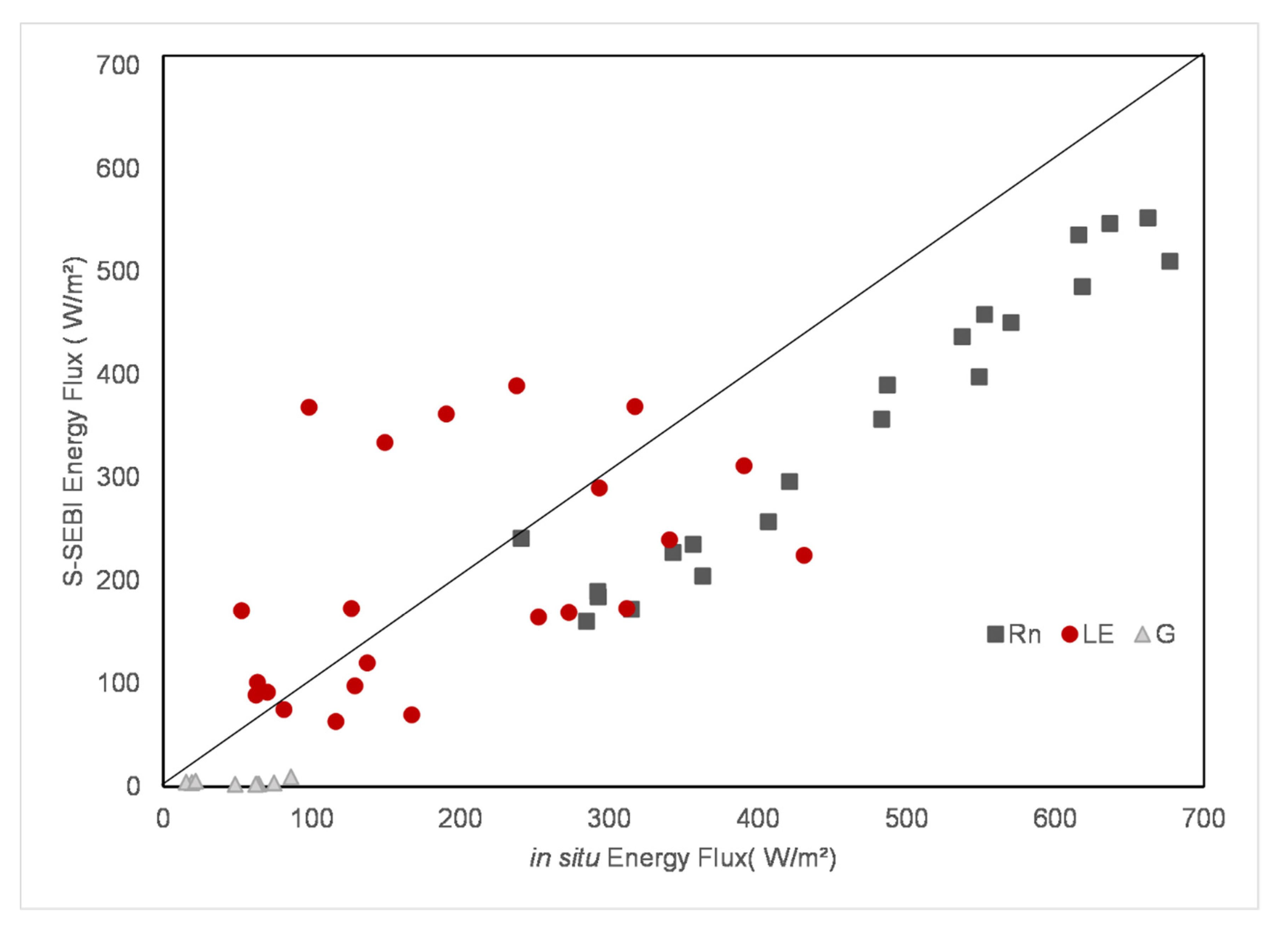
3.1. S-SEBI Validantion
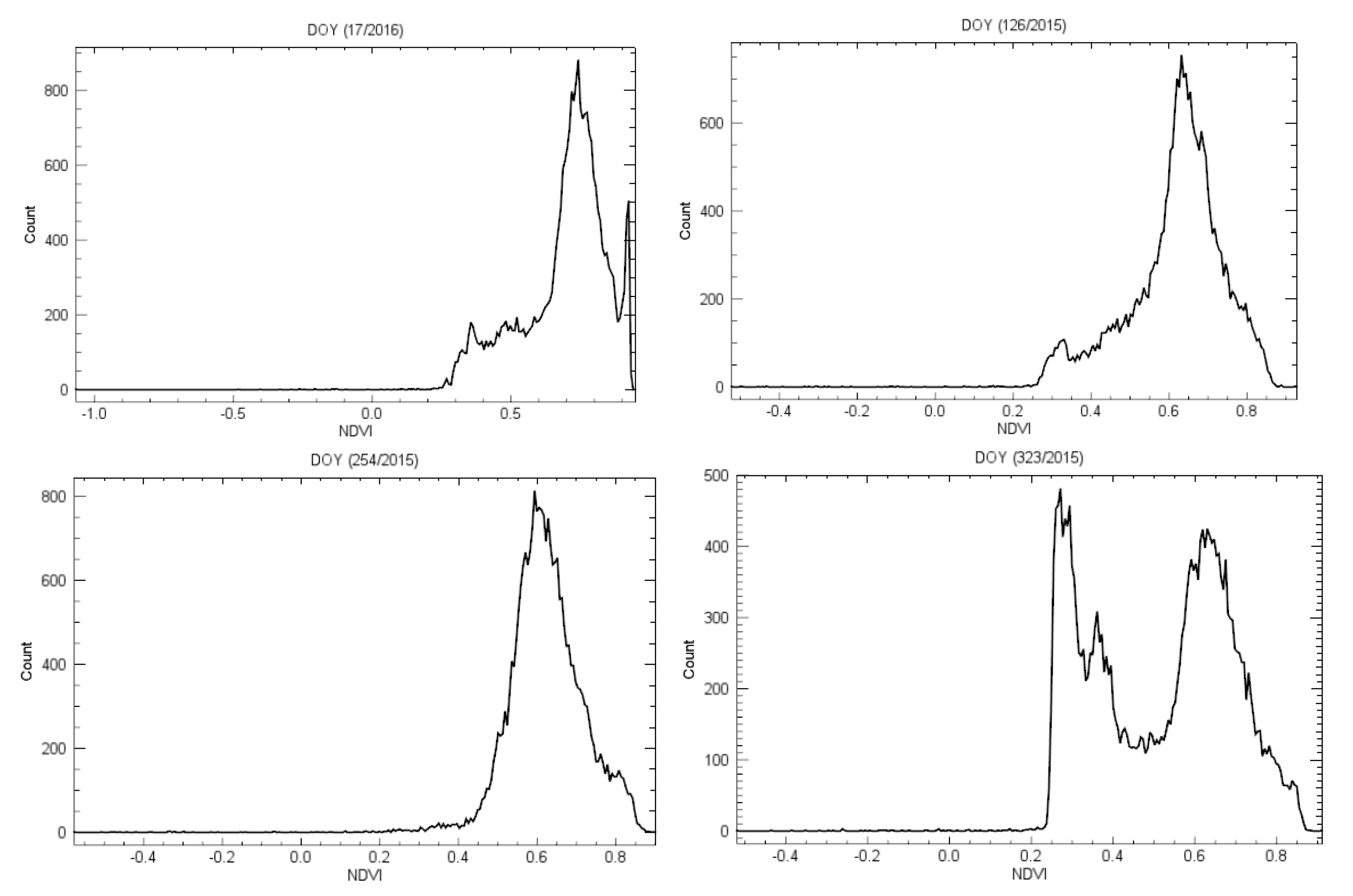
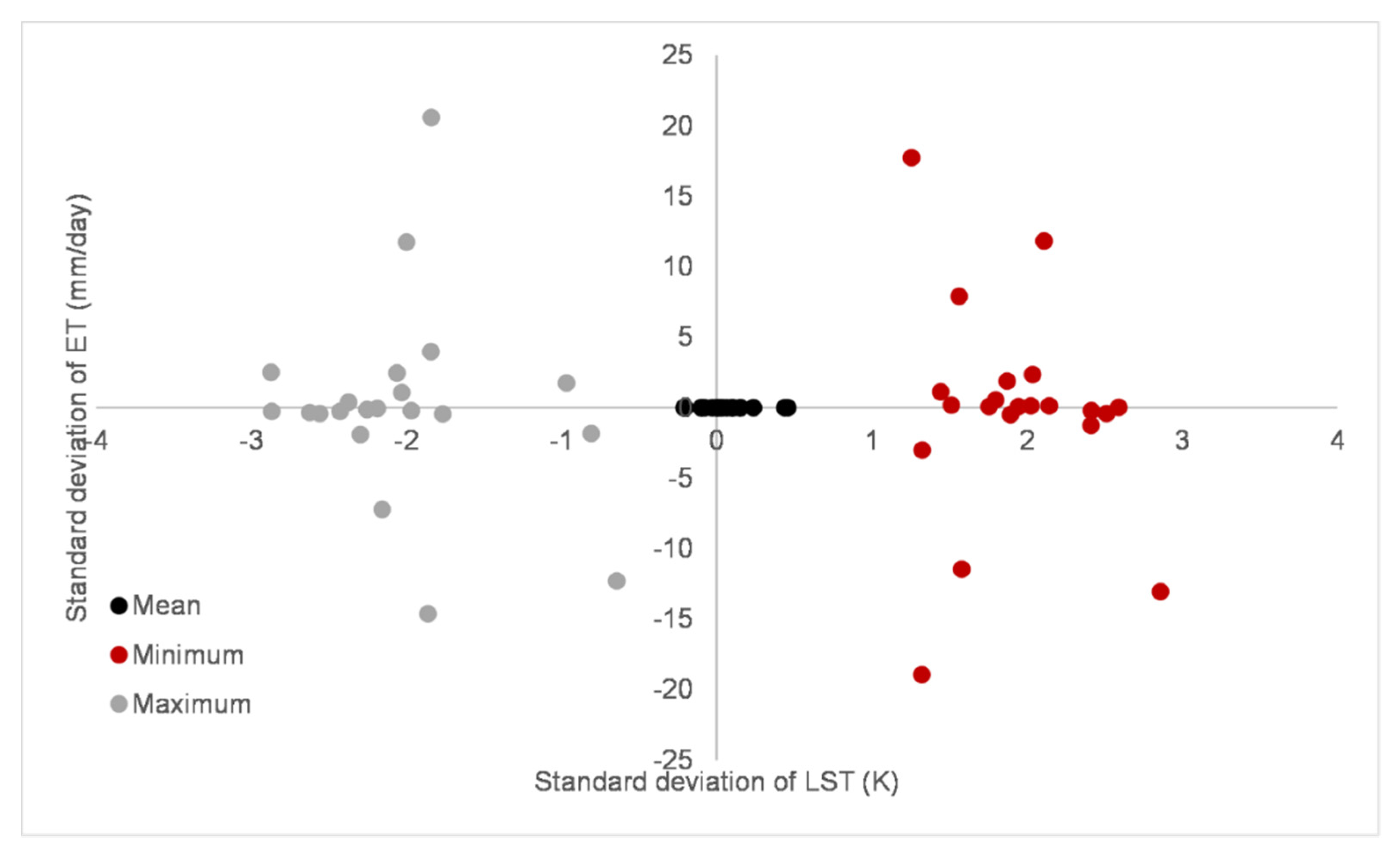
3.2. Heterogeneity of the Study Area
3.3. The Ts Influence on S-SEBI Model
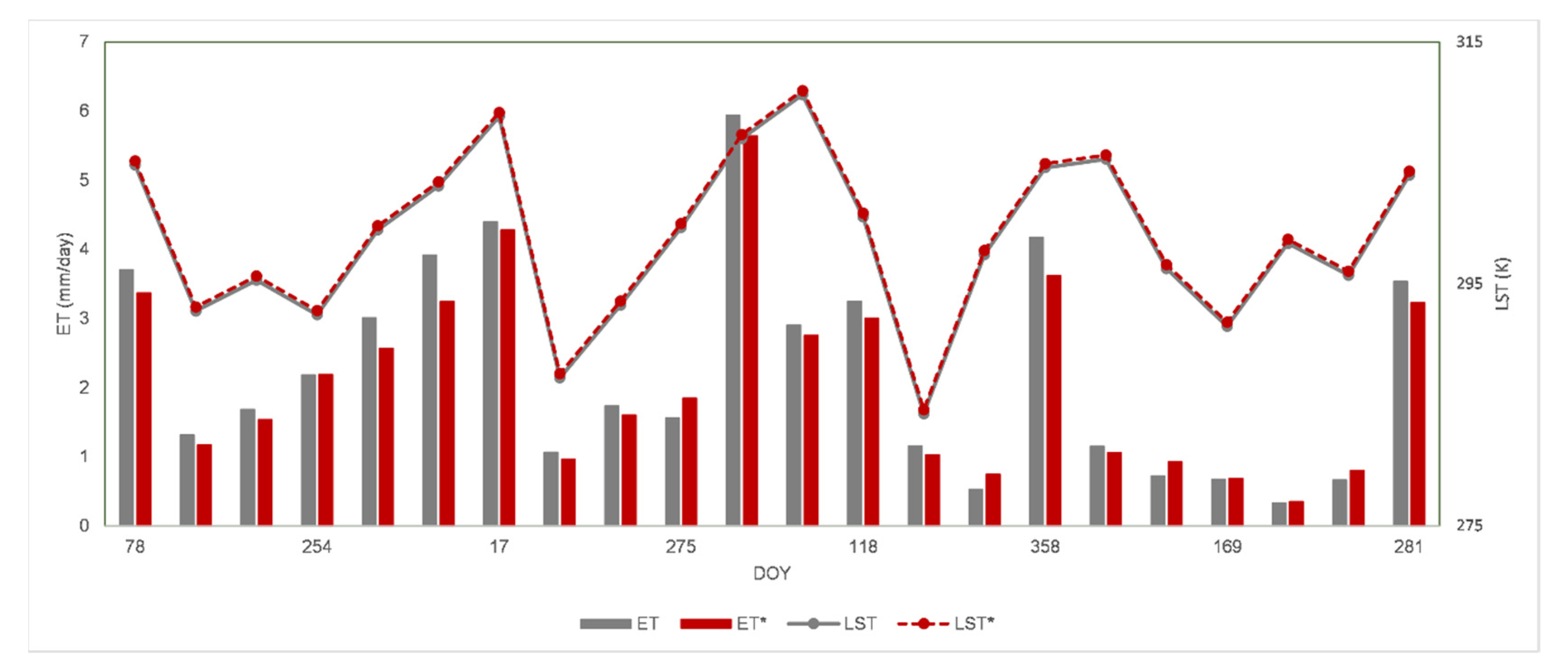
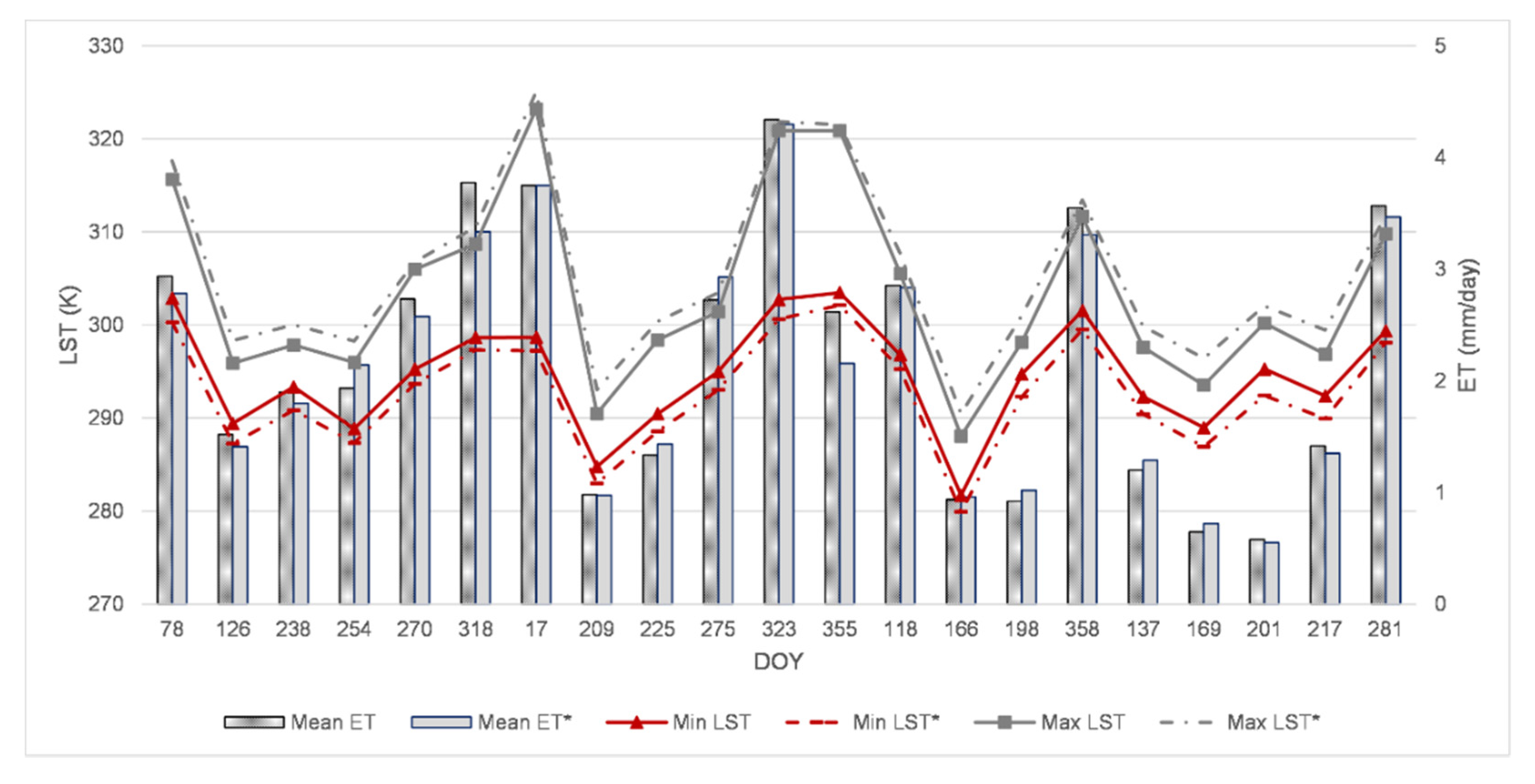
3.4. The Ts Influence on Daily Evapotranspiration
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Olioso, A.; Chauki, H.; Courault, D.; Wigneron, J.-P. Estimation of Evapotranspiration and Photosynthesis by Assimilation of Remote Sensing Data into SVAT Models. Remote Sens. Environ. 1999, 68, 341–356. [Google Scholar] [CrossRef]
- Ehsan Bhuiyan, M.A.; Nikolopoulos, E.I.; Anagnostou, E.N.; Polcher, J.; Albergel, C.; Dutra, E.; Fink, G.; Martínez-de la Torre, A.; Munier, S. Assessment of precipitation error propagation in multi-model global water resource reanalysis. Hydrol. Earth Syst. Sci. 2019, 23, 1973–1994. [Google Scholar] [CrossRef]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surfaceheat flux and evaporation using large-scale parameters. Mon Weather Rev 1972, 100, 81–92. [Google Scholar]
- Wang, T.; Tang, R.; Li, Z.L.; Jiang, Y.; Liu, M.; Niu, L. An improved spatio-temporal adaptive Data fusion algorithm for evapotranspiration mapping. Remote Sens. 2019, 11, 761. [Google Scholar] [CrossRef]
- Cristóbal, J.; Jiménez-Muñoz, J.C.; Prakash, A.; Mattar, C.; Skoković, D.; Sobrino, J.A. An improved single-channel method to retrieve land surface temperature from the landsat-8 thermal band. Remote Sens. 2018, 10, 431. [Google Scholar] [CrossRef]
- Rubert, G.C.; Roberti, D.R.; Pereira, L.S.; Quadros, F.L.; Campos Velho, H.F.D.; Leal de Moraes, O.L. Evapotranspiration of the Brazilian Pampa biome: Seasonality and influential factors. Water 2018, 10, 1864. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Gómez, M.; Jiménez-Muñoz, J.C.; Olioso, A.; Chehbouni, G. A simple algorithm to estimate evapotranspiration from DAIS data: Application to the DAISEX campaigns. J. Hydrol. 2005, 315, 117–125. [Google Scholar] [CrossRef]
- Gibson, L.A.; Münch, Z.; Engelbrecht, J. Particular uncertainties encountered in using a pre-packaged SEBS model to derive evapotranspiration in a heterogeneous study area in South Africa. Hydrol. Earth Syst. Sci. 2011, 15, 295–310. [Google Scholar] [CrossRef]
- Abid, N.; Mannaerts, C.; Bargaoui, Z. Sensitivity of actual evapotranspiration estimation using the sebs model to variation of input parameters (LST, DSSF, aerodynamics parameters, LAI, FVC). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2019, 42, 1193–1200. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global Hydrological Cycles and World Water Resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef]
- Cheng, J.; Kustas, W. Using Very High Resolution Thermal Infrared Imagery for More Accurate Determination of the Impact of Land Cover Differences on Evapotranspiration in an Irrigated Agricultural Area. Remote Sens. 2019, 11, 613. [Google Scholar] [CrossRef]
- Liu, S.; Su, H.; Zhang, R.; Tian, J.; Chen, S.; Wang, W.; Yang, L.; Liang, H. Based on the Gaussian fitting method to derive daily evapotranspiration from remotely sensed instantaneous evapotranspiration. Adv. Meteorol. 2019, 2019. [Google Scholar] [CrossRef]
- Liou, Y.A.; Kar, S.K. Evapotranspiration estimation with remote sensing and various surface energy balance algorithms-a review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef]
- Souza, V.D.A.; Roberti, D.R.; Ruhoff, A.L.; Zimmer, T.; Adamatti, D.S.; Gonçalves, L.G.G.D.; Diaz, M.B.; Alves, R.D.C.M.; Moraes, O.L.L.D. Evaluation of MOD16 Algorithm over Irrigated Rice Paddy Using Flux Tower Measurements in Southern Brazil. Water 2019, 11, 1911. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth, Part B Hydrol. Ocean. Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Gómez, M.; Olioso, A.; Sobrino, J.A.; Jacob, F. Retrieval of evapotranspiration over the Alpilles/ReSeDA experimental site using airborne POLDER sensor and a thermal camera. Remote Sens. Environ. 2005, 96, 399–408. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Gómez, M.; Jiménez-Muñoz, J.C.; Olioso, A. Application of a simple algorithm to estimate daily evapotranspiration from NOAA-AVHRR images for the Iberian Peninsula. Remote Sens. Environ. 2007, 110, 139–148. [Google Scholar] [CrossRef]
- Vargas, L.P.; da Costa Vargas, A.F.; Silveira, V.C.P. Ecosystem services and production systems of family cattle farms: An analysis of animal production in Pampa Biome. Semin. Ciências Agrárias 2020, 41, 661–676. [Google Scholar]
- Rocha, J.M. As Raízes da Crise da Metade Sul: Estudo da formação econômica do Rio Grande do Sul.; UNIPAMPA: Jaguarão-RS, Brazil, 2011. [Google Scholar]
- Pylro, V.S.; Morais, D.K.; Roesch, L.F.W. Microbiome studies need local leaders. Nature 2015, 528, 39. [Google Scholar] [CrossRef]
- Overbeck, G.E.; Müller, S.C.; Pillar, V.D.; Pfadenhauer, J. Floristic composition, environmental variation and species distribution patterns in burned grassland in southern Brazil. Brazilian J. Biol. 2006, 66, 1073–1090. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, L.B.; Soares, E.M.; Jochims, F.; Tiecher, T.; Marques, A.R.; Kuinchtner, B.C.; Rheinheimer, D.S.; De Quadros, F.L.F. Long-Term Effects of Phosphorus on Dynamics of an Overseeded Natural Grassland in Brazil. Rangel. Ecol. Manag. 2015, 68, 445–452. [Google Scholar] [CrossRef]
- Confortin, A.C.C.; Quadros, F.L.F.; Santos, A.B.; Seibert, L.; Severo, P.O.; Ribeiro, B.S.R. Leaf tissue fluxes of Pampa biome native grasses submitted to two grazing intervals. Grass Forage Sci. 2017, 72, 654–662. [Google Scholar] [CrossRef]
- Sauer, T.J.; Horton, R. Soil Heat Flux. In Agronomy Monographs; Hatfield, J.L., Baker, J.M., Eds.; American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America: Madison, WI, USA, 2015; pp. 131–154. ISBN 9780891182689. [Google Scholar]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skokovic, D.; Mattar, C.; Cristobal, J. Land surface temperature retrieval methods from landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Kilic, A.; Allen, R.; Trezza, R.; Ratcliffe, I.; Kamble, B.; Robison, C.; Ozturk, D. Sensitivity of evapotranspiration retrievals from the METRIC processing algorithm to improved radiometric resolution of Landsat 8 thermal data and to calibration bias in Landsat 7 and 8 surface temperature. Remote Sens. Environ. 2016, 185, 198–209. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third ERTS-1 Symposium; NASA: Washington, DC, USA, 1973; pp. 309–317. [Google Scholar]
- Ke, Y.; Im, J.; Park, S.; Gong, H. Downscaling of MODIS One kilometer evapotranspiration using Landsat-8 data and machine learning approaches. Remote Sens. 2016, 8, 215. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Li, Z.L.; Stoll, M.P.; Becker, F. Multi-channel and multi-angle algorithms for estimating sea and land surface temperature with ATSR data. Int. J. Remote Sens. 1996, 17, 2089–2114. [Google Scholar] [CrossRef]
- Buck, A.L. New Equations for Computing Vapor Pressure and Enhancement Factor. J. Appl. Meteorol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martínez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Skokovic, D.; Sobrino, J.A.; Jimenez-Munoz, J.C. Vicarious Calibration of the Landsat 7 Thermal Infrared Band and LST Algorithm Validation of the ETM+ Instrument Using Three Global Atmospheric Profiles. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1804–1811. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Skoković, D. Permanent Stations for Calibration/Validation of Thermal Sensors over Spain. Data 2016, 1, 10. [Google Scholar] [CrossRef]
- Kafer, P.S.; Rolim, S.B.A.; Iglesias, M.L.; da Rocha, N.S.; Diaz, L.R. Land Surface Temperature Retrieval by LANDSAT 8 Thermal Band: Applications of Laboratory and Field Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2332–2341. [Google Scholar] [CrossRef]
- Aubinet, M.; Vesala, T.; Papale, D. Eddy Covariance—A Practical Guide to Measurement and Data Analysis; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple parameterisation for flux footprint predictions. Bound. Layer Meteorol. 2004, 112, 503–523. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- de Oliveira, G.; Brunsell, N.; Moraes, E.; Bertani, G.; dos Santos, T.; Shimabukuro, Y.; Aragão, L. Use of MODIS Sensor Images Combined with Reanalysis Products to Retrieve Net Radiation in Amazonia. Sensors 2016, 16, 956. [Google Scholar] [CrossRef]
- Mayer, D.G.; Butler, D.G. Statistical validation. Ecol. Model. 1993, 68, 21–32. [Google Scholar] [CrossRef]
- Olioso, A.; Chauki, H.; Courault, D.; Wigneron, J. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0034425798001217 (accessed on 23 September 2020).
- Schirmbeck, J.; Fontana, D.C.; Roberti, D.R. Evaluation of OSEB and SEBAL models for energy balance of a crop area in a humid subtropical climate. Bragantia 2018, 77, 609–621. [Google Scholar] [CrossRef]
- Silva Oliveira, B.; Caria Moraes, E.; Carrasco-Benavides, M.; Bertani, G.; Augusto Verola Mataveli, G. Improved Albedo Estimates Implemented in the METRIC Model for Modeling Energy Balance Fluxes and Evapotranspiration over Agricultural and Natural Areas in the Brazilian Cerrado. Remote Sens. 2018, 10, 1181. [Google Scholar] [CrossRef]
- Romio, L.C.; Roberti, D.R.; Buligon, L.; Zimmer, T.; Degrazia, G.A. A Numerical Model to Estimate the Soil Thermal Conductivity Using Field Experimental Data. Appl. Sci. 2019, 9, 4799. [Google Scholar] [CrossRef]
- Zimmer, T.; Buligon, L.; de Arruda Souza, V.; Romio, L.C.; Roberti, D.R. Influence of clearness index and soil moisture in the soil thermal dynamic in natural pasture in the Brazilian Pampa biome. Geoderma 2020, 378, 114582. [Google Scholar] [CrossRef]
- Gomis-Cebolla, J.; Jimenez, J.C.; Sobrino, J.A.; Corbari, C.; Mancini, M. Intercomparison of remote-sensing based evapotranspiration algorithms over amazonian forests. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 280–294. [Google Scholar] [CrossRef]
- Zahira, S.; Abderrahmane, H.; Mederbal, K.; Frederic, D. Mapping Latent Heat Flux in the Western Forest Covered Regions of Algeria Using Remote Sensing Data and a Spatialized Model. Remote Sens. 2009, 1, 795–817. [Google Scholar] [CrossRef]
- KUSTAS, W.P.; NORMAN, J.M. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar] [CrossRef]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Influence of landscape spatial heterogeneity on the non-linear estimation of leaf area index from moderate spatial resolution remote sensing data. Remote Sens. Environ. 2006, 105, 286–298. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, J.; Liang, S.; Feng, J.; Fisher, J.B.; Li, X.; Li, X.; Liu, S.; Ma, Z.; Miyata, A.; et al. Comparison of satellite-based evapotranspiration models over terrestrial ecosystems in China. Remote Sens. Environ. 2014, 140, 279–293. [Google Scholar] [CrossRef]
- Ferreira, T.R.; Da Silva, B.B.; Moura, M.S.B.D.; Verhoef, A.; Nóbrega, R.L.B. The use of remote sensing for reliable estimation of net radiation and its components: A case study for contrasting land covers in an agricultural hotspot of the Brazilian semiarid region. Agric. For. Meteorol. 2020, 291, 108052. [Google Scholar] [CrossRef]
- Cruz, J.C.; Valente, M.L.; Baggiotto, C.; Baumhardt, E. Qualitative characteristics of water resulting from the introduction of Eucalyptus silviculture in Pampa biome, RS. RBRH 2016, 21, 636–645. [Google Scholar] [CrossRef]
- Rubert, G.C.D.; Roberti, D.R.; Diaz, M.B.; Moraes, O.L.L. de Estimativa Da Evapotranspiração Em Área De Pastagem Em Santa Maria—Rs. Ciência e Nat. 2016, 38, 300. [Google Scholar] [CrossRef]
- Fontana, D.C.; Junges, A.H.; Bremm, C.; Schaparini, L.P.; Mengue, V.P.; Wagner, A.P.L.; Carvalho, P. NDVI and meteorological data as indicators of the Pampa biome natural grasslands growth. Bragantia 2018, 77, 404–414. [Google Scholar] [CrossRef]
- Scottá, F.C.; da Fonseca, E.L. Multiscale trend analysis for pampa grasslands using ground data and vegetation sensor imagery. Sensors 2015, 15, 17666–17692. [Google Scholar] [CrossRef] [PubMed]
- Mattar, C.; Franch, B.; Sobrino, J.A.; Corbari, C.; Jiménez-Muñoz, J.C.; Olivera-Guerra, L.; Skokovic, D.; Sória, G.; Oltra-Carriò, R.; Julien, Y.; et al. Impacts of the broadband albedo on actual evapotranspiration estimated by S-SEBI model over an agricultural area. Remote Sens. Environ. 2014, 147, 23–42. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; Van Der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL): 2. Validation. J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Beatriz, A.; Carvalho, P.; Ozorio, C.P. Avaliação Sobre Os Banhados Do Rio Grande Do Sul, Brasil. Rev. Ciências Ambient. 2007, 1, 83–95. [Google Scholar]
- Santos, T.; Trevisan, R. Eucaliptos versus bioma Pampa: Compreendendo as diferenças entre lavouras de arbóreas e o campo nativo. In: TEIXEIRA FILHO, A. (Org.). Lavouras de Destruição A (im)posição do consenso 2009, 299–332. [Google Scholar]
- OVERBECK, G.E.; MÜLLER, S.C.; Fidelis, A.T.; PFADENHAUER, J.; PILLAR, V.; BLANCO, C.C.; BOLDRINI, I.I.; BOTH, R.; FORNECK, E.D. Brazil’s neglected biome: The South Brazilian Campos. Perspect. Plant Ecol. Evol. Syst. 2007, 9, 101–116. [Google Scholar] [CrossRef]
- Käfer, P.S.; da Rocha, N.S.; Diaz, L.R.; Kaiser, E.A.; Santos, D.C.; Veeck, G.P.; Robérti, D.R.; Rolim, S.B.A.; Oliveira, G.G. Artificial neural networks model based on remote sensing to retrieve evapotranspiration over the Brazilian Pampa. J. Appl. Remote Sens. 2020, 14. [Google Scholar] [CrossRef]
- Diaz, M.B.; Roberti, D.R.; Carneiro, J.V.; de Arruda Souza, V.; de Moraes, O.L.L. Dynamics of the superficial fluxes over a flooded rice paddy in southern Brazil. Agric. For. Meteorol. 2019, 276–277, 107650. [Google Scholar] [CrossRef]
- Monteiro, P.F.C.; Fontana, D.C.; dos Santos, T.V.; Roberti, D.R. Estimativa dos componentes do balanço de energia e da evapotranspiração para áreas de cultivo de soja no sul do brasil utilizando imagens do sensor TM landsat 5. Bragantia 2014, 73, 72–80. [Google Scholar] [CrossRef]
- OVERBECK, G.E.; Podgaiski, L.R.; MÜLLER, S.C. Biodiversidade dos campos. In Campos do Sul.; PILLAR, V., Lange, O., Eds.; Rede Campos Sulios: Porto Alegre, Brazil, 2015; pp. 43–50. [Google Scholar]
- Rocha, J.M. Silvio Cezar Arend Desenvolvimento E Sustentabilidade Na Agricultura Da Metade Sul Do Rs: Parâmetros. In Proceedings of the VIII Seminário Internacional sobre Desenvolvimento Regional; Unisc, PPG Desenvolvimento Regional: Santa Cruz do Sul, Brazil, 2017. [Google Scholar]
- Käfer, P.S.; Rolim, S.B.A.; Heinz, L.V.O.; Iglesias, M.L.; da Rocha, N.S.; Diaz, L.R. Assessment of single-channel algorithms for land surface temperature retrieval at two southern Brazil sites. J. Appl. Remote Sens. 2020, 14, 1. [Google Scholar] [CrossRef]


| Data | Source (Online) | Spatial Resolution | Variable Calculated |
|---|---|---|---|
| Landsat 8 OLI | Earth Explorer-USGS | 30 m | NDVI, α, ε |
| Landsat 8 TIRS | 100 m | Ts | |
| Air temperature (Ta) | INMET-SANTA MARIA (83936) | w | |
| Atmospheric pressure (P) | local | ||
| Relative humid (RH) | |||
| Shortwave downward radiation (RS) | NCEP-CFSv2 | 0.205-horizontal resolution | Rn |
| longwave downward radiation (RL) |
| Acquisition Date | DOY | Season | Cloud Cover (%) |
|---|---|---|---|
| 20 March 2015 | 78 | Autumn | 7.56 |
| 07 May 2015 | 126 | Autumn | 0.02 |
| 27 August 2015 | 238 | Winter | 20.58 |
| 12 September 2015 | 254 | Winter | 0.03 |
| 28 September 2015 | 270 | Spring | 4.22 |
| 15 November 2015 | 318 | Spring | 6.08 |
| 18 January 2016 | 17 | Summer | 0.00 |
| 28 July 2016 | 209 | Winter | 28.58 |
| 13 August 2016 | 225 | Winter | 19.8 |
| 03 October 2017 | 275 | Spring | 0.76 |
| 20 November 2017 | 323 | Spring | 0.49 |
| 22 December 2017 | 355 | Summer | 6.38 |
| 29 April 2018 | 118 | Autumn | 27.9 |
| 16 June 2018 | 166 | Autumn | 7.12 |
| 18 July 2018 | 198 | Winter | 12.53 |
| 25 December 2018 | 358 | Summer | 7.85 |
| 26 January 2019 | 25 | Summer | 4.14 |
| 18 May 2019 | 137 | Autumn | 0.89 |
| 19 June 2019 | 169 | Autumn | 1.13 |
| 21 July 2019 | 201 | Winter | 0.01 |
| 06 August 2019 | 217 | Winter | 0.01 |
| 09 October 2019 | 281 | Spring | 0.49 |
| Variable | Equation | Description |
|---|---|---|
| NDVI | NIR is the Near Infrared reflectance of Landsat 8 (0.86 µm) and RED refers to the Red band reflectance of Landsat 8 OLI and (0.65 µm) [28] | |
| A | ρ is the reflectance at each Landsat 8 OLI channel [29] | |
| Ts | ; | Ti and Tj are the at-sensor brightness temperatures at the bands i (10) and j (11) in Kelvins; ε is the mean emissivity, ε = 0.5 (εi + εj), Δε is the emissivity difference, Δε = (εi − εj); w is the total atmospheric water vapor content (in g/cm−2) [26,30] |
| W | Water vapor (in g/cm−2); [31]; where RH is relative humid (%) | |
| w0 | P is atmospheric pressure (mb) and Ta is air temperature (Celcius) | |
| ε | FVC is the Fractional Vegetation Cover and is given by FVC = NDVI − NDVIs/NDVIv − NDVIs; εs and εv are the soil and vegetation emissivity values respectively [32] | |
| Soil Heat Flux (G) | [33] |
| DOY | Average | Min | Min * | Max | Max * |
|---|---|---|---|---|---|
| 78 | 306.68 | 302.88 | 300.28 | 315.66 | 317.63 |
| 126 | 292.18 | 289.41 | 287.27 | 295.89 | 298.33 |
| 238 | 295.16 | 293.35 | 290.84 | 297.85 | 300.04 |
| 254 | 292.82 | 288.85 | 287.34 | 295.97 | 298.27 |
| 270 | 300.09 | 295.25 | 293.67 | 305.98 | 306.79 |
| 318 | 303.27 | 298.64 | 297.31 | 308.68 | 310.52 |
| 17 | 310.67 | 298.67 | 297.23 | 323.209 | 325.068 |
| 209 | 287.41 | 284.77 | 282.97 | 290.48 | 293.037 |
| 225 | 294.04 | 290.46 | 288.57 | 298.381 | 300.38 |
| 275 | 298.41 | 294.98 | 293.03 | 301.437 | 303.466 |
| 323 | 310.17 | 302.73 | 300.62 | 320.88 | 321.847 |
| 355 | 311.41 | 303.47 | 302.15 | 320.889 | 321.532 |
| 118 | 301.04 | 296.82 | 295.25 | 305.507 | 307.662 |
| 166 | 284.88 | 281.68 | 279.92 | 288.066 | 290.438 |
| 198 | 296.68 | 294.71 | 292.3 | 298.152 | 301.019 |
| 358 | 305.54 | 301.55 | 299.52 | 311.657 | 313.422 |
| 137 | 295.52 | 292.28 | 290.41 | 297.604 | 299.857 |
| 169 | 291.57 | 288.96 | 286.92 | 293.546 | 296.418 |
| 201 | 297.32 | 295.28 | 292.42 | 300.20 | 302.042 |
| 217 | 294.43 | 292.37 | 289.95 | 296.84 | 299.462 |
| 281 | 303.99 | 299.38 | 298.12 | 309.80 | 311.864 |
| Variable | Min–Max | Min–Max (*) | r2 | MSD | RMSE | Bias |
|---|---|---|---|---|---|---|
| LE (W/m2) | 52.88–431.22 | 74.51–408.95 | 0.98 | ±21.13 | 19.36 | 11.48 |
| Rn (W/m2) | 142.44–536.05 | 140.33–533.95 | 1 | ±0.14 | 1.98 | 1.97 |
| G (W/m2) | 7.41–86.07 | 7.55–86.48 | 1 | ±19.28 | 0.27 | −0.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocha, N.S.d.; Käfer, P.S.; Skokovic, D.; Veeck, G.; Diaz, L.R.; Kaiser, E.A.; Carvalho, C.M.; Cruz, R.C.; Sobrino, J.A.; Roberti, D.R.; et al. The Influence of Land Surface Temperature in Evapotranspiration Estimated by the S-SEBI Model. Atmosphere 2020, 11, 1059. https://doi.org/10.3390/atmos11101059
Rocha NSd, Käfer PS, Skokovic D, Veeck G, Diaz LR, Kaiser EA, Carvalho CM, Cruz RC, Sobrino JA, Roberti DR, et al. The Influence of Land Surface Temperature in Evapotranspiration Estimated by the S-SEBI Model. Atmosphere. 2020; 11(10):1059. https://doi.org/10.3390/atmos11101059
Chicago/Turabian StyleRocha, Nájila Souza da, Pâmela S. Käfer, Drazen Skokovic, Gustavo Veeck, Lucas Ribeiro Diaz, Eduardo André Kaiser, Cibelle Machado Carvalho, Rafael Cabral Cruz, José A. Sobrino, Débora Regina Roberti, and et al. 2020. "The Influence of Land Surface Temperature in Evapotranspiration Estimated by the S-SEBI Model" Atmosphere 11, no. 10: 1059. https://doi.org/10.3390/atmos11101059
APA StyleRocha, N. S. d., Käfer, P. S., Skokovic, D., Veeck, G., Diaz, L. R., Kaiser, E. A., Carvalho, C. M., Cruz, R. C., Sobrino, J. A., Roberti, D. R., & Rolim, S. B. A. (2020). The Influence of Land Surface Temperature in Evapotranspiration Estimated by the S-SEBI Model. Atmosphere, 11(10), 1059. https://doi.org/10.3390/atmos11101059







