RePLaT-Chaos: A Simple Educational Application to Discover the Chaotic Nature of Atmospheric Advection
Abstract
1. Introduction
2. Chaotic Quantities
2.1. Topological Entropy
2.2. Escape Rate
3. Methods
3.1. Calculation of Particle Trajectories
3.2. Calculation of the Topological Entropy
3.3. Calculation of the Escape Rate
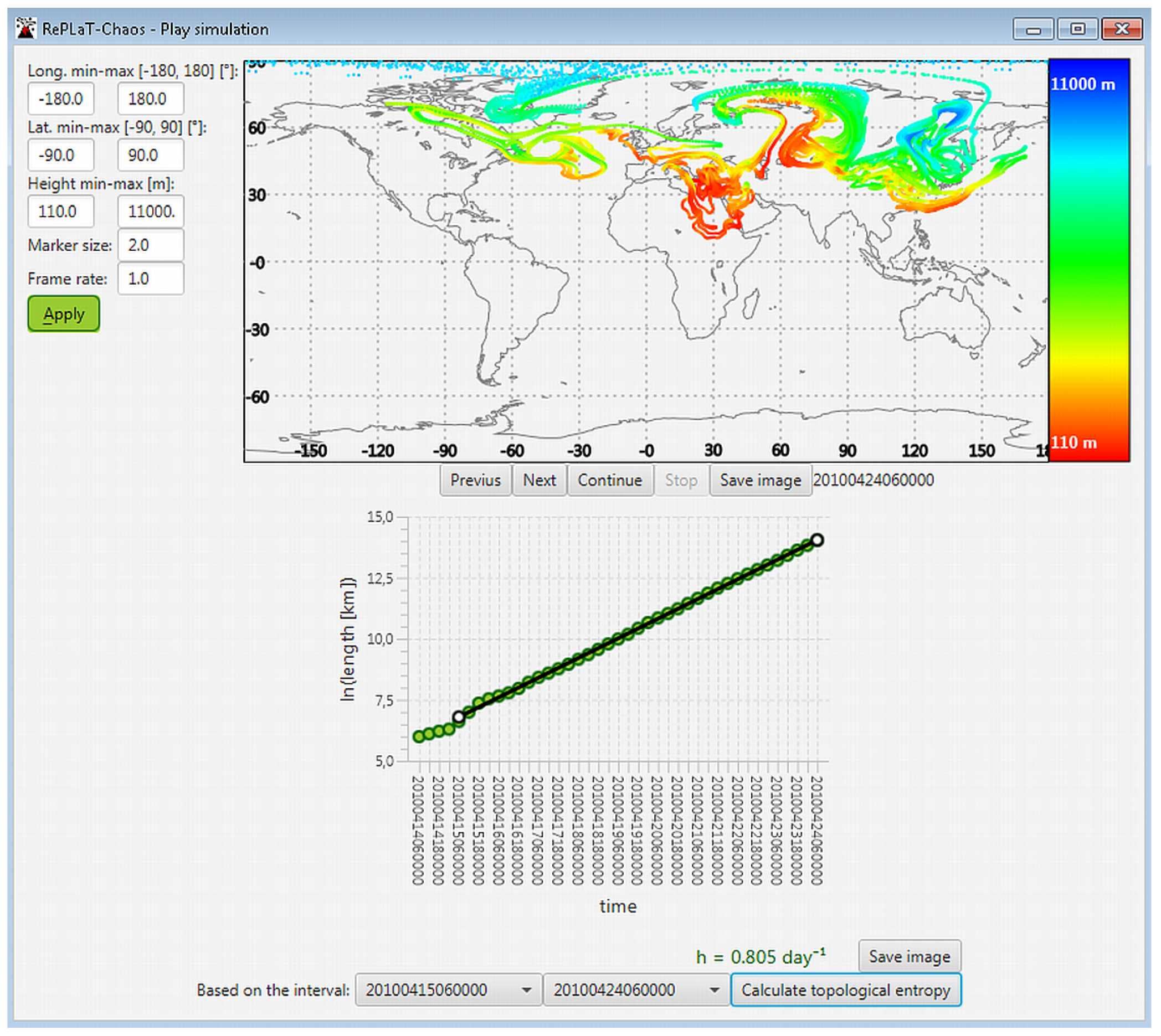
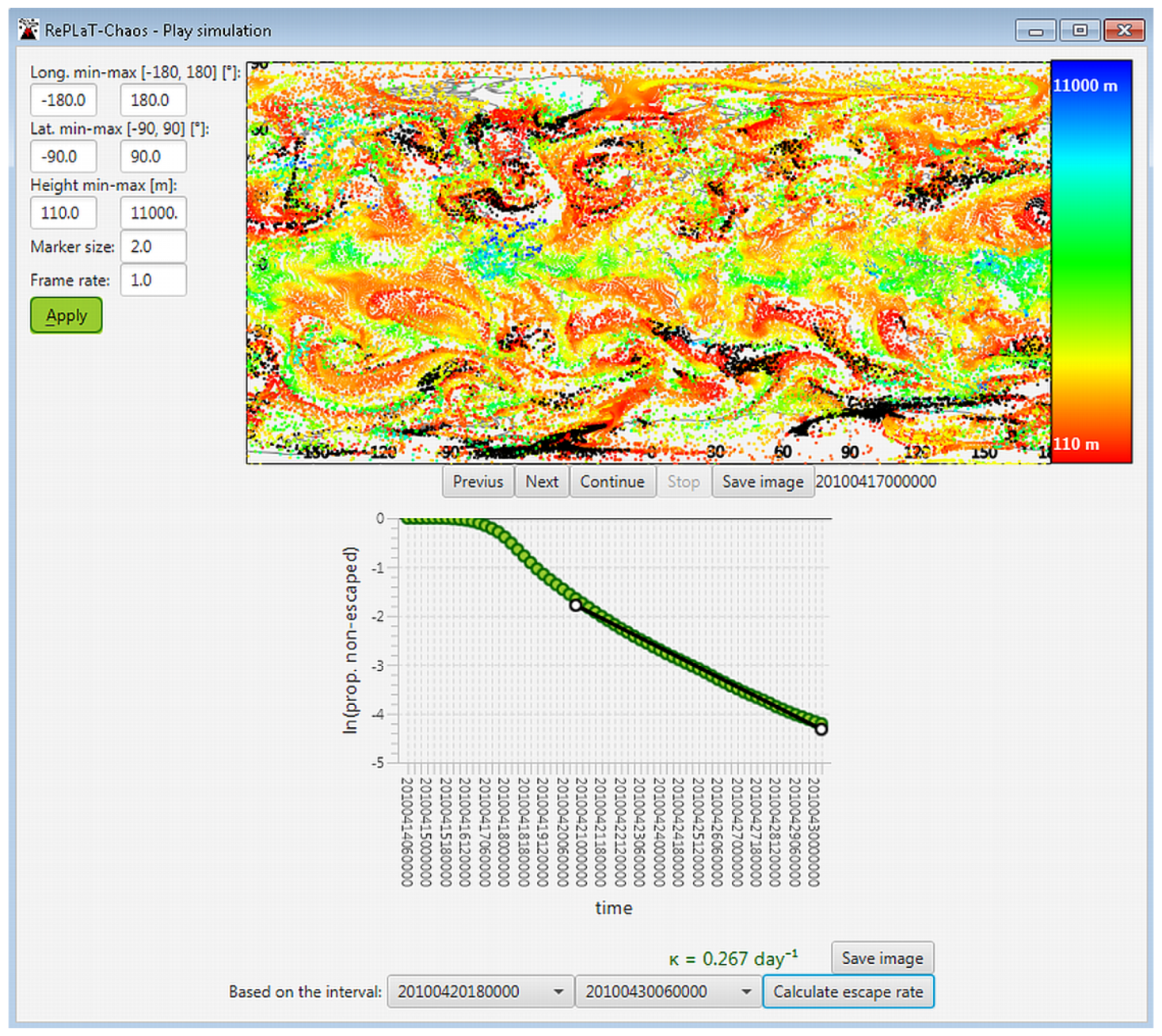
3.4. RePLaT-Chaos in a Nutshell
4. Results from RePLaT-Chaos Simulations
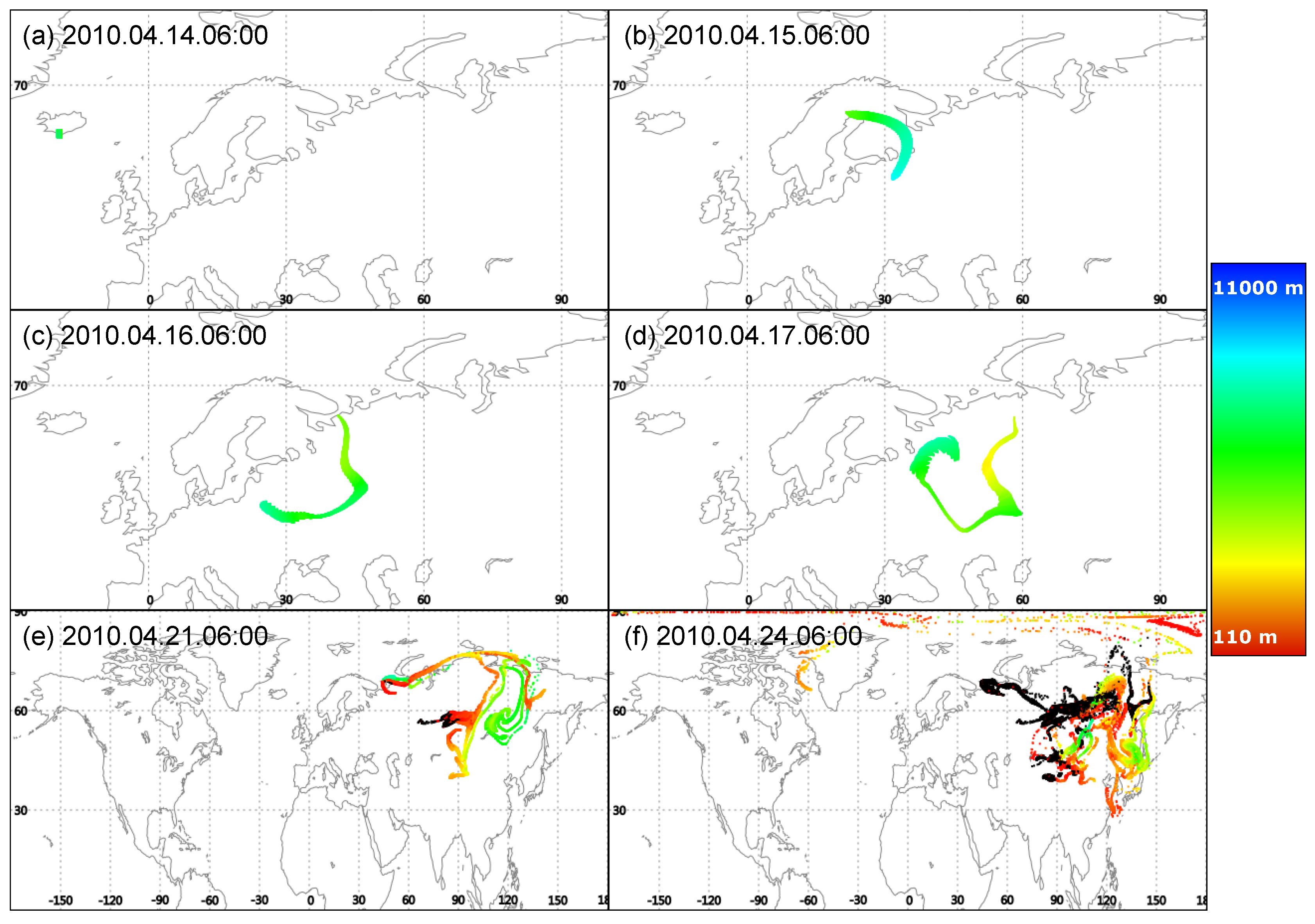
4.1. Spreading of a Volcanic Ash Cloud Emitted during the Eyjafjalljökull Volcano’s Eruption
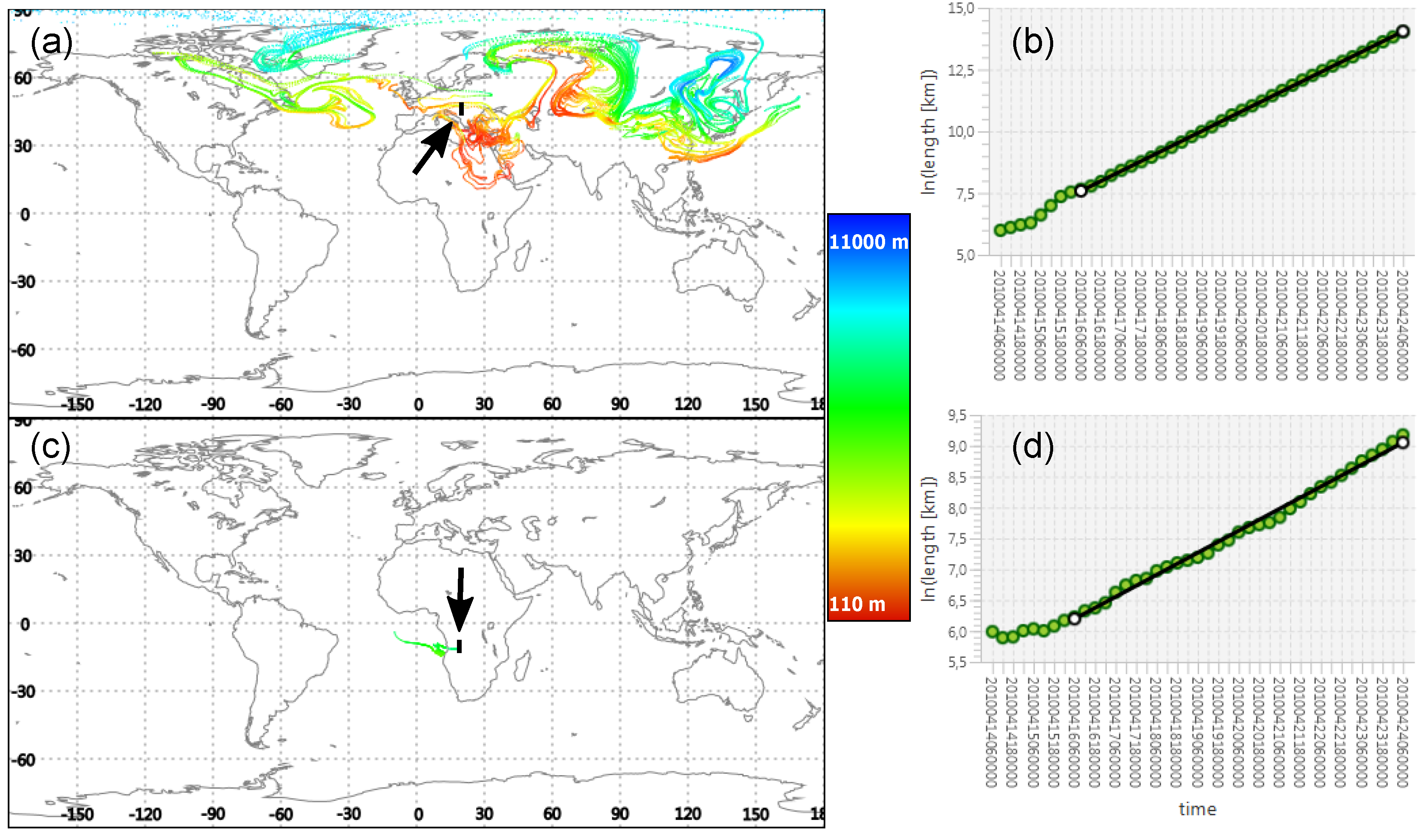
4.2. Stretching of the Pollutant Clouds—The Topological Entropy
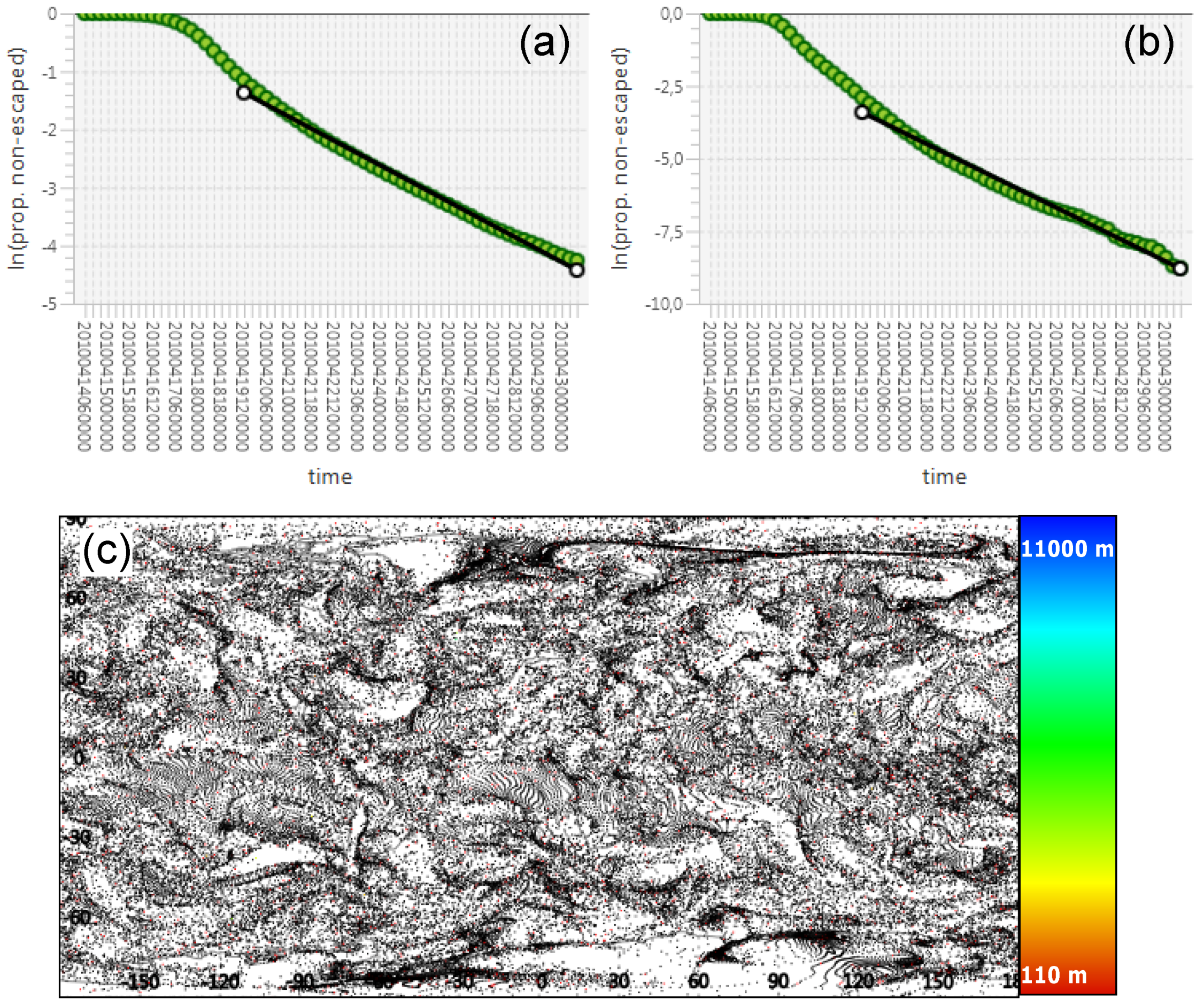
4.3. Deposition of the Particles—The Escape Rate
5. Conclusions
- How much faster do particles with larger size/higher density leave the atmosphere compared to smaller/lighter ones?
- Do the particles deposit on the surface in the shape of patches or in a filamentary structure?
- Is it possible for the particles of an initially small and compact pollutant cloud to cover more or less homogeneously the hemisphere where they are initialized, or the whole globe, and how long does it take?
- How does the initial geographical location of the pollutant clouds affect the rate of their stretching?
- Does the rapidity of the deposition or the stretching of a pollutant cloud depend on initialization time, e.g., the season in a year?
- Can cyclones, jet streams, etc. be revealed by tracking pollutant particles?
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RePLaT | Real Particle Lagrangian Trajectory model |
Appendix A. RePLaT-Chaos Manual
Appendix A.1. First Steps and Data Format Requirements
Appendix A.1.1. Launching RePLaT-Chaos
Appendix A.1.2. Input Meteorological Data
- Meteorological data on a regular longitude–latitude grid () at different pressure levels, where and are the horizontal grid resolutions. The software considers the lowest level as Earth’s surface and the highest one as the “top” of the simulation region.
- Required meteorological variables: zonal [m/s] and meridional [m/s] wind components, vertical velocity component [Pa/s] and temperature [K].
- A meteorological file contains the values of one of the meteorological variables on the above-mentioned grid for a single time instant.
- File name convention: <variable name><yyyyMMddhhmmss>.nc, where the format <yyyyMMddhhmmss> denotes the following: year (yyyy), month (MM), day (dd), hour (hh), minute (mm), second (ss) given in 4, 2, 2, 2, 2, and 2 digits, respectively.
Appendix A.1.3. Output Data
- is the longitude coordinate of the particle [rad] ,
- is the latitude coordinate of the particle [rad] ,
- z is the vertical coordinate of the particle [m] calculated from its pressure coordinate p based on the equations of the standard atmosphere [67],
- r is the particle radius [m] ,
- is the particle density [kg m] ,
- represents whether the particle is in the atmosphere yet [1] or not [0].
Appendix A.2. Running a Simulation
Appendix A.2.1. Setting the Simulation Parameters
- Start: start date and time of the simulation (format: <yyyy.MM.dd.hh:mm:ss>).
- End: end date and time of the simulation (format: <yyyy.MM.dd.hh:mm:ss>).
- Time step: if it is constant then the text field represents the value of the constant time step [s] (format: integer); if it is variable then the text field corresponds to defined in Section 3.1.
- Input folder: folder of the meteorological files. Clicking the Choose input folder button it can be chosen or it can be written directly to the text field.
- File name pattern for the met. fields: the part of the file name before date and time for the meteorological files of the zonal (u), meridional (v), vertical (w) velocity component of air and the temperature (T).
- Reflect from the surface?: if the box is checked each particle bounces back from the lowest meteorological level according to the Reflection coefficient for the surface (format: real). For topological entropy (length) calculation, the box is worth checking and 1 should be given for the reflection coefficient.
- Reflect from the top?: if the box is checked each particle bounces back from the highest meteorological level according to the Reflection coefficient for the top (format: real). Generally, the box is worth checking unless the user especially wants to study how many particles leave the meteorological region at the highest level.
- Save particle data?: should the data of the particles of the pollutant cloud (and the length data and the ratio of the non-escaped particles) be written to file. For example, user should not check the box if he/she carries out test calculations and would like to see the spreading of pollutant cloud only once, i.e., when the user does not need the data later.
- Output folder: the folder of the files for particle data, length data and ratio of the non-escaped particles. Clicking the Choose output folder button it can be chosen or it can be written directly to the text field.
- File name pattern for the output: the part of the particle data file name before date and time.
- Calculate length? (filename): should the length of the pollutant cloud be calculated, and if yes, what should be the name of the length file to which the data are written. The length of the pollutant cloud is computed as the sum of the distances between the subsequent particles as described in Section 3.2. Therefore, the result of the calculation equals to the real length in the unit of km only if the particles are initiated as a one-dimensional “pollutant cloud”, i.e, a line segment.
- Calculate ratio of non-escaped particles? (filename): should the ratio of the non-escaped particles be calculated, and if yes, what should be the name of the escape file to which the data are written.
- Time interval for the output: the time interval [s] for writing the data of the pollutant cloud, of the length and of the ratio of the non-escaped particles to file (format: integer)
- Insert new particles if the distance [km] of two particles: should new particles be inserted in the pollutant cloud if the distance of two subsequent particles is greater than the given distance (format: real). The box is worth checking for length calculation; otherwise subsequent particles may travel far away from each other which results in the underestimation of the length of the pollutant cloud as described in Section 3.2.
- Max. number of particles: The number of the particles in the simulation, including the inserted ones, does not exceed the given number (format: integer).
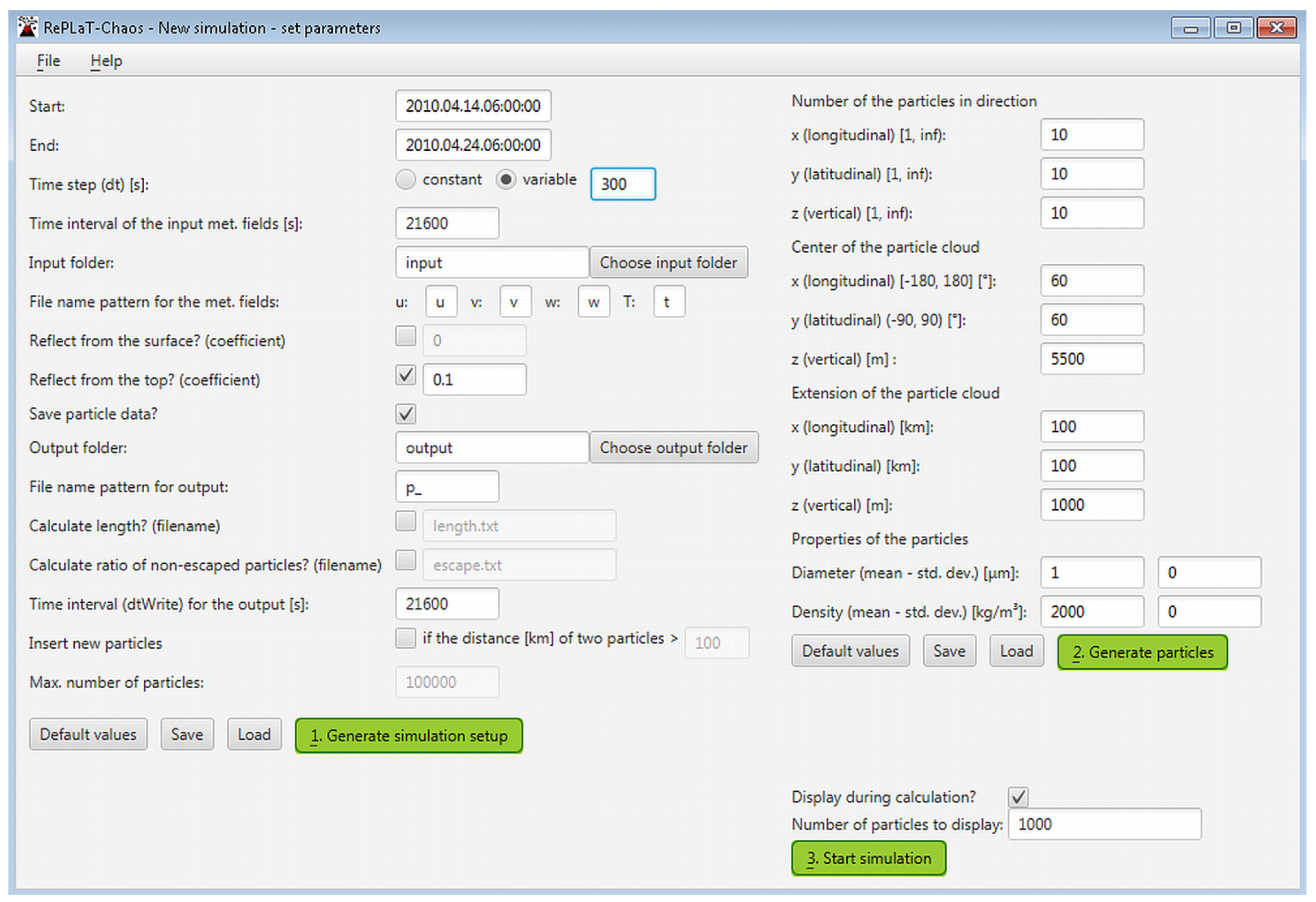
Appendix A.2.2. Setting the Parameters of the Pollutant Cloud
- Number of particles in direction x/y/z: the number of the particles in zonal, meridional and vertical direction (format: integers, greater or equal than 1).
- Center of the particle cloud x/y/z: zonal [], meridional [] and vertical [m] coordinate of the center of the pollutant cloud (format: real numbers in the given intervals)
- Extension of the particle cloud x/y/z: length of the sides of the rectangular cuboid representing the pollutant cloud in zonal [km], meridional [km] and vertical [m] direction (format: non-negative real)
- Diameter (mean–std.dev.): the diameter of the particles is log-normally distributed with the user given mean and standard deviation [m] (format: non-negative real). As mentioned in Section 3.1, the diameter 0 m corresponds to gas particles which are advected by the instantaneous velocity of the atmospheric flow at each time instant (their terminal velocity in Equation (5) is 0).
- Density (mean–std.dev.): the density of the particles is log-normally distributed with the user given mean and standard deviation [kg m] (format: non-negative real).
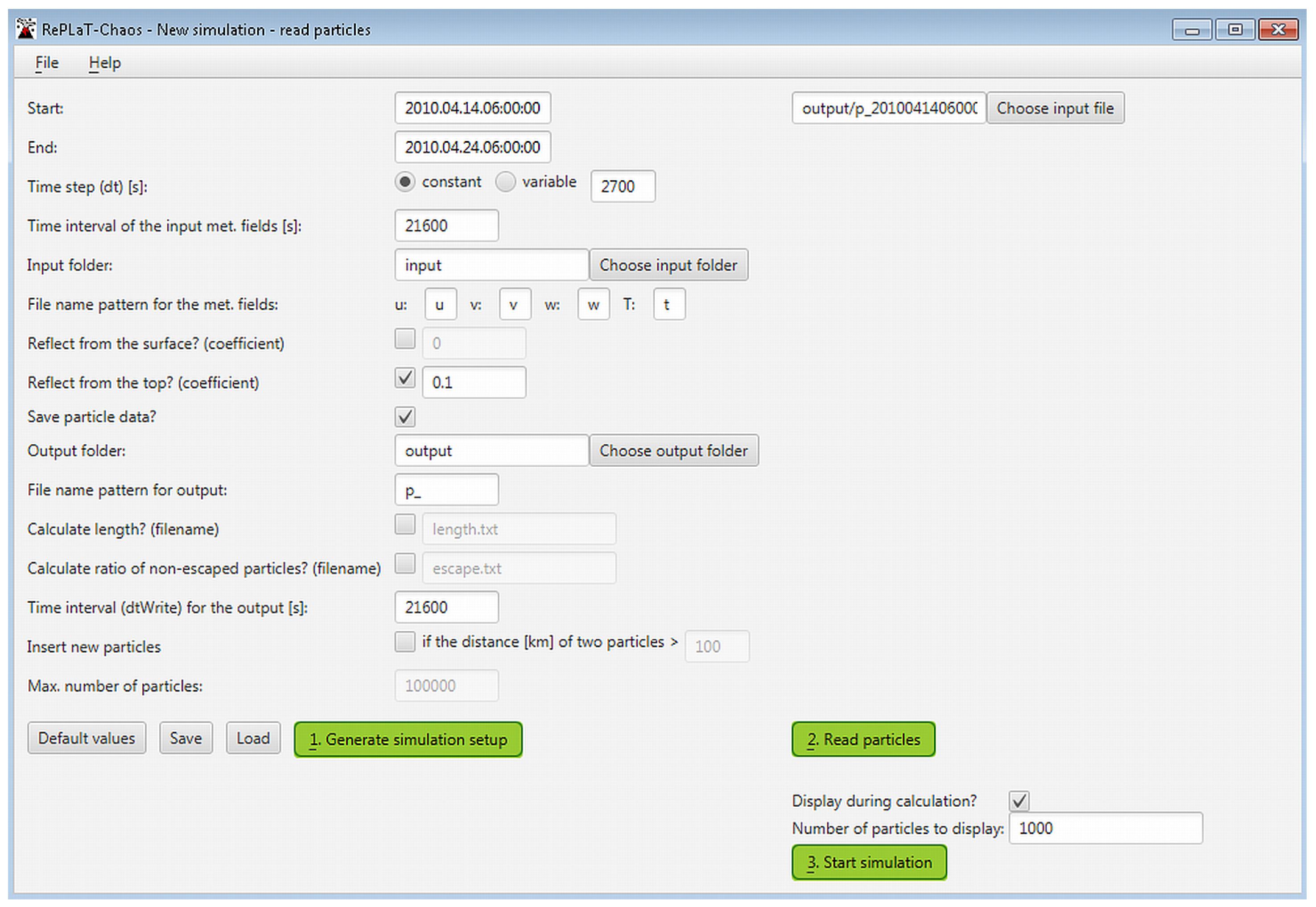
Appendix A.2.3. Reading the Particles of the Pollutant Cloud From File
Appendix A.2.4. Starting a New Simulation
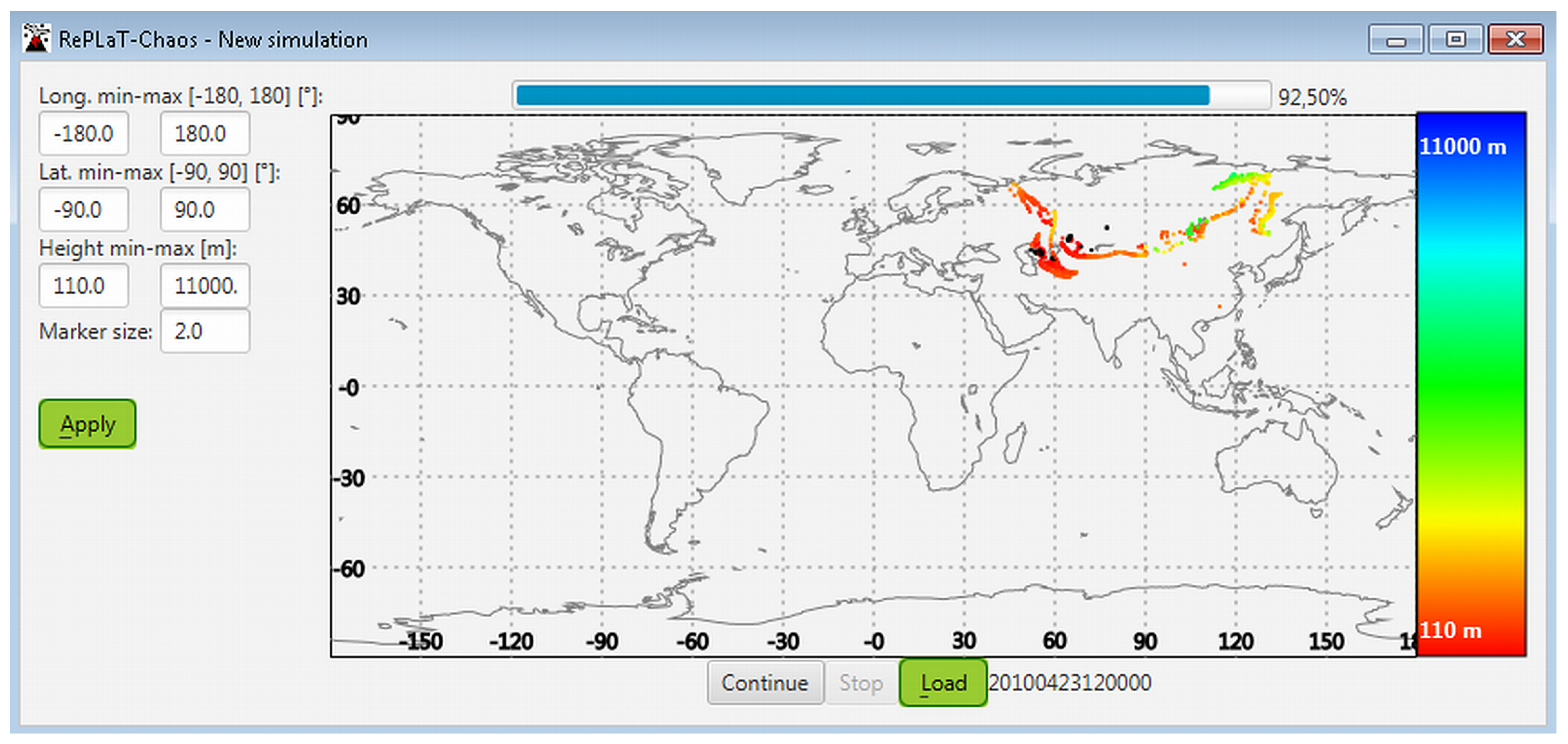
Appendix A.2.5. Setting the Display Properties of the Simulation
Appendix A.3. Replaying a Saved Simulation
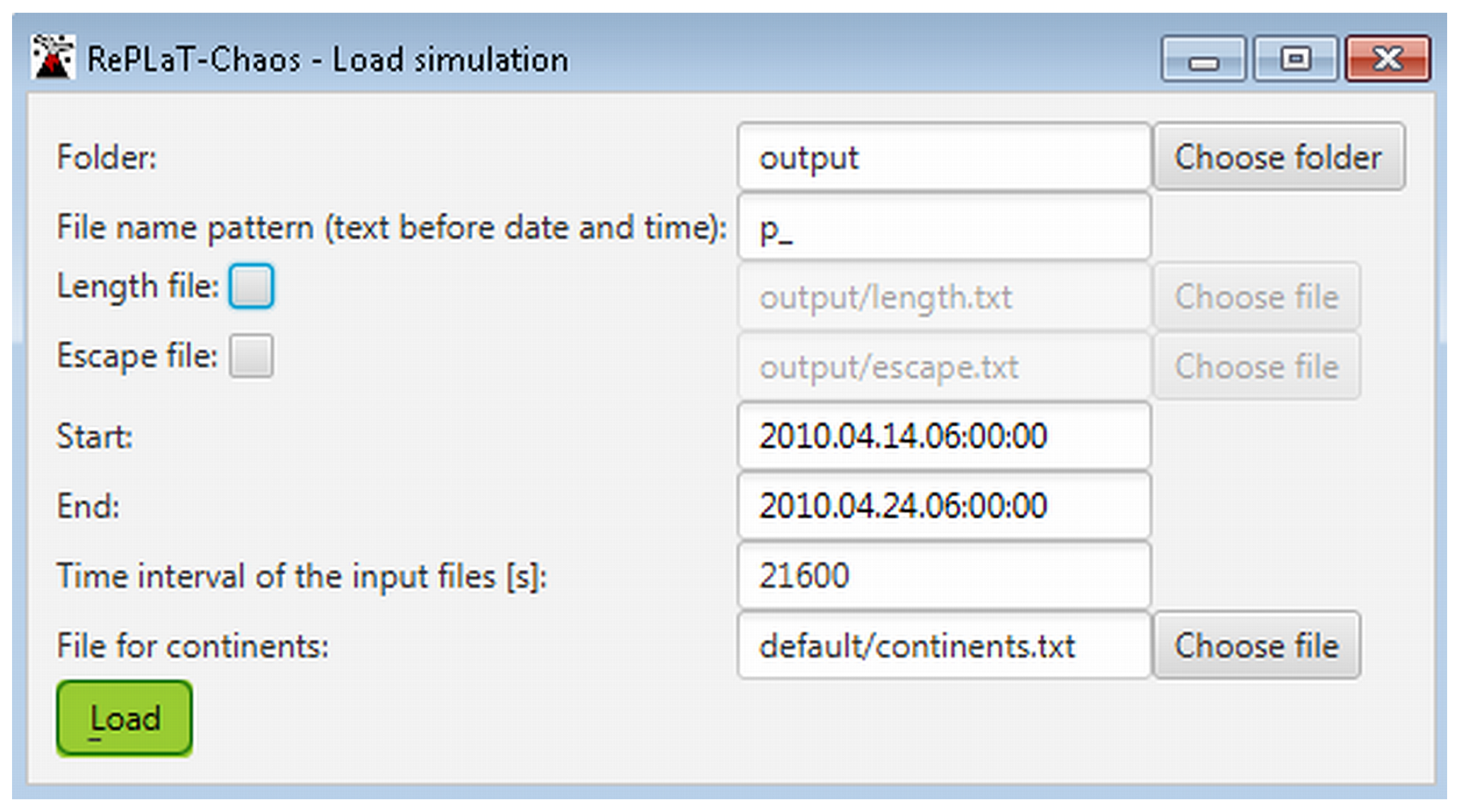
- Folder: folder of the files to be loaded. Clicking the Choose folder button it can be chosen or it can be written directly to the text field.
- File name pattern: the part of the name of the particle files before date and time.
- Length file: should length data be loaded, and if yes from which file. Clicking the Choose file button it can be chosen or it can be written directly to the text field.
- Escape file: should the data of the ratio of non-escaped particles be loaded, and if yes from which file. Clicking the Choose file button it can be chosen or it can be written directly to the text field. The format of the lines of the length and escape file should coincide with the requirements mentioned in Appendix A.1.3.
- Start: start of the display (format: <yyyy.MM.dd.hh:mm:ss>)
- End: end of the display (format: <yyyy.MM.dd.hh:mm:ss>)
- Time interval of the input files: time interval [s] between subsequent files to be displayed (format: integer)
- File for continents: the file which contains the coordinates ( [rad]) of the coastlines of the continents. Clicking the Choose file button it can be chosen, or it can be written directly to the text field.
References
- Ulfarsson, G.F.; Unger, E.A. Impacts and Responses of Icelandic Aviation to the 2010 Eyjafjallajökull Volcanic Eruption: Case Study. Transp. Res. Rec. 2011, 2214, 144–151. [Google Scholar] [CrossRef]
- Wilkinson, S.M.; Dunn, S.; Ma, S. The vulnerability of the European air traffic network to spatial hazards. Nat. Hazards 2012, 60, 1027–1036. [Google Scholar] [CrossRef]
- Arason, P.; Petersen, G.; Bjornsson, H. Observations of the altitude of the volcanic plume during the eruption of Eyjafjallajökull, April–May 2010. Earth Syst. Sci. Data 2011, 3, 9–17. [Google Scholar] [CrossRef]
- Stohl, A.; Prata, A.; Eckhardt, S.; Clarisse, L.; Durant, A.; Henne, S.; Kristiansen, N.I.; Minikin, A.; Schumann, U.; Seibert, P.; et al. Determination of time-and height-resolved volcanic ash emissions and their use for quantitative ash dispersion modeling: The 2010 Eyjafjallajökull eruption. Atmos. Chem. Phys. 2011, 11, 4333–4351. [Google Scholar] [CrossRef]
- Schumann, U.; Weinzierl, B.; Reitebuch, O.; Schlager, H.; Minikin, A.; Forster, C.; Baumann, R.; Sailer, T.; Graf, K.; Mannstein, H.; et al. Airborne observations of the Eyjafjalla volcano ash cloud over Europe during air space closure in April and May 2010. Atmos. Chem. Phys. 2011, 11, 2245–2279. [Google Scholar] [CrossRef]
- Sicard, M.; Guerrero-Rascado, J.L.; Navas-Guzmán, F.; Preißler, J.; Molero, F.; Tomás, S.; Bravo-Aranda, J.A.; Comerón, A.; Rocadenbosch, F.; Wagner, F.; et al. Monitoring of the Eyjafjallajökull volcanic aerosol plume over the Iberian Peninsula by means of four EARLINET lidar stations. Atmos. Chem. Phys. 2012, 12, 3115–3130. [Google Scholar] [CrossRef]
- Pappalardo, G.; Mona, L.; D’Amico, G.; Wandinger, U.; Adam, M.; Amodeo, A.; Ansmann, A.; Apituley, A.; Alados Arboledas, L.; Balis, D.; et al. Four-dimensional distribution of the 2010 Eyjafjallajökull volcanic cloud over Europe observed by EARLINET. Atmos. Chem. Phys. 2013, 13, 4429–4450. [Google Scholar] [CrossRef]
- Burlakov, V.; Dolgii, S.; Nevzorov, A.; Samokhvalov, I.; Nasonov, S.; Zhivotenyuk, I.; El’nikov, A.; Nazarov, E.; Plusnin, I.; Shikhantsov, A. Traces of eruption of Eyjafjallajökull volcano according to data of lidar observations in Tomsk and Surgut. Atmos. Ocean. Opt. 2012, 25, 110–117. [Google Scholar] [CrossRef]
- Zuev, V.V.; Burlakov, V.D.; Nevzorov, A.V.; Pravdin, V.L.; Savelieva, E.S.; Gerasimov, V.V. 30-year lidar observations of the stratospheric aerosol layer state over Tomsk (Western Siberia, Russia). Atmos. Chem. Phys. 2017, 17, 3067–3081. [Google Scholar] [CrossRef]
- Petersen, G.; Bjornsson, H.; Arason, P.; Löwis, S.V. Two weather radar time series of the altitude of the volcanic plume during the May 2011 eruption of Grímsvötn, Iceland. Earth Syst. Sci. Data 2012, 4, 121–127. [Google Scholar] [CrossRef]
- Tesche, M.; Glantz, P.; Johansson, C.; Norman, M.; Hiebsch, A.; Ansmann, A.; Althausen, D.; Engelmann, R.; Seifert, P. Volcanic ash over Scandinavia originating from the Grímsvötn eruptions in May 2011. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Wilkins, K.; Western, L.; Watson, I. Simulating atmospheric transport of the 2011 Grímsvötn ash cloud using a data insertion update scheme. Atmos. Environ. 2016, 141, 48–59. [Google Scholar] [CrossRef]
- Bowyer, T.W.; Biegalski, S.R.; Cooper, M.; Eslinger, P.W.; Haas, D.; Hayes, J.C.; Miley, H.S.; Strom, D.J.; Woods, V. Elevated radioxenon detected remotely following the Fukushima nuclear accident. J. Environ. Radioact. 2011, 102, 681–687. [Google Scholar] [CrossRef] [PubMed]
- Leon, J.D.; Jaffe, D.; Kaspar, J.; Knecht, A.; Miller, M.; Robertson, R.; Schubert, A. Arrival time and magnitude of airborne fission products from the Fukushima, Japan, reactor incident as measured in Seattle, WA, USA. J. Environ. Radioact. 2011, 102, 1032–1038. [Google Scholar] [CrossRef] [PubMed]
- MacMullin, S.; Giovanetti, G.; Green, M.; Henning, R.; Holmes, R.; Vorren, K.; Wilkerson, J. Measurement of airborne fission products in Chapel Hill, NC, USA from the Fukushima Dai-ichi reactor accident. J. Environ. Radioact. 2012, 112, 165–170. [Google Scholar] [CrossRef] [PubMed]
- Masson, O.; Baeza, A.; Bieringer, J.; Brudecki, K.; Bucci, S.; Cappai, M.; Carvalho, F.; Connan, O.; Cosma, C.; Dalheimer, A.; et al. Tracking of airborne radionuclides from the damaged Fukushima Dai-ichi nuclear reactors by European networks. Environ. Sci. Technol. 2011, 45, 7670–7677. [Google Scholar] [CrossRef]
- Bossew, P.; Kirchner, G.; De Cort, M.; De Vries, G.; Nishev, A.; De Felice, L. Radioactivity from Fukushima Dai-ichi in air over Europe; part 1: Spatio-temporal analysis. J. Environ. Radioact. 2012, 114, 22–34. [Google Scholar] [CrossRef]
- Stohl, A.; Seibert, P.; Wotawa, G.; Arnold, D.; Burkhart, J.; Eckhardt, S.; Tapia, C.; Vargas, A.; Yasunari, T. Xenon-133 and caesium-137 releases into the atmosphere from the Fukushima Dai-ichi nuclear power plant: Determination of the source term, atmospheric dispersion, and deposition. Atmos. Chem. Phys. 2012, 12, 2313–2343. [Google Scholar] [CrossRef]
- Manolopoulou, M.; Vagena, E.; Stoulos, S.; Ioannidou, A.; Papastefanou, C. Radioiodine and radiocesium in Thessaloniki, Northern Greece due to the Fukushima nuclear accident. J. Environ. Radioact. 2011, 102, 796–797. [Google Scholar] [CrossRef]
- Pittauerová, D.; Hettwig, B.; Fischer, H.W. Fukushima fallout in Northwest German environmental media. J. Environ. Radioact. 2011, 102, 877–880. [Google Scholar] [CrossRef]
- Bikit, I.; Mrda, D.; Todorovic, N.; Nikolov, J.; Krmar, M.; Veskovic, M.; Slivka, J.; Hansman, J.; Forkapic, S.; Jovancevic, N. Airborne radioiodine in northern Serbia from Fukushima. J. Environ. Radioact. 2012, 114, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Castruccio, A.; Clavero, J.; Segura, A.; Samaniego, P.; Roche, O.; Le Pennec, J.L.; Droguett, B. Eruptive parameters and dynamics of the April 2015 sub-Plinian eruptions of Calbuco volcano (southern Chile). Bull. Volcanol. 2016, 78, 62. [Google Scholar] [CrossRef]
- Romero, J.; Morgavi, D.; Arzilli, F.; Daga, R.; Caselli, A.; Reckziegel, F.; Viramonte, J.; Díaz-Alvarado, J.; Polacci, M.; Burton, M.; et al. Eruption dynamics of the 22–23 April 2015 Calbuco Volcano (Southern Chile): Analyses of tephra fall deposits. J. Volcanol. Geotherm. Res. 2016, 317, 15–29. [Google Scholar] [CrossRef]
- Reckziegel, F.; Bustos, E.; Mingari, L.; Báez, W.; Villarosa, G.; Folch, A.; Collini, E.; Viramonte, J.; Romero, J.; Osores, S. Forecasting volcanic ash dispersal and coeval resuspension during the April–May 2015 Calbuco eruption. J. Volcanol. Geotherm. Res. 2016, 321, 44–57. [Google Scholar] [CrossRef]
- Ivy, D.J.; Solomon, S.; Kinnison, D.; Mills, M.J.; Schmidt, A.; Neely, R.R. The influence of the Calbuco eruption on the 2015 Antarctic ozone hole in a fully coupled chemistry-climate model. Geophys. Res. Lett. 2017, 44, 2556–2561. [Google Scholar] [CrossRef]
- Corsaro, R.A.; Andronico, D.; Behncke, B.; Branca, S.; Caltabiano, T.; Ciancitto, F.; Cristaldi, A.; De Beni, E.; La Spina, A.; Lodato, L.; et al. Monitoring the December 2015 summit eruptions of Mt. Etna (Italy): Implications on eruptive dynamics. J. Volcanol. Geotherm. Res. 2017, 341, 53–69. [Google Scholar] [CrossRef]
- Pompilio, M.; Bertagnini, A.; Del Carlo, P.; Di Roberto, A. Magma dynamics within a basaltic conduit revealed by textural and compositional features of erupted ash: The December 2015 Mt. Etna paroxysms. Sci. Rep. 2017, 7, 4805. [Google Scholar] [CrossRef]
- Athanassiadou, M. The Mt Etna SO2 eruption in December 2015—The view from space. Weather 2016, 71, 273–279. [Google Scholar] [CrossRef]
- Haszpra, T.; Tél, T. Escape rate: A Lagrangian measure of particle deposition from the atmosphere. Nonlinear Process. Geophys. 2013, 20, 867–881. [Google Scholar] [CrossRef]
- Haszpra, T.; Herein, M. Ensemble-based analysis of the pollutant spreading intensity induced by climate change. Sci. Rep. 2019, 9, 3896. [Google Scholar] [CrossRef]
- Haszpra, T.; Tél, T. Topological entropy: A Lagrangian measure of the state of the free atmosphere. J. Atmos. Sci. 2013, 70, 4030–4040. [Google Scholar] [CrossRef]
- Dutton, E.G.; Christy, J.R. Solar radiative forcing at selected locations and evidence for global lower tropospheric cooling following the eruptions of El Chichon and Pinatubo. Geophys. Res. Lett. 1992, 19, 2313–2316. [Google Scholar] [CrossRef]
- Kerr, R.A. Pinatubo global cooling on target. Science 1993, 259, 594–595. [Google Scholar]
- Self, S.; Zhao, J.X.; Holasek, R.E.; Torres, R.C.; King, A.J. The atmospheric impact of the 1991 Mount Pinatubo eruption. In Fire and Mud: The Eruptions and Lahars of Mount Pinatubo, Philippines; Newhall, C.G., Punongbayan, R., Eds.; University of Washington Press: Seattle, WA, USA, 1996; pp. 1089–1116. [Google Scholar]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: New York, NY, USA, 1993; p. 385. [Google Scholar]
- Tél, T.; Gruiz, M. Chaotic Dynamics: An Introduction Based on Classical Mechanics; Cambridge University Press: Cambridge, UK, 2006; p. 393. [Google Scholar]
- Lai, Y.C.; Tél, T. Transient Chaos: Complex Dynamics on Finite Time Scales; Springer-Verlag New York: New York, NY, USA, 2011; Volume 173. [Google Scholar]
- Tél, T. The joy of transient chaos. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 097619. [Google Scholar] [CrossRef]
- Haszpra, T. Intensification of Large-Scale Stretching of Atmospheric Pollutant Clouds due to Climate Change. J. Atmos. Sci. 2017, 74, 4229–4240. [Google Scholar] [CrossRef]
- Stein, A.; Draxler, R.R.; Rolph, G.D.; Stunder, B.J.; Cohen, M.; Ngan, F. NOAA’s HYSPLIT atmospheric transport and dispersion modeling system. Bull. Am. Meteorol. Soc. 2015, 96, 2059–2077. [Google Scholar] [CrossRef]
- Rolph, G.; Stein, A.; Stunder, B. Real-time environmental applications and display sYstem: READY. Environ. Model. Softw. 2017, 95, 210–228. [Google Scholar] [CrossRef]
- Miltenberger, A.K.; Pfahl, S.; Wernli, H. An online trajectory module (version 1.0) for the nonhydrostatic numerical weather prediction model COSMO. Geosci. Model Dev. 2013, 6, 1989–2004. [Google Scholar] [CrossRef]
- Sprenger, M.; Wernli, H. The LAGRANTO Lagrangian analysis tool—Version 2.0. Geosci. Model Dev. 2015, 8, 2569–2586. [Google Scholar] [CrossRef]
- Pisso, I.; Sollum, E.; Grythe, H.; Kristiansen, N.; Cassiani, M.; Eckhardt, S.; Arnold, D.; Morton, D.; Thompson, R.L.; Groot Zwaaftink, C.D.; et al. The Lagrangian particle dispersion model FLEXPART version 10.3. Geosci. Model Dev. Discuss. 2019, 2019, 1–67. [Google Scholar] [CrossRef]
- Costa, A.; Macedonio, G.; Folch, A. A three-dimensional Eulerian model for transport and deposition of volcanic ashes. Earth Planet. Sci. Lett. 2006, 241, 634–647. [Google Scholar] [CrossRef]
- Folch, A.; Costa, A.; Macedonio, G. FALL3D: A computational model for volcanic ash transport and deposition. Comput. Geosci. 2009, 35, 1334–1342. [Google Scholar] [CrossRef]
- Folch, A.; Costa, A.; Macedonio, G. FPLUME-1.0: An integral volcanic plume model accounting for ash aggregation. Geosci. Model Dev. 2016, 9, 431–450. [Google Scholar] [CrossRef]
- RePLaT-Chaos. Available online: http://theorphys.elte.hu/fiztan/volcano/#full (accessed on 21 December 2019).
- Chandler, M.A.; Richards, S.J.; Shopsin, M. EdGCM: Enhancing climate science education through climate modeling research projects. In Proceedings of the 85th Annual Meeting of the American Meteorological Society, 14th Symposium on Education, San Diego, CA, USA, 8–14 January 2005; p. P1. [Google Scholar]
- Fraedrich, K.; Jansen, H.; Kirk, E.; Luksch, U.; Lunkeit, F. The Planet Simulator: Towards a user friendly model. Meteorol. Z. 2005, 14, 299–304. [Google Scholar] [CrossRef]
- Newhouse, S.; Pignataro, T. On the estimation of topological entropy. J. Stat. Phys. 1993, 72, 1331–1351. [Google Scholar] [CrossRef]
- Thiffeault, J.L. Braids of entangled particle trajectories. Chaos 2010, 20, 017516. [Google Scholar] [CrossRef]
- Budišić, M.; Thiffeault, J.L. Finite-time braiding exponents. Chaos 2015, 25, 087407. [Google Scholar] [CrossRef]
- Haszpra, T.; Horányi, A. Some aspects of the impact of meteorological forecast uncertainties on environmental dispersion prediction. Idojaras 2014, 118, 335–347. [Google Scholar]
- Haszpra, T. Intricate features in the lifetime and deposition of atmospheric aerosol particles. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 071103. [Google Scholar] [CrossRef]
- Haszpra, T.; Tél, T. Volcanic ash in the free atmosphere: A dynamical systems approach. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2011; Volume 333, p. 012008. [Google Scholar]
- Haszpra, T.; Tél, T. Individual particle based description of atmospheric dispersion: A dynamical systems approach. In The Fluid Dynamics of Climate; Springer-Verlag Wien: Wien, Austria, 2016; pp. 95–119. [Google Scholar]
- Sutherland, W. LII. The viscosity of gases and molecular force. Philos. Mag. Ser. 1893, 36, 507–531. [Google Scholar] [CrossRef]
- Stohl, A.; Wotawa, G.; Seibert, P.; Kromp-Kolb, H. Interpolation errors in wind fields as a function of spatial and temporal resolution and their impact on different types of kinematic trajectories. J. Appl. Meteorol. 1995, 34, 2149–2165. [Google Scholar] [CrossRef]
- Flentje, H.; Claude, H.; Elste, T.; Gilge, S.; Köhler, U.; Plass-Dülmer, C.; Steinbrecht, W.; Thomas, W.; Werner, A.; Fricke, W. The Eyjafjallajökull eruption in April 2010–detection of volcanic plume using in-situ measurements, ozone sondes and lidar-ceilometer profiles. Atmos. Chem. Phys. 2010, 10, 10085–10092. [Google Scholar] [CrossRef]
- Belosi, F.; Santachiara, G.; Prodi, F. Eyjafjallajökull volcanic eruption: Ice nuclei and particle characterization. Atmos. Clim. Sci. 2011, 1, 48. [Google Scholar]
- Campanelli, M.; Estelles, V.; Smyth, T.; Tomasi, C.; Martìnez-Lozano, M.; Claxton, B.; Muller, P.; Pappalardo, G.; Pietruczuk, A.; Shanklin, J.; et al. Monitoring of Eyjafjallajökull volcanic aerosol by the new European Skynet Radiometers (ESR) network. Atmos. Environ. 2012, 48, 33–45. [Google Scholar] [CrossRef]
- Revuelta, M.; Sastre, M.; Fernández, A.; Martín, L.; García, R.; Gómez-Moreno, F.; Artíñano, B.; Pujadas, M.; Molero, F. Characterization of the Eyjafjallajökull volcanic plume over the Iberian Peninsula by lidar remote sensing and ground-level data collection. Atmos. Environ. 2012, 48, 46–55. [Google Scholar] [CrossRef]
- RePLaT-Chaos-edu. Available online: http://theorphys.elte.hu/fiztan/volcano/#edu (accessed on 21 December 2019).
- Haszpra, T.; Kiss, M.; Izsa, É. RePLaT-Chaos-edu: An interactive educational tool for secondary school students for the illustration of the spreading of volcanic ash clouds. J. Phys. Conf. Ser. 2019. submitted. [Google Scholar]
- ECMWF Public Datasets. Available online: http://apps.ecmwf.int/datasets/ (accessed on 21 December 2019).
- Holton, J.R. An Introduction to Dynamic Meteorology, 4th ed.; Academic Press: Cambridge, MA, USA, 2004; p. 535. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haszpra, T. RePLaT-Chaos: A Simple Educational Application to Discover the Chaotic Nature of Atmospheric Advection. Atmosphere 2020, 11, 29. https://doi.org/10.3390/atmos11010029
Haszpra T. RePLaT-Chaos: A Simple Educational Application to Discover the Chaotic Nature of Atmospheric Advection. Atmosphere. 2020; 11(1):29. https://doi.org/10.3390/atmos11010029
Chicago/Turabian StyleHaszpra, Tímea. 2020. "RePLaT-Chaos: A Simple Educational Application to Discover the Chaotic Nature of Atmospheric Advection" Atmosphere 11, no. 1: 29. https://doi.org/10.3390/atmos11010029
APA StyleHaszpra, T. (2020). RePLaT-Chaos: A Simple Educational Application to Discover the Chaotic Nature of Atmospheric Advection. Atmosphere, 11(1), 29. https://doi.org/10.3390/atmos11010029





