Grapevine Phenology of cv. Touriga Franca and Touriga Nacional in the Douro Wine Region: Modelling and Climate Change Projections
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Datasets
2.2. Phenological Models
2.3. Modelling Tools and Performance Verification
2.4. Future Climate Projections
3. Results
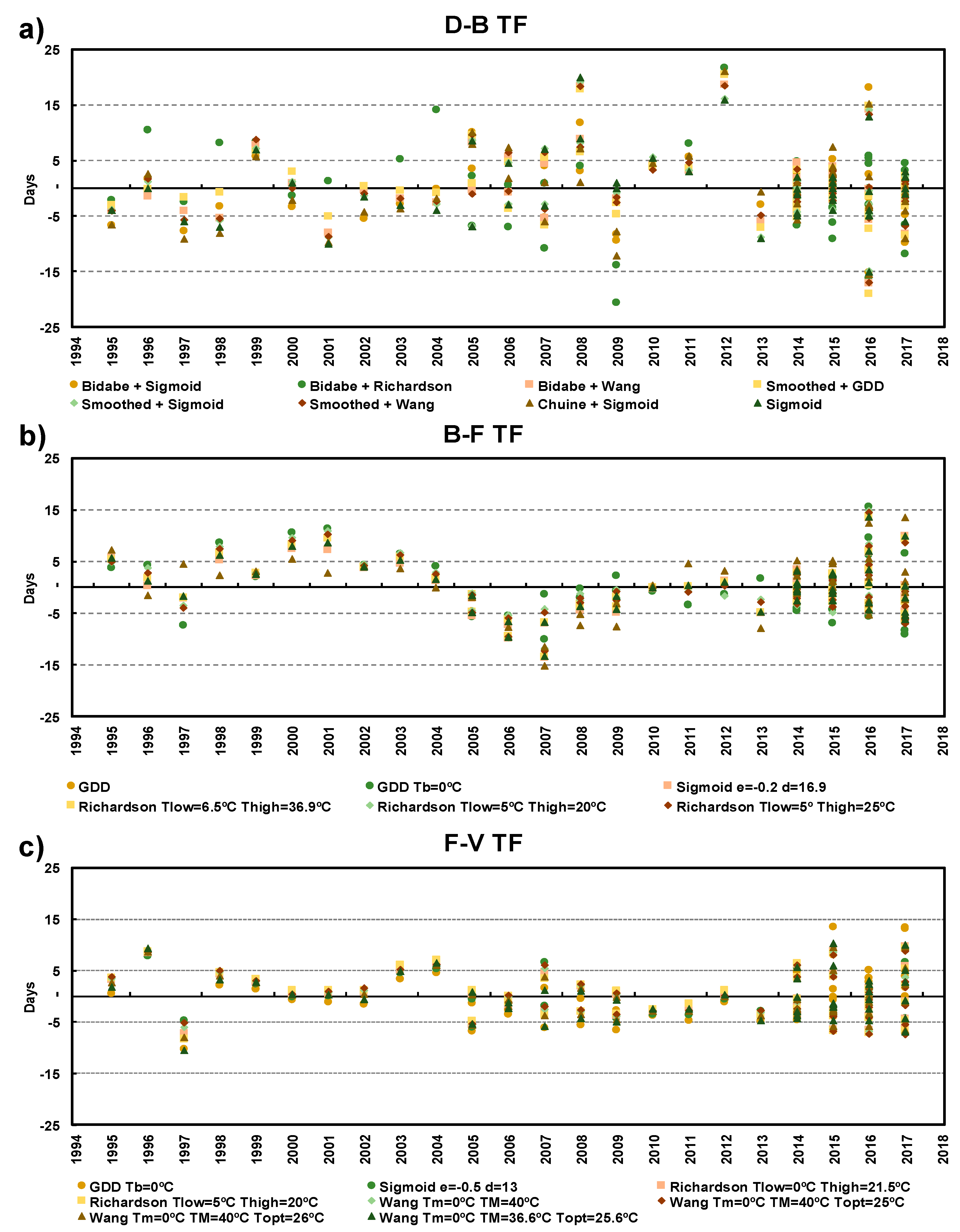
3.1. Model Performance Verification
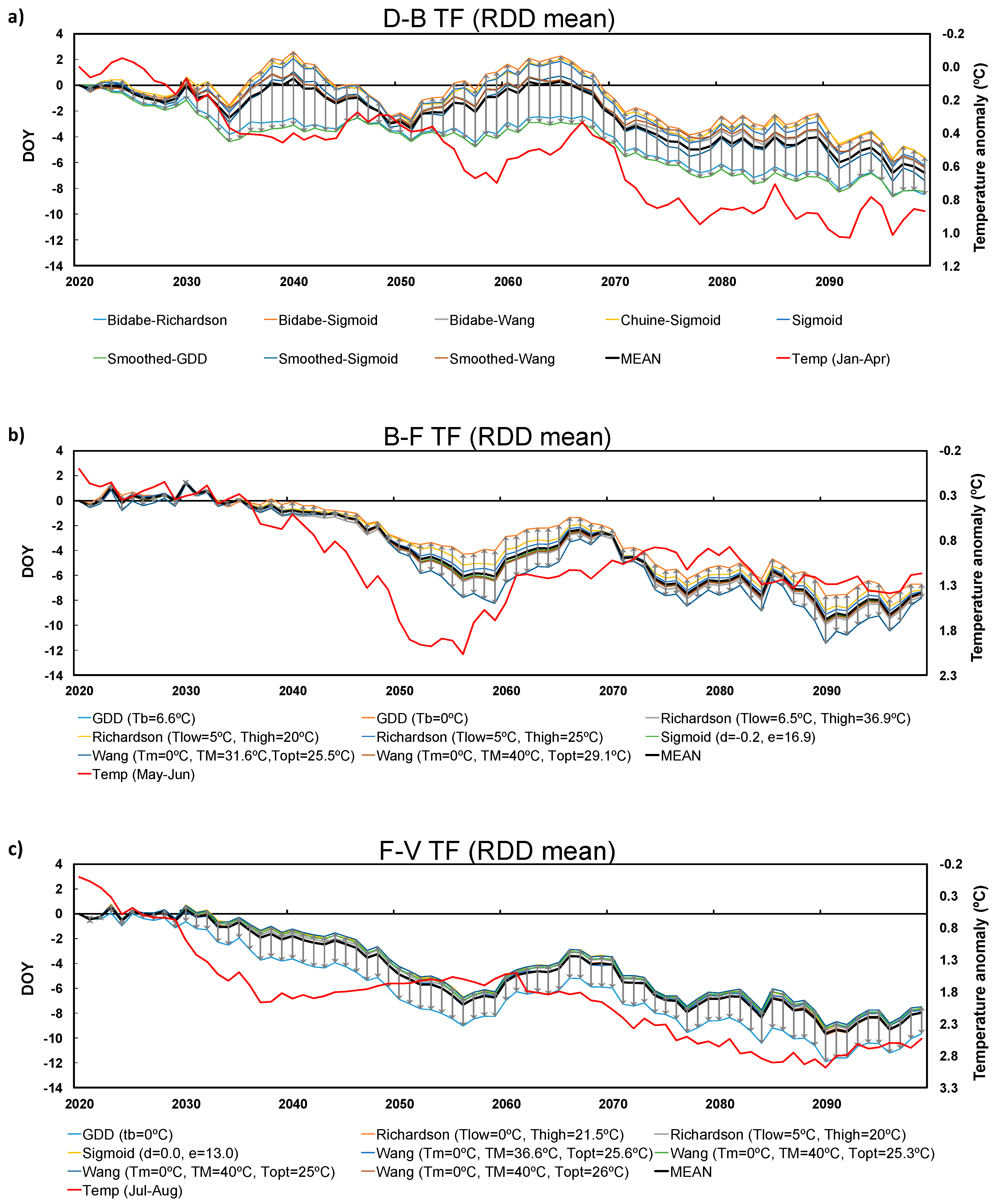
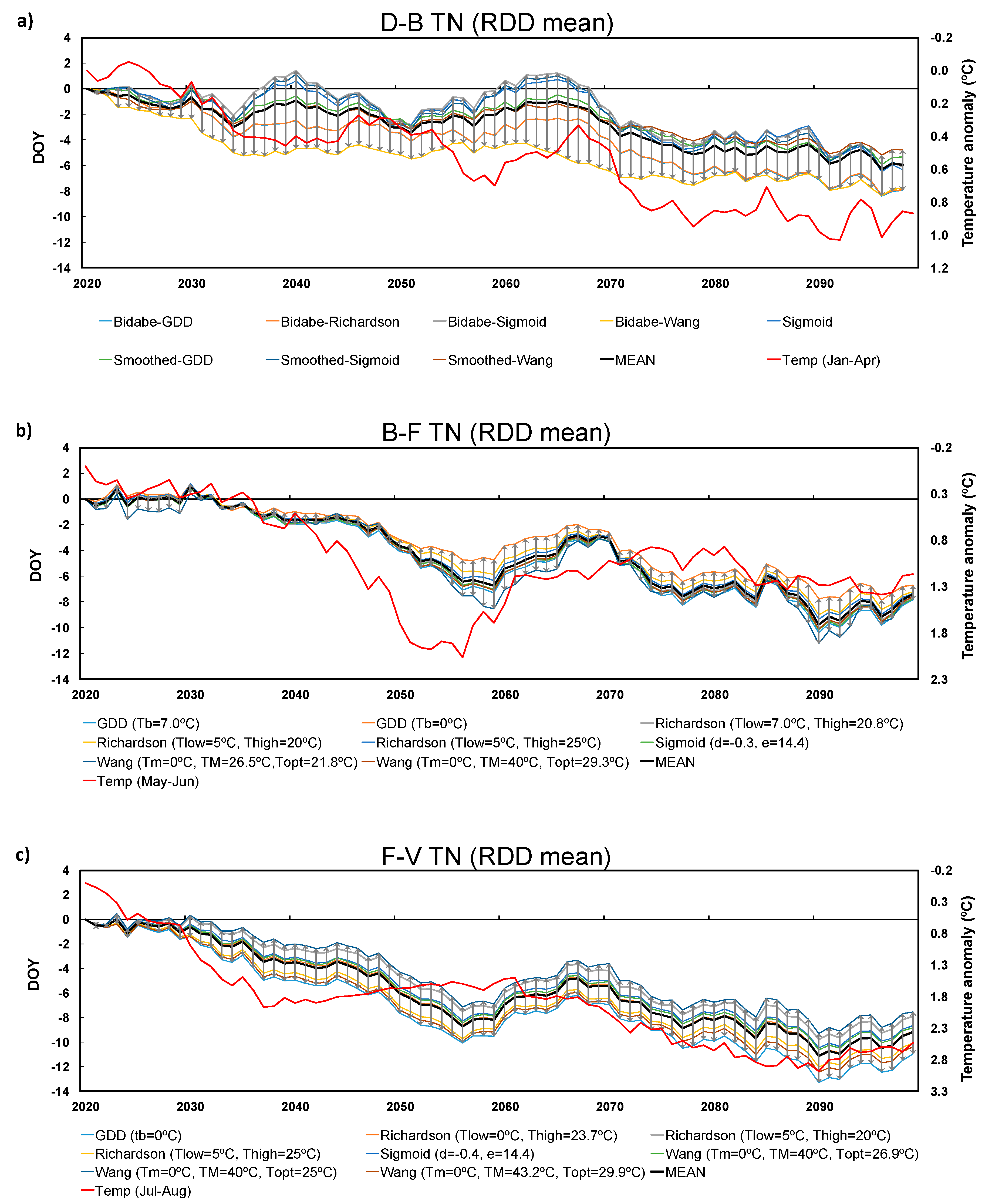
3.2. Future Projections
3.3. Inter-Model Spread
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- OIV. State of the Vitiviniculture World Market; OIV: Paris, France, 2018; p. 14. [Google Scholar]
- IVV. Vinhos e Aguardentes de Portugal, Anuário 2017; Ministério da Agricultura, do Desenvolvimento Rural e das Pescas, Instituto da Vinha e do Vinho: Lisboa, Portugal, 2017; p. 224.
- Fraga, H.; Santos, J.A. Vineyard mulching as a climate change adaptation measure: Future simulations for Alentejo, Portugal. Agric. Syst. 2018, 164, 107–115. [Google Scholar] [CrossRef]
- Fraga, H.; Costa, R.; Santos, J.A. Multivariate clustering of viticultural terroirs in the douro winemaking region. Cienc. Tec. Vitivinic. 2017, 32, 142–153. [Google Scholar] [CrossRef]
- Fraga, H.; Santos, J.A. Daily prediction of seasonal grapevine production in the Douro wine region based on favourable meteorological conditions. Austr. J. Grape Wine Res. 2017, 23, 296–304. [Google Scholar] [CrossRef]
- Keller, M. Phenology and growth cycle. In The Science of Grapevines, 2nd ed.; Keller, M., Ed.; Academic Press: San Diego, CA, USA, 2015; Chapter 2; pp. 59–99. [Google Scholar] [CrossRef]
- Moriondo, M.; Ferrise, R.; Trombi, G.; Brilli, L.; Dibari, C.; Bindi, M. Modelling olive trees and grapevines in a changing climate. Environ. Model. Softw. 2015, 72, 387–401. [Google Scholar] [CrossRef]
- Andreoli, V.; Cassardo, C.; La Iacona, T.; Spanna, F. Description and preliminary simulations with the Italian vineyard integrated numerical model for estimating physiological values (IVINE). Agronomy 2019, 9, 94. [Google Scholar] [CrossRef]
- Winkler, A.J. General Viticulture; University of California Press: Berkly, CA, USA, 1974. [Google Scholar]
- Huglin, P. Nouveau Mode D’évaluation des Possibilités Héliothermiques d’un Milieu Viticole. COMPTES RENDUS de L’académie D’AGRICULTURE; Académie d’agriculture de France: Paris, France, 1978. [Google Scholar]
- Jones, G.V.; Davis, R.E. Climate influences on grapevine phenology, grape composition, and wine production and quality for Bordeaux, France. Am. J. Enol. Viticult. 2000, 51, 249–261. [Google Scholar]
- Jones, G.V.; Duchêne, E.; Tomasi, D.; Yuste, J.; Braslavska, O.; Schultz, H.R.; Martinez, C.; Boso, S.; Langellier, F.; Perruchot, C.; et al. Changes in European winegrape phenology and relationships with climate. In Proceedings of the XIV GESCO Symposium, Geisenheim, Germany, 23–26 August 2005. [Google Scholar]
- Van Leeuwen, C.; Garnier, C.; Agut, C.; Baculat, B.; Barbeau, G.; Besnard, E.; Bois, B.; Boursiquot, J.-M.; Chuine, I.; Dessup, T.; et al. Heat requirements for grapevine varieties is essential information to adapt plant material in a changing climate. In Proceedings of the 7th International Terroir Congress(Agroscope Changins-Wädenswil: Switzerland), Changins, Switzerland, 19–23 May 2008; pp. 222–227. [Google Scholar]
- Chuine, I.; García de Cortázar-Atauri, I.; Kramer, K.; Hänninen, H. Plant development models. In Phenology: An Integrative Environmental Science; Springer: Berlin, Germany, 2013; pp. 275–293. [Google Scholar]
- Orlandi, F.; Bonofiglio, T.; Aguilera, F.; Fornaciari, M. Phenological characteristics of different winegrape cultivars in Central Italy. Vitis 2015, 54, 129–136. [Google Scholar]
- Quenol, H.; García de Cortázar-Atauri, I.; Bois, B.; Sturman, A.; Bonnardot, V.; Le Roux, R. Which climatic modeling to assess climate change impacts on vineyards? Oeno One 2017, 51, 91–97. [Google Scholar] [CrossRef]
- Pouget, R. Le débourrement des bourgeons de la vigne: Méthode de prévision et principes d’établissement d’une échelle de précocité de débourrement. Connaiss. Vigne Vin 1988, 22, 105–123. [Google Scholar] [CrossRef]
- Riou, C.; Carbonneau, A.; Becker, N.; Caló, A.; Costacurta, A.; Castro, R.; Pinto, P.A.; Carneiro, L.C.; Lopes, C.; Clímaco, P.; et al. Le Determinisme Climatique de la Maturation du Raisin: Application au Zonage de la Teneur en Sucre Dans la Communauté Européenne; Office des Publications Officielles des Communautés Européennes: Luxembourg, 1994; p. 319. [Google Scholar]
- García de Cortázar-Atauri, I.; Brisson, N.; Gaudillere, J. Performance of several models for predicting budburst date of grapevine (Vitis vinifera L.). Int. J. Biometeorol. 2009, 53, 317–326. [Google Scholar] [CrossRef]
- Nendel, C. Grapevine bud break prediction for cool winter climates. Int. J. Biometeorol. 2010, 54, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Caffarra, A.; Eccel, E. Projecting the impacts of climate change on the phenology of grapevine in a mountain area. Austr. J. Grape Wine Res. 2011, 17, 5–61. [Google Scholar] [CrossRef]
- Fila, G.; Gardiman, M.; Belvini, P.; Meggio, F.; Pitacco, A. A comparison of different modelling solutions for studying grapevine phenology under present and future climate scenarios. Agr. Forest Meteorol. 2014, 195, 192–205. [Google Scholar] [CrossRef]
- Amerine, M.; Winkler, A. Composition and quality of musts and wines of California grapes. Hilgardia 1944, 15, 493–675. [Google Scholar] [CrossRef]
- Duchene, E.; Huard, F.; Dumas, V.; Schneider, C.; Merdinoglu, D. The challenge of adapting grapevine varieties to climate change. Clim. Res. 2010, 41, 193–204. [Google Scholar] [CrossRef]
- García de Cortázar-Atauri, I.; Chuine, I.; Donatelli, M.; Parker, A.; Van Leeuwen, C. A curvilinear process-based phenological model to study impacts of climatic change on grapevine (Vitis vinifera L.). Proc. Agro 2010, 11, 907–908. [Google Scholar]
- Parker, A.K.; García de Cortázar-Atauri, I.; van Leeuwen, C.; Chuine, I. General phenological model to characterise the timing of flowering and veraison of Vitis vinifera L. Austr. J. Grape Wine Res. 2011, 17, 206–216. [Google Scholar] [CrossRef]
- Parker, A.; García de Cortázar-Atauri, I.; Chuine, I.; Barbeau, G.; Bois, B.; Boursiquot, J.-M.; Cahurel, J.-Y.; Claverie, M.; Dufourcq, T.; Gény, L.; et al. Classification of varieties for their timing of flowering and veraison using a modelling approach: A case study for the grapevine species Vitis vinifera L. Agric. For. Meteorol. 2013, 180, 249–264. [Google Scholar] [CrossRef]
- Molitor, D.; Junk, J.; Evers, D.; Hoffmann, L.; Beyer, M. A High-resolution cumulative degree day-based model to simulate phenological development of grapevine. Am. J. Enol. Viticult. 2014, 65, 72–80. [Google Scholar] [CrossRef]
- García de Cortázar-Atauri, I. Adaptation du modèle STICS à la vigne (Vitis vinifera L.): Utilisation dans le cadre d’une étude d’impact du changement climatique à l’échelle de la France. Ph.D. Thesis, École nationale supérieure agronomique, Montpellier, France, 2006. [Google Scholar]
- Pieri, P. Climate change and grapevines: Main impacts. In Climate Change, Agriculture and Forests in France: Simulations of the Impacts on the Main Species. The Green Book of the CLIMATOR Project (2007–2010); ADEME: Angers, France, 2010; pp. 213–223. [Google Scholar]
- Cuccia, C.; Bois, B.; Richard, Y.; Parker, A.K.; García de Cortázar-Atauri, I.; Van Leeuwen, C.; Castel, T. Phenological Model Performance to Warmer Conditions: Application to Pinot Noir in Burgundy. J. Int. Sci. Vigne Vin 2014, 48, 169–178. [Google Scholar] [CrossRef]
- Molitor, D.; Caffarra, A.; Sinigoj, P.; Pertot, I.; Hoffmann, L.; Junk, J. Late frost damage risk for viticulture under future climate conditions: A case study for the Luxembourgish winegrowing region. Austr. J. Grape Wine Res. 2014, 20, 160–168. [Google Scholar] [CrossRef]
- Moriondo, M.; Bindi, M. Impact of climate change on the phenology of typical mediterranean crops. Italian J. Agrometeorol. 2007, 3, 5–12. [Google Scholar]
- Webb, L.B.; Whetton, P.H.; Barlow, E.W.R. Modelled impact of future climate change on the phenology of winegrapes in Australia. Austr. J. Grape Wine Res. 2007, 13, 165–175. [Google Scholar] [CrossRef]
- Petrie, P.R.; Sadras, V.O. Advancement of grapevine maturity in Australia between 1993 and 2006: Putative causes, magnitude of trends and viticultural consequences. Austr. J. Grape Wine Res. 2008, 14, 33–45. [Google Scholar] [CrossRef]
- Fraga, H.; García de Cortázar-Atauri, I.; Malheiro, A.C.; Santos, J.A. Modelling climate change impacts on viticultural yield, phenology and stress conditions in Europe. Glob. Chang. Biol. 2016, 22, 3774–3788. [Google Scholar] [CrossRef]
- Vivin, P.; Lebon, E.; Dai, Z.; Duchêne, E.; Marguerit, E.; García de Cortázar-Atauri, I.; Zhu, J.; Simonneau, T.; Van Leeuwen, C.; Delrot, S. Combining ecophysiological models and genetic analysis: A promising way to dissect complex adaptive traits in grapevine. Oeno One 2017, 51, 181. [Google Scholar] [CrossRef]
- Van Leeuwen, C.; Seguin, G. The concept of terroir in viticulture. J. Wine Res. 2006, 17, 1–10. [Google Scholar] [CrossRef]
- Wolkovich, E.M.; García de Cortázar-Atauri, I.; Morales-Castilla, I.; Nicholas, K.A.; Lacombe, T. From Pinot to Xinomavro in the world’s future wine-growing regions. Nat. Clim. Chang. 2018, 8, 29–37. [Google Scholar] [CrossRef]
- Magalhães, N. Tratado de Viticultura: A Videira, a Vinha e o Terroir; Chaves Ferreira: Lisboa, Portugal, 2008; p. 605. [Google Scholar]
- Lorenz, D.H.; Eichhorn, K.W.; Bleiholder, H.; Klose, R.; Meier, U.; Weber, E. Growth Stages of the Grapevine: Phenological growth stages of the grapevine (Vitis vinifera L. ssp. vinifera)—Codes and descriptions according to the extended BBCH scale. Austr. J. Grape Wine Res. 1995, 1, 100–103. [Google Scholar] [CrossRef]
- Fonseca, A.; Santos, J. High-resolution temperature datasets in Portugal from a geostatistical approach: Variability and extremes. J. Appl. Meteorol. Climatol. 2018, 57, 627–644. [Google Scholar] [CrossRef]
- Caffarra, A.; Eccel, E. Increasing the robustness of phenological models for Vitis vinifera cv. Chardonnay. Int. J. Biometeorol. 2010, 54, 255–267. [Google Scholar] [CrossRef]
- Bidabe, B. Action of temperature on evolution of buds in apple and comparison of methods used for estimating flowering time. Ann. Physiol. Veg. 1967, 9, 65. [Google Scholar]
- Chuine, I. A unified model for budburst of trees. J. Theor. Biol. 2000, 207, 337–347. [Google Scholar] [CrossRef]
- Bonhomme, M.; Rageau, R.; Lacointe, A. Optimization of endodormancy release models, using series of endodormancy release data collected in france. Acta Hortic. 2010, 872, 51–60. [Google Scholar] [CrossRef]
- De Réaumur, M. Observations du thermometre, faites à Paris pendant l’annee 1735 compareés avec celles qui ont été faites sous la ligne à l’ Ile de France, à Alger et en quelques-unes de nos îles de l’Amérique. Memoires de l’Academie Royale des Sciences 1753, 545–576. [Google Scholar]
- Richardson, E. A model for estimating the completion of rest for’Redhaven’and’Elberta’peach trees. HortScience 1974, 9, 331–332. [Google Scholar]
- Hänninen, H. Modelling bud dormancy release in trees from cool and temperate regions. Acta Forestalia Fennica 1990, 213, 1–47. [Google Scholar] [CrossRef]
- Wang, E.L.; Engel, T. Simulation of phenological development of wheat crops. Agric. Syst. 1998, 58, 1–24. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Chuine, I.; Bonhomme, M.; Legave, J.M.; García de Cortzar-Atauri, I.; Charrier, G.; Lacointe, A.; Améglio, T. Can phenological models predict tree phenology accurately in the future? The unrevealed hurdle of endodormancy break. Glob. Chang. Biol. 2016, 22, 3444–3460. [Google Scholar] [CrossRef]
- Wallach, D.; Makowski, D.; Jones, J.W. Working with Dynamic Crop Models: Evaluation, Analysis, Parameterization, and Applications; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Yang, W.; Andreasson, J.; Graham, L.P.; Olsson, J.; Rosberg, J.; Wetterhall, F. Distribution-based scaling to improve usability of regional climate model projections for hydrological climate change impacts studies. Hydrol. Res. 2010, 41, 211–229. [Google Scholar] [CrossRef]
- Ramos, M.C. Projection of phenology response to climate change in rainfed vineyards in north-east Spain. Agr. Forest Meteorol. 2017, 247, 104–115. [Google Scholar] [CrossRef]
- Fraga, H.; Costa, R.; Moutinho-Pereira, J.; Correia, C.M.; Dinis, L.-T.; Gonçalves, I.; Silvestre, J.; Eiras-Dias, J.; Malheiro, A.C.; Santos, J.A. Modeling phenology, water status, and yield components of three portuguese grapevines using the STICS crop model. Am. J. Enol. Viticult. 2015, 66, 482–491. [Google Scholar] [CrossRef]
- Fraga, H.; Amraoui, M.; Malheiro, A.C.; Moutinho-Pereira, J.; Eiras-Dias, J.; Silvestre, J.; Santos, J.A. Examining the relationship between the enhanced vegetation index and grapevine phenology. Eur. J. Remote Sens. 2014, 47, 753–771. [Google Scholar] [CrossRef]
- Cola, G.; Mariani, L.; Salinari, F.; Civardi, S.; Bernizzoni, F.; Gatti, M.; Poni, S. Description and testing of a weather-based model for predicting phenology, canopy development and source–sink balance in Vitis vinifera L. cv. Barbera. Agric. Forest Meteorol. 2014, 184, 117–136. [Google Scholar] [CrossRef]
- Tomasi, D.; Jones, G.V.; Giust, M.; Lovat, L.; Gaiotti, F. Grapevine phenology and climate change: Relationships and trends in the Veneto Region of Italy for 1964–2009. Am. J. Enol. Viticult. 2011, 62, 329–339. [Google Scholar] [CrossRef]
- Fraga, H.; Santos, J.A.; Moutinho-Pereira, J.; Carlos, C.; Silvestre, J.; Eiras-Dias, J.; Mota, T.; Malheiro, A.C. Statistical modelling of grapevine phenology in Portuguese wine regions: Observed trends and climate change projections. J. Agr. Sci. Camb. 2016, 154, 795–811. [Google Scholar] [CrossRef]
- Bindi, M.; Miglietta, F.; Gozzini, B.; Orlandini, S.; Seghi, L. A simple model for simulation of growth and development in grapevine (Vitis vinifera L.). 2. Model validation. Vitis 1997, 36, 73–76. [Google Scholar]
- Ramos, M.C.; Jones, G.V.; Yuste, J. Phenology of Tempranillo and Cabernet-Sauvignon varieties cultivated in the Ribera del Duero DO: Observed variability and predictions under climate change scenarios. Oeno One 2018, 52, 31–44. [Google Scholar] [CrossRef]
- Oliveira, M. Calculation of budbreak and flowering base temperatures for vitis vinifera cv. touriga francesa in the Douro Region of Portugal. Am. J. Enol. Viticult. 1998, 49, 74–78. [Google Scholar]
- Moncur, M.W.; Rattigan, K.; Mackenzie, D.H.; McIntyre, G.N. Base temperatures for budbreak and leaf appearance of grapevines. Am. J. Enol. Viticult. 1989, 40, 21–26. [Google Scholar]
- Jones, G.V. Climate change in the western united states grape growing regions. Proceedings of the Seventh International Symposium on Grapevine Physiology and Biotechnology. Acta Horticult. 2005, 689, 41–59. [Google Scholar] [CrossRef]
- Bock, A.; Sparks, T.; Estrella, N.; Menzel, A. Changes in the phenology and composition of wine from Franconia, Germany. Clim. Res. 2011, 50, 69–81. [Google Scholar] [CrossRef]
- Jones, G.V.; White, M.A.; Cooper, O.; Storchmann, K. Climate change and global wine quality. Clim. Chang. 2005, 73, 319–343. [Google Scholar] [CrossRef]
- Malheiro, A.C.; Campos, R.; Fraga, H.; Eiras-Dias, J.; Silvestre, J.; Santos, J.A. Winegrape phenology and temperature relationships in the Lisbon Wine Region, Portugal. J. Int. Sci. Vigne Vin. 2013, 47, 287–299. [Google Scholar] [CrossRef]
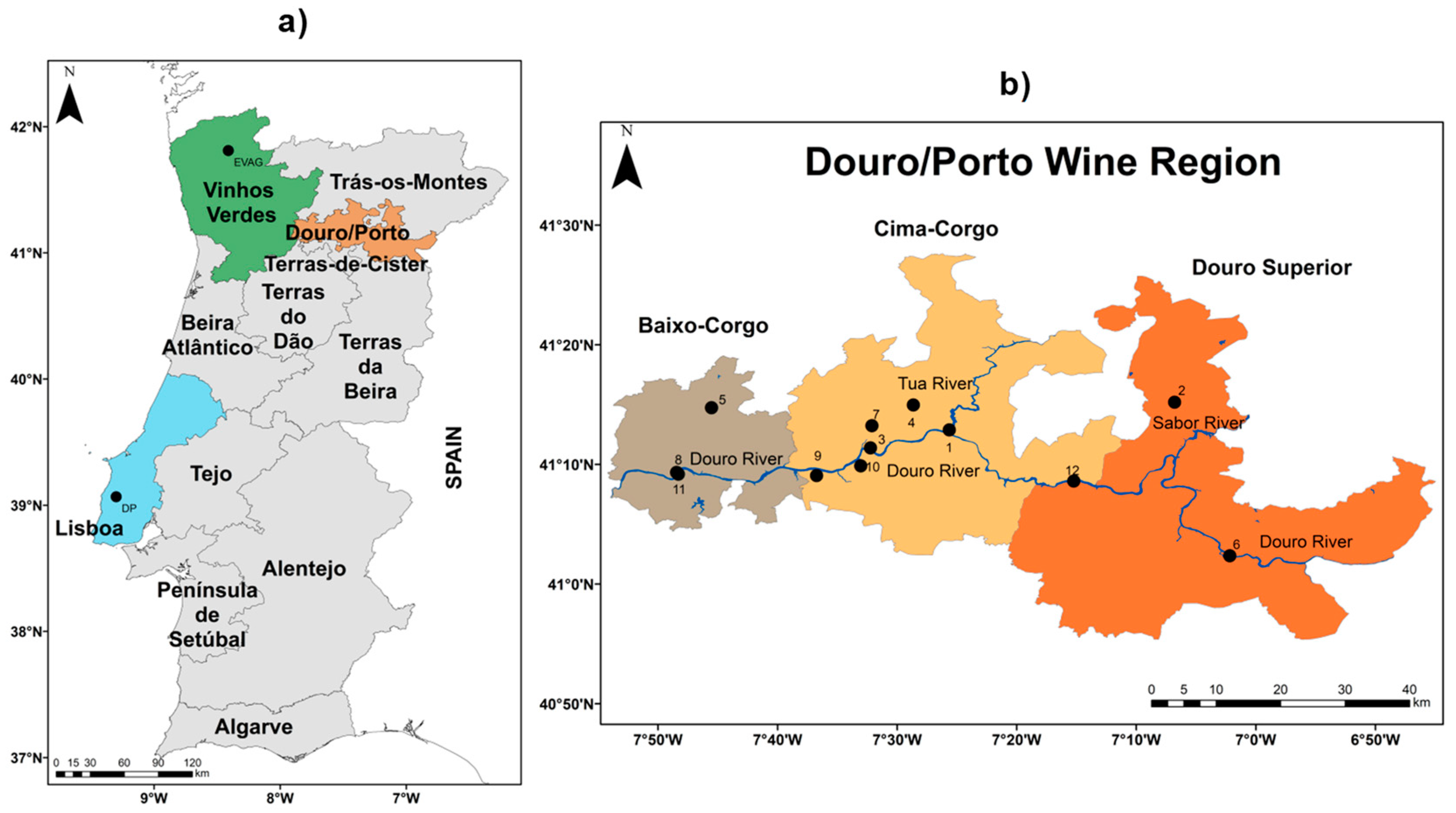
| Wine Region | Latitude (°N) | Longitude (°W) | Altitude (meters) | Variety (cv.) | Available Time Period | ||
|---|---|---|---|---|---|---|---|
| Budburst 1 | Flowering 2 | Veraison 3 | |||||
| Douro/Porto | 41°14′24″ N–41°02′24″ N | 7°01′48″ W–°47′24″ W | 85–588 | Touriga Franca | 2014–2017 | 2014–2017 | 2014–2017 |
| Douro/Porto | 41°14′24″ N–41°02′24″ N | 7°01′48″ W–7°47′24″ W | 85–588 | Touriga Nacional | 2014–2017 | 2014–2017 | 2014–2017 |
| Lisboa | 39°02′24″ N | 9°10′48″ W | 85 | Touriga Franca | 1995–2014 | 1995–2014 | 1995–2014 |
| Lisboa | 39°02′24″ N | 9°10′48″ W | 85 | Touriga Nacional | 1990–2000; 2006–2014 | 1990–2000; 2006–2014 | 1990–2000; 2006–2014 |
| Vinhos Verdes | 41°48′36″ N | 8°24′36″ W | 70 | Touriga Franca | 2005–2009 | 2005–2009 | 2005–2009 |
| Vinhos Verdes | 41°48′36″ N | 8°24′36″ W | 70 | Touriga Nacional | 2005–2009 | 2005–2009 | 2005–2009 |
| Type of Model | Model Name | Reference | Starting Date |
|---|---|---|---|
| Chilling model–Dormancy | Bidabe | [44] | August 1st of previous year |
| Chuine | [45] | ||
| Smoothed Utah (SU) | [46] | ||
| Forcing model, Post-Dormancy, Flowering, Veraison | Growing degree-days (GDD) | [47] | January 1st, previous phenological stage |
| Richardson | [48] | ||
| Sigmoid | [49] | ||
| Wang | [50] |
| Model | Equation | Parameters * |
|---|---|---|
| Bidabe | ||
| Chuine | ||
| GDD | ||
| Richardson | , | |
| Sigmoid | ||
| Smoothed Utah | ; ; ; | ,,, min |
| Wang | ; |
| GCM | RCM | Abbreviation |
|---|---|---|
| CNRM-CERFACS-CNRM-CM5 | SMHI-RCA4 | CNRMSMHI |
| MPI-M-MPI-ESM-LR | CLMcom-CCLM4-8-17 | MPICLM |
| Phenophase | Model | Description | Model Performance | |||
|---|---|---|---|---|---|---|
| Dormancy-Budburst | With dormancy | RMSEP | EF | R2 | AIC | |
| Bidabe + Wang | Q10 = 0.9, Tm = 5.5, TM = 34.3, Topt = 14.7 | 6.4 | 0.36 | 0.62 | 185.1 | |
| Bidabe + Sigmoid | Q10 = 1.0, d = −22.4, e = 7.4 | 6.5 | 0.35 | 0.58 | 186.5 | |
| SU + Sigmoid | Tm1 = −13.4, Topt = 29.2, Tn2 = 44.6, min = −0.5, d = −39.9, e = 7.5 | 6.2 | 0.41 | 0.64 | 187.4 | |
| SU + GDD | Tm1 = −2.8, Topt = 29.2, Tn2 = 36.6, min = −0.3, Tb = 0 | 6.5 | 0.35 | 0.59 | 190.1 | |
| SU + Wang | Tm1 = −32.2, Topt = 29.3, Tn2 = 35.7, min = −0.3, Tm = 5.3, TM = 34.8, Topt = 15.1 | 6.4 | 0.37 | 0.63 | 190.4 | |
| Chuine + Sigmoid | a = 0.3, b = −21.1, c = −2.5, d = −40, e = 7.5 | 6.4 | 0.38 | 0.57 | 192.3 | |
| Bidabe + Richardson | Q10 = 0.9, Tlow = 0.2, Thigh = 43.2 | 6.5 | 0.35 | 0.54 | 201.4 | |
| Without dormancy | ||||||
| Sigmoid | d = −40, e = 7.5 | 6.4 | 0.38 | 0.61 | 181.6 | |
| Budburst-Flowering | GDD | Tb = 6.6 | 5.1 | 0.69 | 0.85 | 159.1 |
| Sigmoid | d = −0.2, e = 16.9 | 5.1 | 0.70 | 0.86 | 159.4 | |
| Richardson | Tlow = 6.5, Thigh = 36.9 | 5.1 | 0.69 | 0.85 | 161.1 | |
| Wang | Tm = 0, TM = 40, Topt = 29.1 | 5.1 | 0.69 | 0.86 | 161.9 | |
| Richardson | Tlow = 5, Thigh = 25 | 5.2 | 0.68 | 0.84 | 162.6 | |
| Richardson | Tlow = 5, Thigh = 20 | 5.3 | 0.67 | 0.83 | 164.1 | |
| GDD | Tb = 0 | 5.9 | 0.60 | 0.78 | 171.1 | |
| Wang | Tm = 0, TM = 31.6, Topt = 25.5 | 5.6 | 0.62 | 0.87 | 172.3 | |
| Flowering-Veraison | Sigmoid | d = 0.0, e = 13.0 | 4.3 | 0.83 | 0.92 | 141.1 |
| Richardson | Tlow = 0.0, Thigh = 21.5 | 4.2 | 0.83 | 0.91 | 142.1 | |
| Wang | Tm = 0, TM = 40, Topt = 25.3 | 4.2 | 0.84 | 0.92 | 142.6 | |
| Wang | Tm = 0, TM = 40, Topt = 25 | 4.2 | 0.84 | 0.92 | 143.1 | |
| Wang | Tm = 0, TM = 40, Topt = 26 | 4.2 | 0.83 | 0.91 | 144.2 | |
| Richardson | Tlow = 5, Thigh = 20 | 4.3 | 0.82 | 0.91 | 144.9 | |
| Wang | Tm = 0, TM = 36.6, Topt = 25.6 | 4.4 | 0.82 | 0.91 | 148.9 | |
| GDD | Tb = 0 | 5.1 | 0.76 | 0.90 | 157.6 | |
| Phenophase | Model | Description | Model Performance | |||
|---|---|---|---|---|---|---|
| Dormancy-Budburst | With dormancy | RMSEP | EF | R2 | AIC | |
| Bidabe + GDD | Q10 = 0.9, Tb = 0 | 7.8 | 0.18 | 0.43 | 190.5 | |
| Bidabe + Wang | Q10 = 0.7, Tm = −36.7, TM = 34, Topt = 18 | 7.7 | 0.20 | 0.44 | 193.7 | |
| Bidabe + Richardson | Q10 = 0.9, Tlow = 0, Thigh = 37.3 | 7.8 | 0.18 | 0.42 | 193.9 | |
| SU + Sigmoid | Tm1 = −34.1, Topt = 29.9, Tn2 = 43, min = −0.2, d = −39.7, e = 7.5 | 7.6 | 0.23 | 0.48 | 196.0 | |
| SU + GDD | Tm1 = −31.1, Topt = 29.5, Tn2 = 32.1, min = −0.1, Tb = 0 | 8.0 | 0.15 | 0.41 | 197.8 | |
| Bidabe + Sigmoid | Q10 = 1, d = −38.3, e = 7.5 | 7.8 | 0.19 | 0.41 | 197.9 | |
| SU + Wang | Tm1 = −31.1, Topt = 30, Tn2 = 32.2, min = −0.4, Tm = −16.1, TM = 25.1, Topt = 16.4 | 7.9 | 0.17 | 0.42 | 201.0 | |
| Without dormancy | ||||||
| Sigmoid | d = −40, e = 7.5 | 7.2 | 0.20 | 0.42 | 190.9 | |
| Budburst-Flowering | GDD | Tb = 7.0 | 5.4 | 0.68 | 0.83 | 169.6 |
| Sigmoid | d = −0.3, e = 14.4 | 5.4 | 0.69 | 0.84 | 170.5 | |
| Richardson | Tlow = 7.0, Thigh = 20.8 | 5.4 | 0.69 | 0.83 | 171.1 | |
| Wang | Tm = 0, TM = 40, Topt = 29.3 | 5.3 | 0.69 | 0.83 | 172.5 | |
| Richardson | Tlow = 5, Thigh = 25 | 5.7 | 0.67 | 0.82 | 173.6 | |
| Richardson | Tlow = 5, Thigh = 20 | 5.8 | 0.67 | 0.82 | 173.7 | |
| Wang | Tm = 0, TM = 26.5, Topt = 21.8 | 5.3 | 0.66 | 0.84 | 177.3 | |
| GDD | Tb = 0 | 6.8 | 0.61 | 0.78 | 180.1 | |
| Flowering-Veraison | Sigmoid | d = −0.4, e = 14.4 | 6.0 | 0.85 | 0.93 | 151.3 |
| Richardson | Tlow = 0, Thigh = 23.7 | 5.6 | 0.86 | 0.93 | 151.6 | |
| GDD | Tb = 0 | 5.6 | 0.85 | 0.92 | 154.8 | |
| Wang | Tm = 0, TM = 40, Topt = 26.9 | 5.7 | 0.86 | 0.93 | 155.7 | |
| Wang | Tm = 0, TM = 40, Topt = 25 | 6.2 | 0.85 | 0.91 | 161.0 | |
| Richardson | Tlow = 5, Thigh = 20 | 6.1 | 0.83 | 0.92 | 161.7 | |
| Richardson | Tlow = 5, Thigh = 25 | 5.9 | 0.83 | 0.91 | 161.8 | |
| Wang | Tm = 0, TM = 43.2, Topt = 29.9 | 5.9 | 0.83 | 0.91 | 164.9 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, R.; Fraga, H.; Fonseca, A.; García de Cortázar-Atauri, I.; Val, M.C.; Carlos, C.; Reis, S.; Santos, J.A. Grapevine Phenology of cv. Touriga Franca and Touriga Nacional in the Douro Wine Region: Modelling and Climate Change Projections. Agronomy 2019, 9, 210. https://doi.org/10.3390/agronomy9040210
Costa R, Fraga H, Fonseca A, García de Cortázar-Atauri I, Val MC, Carlos C, Reis S, Santos JA. Grapevine Phenology of cv. Touriga Franca and Touriga Nacional in the Douro Wine Region: Modelling and Climate Change Projections. Agronomy. 2019; 9(4):210. https://doi.org/10.3390/agronomy9040210
Chicago/Turabian StyleCosta, Ricardo, Helder Fraga, André Fonseca, Iñaki García de Cortázar-Atauri, Maria C. Val, Cristina Carlos, Samuel Reis, and João A. Santos. 2019. "Grapevine Phenology of cv. Touriga Franca and Touriga Nacional in the Douro Wine Region: Modelling and Climate Change Projections" Agronomy 9, no. 4: 210. https://doi.org/10.3390/agronomy9040210
APA StyleCosta, R., Fraga, H., Fonseca, A., García de Cortázar-Atauri, I., Val, M. C., Carlos, C., Reis, S., & Santos, J. A. (2019). Grapevine Phenology of cv. Touriga Franca and Touriga Nacional in the Douro Wine Region: Modelling and Climate Change Projections. Agronomy, 9(4), 210. https://doi.org/10.3390/agronomy9040210







