Partition Function Zeros and Heat Capacity Decomposition Reveal HP Protein Foldability
Abstract
1. Introduction
2. Method
2.1. Heat Capacity Decomposition
2.2. Kinetic Monte Carlo Simulation
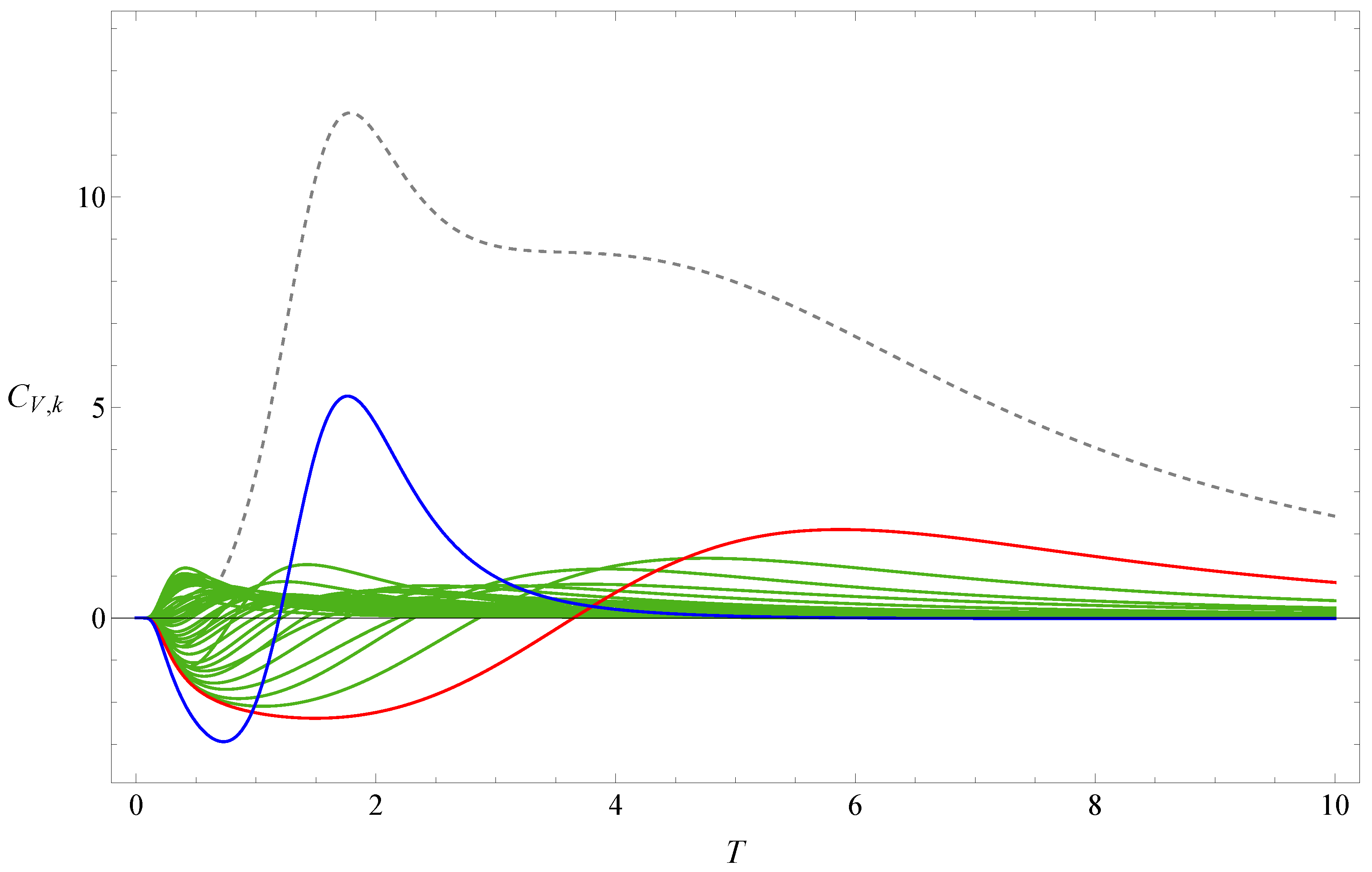
3. Result
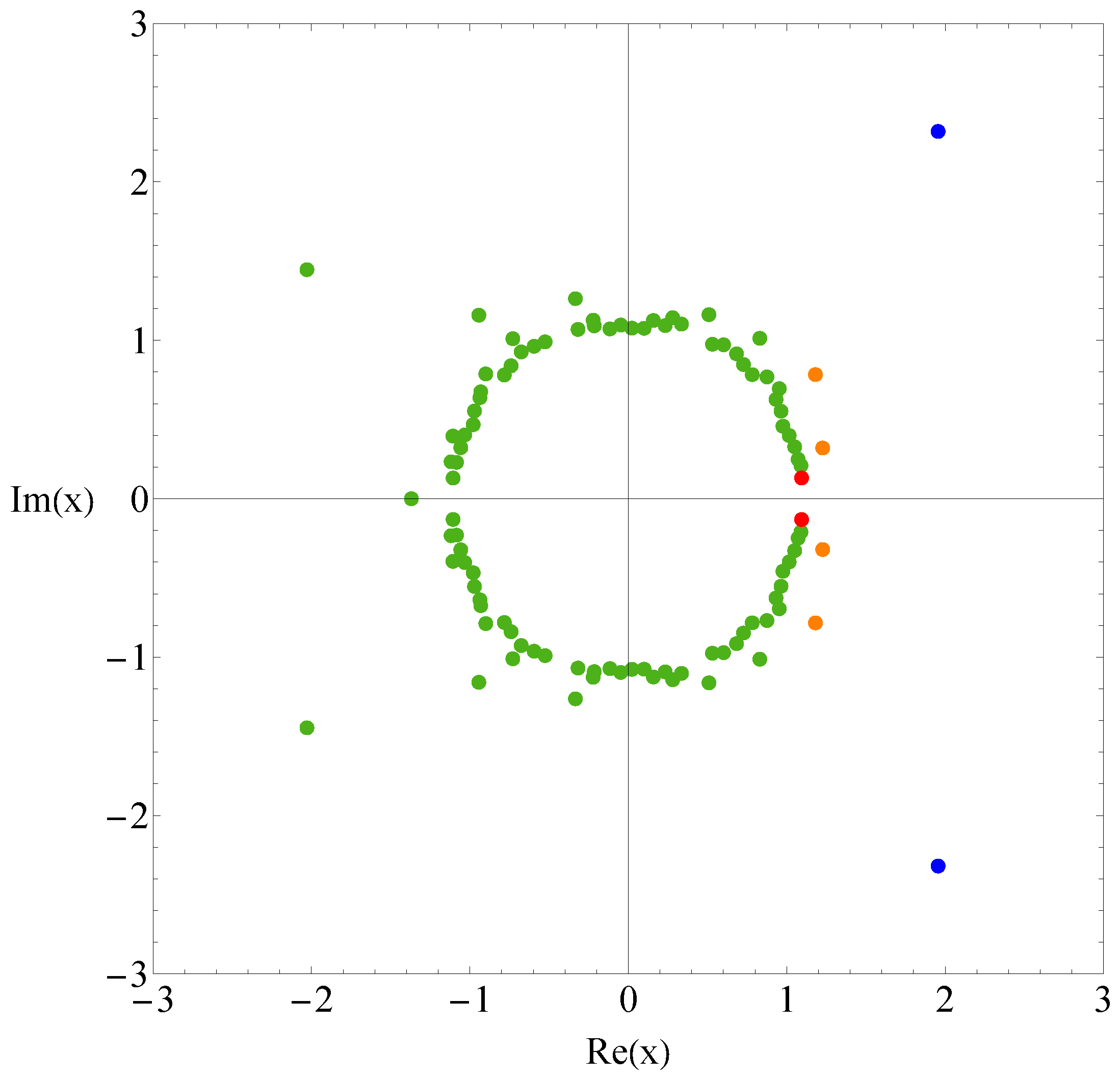

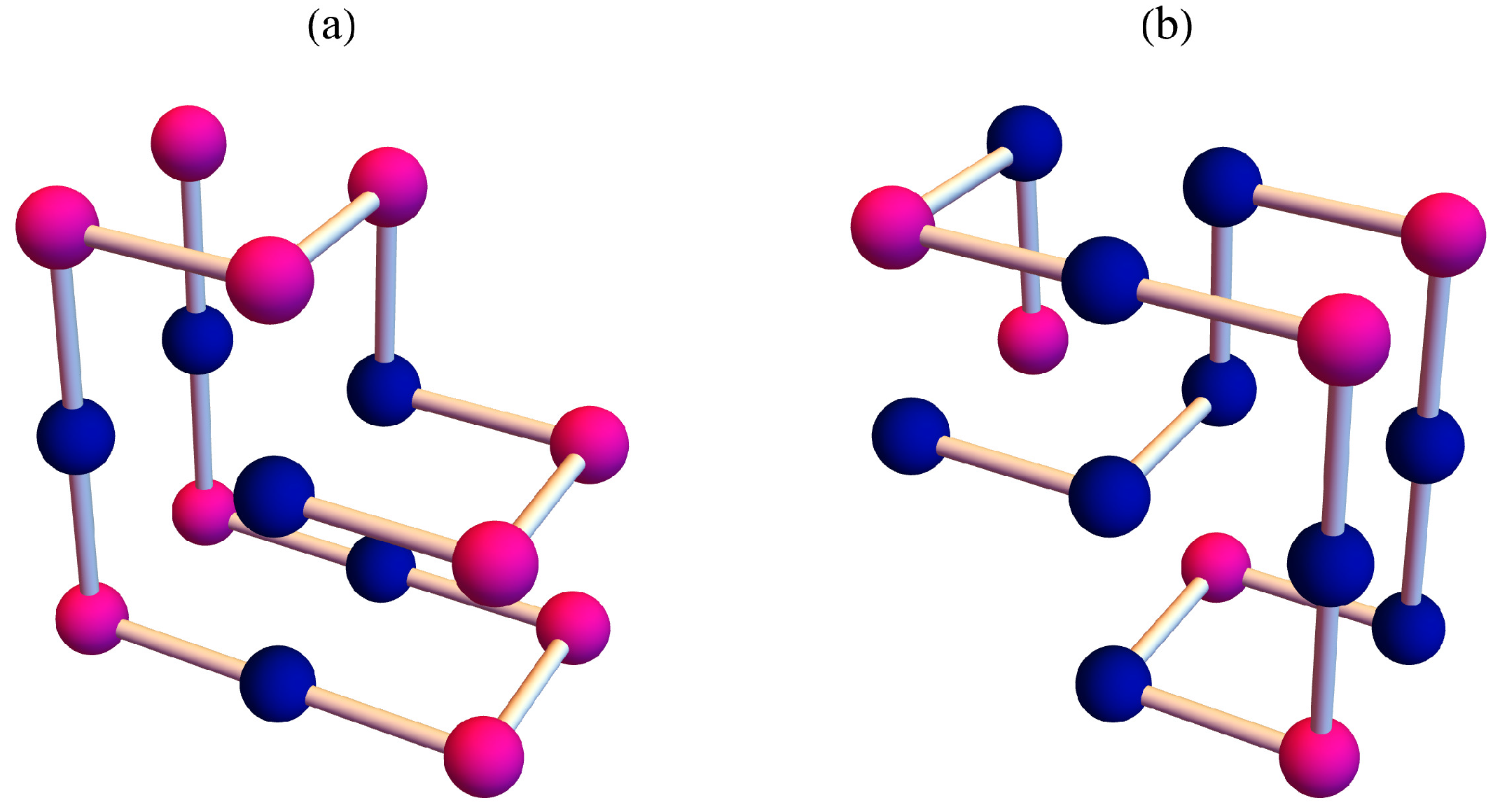
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Anfinson, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef]
- Levinthal, C. Are there pathways for protein folding? Ext. J. Chim. Phys. 1968, 65, 44–45. [Google Scholar] [CrossRef]
- Leopold, P.E.; Montal, M.; Onuchic, J.N. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. USA 1992, 89, 8721–8725. [Google Scholar] [CrossRef]
- Bryngelson, D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar] [CrossRef]
- Dill, K.A.; Chan, H.S. From Levinthal to pathways to funnels. Nat. Struc. Bio. 1997, 4, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Onuchic, J.N.; Luthey-Schulten, Z.; Wolynes, P.G. Theory of protein folding: The energy landscape perspective. Annu. Rev. Phys. Chem. 1997, 48, 545–600. [Google Scholar] [CrossRef] [PubMed]
- Dobson, C.M. Protein folding and misfolding. Nature 2003, 426, 884–890. [Google Scholar] [CrossRef]
- Dill, K.A.; MacCallum, J.L. The protein-folding problem, 50 years on. Science 2012, 3388, 1042–1046. [Google Scholar] [CrossRef] [PubMed]
- Nassar, R.; Dignon, G.L.; Razban, R.M.; Dill, K.A. The Protein folding problem: The role of theory. J. Mol. Bio. 2021, 433, 167126. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Varadi, M.; Bertoni, D.; Magana, P.; Paramval, U.; Pidruchna, I.; Radhakrishnan, M.; Tsenkov, M.; Nair, S.; Mirdita, M.; Yeo, J.; et al. AlphaFold Protein Structure Database in 2024: Providing structure coverage for over 214 million protein sequences. Nucleic Acids Res. 2024, 52, D368–D375. [Google Scholar] [CrossRef] [PubMed]
- Abramson, J.; Adler, J.; Dunger, J.; Evans, R.; Green, T.; Pritzel, A.; Ronneberger, O.; Willmore, L.; Ballard, A.J.; Bambrick, J.; et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 2024, 630, 493–500. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.N.; Lee, T.D. Statistical theory of equations of state and phase transitions. I. Theory of condensation. Phys. Rev. 1952, 87, 404–409. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Statistical theory of equations of state and phase transitions. II. Lattice gas and Ising model. Phys. Rev. 1952, 87, 410–419. [Google Scholar] [CrossRef]
- Borrmann, P.; Mulken, O.; Harting, J. Classification of phase transitions in small systems. Phys. Rev. Lett. 2000, 84, 3511–3514. [Google Scholar] [CrossRef]
- Janke, W.; Kenna, R. The strength of first and second order phase. J. Stat. Phys. 2001, 102, 1211–1227. [Google Scholar] [CrossRef]
- Janke, W.; Johnston, D.A.; Kenna, R. Phase transition strength through densities of general distributions of zeroes. Nucl. Phys. B 2004, 682, 618–634. [Google Scholar] [CrossRef]
- Lau, K.F.; Dill, K.A. A lattice statistical mechanics model of the conformational and sequence spaces of proteins. Macromolecules 1989, 22, 3986–3997. [Google Scholar] [CrossRef]
- Chen, C.N.; Lin, C.Y. Partition function zeros of the two-dimensional HP model for protein folding. Physica A 2005, 350, 45–51. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, S.Y.; Lee, J. Study on collapse and folding transitions of a lattice protein using exact enumeration. AIP Adv. 2015, 5, 127211. [Google Scholar] [CrossRef]
- Chen, C.N.; Hsieh, Y.H.; Hu, C.K. Heat capacity decomposition by partition function zeros for interacting self-avoiding walks. Europhys. Lett. 2013, 104, 20005. [Google Scholar] [CrossRef]
- Dill, K.A. Dominant forces in protein folding. Biochemistry 1990, 29, 7133–7155. [Google Scholar] [CrossRef]
- Li, H.; Tang, C.; Wingreen, N.S. Nature of driving force for protein folding: A result from analyzing the statistical potential. Phys. Rev. Lett. 1997, 79, 765–768. [Google Scholar] [CrossRef]
- Chen, H.; Zhow, X.; Ou-Yang, Z.C. Difference between proteinlike and nonproteinlike heteropolymers. Phys. Rev. E 2001, 63, 031913. [Google Scholar] [CrossRef]
- Berger, B.; Leighton, T. Protein folding in the HP model is NP-complete. In Proceedings of the Second Annual International Conference on Computational Molecular Biology, New York, NY, USA, 22–25 March 1998; pp. 30–39. [Google Scholar]
- Wüst, T.; Landau, D.P. Versatile approach to access the low temperature thermodynamics of lattice polymers and proteins. Phys. Rev. Lett. 2009, 102, 178101. [Google Scholar] [CrossRef] [PubMed]
- Fisher, M.E. The nature of critical points. In Lectures in Theoretical Physics; University of Colorado Press: Boulder, CO, USA, 1965; Volume 7C, pp. 1–159. [Google Scholar]
- Gross, D.H.E.; Votyakov, E.V. Phase transitions in small systems. Eur. Phys. J. B. 2000, 15, 115–126. [Google Scholar] [CrossRef]
- Dunkel, J.; Hilbert, S. Phase transitions in small systems Microcanonical vs. canonical ensembles. Physica A 2006, 370, 390–406. [Google Scholar] [CrossRef]
- Vogel, T.; Bachmann, M.; Janke, W. Freezing and collapse of flexible polymers on regular lattices in three dimensions. Phys. Rev. E 2007, 76, 061803. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Bortz, A.B.; Kalos, M.H.; Lebowitz, J.L. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 1975, 17, 10–18. [Google Scholar] [CrossRef]
- Dinner, A.R.; Abkevich, V.; Shakhnovich, E.; Karplus, M. Factors That Affect the Folding Ability of Proteins. Proteins 1999, 35, 34–40. [Google Scholar] [CrossRef]
- Hsieh, Y.H.; Chen, C.N.; Hu, C.K. Efficient algorithm for computing exact partition functions of lattice polymer models. Comput. Phys. Commun. 2016, 209, 27–33. [Google Scholar] [CrossRef]
- Huang, S.S.; Hsieh, Y.H.; Chen, C.N. Exact enumeration approach to estimate the theta temperature of interacting self-avoiding walks on the simple cubic lattice. Polymers 2022, 14, 4536. [Google Scholar] [CrossRef] [PubMed]
- Lesh, N.; Mitzenmacher, M.; Whitesides, S. A complete and effective move set for simplified protein folding. In Proceedings of the 7th Annual International Conference on Research in Computational Molecular Biology, Berlin, Germany, 10–14 April 2003; pp. 188–195. [Google Scholar]
- Madras, N.; Sokal, A.D. The pivot algorithm A highly efficient Monte Carlo method for the self-avoiding walk. J. Stat. Phys. 1988, 50, 109–186. [Google Scholar] [CrossRef]
- Deutsch, J.M. Long range moves for high density polymer simulations. J. Chem. Phys. 1997, 106, 8849–8854. [Google Scholar] [CrossRef]
- Chen, C.N.; Chou, C.I.; Hwang, C.R.; Kang, J.; Lee, T.K.; Li, S.P. Monte Carlo dynamics in global optimization. Phys. Rev. E 1999, 60, 2388–2393. [Google Scholar] [CrossRef]
- Klimov, D.; Thirumalai, D. Criterion that determines the foldability of proteins. Phys. Rev. Lett. 1996, 76, 4070–4073. [Google Scholar] [CrossRef]
- Alves, N.A.; Hansmann, U.H.E. Partition Function Zeros and Finite Size Scaling of Helix-Coil Transitions in a Polypeptide. Phys. Rev. Lett. 2000, 84, 1836–1839. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D.P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050–2053. [Google Scholar] [CrossRef]
- Farris, A.C.K.; Landau, D.P. Replica exchange Wang–Landau sampling of long HP model sequences. Physica A 2021, 569, 125778. [Google Scholar] [CrossRef]


| No. | HP Sequence | # of H | |||
|---|---|---|---|---|---|
| 1 | PHPPPPHPPHPHPPPP | 4 | −72 | 0.811420 | 5.140083 |
| 2 | HPPPHPPPPPPHHPHP | 5 | −78 | 0.861228 | 5.275736 |
| 3 | PHPPPHPPPPPPHPHH | 5 | −78 | 0.631339 | 5.341242 |
| 4 | PHPHHPPHHHPPPPPP | 6 | −81 | 0.632632 | 6.053996 |
| 5 | PHPHHPHPPHPPPPHP | 6 | −87 | 1.646424 | 5.776825 |
| 6 | HPPHPPPHPHPPHPHP | 6 | −91 | 1.763969 | 5.876219 |
| 7 | PHHHPPPHPPHHPPHP | 7 | −90 | 1.193511 | 6.236811 |
| 8 | PHPHHPPHPPPHHPHP | 7 | −90 | 1.471768 | 6.260434 |
| 9 | HPPPPHPPPHHPHPHH | 7 | −93 | 0.235701 | 6.140142 |
| 10 | HHHPPHPPPPHPHHPP | 7 | −93 | 1.069987 | 6.278046 |
| 11 | HHHPHPPPPHPPHHPP | 7 | −93 | 1.790133 | 6.379248 |
| 12 | HHHPHHPHHPPPHPPP | 8 | −95 | 0.788043 | 6.769531 |
| 13 | HHPPHHPPHHHPPPHP | 8 | −96 | 0.810405 | 6.598124 |
| 14 | HHHHPHPHPPHPPHPP | 8 | −97 | 1.226218 | 6.722472 |
| 15 | HHHPPHPPPHPHPPHH | 8 | −100 | 0.943834 | 6.640664 |
| 16 | HPHHPHHHPPHPHPHP | 9 | −100 | 0.820632 | 7.186494 |
| 17 | HHHPHHPPHHHPPHPP | 9 | −103 | 1.008023 | 7.196576 |
| 18 | HHHHPHHPHPHPHPHP | 10 | −103 | 0.758160 | 7.512336 |
| 19 | HPHHHHPHHPHPHPHP | 10 | −103 | 0.725455 | 7.638136 |
| 20 | HHHPHHPHHPPPHPPP | 11 | −112 | 0.236975 | 7.923537 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.-S.; Chen, C.-N. Partition Function Zeros and Heat Capacity Decomposition Reveal HP Protein Foldability. Polymers 2025, 17, 2956. https://doi.org/10.3390/polym17212956
Huang S-S, Chen C-N. Partition Function Zeros and Heat Capacity Decomposition Reveal HP Protein Foldability. Polymers. 2025; 17(21):2956. https://doi.org/10.3390/polym17212956
Chicago/Turabian StyleHuang, Sing-Shuo, and Chi-Ning Chen. 2025. "Partition Function Zeros and Heat Capacity Decomposition Reveal HP Protein Foldability" Polymers 17, no. 21: 2956. https://doi.org/10.3390/polym17212956
APA StyleHuang, S.-S., & Chen, C.-N. (2025). Partition Function Zeros and Heat Capacity Decomposition Reveal HP Protein Foldability. Polymers, 17(21), 2956. https://doi.org/10.3390/polym17212956





