Applicability of the Cox-Merz Rule to High-Density Polyethylene Materials with Various Molecular Masses
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
- Material 1 was a high viscosity hexene copolymer polyethylene compound (HDPE) for pipe applications (PE 100) with high density and an outstanding resistance to slow crack growth.
- Material 2 was a high-density polyethylene for injection and compression moulding.
- Material 3 was another high-density polyethylene for injection and compression moulding.
2.2. Parallel-Plate Rheometer
2.3. High-Pressure Capillary Rheometer (HPCR)
2.4. Slit-Die Extrusion Rheometer
3. Simulation
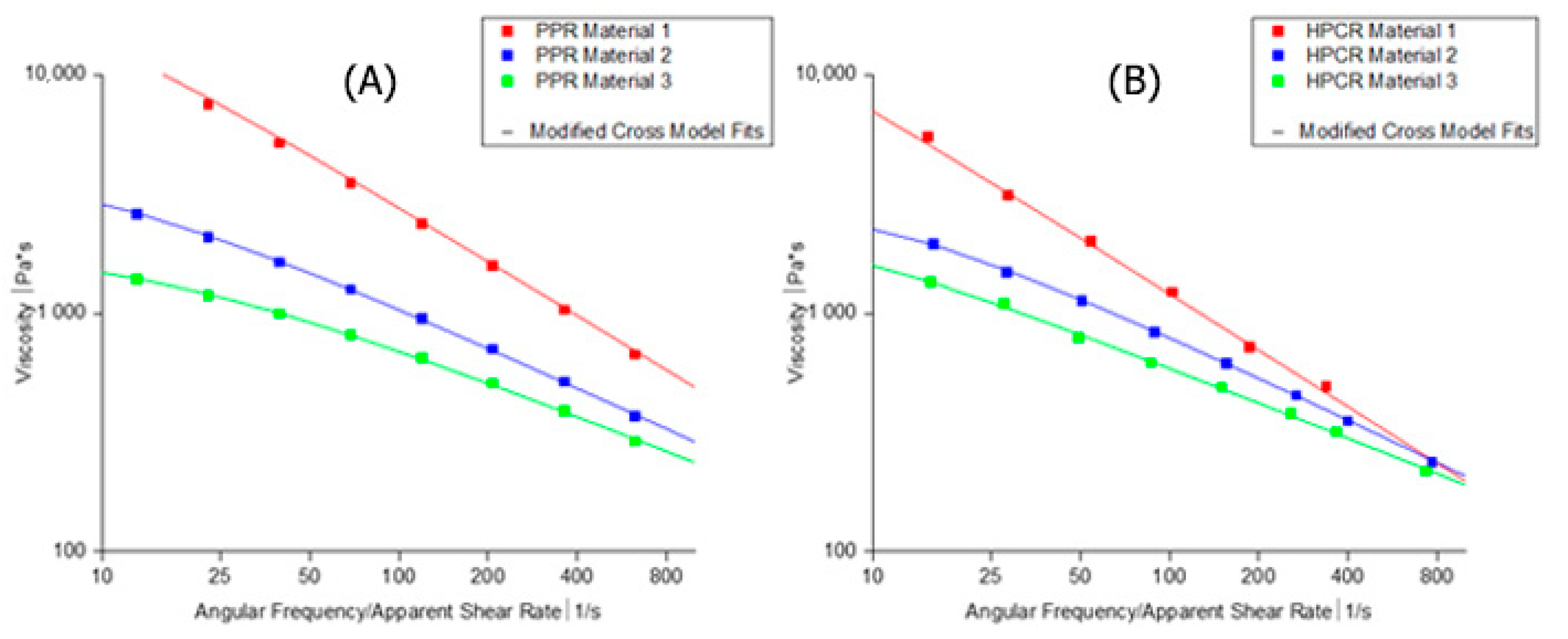
3.1. Fitting of Experimental Data
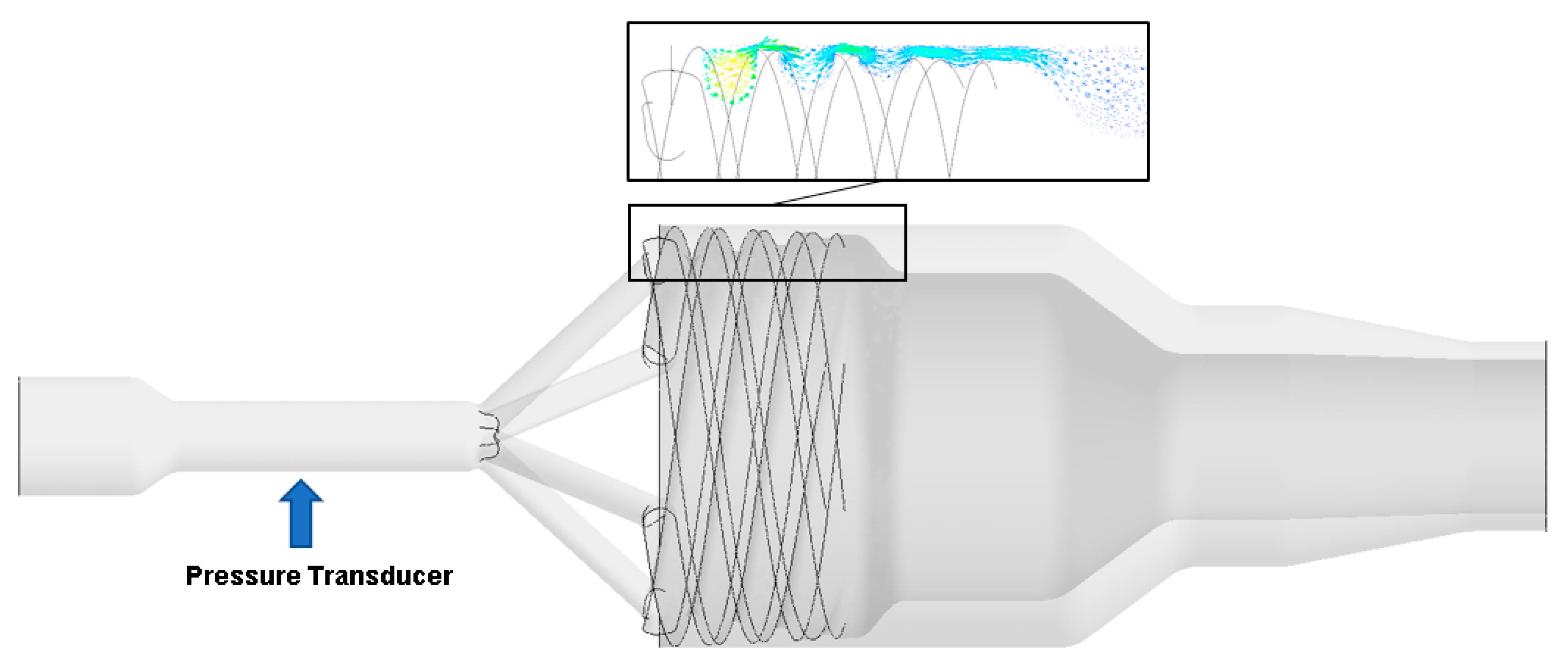
3.2. Simulation of Extrusion Equipment
3.3. Extrusion Experiments with the Real Pipe Head
4. Results and Discussion
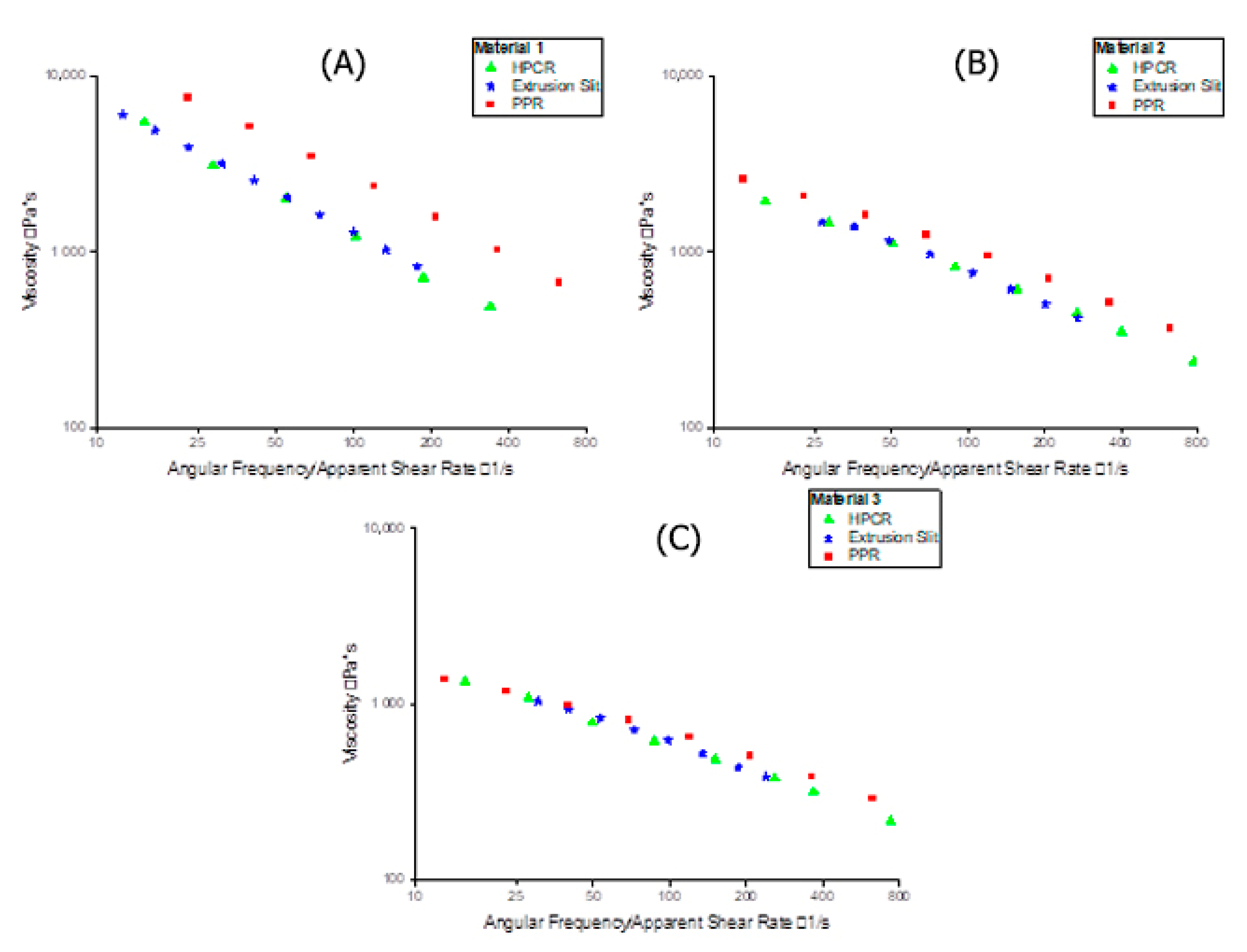
4.1. Comparison of Plate-Plate Rheometry (PPR) to High-Pressure Capillary Rheometry (HPCR) and Extrusion Slit Rheometry
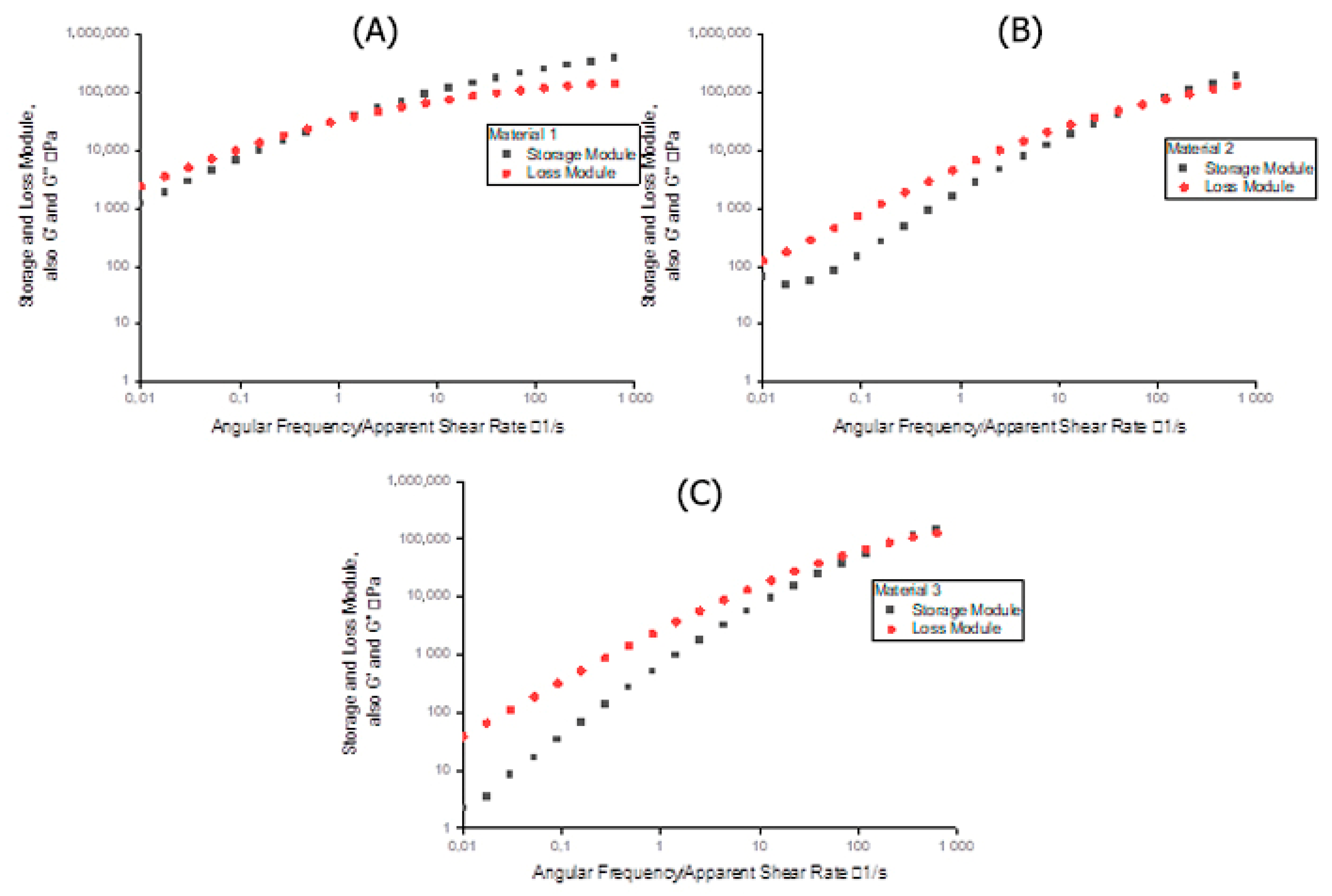
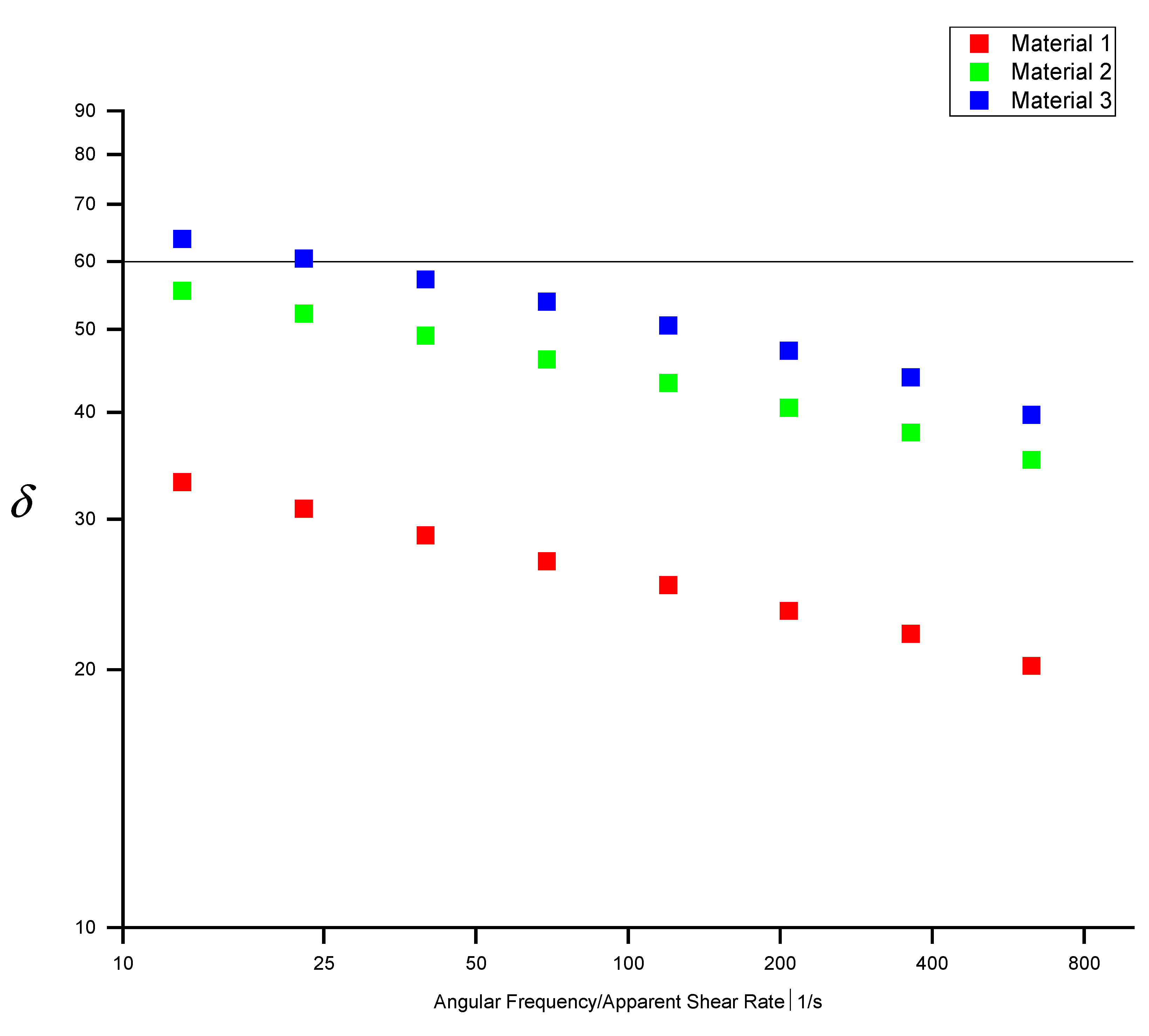
4.2. Viscoelasticity of HDPE Materials
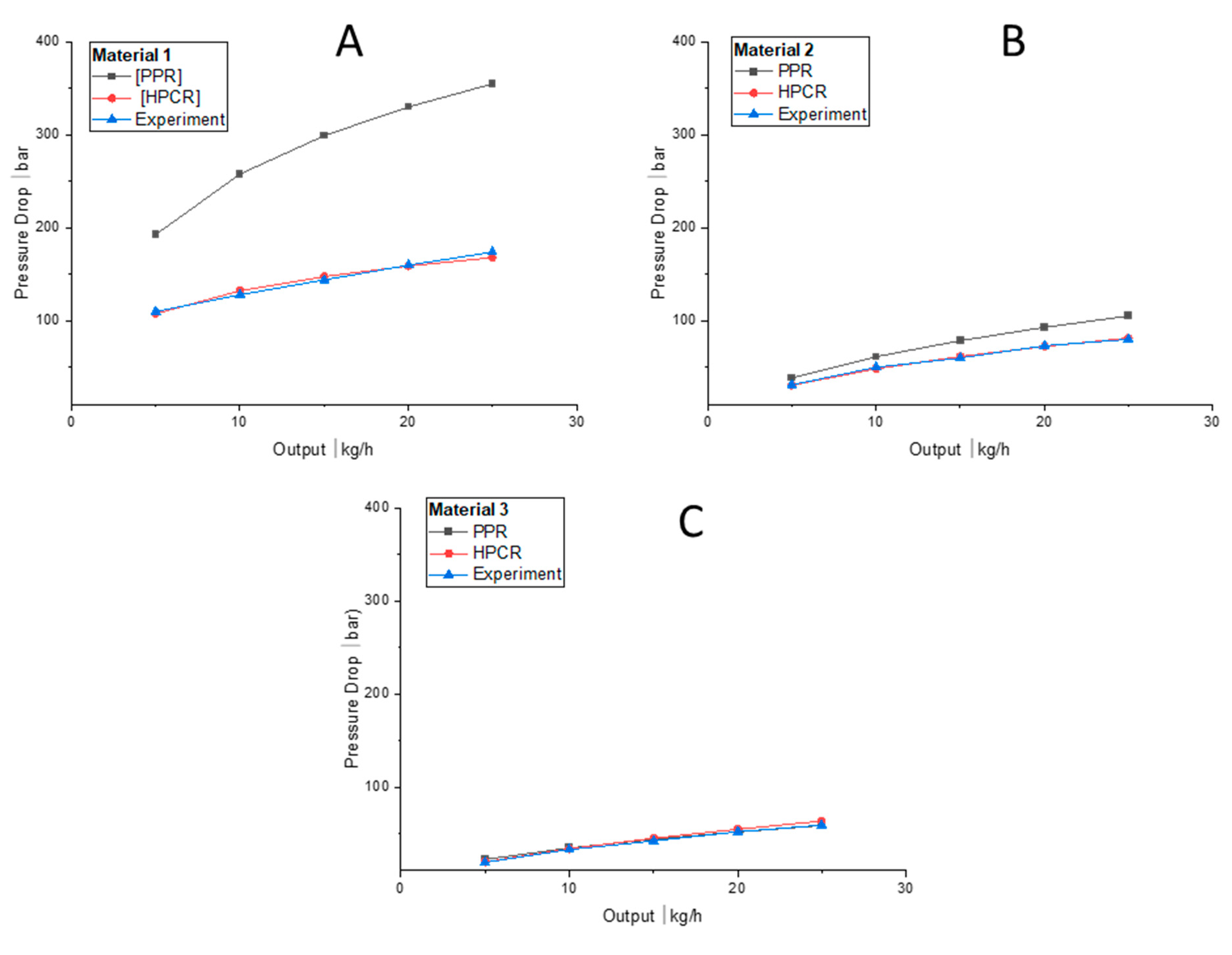
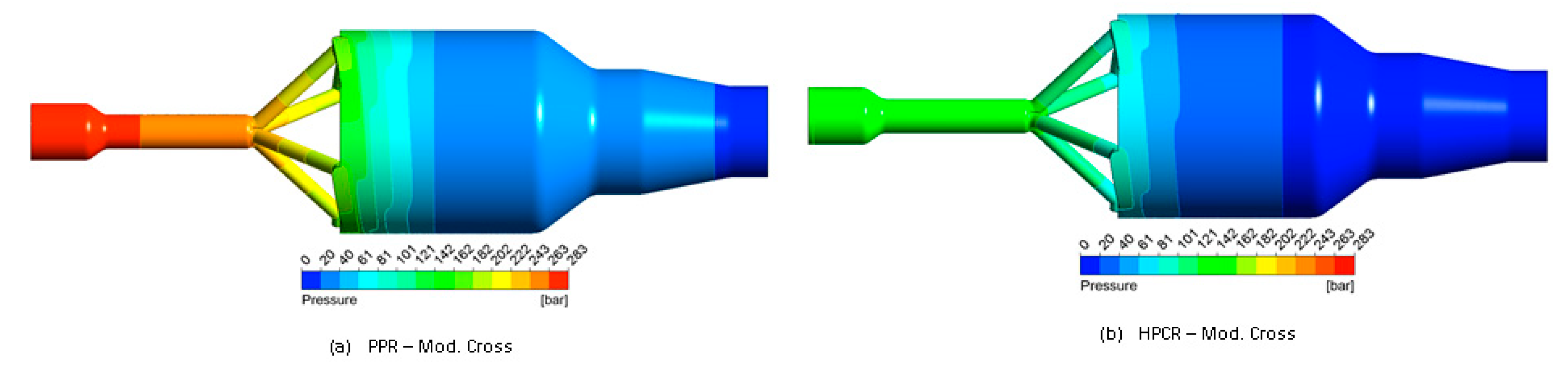
4.3. Comparison of Pipe-Head Simulations with Measured Rheology Curves
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roller, M.B. Rheology of curing thermosets: A review. Polym. Eng. Sci. 1986, 26, 432–440. [Google Scholar] [CrossRef]
- Rueda, M.M.; Auscher, M.-C.; Fulchiron, R.; Périé, T.; Martin, G.; Sonntag, P.; Cassagnau, P. Rheology and applications of highly filled polymers: A review of current understanding. Prog. Polym. Sci. 2017, 66, 22–53. [Google Scholar] [CrossRef]
- Köpplmayr, T.; Luger, H.-J.; Burzic, I.; Battisti, M.G.; Perko, L.; Friesenbichler, W.; Miethlinger, J. A novel online rheometer for elongational viscosity measurement of polymer melts. Polym. Test. 2016, 50, 208–215. [Google Scholar] [CrossRef]
- Włoch, M.; Datta, J. Rheology of polymer blends. In Rheology of Polymer Blends and Nanocomposites: Theory, Modelling and Applications; Thomas, S., Sarathchandran, C., Chandran, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 19–29. ISBN 9780128169575. [Google Scholar]
- Kamal, M.R.; Utracki, L.A.; Mirzadeh, A. Rheology of Polymer Alloys and Blends. In Polymer Blends Handbook, 2nd ed.; Utracki, L.A., Wilkie, C.A., Eds.; Springer: New York, NY, USA, 2014; pp. 725–873. ISBN 978-94-007-6064-6. [Google Scholar]
- Sperling, L.H. Polymer alloys and blends thermodynamics and rheology, by L. A. Utracki, Hanser, Munich, 1989, 356 pp. Price: $90.00. J. Polym. Sci. C Polym. Lett. 1990, 28, 387. [Google Scholar] [CrossRef]
- Schroyen, B.; Vlassopoulos, D.; van Puyvelde, P.; Vermant, J. Bulk rheometry at high frequencies: A review of experimental approaches. Rheol Acta 2020, 59, 1–22. [Google Scholar] [CrossRef]
- Laun, M.; Auhl, D.; Brummer, R.; Dijkstra, D.J.; Gabriel, C.; Mangnus, M.A.; Rüllmann, M.; Zoetelief, W.; Handge, U.A. Guidelines for checking performance and verifying accuracy of rotational rheometers: Viscosity measurements in steady and oscillatory shear (IUPAC Technical Report). Pure Appl. Chem. 2014, 86, 1945–1968. [Google Scholar] [CrossRef]
- Cox, W.P.; Merz, E.H. Correlation of dynamic and steady flow viscosities. J. Polym. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Bair, S.; Yamaguchi, T.; Brouwer, L.; Schwarze, H.; Vergne, P.; Poll, G. Oscillatory and steady shear viscosity: The Cox-Merz rule, superposition, and application to EHL friction. Tribol. Int. 2014, 79, 126–131. [Google Scholar] [CrossRef]
- Mead, D.W. Analytic derivation of the Cox-Merz rule using the MLD “toy” model for polydisperse linear polymers. Rheol Acta 2011, 50, 837–866. [Google Scholar] [CrossRef]
- Wen, Y.H.; Lin, H.C.; Li, C.H.; Hua, C.C. An experimental appraisal of the Cox-Merz rule and Laun’s rule based on bidisperse entangled polystyrene solutions. Polymer 2004, 45, 8551–8559. [Google Scholar] [CrossRef]
- Shan, L.; Tan, Y.; Richard Kim, Y. Applicability of the Cox-Merz relationship for asphalt binder. Constr. Build. Mater. 2012, 37, 716–722. [Google Scholar] [CrossRef]
- Ahmad, N.H.; Ahmed, J.; Hashim, D.M.; Manap, Y.A.; Mustafa, S. Oscillatory and steady shear rheology of gellan/dextran blends. J. Food Sci. Technol. 2015, 52, 2902–2909. [Google Scholar] [CrossRef] [PubMed]
- Stieger, S.; Kerschbaumer, R.C.; Mitsoulis, E.; Fasching, M.; Berger-Weber, G.R.; Friesenbichler, W.; Sunder, J. Contraction and capillary flow of a carbon black filled rubber compound. Polym. Eng. Sci. 2020, 60, 32–43. [Google Scholar] [CrossRef]
- Miao, X.; Guo, Y.; He, L.; Meng, Y.; Li, X. Rheological behaviors of a series of hyperbranched polyethers. Chin. J. Polym. Sci. 2015, 33, 1574–1585. [Google Scholar] [CrossRef]
- Ebagninin, K.W.; Benchabane, A.; Bekkour, K. Rheological characterization of poly(ethylene oxide) solutions of different molecular weights. J. Colloid Interface Sci. 2009, 336, 360–367. [Google Scholar] [CrossRef] [PubMed]
- Yüce, C.; Willenbacher, N. Challenges in Rheological Characterization of Highly Concentrated Suspensions-A Case Study for Screen-printing Silver Pastes. J. Vis. Exp. 2017, 122, e55377. [Google Scholar] [CrossRef]
- Snijkers, F.; Vlassopoulos, D. Appraisal of the Cox-Merz rule for well-characterized entangled linear and branched polymers. Rheol Acta 2014, 53, 935–946. [Google Scholar] [CrossRef]
- Robertson, C.G.; Roland, C.M.; Puskas, J.E. Nonlinear rheology of hyperbranched polyisobutylene. J. Rheol. 2002, 46, 307–320. [Google Scholar] [CrossRef][Green Version]
- Järvelä, P.; Shucai, L.; Järvelä, P. Dynamic mechanical properties and morphology of polypropylene/maleated polypropylene blends. J. Appl. Polym. Sci. 1996, 62, 813–826. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hitomi, C.; Onogi, S. Rheological Properties of Disperse Systems of Spherical Particles in Polystyrene Solution at Long Time-Scales. Trans. Soc. Rheol. 1975, 19, 541–555. [Google Scholar] [CrossRef][Green Version]
- Kulicke, W.-M.; Porter, R.S. Relation between steady shear flow and dynamic rheology. Rheol Acta 1980, 19, 601–605. [Google Scholar] [CrossRef]
- Venkatraman, S.; Okano, M. A comparison of torsional and capillary rheometry for polymer melts: The Cox-Merz rule revisited. Polym. Eng. Sci. 1990, 30, 308–313. [Google Scholar] [CrossRef]
- Schulken, R.M.; Cox, R.H.; Minnick, L.A. Dynamic and steady-state rheological measurements on polymer melts. J. Appl. Polym. Sci. 1980, 25, 1341–1353. [Google Scholar] [CrossRef]
- Booij, H.C.; Leblans, P.; Palmen, J.; Tiemersma-Thoone, G. Nonlinear viscoelasticity and the Cox-Merz relations for polymeric fluids. J. Polym. Sci. Polym. Phys. Ed. 1983, 21, 1703–1711. [Google Scholar] [CrossRef]
- Ferri, D.; Lomellini, P. Melt rheology of randomly branched polystyrenes. J. Rheol. 1999, 43, 1355–1372. [Google Scholar] [CrossRef]
- Al-Hadithi, T.S.R.; Barnes, H.A.; Walters, K. The relationship between the linear (oscillatory) and nonlinear (steady-state) flow properties of a series of polymer and colloidal systems. Colloid Polym. Sci. 1992, 270, 40–46. [Google Scholar] [CrossRef]
- Tam, K.C.; Tiu, C. Modified cox-merz rule for charged polymer systems in solution. J. Macromol. Sci. Part B 1994, 33, 173–184. [Google Scholar] [CrossRef]
- Doraiswamy, D.; Mujumdar, A.N.; Tsao, I.; Beris, A.N.; Danforth, S.C.; Metzner, A.B. The Cox-Merz rule extended: A rheological model for concentrated suspensions and other materials with a yield stress. J. Rheol. 1991, 35, 647–685. [Google Scholar] [CrossRef]
- Marrucci, G. Dynamics of entanglements: A nonlinear model consistent with the Cox-Merz rule. J. Non-Newton. Fluid Mech. 1996, 62, 279–289. [Google Scholar] [CrossRef]
- Kissin, Y.V. Polyethylene: End-Use Properties and Their Physical Meaning; Kissin, Y.V., Ed.; Hanser Publishers: Munich, Germany, 2013; ISBN 978-1-56990-520-3. [Google Scholar]
- Winter, H.H. Three views of viscoelasticity for Cox-Merz materials. Rheol. Acta 2009, 48, 241–243. [Google Scholar] [CrossRef]
- Raj, A.; Rajak, D.K.; Gautam, S.; Guria, C.; Pathak, A.K. Shear Rate Estimation: A Detailed Review. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2 May 2016. [Google Scholar]
- Bagley, E.B. End Corrections in the Capillary Flow of Polyethylene. J. Appl. Phys. 1957, 28, 624–627. [Google Scholar] [CrossRef]
- Allen, G.M. Rheology of polymeric systems, principles and applications. By P. J. Carreau, D.C.R. De Kee, and R. P. Chhabra, Hanser/Gardner Publications, Cincinnati, OH, 1997, 520 pp., $197.50. AIChE J. 1999, 45, 1836–1837. [Google Scholar] [CrossRef]
- ANSYS POLYFLOW. User Manual 18.1; ANSYS: Canonsburg, PA, USA, 2017. [Google Scholar]
- Cross, M.M. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Wasserman, S.H.; Graessley, W.W. Prediction of linear viscoelastic response for entangled polyolefin melts from molecular weight distribution. Polym. Eng. Sci. 1996, 36, 852–861. [Google Scholar] [CrossRef]
| MFR (g/10 min) | MW (g/mol) | MZ (g/mol) | |
|---|---|---|---|
| Material 1 | 0.25 | 230,000 | 1,190,000 |
| Material 2 | 1.5 | 110,000 | 550,000 |
| Material 3 | 4.0 | 85,500 | 387,000 |
| Parameter | Unit | Material 1 | Material 2 | Material 3 |
|---|---|---|---|---|
| Pa.s | 43,226 | 4559 | 1930 | |
| s | 0.362 | 0.125 | 0.0711 | |
| - | 0.761 | 0.571 | 0.491 |
| Parameter | Unit | Material 1 | Material 2 | Material 3 |
|---|---|---|---|---|
| Pa.s | 56,796 | 3715 | 3175 | |
| s | 0.323 | 0.124 | 0.097 | |
| - | 0.788 | 0.598 | 0.494 |
| PPR | HPCR | |
|---|---|---|
| α | 3.09 | 3.12 |
| β | 0.43 | 0.45 |
| κ | 1.59 | 1.23 |
| Material 1 | Material 2 | Material 3 | |
|---|---|---|---|
| 5 | 2.12 | 1.27 | 1.05 |
| 50 | 2.22 | 1.29 | 1.13 |
| 150 | 2.33 | 1.32 | 1.20 |
| 400 | 2.41 | 1.36 | 1.23 |
| Output | Material 1 | Material 2 | Material 3 | |||
|---|---|---|---|---|---|---|
| kg/h | ||||||
| 5 | 1.74 | 0.98 | 1.23 | 1 | 1.16 | 1 |
| 10 | 2.01 | 1.03 | 1.22 | 0.96 | 1.03 | 1 |
| 15 | 2.08 | 1.03 | 1.31 | 1.02 | 1.07 | 1.04 |
| 20 | 2.06 | 0.99 | 1.27 | 0.99 | 1 | 1.05 |
| 25 | 2.04 | 0.97 | 1.31 | 1.01 | 1 | 1.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathner, R.; Roland, W.; Albrecht, H.; Ruemer, F.; Miethlinger, J. Applicability of the Cox-Merz Rule to High-Density Polyethylene Materials with Various Molecular Masses. Polymers 2021, 13, 1218. https://doi.org/10.3390/polym13081218
Rathner R, Roland W, Albrecht H, Ruemer F, Miethlinger J. Applicability of the Cox-Merz Rule to High-Density Polyethylene Materials with Various Molecular Masses. Polymers. 2021; 13(8):1218. https://doi.org/10.3390/polym13081218
Chicago/Turabian StyleRathner, Raffael, Wolfgang Roland, Hanny Albrecht, Franz Ruemer, and Jürgen Miethlinger. 2021. "Applicability of the Cox-Merz Rule to High-Density Polyethylene Materials with Various Molecular Masses" Polymers 13, no. 8: 1218. https://doi.org/10.3390/polym13081218
APA StyleRathner, R., Roland, W., Albrecht, H., Ruemer, F., & Miethlinger, J. (2021). Applicability of the Cox-Merz Rule to High-Density Polyethylene Materials with Various Molecular Masses. Polymers, 13(8), 1218. https://doi.org/10.3390/polym13081218






