DEM-FEM Simulation of Double Compaction of Cu and Al Composite Metal Powders with Multiple Particle Sizes
Abstract
1. Introduction
2. Materials and Methods
2.1. Molding Analysis of Mixed Metal Powder Particles at a Particle Size Ratio of 1:2
2.1.1. Geometric Modeling
2.1.2. Validation of Model Validity and Mesh Independence
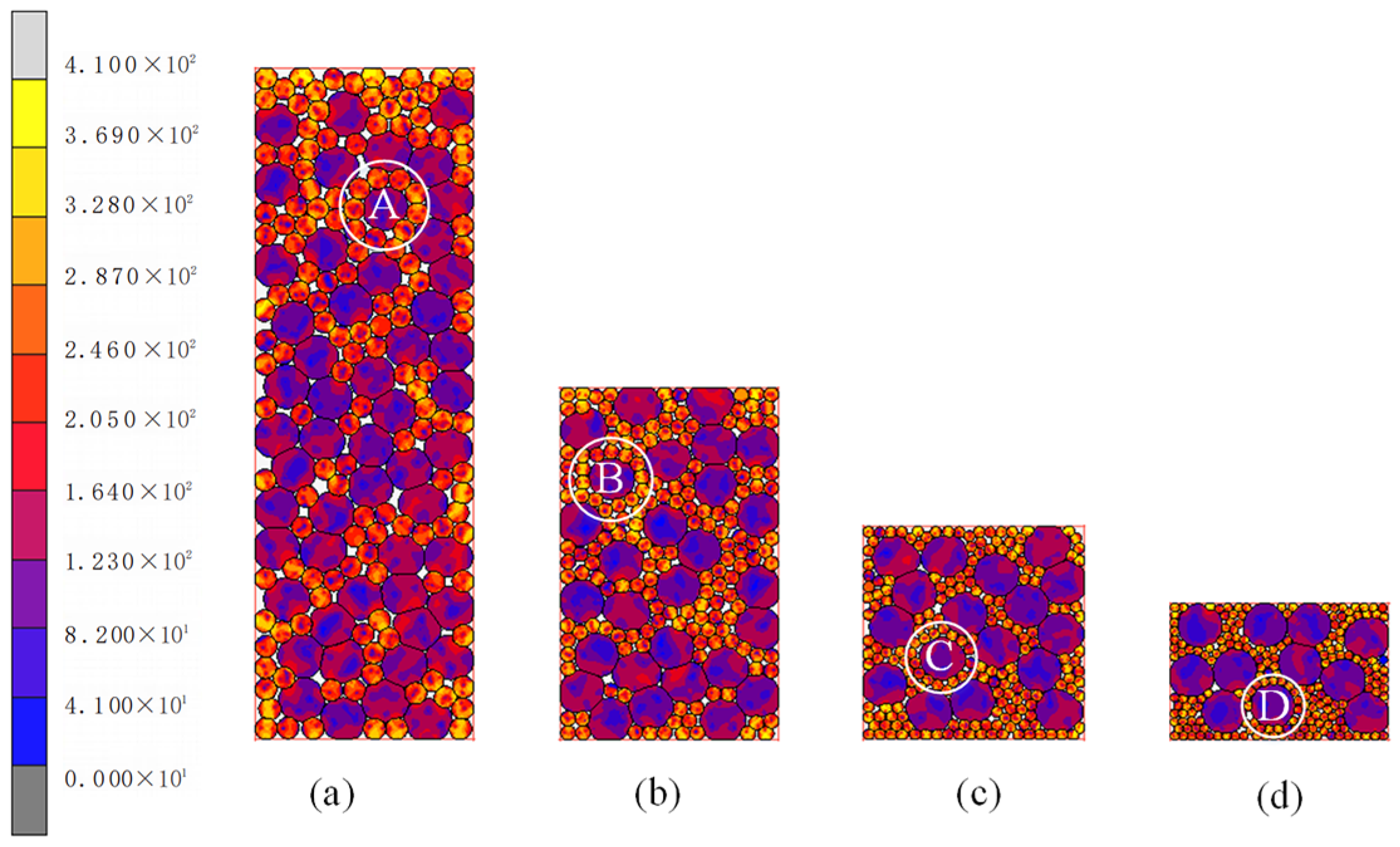
2.2. Numerical Simulation of Cu and Al Composite Metal Powder Particle Molding Process at Various Particle Size Ratios
3. Results and Discussion
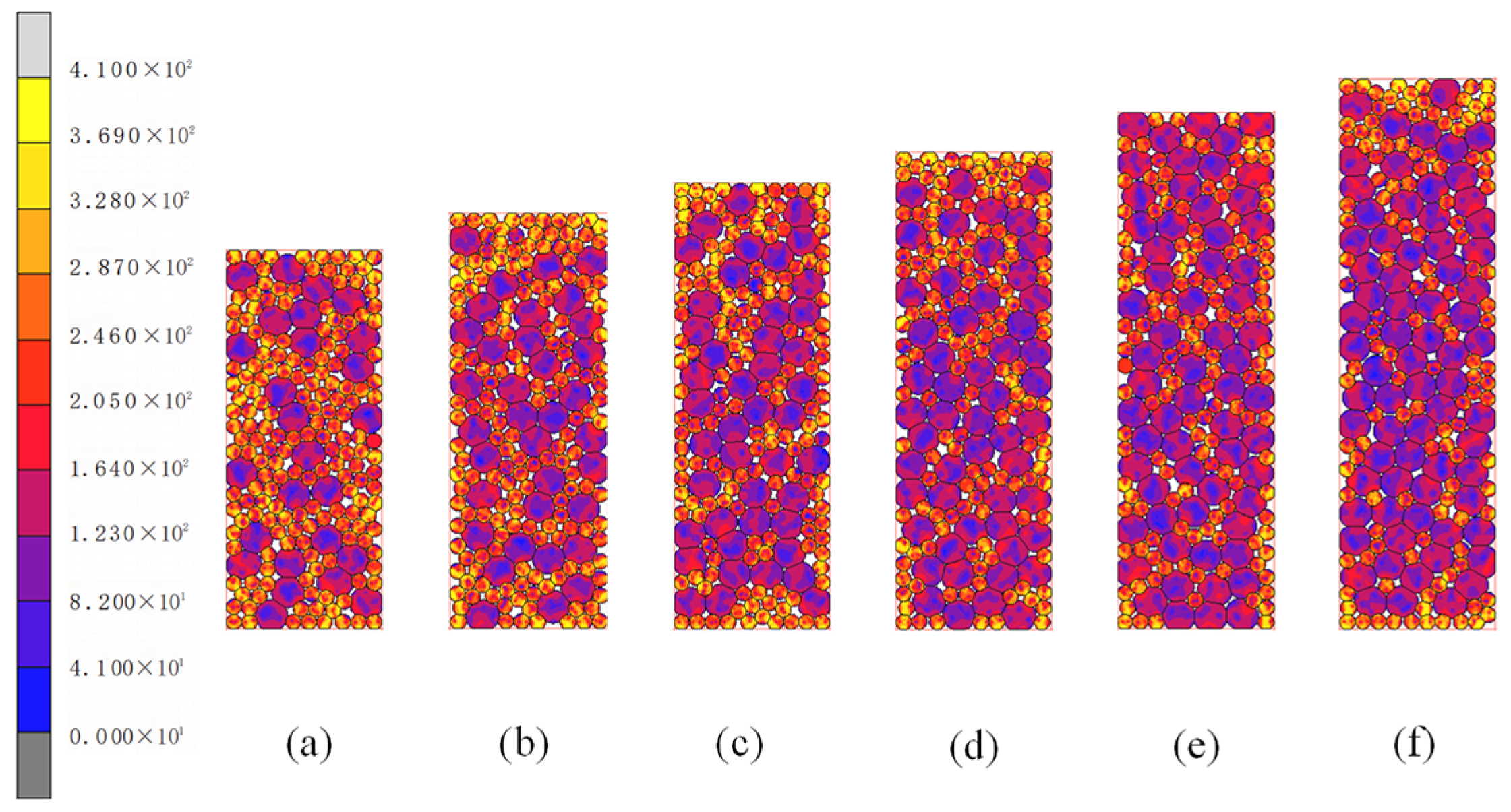
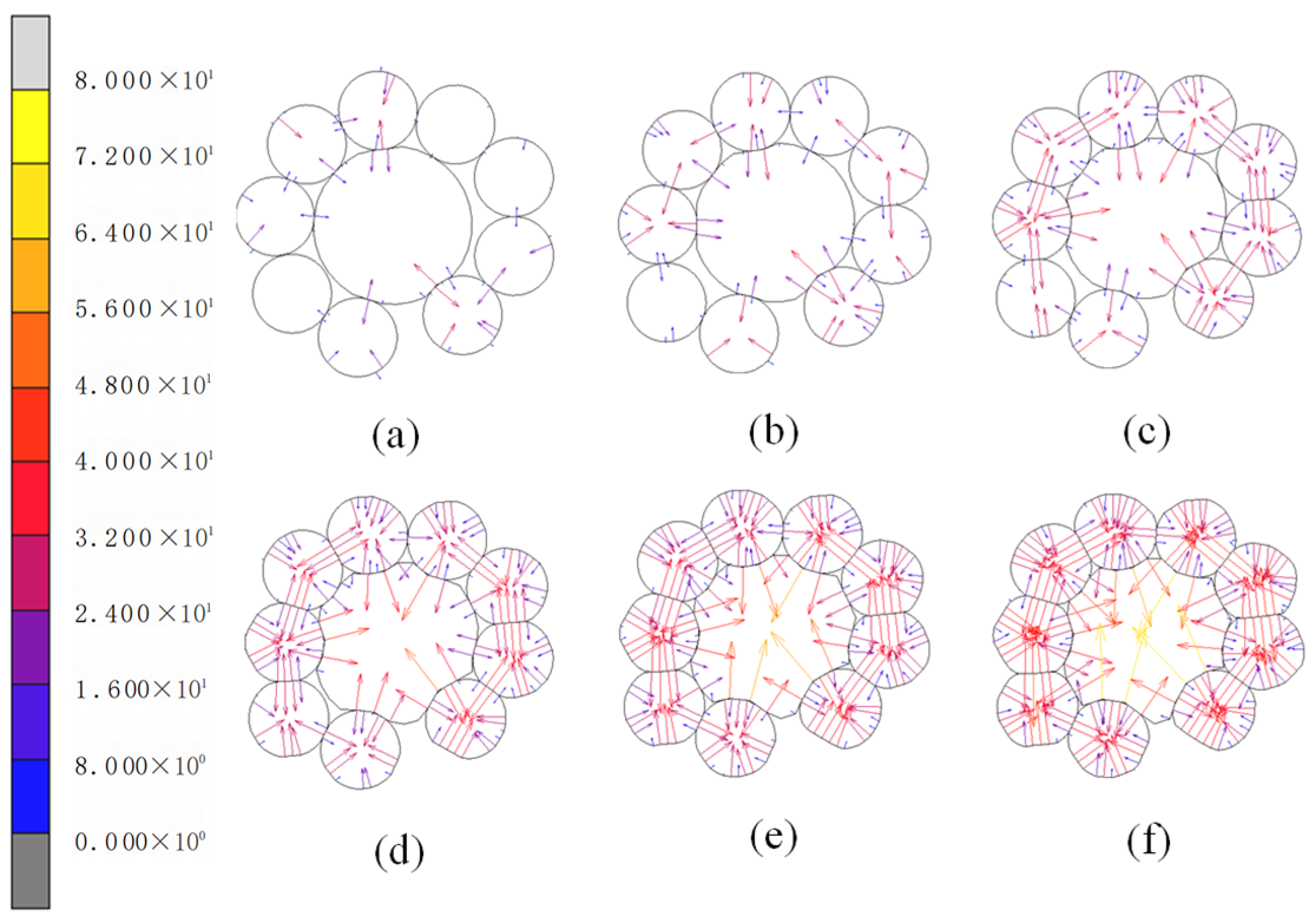
3.1. Stress and Deformation Analysis of Cu and Al Composite Powders
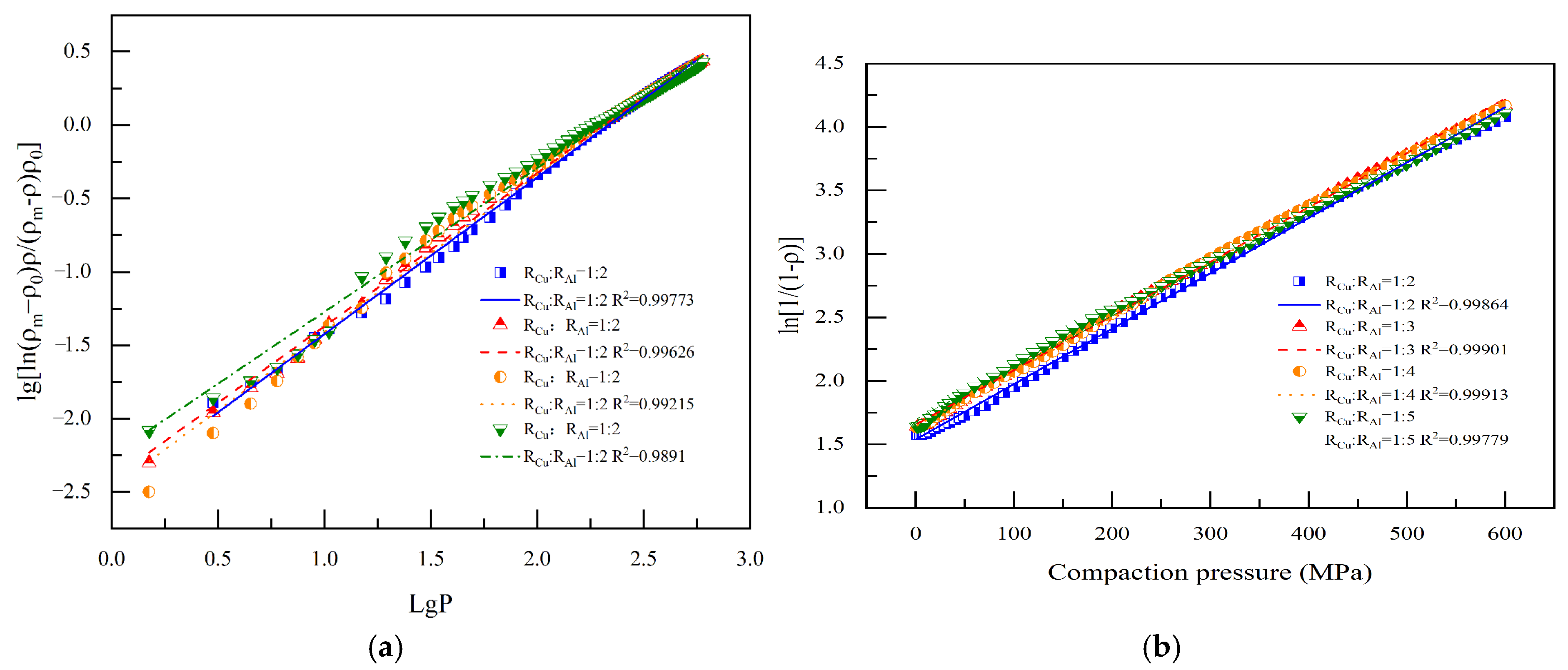
3.2. Effect of Particle Size Ratio on Densification
4. Conclusions
- The larger the difference in the Cu and Al particle size ratio, the better the densification of the press blanks during the compact of the composite powder particles. The smaller Cu particles preferentially fill the inter-particle voids formed by the larger Al particles during the initial compaction stage, reducing the pore volume by up to 12.3% with a 1:5 size ratio. This rearrangement-dominated densification is more pronounced at lower pressures, while plastic deformation of the Al particles dominates pore filling at higher pressures. When the size ratio is changed from 1:2 to 1:5, the relative density of the briquette increases from 0.7915 to 0.8047, the critical role of particle size gradient in optimizing the pore elimination pathway is demonstrated.
- The average relative density of the briquette increases with the increase in Al content in the composite metal powder at a certain particle size ratio, but the equivalent Mises stress decreases gradually due to the excellent plasticity of Al. the Cu particles form a rigid force network that hinders densification, while the Al particles alleviate the stress concentration through large-scale plastic deformation. Under the same conditions, the stress value in Cu particles is still higher than that in Al particles.
- Inside the billet, the stress value of Cu particles is larger but the deformation is smaller. The stress value of Al particles is small, but the deformation is larger than that of Cu particles. But with the continuous increase in the difference in particle size, the deformation of Al particles began to decrease, and the comparison found that Al particles can better maintain its own shape.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ding, W.; Tao, Q.; Liu, C.; Chen, G.; Yoo, S.; Cai, W.; Cao, P.; Jia, B.; Wu, H.; Zhang, D.; et al. Lean design of a strong and ductile dual-phase titanium–oxygensteel. Nat. Mater. 2025, 24, 506–512. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Ma, Y.; Raabe, D. One step from oxides to sustainable bulk alloys. Nature 2024, 633, 816–822. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zhang, Y.; Liu, J.; Chen, W.; Wang, K.; Cui, B.; Zou, B.; Ouyang, Q.; Zhang, Y.; Hu, Z.; et al. Dispersion hardening using amorphous nanoparticles deployed via additive manufacturing. Nat. Commun. 2025, 16, 3589. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Hong, Y. High-cycle and very-high-cycle fatigue of an additively manufactured aluminium alloy under axial cycling at ultrasonic and conventional frequencies. Int. J. Fatigue 2024, 185, 108363. [Google Scholar] [CrossRef]
- Liu, J.; Li, M.; Jiang, C.; Long, Y.; An, X.; Zhu, G.; Xu, H.; Xu, J. Numerical investigation on the densification of granulated porous indium tin oxide powders before compaction. Powder Technol. 2024, 438, 119676. [Google Scholar] [CrossRef]
- Wang, W.; Qi, H.; Liu, P.; Zhao, Y.; Chang, H. Numerical simulation of densification of Cu and Al mixed metal powder during axial compaction. Metals 2018, 8, 537. [Google Scholar] [CrossRef]
- He, Y.; Evans, T.J.; Yu, A.; Yang, R. A GPU-based DEM for modelling large scale powder compaction with wide size distributions. Powder Technol. 2018, 333, 219–228. [Google Scholar] [CrossRef]
- Skrinjar, O.; Larsson, P.-L. Cold compaction of composite powders with size ratio. Acta Mater. 2004, 52, 1871–1884. [Google Scholar] [CrossRef]
- Gethin, D.T.; Lewis, R.W.; Ransing, R.S. A discrete deformable element approach for the compaction of powder systems. Model. Simul. Mater. Sci. Eng. 2003, 11, 101–114. [Google Scholar] [CrossRef]
- Olsson, E.; Larsson, P.-L. A numerical analysis of cold powder compaction based on micromechanical experiments. Powder Technol. 2013, 243, 71–78. [Google Scholar] [CrossRef]
- Zavaliangos, A. A Multiparticle Simulation of Powder Compaction Using Finite Element Discretization of Individual Particles. Mater. Res. Soc. Symp. Proc. 2002, 731, W7.1.1–W7.1.7. [Google Scholar] [CrossRef]
- Sun, R.; Mi, G. Investigations on the surface temperature field of Ti–6Al and Ti–48Al alloy under continuous laser ablation. Rare Met. Mater. Eng. 2024, 53, 2405–2412. [Google Scholar]
- Wang, T.; Li, X.; Li, Z.; Liu, T.; Wang, X.; Devaraj, A.; Powell, C.A.; dos Santos, J.F. Upcycled high-strength Al alloys from scrap through solid-phase alloying. Nat. Commun. 2024, 15, 10664. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Jiang, H.; Liu, Y.; Hu, Y.; Palakkal, A.S.; Zhou, Y.; Sun, M.; Du, E.; Gong, W.; Zhang, Q.; et al. Metal-halide porous framework superlattices. Nature 2025, 638, 418–424. [Google Scholar] [CrossRef]
- Sun, R.; Mi, G. Influence of alloying elements content on high temperature properties of Ti–V–Cr and Ti–Al–V series titanium alloys: A JMatPro Program Calculation Study. J. Phys. Conf. Ser. 2023, 2639, 012019. [Google Scholar] [CrossRef]
- Zou, Q.; Wu, D.; Yu, X.; Li, M.; An, X.; Jie, J. Elaborating Cu-network structure of W@20Cu composites with Cu-coated W powders via oscillating pressure sintering. J. Alloys Compd. 2025, 1014, 178629. [Google Scholar] [CrossRef]
- Zheng, W.; Shi, Y.; Zhao, L.; Jia, S.; Li, L.; Gan, C.L.; Zhang, D.; Guo, Q. Realizing reversible phase transformation of shape memory ceramics constrained in Al. Nat. Commun. 2023, 14, 7103. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, N.; Yu, Q.; Liu, Z.; Qu, R.; Zhang, J.; Li, S.; Ren, D.; Berto, F.; Zhang, Z.; et al. On the damage tolerance of 3-D printed Mg-Ti interpenetrating-phase composites with bioinspired architectures. Nat. Commun. 2022, 13, 3247. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Y.; Wang, L.; Li, Y.; Lin, F.; Yan, W. Dispersion of reinforcing micro-particles in the powder bed fusion additive manufacturing of metal matrix composites. Acta Mater. 2022, 235, 118086. [Google Scholar] [CrossRef]
- Wang, W.C.; Liu, P.A.; Qi, H.; Liu, J.J.; Liu, T.Y.; Zheng, L. Finite element analysis of densification of Fe-40at%Al composite powders. AIP Adv. 2019, 9, 015311. [Google Scholar] [CrossRef]
- Wang, C.; Gong, Y.; Cunning, B.V.; Lee, S.; Le, Q.; Joshi, S.R.; Buyukcakir, O.; Zhang, H.; Seong, W.K.; Huang, M.; et al. A general approach to composites containing nonmetallic fillers and liquid gallium. Sci. Adv. 2021, 7, eabe3767. [Google Scholar] [CrossRef] [PubMed]
- Han, P.; An, X.; Wang, D.; Fu, H.; Yang, X.; Zhang, H.; Zou, Z. MPFEM simulation of compaction densification behavior of Fe-Al composite powders with different size ratios. J. Alloys Compd. 2018, 741, 473–481. [Google Scholar] [CrossRef]
- Han, P.; An, X.; Zhang, Y.; Huang, F.; Yang, T.; Fu, H.; Yang, X.; Zou, Z. Particulate scale MPFEM modeling on compaction of Fe and Al composite powders. Powder Technol. 2017, 314, 69–77. [Google Scholar] [CrossRef]
- Sun, R.; Mi, G.; Huang, X.; Sui, N. Molecular dynamic simulations of ti-6al and fe-12cr alloys for their heat transfer and oxygen transport behaviors. Mod. Phys. Lett. B Condens. Matter Phys. Stat. Phys. Appl. Phys. 2024, 38, 2350263. [Google Scholar] [CrossRef]
- Pan, X.; Du, L.; Qian, G.; Hong, Y. Microstructure features induced by fatigue crack initiation up to very-high-cycle regime for an additively manufactured aluminium alloy. J. Mater. Sci. Technol. 2024, 173, 247–260. [Google Scholar] [CrossRef]
- Song, J.; Barriere, T.; Liu, S.; Gelin, J.-C. Behaviors of sintering densification for injection molded components in 316L stainless steel powders. Cailiao Kexue Yu Gongyi/Mater. Sci. Technol. 2010, 18, 330–334. [Google Scholar]
- Deng, S.; Zhao, H.; Li, R.; Yuan, T.; Li, L.; Cao, P. The influence of the local effect of electric current on densification of tungsten powder during spark plasma sintering. Powder Technol. 2019, 356, 769–777. [Google Scholar] [CrossRef]
- Pan, X.; Su, H.; Liu, X.; Hong, Y. Multi-scale fatigue failure features of titanium alloys with equiaxed or bimodal microstructures from low-cycle to very-high-cycle loading numbers. Mater. Sci. Eng. A 2024, 890, 145906. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, J.; Ngan, A.H.W.; Ning, Z.; Fan, H.; Huang, Y. Heterogeneity of microstructures in a Cu–Zr based amorphous alloy composite reinforced by crystalline phases. Compos. Part B Eng. 2023, 262, 110823. [Google Scholar] [CrossRef]
- Liu, Y.; Lyu, F.; Ding, F.; Wang, E.; Xu, Y.; Yuan, T.; Deng, C.; Luo, C. Numerical Study on Confinement Effect and Efficiency of Concentrically Loaded RACFRST Stub Columns. Front. Mater. 2021, 8, 630774. [Google Scholar] [CrossRef]
- Long, S.; Yao, X.; Wang, H.; Zhang, X. A dynamic constitutive model for fiber-reinforced composite under impact loading. Int. J. Mech. Sci. 2020, 166, 105226. [Google Scholar] [CrossRef]
- Shima, S.; Oyane, M. Plasticity theory for porous metals. Int. J. Mech. Sci. 1976, 18, 285–291. [Google Scholar] [CrossRef]
- Huang, P.Y. Further study on compaction equations in powder metallurgy. Powder Metall. Technol. 1980, 2, 15–20. [Google Scholar]
- Heckel, R.W. Density-Pressure Relationships in Powder Compaction. Trans. Metall. Soc. AIME 1961, 221, 671–675. [Google Scholar]
- Huang, F.; An, X.; Zhang, Y.; Yu, A. Multi-particle FEM simulation of 2D compaction on binary Al/SiC composite powders. Powder Technol. 2017, 314, 39–48. [Google Scholar] [CrossRef]
- Zhang, Y.; An, X.; Zhang, Y. Multi-particle FEM modeling on microscopic behavior of 2D particle compaction. Appl. Phys. A 2015, 118, 1015–1021. [Google Scholar] [CrossRef]










| Proposer | , , and as a Function of | Equation | Prerequisite |
|---|---|---|---|
| Shima & Oyane [32] | ; | ||
| Stacked Structure | Particle Size Ratio RCu:RAl | Al Content wt.% | Number of Cu Particles | Number of Al Particles | Initial Packing Density |
|---|---|---|---|---|---|
| Random I | 1:2 | 30% | 174 | 26 | 0.7915 |
| Random II | 1:3 | 30% | 172 | 28 | 0.8054 |
| Random III | 1:4 | 30% | 183 | 17 | 0.8035 |
| Random IV | 1:5 | 30% | 189 | 11 | 0.8047 |
| Certain Year | Inventor | Equation | Parameter Introduction |
|---|---|---|---|
| 1961 | Heckel | (3) | , —ratio |
| 1964–1980 | Huangpei Yun | (4) | —dense metal density —Initial billet density —Density of compression blanks —repressive —Equivalent to pressing module —Equivalent to the inverse of the sclerosis index —Equivalent to sclerosis index |
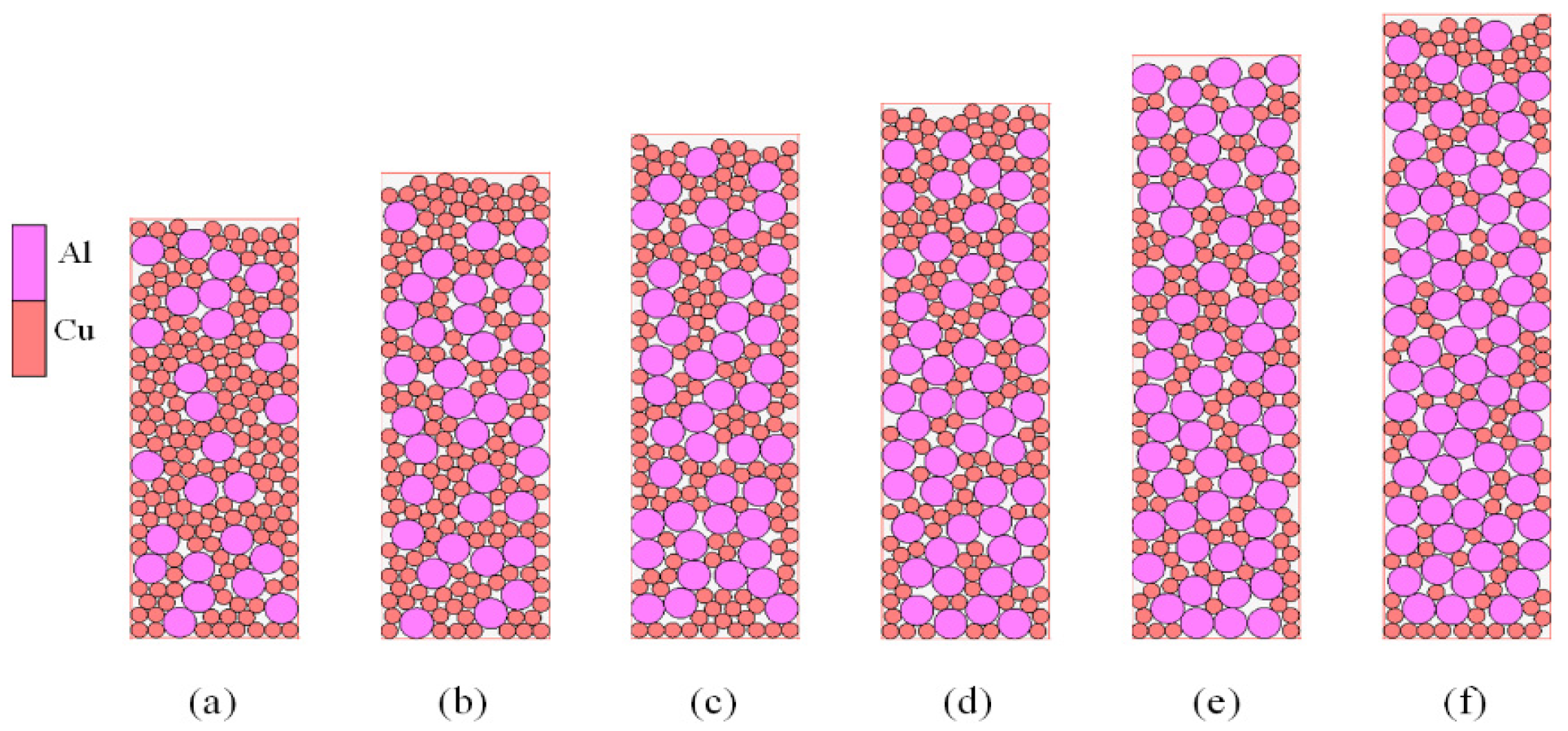
| Stacked Structure | Particle Size Ratio | Al Content wt.% | Number of Cu Particles | Number of Al Particles | Initial Relative Density |
|---|---|---|---|---|---|
| Random (a) | 1:2 | 15% | 174 | 26 | 0.7855 |
| Random (b) | 1:2 | 20% | 165 | 35 | 0.7809 |
| Random (c) | 1:2 | 25% | 156 | 44 | 0.7804 |
| Random (d) | 1:2 | 30% | 147 | 53 | 0.7915 |
| Random (e) | 1:2 | 35% | 138 | 62 | 0.7863 |
| Random (f) | 1:2 | 40% | 129 | 71 | 0.7839 |
| Materials | Young’s Modulus E (GPa) | Poisson’s Ratio υ | Strength Factor A (MPa) | Hardening Index m |
|---|---|---|---|---|
| Cu | 120 | 0.3 | 448 | 0.126 |
| Materials | Young’s Modulus E (GPa) | Poisson’s Ratioυ | Strength Factor A (MPa) | Hardening Index m |
|---|---|---|---|---|
| Al | 62.59 | 0.33 | 225.9 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhao, Y.; Weng, M.; Dong, K.; Qi, H.; Wang, W.; Li, C. DEM-FEM Simulation of Double Compaction of Cu and Al Composite Metal Powders with Multiple Particle Sizes. Crystals 2025, 15, 526. https://doi.org/10.3390/cryst15060526
Wang W, Zhao Y, Weng M, Dong K, Qi H, Wang W, Li C. DEM-FEM Simulation of Double Compaction of Cu and Al Composite Metal Powders with Multiple Particle Sizes. Crystals. 2025; 15(6):526. https://doi.org/10.3390/cryst15060526
Chicago/Turabian StyleWang, Wenchao, Yuanbo Zhao, Mengyao Weng, Kangxing Dong, Hui Qi, Wenzhe Wang, and Chongming Li. 2025. "DEM-FEM Simulation of Double Compaction of Cu and Al Composite Metal Powders with Multiple Particle Sizes" Crystals 15, no. 6: 526. https://doi.org/10.3390/cryst15060526
APA StyleWang, W., Zhao, Y., Weng, M., Dong, K., Qi, H., Wang, W., & Li, C. (2025). DEM-FEM Simulation of Double Compaction of Cu and Al Composite Metal Powders with Multiple Particle Sizes. Crystals, 15(6), 526. https://doi.org/10.3390/cryst15060526





