Abstract
Batteries based on heavier alkali ions are considered promising candidates to substitute for current Li-based technologies. In this theoretical study, we characterize the structural properties of a novel material, i.e., F-doped RbTiOPO (RbTiPOF, RTP:F), and discuss aspects of its electrochemical performance in Rb-ion batteries (RIBs) using density functional theory (DFT). According to our calculations, RTP:F is expected to retain the so-called KTiOPO (KTP)-type structure, with lattice parameters of Å, Å, and Å. Due to the doping with F, the crystal features eight extra electrons per unit cell, whereby each of these electrons is trapped by one of the surrounding Ti atoms in the cell. Notably, the ground state of the system corresponds to a ferromagnetic spin configuration (i.e., ). The deintercalation of Rb leads to the oxidation of the Ti atoms in the cell (i.e., from Ti to Ti) and to reduced magnetic moments. The material promises interesting electrochemical properties for the cathode: rather high average voltages above V and modest volume shrinkages below 13% even in the fully deintercalated case are predicted.
1. Introduction
Although lithium-ion batteries (LIBs) have gradually replaced traditional dry-cell batteries, e.g., in portable devices and electric vehicles [1,2,3,4,5], the low abundance of lithium (Li) in the Earth’s crust prevent the direct application of these technologies for the energy storage on the large scale required for, e.g., the development of renewable forms of energy. Showing higher abundances and similar properties, heavier alkali ions like sodium (Na) and potassium (K) are therefore obvious candidates to substitute for Li in batteries [6,7,8,9,10,11,12,13,14,15,16,17,18].
In this context, although the higher cost of rubidium (Rb) might hinder its application on the large scale, rubidium-based technologies (RIBs) are also of increasing interest [19,20]. These technologies are not only expected to lead to high working voltages, given the closeness of the standard redox potentials of Li/Li and Rb/Rb [21]. Some recent studies have suggested that they are also characterized by very low activations barriers for the ionic migration through the material [18,19,20]. In addition, RIBs are discussed to be excellent devices in cold-atom physics for the generation of alkali vapors [22,23,24,25]. Nevertheless, finding appropriate electrode materials represents a major challenge for the realization of RIBs [19]. In fact, the larger ionic radius hampers the intercalation/deintercalation cycles, since it could cause more significative volume distortions, which in turn could damage the electrodes. This is of particular relevance for the anode material, since standard graphite-based anodes are not suitable to accommodate for the larger Rb atoms. Here, H-MoS monolayers [20] as well as porous graphene [19] are discussed as promising alternatives. However, since RIBs are still in an early stage of their development, the basic electrochemical properties of potential new electrode materials must be investigated.
Already well-established in optics, the application field of the ferroelectric potassium titanyl phosphate (KTiOPO, KTP) crystal family has been recently further extended to electrochemistry [17,18,26,27,28,29,30,31,32,33,34,35,36,37]: These materials are expected to lead to high working voltages upon the (de)intercalation of alkali atoms. In addition, they promise efficient charging of batteries. The reason for this can be found in their peculiar crystal structure. More precisely, the ferroelectric properties of KTP-type compounds are determined by the mobility of the alkali ions, along the crystal direction, which are characterized by low activation barriers for the ion migration [38].
The (electrochemical) properties of the KTP can be further modified by F doping, i.e., replacing the Ti-Ti coordinated oxygen with F. In KTP, this type of F doping has been reported to introduce ferromagnetic properties into the material [17]. In this theoretical ab initio study, we want to evaluate F doping in connection with the KTP-type crystal family adapted to rubidium-based technology (RIB). More specifically, we evaluate F-doped RbTiOPO (RbTiPOF, RTP:F), for Rb-ion electrodes, which also holds the advantage of not containing any hazardous element like arsenic or vanadium.
2. Materials and Methods
The general constitution formula of the KTP-type family reads MTiOXO. Here, the M sites are occupied by (a mixture of) alkali metals or NH. X, on the other hand, stands for P or As [38,39,40,41]. In addition, the Ti sites can alternatively be occupied by vanadium (V) [18,30,31,32,33], and also a Si/Nb co-doping was possible by a partial variation of the X and Ti sites, respectively [42].
KTP-type crystals adopt an orthorhombic crystal structure with the space group . The unit cell contains 64 atoms, which can be reduced to each two nonequivalent Ti, X, and M sites and ten nonequivalent O sites [38,39,40,41]. A schematic representation of the crystal is shown in Figure 1. Note that all the crystal geometries as well as spin densities shown in this work are visualized using the open-access program Visualization for Electronic and Structural analysis (VESTA) [43]. Clearly, two substructures can be identified in Figure 1a: (i) the M atoms are ionized and only weakly bonded in the lattice and (ii) chains of distorted TiO octahedra and XO tetrahedra cross the crystal along the and the crystal directions. The polyhedra are thereby connected via mutual O atoms, which can be thus further classified according to their coordination into two groups. More precisely, eight atoms (i.e., O(1)–O(8)) are each coordinated to one Ti and one P atom; the remaining two (i.e., O(9) and O(10)), on the other hand, are coordinated to Ti, exclusively. The two nonequivalent Ti sites differ with respect to the angle these O atoms form with the central Ti atom. More precisely, the bond angle amounts to about and in the case of Ti(1) and Ti(2) [41], respectively (see also Figure 1b). Regarding the M sites, on the other hand, and are coordinated to eight and nine O atoms, respectively, whereby the cage is larger by about 25% compared to the cage [44]. Consequently, Rb substitutional atoms are more likely to occupy the latter site [45].
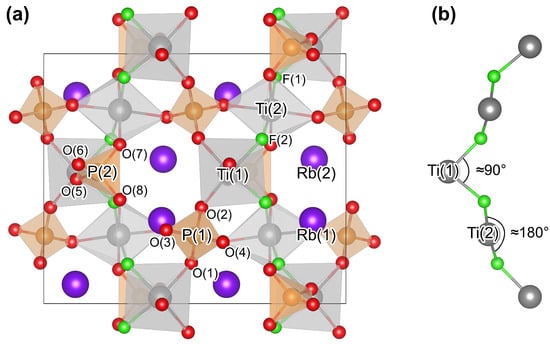
Figure 1.
(a) The crystal structure of F-doped RbTiOPO (RTP:F) is shown to illustrate the KTP-type crystal structure. The green atoms correspond to the fluorine (F) atoms located at the lattice sites O(9) and O(10). Chains of TiOF octahedra and PO tetrahedra cross the crystal along the and crystal directions. The Rb ions, on the other hand, form a positively charged sublattice. (b) Visualization of the difference between F F and F F bond angles.
For the desired F-doped rubidium titanyl phosphate (RbTiPOF, RTP:F), we start from the RbTiOPO (RTP) unit cell and replace all the Ti-Ti coordinated O atoms with fluorine (F), see Figure 1a. The resulting structure is modeled and fully relaxed using periodic boundary conditions and density functional theory (DFT). The calculations are performed using the open-source Quantum ESPRESSO package (v. 6.3) [46,47]; the DFT-predicted crystallographic and electric properties of the resulting structure are presented and discussed in Section 3.1. During structure optimization, atomic positions and lattice parameters are relaxed until the fluctuations in the total energy (residual forces) are below Ry ( Ry/bohrs). Thereby, converged ground-state geometries are obtained by expanding the electron wave functions into plane waves using 90 Ry as the cut off. Due to the small band dispersion, the Brillouin sampling can be reduced without loss of accuracy to the Baldereschi point [48]. Norm-conserving pseudopotentials are applied for the description of electron–ion interactions. These have been generated using the following occupations: Ti , Rb , P , O , and F. For the modeling of the electronic exchange and correlation (XC) effects the generalized gradient approximation (GGA), more precisely, the revised formulation for solid-state systems by Perdew, Burke, and Ernzerhof (PBEsol) [49], is used as a starting point.
Upon F doping, the crystal under consideration features eight additional electrons per unit cell compared to the stoichiometric RbTiOPO host. The excess electrons are thereby trapped by the Ti sites in the cell. As F doping thus alters the occupation of the Ti shell, a correct description of the electronic properties of the strongly correlated Ti electrons is crucial. Here, we apply either hybrid functionals or a Hubbard energy correction (restricted to the Ti shell). Both methods, assure a correct localization of states by promoting an integer occupation number. For the inclusion of the Hubbard correction, the simplified scheme by Cococcioni and de Gironcoli [50] is applied. To determine the magnitude of the energy correction, we adopt the self-consistent scheme described in Ref. [50]. This results in eV and eV for the sites Ti(1) and Ti(2), respectively. Since the values are very close, we decide to apply the same value of eV to both Ti sites. The use of a common effective-U value is evaluated by recalculating the electrochemical properties of the PBEsol-relaxed geometries using different hybrid functionals (i.e., B3LYP [51,52,53], HSE [54], and PBE0 [55]), featuring specific fractions of exact exchange (EXX) from Hartree–Fock theory. These functionals, in fact, are known to lead to (i) a reliable description of electronic structures [56,57,58] and (ii) an accurate prediction of voltages [59].
To evaluate the potential electrochemical performance of RTP:F in Rb-ion batteries, we focus on the computation of the average open circuit voltages and volume deformations arising from (i) the deintercalation of Rb atoms from the crystal for the simulation of the cathode and (ii) the intercalation of additional Rb for anode application. In both cases, the related volume deformation should be moderate, in order to allow a robust long-term cycling of the battery. On the other hand, the cathode should ideally feature a rather high value, while the anode a rather low value for , in order to allow for high working voltages, whereby the open circuit voltage (OCV) averaged over a full charge/discharge cycle is defined as follows [27,60,61,62,63,64]
where x is the concentration of (de)intercalated Rb per formula unit and the elementary charge. , on the other hand, is the change in Gibbs free energy referring to the reactions and their explicit directions
taking place at the cathode and anode during charging, respectively. However, in the simplest approximation, DFT calculations are performed at K and vanishing pressure so that can be approximated by the change in the DFT total (internal) energy , yielding
whereby the quantity corresponds to the (de)intercalation energy per formula unit, which is defined as
with , and indicating the energy of one formula unit of stoichiometric RbTiPOF, RbTiPOF and RbTiPOF, respectively. , on the other hand, is the energy of an isolated, (quasi-)interaction-free Rb atom.
In addition, we determine the gravimetric energy density , which is a measure of the amount of charge which can be stored per unit mass, as [64]
with as the molar mass of one formula unit of RbTiPOF and F as the Faraday constant. Combining the average voltage and the capacity, one can then determine the energy density as [64]
3. Results and Discussion
3.1. Crystallographic and Electric Properties of Stoichiometric RTP:F
Due to the F doping, eight extra electrons are introduced in the RTP:F unit cell compared to the pristine RTP host. Each of these extra electrons are trapped by one nearby Ti atom, which consequently transforms into the oxidation state +3 (see also Figure 2a). The extra electrons are instrumental for both the electrochemical as well as the electronic properties. Notably, as it has also been reported for F-doped KTiOPO (KTiPOF, KTP:F) [17], the resulting material provides specific ferromagnetic properties. The corresponding ground state of the system provides a ferromagnetic spin configuration with eight unpaired electrons, i.e., with total spin . This can also be seen from the spin-polarized density of states (pDOS) plotted in Figure 2a: The spin-up channel features eight additional occupied states compared to the spin-down channel, with the Ti(1) states clearly separated from the Ti(2) states. Since the unpaired spin-up states are depopulated during the deintercalation of Rb from the cell, we refer to these states as occupied defect states in the following.
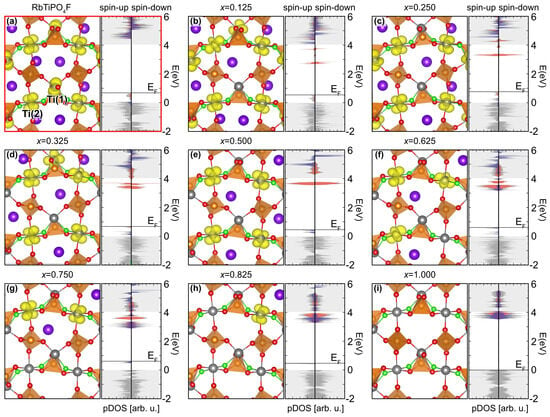
Figure 2.
(a) Geometry (l.h.s.) and pDOS (r.h.s.) of the stoichiometric RTP:F unit cell after geometry relaxation. The Ti(1) and T(2) states are depicted in red and blue, respectively. Notably, they are clearly separated from each other. (b–i) Geometries and pDOS of RbTiPOF after the deintercalation of different concentrations – of Rb. The yellow isosurfaces represent the spin-density difference of the spin-up and the spin-down channel, clearly showing the localization of the occupied defect states at the Ti sites and their consequent oxidation from Ti to Ti upon the deintercalation of Rb. Note that for (i.e., structures (b–e)) only Ti(1) have been oxidized. indicates the Fermi level position.
After geometry relaxation, the basic KTP-type structure is still retained, and the atomic positions do not change significantly compared to those in RTP. The lattice constants of RTP:F are predicted to be Å, Å, and Å, resulting in a unit cell volume of Å. To the best of our knowledge, RTP:F has not been synthesized yet, so experimental data on its crystal structure are not available. It is thus illustrative to compare the calculated lattice parameters of RTP:F with other related crystals, compiled in Table 1: They are slightly larger than the one reported for stoichiometric RTP [65,66]: More precisely, the unit-cell volume of RTP:F is larger by % than the DFT one calculated for RTP in Ref. [65]. Interestingly, this deviation is similar to the one (i.e., %) between the DFT () volumes reported for stoichiometric [67] and F-doped KTP [17]. Thus, our values appear to be reasonable. For a conclusive proof, however, the F-doped crystal needs to be synthesized and structurally analyzed, e.g., via powder X-ray diffraction (XRD).

Table 1.
Lattice constants (, and c) and unit-cell volumes (V) of different KTP-type compounds.
3.2. Electrochemical Performance of RTP:F
For the cathode, Rb-deficient RbTiPOF, with –, is modeled by deintercalating up to eight Rb atoms from the stoichiometric RTP:F unit cell. For each concentration x, one defect geometry is simulated. As mentioned before, due to the different cage sizes, the Rb atoms preferentially occupy the sites in the cell. Thus, for we only deintercalate Rb(1) atoms from the cell. The Rb(2) atoms are then deintercalated for higher vacancy concentrations.
The so-obtained ground-state geometries, together with the corresponding pDOS, are depicted in Figure 2b–i. According to our calculations, for each deintercalated atom, one of the nearby Ti atoms oxidizes (from Ti to Ti). This is clearly shown by the spin density (i.e., the yellow isosurfaces) plotted in Figure 2b–i. Due to the peculiar magnetic properties of RTP:F, in fact, we can refer to the spin density as a direct measure for the charge transfer in the material. Consequently, additional charge analyses [68,69] are not required in this specific case.
Upon oxidation of the Ti atoms, the initially occupied defect states of the spin-up channel are emptied and additional empty defect states arise in the fundamental band gap. Notably, the position of the F atoms in the TiOF octahedra has a major influence on the oxidation of the central Ti atom. In fact, as already pointed out in Ref. [17], the Ti(1) sites (cis-positioning) are more prone to oxidize compared to the Ti(2) sites (trans-positioning): the oxidation of the latter only takes place if all the Ti(1) present in the cell has already been oxidized (i.e., ).
Using the PBEsol ground-state energies to calculate the average voltages for each concentration x of deintercalated Rb via Equation (4), we obtain the red curve plotted in Figure 3a. Interestingly, our data suggest a V-shaped voltage profile: for , in fact, our calculations already predict a high voltage of about V. Then, by deintercalating up to four Rb atoms, the voltage slightly decreases to the minimum value of V. Finally, for high concentrations x, the voltage increases again to the intermediate value of V.
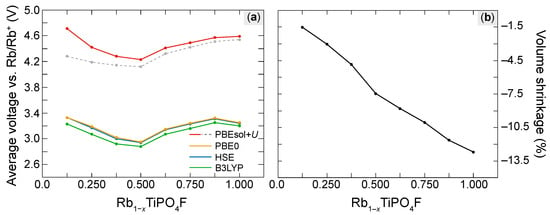
Figure 3.
(a) Average voltage of the RTP:F cathode as predicted under the application of different levels of theory: The red solid and the grey dashed curve are obtained using the PBEsol formalism, whereby the latter implies the DFT ground-state energy of a local minimum of the stoichiometric unit cell. The remaining orange, blue, and green voltage curves are obtained under the application of hybrid functionals, i.e., PBE0, HSE, and B3LYP, respectively. (b) Volume shrinkage of the cathode upon the deintercalation of Rb (calculated using the PBEsol formalism).
Despite the structural similarities between RTP:F and KTP:F, the voltage profile predicted here is in some qualitative contrast to the one discussed by Fedotov et al. in Ref. [17]. Nevertheless, also in KTP:F, a sequential reduction in the different Ti sites is reported, which also has a major influence on the voltage profile: For , the voltage rises steadily with the concentration of deintercalated K. For higher values of x, on the other hand, a potential step of V and a consequent voltage plateau is reported. The voltage plateau is explained by the fact that only thermodynamically stable phases have been considered for the computation of the average voltages. The potential step, on the other hand, was attributed to (i) different redox potential of the two nonequivalent Ti sites and mainly to (ii) electrostatic interactions between the remaining K in the cell.
Although we have modeled only one of the possible configurations for each concentration x, which does not necessarily match with the energetically most favorable ones, there is clear evidence that the lineshape is indeed related to the tendency toward high-spin states as well as to the stronger electrostatic interactions between the Rb ions. In fact, the resulting forces hamper the structural relaxation of the system. As a consequence, the material features plenty of different local minima. These differ mainly by the magnitude of the energy contributions caused by the Coulomb interactions, whereby the energetically most favorable configuration corresponds to the structure featuring higher values for the Coulomb interactions. Notably, the ground-state energy of the stoichiometric RTP:F cell has a strong influence on the qualitative shape of the calculated voltage profile: Recalculating the PBEsol voltages using the ground-state energy of a local minimum for the stoichiometric bulk cell, we obtain the dashed gray curve in Figure 3a. Clearly, the deviation from the red curve is more pronounced the more Rb (and as a consequence, interacting ions) is present in the cell. To validate our data, we thus introduce different hybrid functionals onto the PBEsol-relaxed geometries. The hybrid functionals yield the orange (PBE0), the blue (HSE), and the green (B3LYP) voltage curves in Figure 3a. Although these values are lower by up to V compared to the corresponding PBEsol voltages, the hybrid voltage curves are in good qualitative agreement with the red PBEsol curve. Thus, we expect the shape of the PBEsol curve related to the more energetically favorable structure to be reliable. Even when assuming the smaller values of the hybrid functionals (3.2 eV in average), the predicted voltage is still comparable with those of current Li-ion cathodes, e.g., 3.5 eV for LiFePO[70] or roughly 4 V for LiCoO [71].
Upon continuous removal of Rb from the cathode, the molar mass of the crystal is decreasing. According to Equation (7), RTP:F can reach a maximum gravimetric capacity of mAh/g in the fully deintercalated case. This value is between the ones of KTP and KVPOF, i.e., mAh/g [26] and 162.5 mAh/g [26], respectively. As a result, its PBEsol gravimetric energy density amounts to Wh/kg, which is very close to the one predicted for KTP (i.e., Wh/kg) [26], but higher compared to the one of KTA and KVPOF, i.e., Wh/kg [37], and Wh/kg [26], respectively. The theoretical maximum capacity of RTP:F is also almost identical to the one of LiFePO of 170 mAh/g [72,73], which is commonly applied in LIBs. Nevertheless, the actual performance of the KTP:F electrode depends critically on whether, technologically, the fully deintercallated case can be reached. Future experimental studies are required for final clarification. However, our DFT calculations are promising. Even in the fully deintercalled case, there is no hint for critical structural transformations. The volume is compressed, but the KTP-type crystal structure is retained. The volume compression upon the deintercalation of Rb in dependence of the concentration of deintercalated Rb is plotted in Figure 3b. The volume shrinks almost linearly with the concentration x, reaching the maximum compression of % when all Rb are removed from the cell. Note that the slight deviation from a linear behavior at could be related to the high-symmetry configuration adopted by the Rb atoms retained in the cell. The maximum volume shrinkage of RTP:F is larger than that of KTP:F (%) [17], but it is in good agreement with the value % predicted for RbVPOF [18]. This finding is explained by the larger ionic radius of Rb compared to K. As already mentioned above, our calculations do not hint at any drastic geometric transformation, which could hamper a reversible intercalation/deintercalation of Rb atoms. In fact, the polyhedral network is barely affected by the deintercalation of Rb. This observation and the other strong similarities with KTP:F [17] suggest that RTP:F should also be very robust upon cycling.
Since other KTP-type compounds have already been discussed to be promising under the application as anodes [27,30,34,35,36,37], we also evaluate its use as anode material. According to our DFT total-energy calculations, the intercalation of one additional Rb atom in the RTP:F unit cell (i.e., RbTiPOF) causes the reduction of a nearby Ti(2) atom (i.e., a Ti center). This results in a still promising average PBEsol voltage of V and a volume expansion of 2%, which is only slightly higher compared to the volume expansion per intercalated K atom in KTP [27] or KTiOAsO [37]. Nevertheless, we do not succeed in converging calculations with a larger number of extra Rb atoms. Obviously, the intercalation of large amounts of Rb in the material could be hampered by the strong electrostatic as well as spin interactions present in the material.
4. Conclusions
In this work, the novel material RbTiPOF (RTP:F) has been (i) structurally characterized and (ii) investigated as an electrode for Rb-ion batteries (RIBs) using density functional theory (DFT). Particular attention was given to the average voltages and the volume deformation caused by the deintercalation of Rb atoms from the crystal.
We found that the the material retains the so-called KTP-type structure with lattice parameters of Å, Å, and Å, even in the fully deintercallated case. Furthermore, we found that the F doping causes excess electrons in the crystal, which are localized at Ti sites. Each unpaired electron thereby occupies an individual orbital, resulting in a ferromagnetic ground-state spin configuration. Therefore, the application of the Hubbard correction (or hybrid functionals) is crucial to properly describe the localization of the Ti electrons. Moreover, a sequential oxidation was observed during the deintercalation process, whereby all Ti(1) sites oxidize before the Ti(2) sites.
The cathode material is predicted to give rise to rather high average voltages, i.e., up to V and V under the application of the PBEsol formalism and hybrid DFT, respectively. In addition, the volume shrinkage is relatively modest, i.e., less than 13% in the fully deintercalated case. The anode, on the other hand, features a still promising PBEsol voltage (i.e., V for one intercalated Rb), but the intercalation of further Rb atoms seems to be hindered by the strong electrostatic as well as spin interactions within the material. Whereas this effect seems to be detrimental for anode application, the magnetic interaction promises to be beneficial in case of cathode application. Our DFT-calculated data suggest a decent electrochemical performance of RTP:F, where the ferromagnetic spin configuration might be exploited during applications. In fact, recent studies have shown that the application of external magnetic fields can enhance the performance of electrodes [74,75]. This effect might be even more pronounced by the ferromagnetic properties of RTP:F.
Author Contributions
Conceptualization, A.B. and U.G.; methodology, A.B., Y.X. and U.G.; investigation, A.B. and Y.X.; writing—original draft preparation, A.B., Y.X., W.G.S. and U.G.; writing—review and editing, A.B., W.G.S. and U.G.; visualization, A.B. and Y.X.; project administration, A.B. and U.G.; funding acquisition, W.G.S. and U.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG) from TRR 142/3- 2023, Project No. 231447078.
Data Availability Statement
The data that support the findings of this study are contained within the article or are available from the corresponding author upon reasonable request.
Acknowledgments
The authors gratefully acknowledge the Paderborn Center for Parallel Computing (PC) and the High Performance Computing Center Stuttgart (HLRS) for the provided computational resources.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Placke, T.; Kloepsch, R.; Dühnen, S.; Winter, M. Lithium ion, lithium metal, and alternative rechargeable battery technologies: The odyssey for high energy density. J. Solid State Electrochem. 2017, 21, 1939–1964. [Google Scholar] [CrossRef]
- Blomgren, G.E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2016, 164, A5019. [Google Scholar] [CrossRef]
- Winter, M.; Brodd, R.J. What Are Batteries, Fuel Cells, and Supercapacitors? Chem. Rev. 2004, 104, 4245–4270. [Google Scholar] [CrossRef] [PubMed]
- Andre, D.; Kim, S.J.; Lamp, P.; Lux, S.F.; Maglia, F.; Paschos, O.; Stiaszny, B. Future generations of cathode materials: An automotive industry perspective. J. Mater. Chem. A 2015, 3, 6709–6732. [Google Scholar] [CrossRef]
- Patry, G.; Romagny, A.; Martinet, S.; Froelich, D. Cost modeling of lithium-ion battery cells for automotive applications. Energy Sci. Eng. 2015, 3, 71–82. [Google Scholar] [CrossRef]
- Slater, M.D.; Kim, D.; Lee, E.; Johnson, C.S. Sodium-Ion Batteries. Adv. Funct. Mater. 2013, 23, 947–958. [Google Scholar] [CrossRef]
- Rudola, A.; Rennie, A.J.R.; Heap, R.; Seyyed Meysami, S.; Lowbridge, A.; Mazzali, F.; Sayers, R.; Wright, C.J.; Barker, J. Commercialisation of high energy density sodium-ion batteries: Faradion’s journey and outlook. J. Mater. Chem. A 2021, 9, 8279–8302. [Google Scholar] [CrossRef]
- Komaba, S.; Murata, W.; Ishikawa, T.; Yabuuchi, N.; Ozeki, T.; Nakayama, T.; Ogata, A.; Gotoh, K.; Fujiwara, K. Electrochemical Na Insertion and Solid Electrolyte Interphase for Hard-Carbon Electrodes and Application to Na-Ion Batteries. Adv. Funct. Mater. 2011, 21, 3859–3867. [Google Scholar] [CrossRef]
- Kim, S.W.; Seo, D.H.; Ma, X.; Ceder, G.; Kang, K. Electrode Materials for Rechargeable Sodium-Ion Batteries: Potential Alternatives to Current Lithium-Ion Batteries. Adv. Energy Mater. 2012, 2, 710–721. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Myung, S.T.; Sun, Y.K. Sodium-ion batteries: Present and future. Chem. Soc. Rev. 2017, 46, 3529–3614. [Google Scholar] [CrossRef]
- Pan, H.; Hu, Y.S.; Chen, L. Room-temperature stationary sodium-ion batteries for large-scale electric energy storage. Energy Environ. Sci. 2013, 6, 2338–2360. [Google Scholar] [CrossRef]
- Xu, Y.; Titirici, M.; Chen, J.; Cora, F.; Cullen, P.L.; Edge, J.S.; Fan, K.; Fan, L.; Feng, J.; Hosaka, T.; et al. 2023 roadmap for potassium-ion batteries. J. Phys. Energy 2023, 5, 021502. [Google Scholar] [CrossRef]
- Rajagopalan, R.; Tang, Y.; Ji, X.; Jia, C.; Wang, H. Advancements and Challenges in Potassium Ion Batteries: A Comprehensive Review. Adv. Funct. Mater. 2020, 30, 1909486. [Google Scholar] [CrossRef]
- Min, X.; Xiao, J.; Fang, M.; Wang, W.; Zhao, Y.; Liu, Y.; Abdelkader, A.M.; Xi, K.; Kumar, R.V.; Huang, Z. Potassium-ion batteries: Outlook on present and future technologies. Energy Environ. Sci. 2021, 14, 2186–2243. [Google Scholar] [CrossRef]
- Wu, X.; Leonard, D.P.; Ji, X. Emerging Non-Aqueous Potassium-Ion Batteries: Challenges and Opportunities. Chem. Mater. 2017, 29, 5031–5042. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Guo, Z. Approaching high-performance potassium-ion batteries via advanced design strategies and engineering. Sci. Adv. 2019, 5, eaav7412. [Google Scholar] [CrossRef]
- Fedotov, S.S.; Luchinin, N.D.; Aksyonov, D.A.; Morozov, A.V.; Ryazantsev, S.V.; Gaboardi, M.; Plaisier, J.R.; Stevenson, K.J.; Abakumov, A.M.; Antipov, E.V. Titanium-based potassium-ion battery positive electrode with extraordinarily high redox potential. Nat. Commun. 2020, 11, 1484. [Google Scholar] [CrossRef] [PubMed]
- Fedotov, S.S.; Samarin, A.S.; Nikitina, V.A.; Aksyonov, D.A.; Sokolov, S.A.; Zhugayevych, A.; Stevenson, K.J.; Khasanova, N.R.; Abakumov, A.M.; Antipov, E.V. Reversible facile Rb+ and K+ ions de/insertion in a KTiOPO4-type RbVPO4F cathode material. J. Mater. Chem. A 2018, 6, 14420–14430. [Google Scholar] [CrossRef]
- Lu, B.; Ru, N.; Duan, J.; Li, Z.; Qu, J. In-Plane Porous Graphene: A Promising Anode Material with High Ion Mobility and Energy Storage for Rubidium-Ion Batteries. ACS Omega 2023, 8, 21842–21852. [Google Scholar] [CrossRef]
- Lu, B.; Liu, X.; Qu, J.; Li, Z. Monolayer H-MoS2 with high ion mobility as a promising anode for rubidium (cesium)-ion batteries. Nanoscale Adv. 2022, 4, 3756–3763. [Google Scholar] [CrossRef]
- Sultana, I.; Rahman, M.M.; Ramireddy, T.; Chen, Y.; Glushenkov, A.M. High capacity potassium-ion battery anodes based on black phosphorus. J. Mater. Chem. A 2017, 5, 23506–23512. [Google Scholar] [CrossRef]
- McGilligan, J.P.; Moore, K.R.; Kang, S.; Mott, R.; Mis, A.; Roper, C.; Donley, E.A.; Kitching, J. Dynamic Characterization of an Alkali-Ion Battery as a Source for Laser-Cooled Atoms. Phys. Rev. Appl. 2020, 13, 044038. [Google Scholar] [CrossRef]
- Kang, S.; Mott, R.P.; Gilmore, K.A.; Sorenson, L.D.; Rakher, M.T.; Donley, E.A.; Kitching, J.; Roper, C.S. A low-power reversible alkali atom source. Appl. Phys. Lett. 2017, 110, 244101. [Google Scholar] [CrossRef]
- Kang, S.; Mott, R.P.; Mis, A.V.; Roper, C.S.; Donley, E.A.; Kitching, J. Active stabilization of alkali-atom vapor density with a solid-state electrochemical alkali-atom source. Opt. Express 2018, 26, 3696–3701. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Moore, K.R.; McGilligan, J.P.; Mott, R.; Mis, A.; Roper, C.; Donley, E.A.; Kitching, J. Magneto-optic trap using a reversible, solid-state alkali-metal source. Opt. Lett. 2019, 44, 3002–3005. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Cai, X.; Yin, H.; Li, Y.; Lin, W.; Huang, S.; Zhang, Y. A new candidate in polyanionic compounds for a potassium-ion battery cathode: KTiOPO4. J. Phys. Chem. Lett. 2021, 12, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Cai, X.; Li, Y.; Fang, Z.; Li, Y.; Lin, W.; Huang, S.; Zhang, Y. DFT investigations of KTiOPO4Mx (M = K, Na, and Li) anodes for alkali-ion battery. J. Chem. Phys. 2022, 156, 204702. [Google Scholar] [CrossRef] [PubMed]
- Fedotov, S.S.; Samarin, A.S.; Antipov, E.V. KTiOPO4-structured electrode materials for metal-ion batteries: A review. J. Power Sources 2020, 480, 228840. [Google Scholar] [CrossRef]
- Katorova, N.S.; Fedotov, S.S.; Rupasov, D.P.; Luchinin, N.D.; Delattre, B.; Chiang, Y.M.; Abakumov, A.M.; Stevenson, K.J. Effect of Concentrated Diglyme-Based Electrolytes on the Electrochemical Performance of Potassium-Ion Batteries. ACS Appl. Energy Mater. 2019, 2, 6051–6059. [Google Scholar] [CrossRef]
- Tan, H.; Du, X.; Huang, J.Q.; Zhang, B. KVPO4F as a novel insertion-type anode for potassium ion batteries. Chem. Commun. 2019, 55, 11311–11314. [Google Scholar] [CrossRef]
- Fedotov, S.S.; Khasanova, N.R.; Samarin, A.S.; Drozhzhin, O.A.; Batuk, D.; Karakulina, O.M.; Hadermann, J.; Abakumov, A.M.; Antipov, E.V. AVPO4F (A = Li, K): A 4 V Cathode Material for High-Power Rechargeable Batteries. Chem. Mater. 2016, 28, 411–415. [Google Scholar] [CrossRef]
- Chihara, K.; Katogi, A.; Kubota, K.; Komaba, S. KVPO4F and KVOPO4 toward 4 volt-class potassium-ion batteries. Chem. Commun. 2017, 53, 5208–5211. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Lin, Y.C.; Liu, J.; Rana, J.; Zhang, H.; Zhou, H.; Chu, I.H.; Wiaderek, K.M.; Omenya, F.; Chernova, N.A.; et al. KVOPO4: A New High Capacity Multielectron Na-Ion Battery Cathode. Adv. Energy Mater. 2018, 8, 1800221. [Google Scholar] [CrossRef]
- Mu, L.; Ben, L.; Hu, Y.S.; Li, H.; Chen, L.; Huang, X. Novel 1.5 V anode materials, ATiOPO4 (A = NH4, K, Na), for room-temperature sodium-ion batteries. J. Mater. Chem. A 2016, 4, 7141–7147. [Google Scholar] [CrossRef]
- Galceran, M.; Rikarte, J.; Zarrabeitia, M.; Pujol, M.C.; Aguiló, M.; Casas-Cabanas, M. Investigation of NaTiOPO4 as Anode for Sodium-Ion Batteries: A Solid Electrolyte Interphase Free Material? ACS Appl. Energy Mater. 2019, 2, 1923–1931. [Google Scholar] [CrossRef]
- Liu, S.; Shao, L.; Zhang, X.; Zhou, M.; Tao, Z.; Chen, J. KTiOPO4 as a novel anode material for sodium-ion batteries. J. Alloys Compd. 2018, 754, 147–152. [Google Scholar] [CrossRef]
- Bocchini, A.; Gerstmann, U.; Bartley, T.; Steinrück, H.G.; Henkel, G.; Schmidt, W.G. Electrochemical performance of KTiOAsO4 (KTA) in potassium-ion batteries from density-functional theory. Phys. Rev. Mater. 2022, 6, 105401. [Google Scholar] [CrossRef]
- Roth, M. Stoichiometry and Domain Structure of KTP-Type Nonlinear Optical Crystals. In Springer Handbook of Crystal Growth; Dhanaraj, G., Byrappa, K., Prasad, V., Dudley, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Masse, R.; Grenier, J.C. Étude des monophosphates du type MITiOPO4 avec MI = K, Rb et Tl. Bull. Minéral. 1971, 94, 437–439. [Google Scholar]
- Bierlein, J.D.; Vanherzeele, H. Potassium titanyl phosphate: Properties and new applications. J. Opt. Soc. Am. B Opt. Phys. 1989, 6, 622–633. [Google Scholar] [CrossRef]
- Tordjman, P.I.; Masse, E.; Guitel, J.C. Structure cristalline du monophosphate KTiPO5. Z. Krist. 1974, 139, 103–115. [Google Scholar] [CrossRef]
- Rangan, K.K.; Prasad, B.R.; Subramanian, C.K.; Gopalakrishnan, J. Coupled substitution of niobium and silicon in potassium titanyl phosphate and arsenate KTiOPO4 and KTiOAsO4. Synthesis and nonlinear optical properties of KTi1-xNbxOX1-xSixO4 (X = P, As). Inorg. Chem. 1993, 32, 4291–4293. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Allan, D.R.; Loveday, J.S.; Nelmes, R.J.; Thomas, P.A. A high-pressure structural study of potassium titanyl phosphate (KTP) up to 5 GPa. J. Phys. Condens. Matter 1992, 4, 2747. [Google Scholar] [CrossRef]
- Thomas, P.A.; Duhlev, R.; Teat, S.J. A comparative structural study of a flux-grown crystal of K0.86Rb0.14TiOPO4 and an ion-exchanged crystal of K0.84Rb0.16TiOPO4. Acta Crystallogr. Sect. B 1994, 50, 538–543. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Baldereschi, A. Mean-Value Point in the Brillouin Zone. Phys. Rev. B 1973, 7, 5212–5215. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Deák, P.; Lorke, M.; Aradi, B.; Frauenheim, T. Optimized hybrid functionals for defect calculations in semiconductors. J. Appl. Phys. 2019, 126, 130901. [Google Scholar] [CrossRef]
- Janotti, A.; Varley, J.B.; Rinke, P.; Umezawa, N.; Kresse, G.; Van de Walle, C.G. Hybrid functional studies of the oxygen vacancy in TiO2. Phys. Rev. B 2010, 81, 085212. [Google Scholar] [CrossRef]
- Komsa, H.P.; Broqvist, P.; Pasquarello, A. Alignment of defect levels and band edges through hybrid functionals: Effect of screening in the exchange term. Phys. Rev. B 2010, 81, 205118. [Google Scholar] [CrossRef]
- Chevrier, V.L.; Ong, S.P.; Armiento, R.; Chan, M.K.Y.; Ceder, G. Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds. Phys. Rev. B 2010, 82, 075122. [Google Scholar] [CrossRef]
- Ceder, G.; Aydinol, M.; Kohan, A. Application of first-principles calculations to the design of rechargeable Li-batteries. Comput. Mater. Sci. 1997, 8, 161–169. [Google Scholar] [CrossRef]
- Krishnamurthy, V.; Viswanathan, V. Beyond Transition Metal Oxide Cathodes for Electric Aviation: The Case of Rechargeable CFx. ACS Energy Lett. 2020, 5, 3330–3335. [Google Scholar] [CrossRef]
- Ghosh, A.; Pal, S.; Sarkar, P. Rational Design of Two-Dimensional Porous Boron Phosphide as Efficient Cathode Material for Li and Na Ion Batteries: A First-Principles Study. J. Phys. Chem. C 2022, 126, 5092–5100. [Google Scholar] [CrossRef]
- Lv, X.; Li, F.; Gong, J.; Gu, J.; Lin, S.; Chen, Z. Metallic FeSe monolayer as an anode material for Li and non-Li ion batteries: A DFT study. Phys. Chem. Chem. Phys. 2020, 22, 8902–8912. [Google Scholar] [CrossRef] [PubMed]
- Van der Ven, A.; Deng, Z.; Banerjee, S.; Ong, S.P. Rechargeable Alkali-Ion Battery Materials: Theory and Computation. Chem. Rev. 2020, 120, 6977–7019. [Google Scholar] [CrossRef] [PubMed]
- Neufeld, S.; Schindlmayr, A.; Schmidt, W.G. Quasiparticle energies and optical response of RbTiOPO4 and KTiOAsO4. J. Phys. Mater. 2021, 5, 015002. [Google Scholar] [CrossRef]
- Zumsteg, F.C.; Bierlein, J.D.; Gier, T.E. KxRb1-xTiOPO4: A new nonlinear optical material. J. Appl. Phys. 1976, 47, 4980–4985. [Google Scholar] [CrossRef]
- Neufeld, S.; Bocchini, A.; Gerstmann, U.; Schindlmayr, A.; Schmidt, W.G. Potassium titanyl phosphate (KTP) quasiparticle energies and optical response. J. Phys. Mater. 2019, 2, 045003. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in molecules. Accounts Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Whittingham, M.S. Lithium Batteries and Cathode Materials. Chem. Rev. 2004, 104, 4271–4302. [Google Scholar] [CrossRef]
- Ohzuku, T.; Ueda, A. Solid-State Redox Reactions of LiCoO2 (R3m) for 4 Volt Secondary Lithium Cells. J. Electrochem. Soc. 1994, 141, 2972. [Google Scholar] [CrossRef]
- Lung-Hao Hu, B.; Wu, F.Y.; Lin, C.T.; Khlobystov, A.N.; Li, L.J. Graphene-modified LiFePO4 cathode for lithium ion battery beyond theoretical capacity. Nat. Commun. 2013, 4, 1687. [Google Scholar] [CrossRef] [PubMed]
- Franger, S.; Cras, F.L.; Bourbon, C.; Rouault, H. LiFePO4 Synthesis Routes for Enhanced Electrochemical Performance. Electrochem. Solid-State Lett. 2002, 5, A231. [Google Scholar] [CrossRef]
- Shen, K.; Xu, X.; Tang, Y. Recent progress of magnetic field application in lithium-based batteries. Nano Energy 2022, 92, 106703. [Google Scholar] [CrossRef]
- Costa, C.M.; Merazzo, K.J.; Gonçalves, R.; Amos, C.; Lanceros-Méndez, S. Magnetically active lithium-ion batteries towards battery performance improvement. iScience 2021, 24, 102691. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).