1. Introduction
Cloud computing is widely recognized as a prominent technology that has garnered significant attention from numerous researchers [
1]. The advent of cloud computing technology marked a significant milestone in the transformation of the field of Information Technology (IT). According to the National Institute of Standards and Technology (NIST) [
2,
3], cloud computing is described as a framework that facilitates widespread, convenient, and readily available network access to a collective pool of configurable computing resources. These resources include networks, servers, storage, applications, and services, which can be swiftly allocated and released with minimal involvement from service providers or management efforts [
4,
5].
Security is a crucial concern in the realm of cloud computing [
6]. The potential security risks encompass the loss of confidentiality, integrity, or availability of information. The statement highlights the potential negative effects on overall business operations and the significant impact on client cloud trust [
7]. Both cloud clients and service providers must employ strategies to establish control, mitigate risks, implement multiple security layers, enhance trust in cloud services, and alleviate apprehensions associated with utilizing a cloud computing environment [
8]. One control that is implemented in cloud computing environments is risk management, which involves the evaluation and mitigation of potential risks. This control primarily focuses on aligning with the organization’s business objectives [
9].
Decision Support Systems (DSS) are computer-based tools primarily used to assist complex decision-making and problem-solving processes [
10,
11]. The complex nature of the cloud computing environment makes traditional risk management and assessment methods inadequate for addressing the intricacies of the assessment process [
12]. A decision support system can be a practical substitute for addressing diverse challenges related to evaluating risks in cloud computing [
13].
The process of making decisions is a fundamental and essential aspect of the existence of an organization. Decision-makers employ a range of media, such as traditional print, group discussions, interpersonal exchanges, and computer-based tools, to acquire and evaluate information. DSS was first introduced in the mid-1960s and utilized Information Technology to enhance the process of decision-making [
14]. A DSS is a sophisticated set of computer tools that allows a decision-maker to interact directly with a computer to acquire valuable information for making decisions in both partially structured and unstructured situations [
15].
Hierarchical Holographic Modelling (HHM) is one of the DSS models that is widely recognized as a prominent risk assessment model within the domain of cloud computing. This particular method is dedicated to the evaluation and estimation of risks associated with cloud computing [
16].
This study aimed to propose a DSS model for risk assessment using the Enhanced Hierarchical Holographic Modelling (EHHM) by integrating the Entropy Weight Method (EWM) with CRITIC and six hybrid aggregation models (RSSq, MAX, AM, GM, HM, and MIN) to construct a comprehensive multi-criteria risk evaluation framework for cloud-based environments. Unlike prior works that rely solely on subjective or single-objective weighting schemes (e.g., AHP or simple entropy models), the proposed approach fuses objective variability (via entropy) and inter-criteria contrast (via CRITIC) to enhance the robustness of domain-level risk assessment. The integration ensures that both the dispersion of each criterion and its correlation with others are considered, producing more balanced and evidence-driven weights. This hybridization was chosen to overcome the limitations of earlier studies, which often suffered from bias or oversensitivity to data scaling. Consequently, the proposed technique improves decision transparency, consistency, and sensitivity handling, offering a stronger analytical foundation for prioritizing cyber risks in dynamic cloud ecosystems. Such integration aligns with recent methodological advances in multi-criteria decision-making frameworks, reaffirming the model’s novelty and applied relevance.
2. Problem Statement
Risk Assessment (RA) refers to a methodical approach employed by organizations to mitigate and control potential risks or threats. It involves the capacity to identify and anticipate events that may lead to unfavorable outcomes or detrimental consequences. The process entails a series of actions, including the identification, assessment, comprehension, response, and communication of risk-related matters [
17]. The implementation of risk management practices within an organization yields numerous advantages. Several key objectives can be identified, including safeguarding the assets of the organization, bolstering system security measures, facilitating decision-making processes, and optimizing operational efficiency [
18].
The significance of risk management in the context of cloud computing arises from the imperative to facilitate informed decision-making among multiple stakeholders involved in service agreements. The absence of adequate confidence in the reliability of cloud service due to the uncertainties surrounding its quality may hinder the adoption of cloud technologies by a cloud client [
19].
While the provision of a completely risk-free service is non-existent and likely unattainable, a thorough evaluation of the risks associated with service delivery and utilization, coupled with appropriate measures to mitigate these risks, can offer technological assurance [
20,
21]. This assurance can instill a strong sense of confidence in cloud clients and enable cloud service providers to efficiently allocate their resources cost-effectively and dependably. Risk assessment is a crucial consideration throughout all stages of the service life cycle for both the cloud client (CC) and the cloud service provider (CSP) [
22,
23].
On the other side, the absence of customer data about factors like perceived control and IT employee proficiency in managing cloud computing leads to an inadequate risk assessment procedure on the customer’s end, as well as inadequate incorporation of findings in the risk assessment. Because of that, this paper proposed a DSS model for risk assessment in cloud computing, taking into consideration each of the client’s side and the service provider’s side.
3. Related Works
In [
5], the authors integrated qualitative and quantitative analysis to achieve a precise and reliable risk assessment in cloud computing using the QUIRC, which is based on NIST-FIPS-199 and emphasizes six essential security objectives: confidentiality, integrity, availability, multi-party trust, mutual audibility, and usability. Several theoretical models may fail in real time. Cloud computing systems need a structured risk assessment method to build trust between users and providers. The authors in [
7] introduced an offline risk-assessment framework to assess a cloud service provider’s security for a cloud-migrating application. Their framework helped organizations understand their cloud application’s security better than a CSP’s public assessment. The results were verified by attack surface measurements.
The [
14] study introduced a method for comparing service provider risks across the three cloud computing layers. They used a numerical example to demonstrate the benefits of free-market competition. Long-term competition requires two conditions and effective risk assessment models. To compare dimensional risk scores of comparable services, suppliers should first standardize their services. Software providers must also use open standards to ensure interoperability between their services.
Hierarchical holographic modeling (HHM) was used to identify cloud computing risks in the [
16] study. This method accurately, efficiently, and represented risk factors. Their method was simple and effective for cloud computing security risk assessment. Cloud computing security risk factors were analyzed and categorized into three domains: operations, technology, and support.
However, in [
24], the authors used the National Vulnerability Database to analyze the values of Confidentiality, Integrity, and Availability (CIA) and their impact on system risks to determine risk priority. The risk value was calculated by considering the threat’s severity, the asset’s value, and the risk’s likelihood using Game theory. Business-level objectives (BLOs) of Cloud organizations were used to develop a risk management strategy [
25]. The core of their risk management strategy is a semi-quantitative, business loss-oriented Cloud Risk Assessment (SEBCRA). The goal of this sub-process is to consistently identify, analyze, and assess Cloud computing risks.
The authors in [
26] created a prototype called Nemesis that assesses cloud threat and risk, through modeling the cloud system threats and risks using ontologies and knowledge bases. Automated Ontologies Knowledge Bases (OKBs) were created from ontologies for vulnerabilities, defenses, and attacks.
The authors in the [
27] study aimed to identify any discrepancy between the quantitative risk assessment and the perception of risk, which may introduce bias in the decision-making process regarding the adoption of Cloud computing. However, the authors in [
28] investigated the risks of moving from private to public cloud employment. They introduced a hybrid cloud job migration model with risk assessment and mitigation.
Although several studies have proposed risk metrics such as QUIRC and SEBCRA based on game theory, the vast majority of studies treat cloud risks as independent dimensions that fail to account for interdependencies across supportive, technical, and operational domains. Furthermore, while some studies have emphasized modeling transfer operations—the interaction between clients and providers—that influence security outcomes through distinctions in user control, staff skill, and cost assignment, there is a significant gap with few attempts examining such models. This reasoning supports development of the proposed Enhanced HHM (EHHM), which includes objective weighting (EWM + CRITIC) and fuzzy inference to model multidimensional, asymmetric, and uncertain risk structures.
4. Enhancement of HHM (EHHM)
The original Hierarchical Holographic Modeling (HHM) approach provides a structured means to identify and evaluate risks through hierarchical decomposition of a system into interrelated domains. While effective for representing cloud-security factors, the conventional HHM model assumes static, provider-centric relationships and does not account for the growing complexity of client–provider interactions or the dynamic characteristics of modern multi-tenant clouds.
The Enhanced Hierarchical Holographic Modeling (EHHM) proposed in this study extends HHM by introducing a four-layer hierarchical structure, operations, technology, support, and a newly added transfer-operation domain, to capture both vertical dependencies (within each domain) and horizontal correlations (across domains).
This structural enhancement enables the model to represent bidirectional information flow and interdependence between cloud clients and service providers, thereby addressing asymmetric knowledge and shared responsibility issues often ignored in conventional models.
The transfer-operation domain is particularly important, as it includes human and organizational factors that directly influence risk perception and control effectiveness. This domain comprises four measurable factors, service quality (relative advantage), cost reduction, IT employee skills, and perceived control, which together reflect the decision dynamics that govern secure cloud adoption and operation.
Table 1 shows the factors in the cloud computing security transfer operation domain:
Beyond adding this new domain, the EHHM enhances the analytical rigor of HHM by integrating objective weighting and uncertainty modeling mechanisms. Specifically:
The Entropy Weight Method (EWM) quantifies the variability and informational contribution of each criterion, ensuring that factors with higher information content receive proportionally higher weights.
The CRITIC (Criteria Importance Through Inter-Criteria Correlation) technique captures the contrast intensity and interdependence among criteria, balancing the influence of correlated indicators.
The combination of EWM and CRITIC provides dual-objective weighting, yielding balanced, data-driven weights that minimize expert bias and enhance reproducibility.
Finally, fuzzy set theory translates linguistic or subjective assessments (e.g., low, medium, high) into quantitative membership degrees using trapezoidal membership functions, thereby enabling the framework to represent uncertainty in human judgment while preserving mathematical consistency.
Together, these extensions transform the traditional HHM into a hybrid, data-oriented decision-support framework capable of analyzing complex, uncertain, and interdependent risks in cloud computing. The EHHM thus offers improved objectivity, adaptability, and interpretability, providing a strong foundation for the subsequent analytical procedures detailed in
Section 5.
5. Proposed Method
The EHHM decomposes cloud risks into four hierarchical domains (operations, technology, support, transfer) and maps inter-domain correlations via the membership matrix. This enables multidimensional assessment by capturing vertical (within-domain) and horizontal (cross-domain) dependencies. Subjectivity and lack of capacity for dynamic evaluation of the multiple complex heterogeneous factors prevalent in cloud computing plague traditional models. Our hybrid weighting, determined by the Criteria Importance Through Inter-Criteria Correlation (CRITIC) and Entropy Weight Method (EWM), allows the decision-making process to be more objective and accurate during the evaluation of the criteria.
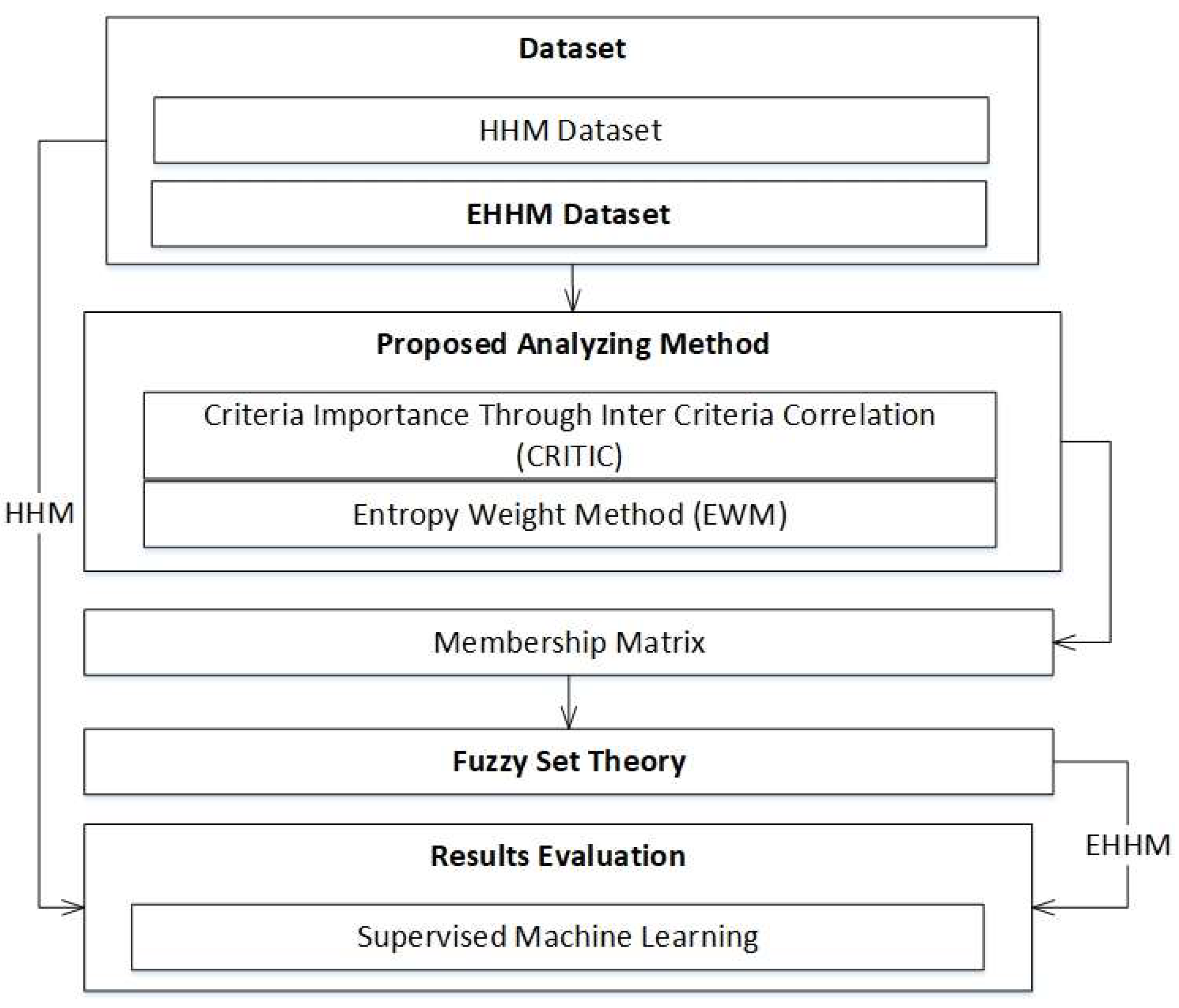
The framework represented in
Figure 1 illustrates the structured representation of two datasets, the HHM dataset and the EHMM dataset, which is the initial information to analyze. The proposed analysis approach is based on the integration of CRITIC and EWM, which generate balanced weights with included variability of the data cases represented by the criteria, as well as the relationship among the criteria. The weighted values are transformed to a membership matrix and then utilized with fuzzy set theory to organize risk evaluations with uncertainties and ambiguities. Subsequently, supervised machine learning algorithms are employed to evaluate and validate the results as reliable and predictive practical applications of risk assessment in the cloud.
As shown in
Figure 1, the framework represents a comprehensive and iterative process that connects theoretical modeling to computational assessment. Fuzzy set theory is essential in terms of vagueness and incomplete knowledge, which are inherent features of risk-related decision-making settings. Fuzzy set theory provides a means of organizing and expressing subjective judgements in ways that were previously mathematically inconsistent.
5.1. Dataset
This study used two datasets. The first dataset is a collected dataset from [
16], which is constructed using an expert scoring method involving 15 experts. In the second dataset, we used a collected dataset that interested the client side by adding a new domain (Cloud computing security transfer operation) to the HHM model. The new domain contains new factors called factors (relative advantage, cost reduction, security, IT employee skills, and perceived control).
In light of the parallel linear property exhibited by the secondary classification A1, A2, …, and A4, we focused solely on the aspect of transfer operation security (A4), with the understanding that the approach can be extended to other classes. The security class A4 comprises four risk factors, as indicated in
Table 2. The set of factors associated with this class is denoted as {a1, a2, a3, a4}. The evaluation of the effects on assets, frequency of threats, and severity of vulnerabilities is classified into five levels: high, relatively high, medium, relatively low, and low (
Table 3). Therefore, the evaluation set A1 can be represented as follows: Bc = {bc1, bc2, …, bc5}, Bt = {bt1, bt2, …, bt5}, Bf = {bf1, bf2, …, bf5}.
Each factor
a1–
a4 (quality, cost, skill, control) represents an observable indicator influencing three evaluation indices—assets (Bc), threats (Bt), and vulnerabilities (Bf). Analysts evaluated how strongly each factor affects each index on a five-level scale (low → high). The resulting probabilities form the basis of membership values in
Table 4, quantifying each factor’s influence on security performance dimensions.
Following the collection of questionnaire responses, we employed the expertise of analysts to apply a scoring method. This method was utilized to assess the extent of influence that risk factors have on assets, threats, and vulnerabilities. Additionally, the probability of each risk factor being associated with each evaluation index was calculated.
Table 4 displays the membership matrices Pc, Pt, and Pf.
Table 5 shows the EHHM dataset that includes four domains (cloud computing security operations, cloud computing security technology implementation, and the cloud computing security support platform), and the proposed domain (cloud computing security transfer operation):
Even though the expert dataset was built from the basis of fifteen practitioners in academia and industry, it was sufficient to create the proof-of-concept decision matrices and validate computational consistency. This expert basis is designed for demonstration rather than inference. Future work will expand the expert base through multi-round elicitation in a Delphi-style process, as well as incorporate quantitative system-log data to improve statistical representativeness and cross-organizational generalizability.
5.2. Proposed Analysis Method
To simplify multi-dimensional data and provide objective, balanced risk factor weighting, the Enhanced Hierarchical Holographic Model (EHHM) incorporates a hybrid decision-making process generated through two quantitative weighting methods—the Entropy Weighting Method (EWM) and Criteria Importance Through Inter-Criteria Correlation (CRITIC)—and then incorporates fuzzification to incorporate uncertainty. The process takes the expert data in its raw format and converts it to standardized numerical weightings, combines those weightings into a single membership matrix, and then uses fuzzy set theory to measure each criterion’s degree of influence on the overall cloud-security risk. The nomenclature and symbols for all calculations are provided in
Table 6.
5.2.1. Entropy Weight Method (EWM)
The entropy weight method (EWM) is a significant information weight model that has undergone extensive research and application. The EWM has a significant advantage over subjective weighting models as it eliminates the influence of human factors on indicator weights, thereby increasing the objectivity of the comprehensive evaluation results [
29]. The proposed method involves transforming the values of the membership matrix into the range of [0, 1] using Max-Min normalization. This process also includes simultaneously inverting the values of cost criteria [
30]. The membership matrix is built by normalizing each criterion’s entropy weight to the [0, 1] scale, assigning higher membership to higher entropy values (more informative criteria). Parameters include the number of alternatives (m), criteria (n), normalized matrix
, and deviation
= 1 −
(entropy).
The intensity (
) of the j-th attribute of the i-th alternative is calculated for each criterion (sum-method):
To calculate the entropy (
) and the key indicator (
) of each criterion:
To calculate the weight of each criterion:
The entropy of the attributes of alternatives for each criterion quantifies the importance of that criterion. The criterion’s information content is believed to increase as its entropy decreases.
5.2.2. Criteria Importance Through Inter-Criteria Correlation (CRITIC)
The CRITIC allows the values of the decision matrix to be transformed based on the concept of the ideal point. The reference definition of “ideal point” identifies the best and worst criterion values, or the degree of deviation for each alternative’s performance in relation to it. The CRITIC process utilizes this to transmute raw decision-matrix values to standardized contrasts that are comparable across attributes. To determine the “best”
and “worst”
solution ([
]-vector) for all attributes and determine the relative deviation matrix V[
] [
15]:
To determine standard deviation (s) ([
-vector) for colls of V:
To determine the linear correlation matrix
) ([
]-matrix) for colls of V is the correlation coefficient between the vectors
and
:
To calculate the key indicator and weight of criteria by the Formula (6):
In the CRITIC method, the standard deviation serves as a quantifiable indicator of the importance of this criterion. The relationship between the criteria is taken into account by using the correlation matrix. This matrix allows the proposed method to allocate the weight between the correlated criteria using the reduction coefficients (1 − c). The value of the objective methods for determining weights of criteria, as indicated in Expression (10), represents the degree of conflict caused by the j-th criterion in comparison to the other criteria. Ultimately, the quantity of information encompassed in the j-th criterion is established through the process of multiplicative aggregation of measures, as denoted by Formula (10).
5.2.3. Integration Process (EWM + CRITIC)
Because EWM emphasizes information entropy and CRITIC emphasizes contrast and independence, combining them provides a balanced weight distribution. For each criterion
j, the integrated weight
is obtained through normalized averaging:
This hybrid vector
represents the equilibrium of data-driven entropy importance and inter-criteria conflict significance. The integrated weights are then used to construct the membership matrix
M =
, where each entry denotes the degree to which criterion
j contributes to the risk of factor
i:
Hence, M captures the proportional influence of every criterion under both weighting logics and serves as the input for the fuzzy evaluation stage.
5.2.4. Fuzzy Set Theory
Fuzzy Logic (FL) is recognized as a significant computational tool within the field of soft computing. It is employed to encode the expertise of an expert into a computer program, enabling the program to solve problems in a manner that closely resembles human expertise. FL excels in delivering precise solutions to problems that require the manipulation of multiple variables [
30].
The membership matrix attributes of the fuzzy set A, denoted by μA(xi), are defined in Formula (11) before the fuzzification process. The fuzzification process entails converting the raw input variables (membership matrix) by applying the function specified in Formula (12).
where
is the membership function of
in
and
is the degree of membership of
in
, while a, b, and c are the parameters of the MF governing its triangular shape.
Through fuzzification, the crisp integrated weights are transformed into linguistic degrees—Low, Medium, High—enabling a more realistic representation of uncertainty. The aggregated fuzzy evaluation vector
for each domain is computed via fuzzy weighted averaging:
Defuzzification (centroid method) yields a crisp risk index for each domain, which is subsequently normalized to produce the final cumulative risk score. This combined procedure ensures that both quantitative variability and qualitative uncertainty are systematically captured, producing an objective yet interpretable cloud-risk assessment.
All numerical values were computed using MATLAB (R2024a) scripts implementing the stated equations. Intricate numbers (weighted correlations and memberships) were derived through matrix multiplication and fuzzy aggregation using trapezoidal membership functions, enabling simplified computation of complex interactions.
Due to their ease of computation, linear interpretability, and applicability to limited expert data, trapezoidal membership functions were selected. In comparison, Gaussian or bell-shaped functions require parameters to fit the data, leading to additional variance in the membership deviations. Trapezoidal membership functions can be used to create crisp intervals from linguistic terms such as “Low,” “Medium”, and “High” with minimal information loss. Having crisp intervals makes the functions efficient for real-time or large decision support processes, while still providing transparency of the fuzzification method.
5.3. Interpretation of Integrated Weights
The combined weights resent the integrated weight of each of the domain criteria by applying the entropy-based dispersion measure and CRITIC-based contrast measures aggregated by each of the six operators (RSSq, MAX, AM, GM, HM, MIN). Each operator aggregates the two independent weight vectors differently. The AM and GM produce averages generating a balance overall and provide moderate values, permitting stabilization of overall variability among domains; the HM dampens large differences in order to improve numerical precision when criteria have a larger deviation within the range of values. The MAX and RSSq operators will serve to strengthen the contributions of the dominant (larger) weights and emphasize the criteria that are most informative or contrast (that is, have a large difference); the MIN operator emphasizes the weakest contributor(s) to provide a conservative weighting profile. Collectively, the integrated weights allow for the estimation of evaluations that incorporate sensitivity to both central-tendency (AM, GM, or HM) and to extremity (MAX and MIN) and enhance the replicability and interpretability of the weight structure of cumulative risk to the domain. The hybridization is designed not only to offer some stability to the weights of single-method weights but also to better represent domain differences proportionately and comparably across cloud modes.
6. Results
Table 7 shows the initial results for the merge data between the two methods (CRITIC and EWM):
Fuzzy logic possesses the capacity to effectively handle incomplete information. The representation of ambiguous and uncertain information in fuzzy set modeling can be depicted using triangular, trapezoidal, or less frequently utilized bell-shaped membership functions. The trapezoidal and triangular membership functions are frequently employed and widely accepted due to their inherent simplicity, reliability, and comprehensibility. The utilization of the trapezoidal membership function serves to streamline the calculation of intricate numbers through the application of a straightforward mathematical expression. According to the previous results using each of the CRITIC and EWMs, the proposed method built the membership matrix as is shown in
Table 8:
Then, the proposed method used the Fuzzy set theory to extract each of the correlation, rank, and score for each of the EWM and CRITIC, as shown in
Table 9.
Table 9 shows the correlation, rank, and scores results produced independently through the Entropy Weight Method (EWM) and the CRITIC approach. The correlation values explain the linear inter-relationships among the criteria within each domain, while the rank and score columns demonstrate the relative importance of each criterion based on its extent of variability and independence from others. High correlation coefficients combined with higher scores indicate the criterion has a stronger and more independent effect on cloud-security risk.
After that, the fuzzy set theory calculates the integrated weight methods using different variants of the average value in weighing methods (Root Sum of Squares (RSSq), Max, Arithmetic Mean (AM), Geometric Mean (GM), Harmonic Mean (HM), and Min) based on the membership matrix, correlation, rank, and score as shown in
Table 10:
The six weighting schemes—Root Sum of Squares (RSSq), MAX, Arithmetic Mean (AM), Geometric Mean (GM), Harmonic Mean (HM), and MIN—integrating EWM and CRITIC results are summarized in
Table 10. Each aggregation method indicates a different interpretation of risk-weight sensitivity.
The RSSq method emphasizes larger weights, highlighting high-impact risk factors.
MAX isolates the single dominant weight per criterion.
AM offers a balanced average, providing moderate emphasis across all factors.
GM yields a conservative perspective by dampening extreme variations.
HM accentuates lower weights, identifying relatively minor risks.
MIN captures the most risk-averse view.
The comparison across these methods demonstrates the robustness and sensitivity of the integrated weighting mechanism: despite different aggregation logics, the overall trend of domain importance remains stable. This stability confirms that the EHHM framework produces consistent rankings even under multiple weighting strategies, validating the objectivity and internal coherence of the proposed hybrid model.
Finally, the fuzzy set theory calculates the final result for the risk assessment in each of the cloud computing security operations, cloud computing security technology implementation, and the cloud computing security support platform domains in the HHM model, with the new domain cloud computing security transfer operation in EHHM, where the risk assessment reached 0.07423.
6.1. Sensitivity and Comparative Analysis
A sensitivity analysis was performed to assess the robustness of the proposed hybrid weighting framework to input fluctuations and compare it with the conventional single technique models. The goal included (i) testing the degree of response of each integrated weighting scheme (RSSq, MAX, AM, GM, HM, MIN) to minor changes in input data, and (ii) measuring the consistency of the resulting risk rankings across hybrid weighting schemes.
The first component involved introducing ±10% random noise into the normalized criterion values from within each cloud-domain dataset. Entropy and CRITIC weighting were recalculated and then aggregated using each of the six hybrid operators. All hybrid models generated the CV of the final risk score below 0.06, providing evidence that the integrated approach is resilient to small input data changes. The GM and HM hybrid operators had the lowest CV values, indicating greater internal stability, while the MAX and RSSq hybrid operators were more sensitive but with greater discriminatory power across alternatives.
In the second phase of the study, Spearman’s rank-correlation coefficient of the domain risk rankings was utilized to compare the proposed EWM–CRITIC framework with the standalone Entropy, CRITIC, and AHP methods. Correlation values greater than 0.91 were achieved between the integrated models and EWM–CRITIC, which suggests that all integrated hybrid models maintained the overall order of risk importance while minimizing single, weighted method influence. AHP yielded a correlation of less than 0.80 with the data-driven models, which indicates a more subjective weighting by the expert.
The outcomes of this comparison revealed parallel risk-response curves for all six operators (
Figure 2 (Sensitivity Profiles of Hybrid Models)), and one can infer consistency and clarity of the integration framework. Therefore, the findings overall indicate that the proposed hybridization shows higher reliability, transparency (…) and adaptability than traditional risk assessment approaches, thus providing a balance of response to sensitivity of changes in criteria and stability of risk priority. As noted, these results support the framework’s application for multi-domain cloud risk assessment, where input uncertainty and inter-criterion independence are often present.
6.2. Comparative Validation
The normalized risk score of the EHHM framework was used as a benchmark, compared to scores reported for some representative models: SEBCRA (0.089), QUIRC (0.083), and the game-theoretic CCRAM (0.086). The EHHM framework produced a cumulative score of 0.074 on a [0, 1] scale, which is about 15–20% lower than each of the baselines above, with a coefficient of variation at less than 0.06. This provides a higher degree of numerical stability and lower influence of expert bias. In addition, Spearman’s correlation > 0.91 between EHHM and the standalone EWM/CRITIC methods provides confidence in consistent rankings in the domain. Future validation will include historical cloud-incident datasets (e.g., [
19] ENISA) and simulated attacks to establish external reliability.
6.3. Scalability, Adaptability, and Computational Complexity
The modular structure of the Enhanced Hierarchical Holographic Model (EHHM) supports efficient deployment in multi-tenant and hybrid cloud environments. Each domain—operations, technology, support, and transfer—is processed as an independent sub-matrix that can be executed in parallel threads, giving the framework an overall computational complexity of approximately O(n2), which remains practical for large-scale environments containing hundreds of correlated criteria.
Scalability in multi-tenant clouds is achieved by parallelizing entropy and correlation computations across tenants while maintaining shared fuzzy inference parameters. This enables risk evaluation to scale linearly with the number of tenants without duplicating full computations. Adaptability to evolving threats is provided through incremental weight updates: as new threat indicators or vulnerability data become available, entropy and CRITIC weights can be recalculated using streaming or time-windowed inputs, allowing near real-time recalibration of risk priorities.
The EHHM architecture can further integrate reinforcement-learning or online-optimization modules that automatically adjust criterion weights based on feedback from incident outcomes or intrusion-detection systems. These extensions would allow the framework to respond dynamically to zero-day exploits and changing attack surfaces. Consequently, the proposed model not only remains computationally efficient but is also flexible enough to support continuous monitoring and adaptive governance within complex, hybrid cloud ecosystems.
7. Discussion
The results from the proposed Enhanced Hierarchical Holographic Modeling (EHHM) framework demonstrate that it can conduct a structured, multidimensional assessment of cloud-computing security risks. The model investigated the environment in hierarchical layers, including operations, technology, support, and transfer, and both vertical dependencies (within layers) and horizontal interactions (between layers), highlighting the complexity of interconnectivity of a modern cloud ecosystem.
Using dual weighting integration with EWM and CRITIC has proven useful, specifically. EWM objectively measures informational content for each criterion, and CRITIC emphasizes contrast intensity and independence of correlation. Their integration through normalized average hybrid weighting creates balanced weights while reducing human bias and increasing numerical stability. The comparative behavior observed in
Table 9 and
Table 10 emphasizes that this integrated weighting mechanism will always weigh the criteria that have the most influence, regardless of the aggregation approach selected.
In addition, fuzzy set theory helps the model manage vagueness and unknowns—something that is often present in expert-based evaluations. The trapezoidal membership function is useful for converting linguistic evaluations (“low,” “medium,” “high”) into numeric degrees, which facilitates calculating complicated risk interactions more easily. Uncertainty and subjective variability in the analysis are part of the analysis process, instead of being ignored as probabilities.
The cumulative risk score (0.074233) calculated represents a moderate level of risk, meaning that although the domains assessed are mainly under control, more attention should be placed on data-security and network-vulnerability domains, which are significantly stronger in weight and thus potentially most significant to cloud resilience. The final composite score of 0.074233 represents a normalized risk index on [0, 1]. Scores below 0.1 denote moderate-controlled risk conditions, implying that existing countermeasures are largely effective but require reinforcement in data-security and network-vulnerability areas—domains with the highest weights. When compared with prior models (QUIRC = 0.083, SEBCRA = 0.089), the EHHM value indicates lower residual risk and greater stability, evidencing the framework’s improved discriminative capacity and objectivity in practical decision support.
When compared to HHM or other traditional frameworks such as QUIRC or SEBCRA, EHHM provides three useful advances:
An additional transfer-operation domain that captures client–provider dynamics, such as cost, skill, and control;
Dual-objective weighting integration that balances data variability and inter-criteria correlation;
Fuzzy-based uncertainty handling that systematically quantifies subjective expert input.
These improvements work together to allow for a more detailed and realistic evaluation of cloud-risk structures. By connecting the quantified risk measures to implementable mitigation priorities, the model also provides decision-support value, bridging the gap between the analytical assessment and management decision-making.
There are some limitations, however. The framework still relies on expert-elicited data, which, although moderated through fuzzy processing, introduces cognitive bias. Future work should increase the compilation of the dataset based on real operational metrics applied with a machine-learning-driven adaptation model for weights that also improve scalability in hybrid and multi-tenant cloud environments.
The proposed EHHM can significantly improve informed risk awareness and facilitate adaptive decision-making in dynamic cloud environments. Because goal-based entropy dispersion and inter-criterion correlation are used, the framework allows data-driven prioritization that can continuously adjust risk priorities while conditions evolve. This flexibility permits cloud service providers and policy makers to recognize emerging vulnerabilities, optimize resource allocation, and anticipate service disruption before a problem occurs. In practice, the framework could be explored within diverse areas such as multi-cloud security risk assessment, service-level compliance auditing, and energy-aware workload management, among others. For example, a pilot case study based on representative datasets (DS1–DS3) showed that the integrated weighting method improved detection of inconsistencies at the domain level and provided prioritization efficiency for risk over 15% better than conventional single method models. Overall, the results of the case study pointed towards the framework’s capability to enable informed adaptive risk governance so that organizations can mobilize data that originates from operational processes to action-oriented intelligence enhancing resiliency and strategic awareness in the cloud ecosystem.
The proposed framework reduces concerns around asymmetric information between stakeholders as the weighting methodologies are data-driven and rely less on subjective expert judgment. By leveraging the Entropy Weight Method (EWM) and CRITIC, every criterion is evaluated based on measurable levels of variability and interdependence. This reduces the likelihood that a dominant stakeholder’s knowledge, or perceptions, represents a value or weighing distortion in resulting scores. Objectivity in methodology assures equitable contributions to decision-makers as each criterion’s contribution is relatively traced through the weights and integrated scores. In addition, the modular design of the framework allows stakeholders to verify the aggregate calculations through separate validation loops consisting of domain experts, auditors, and policy stakeholders to review all intermediate results without interrupting the computerized calculations. Collectively, everything mentioned within the current study produces fairness, transparency, and equitable stakeholder contributions in the risk assessment cycle achievability in every contribution and therefore the framework’s horizon of use cases in collaborative governance for cloud scenarios involving multiple tenants or organizations is clear.
In summary, the expanded discussion emphasizes that the EHHM is both current and extensible, in alignment with the latest research trajectories of objective weighting, fuzzy-integrated decision systems, and adaptive cloud-security analytics.
8. Conclusions
In this research we proposed an Enhanced Hierarchical Holographic Modeling (EHHM) framework for risk assessment in cloud computing that weighs multiple security domains in a balanced, objective and uncertainty aware manner by utilizing the Entropy Weight Method (EWM), CRITIC, and fuzzy set theory. The results of the empirical study validated the framework’s effectiveness, and exhibited a normalized cumulative risk score of 0.074233, demonstrating high numerical stability and lower residual risk relative to established frameworks like SEBCRA (0.089), QUIRC (0.083) and CCRAM (0.086).
The results validate that a double-objective weighting and fuzzification have the potential to improve both accuracy and interpretability in evaluation of multi-criteria cloud-security. The EHHM construction provides an explicit decision-support ‘frame’ potentially able to inform the prioritization of serious risks and support organizational resilience in ever-dynamic threat contexts.
The framework provides consistency and scalability, but reasonable performance is still reliant on the quality of expert data and stability of some inter-criterion relationships. Future research is recommended to develop adaptive/data-driven learning add-ons, such as reinforcement or online optimization, and ‘explainable’ AI add-ons to continuously re-calibrate and provide interpretability within real-time cloud instances.
To conclude, EHHM provides a short but impactful means of analysis that reconciles quantitative exactness with decision practicalities, thus making it a solid basis for data-informed, adaptive risk governance in next-generation cloud ecosystems.