Radiobiological Meta-Analysis of the Response of Prostate Cancer to Different Fractionations: Evaluation of the Linear–Quadratic Response at Large Doses and the Effect of Risk and ADT
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Clinical Dataset
2.2. Radiobiological Modelling: Dose–Response
2.3. Statistical Methods
2.4. Radiobiological Modelling: and Number of Clonogens
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brenner, D.J.; Hall, E.J. Fractionation and protraction for radiotherapy of prostate carcinoma. Int. J. Radiat. Oncol. Biol. Phys. 1999, 43, 1095–1101. [Google Scholar] [CrossRef] [PubMed]
- Bentzen, S.M.; Ritter, M.A. The alpha/beta ratio for prostate cancer: What is it, really? Radiother. Oncol. 2005, 76, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Fowler, J.F. The radiobiology of prostate cancer including new aspects of fractionated radiotherapy. Acta Oncol. 2005, 44, 265–276. [Google Scholar] [CrossRef] [PubMed]
- Miralbell, R.; Roberts, S.A.; Zubizarreta, E.; Hendry, J.H. Dose-fractionation sensitivity of prostate cancer deduced from radiotherapy outcomes of 5969 patients in seven international institutional datasets: α/β = 1.4 (0.9–2.2) Gy. Int. J. Radiat. Oncol. Biol. Phys. 2012, 82, e17–e24. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, R.; Pickles, T.; Lee, R.; Moiseenko, V. Deriving prostate alpha-beta ratio using carefully matched groups, long follow-up and the phoenix definition of biochemical failure. Int. J. Radiat. Oncol. Biol. Phys. 2011, 79, 1029–1036. [Google Scholar] [CrossRef]
- Oliveira, S.M.; Teixeira, N.J.; Fernandes, L. What do we know about the alpha/beta for prostate cancer? Med. Phys. 2012, 39, 3189–3201. [Google Scholar] [CrossRef]
- Dasu, A. Is the alpha/beta value for prostate tumours low enough to be safely used in clinical trials? Clin. Oncol. 2007, 19, 289–301. [Google Scholar] [CrossRef]
- Nahum, A.E.; Movsas, B.; Horwitz, E.M.; Stobbe, C.C.; Chapman, J.D. Incorporating clinical measurements of hypoxia into tumour local control modelling of prostate cancer: Implications for the alpha/beta ratio. Int. J. Radiat. Oncol. Biol. Phys. 2003, 57, 391–401. [Google Scholar] [CrossRef]
- Pedicini, P.; Strigari, L.; Benassi, M. Estimation of a self-consistent set of radiobiological parameters from hypofractionated versus standard radiation therapy of prostate cancer. Int. J. Radiat. Oncol. Biol. Phys. 2013, 85, e231–e237. [Google Scholar] [CrossRef]
- Datta, N.R.; Stutz, E.; Rogers, S.; Bodis, S. Clinical estimation of α/β values for prostate cancer from isoeffective phase III randomized trials with moderately hypofractionated radiotherapy. Acta Oncol. 2018, 57, 883–894. [Google Scholar] [CrossRef]
- Vogelius, I.R.; Bentzen, S.M. Diminishing Returns From Ultrahypofractionated Radiation Therapy for Prostate Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2020, 107, 299–304. [Google Scholar] [CrossRef]
- Lo, S.S.; Fakiris, A.J.; Chang, E.L.; Mayr, N.A.; Wang, J.Z.; Papiez, L.; Teh, B.S.; McGarry, R.C.; Cardenes, H.R.; Timmerman, R.D. Stereotactic body radiation therapy: A novel treatment modality. Nat. Rev. Clin. Oncol. 2010, 7, 44–54. [Google Scholar] [CrossRef]
- Zietman, A.L.; Bae, K.; Slater, J.D.; Shipley, W.U.; Efstathiou, J.A.; Coen, J.J.; Bush, D.A.; Lunt, M.; Spiegel, D.Y.; Skowronski, R.; et al. Randomized trial comparing conventional-dose with high-dose conformal radiation therapy in early-stage adenocarcinoma of the prostate: Long-term results from proton radiation oncology group/american college of radiology 95-09. J. Clin. Oncol. 2010, 28, 1106–1111. [Google Scholar] [CrossRef]
- Arcangeli, G.; Saracino, B.; Arcangeli, S.; Gomellini, S.; Petrongari, M.G.; Sanguineti, G.; Strigari, L. Moderate hypofractionation in high-risk, organ-confined prostate cancer: Final results of a phase III randomized trial. J. Clin. Oncol. 2017, 35, 1891–1897. [Google Scholar] [CrossRef]
- Dearnaley, D.P.; Jovic, G.; Syndikus, I.; Khoo, V.; Cowan, R.A.; Graham, J.D.; Aird, E.G.; Bottomley, D.; Huddart, R.A.; Jose, C.C.; et al. Escalated-dose versus control-dose conformal radiotherapy for prostate cancer: Long-term results from the MRC RT01 randomised controlled trial. Lancet Oncol. 2014, 15, 464–473. [Google Scholar] [CrossRef]
- Kirkpatrick, J.P.; Meyer, J.J.; Marks, L.B. The linear–quadratic model is inappropriate to model high dose per fraction effects in radiosurgery. Semin. Radiat. Oncol. 2008, 18, 240–243. [Google Scholar] [CrossRef]
- Brenner, D.J. The linear–quadratic model is an appropriate methodology for determining isoeffective doses at large doses per fraction. Semin. Radiat. Oncol. 2008, 18, 234–239. [Google Scholar] [CrossRef]
- Sperduto, P.W.; Song, C.W.; Kirkpatrick, J.P.; Glatstein, E. A hypothesis: Indirect cell death in the radiosurgery era. Int. J. Radiat. Oncol. Biol. Phys. 2015, 91, 11–13. [Google Scholar] [CrossRef]
- Guerrero, M.; Li, X.A. Extending the linear–quadratic model for large fraction doses pertinent to stereotactic radiotherapy. Phys. Med. Biol. 2004, 49, 4825–4835. [Google Scholar] [CrossRef]
- Wang, J.Z.; Huang, Z.; Lo, S.S.; Yuh, W.T.C.; Mayr, N.A. A generalized linear–quadratic model for radiosurgery, stereotactic body radiation therapy, and high-dose rate brachytherapy. Sci. Transl. Med. 2010, 2, 39ra48. [Google Scholar] [CrossRef]
- Song, C.W.; Lee, Y.J.; Griffin, R.J.; Park, I.; Koonce, N.A.; Hui, S.; Kim, M.-S.; Dusenbery, K.E.; Sperduto, P.W.; Cho, L.C. Indirect Tumour Cell Death after High-Dose Hypofractionated Irradiation: Implications for Stereotactic Body Radiation Therapy and Stereotactic Radiation Surgery. Int. J. Radiat. Oncol. Biol. Phys. 2015, 93, 166–172. [Google Scholar] [CrossRef] [PubMed]
- Song, C.W.; Glatstein, E.; Marks, L.B.; Emami, B.; Grimm, J.; Sperduto, P.W.; Kim, M.-S.; Hui, S.; Dusenbery, K.E.; Cho, L.C. Biological Principles of Stereotactic Body Radiation Therapy (SBRT) and Stereotactic Radiation Surgery (SRS): Indirect Cell Death. Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 21–34. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Barbeito, P.; Díaz-Botana, P.; Gago-Arias, A.; Feijoo, M.; Neira, S.; Guiu-Souto, J.; López-Pouso, Ó.; Gómez-Caamaño, A.; Pardo-Montero, J. A model of indirect cell death caused by tumour vascular damage after high-dose radiotherapy. Cancer Res. 2019, 79, 6044–6053. [Google Scholar] [CrossRef] [PubMed]
- Serre, R.; Benzekry, S.; Padovani, L.; Meille, C.; André, N.; Ciccolini, J.; Barlesi, F.; Muracciole, X.; Barbolosi, D. Mathematical Modelling of Cancer Immunotherapy and Its Synergy with Radiotherapy. Cancer Res. 2016, 76, 4931–4940. [Google Scholar] [CrossRef] [PubMed]
- Poleszczuk, J.; Enderling, H. The optimal radiation dose to induce robust systemic anti-tumour immunity. Int. J. Mol. Sci. 2018, 19, 3377. [Google Scholar] [CrossRef]
- Gago-Arias, A.; Neira, S.; Pombar, M.; Gómez-Caamaño, A.; Pardo-Montero, J. Evaluation of indirect damage and damage saturation effects in dose–response curves of hypofractionated radiotherapy of early-stage NSCLC and brain metastases. Radiother. Oncol. 2021, 2021 161, 1–8. [Google Scholar] [CrossRef]
- González-Crespo, I.; Gómez-Caamaño, A.; Pouso, O.L.; Fenwick, J.D.; Pardo-Montero, J. A biomathematical model of tumour response to radioimmunotherapy with αPDL1 and αCTLA4. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 808–821. [Google Scholar] [CrossRef]
- Royce, T.J.; Mavroidis, P.; Wang, K.; Falchook, A.D.; Sheets, N.C.; Fuller, D.B. Tumour Control Probability Modelling and Systematic Review of the Literature of Stereotactic Body Radiation Therapy for Prostate Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 227–236. [Google Scholar] [CrossRef]
- Alayed, Y.; Cheung, P.; Pang, G.; Mamedov, A.; D’Alimonte, L.; Deabreu, A.; Commisso, K.; Commisso, A.; Zhang, L.; Quon, H.C.; et al. Dose escalation for prostate stereotactic ablative radiotherapy (SABR): Late outcomes from two prospective clinical trials. Radiother. Oncol. 2018, 127, 213–218. [Google Scholar] [CrossRef]
- Arcangeli, S.; Strigari, L.; Gomellini, S.; Saracino, B.; Petrongari, M.G.; Pinnarò, P.; Pinzi, V.; Arcangeli, G. Updated Results and Patterns of Failure in a Randomized Hypofractionation Trial for High-risk Prostate Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2012, 84, 1172–1184. [Google Scholar] [CrossRef]
- Bernetich, M.; Oliai, C.; Lanciano, R.; Hanlon, A.; Lamond, J.; Arrigo, S.; Yang, J.; Good, M.; Feng, J.; Brown, R.; et al. SBRT for the primary treatment of localized prostate cancer: The effect of Gleason score, dose and heterogeneity of intermediate risk on outcome utilizing 2.2014 NCCN risk stratification guidelines. Front. Oncol. 2014, 4, 312. [Google Scholar] [CrossRef]
- Catton, C.N.; Lukka, H.; Gu, C.; Martin, J.M.; Supiot, S.; Chung, P.W.M.; Bauman, G.S.; Bahary, J.; Ahmed, S.; Cheung, P.; et al. Randomized Trial of a Hypofractionated Radiation Regimen for the Treatment of Localized Prostate Cancer. J. Clin. Oncol. 2017, 35, 1884–1890. [Google Scholar] [CrossRef]
- Davis, J.; Sharma, S.; Shumway, R.; Perry, D.; Bydder, S.; Simpson, C.K.; D’Ambrosio, D. Stereotactic Body Radiotherapy for Clinically Localized Prostate Cancer: Toxicity and Biochemical Disease-Free Outcomes from a Multi-Institutional Patient Registry. Cureus 2015, 7, e395. [Google Scholar] [CrossRef]
- Dearnaley, D.; Syndikus, I.; Mossop, H.; Khoo, V.; Birtle, A.; Bloomfield, D.; Graham, J.; Kirkbride, P.; Logue, J.; Malik, Z.; et al. Conventional versus hypofractionated high-dose intensity-modulated radiotherapy for prostate cancer: 5-year outcomes of the randomised, non-inferiority, phase 3 CHHiP trial. Lancet Oncol. 2016, 17, 1047–1060. [Google Scholar] [CrossRef]
- Fuller, D.F.; Naitoh, J.; Mardirossian, G. Virtual HDR CyberKnife SBRT for localized prostatic carcinoma: 5-year disease-free survival and toxicity observations. Front. Oncol. 2014, 4, 321. [Google Scholar] [CrossRef]
- Hannah, R.; Tumati, V.; Xie, X.; Cho, C.; Kavanagh, B.D.; Brindle, J.; Raben, D.; Nanda, A.; Cooley, S.; Kim, D.W.N.; et al. Stereotactic body radiation therapy for low and intermediate risk prostate cancer—Results from a multi-institutional clinical trial. Eur. J. Cancer 2016, 59, 142–151. [Google Scholar] [CrossRef]
- Incrocci, L.; Wortel, R.C.; Alemayehu, W.G.; Aluwini, S.; Schimmel, E.; Krol, S.; van der Toorn, P.; de Jager, H.; Heemsbergen, W.; Heijmen, B.; et al. Hypofractionated versus conventionally fractionated radiotherapy for patients with localised prostate cancer (HYPRO): Final efficacy results from a randomised, multicentre, open-label, phase 3 trial. Lancet Oncol. 2016, 17, 1061–1069. [Google Scholar] [CrossRef]
- Kang, J.; Cho, C.K.; Choi, C.W.; Yoo, S.; Kim, M.; Yang, K.; Yoo, H.; Kim, J.H.; Seo, Y.S.; Lee, D.H.; et al. Image-guided stereotactic body radiation therapy for localized prostate cancer. Tumori 2011, 97, 43–48. [Google Scholar] [CrossRef]
- Katz, A.; Formenti, S.C.; Kang, J. Predicting Biochemical Disease-Free survival after Prostate stereotactic Body radiotherapy: Risk-stratification and Patterns of Failure. Front. Oncol. 2016, 6, 168. [Google Scholar] [CrossRef]
- King, C.R.; Brooks, J.D.; Gill, H.; Presti, J.C. Long-term outcomes from a prospective trial of stereotactic body radiotherapy for low-risk prostate cancer. Int. J. Radiat. Oncol. Biol. Phys. 2012, 82, 877–882. [Google Scholar] [CrossRef]
- Kuban, D.A.; Nogueras-Gonzalez, G.M.; Hamblin, L.; Lee, A.K.; Choi, S.; Frank, S.J.; Nguyen, Q.N.; Hoffman, K.E.; McGuire, S.E.; Munsell, M.F. Preliminary Report of a Randomized Dose Escalation Trial for Prostate Cancer using Hypofractionation. Int. J. Radiat. Oncol. Biol. Phys. 2010, 78, S58–S59. [Google Scholar] [CrossRef]
- Kupelian, P.A.; Willoughby, T.R.; Reddy, C.A.; Klein, E.A.; Mahadevan, A. Hypofractionated intensity-modulated radiotherapy (70 Gy at 2.5 Gy per fraction) for localized prostate cancer: Cleveland Clinic experience. Int. J. Radiat. Oncol. Biol. Phys. 2007, 68, 1424–1430. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.R.; Dignam, J.J.; Amin, M.B.; Bruner, D.W.; Low, D.; Swanson, G.P.; Shah, A.B.; D’Souza, D.P.; Michalski, J.M.; Dayes, I.S.; et al. Randomized Phase III Noninferiority Study Comparing Two Radiotherapy Fractionation Schedules in Patients With Low-Risk Prostate Cancer. J. Clin. Oncol. 2016, 34, 2325–2332. [Google Scholar] [CrossRef] [PubMed]
- Levin-Epstein, R.G.; Jiang, N.Y.; Wang, X.; Upadhyaya, S.K.; Collins, S.P.; Guy, S.; Aghdam, N.; Mantz, C.; Katz, A.J.; Miszczyk, L.; et al. Dose–response with stereotactic body radiotherapy for prostate cancer: A multi-institutional analysis of prostate-specific antigen kinetics and biochemical control. Radiother. Oncol. 2021, 154, 207–213. [Google Scholar] [CrossRef]
- Lukka, H.; Hayter, C.; Julian, J.A.; Warde, P.; Morris, W.J.; Gospodarowicz, M.; Levine, M.; Sathya, J.; Choo, R.; Prichard, H.; et al. Randomized Trial Comparing Two Fractionation Schedules for Patients With Localized Prostate Cancer. J. Clin. Oncol. 2005, 23, 6132–6138. [Google Scholar] [CrossRef]
- Madsen, B.L.; Hsi, R.A.; Pham, H.T.; Fowler, J.F.; Esagui, L.; Corman, J. Stereotactic hypofractionated accurate radiotherapy of the prostate (SHARP), 33.5 Gy in five fractions for localized disease: First clinical trial results. Int. J. Radiat. Oncol. Biol. Phys. 2007, 67, 1099–1105. [Google Scholar] [CrossRef]
- Mantz, C. A phase II trial of stereotactic ablative body radiotherapy for low-risk prostate cancer using a non-robotic linear accelerator and real-time target tracking: Report of toxicity, quality of life, and disease control outcomes with 5-year minimum follow-up. Front. Oncol. 2014, 4, 279. [Google Scholar] [CrossRef]
- McBride, S.M.; Wong, D.S.; Dombrowski, J.J.; Harkins, B.; Tapella, P.; Hanscom, H.N.; Collins, S.P.; Kaplan, I.D. Hypofractionated Stereotactic Body Radiotherapy in Low-Risk Prostate Adenocarcinoma. Cancer 2012, 118, 3681–3690. [Google Scholar] [CrossRef]
- Yeoh, E.E.; Holloway, R.H.; Fraser, R.J.; Botten, R.J.; Di Matteo, A.C.; Butters, J.; Weerasinghe, S.; Abeysinghe, P. Hypofractionated versus conventional fractionated radiation therapy for prostate carcinoma: Updated results of a phase III randomized trial. Int. J. Radiat. Oncol. Biol. Phys. 2006, 66, 1072–1083. [Google Scholar] [CrossRef]
- Zelefsky, M.J.; Fuks, Z.; Hunt, M.; Yamada, Y.; Marion, C.; Ling, C.C.; Amols, H.; Venkatraman, E.S.; Leibel, S.A. High-dose intensity modulated radiation therapy for prostate cancer: Early toxicity and biochemical outcome in 772 patients. Int. J. Radiat. Oncol. Biol. Phys. 2002, 53, 1111–1116. [Google Scholar] [CrossRef]
- Bentzen, S.M.; Tucker, S.L. Quantifying the position and steepness of radiation dose–response curves. Int. J. Radiat. Biol. 1997, 71, 531–542. [Google Scholar]
- Royston, P. Profile likelihood for estimation and confidence intervals. Stata J. 2007, 7, 376–387. [Google Scholar] [CrossRef]
- Rao, S.S. The Profile Likelihood. Available online: https://web.stat.tamu.edu/suhasini/teaching613/chapter3.pdf (accessed on 1 January 2023).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Webb, S.; Nahum, A.E. A model for calculating tumour control probability in radiotherapy including the effects of inhomogeneous distributions of dose and clonogenic cell density. Phys. Med. Biol. 1993, 38, 653–666. [Google Scholar] [CrossRef]
- Fowler, J.F. 21 years of biologically effective dose. Br. J. Radiol. 2010, 83, 554–568. [Google Scholar] [CrossRef]
- Shuryak, I.; Carlson, D.J.; Brown, M.; Brenner, D.J. High-dose and fractionation effects in stereotactic radiotherapy: Analysis of tumour control data from 2965 patients. Radiother. Oncol. 2015, 115, 327–334. [Google Scholar] [CrossRef]
- Symonds, M.R.; Moussalli, A. A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behav. Ecol. Sociobiol. 2011, 65, 13–21. [Google Scholar] [CrossRef]
- Kuperman, V.Y.; Lubich, L.M. Effect of reoxygenation on hypofractionated radiotherapy of prostate cancer. Med. Phys. 2020, 47, 5383–5391. [Google Scholar] [CrossRef]
- Kerns, S.L.; Fachal, L.; Dorling, L.; Barnett, G.C.; Baran, A.; Peterson, D.R.; Hollenberg, M.; Hao, K.; Narzo, A.D.; Ahsen, M.E.; et al. Radiogenomics Consortium Genome-Wide Association Study Meta-Analysis of Late Toxicity After Prostate Cancer Radiotherapy. JNCI J. Natl. Cancer Inst. 2020, 112, 179–190. [Google Scholar] [CrossRef]
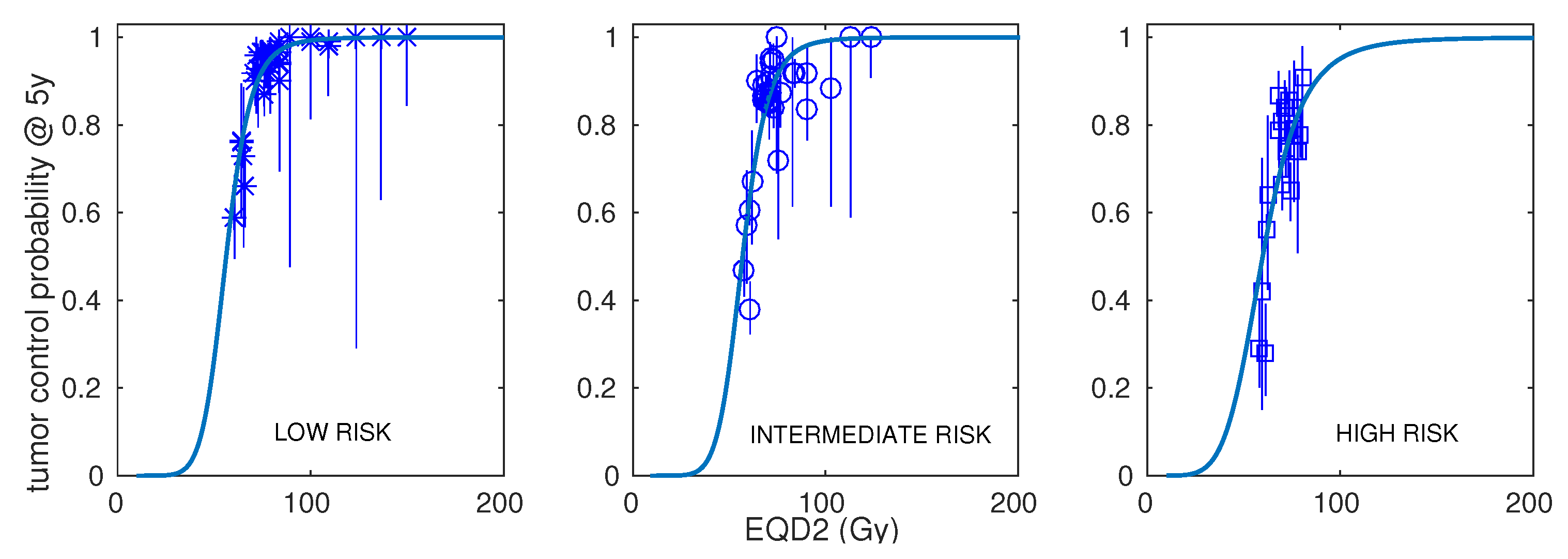
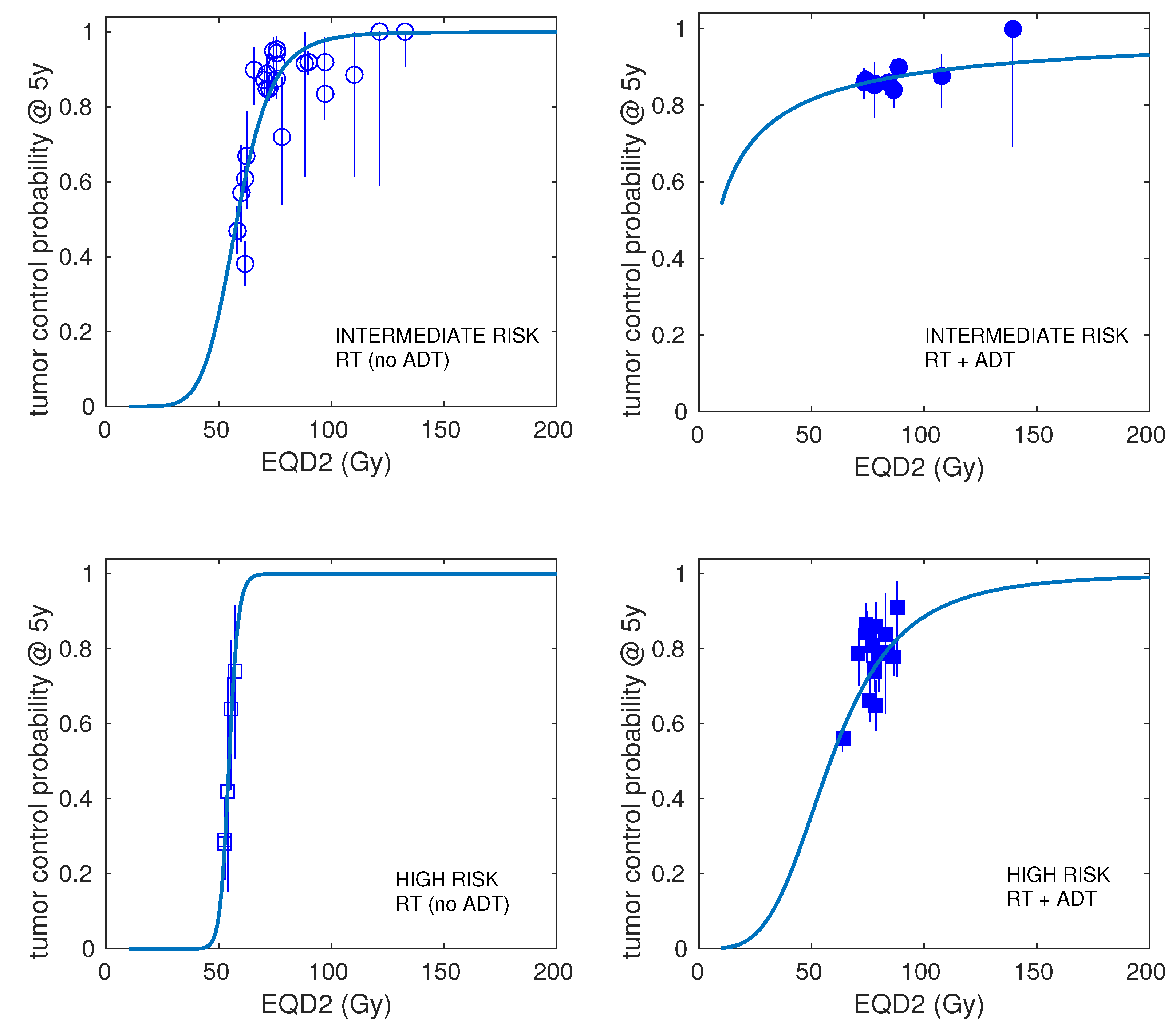
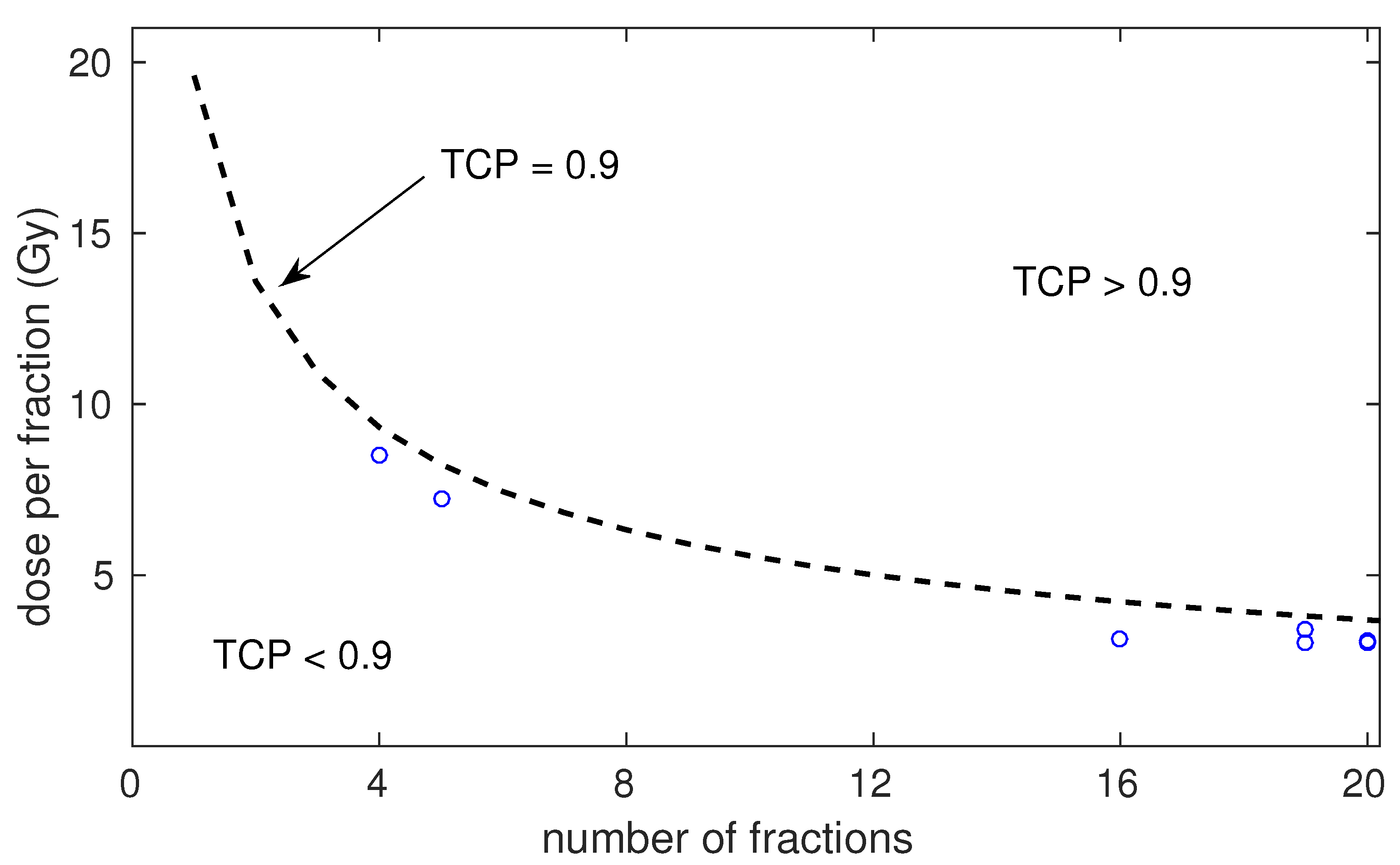
| Risk | Number of Schedules | Number of Patients (Range) | Dose per Fraction (Range) | Total Dose (Range) | Treatment Time (Range) | ADT (Fraction of Schedules) | Control at 5 Years (Range) |
|---|---|---|---|---|---|---|---|
| LR | 35 | 3–550 | 1.8–10 Gy | 33.5–81 Gy | 3–62 days | 3/35 | 0.59–1.00 |
| IR | 32 | 7–839 | 1.8–10 Gy | 34–81 Gy | 3–62 days | 9/32 | 0.38–1.00 |
| HR | 20 | 12–812 | 1.8–8.5 Gy | 34–81 Gy | 3–62 days | 15/20 | 0.28–0.908 |
| Risk | Model | Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (Gy) | (Gy day) | (day) | (Gy) | (Gy) | (Gy) | ||||||
| LR | LQ | 2.0 | 0.00 | - | - | - | 56.2 | 2.17 | 89.4 | 190.8 | - |
| LQL | 2.0 | 0.00 | - | 0.00 | - | 56.2 | 2.17 | 89.4 | 193.7 | −2.9 | |
| LQ | 2.6 | 0.00 | - | - | 0.07 | 55.8 | 2.11 | 89.2 | 193.4 | −2.6 | |
| IR | LQ | 3.4 | 0.41 | 24.0 | - | - | 56.9 | 2.14 | 220.9 | 454.2 | - |
| LQL | 0.4 | 0.00 | - | 0.28 | - | 62.8 | 2.18 | 201.3 | 418.0 | 36.2 | |
| LQ | 3.5 | 0.41 | 23.9 | - | 0.00 | 56.8 | 2.15 | 220.9 | 457.2 | −3.0 | |
| HR | LQ | 2.8 | 0.35 | 21.0 * | - | - | 59.8 | 1.45 | 105.0 | 224.4 | - |
| LQL | 2.8 | 0.35 | 21.0 * | 0.00 | - | 59.8 | 1.45 | 105.0 | 228.5 | −4.2 | |
| LQ | 11.2 | 0.34 | 21.0 * | - | 0.75 | 58.7 | 1.47 | 103.9 | 226.2 | −1.8 | |
| IR | LQ | 2.8 | 0.32 | 21.0 * | - | - | 58.1 | 1.85 | 157.6 | 328.7 | - |
| (no ADT) | LQL | 0.5 | 0.00 | - | 0.24 | - | 63.6 | 2.01 | 138.7 | 294.6 | 34.1 |
| LQ | 2.8 | 0.32 | 21.0 * | - | 0.00 | 58.1 | 1.85 | 157.6 | 332.4 | −3.7 | |
| HR | LQ | 2.1 | 0.00 | - | - | - | 58.5 | 0.95 | 72.6 | 161.8 | - |
| (ADT) | LQL | 2.1 | 0.00 | - | 0.00 | - | 58.5 | 0.95 | 72.5 | 167.6 | -5.8 |
| LQ | 18.7 | 0.00 | - | - | 1.99 | 56.8 | 0.88 | 71.2 | 164.9 | −3.1 | |
| (Gy) | (Gy day) | (day) | (Gy) | ||
|---|---|---|---|---|---|
| LR | 2.0 | 0 | - | 56.2 | 2.17 |
| (1.7, 2.3) | (0, 0.13) | (54.4, 58.0) | (1.90, 2.47) | ||
| IR | 3.4 | 0.41 | 24.0 | 56.9 | 2.14 |
| (3.0, 4.0) | (0.31, 0.49) | (21.0, 25.5) | (55.5, 57.9) | (1.92, 2.40) | |
| HR | 2.8 | 0.35 | 21.0 | 59.8 | 1.45 |
| (1.4, 4.2) | (0, ∞) | (21.0, ∞) | (57.1, 63.9) | (1.07, 1.83) | |
| IR | 2.8 | 0.32 | 21.0 | 58.1 | 1.85 |
| (no ADT) | (2.1, 3.5) | (0.09, 0.46) | (21.0, 27.3) | (56.5, 60.0) | (1.55, 2.14) |
| HR | 2.1 | 0 | - | 58.5 | 0.95 |
| (ADT) | (1.5, 3.5) | (0, 0.31) | (54.3, 61.5) | (0.75, 1.25) | |
| IR | 0.1 | 0 | - | 8.1 | 0.20 |
| (ADT) | (0, ∞) | (0, ∞) | (0.4, 40.5) | (0.11, 0.80) | |
| HR | 100.0 | 3.31 | 39.9 | 54.6 | 6.68 |
| (no ADT) | (7.1, ∞) | (1.09, ∞) | (21.0, 40.8) | (49.8, 60.5) | (2.70, 10.67) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pardo-Montero, J.; González-Crespo, I.; Gómez-Caamaño, A.; Gago-Arias, A. Radiobiological Meta-Analysis of the Response of Prostate Cancer to Different Fractionations: Evaluation of the Linear–Quadratic Response at Large Doses and the Effect of Risk and ADT. Cancers 2023, 15, 3659. https://doi.org/10.3390/cancers15143659
Pardo-Montero J, González-Crespo I, Gómez-Caamaño A, Gago-Arias A. Radiobiological Meta-Analysis of the Response of Prostate Cancer to Different Fractionations: Evaluation of the Linear–Quadratic Response at Large Doses and the Effect of Risk and ADT. Cancers. 2023; 15(14):3659. https://doi.org/10.3390/cancers15143659
Chicago/Turabian StylePardo-Montero, Juan, Isabel González-Crespo, Antonio Gómez-Caamaño, and Araceli Gago-Arias. 2023. "Radiobiological Meta-Analysis of the Response of Prostate Cancer to Different Fractionations: Evaluation of the Linear–Quadratic Response at Large Doses and the Effect of Risk and ADT" Cancers 15, no. 14: 3659. https://doi.org/10.3390/cancers15143659
APA StylePardo-Montero, J., González-Crespo, I., Gómez-Caamaño, A., & Gago-Arias, A. (2023). Radiobiological Meta-Analysis of the Response of Prostate Cancer to Different Fractionations: Evaluation of the Linear–Quadratic Response at Large Doses and the Effect of Risk and ADT. Cancers, 15(14), 3659. https://doi.org/10.3390/cancers15143659






