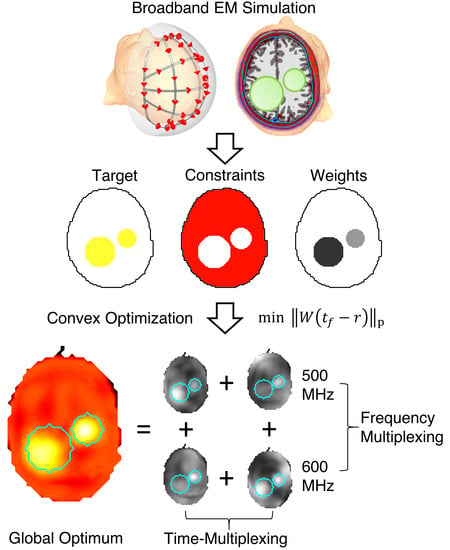
Solving the Time- and Frequency-Multiplexed Problem of Constrained Radiofrequency Induced Hyperthermia
Abstract
1. Introduction
2. Materials and Methods
2.1. Problem Statement
2.2. Semidefinite Relaxation
2.3. Time-Multiplexed Radiofrequency (RF) Heating
- A rank >1 solution to the semidefinite relaxation corresponds to the time-multiplexed excitation scenario.
- The individual excitation vectors for the time-multiplexed application can be retrieved using the eigendecomposition of X.
- Any arbitrary number of excitation vectors can be effectively compressed to at most N vectors.
2.4. Arbitrary Heating Patterns
2.5. Frequency-Multiplexed RF Heating
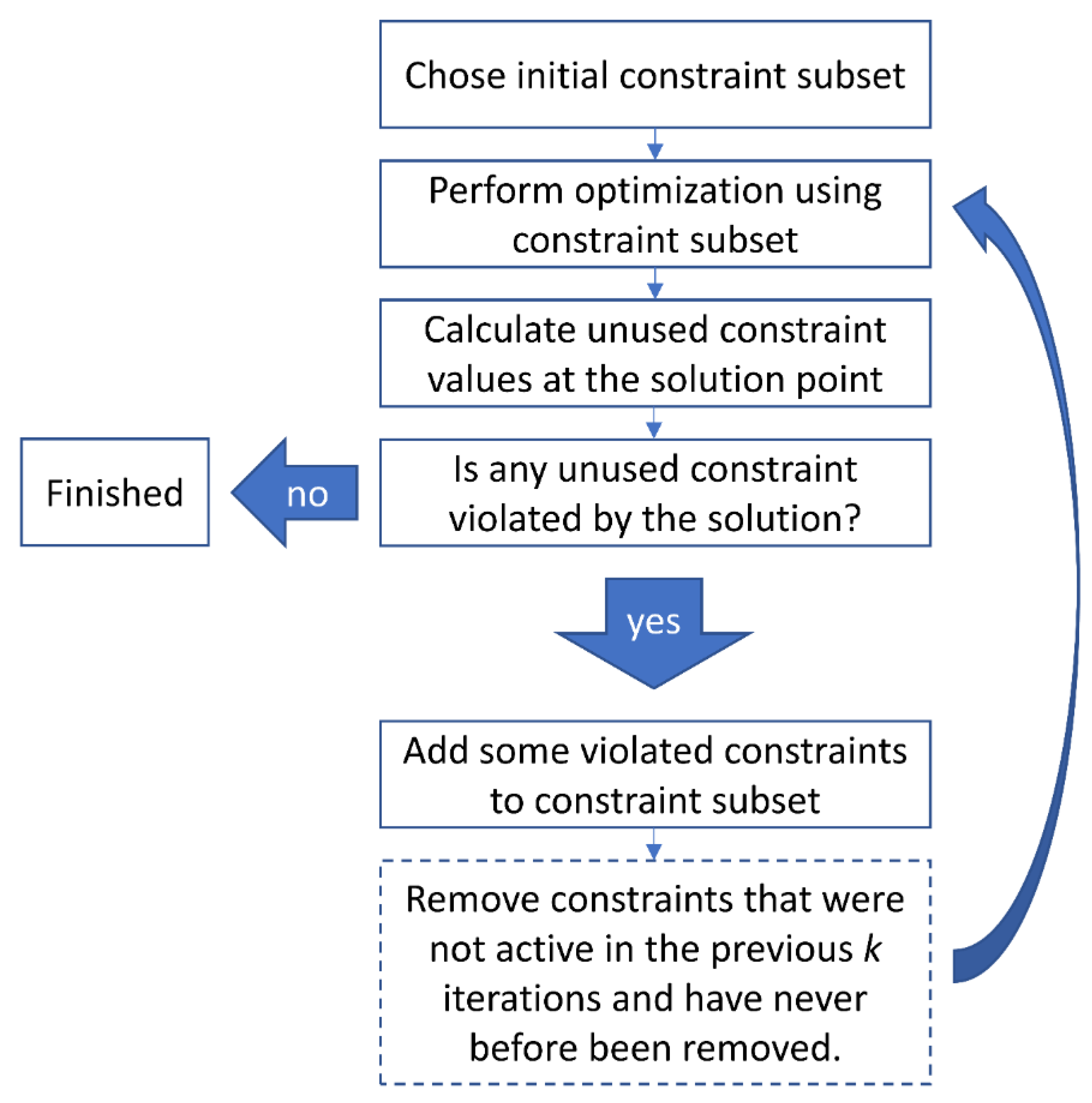
2.6. Iterative Solution
- EMF simulation of the RF applicator with an appropriate model of the object under investigation for the desired frequencies.
- Calculation of appropriately averaged SAR matrices for regions targeted for RF heating and for regions outside the target region for all frequencies.
- Solution of the optimization problem using the calculated SAR and target matrices.
- Retrieval of the individual excitation vectors for each frequency.
2.7. Retrieval of Excitation Vectors
- Perform an eigendecomposition of each matrix Xf, each yielding N eigenvectors vk and their associated eigenvalues λk. Very often, the solutions will be strongly rank-deficient, having only a few large eigenvalues. Each individual excitation vector is given by .
- Compute the local SAR distribution for each of the N · F excitations and evaluate their respective influence on the target region (e.g., by calculating their maximum and mean SAR inside the target region).
- Discard all excitations that do not significantly contribute to the solution (e.g., all excitations whose maximum SAR contribution to the target region falls below a certain threshold). In our examples, we chose to discard all vectors contributing less than 0.1% to the overall solution.
- Scale the remaining vectors for time-multiplexing. If M solutions belonging to the same frequency remain, this indicates that time-multiplexing is required (i.e., the excitations are played out in succession during the application and each solution vector needs to be scaled by . Excitations at different frequencies do not interact coherently and can in principle be played out concurrently (i.e., their SAR patterns are purely additive). If the different frequency solutions are also applied in a time-multiplexed fashion, a similar scaling needs to be performed.
2.8. Implementation and Validation
3. Results
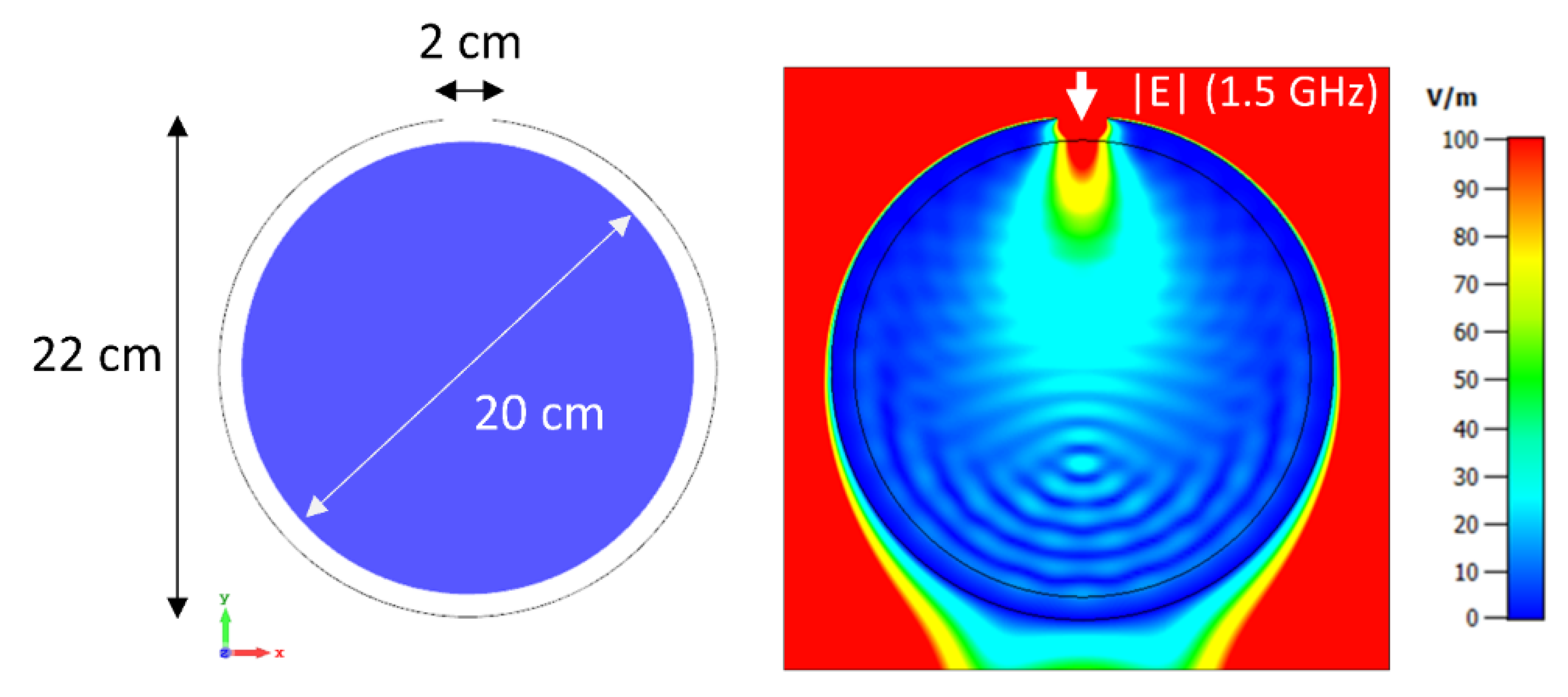
3.1. Phantom Setup Using a 32-Channel 2D Applicator
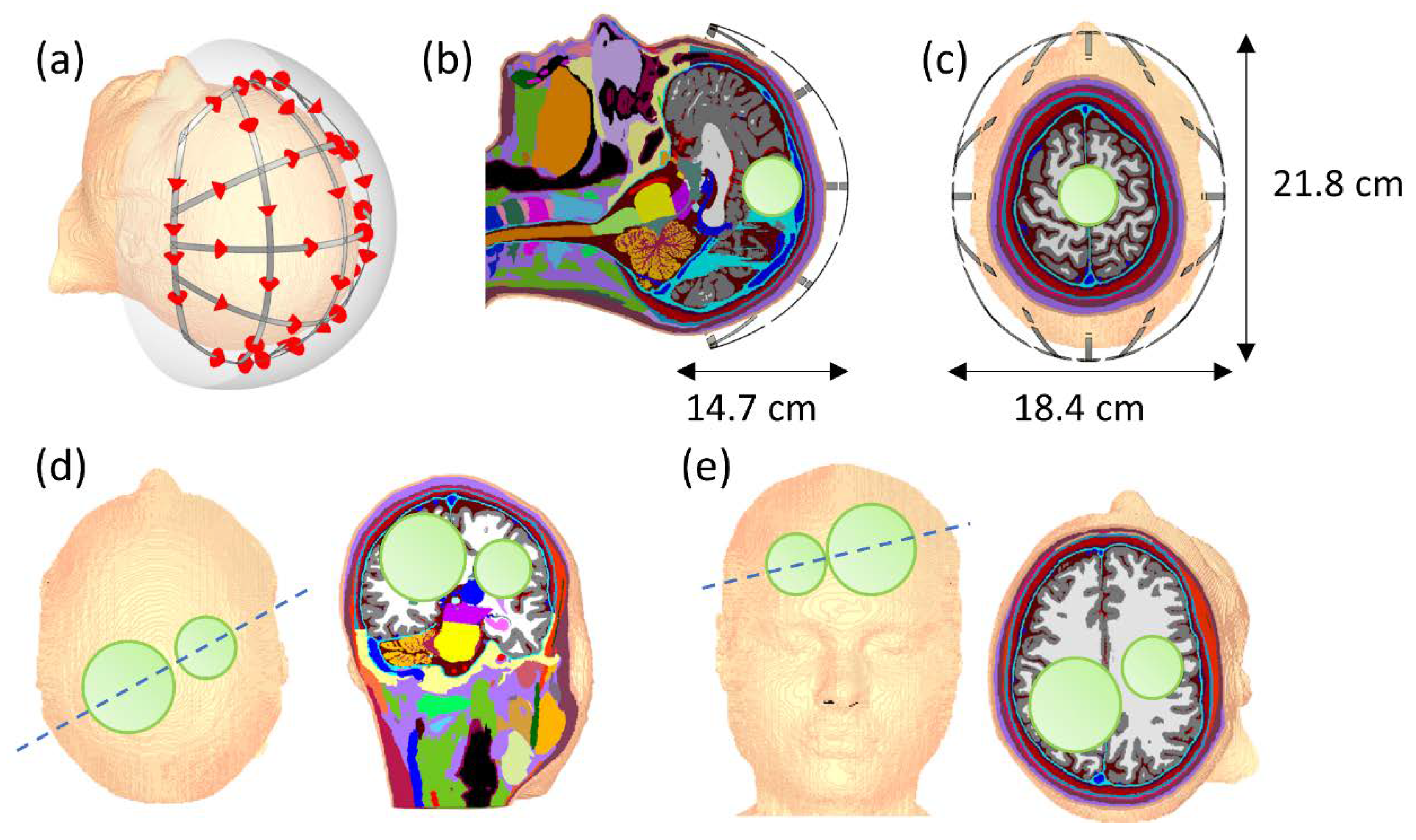
3.2. Human Brain Model Setup Using a 40-Channel 3D Helmet Grid Applicator
3.3. Runtimes of Demonstration Examples
3.4. Iterative vs. Non-Iterative Approach
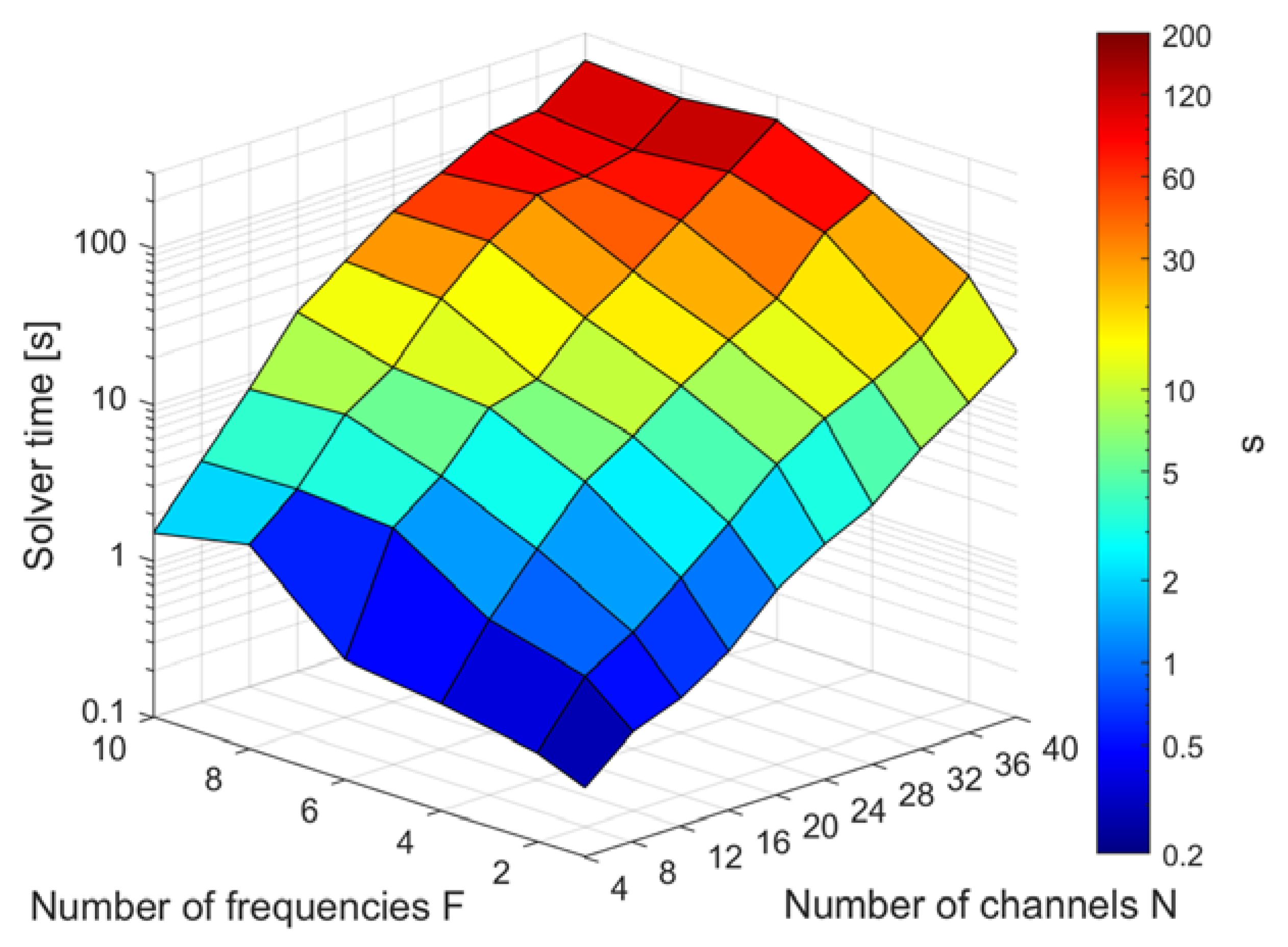
3.5. Dependence on Frequency and Channel Number
3.6. Comparison of Multiplexed Vector Field Shaping (MVFS) to Focused Constrained Power Optimization (FOCO)
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lo, Y.; Lee, S.W. Antenna Handbook; Lo, Y.T., Lee, S.W., Eds.; Springer: Boston, MA, USA, 1988; ISBN 978-1-4615-6461-4. [Google Scholar]
- Lin, J.C. Electromagnetic Fields in Biological Systems; Lin, J.C., Ed.; CRC Press: Boca Raton, FL, USA, 2016; ISBN 9780429106958. [Google Scholar]
- Brace, C.L. Microwave Tissue Ablation: Biophysics, Technology, and Applications. Crit. Rev. Biomed. Eng. 2010, 38, 65–78. [Google Scholar] [CrossRef] [PubMed]
- Brace, C. Thermal Tumor Ablation in Clinical Use. IEEE Pulse 2011, 2, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Besse, H.; Barten-van Rijbroek, A.; van der Wurff-Jacobs, K.; Bos, C.; Moonen, C.; Deckers, R. Tumor Drug Distribution after Local Drug Delivery by Hyperthermia, In Vivo. Cancers 2019, 11, 1512. [Google Scholar] [CrossRef]
- Oldenborg, S.; van Os, R.; Oei, B.; Poortmans, P. Impact of Technique and Schedule of Reirradiation Plus Hyperthermia on Outcome after Surgery for Patients with Recurrent Breast Cancer. Cancers 2019, 11, 782. [Google Scholar] [CrossRef] [PubMed]
- Mei, X.; ten Cate, R.; van Leeuwen, C.M.; Rodermond, H.M.; de Leeuw, L.; Dimitrakopoulou, D.; Stalpers, L.J.A.; Crezee, J.; Kok, H.P.; Franken, N.A.P.; et al. Radiosensitization by Hyperthermia: The Effects of Temperature, Sequence, and Time Interval in Cervical Cell Lines. Cancers 2020, 12, 582. [Google Scholar] [CrossRef] [PubMed]
- Moroz, P.; Jones, S.K.; Gray, B.N. Status of hyperthermia in the treatment of advanced liver cancer. J. Surg. Oncol. 2001, 77, 259–269. [Google Scholar] [CrossRef]
- Wust, P.; Hildebrandt, B.; Sreenivasa, G.; Rau, B.; Gellermann, J.; Riess, H.; Felix, R.; Schlag, P. Hyperthermia in combined treatment of cancer. Lancet Oncol. 2002, 3, 487–497. [Google Scholar] [CrossRef]
- Paulides, M.M.; Bakker, J.F.; Neufeld, E.; Zee, J.; van der Jansen, P.P.; Levendag, P.C.; van Rhoon, G.C. The HYPERcollar: A novel applicator for hyperthermia in the head and neck. Int. J. Hyperth. 2007, 23, 567–576. [Google Scholar] [CrossRef]
- Crezee, J.; Van Haaren, P.M.A.; Westendorp, H.; De Greef, M.; Kok, H.P.; Wiersma, J.; Van Stam, G.; Sijbrands, J.; Zum Vörde Sive Vörding, P.; Van Dijk, J.D.P.; et al. Improving locoregional hyperthermia delivery using the 3-D controlled AMC-8 phased array hyperthermia system: A preclinical study. Int. J. Hyperth. 2009, 25, 581–592. [Google Scholar] [CrossRef]
- Gellermann, J.; Wlodarczyk, W.; Feussner, A.; Fähling, H.; Nadobny, J.; Hildebrandt, B.; Felix, R.; Wust, P. Methods and potentials of magnetic resonance imaging for monitoring radiofrequency hyperthermia in a hybrid system. Int. J. Hyperth. 2005, 21, 497–513. [Google Scholar] [CrossRef]
- Guérin, B.; Villena, J.F.; Polimeridis, A.G.; Adalsteinsson, E.; Daniel, L.; White, J.K.; Rosen, B.R.; Wald, L.L. Computation of ultimate SAR amplification factors for radiofrequency hyperthermia in non-uniform body models: Impact of frequency and tumour location. Int. J. Hyperth. 2017, 34, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Winter, L.; Niendorf, T. Electrodynamics and radiofrequency antenna concepts for human magnetic resonance at 23.5 T (1 GHz) and beyond. Magn. Reson. Mater. Phys. Biol. Med. 2016, 29, 641–656. [Google Scholar] [CrossRef] [PubMed]
- Winter, L.; Oezerdem, C.; Hoffmann, W.; van de Lindt, T.; Periquito, J.; Ji, Y.; Ghadjar, P.; Budach, V.; Wust, P.; Niendorf, T. Thermal magnetic resonance: Physics considerations and electromagnetic field simulations up to 23.5 Tesla (1GHz). Radiat. Oncol. 2015, 10, 201. [Google Scholar] [CrossRef] [PubMed]
- Oberacker, E.; Kuehne, A.; Nadobny, J.; Zschaeck, S.; Weihrauch, M.; Waiczies, H.; Ghadjar, P.; Wust, P.; Niendorf, T.; Winter, L. Radiofrequency applicator concepts for simultaneous MR imaging and hyperthermia treatment of glioblastoma multiforme. Curr. Dir. Biomed. Eng. 2017, 3, 473–477. [Google Scholar] [CrossRef]
- Trefná, H.D.; Vrba, J.; Persson, M. Time-reversal focusing in microwave hyperthermia for deep-seated tumors. Phys. Med. Biol. 2010, 55, 2167–2185. [Google Scholar] [CrossRef]
- Takook, P.; Trefna, H.D.; Zeng, X.; Fhager, A.; Persson, M. A computational study using time reversal focusing for hyperthermia treatment planning. Prog. Electromagn. Res. B 2017, 73, 117–130. [Google Scholar] [CrossRef]
- Rijnen, Z.; Bakker, J.F.; Canters, R.A.M.; Togni, P.; Verduijn, G.M.; Levendag, P.C.; Van Rhoon, G.C.; Paulides, M.M. Clinical integration of software tool VEDO for adaptive and quantitative application of phased array hyperthermia in the head and neck. Int. J. Hyperth. 2013, 29, 181–193. [Google Scholar] [CrossRef]
- Bardati, F.; Borrani, A.; Gerardino, A.; Lovisolo, G.A. SAR optimization in a phased array radiofrequency hyperthermia system. IEEE Trans. Biomed. Eng. 1995, 42, 1201–1207. [Google Scholar] [CrossRef]
- Böhm, M.; Louis, A. Efficient algorithm for computing optimal control of antennas in hyperthermia. Surv. Math. Indust 1993, 3, 233–251. [Google Scholar]
- Mestrom, R.M.C.; van Engelen, J.P.; van Beurden, M.C.; Paulides, M.M.; Numan, W.C.M.; Tijhuis, A.G. A Refined Eigenvalue-Based Optimization Technique for Hyperthermia Treatment Planning. In Proceedings of the The 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2010–2013. [Google Scholar]
- Köhler, T.; Maass, P.; Wust, P.; Seebass, M. A fast algorithm to find optimal controls of multiantenna applicators in regional hyperthermia. Phys. Med. Biol. 2001, 46, 2503–2514. [Google Scholar] [CrossRef]
- Cappiello, G.; Drizdal, T.; Mc Ginley, B.; O’Halloran, M.; Glavin, M.; Van Rhoon, G.C.; Jones, E.; Paulides, M.M. The potential of time-multiplexed steering in phased array microwave hyperthermia for head and neck cancer treatment. Phys. Med. Biol. 2018, 63, 135023. [Google Scholar] [CrossRef] [PubMed]
- Zastrow, E.; Hagness, S.C.; Van Veen, B.D.; Medow, J.E. Time-Multiplexed Beamforming for Noninvasive Microwave Hyperthermia Treatment. IEEE Trans. Biomed. Eng. 2011, 58, 1574–1584. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; Van Stam, G.; Bel, A.; Crezee, J. A Mixed Frequency Approach to Optimize Locoregional RF Hyperthermia. In Proceedings of the 2015 European Microwave Conference (EuMC), Paris, France, 7–10 September 2015; pp. 773–776. [Google Scholar]
- Converse, M.; Bond, E.J.; Van Veen, B.D.; Hagness, S.C. A computational study of ultra-wideband versus narrowband microwave hyperthermia for breast cancer treatment. IEEE Trans. Microw. Theory Tech. 2006, 54, 2169–2180. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Crocco, L.; Battaglia, G.M.; Isernia, T. Multi-frequency constrained SAR focusing for patient specific hyperthermia treatment. IEEE J. Electromagn. RF Microwaves Med. Biol. 2017, 1, 74–80. [Google Scholar] [CrossRef]
- Takook, P.; Persson, M.; Gellermann, J.; Trefná, H.D. Compact self-grounded Bow-Tie antenna design for an UWB phased-array hyperthermia applicator. Int. J. Hyperth. 2017, 33, 387–400. [Google Scholar] [CrossRef]
- Jacobsen, S.; Melandsø, F. The Concept of Using Multifrequency Energy Transmission to Reduce Hot Spots during Deep-Body Hyperthermia. Ann. Biomed. Eng. 2002, 30, 34–43. [Google Scholar] [CrossRef]
- Bucci, O.M.; D’elia, G.; Mazzarella, G.; Panariello, G. Antenna Pattern Synthesis: A New General Approach. Proc. IEEE 1994, 82, 358–371. [Google Scholar] [CrossRef]
- Liontas, C.A.; Knott, P. An Alternating Projections Algorithm for Optimizing Electromagnetic Fields in Regional Hyperthermia. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Liontas, C.A. Alternating Projections of Auxiliary Vector Fields for Electric Field Optimization in Temperature-guided Hyperthermia. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Bellizzi, G.G.; Drizdal, T.; Van Rhoon, G.C.; Crocco, L.; Isernia, T.; Paulides, M.M. The potential of constrained SAR focusing for hyperthermia treatment planning: Analysis for the head & neck region. Phys. Med. Biol. 2019, 64, 1. [Google Scholar]
- Iero, D.; Isernia, T.; Morabito, A.F.; Catapano, I.; Crocco, L. Optimal constrained field focusing for hyperthermia cancer therapy: A feasibility assessment on realistic phantoms. Prog. Electromagn. Res. 2010, 102, 125–141. [Google Scholar] [CrossRef][Green Version]
- Iero, D.A.M.; Crocco, L.; Isernia, T. Thermal and microwave constrained focusing for patient-specific breast cancer hyperthermia: A robustness assessment. IEEE Trans. Antennas Propag. 2014, 62, 814–821. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Battaglia, G.M.; Bevacqua, M.T.; Crocco, L.; Isernia, T. FOCO: A Novel Versatile Tool in Hyperthermia Treatment Planning. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–4. [Google Scholar]
- Kuehne, A.; Goluch, S.; Waxmann, P.; Seifert, F.; Ittermann, B.; Moser, E.; Laistler, E. Power balance and loss mechanism analysis in RF transmit coil arrays. Magn. Reson. Med. 2015, 74, 1165–1176. [Google Scholar] [CrossRef] [PubMed]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Boulant, N.; Wu, X.; Adriany, G.; Schmitter, S.; Uʇurbil, K.; Van De Moortele, P.F. Direct control of the temperature rise in parallel transmission by means of temperature virtual observation points: Simulations at 10.5 tesla. Magn. Reson. Med. 2016, 75, 249–256. [Google Scholar] [CrossRef] [PubMed]
- Kowalski, M.; Behnia, B.; Webb, A.G.; Jin, J.M. Optimization of electromagnetic phased-arrays for hyperthermia via magnetic resonance temperature estimation. IEEE Trans. Biomed. Eng. 2002, 49, 1229–1241. [Google Scholar] [CrossRef]
- Luo, Z.; Ma, W.; So, A.; Ye, Y.; Zhang, S. Semidefinite Relaxation of Quadratic Optimization Problems. IEEE Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Iero, D.A.M.; Crocco, L.; Isernia, T. Three-Dimensional Field Intensity Shaping: The Scalar Case. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 360–363. [Google Scholar] [CrossRef]
- Vandenberghe, L.; Boyd, S. Semidefinite Programming. SIAM Rev. 1996, 38, 49–95. [Google Scholar] [CrossRef]
- Sturm, J.F. Using SeDuMi 1.02, A Matlab toolbox for optimization over symmetric cones. Optim. Methods Softw. 1999, 11, 625–653. [Google Scholar] [CrossRef]
- Toh, K.C.; Todd, M.J.; Tütüncü, R.H. SDPT3—A Matlab software package for semidefinite programming, Version 1.3. Optim. Methods Softw. 1999, 11, 545–581. [Google Scholar] [CrossRef]
- Tütüncü, R.H.; Toh, K.C.; Todd, M.J. Solving semidefinite-quadratic-linear programs using SDPT3. Math. Program. 2003, 95, 189–217. [Google Scholar] [CrossRef]
- Yamashita, M.; Fujisawa, K.; Kojima, M. Implementation and evaluation of SDPA 6.0 (Semidefinite Programming Algorithm 6.0). Optim. Methods Softw. 2003, 18, 491–505. [Google Scholar] [CrossRef]
- Yamashita, M.; Fujisawa, K.; Fukuda, M.; Kobayashi, K.; Nakata, K.; Nakata, M. Handbook on Semidefinite, Conic and Polynomial Optimization; Springer: Boston, MA, USA, 2012; pp. 687–713. [Google Scholar]
- Borchers, B. CSDP, A C library for semidefinite programming. Optim. Methods Softw. 1999, 11, 613–623. [Google Scholar] [CrossRef]
- Mosep ApS, The MOSEK Optimization Toolbox for MATLAB Manual, Version 9.2.; Mosep ApS: Copenhagen, Denmark, 2019.
- Löfberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the CACSD Conference, New Orleans, LA, USA, 2–4 September 2004. [Google Scholar]
- CVX Research, Inc. CVX: Matlab Software for Disciplined Convex Programming. version 2.0. 2012. [Google Scholar]
- Graesslin, I.; Homann, H.; Biederer, S.; Börnert, P.; Nehrke, K.; Vernickel, P.; Mens, G.; Harvey, P.; Katscher, U. A specific absorption rate prediction concept for parallel transmission MR. Magn. Reson. Med. 2012, 68, 1664–1674. [Google Scholar] [CrossRef] [PubMed]
- Gebhardt, M. Method and High-Frequency Check Device for Checking a High-Frequency Transmit Device of a Magnetic Resonance Tomography System. U.S. Patent 9,229,072, 2012. [Google Scholar]
- Pendse, M.; Rutt, B.K. A Vectorized Formalism for Efficient SAR Computation in Parallel Transmission. In Proceedings of the ISMRM, Toronto, ON, Canada, 30 May–5 June 2015; p. 0379. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Pendse, M.; Rutt, B.K. Method and Apparatus for SAR Focusing with an Array of RF Transmitters. U.S. Patent 10,088,537 B2, 2 October 2018. [Google Scholar]
- Pendse, M.; Stara, R.; Mehdi Khalighi, M.; Rutt, B. IMPULSE: A scalable algorithm for design of minimum specific absorption rate parallel transmit RF pulses. Magn. Reson. Med. 2018, 1–15. [Google Scholar] [CrossRef]
- Eichfelder, G.; Gebhardt, M. Local specific absorption rate control for parallel transmission by virtual observation points. Magn. Reson. Med. 2011, 66, 1468–1476. [Google Scholar] [CrossRef]
- Lee, J.; Gebhardt, M.; Wald, L.L.; Adalsteinsson, E. Local SAR in parallel transmission pulse design. Magn. Reson. Med. 2012, 67, 1566–1578. [Google Scholar] [CrossRef]
- Kuehne, A.; Waiczies, H.; Niendorf, T. Massively accelerated VOP compression for population-scale RF safety models. In Proceedings of the ISMRM, Honolulu, HI, USA, 2017; p. 0478. [Google Scholar]
- Volken, W.; Frei, D.; Manser, P.; Mini, R.; Born, E.J.; Fix, M.K. An integral conservative gridding--algorithm using Hermitian curve interpolation. Phys. Med. Biol. 2008, 53, 6245–6263. [Google Scholar] [CrossRef]
- Iacono, M.I.; Neufeld, E.; Akinnagbe, E.; Bower, K.; Wolf, J.; Oikonomidis, I.V.; Sharma, D.; Lloyd, B.; Wilm, B.J.; Wyss, M.; et al. MIDA: A multimodal imaging-based detailed anatomical model of the human head and neck. PLoS ONE 2015, 10, e0124126. [Google Scholar] [CrossRef] [PubMed]
- Paska, J.; Raya, J.; Cloos, M.A. Fast and Intuitive RF-Coil Optimization Pipeline Using a Mesh-Structure. In Proceedings of the ISMRM, Montréal, QC, Canada, 11–16 May 2019; p. 0571. [Google Scholar]
- Hasgall, P.; Neufeld, E.; Gosselin, M.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues, Version 4.0. Available online: www.itis.ethz.ch/database (accessed on 4 March 2020).
- Lu, Y.; Li, B.; Xu, J.; Yu, J. Dielectric properties of human glioma and surrounding tissue. Int. J. Hyperth. 1992, 8, 755–760. [Google Scholar] [CrossRef] [PubMed]
- Kuehne, A.; Seifert, F.; Ittermann, B. GPU-accelerated SAR computation with arbitrary averaging shapes. In Proceedings of the ISMRM, Melbourne, Australia, 5–11 May 2012; p. 4260. [Google Scholar]
- Lee, H.K.; Antell, A.G.; Perez, C.A.; Straube, W.L.; Ramachandran, G.; Myerson, R.J.; Emami, B.; Molmenti, E.P.; Buckner, A.; Lockett, M.A. Superficial hyperthermia and irradiation for recurrent breast carcinoma of the chest wall: Prognostic factors in 196 tumors. Int. J. Radiat. Oncol. 1998, 40, 365–375. [Google Scholar] [CrossRef]
- Myerson, R.J.; Perez, C.A.; Emami, B.; Straube, W.; Kuske, R.R.; Leybovich, L.; Von Gerichten, D. Tumor control in long-term survivors following superficial hyperthermia. Int. J. Radiat. Oncol. 1990, 18, 1123–1129. [Google Scholar] [CrossRef]
- Canters, R.A.M.; Wust, P.; Bakker, J.F.; Van Rhoon, G.C. A literature survey on indicators for characterisation and optimisation of SAR distributions in deep hyperthermia, a plea for standardisation. Int. J. Hyperth. 2009, 25, 593–608. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Drizdal, T.; van Rhoon, G.C.; Crocco, L.; Isernia, T.; Paulides, M.M. Predictive value of SAR based quality indicators for head and neck hyperthermia treatment quality. Int. J. Hyperth. 2019, 36, 456–465. [Google Scholar] [CrossRef]
- Grissom, W.A.; Xu, D.; Kerr, A.B.; Fessler, J.A.; Noll, D.C. Fast Large-Tip-Angle Multidimensional and Parallel RF Pulse Design in MRI. IEEE Trans. Med. Imaging 2009, 28, 1548–1559. [Google Scholar] [CrossRef]
- Eryaman, Y.; Akin, B.; Atalar, E. Reduction of implant RF heating through modification of transmit coil electric field. Magn. Reson. Med. 2011, 65, 1305–1313. [Google Scholar] [CrossRef]
- Eryaman, Y.; Turk, E.A.; Oto, C.; Algin, O.; Atalar, E. Reduction of the radiofrequency heating of metallic devices using a dual-drive birdcage coil. Magn. Reson. Med. 2013, 69, 845–852. [Google Scholar] [CrossRef]
- Guerin, B.; Angelone, L.M.; Dougherty, D.; Wald, L.L. Parallel transmission to reduce absorbed power around deep brain stimulation devices in MRI: Impact of number and arrangement of transmit channels. Magn. Reson. Med. 2020, 83, 299–311. [Google Scholar] [CrossRef]
- Oberacker, E.; Kuehne, A.; Oezerdem, C.; Millward, J.M.; Diesch, C.; Eigentler, T.W.; Zschaeck, S.; Ghadjar, P.; Wust, P.; Winter, L.; et al. Power Considerations for Radiofrequency Applicator Concepts for Thermal Magnetic Resonance Interventions in the Brain at 297 MHz. In Proceedings of the ISMRM, Montréal, QC, Canada, 11–16 May 2019; p. 3828. [Google Scholar]
- Oberacker, E.; Kuehne, A.; Waiczies, H.; Nadobny, J.; Zschaeck, S.; Ghadjar, P.; Wust, P.; Niendorf, T.; Winter, L. Radiofrequency Applicator Concepts for Simultaneous MR Imaging and Hyperthermia Treatment of Glioblastoma Multiforme: A 7.0 T (298 MHz) Study. In Proceedings of the ISMRM, Honolulu, HI, USA, 22–27 April 2017; p. 2604. [Google Scholar]
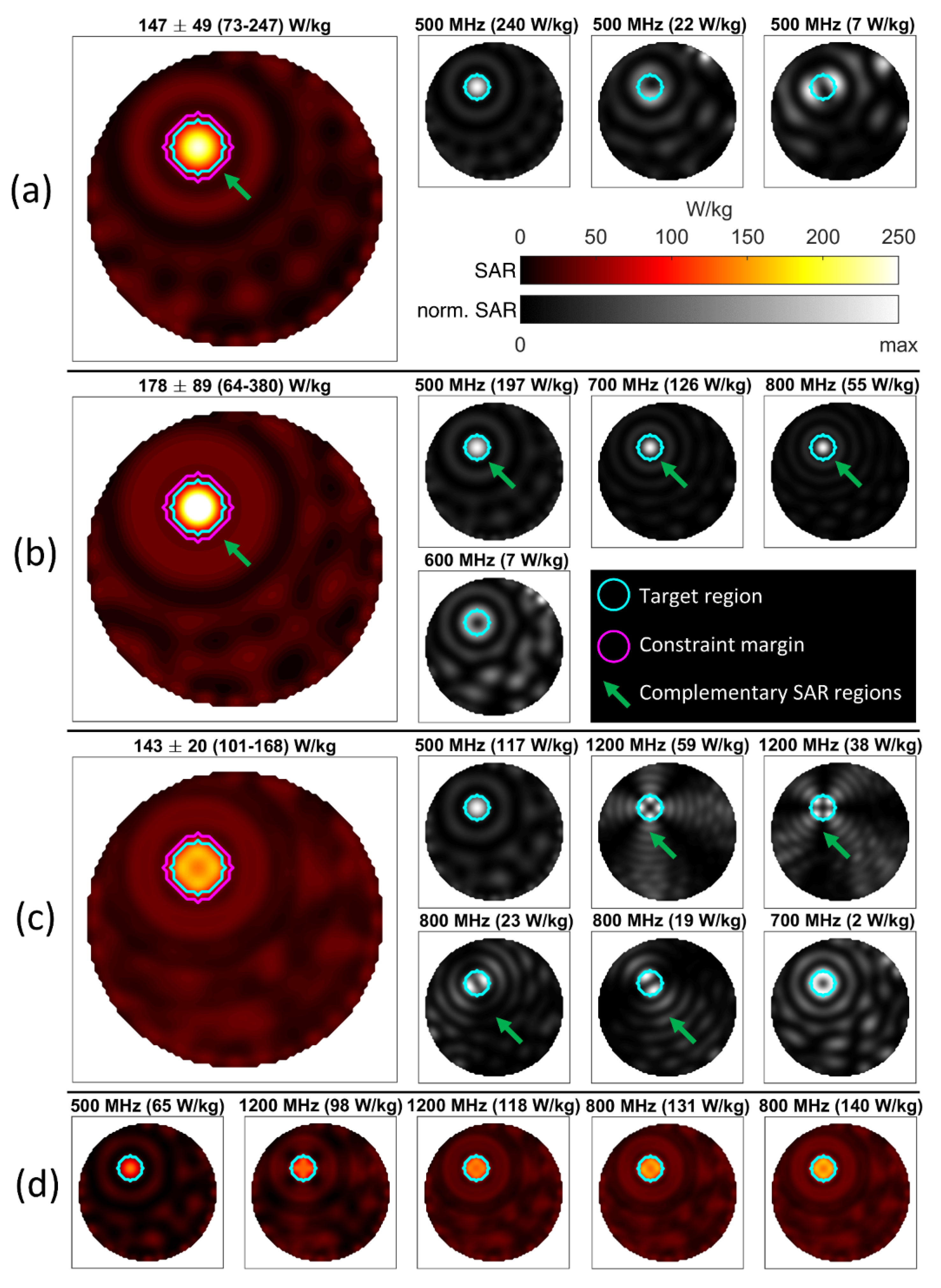

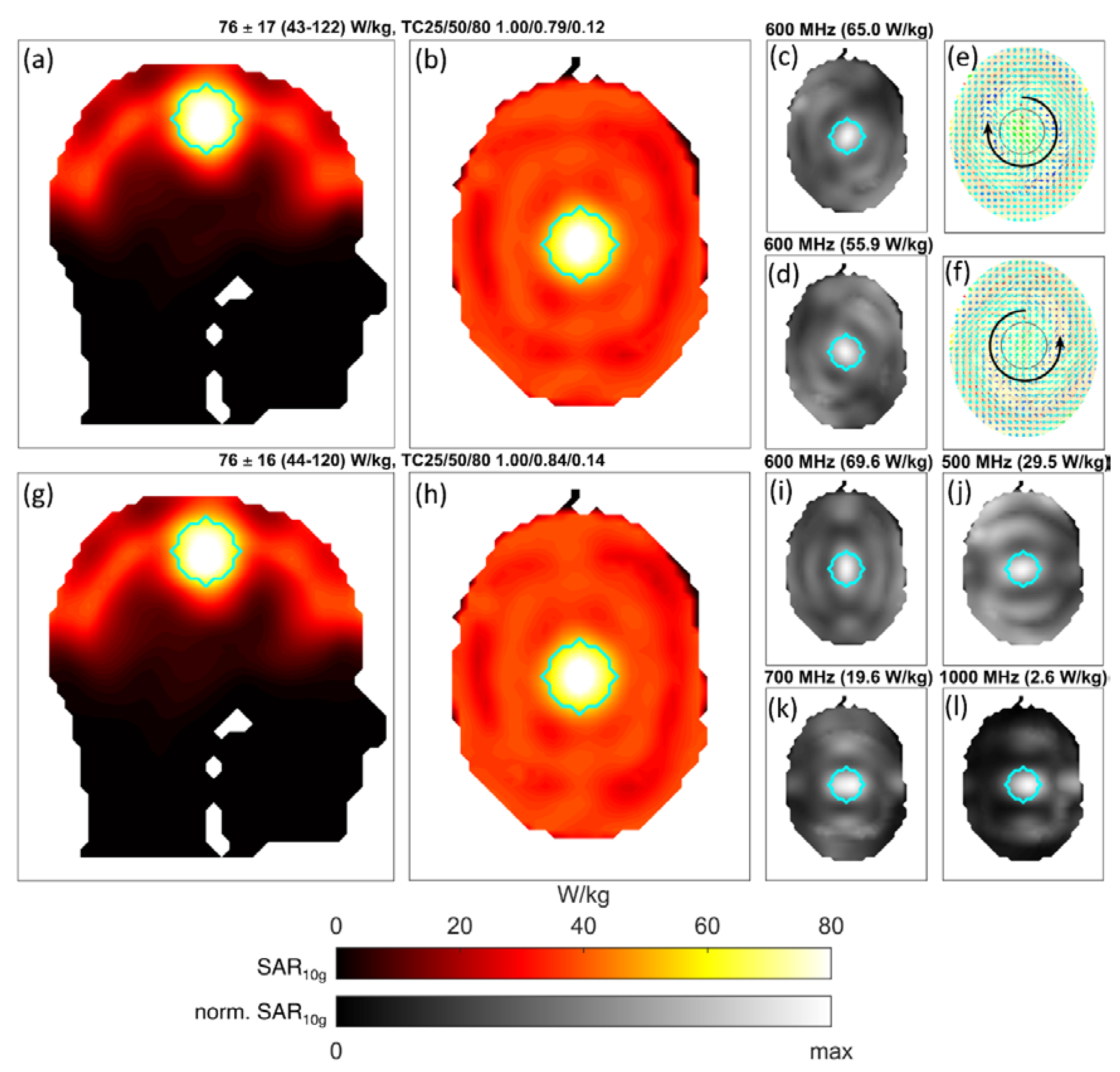
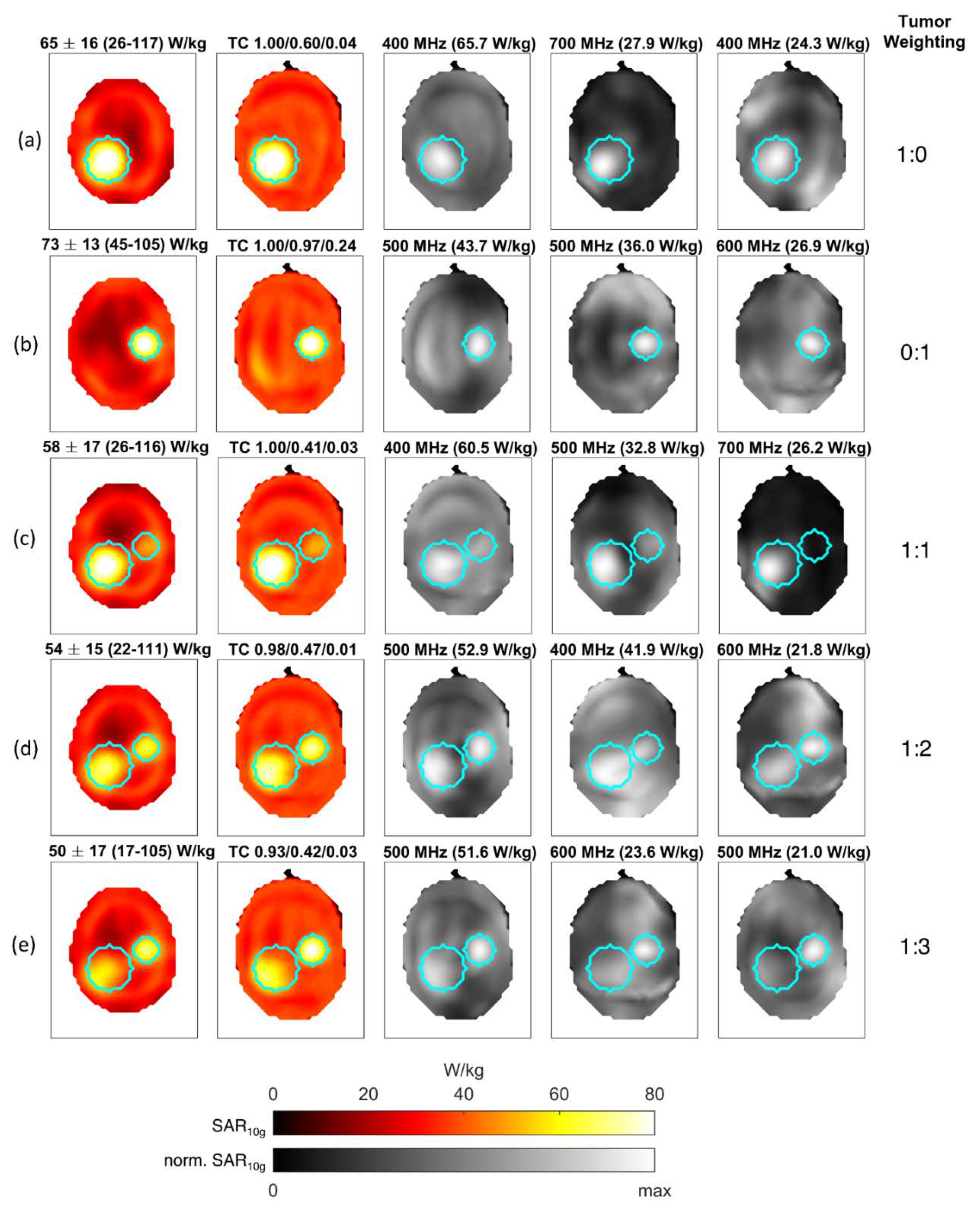
| Example Figure # | # of Channels | # of Target Points | # of Frequencies | # of Constraint Voxels | % of Used Constraint Voxels | # of Iterations | Computation Time [hh:mm:ss] |
|---|---|---|---|---|---|---|---|
| 4 (a) | 32 | 149 | 1 | 4952 | 17.4 | 25 | 00:00:52 |
| 4 (b) | 32 | 149 | 10 | 4952 | 15.3 | 10 | 00:03:21 |
| 4 (c) | 32 | 149 | 10 | 4952 | 13.9 | 16 | 00:04:42 |
| 5 | 32 | 8693 | 16 | 22,289 | 1.7 | 19 | 02:36:18 |
| 6 (a–f) | 40 | 257 | 1 | 29,914 | 0.7 | 9 | 00:00:22 |
| 6 (g–l) | 40 | 257 | 10 | 29,914 | 0.8 | 10 | 00:03:24 |
| 7 (a) | 40 | 247 | 10 | 29,908 | 0.6 | 8 | 00:03:10 |
| 7 (b) | 40 | 67 | 10 | 29,908 | 0.4 | 9 | 00:02:52 |
| 7 (c) | 40 | 314 | 10 | 29,908 | 0.6 | 8 | 00:03:04 |
| 7 (d) | 40 | 314 | 10 | 29,908 | 0.5 | 9 | 00:03:16 |
| 7 (e) | 40 | 314 | 10 | 29,908 | 0.6 | 8 | 00:03:03 |
| Performance | MVFS | |||||||
|---|---|---|---|---|---|---|---|---|
| Metrics | FOCO | Center | Averaged | S2 150 | S2 75 | S∞ 150 | S∞ 75 | |
| Local 10 g-SAR [W/kg] | Mean | 69 | 75 | 76 | 76 | 68 | 69 | 68 |
| Max | 107 | 120 | 123 | 122 | 95 | 103 | 99 | |
| Min | 33 | 41 | 43 | 43 | 45 | 51 | 51 | |
| SD | 15 | 17 | 17 | 17 | 11 | 12 | 12 | |
| Coverage | TC25 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| TC50 | 0.87 | 0.80 | 0.77 | 0.79 | 0.99 | 0.95 | 1.00 | |
| TC80 | 0.13 | 0.14 | 0.12 | 0.12 | 0.23 | 0.16 | 0.18 | |
| Solution | Time [s] | 16.5 | 14 | 22.2 | 22.8 | 21.7 | 24 | 26 |
| Rank | 1 | 2 | 2 | 2 | 3 | 3 | 3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuehne, A.; Oberacker, E.; Waiczies, H.; Niendorf, T. Solving the Time- and Frequency-Multiplexed Problem of Constrained Radiofrequency Induced Hyperthermia. Cancers 2020, 12, 1072. https://doi.org/10.3390/cancers12051072
Kuehne A, Oberacker E, Waiczies H, Niendorf T. Solving the Time- and Frequency-Multiplexed Problem of Constrained Radiofrequency Induced Hyperthermia. Cancers. 2020; 12(5):1072. https://doi.org/10.3390/cancers12051072
Chicago/Turabian StyleKuehne, Andre, Eva Oberacker, Helmar Waiczies, and Thoralf Niendorf. 2020. "Solving the Time- and Frequency-Multiplexed Problem of Constrained Radiofrequency Induced Hyperthermia" Cancers 12, no. 5: 1072. https://doi.org/10.3390/cancers12051072
APA StyleKuehne, A., Oberacker, E., Waiczies, H., & Niendorf, T. (2020). Solving the Time- and Frequency-Multiplexed Problem of Constrained Radiofrequency Induced Hyperthermia. Cancers, 12(5), 1072. https://doi.org/10.3390/cancers12051072