An Overmoded-Waveguide-Based Permittivity Measurement Method with High Accuracy and Ultra-Broadband over 8–110 GHz
Abstract
1. Introduction
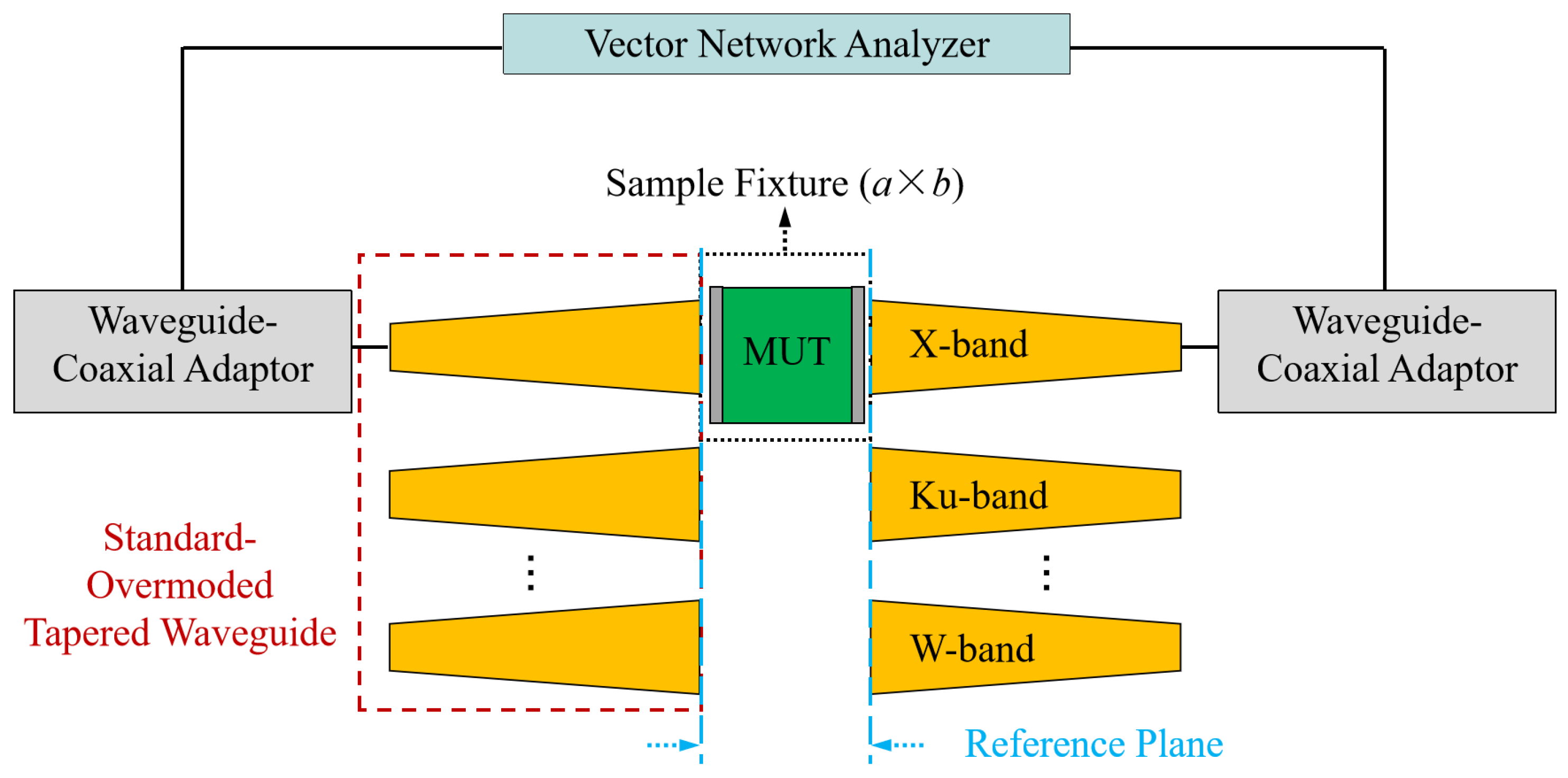
2. Design of the OWM-Based Measurement Kit
3. Measurement Results
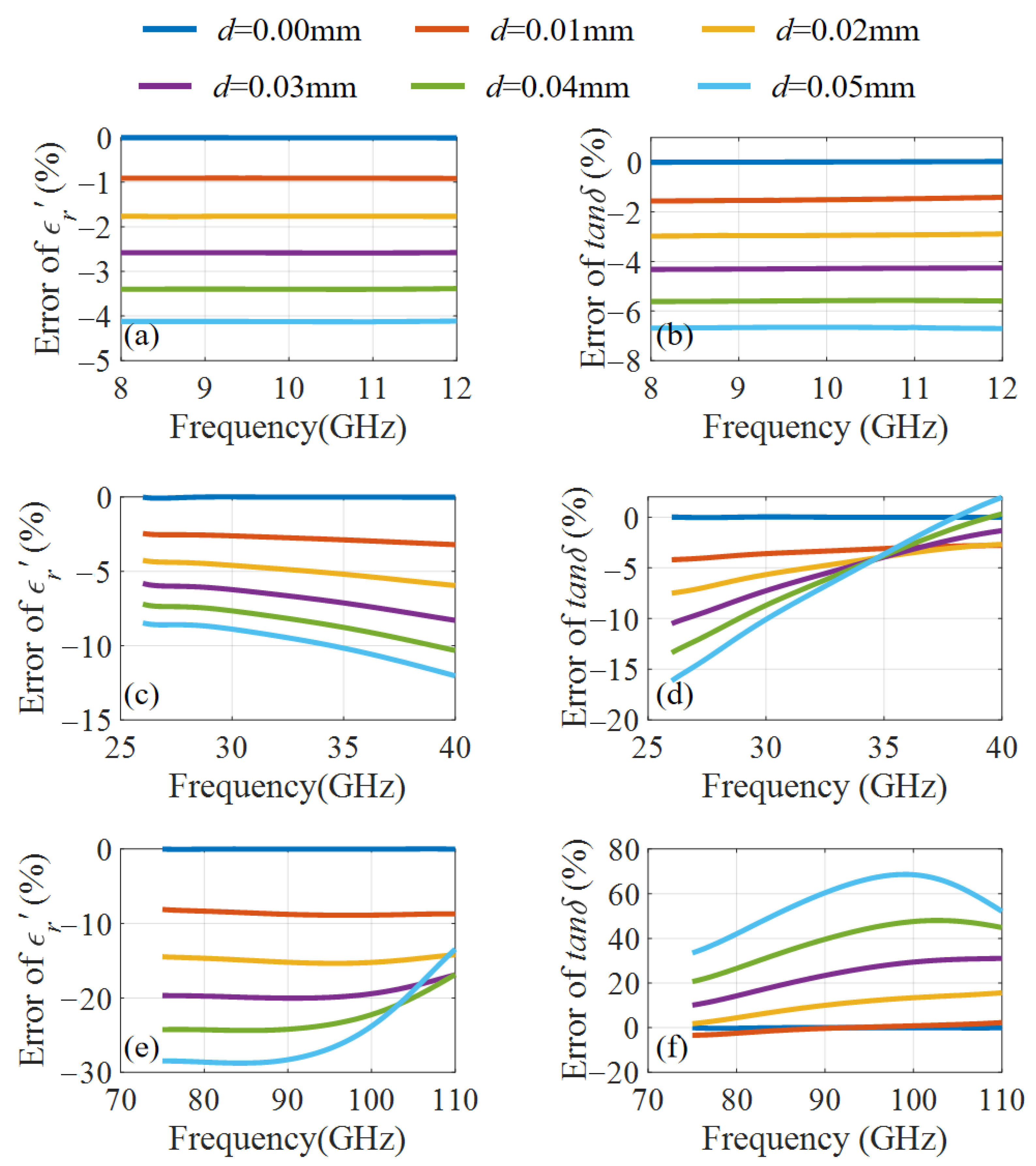
3.1. Measurement Verification of the PTFE
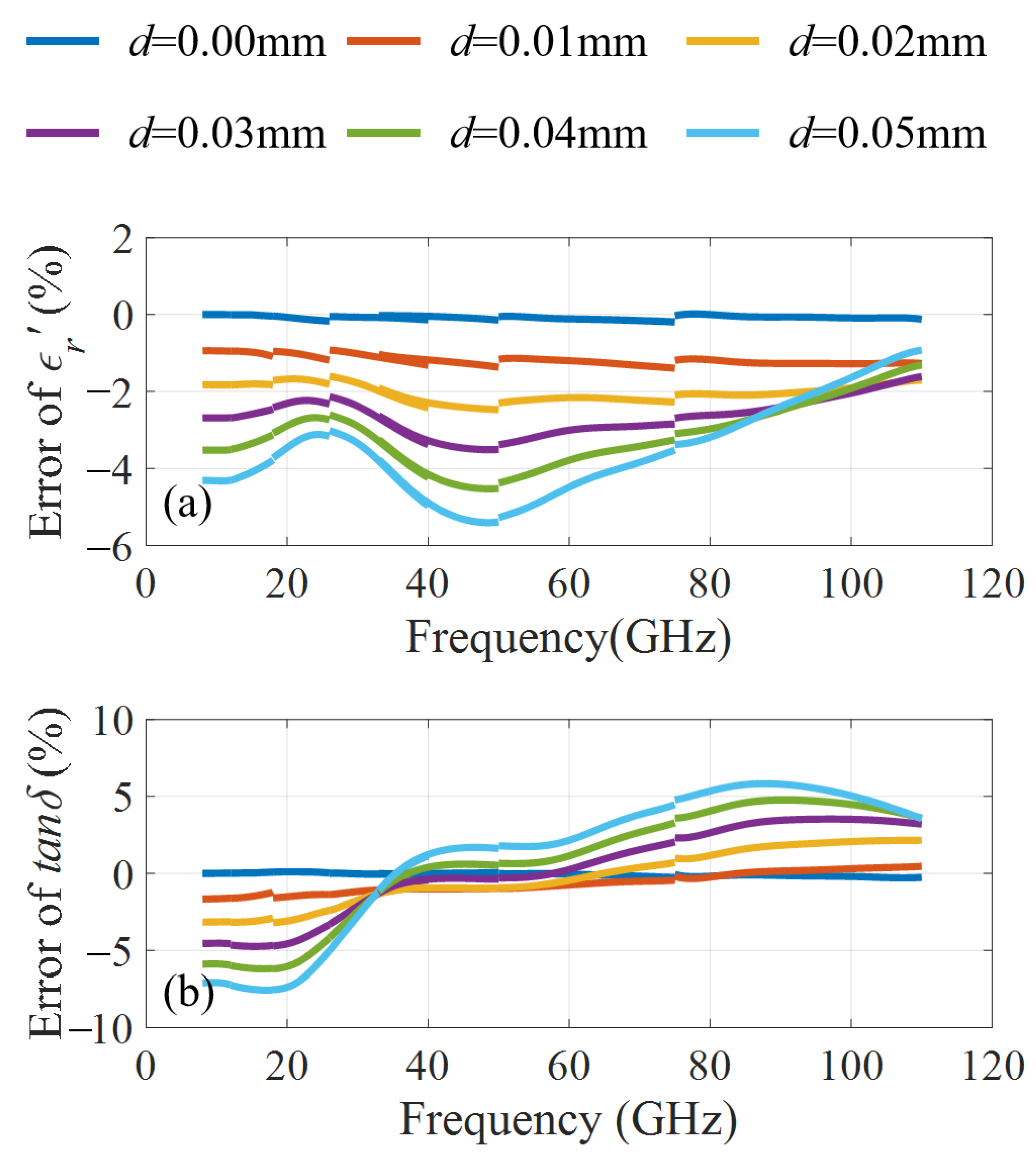
3.2. Application in Lossy Material Measurement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, H.J.; Nagatsuma, T. Present and future of terahertz communications. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 256–263. [Google Scholar] [CrossRef]
- Cohick, Z.W.; Schaub, S.C.; Hoff, B.; Dynys, F.W.; Baros, A.E.; Telmer, M.; Orozco, H.; Grudt, R.O.; Hayden, S.C.; Rittersdorf, I.M.; et al. High temperature W-band complex permittivity measurements of thermally cycled ceramic-metal composites: AlN:Mo with 0.25 to 4.0 vol% Mo from 25 °C to 1000 °C in air. IEEE Trans. Terahertz Sci. Technol. 2021, 33, 015901. [Google Scholar] [CrossRef]
- Calame, J.P.; Abe, D.K. Applications of advanced materials technologies to vacuum electronic devices. IEEE Trans. Terahertz Sci. Technol. 1999, 87, 840–864. [Google Scholar] [CrossRef]
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; Wiley: West Sussex, UK, 2004. [Google Scholar][Green Version]
- Wilson, S.B. Modal analysis of the ’gap effect’ in waveguide dielectric measurements. IEEE Trans. Microw. Theory Tech. 1988, 36, 752–756. [Google Scholar] [CrossRef]
- Foudazi, A.; Donnell, K.M. Effect of sample preparation on microwave material characterization by loaded waveguide technique. IEEE Trans. Instrum. Meas. 2016, 65, 1669–1677. [Google Scholar] [CrossRef]
- Yang, G.F.; Zhou, S.H.; Liang, W.; Li, X.; Huang, H.; Yang, J.H. Effect of different shapes on the measurement of dielectric constants of low-loss materials with rectangular waveguides at X-band. IEEE Microw. Wireless Compon. Lett. 2022, 32, 1471–1474. [Google Scholar] [CrossRef]
- Baker-Jarvis, J.R. Measuring Permittivity and Permeability of Lossy Materials: Solids, Liquids, Metals, and Negative-Index Materials; Technical Report; National Institute of Standards and Technology: Washington, DC, USA, 2005.[Green Version]
- Wang, W.J.; Jiang, W.; Yao, Y.L.; Wang, J.X.; Liu, G. An air gap correction method for permittivity extraction of high-loss materials. J. Electromagn. Waves Appl. 2024, 38, 1435–1449. [Google Scholar] [CrossRef]
- Wang, Y.; Hooper, I.; Edwards, E.; Grant, P.S. Gap-corrected thin-film permittivity and permeability measurement with a broadband coaxial line technique. IEEE Trans. Terahertz Sci. Technol. 2016, 64, 924–930. [Google Scholar] [CrossRef]
- Xu, H.; Liang, W.; Gao, Q. A self-gap-correction method for accurate permittivity measurement using the hybrid optimization algorithm. IEEE Trans. Instrum. Meas. 2019, 68, 1781–1787. [Google Scholar] [CrossRef]
- Wang, W.J.; Jiang, W.; Yao, Y.L.; Wang, J.X.; Liu, G. An improved waveguide method for accurate complex permittivity measurement of medium/high-loss material. Meas. Sci. Technol. 2024, 35, 066005. [Google Scholar] [CrossRef]
- Wang, W.J.; Liu, G.; Wang, Y.; Jiang, W.; Zheng, Q.; Wang, J.X.; Luo, Y. A more accurate measurement method of the dielectric material properties with high tolerance using an overmoded waveguide. IEEE Trans. Microw. Theory Tech. 2022, 70, 2363–2369. [Google Scholar] [CrossRef]
- Gong, X.Q.; Wang, W.J.; Liu, G.; Cao, Y.J.; Wang, Y.; Jiang, W.; Yao, Y.L.; Shu, G.X.; Wang, J.X.; Luo, Y. An improved overmoded-waveguide method for the accurate measurement of dielectric properties in the sub-terahertz band. J. Infrared. Milli. Terahz Waves 2023, 44, 265–280. [Google Scholar] [CrossRef]
- Wang, X.C.; Tretyakov, S.A. Fast and robust characterization of lossy dielectric slabs using rectangular waveguides. IEEE Trans. Microw. Theory Tech. 2022, 70, 2341–2350. [Google Scholar] [CrossRef]
- Choi, H.E.; Choi, W.; Simakov, E.I.; Zuboraj, M.; Carlsten, B.E.; Choi, E. Error tolerant method of dielectric permittivity determination using a TE01 mode in a circular waveguide at the W-band. IEEE Trans. Microw. Theory Tech. 2020, 68, 808–815. [Google Scholar] [CrossRef]
- CST-Computer Simulation Technology. Available online: http://www.cst.com/products/cstmws (accessed on 1 January 2025).[Green Version]
- Baker-Jarvis, J.; Vanzura, E.J.; Kissick, W.A. Improved technique for determining complex permittivity with the transmission/reflection method. IEEE Trans. Microw. Theory Tech. 1990, 38, 1096–1103. [Google Scholar] [CrossRef]
- Engen, G.F.; Hoer, C.A. Thru-reflect-line: An improved technique for calibrating the dual six-port automatic network analyzer. IEEE Trans. Microw. Theory Tech. 1979, 27, 987–993. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, X.B.; Ridler, N.M.; Naftaly, M.; Dimitriadis, A.I.; Huang, T.D.; Wu, W. Material measurements using VNA-based material characterization kits subject to Thru-reflect-line calibration. IEEE Trans. Terahertz Sci. Technol. 2020, 10, 466–473. [Google Scholar] [CrossRef]
- Ma, D.D.; Shang, X.B.; Ridler, N.M.; Wu, W. Assessing the impact of data filtering techniques on material characterization at millimeter-wave frequencies. IEEE Trans. Instrum. Meas. 2021, 70, 6005904. [Google Scholar] [CrossRef]
- Baker-Jarvis, J. Transmission/Reflection and Short-Circuit Line Permittivity Measurements; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1990.[Green Version]
- Abbas, Z.; Pollard, R.D.; Kelsall, R.W. Complex permittivity measurements at ka-band using rectangular dielectric waveguide. IEEE Trans. Instrum. Meas. 2001, 50, 1334–1342. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, X.; Ridler, N.; Huang, T.; Wu, W. Characterization of dielectric materials at wr-15 band (50–75 ghz) using VNA-based technique. IEEE Trans. Instrum. Meas. 2020, 69, 4930–4939. [Google Scholar] [CrossRef]
- Choi, H.E.; Choi, E. High-precision complex permittivity measurement of high loss dielectric materials using a geometrical gap in millimeter wave frequency. J. Infrared Milli. Terahz Wave 2024, 45, 97–115. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, Y. Measuring method of complex dielectric constant with monostatic horn antenna in w-band using multiple distance measurements and analysis. In Proceedings of the IEEE Asia–Pacific Microwave Conference (APMC), Kuala Lumpar, Malaysia, 13–16 November 2017; pp. 666–669. [Google Scholar][Green Version]
- Kiiko, V.S.; Pavlov, A.V.; Bykov, V.A. Production and thermophysical properties of BeO ceramics with the addition of nanocrystalline titanium dioxide. Refract. Ind. Ceram. 2019, 59, 616–622. [Google Scholar] [CrossRef]
- Eichhorn, R.; Conway, J.; He, Y.; Li, Y.; O’Connel, T.; Quigley, P.; Sears, J.; Shemelin, V. Higher order mode absorbers for high current ERL applications. In Proceedings of the 5th International Particle Accelerator Conference, Dresden, Germany, 15–20 June 2014; pp. 4037–4039. [Google Scholar][Green Version]
- Liu, G.; Jiang, W.; Yao, Y.L.; Wang, W.J.; Cao, Y.J.; Wang, J.X.; Luo, Y. High average power test of a W-band broadband gyrotron traveling wave tube. IEEE Electron. Device Lett. 2022, 43, 950–953. [Google Scholar] [CrossRef]
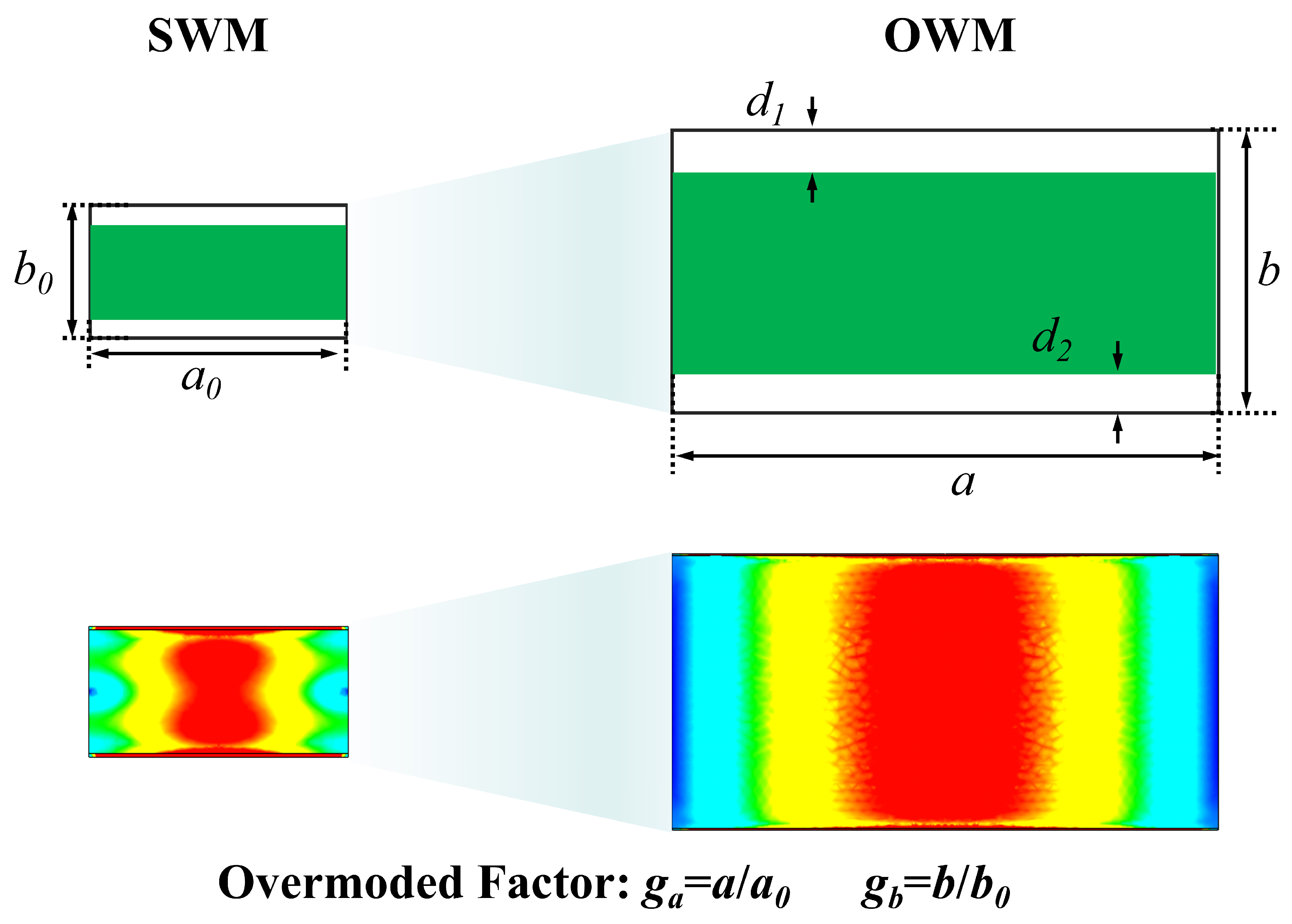



| Frequency Band | X | Ku | K | Ka | Q | V | W |
|---|---|---|---|---|---|---|---|
| Frequency Range (GHz) | 8–12 | 12–18 | 18–26 | 26–40 | 33–50 | 50–75 | 75–110 |
| Overmoded Factor | 1 | 1.45 | 2.14 | 3.21 | 4.02 | 6.08 | 9.00 |
| Overmoded Factor | 1 | 1.29 | 1.90 | 2.86 | 3.57 | 5.41 | 8.00 |
| Taper length (mm) | 140 | 140 | 140 | 160 | 180 | 250 | 300 |
| Line length (mm) | 9.8 | 5.7 | 3.6 | 2.4 | 2.0 | 1.5 | 1.0 |
| Sample Fixture Size (mm) | 22.86 × 10.16 mm | ||||||
| Reference | Measurement Frequency | Measurement Method | |
|---|---|---|---|
| [22] | 1–18 GHz | 2.03–2.04 | Coaxial Line |
| [23] | 26–40 GHz | 1.95 | Dielectric Waveguide |
| [24] | 50–75 GHz | 1.99–2.01 | Guided Free-space |
| [25] | 80–105 GHz | 1.99–2.00 | Circular Waveguide |
| [26] | 75–110 GHz | 2.05 | Free-space Method |
| This work | 8–110 GHz | 2.00–2.03 | OWM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Cao, Y.; Wang, T.; Song, F.; Fang, S.; Tang, X.; Li, X.; Shu, G.; Liu, G. An Overmoded-Waveguide-Based Permittivity Measurement Method with High Accuracy and Ultra-Broadband over 8–110 GHz. Micromachines 2025, 16, 1045. https://doi.org/10.3390/mi16091045
Wang W, Cao Y, Wang T, Song F, Fang S, Tang X, Li X, Shu G, Liu G. An Overmoded-Waveguide-Based Permittivity Measurement Method with High Accuracy and Ultra-Broadband over 8–110 GHz. Micromachines. 2025; 16(9):1045. https://doi.org/10.3390/mi16091045
Chicago/Turabian StyleWang, Weijie, Yingjian Cao, Tieyang Wang, Fangfang Song, Shuanzhu Fang, Xianfeng Tang, Xiangqiang Li, Guoxiang Shu, and Guo Liu. 2025. "An Overmoded-Waveguide-Based Permittivity Measurement Method with High Accuracy and Ultra-Broadband over 8–110 GHz" Micromachines 16, no. 9: 1045. https://doi.org/10.3390/mi16091045
APA StyleWang, W., Cao, Y., Wang, T., Song, F., Fang, S., Tang, X., Li, X., Shu, G., & Liu, G. (2025). An Overmoded-Waveguide-Based Permittivity Measurement Method with High Accuracy and Ultra-Broadband over 8–110 GHz. Micromachines, 16(9), 1045. https://doi.org/10.3390/mi16091045








