Interaction Energy Dependency on Pulse Width in ns NIR Laser Scanning of Silicon
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
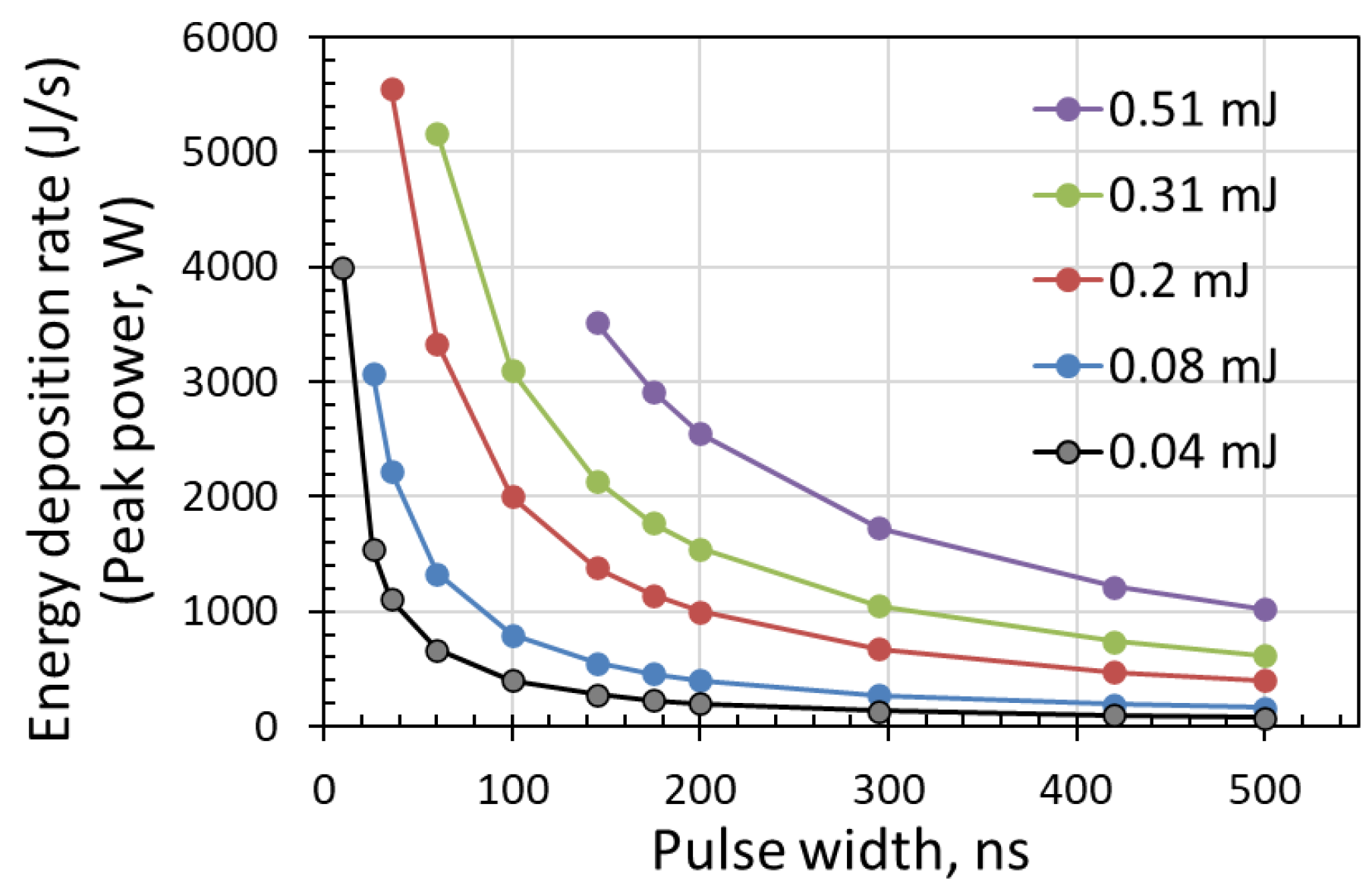
3.1. Interaction Energy Dependence on Pulse Width
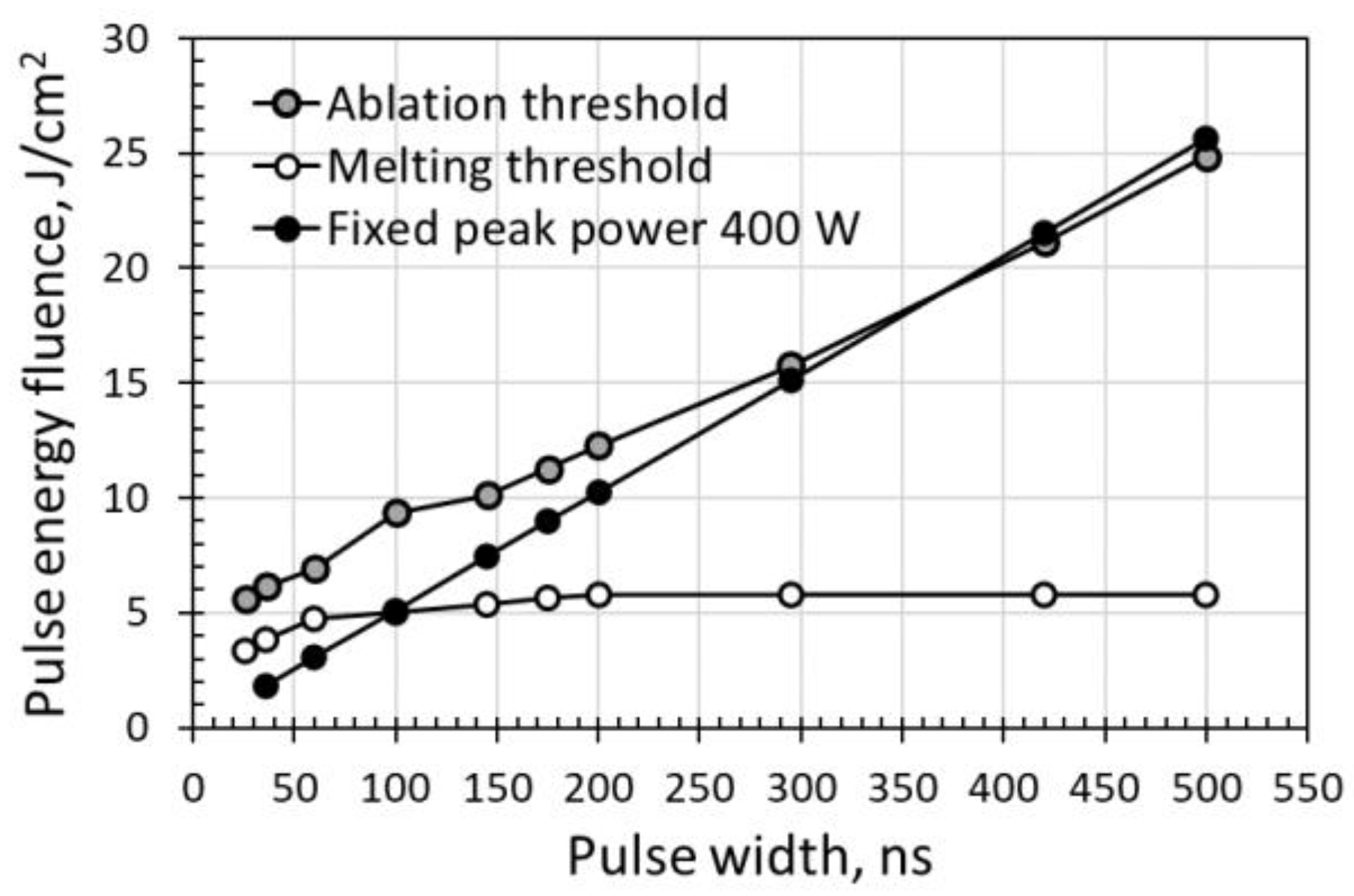
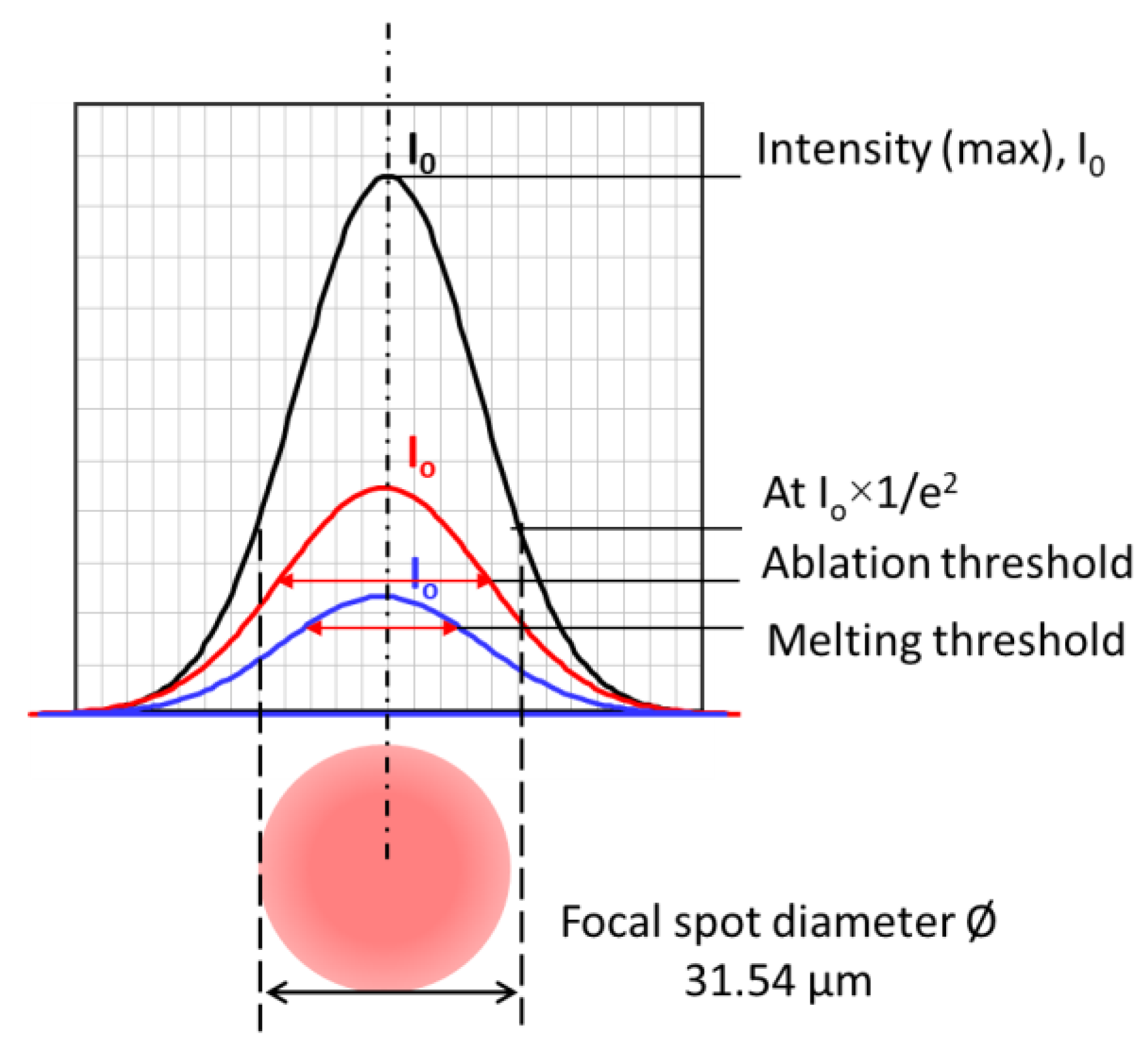
3.2. Laser Fluence Threshold Dependence on Pulse Width
3.3. Identical Peak Power at Various Pulse Widths
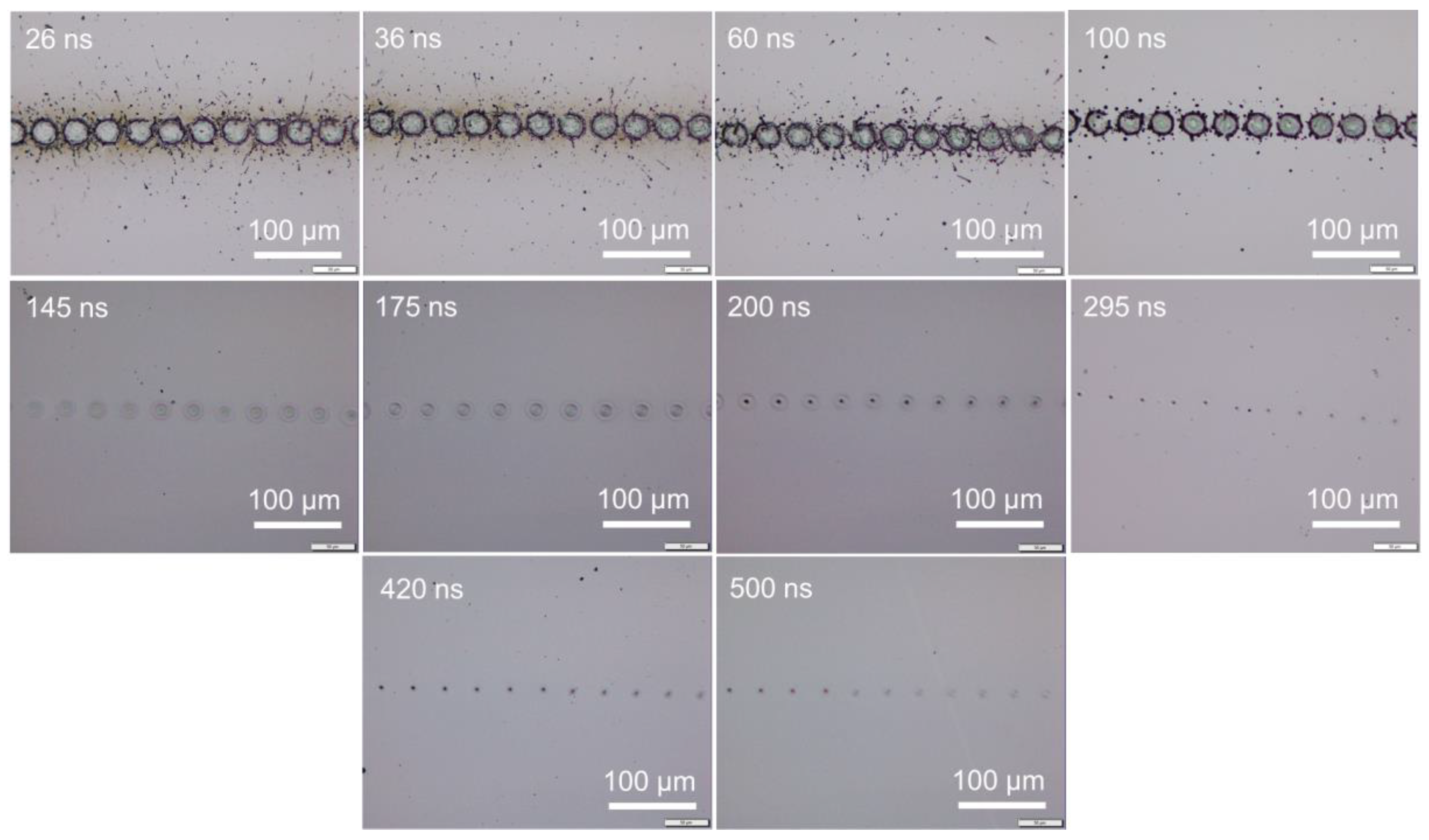
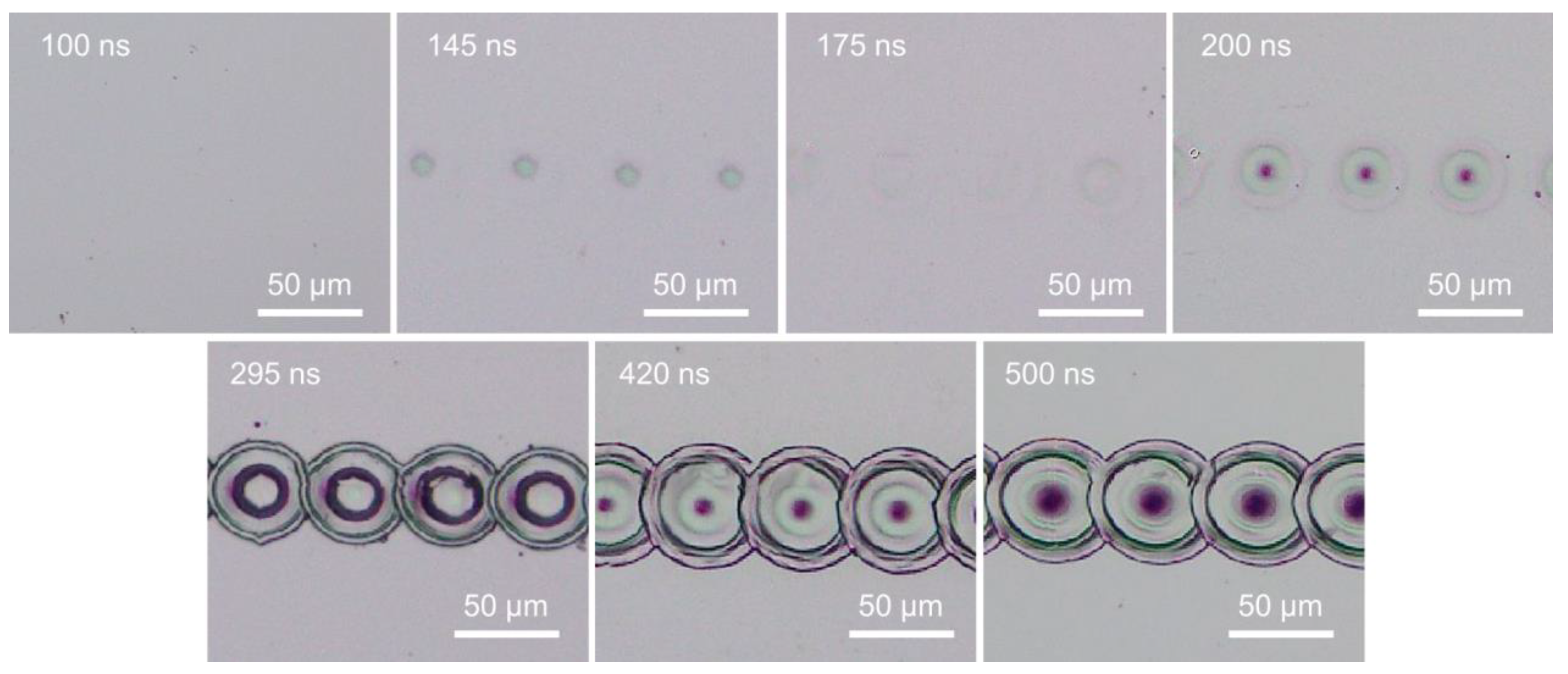
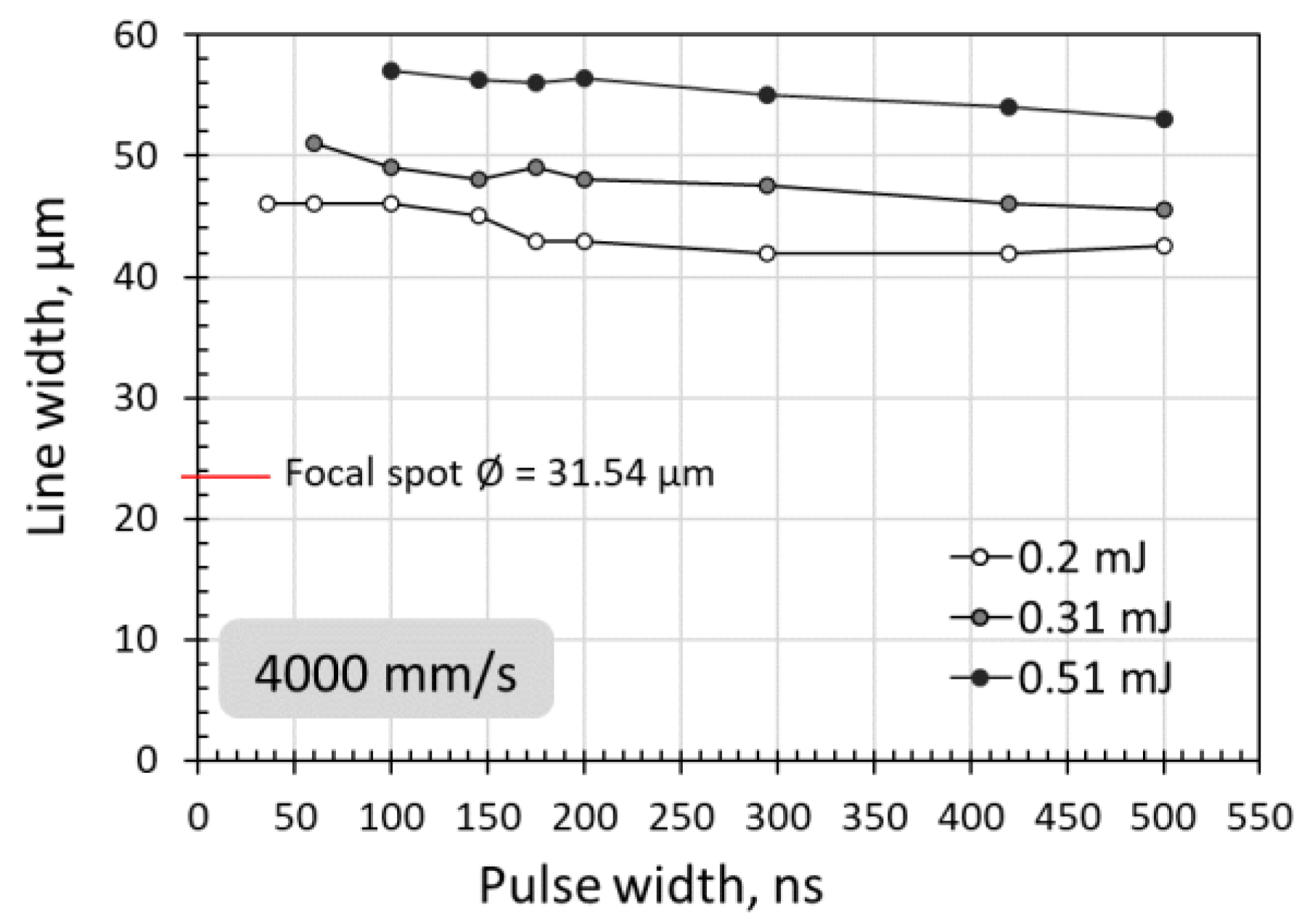
3.4. Scanning Line Width at Various Pulse Widths
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Preuss, S.; Demchuk, A.; Stuke, M. Sub-picosecond UV laser-ablation of metals. Appl. Phys. A 1995, 61, 33–37. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Notle, S.; VonAlvensleben, F.; Tunnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Bulgakova, N.M.; Bulgakov, A.V. Pulsed laser ablation of solids: Transition from normal vaporization to phase explosion. Appl. Phys. A 2001, 73, 199–208. [Google Scholar] [CrossRef]
- Perez, D.; Lewis, L.J. Ablation of solids under femtosecond laser pulses. Phys. Rev. Lett. 2002, 89, 255504. [Google Scholar] [CrossRef]
- Bogaerts, A.; Chen, Z. Effect of laser parameters on laser ablation and laser-induced plasma formation: A numerical modeling investigation. Spectrochim. Acta Part B 2005, 60, 1280–1307. [Google Scholar] [CrossRef]
- Gravel, J.F.Y.; Boudreau, D. Study by focused shadowgraphy of the effect of laser irradiance on laser-induced plasma formation and ablation rate in various gases. Spectrochim. Acta Part B 2009, 64, 56–66. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, B.; Tao, S.; Forsman, A.; Gao, Y. Physical mechanism of silicon ablation with long nanosecond laser pulses at 1064 nm through time-resolved observation. Appl. Surf. Sci. 2011, 257, 2886–2890. [Google Scholar] [CrossRef]
- Stafe, M.; Marcu, A.; Puscas, N.N. Pulsed Laser Ablation of Solids; Springer: Berlin/Heidelberg, Germany, 2014; Volume 62, pp. 758–770. [Google Scholar] [CrossRef]
- Shaheen, M.E.; Gagnon, J.E.; Fryer, B.J. Femtosecond laser ablation behavior of gold, crystalline silicon, and fused silica: A comparative study. Laser. Phys. 2014, 24, 106102. [Google Scholar] [CrossRef]
- Pangovski, K.; Otanocha, O.B.; Zhong, S.; Sparkes, M.; Liu, Z.; O’Neill, W.; Li, L. Investigation of plume dynamics during picosecond laser ablation of H13 steel using high-speed digital holography. Appl. Phys. A 2017, 123, 114. [Google Scholar] [CrossRef]
- Maclean, J.O.; Hodson, J.R.; Tangkijcharoenchai, C.; Al-Ojaili, S.; Rodsavas, S.; Coomber, S.; Voisey, K.T. Laser drilling of microholes in single crystal silicon using continuous wave (CW) 1070 nm fiber lasers with millisecond pulse widths. Laser. Eng. 2018, 39, 53–65. [Google Scholar] [CrossRef]
- Richard, F.; Haglund, J.R. Mechanisms of Laser-Induced Desorption and Ablation. Exp. Methods Phys. Sci. 1997, 30, 15–138. [Google Scholar] [CrossRef]
- Bauerle, D.W. Laser Processing and Chemistry; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Phipps, C. Laser Ablation and Its Application; Springer: Berlin/Heidelberg, Germany, 2007; Volume 7, pp. 159–184. [Google Scholar] [CrossRef]
- Gower, M.C. Industrial applications of laser micromachining. Opt. Express 2000, 7, 56–67. [Google Scholar] [CrossRef]
- Calderón Urbina, J.P. Efficient Material Laser Beam Ablation with a Picosecond Laser; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Schittenhelm, H.; Callies, G.; Straub, A.; Berger, P.; Hügel, H. Measurements of wavelength-dependent transmission in excimer laser-induced plasma plumes and their interpretation. J. Phys. D Appl. Phys. 1998, 31, 418–427. [Google Scholar] [CrossRef]
- Breitling, D.; Schittenhelm, H.; Berger, P.; Dausinger, F.; Hugel, H. Shadowgraphic and interferometric investigations on Nd: YAG laser-induced vapor/plasma plumes for different processing wavelengths. Appl. Phys. A 1999, 69, S505–S508. [Google Scholar] [CrossRef]
- Tao, S.; Zhou, Y.; Wu, B.; Gao, Y. Infrared long nanosecond laser pulse ablation of silicon: Integrated two-dimensional modeling and time-resolved experimental study. Appl. Surf. Sci. 2012, 258, 7766–7773. [Google Scholar] [CrossRef]
- Peng, Y.; Hong, M.; Zhou, Y.Y.; Fang, D.; Chen, X.Q.; Cai, B.; Zhu, Y.M. Influence of Femtosecond Laser Pulse Number on Spike Geometry of Microstructured Silicon. Appl. Phys. Express 2013, 6, 051303. [Google Scholar] [CrossRef]
- Mills, B.; Heath, D.J.; Feinaeugle, M.; Grant-Jacob, J.A.; Eason, R.W. Laser ablation via programmable image projection for submicron dimension machining in diamond. J. Laser. Appl. 2014, 26, 041501. [Google Scholar] [CrossRef]
- Singh, K.S.; Sharma, A.K. Effect of variation of magnetic field on laser ablation depth of copper and aluminum targets in air atmosphere. J. Appl. Phys. 2016, 119, 183301. [Google Scholar] [CrossRef]
- Heath, D.J.; Grant-Jacob, J.A.; Feinaeugle, M.; Mills, B.; Eason, R.W. Sub-diffraction limit laser ablation via multiple exposures using a digital micromirror device. Appl. Opt. 2017, 56, 6398–6404. [Google Scholar] [CrossRef]
- Casalino, G. Computational intelligence for smart laser materials processing. Opt. Laser. Technol. 2018, 100, 165–175. [Google Scholar] [CrossRef]
- Semerok, A.; Chaleard, C.; Dettalle, V.; Kocon, S.; Lacour, J.L.; Mauchien, P.; Meynadier, P.; Nouvellon, C.; Palianov, P.; Perdrix, M.; et al. Laser ablation efficiency of pure metals with femtosecond, picosecond and nanosecond pulses. SPIE Proc. 1998, 3343, 1049–1055. [Google Scholar] [CrossRef]
- Ren, J.; Kelly, M.; Hesselink, L. Laser ablation of silicon in water with nanosecond and femtosecond pulses. Opt. Lett. 2005, 30, 1740–1742. [Google Scholar] [CrossRef]
- Shaheen, M.E.; Gagnon, J.E.; Fryer, B.J. Excimer laser ablation of aluminum: Influence of spot size on ablation rate. Laser. Phys. 2016, 26, 116102. [Google Scholar] [CrossRef]
- Parmar, V.; Shin, Y.C. Wideband anti-reflective silicon surface structures fabricated by femtosecond laser texturing. Appl. Surf. Sci. 2018, 459, 86–91. [Google Scholar] [CrossRef]
- Shaheen, M.E.; Gagnon, J.E.; Fryer, B.J. Studies on laser ablation of silicon using near IR picosecond and deep UV nanosecond lasers. Opt. Laser Eng. 2019, 119, 18–25. [Google Scholar] [CrossRef]
- Maksimovic, J.; Ng, S.H.; Katkus, T.; An Le, H.; Chon, J.W.M.; Cowie, C.C.; Yang, T.; Bellouard, Y.; Juodkazis, S. Ablation in Externally Applied Electric and Magnetic Fields. Nanomaterials 2020, 10, 182. [Google Scholar] [CrossRef]
- Marks, M.R.; Cheong, K.Y.; Hassan, Z. A review of laser ablation and dicing of Si wafers. Precis. Eng. 2022, 73, 377–408. [Google Scholar] [CrossRef]
- Yates, J.T. A new opportunity in silicon-based microelectronics. Science 1998, 279, 335–336. [Google Scholar] [CrossRef]
- Li, K.; Sparkes, M.; O’Neill, W. Comparison between single shot micromachining of silicon with nanosecond pulse shaped IR fiber laser and DPSS UV laser. IEEE J. Set. Top. Quant. 2014, 20, 0900807. [Google Scholar] [CrossRef]
- Garban-Labaune, C.; Fabre, E.; Max, C.E.; Fabbro, R.; Amiranoff, F.; Virmont, J.; Weinfeld, M.; Michard, A. Effect of Laser Wavelength and Pulse Duration on Laser-Light Absorption and Back Reflection. Phys. Rev. Lett. 1982, 48, 1018–1021. [Google Scholar] [CrossRef]
- Sanchez, F.; Morenza, J.L.; Aguiar, R.; Delgado, J.C.; Varela, M. Whiskerlike structure growth on silicon exposed to ArF: Excimer laser irradiation. Appl. Phys. Lett. 1996, 69, 620–622. [Google Scholar] [CrossRef]
- Colina, M.; Molpeceres, C.; Morales, M.; Allens-Perkins, F.; Guadano, G.; Ocana, J.L. Laser ablation modelling of aluminium, silver and crystalline silicon for applications in photovoltaic technologies. Surf. Eng. 2011, 27, 414–423. [Google Scholar] [CrossRef]
- Demirci, E.; Kaya, E.T.A.; Sahin, R. Nanosecond laser ablation of Si (111) under an aqueous medium. Optik 2019, 181, 1049–1056. [Google Scholar] [CrossRef]
- Zhang, J.J.; Zhao, L.; Rosenkranz, A.; Song, C.W.; Yan, Y.D.; Sun, T. Nanosecond pulsed laser ablation of silicon-finite element simulation and experimental validation. J. Micromech. Microeng. 2019, 29, 29075009. [Google Scholar] [CrossRef]
- Van Brug, H.; Murakami, K.; Bijkerk, F.; Van der Wiel, M.J. Time-resolved x-ray monitoring of laser ablation of and plasma formation from Si. J. Appl. Phys. 1986, 60, 3438. [Google Scholar] [CrossRef][Green Version]
- Fauchet, P.M.; Siegman, A.E. Surface ripples on silicon and gallium arsenide under picosecond laser illumination. Appl. Phys. Lett. 1982, 40, 824–826. [Google Scholar] [CrossRef]
- Young, J.F.; Sipe, J.E.; Preston, J.S.; Van Driel, H.M. Laser-induced periodic surface damage and radiation remnants. Appl. Phys. Lett. 1982, 41, 261. [Google Scholar] [CrossRef]
- Gorodetsky, G.; Kanicki, J.; Kazyaka, T.; Melcher, R.L. Far UV pulsed laser melting of silicon. Appl. Phys. Lett. 1985, 46, 547–549. [Google Scholar] [CrossRef]
- Bullock, J.; Hettick, M.; Geissbühler, J.; Ong, A.J.; Allen, T.; Sutter-Fella, C.M.; Chen, T.; Ota, H.; Schaler, E.W.; De Wolf, S.; et al. Efficient silicon solar cells with dopant-free asymmetric heterocontacts. Nat. Energy 2016, 1, 15031. [Google Scholar] [CrossRef]
- Armbruster, O.; Naghilou, A.; Kitzler, M.; Kautek, W. Spot size and pulse number dependence of femtosecond laser ablation thresholds of silicon and stainless steel. Appl. Surf. Sci. 2017, 396, 1736–1740. [Google Scholar] [CrossRef]
- Choo, K.L.; Ogawa, Y.; Kanbargi, G.; Otra, V.; Raff, L.M.; Komanduri, R. Micromachining of silicon by short-pulse laser ablation in air and under water. Mater. Sci. Eng. A-Struct. 2004, 372, 145–162. [Google Scholar] [CrossRef]
- Wee, L.M.; Ng, E.Y.K.; Prathama, A.H.; Zheng, H. Micro-machining of silicon wafer in air and under water. Opt. Laser Technol. 2011, 43, 62–71. [Google Scholar] [CrossRef]
- Karimzadeh, R.; Anvari, J.Z.; Mansour, N. Nanosecond pulsed laser ablation of silicon in liquids. Appl. Phys. A 2009, 94, 949–955. [Google Scholar] [CrossRef]
- Charee, W.; Tangwarodomnukun, V. Laser ablation of silicon in water at different temperatures. Int. J. Adv. Manuf. Techol. 2020, 107, 2333–2344. [Google Scholar] [CrossRef]
- Farrokhi, H.; Gruzdev, V.; Zheng, H.Y.; Rawat, R.S.; Zhou, W. Magneto-absorption effects in magnetic-field assisted laser ablation of silicon by UV nanosecond pulses. Appl. Phys. Lett. 2016, 108, 254103. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Zhang, Z.; Zhang, Y.; Liu, D.; Wu, J.; Huang, Y.; Zhang, G. Study on machining characteristics of magnetically controlled laser induced plasma micromachining single-crystal silicon. J. Adv. Res. 2021, 30, 39–51. [Google Scholar] [CrossRef]
- Gao, W.; Zheng, K.; Liao, Y.; Du, H.; Liu, C.; Ye, C.; Liu, K.; Xie, S.; Chen, C.; Chen, J.; et al. High-quality femtosecond laser surface micro/nano-structuring assisted by a thin frost layer. arXiv 2022, arXiv:2205.09650. [Google Scholar] [CrossRef]
- Lei, W.S.; Kumar, A.; Yalamanchili, R. Die singulation technologies for advanced packaging: A critical review. J. Vac. Sci. Technol. B 2012, 30, 040801. [Google Scholar] [CrossRef]
- Wang, H.J.; Yang, T. A review on laser drilling and cutting of silicon. J. Eur. Ceram. Soc. 2021, 41, 4997–5015. [Google Scholar] [CrossRef]
- Shirk, M.D.; Molian, P.A. A review of ultrashort pulsed laser ablation of materials. J. Laser Appl. 1998, 10, 18. [Google Scholar] [CrossRef]
- Phillips, K.C.; Gandhi, H.H.; Mazur, E.; Sundaram, S.K. Ultrafast laser processing of materials: A review. Adv. Opt. Photonics 2015, 7, 684. [Google Scholar] [CrossRef]
- Tull, B.R.; Carey, J.E.; Mazur, E.; McDonald, J.P.; Yalisove, S.M. Silicon surface morphologies after femtosecond laser irradiation. MRS Bull. 2006, 31, 626–633. [Google Scholar] [CrossRef]
- Trtica, M.S.; Gakovic, B.M.; Maravic, D.; Batani, D.; Desai, T.; Redaelli, R. Surface modifications of crystalline silicon created by high intensity 1064 nm picosecond Nd:YAG laser pulses. Appl. Surf. Sci. 2007, 253, 9315–9318. [Google Scholar] [CrossRef]
- Jellison, G.E.; Lowndes, D.H. Optical-Absorption Coefficient of Silicon at 1.152 μm at Elevated-Temperatures. Appl. Phys. Lett. 1982, 41, 594–596. [Google Scholar] [CrossRef]
- Herrmann, R.F.W.; Gerlach, J.; Campbell, E.E.B. Ultrashort pulse laser ablation of silicon: An MD simulation study. Appl. Phys. A 1998, 66, 35–42. [Google Scholar] [CrossRef]
- von der Linde, D.; SokolowskiTinten, K.; Bialkowski, J. Laser–solid interaction in the femtosecond time regime. Appl. Surf. Sci. 1997, 109, 1–10. [Google Scholar] [CrossRef]
- Zeng, X.; Mao, X.; Greif, R.; Russo, R.E. Ultraviolet femtosecond and nanosecond laser ablation of silicon: Ablation efficiency and laser-induced plasma expansion. Proc. SPIE 2004, 5448, 1150–1158. [Google Scholar] [CrossRef]
- Jeschke, H.O.; Garcia, M.E.; Lenzner, M.; Bonse, J.; Kruger, J.; Kautek, W. Laser ablation thresholds of silicon for different pulse durations: Theory and experiment. Appl. Surf. Sci. 2002, 197, 839–844. [Google Scholar] [CrossRef]
- Hodgson, N.; Heming, S.; Steinkopff, A.; Haloui, H.; Lee, T.S. Ultrafast Laser Ablation at 1035 nm, 517 nm and 345 nm as a Function of Pulse Duration and Fluence. In Proceedings of the Lasers in Manufacturing Conference 2019, Munich, Germany, 24–27 July 2019; Available online: https://www.wlt.de/lim/proceedings2019/data/1.html (accessed on 23 December 2022).
- Yoo, J.H.; Jeong, S.H.; Mao, X.L.; Greif, R.; Russo, R.E. Evidence for phase-explosion and generation of large particles during high power nanosecond laser ablation of silicon. Appl. Phys. Lett. 2000, 76, 783–785. [Google Scholar] [CrossRef]
- Lu, Q.; Mao, S.S.; Mao, X.L.; Russo, R.E. Delayed phase explosion during high- power nanosecond laser ablation of silicon. Appl. Phys. Lett. 2002, 80, 3072–3074. [Google Scholar] [CrossRef]
- Raskovskaya, I.L.; Rinkevichyus, B.S.; Tolkachev, A.V. Structured beams in laser refractography applications. In Laser beams: Theory, Properties and Applications; Thys, M., Desmet, E., Eds.; Nova Science Publishers, Inc.: New York, NY, USA, 2011; p. 418. [Google Scholar]
- Mingareev, I.; Fornaroli, C.; Gillner, A. Laser Dicing of Silicon and Electronics Substrates. In Advances in Laser Materials Processing; Lawrence, J., Ed.; Woodhead Publishing: Sawston, UK, 2018; p. 99. [Google Scholar] [CrossRef]
- Bonse, J.; Baudach, S.; Krüger, J.; Kautek, W.; Lenzner, M. Femtosecond laser ablation of silicon–modification thresholds and morphology. Appl. Phys. A 2002, 74, 19–25. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wang, X.; Chen, G.; Wang, Z. Interaction Energy Dependency on Pulse Width in ns NIR Laser Scanning of Silicon. Micromachines 2023, 14, 119. https://doi.org/10.3390/mi14010119
Li S, Wang X, Chen G, Wang Z. Interaction Energy Dependency on Pulse Width in ns NIR Laser Scanning of Silicon. Micromachines. 2023; 14(1):119. https://doi.org/10.3390/mi14010119
Chicago/Turabian StyleLi, Shunping, Xinchang Wang, Guojie Chen, and Zhongke Wang. 2023. "Interaction Energy Dependency on Pulse Width in ns NIR Laser Scanning of Silicon" Micromachines 14, no. 1: 119. https://doi.org/10.3390/mi14010119
APA StyleLi, S., Wang, X., Chen, G., & Wang, Z. (2023). Interaction Energy Dependency on Pulse Width in ns NIR Laser Scanning of Silicon. Micromachines, 14(1), 119. https://doi.org/10.3390/mi14010119





