Optical Sensor, Based on an Accelerometer, for Low-Frequency Mechanical Vibrations
Abstract
:1. Introduction
2. Design of the Optical Sensor and Test Bench
2.1. Vibration Sensor Design
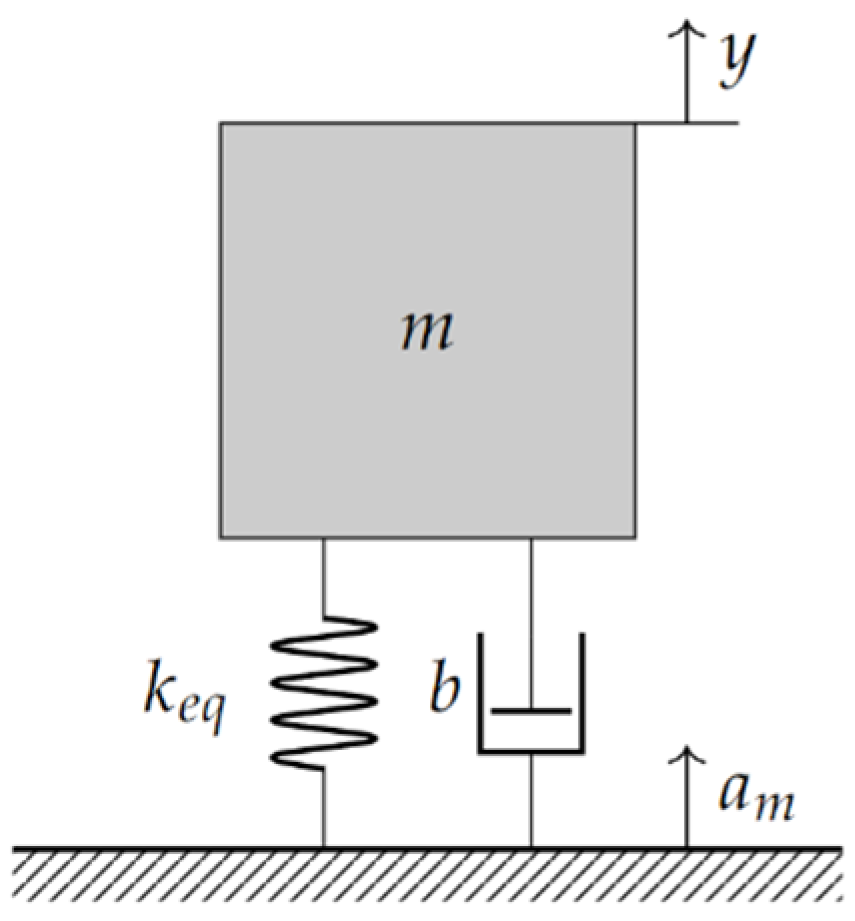
2.1.1. Analytical Accelerometer Modeling
2.1.2. Optical Detection
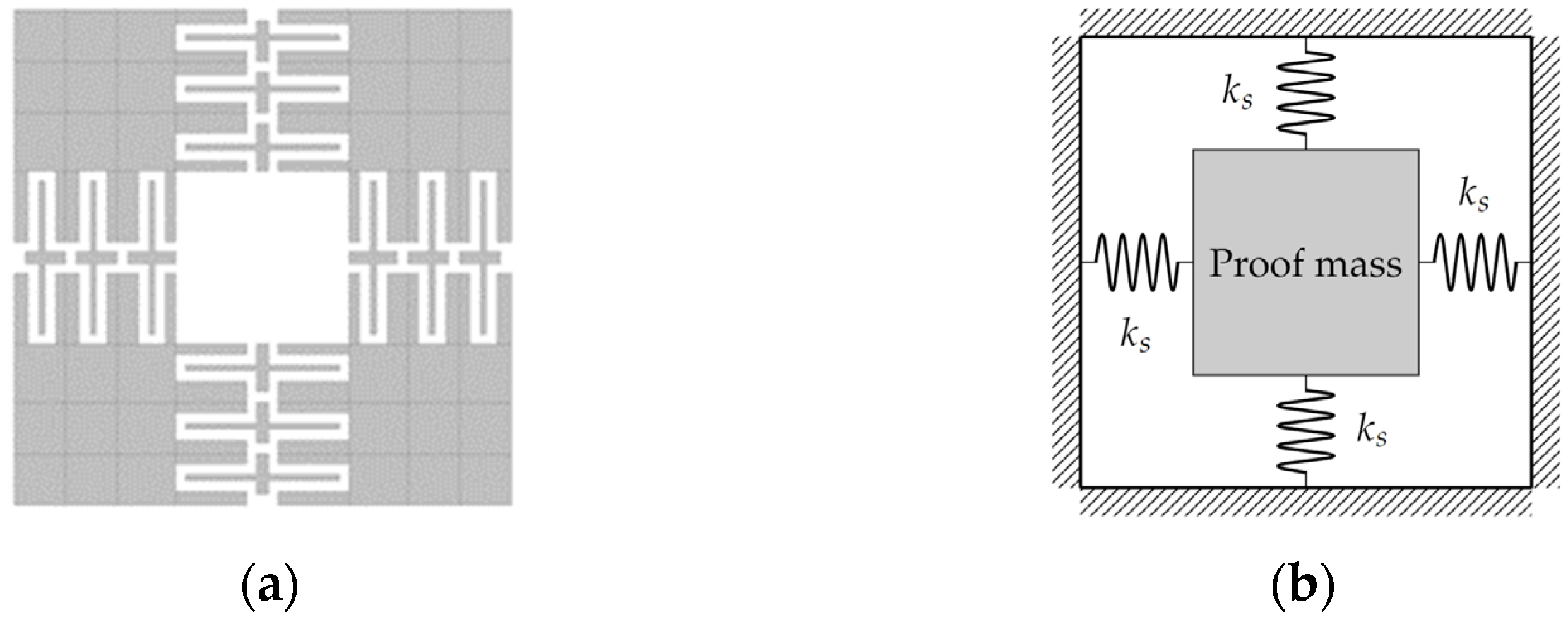
2.1.3. Silicon Microstructure Design
2.2. Finite Element Analysis
Modelling
- i.
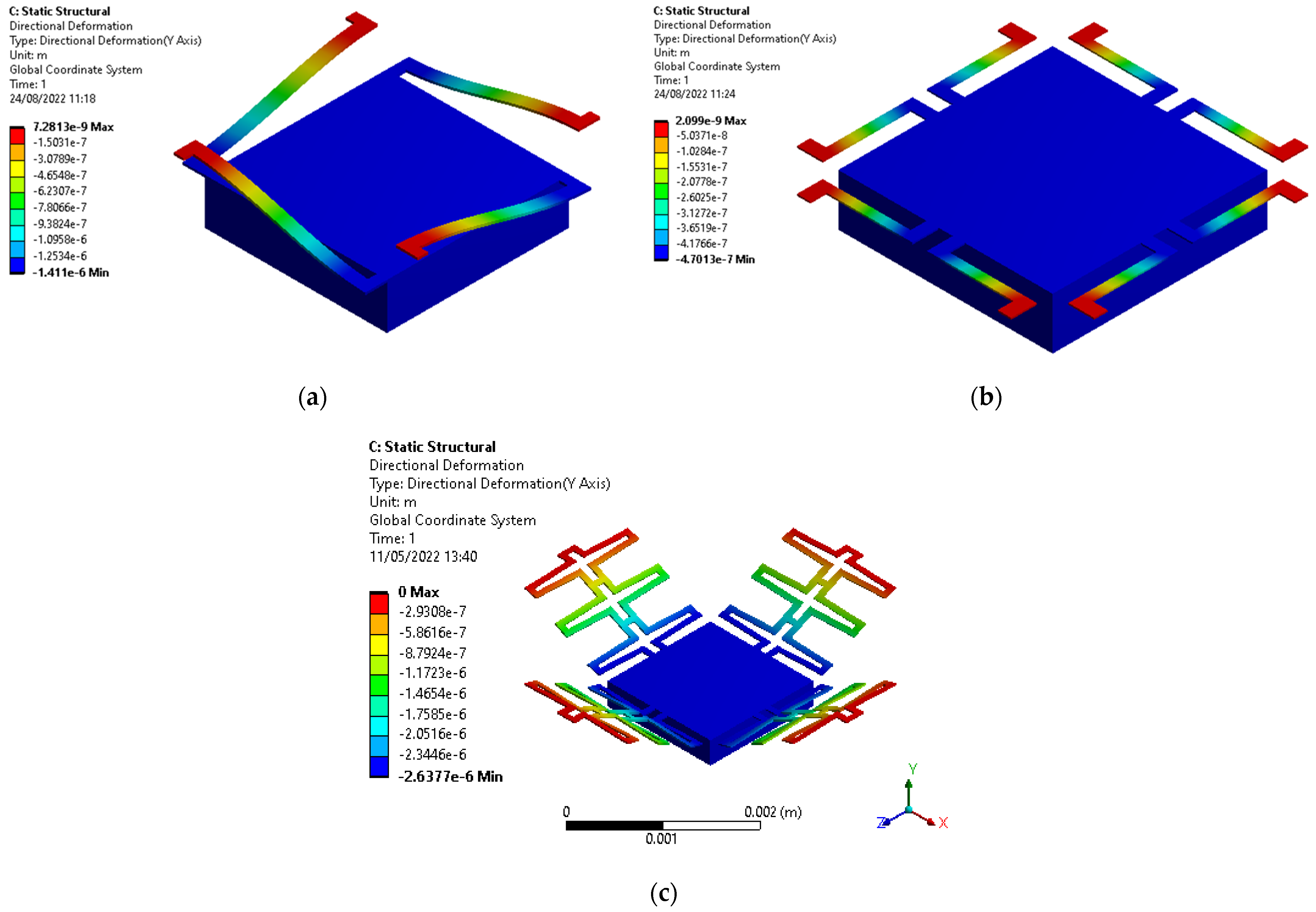
- A steady-state study to verify the maximum displacement amplitude at a given acceleration and the static effects, mainly the sensitivity to gravitational attraction as a function of the orientation of the microstructure with respect to the Earth (Section 2.3.1).
- ii.
- A modal study to determine the natural resonance modes and their frequencies is performed in Section 2.3.2.
- iii.
- A harmonic study to find the frequency response of the microstructure subjected to vibrations at a known frequency (Section 2.3.3).
2.3. Simulation Results
2.3.1. Steady-State Study
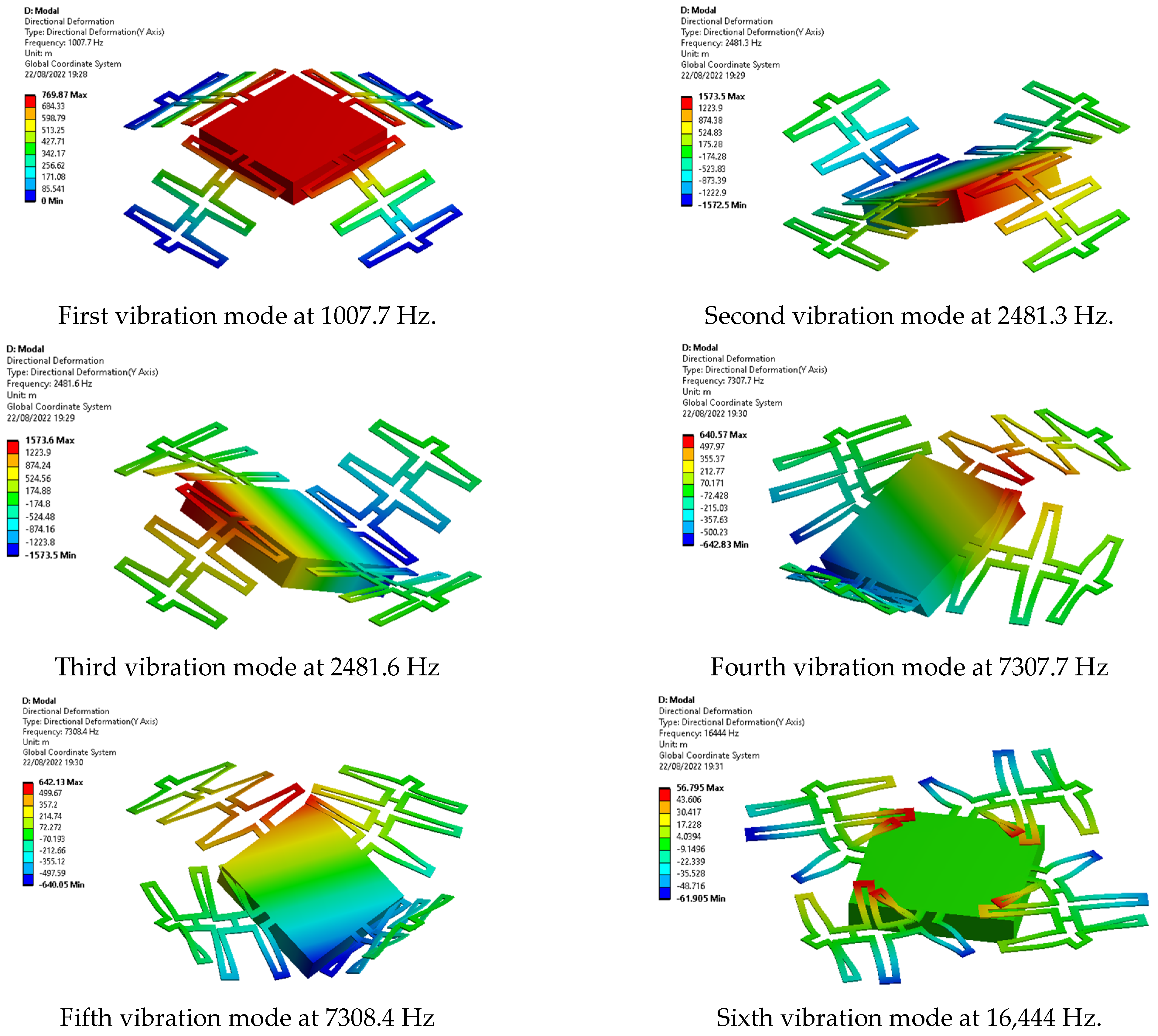
2.3.2. Modal Analysis
2.3.3. Harmonic Analysis
- Its vibration amplitude is the largest, reaching a displacement of 1 μm at 10 g, which will allow the performance of the optical detection system to be evaluated.
- It has its second vibration mode of 2481 Hz further away from the frequency of the first one of 1007 Hz, in comparison with other designs, which allows more stability in the experimental test range.
- The seismic mass can be adjusted to various dimensions, and even consider circular shapes.
2.4. Vibration Sensor Package Design
- (a)
- A support for the microstructure (in green)
- (b)
- The encapsulation made in Steel SAE 304 (in metallic color)
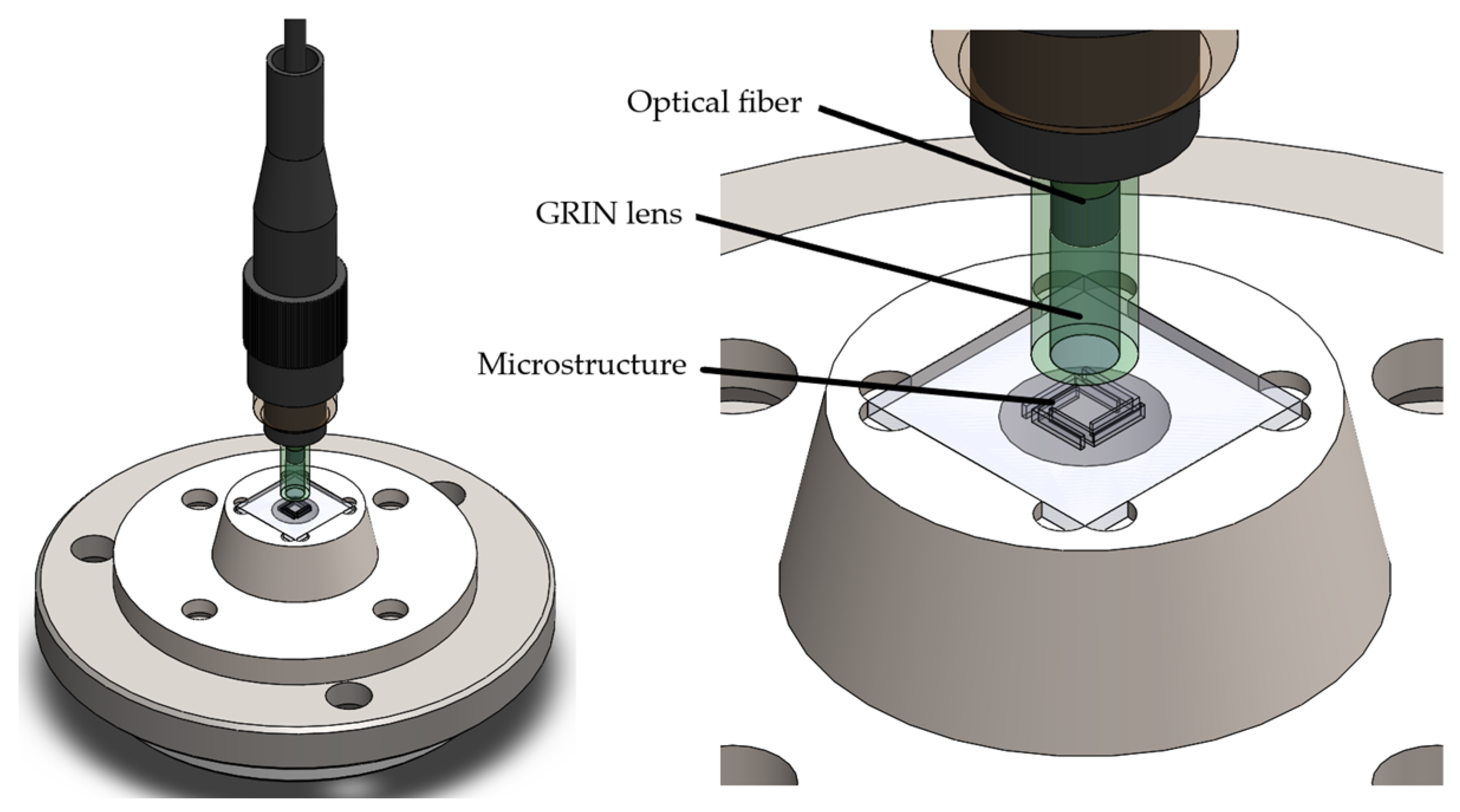
2.5. Test Bench Design
2.5.1. Interferometer Scheme
- Light source: Linearly polarized He-Ne laser, with wavelength of 633 nm, power of 2 mW, divergence of 1.3 mrad, and polarization ratio of 500:1.
- Beam splitter: 50:50 in non-polarizing cube in the range of 400 to 700 nm.
- Microestructure mirror: Monocrystalline silicon microstructure under test
- Mechanical support: Two-degree-of-freedom circular mirror assembly and 8.3 mrad/rev. resolution adjustment.
- Projection objective: With 10× magnification and 0.25 aperture
- Reference mirror: Dielectric fused silica mirror with reflective coating for a 400 to 700 nm range.
- Photodiode: With integrated preamplifier OPT101, detection area of 2.29 mm × 2.29 mm, sensitivity of 0.45 A/W (at 650 nm), and bandwidth of 14 kHz.

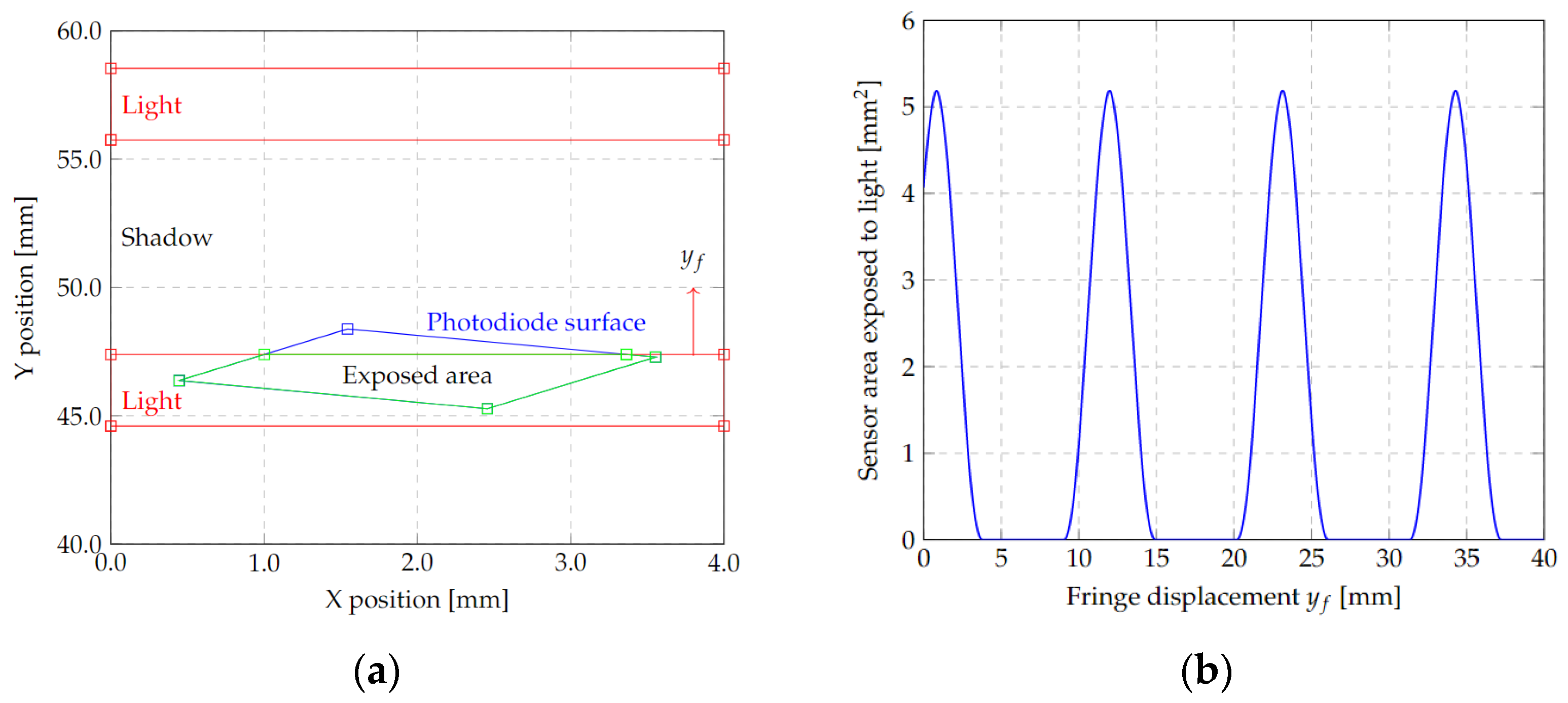
2.5.2. Photodiode Response
3. Manufacturing
3.1. Manufacture of Accelerometers
- i.
- A 100 mm diameter, 400 μm-thick monocrystalline silicon wafer with a polished top side (with a thickness roughness less than 10 nm) and <100> crystalline orientation is used.
- ii.
- Silicon nitride (300 nm) and silicon oxide (1.5 μm) layers are deposited through a sputtering process on both faces. Their roughness is not relevant because these layers will be used as sacrificial material.
- iii.
- A pattern is etched on the oxide and nitride layers of both faces by the next steps:
- a.
- A chromium deposit (300 nm) is made by electron-beam deposition
- b.
- By means of a photolithography process, a pattern is etched on the chromium with wet etching by chrome etchant.
- c.
- The oxide pattern is etched with hydrofluoric acid. The chromium acts as a protective layer for the regions not to be etched, until the silicon is exposed.
- iv.
- Deep reactive ion etching (DRIE) is performed on both sides of the wafer, one after the other. The back side is etched first; the duration of the etching sets the proof mass thickness of the microstructure. Subsequently, the pattern of the beam supports is etched on the top (polished) side until it is transferred to the cavity formed on the bottom side.
- v.
- The sacrificial layers, made of nitride, oxide, chromium, and photoresist residues, were removed. For the sake of simplicity, the photo resin process is not shown. The liberated microstructure was obtained.
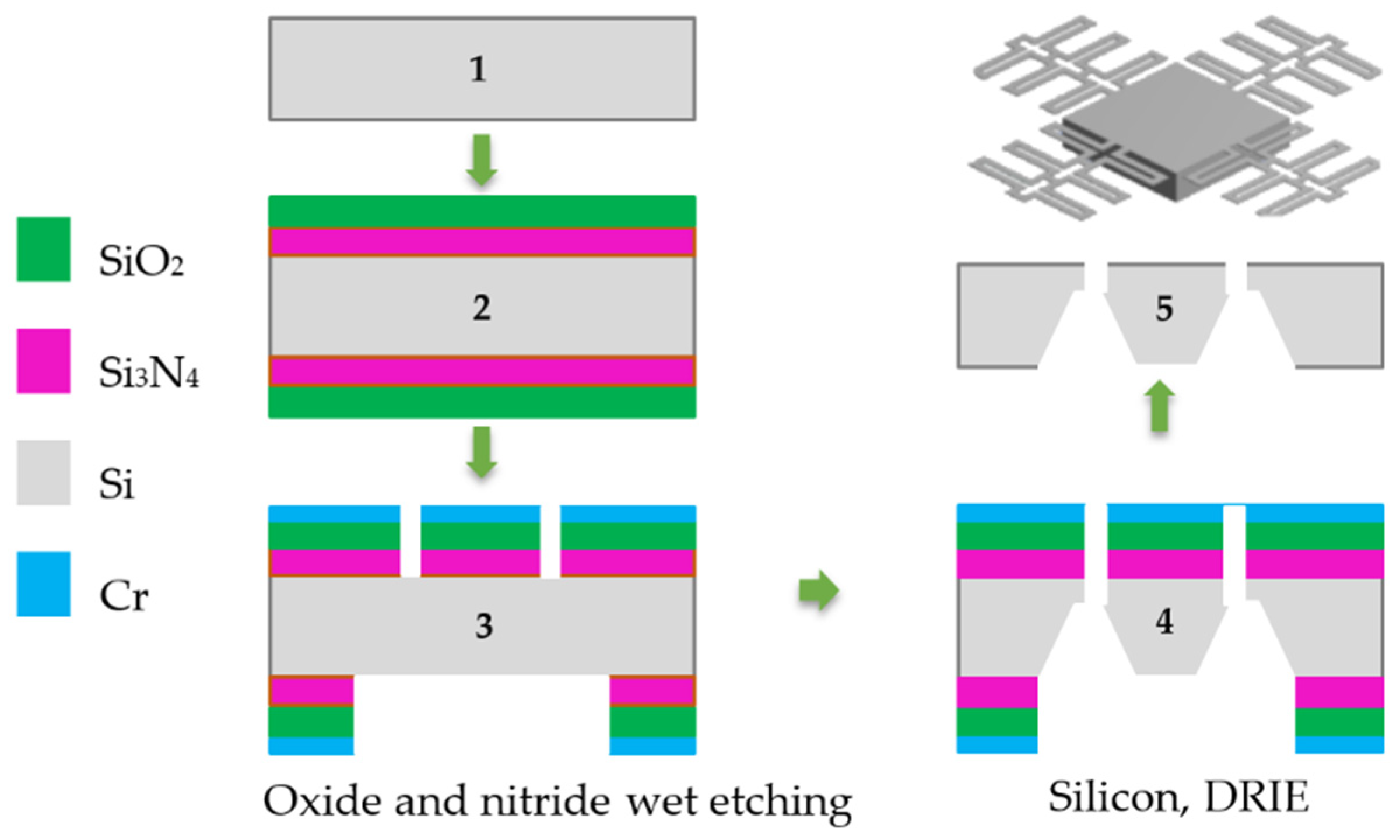
3.2. Vibration Measurement Probe Housing
3.3. Implementation of the Test Bench
4. Experimental Tests
4.1. Optical System Evaluation
- The polished monocrystalline silicon substrate has optical properties in the visible wavelength range, which is sufficient for use in an interferometric vibration detection scheme.
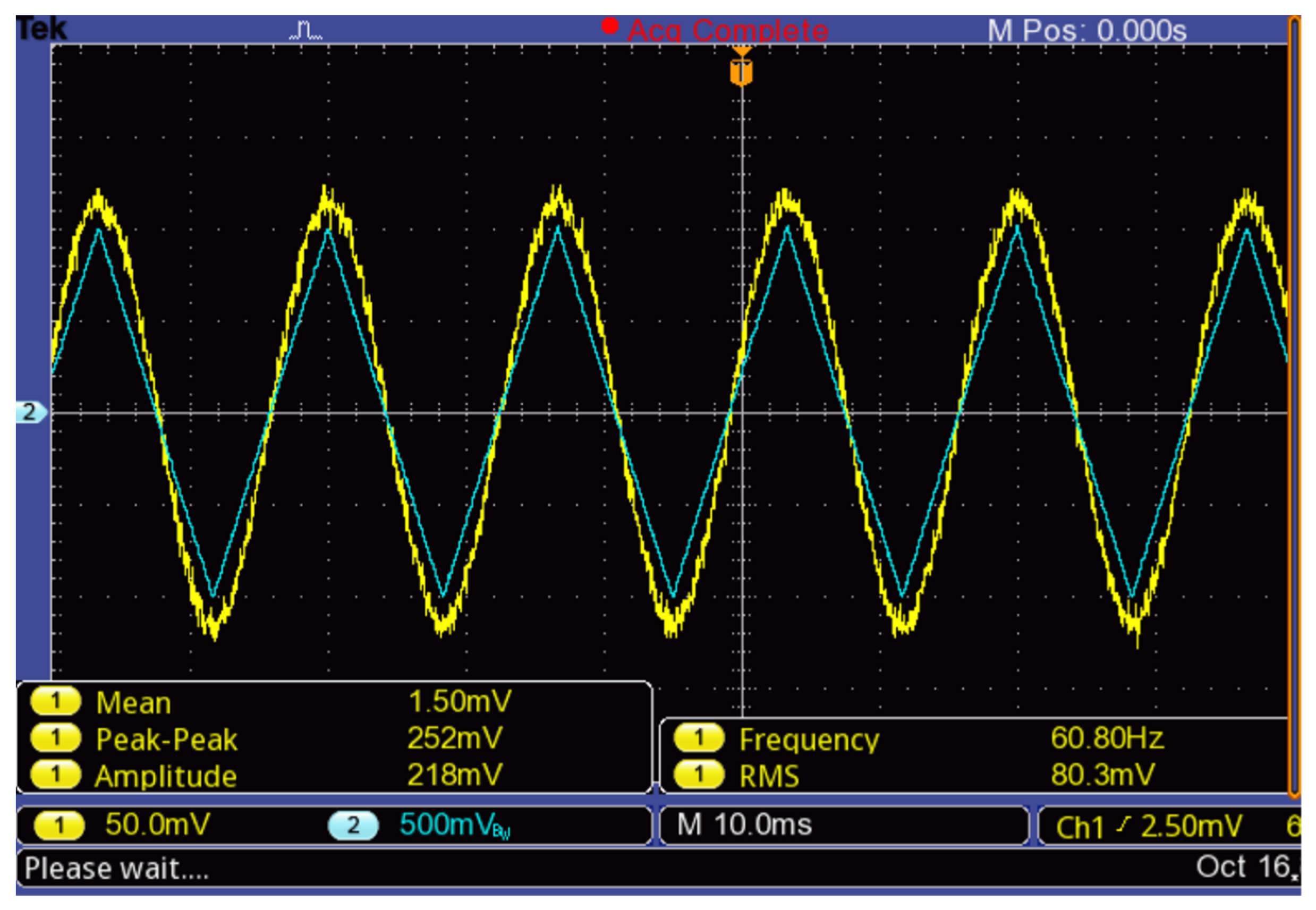
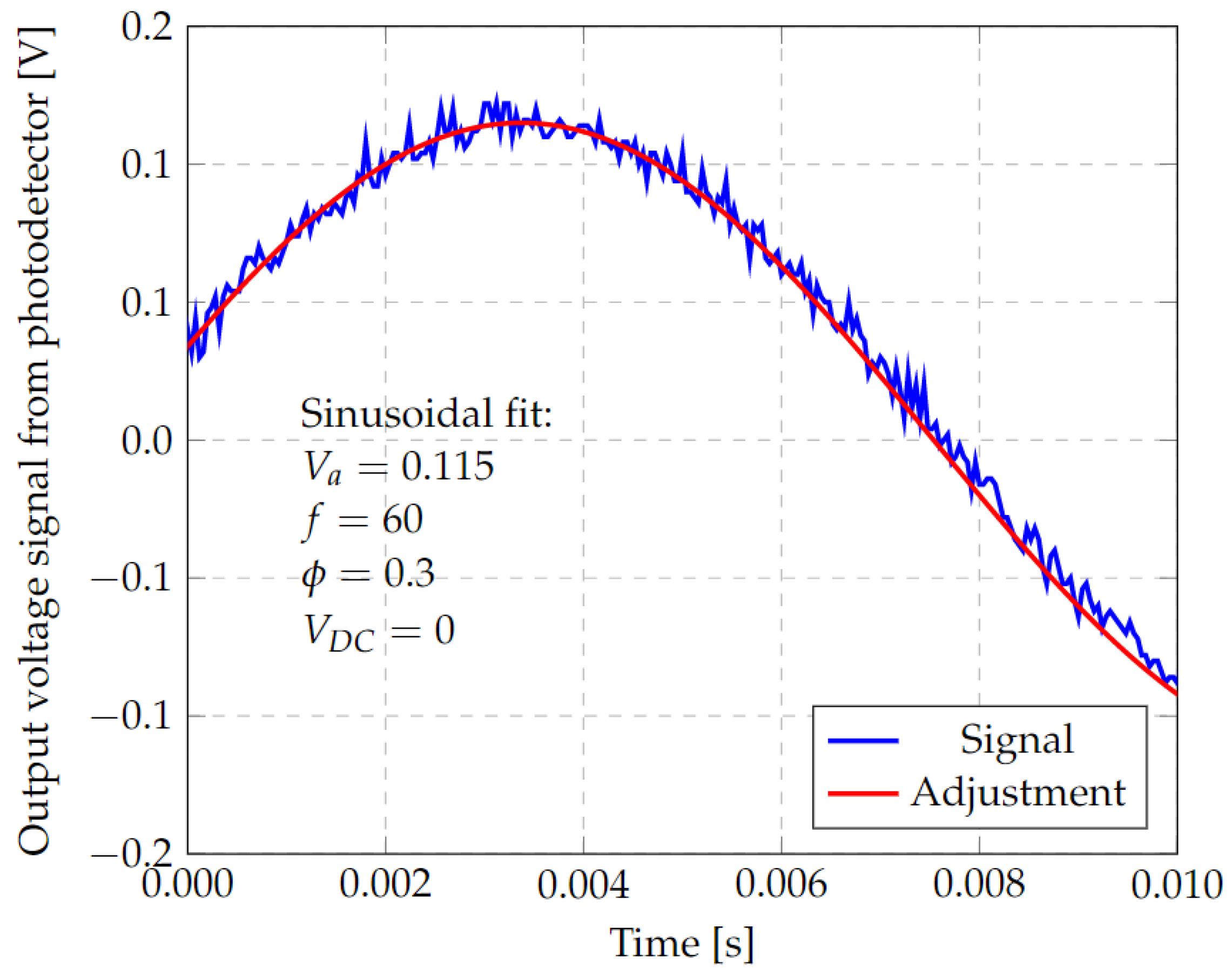
- The fringe shift coincides with the ratio of λ/2 = 316.5 nm. Consequently, from Figure 24, where the amplitude of the applied triangular signal is Apiezo = 1 V, the vibration generated has an amplitude of ±Apiezo∙Spiezo = ±200 nm.
- From the photodetector response to the measured deflection amplitude of ±200 nm, the sensitivity of the entire system to the sensor can be calculated by a linear approximation as Ssys = 200 nm/0.115 V = 1.74 μm/V.
- The optical system cannot be used to measure signals with frequencies that are higher than 14 kHz due to the bandwidth of the photodetector selected.
- To measure the relative position of the microstructure, the measurement system must have a vibration in phase with its reference frame.
- With this setup, a peak-to-peak noise voltage () lower than 10 mV is achieved without further signal processing. Therefore, vibration resolution can be calculated using the linear sensitivity approximation as:
4.2. Microstructure Performance Test
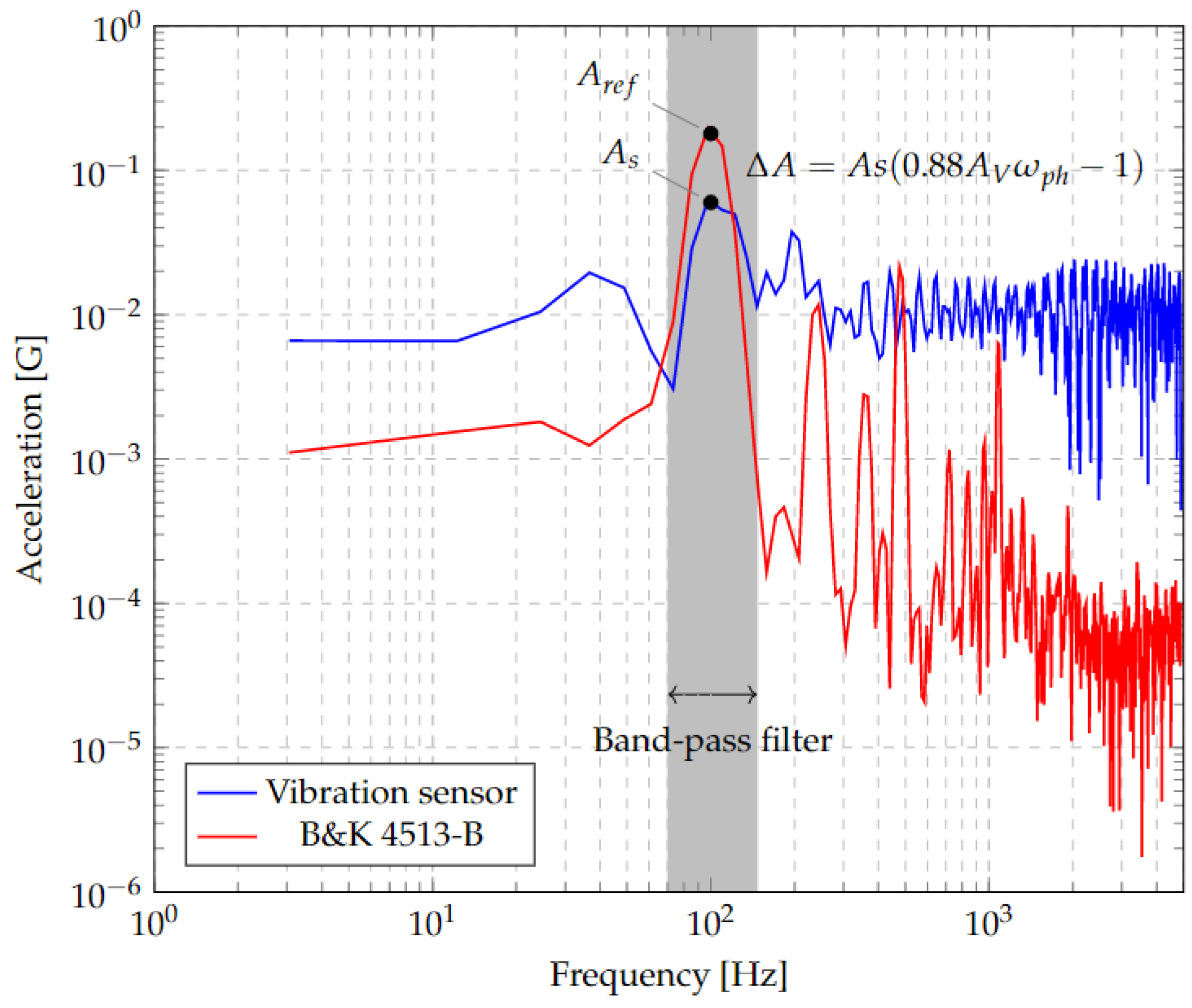
- There is a small distortion of the reference accelerometer signal due to the adaptation of the accelerometer manufactured, which is not concentric and is made by means of a screw that does not ideally approximate a rigid solid. The effect is negligible and can be reduced by placing the accelerometer concentrically to the microstructure support for future evaluations.
- To obtain the vibration signal of the microstructure with reference to its local coordinate system, it is required that the interferometer be vibrating next to the reference of the support to avoid the modification of the trajectory with the main vibration. Therefore, the result of this test corresponds to a composite signal between the vibration of the support plus the vibration of the microstructure.
- Because of the previous point, there is a limitation on the spectrum and amplitude that can be measured, because to produce a significant vibration in the microstructure, a minimum acceleration, which depends on the used frequency, is required. This acceleration cannot be increased arbitrarily, since if the total amplitude (of the support plus the microstructure) exceeds the maximum range and the change of fringes produces a saturation of peaks in the response, it is not possible to distinguish between them.

- The proposed methodology can be used to detect the vibrational spectrum of the microstructure with a 17.5 nm amplitude resolution in a frequency range from 5 Hz up to 13 kHz due to the shaker limitation.
- The response of the microstructure to inertial stimuli can be adjusted by geometric modifications to improve the resolution in a smaller frequency range or to increase the frequency range but reducing the resolution.
- An operational probe can be designed and manufactured from materials that can be used at higher than 85 °C without significant variations in response
- It is feasible to design and manufacture a vibration measurement system for testing under relevant conditions.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| % Data initialization lw = 8.36; % Light width in pixels dw = 2.79; % Dark widht in pixels fr = 6; % Fringe repetitions wp = 4; % Frige projection width % Varible initiallization cx = 0; cy = 0; a1 = 0; a2 = 0; a3 = 0; a4 = 0; a5 = 0; a6 = 0; % Sensor size = 2.29; % Size (square) of sensor xs = wp/2; % Sensor center x point ys = fr*(lw + dw)*0.7; % Sensor center y point theta = 0.5; % Sensor rotation angle refp = [xs ys;xs ys;xs ys;xs ys;xs ys]; sensor_nr = [ xs-size/2 ys-size/2 xs + size/2 ys-size/2 xs + size/2 ys + size/2 xs-size/2 ys + size/2 xs-size/2 ys-size/2 ]; % Sensor area rotation R = [cos(theta) − sin(theta); sin(theta) cos(theta)]; sensor = refp + (sensor_nr-refp)*R; % Step calculation samples = 1000; range = 4*(lw + dw); step = range/samples; av = zeros(samples,1); at = av; at2 = av; av2 = av; index = 1; % Base shadow sh0 = [ 0 0 ; wp 0 ; wp dw ; 0 dw ; 0 0]; for j = 0:step:range % Shadows generation sh1 = [sh0(:,1) sh0(:,2) + 0*(lw + dw) + j]; sh2 = [sh0(:,1) sh0(:,2) + 1*(lw + dw) + j]; sh3 = [sh0(:,1) sh0(:,2) + 2*(lw + dw) + j]; sh4 = [sh0(:,1) sh0(:,2) + 3*(lw + dw) + j]; sh5 = [sh0(:,1) sh0(:,2) + 4*(lw + dw) + j]; sh6 = [sh0(:,1) sh0(:,2) + 5*(lw + dw) + j]; % Intersection [rx1,ry1] = oc_polybool(sensor,sh1,’and’); i = numel(rx1); if(i > 0) a1 = polyarea(rx1(2:i-1),ry1(2:i-1)); endif [rx2,ry2] = oc_polybool(sensor,sh2,’and’); i = numel(rx2); if(i > 0) a2 = polyarea(rx2(2:i-1),ry2(2:i-1)); endif [rx3,ry3] = oc_polybool(sensor,sh3,’and’); i = numel(rx3); if(i > 0) a3 = polyarea(rx3(2:i-1),ry3(2:i-1)); endif [rx4,ry4] = oc_polybool(sensor,sh4,’and’); i = numel(rx4); if(i > 0) a4 = polyarea(rx4(2:i-1),ry4(2:i-1)); endif [rx5,ry5] = oc_polybool(sensor,sh5,’and’); i = numel(rx5); if(i > 0) a5 = polyarea(rx5(2:i-1),ry5(2:i-1)); endif [rx6,ry6] = oc_polybool(sensor,sh6,’and’); i = numel(rx6); if(i > 0) a6 = polyarea(rx6(2:i-1),ry6(2:i-1)); endif av(index) = a1 + a2 + a3 + a4 + a5 + a6; at(index) = j; a1 = 0; a2 = 0; a3 = 0; a4 = 0; a5 = 0; a6 = 0; index = index + 1; endfor |
References
- Burian, Y.A.; Sorokin, V.N.; Lizunov, V.V. Multifunctional Vibrational Source of Seismic Waves. J. Phys. Conf. Ser. 2018, 1050, 012016. [Google Scholar] [CrossRef]
- Chin, W.K.; Ong, Z.C.; Kong, K.K.; Khoo, S.Y.; Huang, Y.; Chong, W.T. Enhancement of Energy Harvesting Performance by a Coupled Bluff Splitter Body and PVEH Plate through Vortex Induced Vibration near Resonance. Appl. Sci. 2017, 7, 921. [Google Scholar] [CrossRef]
- Alizad, A.; Urban, M.W.; Kinnick, R.R.; Greenleaf, J.F.; Fatemi, M. Applications of Low-frequency Vibration in Assessment of Biological Tissues. In Proceedings of the 17th International Congress on Sound and Vibration 2010, ICSV 2010, Cairo, Egypt, 18–22 July 2010; Volume 5, pp. 3617–3624. [Google Scholar]
- Benevicius, V.; Ostasevicius, V.; Gaidys, R. Identification of Capacitive MEMS Accelerometer Structure Parameters for Human Body Dynamics Measurements. Sensors 2013, 13, 11184–11195. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Pillay, P.; Omekanda, A. Low Vibration Design of SRMs for Automotive Applications using Modal Analysis. In Proceedings of the IEMDC 2001. IEEE International Electric Machines and Drives Conference (Cat. No.01EX485), Cambrigde, MA, USA, 17–29 June 2001; pp. 261–266. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, J.; Cai, C.; Pan, Z.; Zhai, W. Application of Dynamic Vibration Absorbers in Designing a Vibration Isolation Track at Low-frequency Domain. In Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit; Urbana Champaign: Urbana, IL, USA, 2017; Volume 231, pp. 546–557. [Google Scholar]
- Bernstein, J.; Miller, R.; Kelley, W.; Ward, P. Low-Noise MEMS Vibration Sensor for Geophysical Applications. J. Microelectromechanical Syst. 1999, 8, 433–438. [Google Scholar] [CrossRef]
- MEMS Applications Overview. MEMS Applications PK, MEMS Applications Activity. Participant Guide; Southwest Center for Microsystems Education. SCME. Available online: http://nanotechradar.com/sites/default/files/inano10_mems_applications_overview.pdf (accessed on 15 July 2022).
- Girish, K.; Chaitanya, U.; Kshisagar, G.K.; Ananthasuresh, N.B. Micromachines High-resolution Accelerometers. J. Indian Inst. Sci. 2007, 87, 333–361. [Google Scholar]
- Loone, M. Introduction to MEMS Vibration Monitoring. Analog. Dialogue 2014, 48, 1–3. Available online: https://www.analog.com/en/analog-dialogue/articles/intro-to-mems-vibration-monitoring.html (accessed on 10 July 2022).
- Liu, Y.; Wang, H.; Qin, H.; Zhao, W.; Wang, P. Geometry and Profile Modification of Microcantilevers for Sensitivity Enhancement in Sensing Applications. Sens. Mater. 2017, 29, 1. [Google Scholar]
- Graak, P.; Gupta, A.; Kaur, S.; Chhabra, P.; Kumar, D.; Shetty, A. Simulation of Various Shapes of Cantilever Beam for Piezoelectric Power Generator. In Proceedings of the 2015 COMSOL Conference, Pune, India, 29 October 2015. [Google Scholar]
- Andrejasic, M. MEMS Accelerometers Seminar, University of Ljubljana. Marec. 2008. Available online: http://mafija.fmf.uni-lj.si/seminar/files/2007_2008/MEMS_accelerometers-koncna.pdf (accessed on 16 January 2020).
- Zhou, X.; Che, L.; Liang, S.; Lin, Y.; Li, X.; Wang, Y. Design and Fabrication of a MEMS Capacitive Accelerometer with Fully Symmetrical Double-sided H-shaped Beam Structure. Microelectron. Eng. 2015, 131, 51–57. [Google Scholar] [CrossRef]
- Xiao, D.B.; Li, Q.S.; Hou, Z.Q.; Wang, X.H.; Chen, Z.H.; Xia, D.W.; Wu, X.Z. A Novel Sandwich Differential Capacitive Accelerometer with Symmetrical Double-sided Serpentine Beam-mass Structure. J. Micromech. Microeng. 2015, 26, 025005. [Google Scholar] [CrossRef]
- Xu, W.; Yang, J.; Xie, G.; Wang, B.; Qu, M.; Wang, X.; Liu, X.; Tang, B. Design and Fabrication of a Slanted-Beam MEMS Accelerometer. Micromachines 2017, 8, 77. [Google Scholar] [CrossRef]
- Avinash, K.; Siddheshwar, K. Comparative Study of Different Flexures of MEMS Accelerometers. Int. J. Eng. Adv. Technol. 2015, 4, 2249–8958. [Google Scholar]
- Aoyagi, S.; Makihira, K.; Yoshikawa, D.; Tai, Y. Parylene Accelerometer Utilizing Spiral Beams. In Proceedings of the 19th IEEE International Conference on Micro Electro Mechanical Systems, Istanbul, Turkey, 22–26 January 2006. [Google Scholar]
- Solai, K.; Rathnasami, J.D.; Koilmani, S. Superior Performance Area Changing Capacitive MEMS Accelerometer Employing Additional Lateral Springs for Low Frequency Applications. Microsyst. Technol. 2020, 26, 1–18. [Google Scholar] [CrossRef]
- Keshavarzi, M.; Hasani, J.Y. Design and Optimization of Fully Differential Capacitive MEMS Accelerometer Based on Surface Micromachining. Microsyst. Technol. 2018, 25, 1369–1377. [Google Scholar] [CrossRef]
- Benmessaoud, M.; Nasreddine, M.M. Optimization of MEMS Capacitive Accelerometer. Microsyst. Technol. 2013, 19, 713–720. [Google Scholar] [CrossRef]
- Kaajakari, V. Practical MEMS; Small Gear Publishing: Las Vegas, NV, USA, 2009; ISBN 978-0-9822991-0-4. [Google Scholar]
- Denishev, K.H.; Petrova, M.R. Accelerometer Design. In Proceedings of the ELECTRONICS 2007, Sozopol, Bulgaria, 19–21 September 2007; pp. 159–164. [Google Scholar]
- Rao, K.; Wei, X.; Zhang, S.; Zhang, M.; Hu, C.; Liu, H.; Tu, L.-C. A MEMS Micro-g Capacitive Accelerometer Based on Through-Silicon-Wafer-Etching Process. Micromachines 2019, 10, 380. [Google Scholar] [CrossRef]
- Wai-Chi, W.; Azid, A.A.; Majlis, B.Y. Formulation of stiffness constant and effective mass for a folded beam. Arch. Mech. 2010, 62, 405–418. [Google Scholar]
- Chae, J.S.; Kulah, H.; Salian, A.; Najafi, K. A High Sensitivity Silicon on Glass Lateral μg Microaccelerometer. In Proceedings of the Third Annual Micro/NanoTechnology Conference, Houston, TX, USA, 10–30 June 2000. [Google Scholar]
- Vanhellemont, J.; Swarnakar, A.K.; van der Biest, O. Temperature Dependent Young’s Modulus of Si and Ge. ECS Trans. 2014, 64, 283–292. [Google Scholar] [CrossRef]
- Shi, S.; Geng, W.; Bi, K.; Shi, Y.; Li, F.; He, J.; Chou, X. High Sensitivity MEMS Accelerometer Using PZT-Based Four L-Shaped Beam Structure. IEEE Sens. J. 2022, 22, 7627–7636. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, X.; Wen, D. Fabrication and Characteristics of a Three-Axis Accelerometer with Double L-Shaped Beams. Sensors 2020, 20, 1780. [Google Scholar] [CrossRef]
- Ikehara, T.; Tsuchiya, T. Crystal orientation-dependent fatigue characteristics in micrometer-sized single-crystal silicon. Microsyst. Nanoeng. 2016, 2, 16027. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Q.A.; Yu, H. Size and Temperature Dependence of Young’s Modulus of a Silicon Nano-plate. J. Phys. D Appl. Phys. 2008, 41, 165406. [Google Scholar] [CrossRef]
- Wang, M.C.; Chao, S.Y.; Lin, C.Y.; Chang, C.H.T.; Lan, W.H. Low-Frequency Vibration Sensor with Dual-Fiber Fabry–Perot Interferometer Using a Low-Coherence LED. Crystals 2022, 12, 1079. [Google Scholar] [CrossRef]


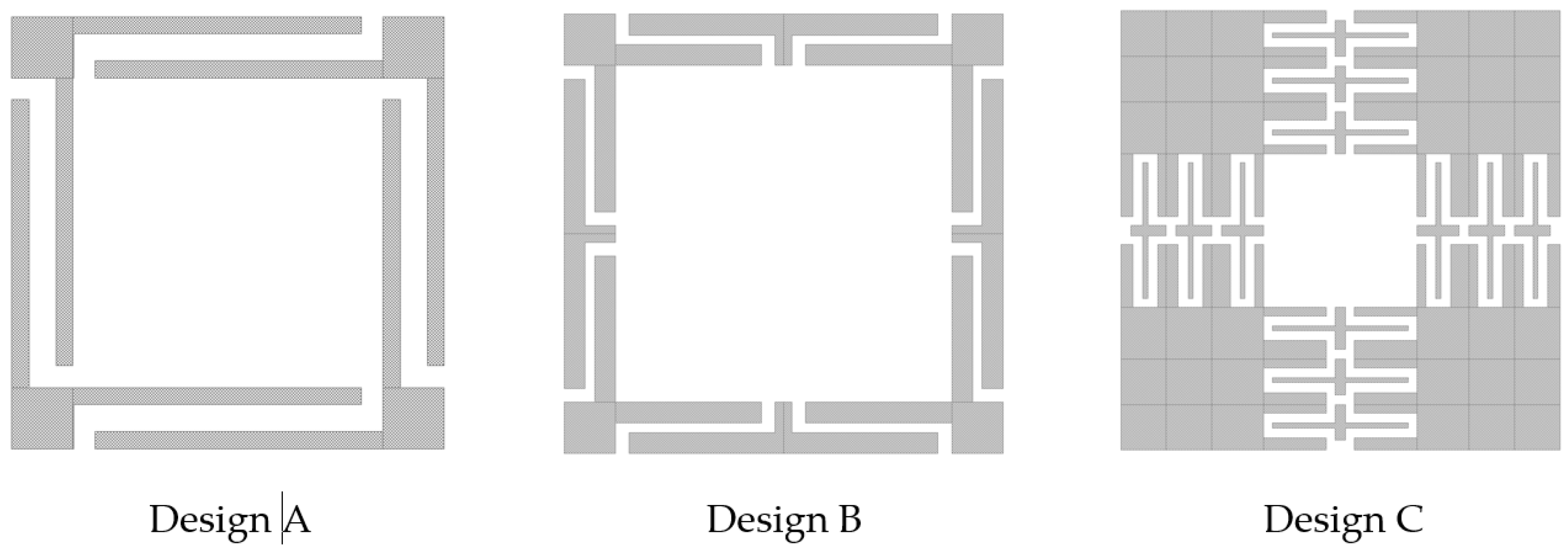










| Parameter | Description | Size (µm) | ||
|---|---|---|---|---|
| Design A | Design B | Design C | ||
| Hm | Mass thickness | 378 | 362 | 490.36 |
| Lm | Mass length | 1500 | 1500 | 1500 |
| W1 | Beam width | 106.9 | 69.55 | 86.02 |
| W2 | Joint width between supports and mass | 83.6 | 94.15 | 96.21 |
| L2 | Length of the joint between supports and mass | 86.6 | 124.2 | 86.6 |
| Hb | Beam thickness | 19.4 | 11.4 | 18.9 |
| Device | Solver Target | Element Type/Mesh | Convergence | |||
|---|---|---|---|---|---|---|
| Total Number of Nodes | Total Number of Elements | Change % | Total Mass (Kg) | |||
| Design A | Mechanical APDL | SOLID187/Refinement controlled program (Tet10) | 83,842 | 54,922 | 4.02 | 1.9868 × 10−6 |
| Design B | 157,411 | 100,226 | 3.03 | 1.8877 × 10−6 | ||
| Design C | 19,845 | 8577 | 0 | 1.7624 × 10−6 | ||
| Vibration Mode | Frequency (Hz) | ||
|---|---|---|---|
| Design A | Design B | Design C | |
| 1 | 1390.6 | 2445.4 | 1007.7 |
| 2 | 2232.6 | 3672.8 | 2481.3 |
| 3 | 2235.4 | 3676.3 | 2481.6 |
| 4 | 49,157 | 53,924 | 7307.7 |
| 5 | 49,212 | 53,943 | 7308.4 |
| 6 | 75,224 | 95,190 | 16,444 |
| Parameter | Description | Design C | Error, % | |
|---|---|---|---|---|
| Designed Sizes (µm) | Fabricated Sizes (µm) | |||
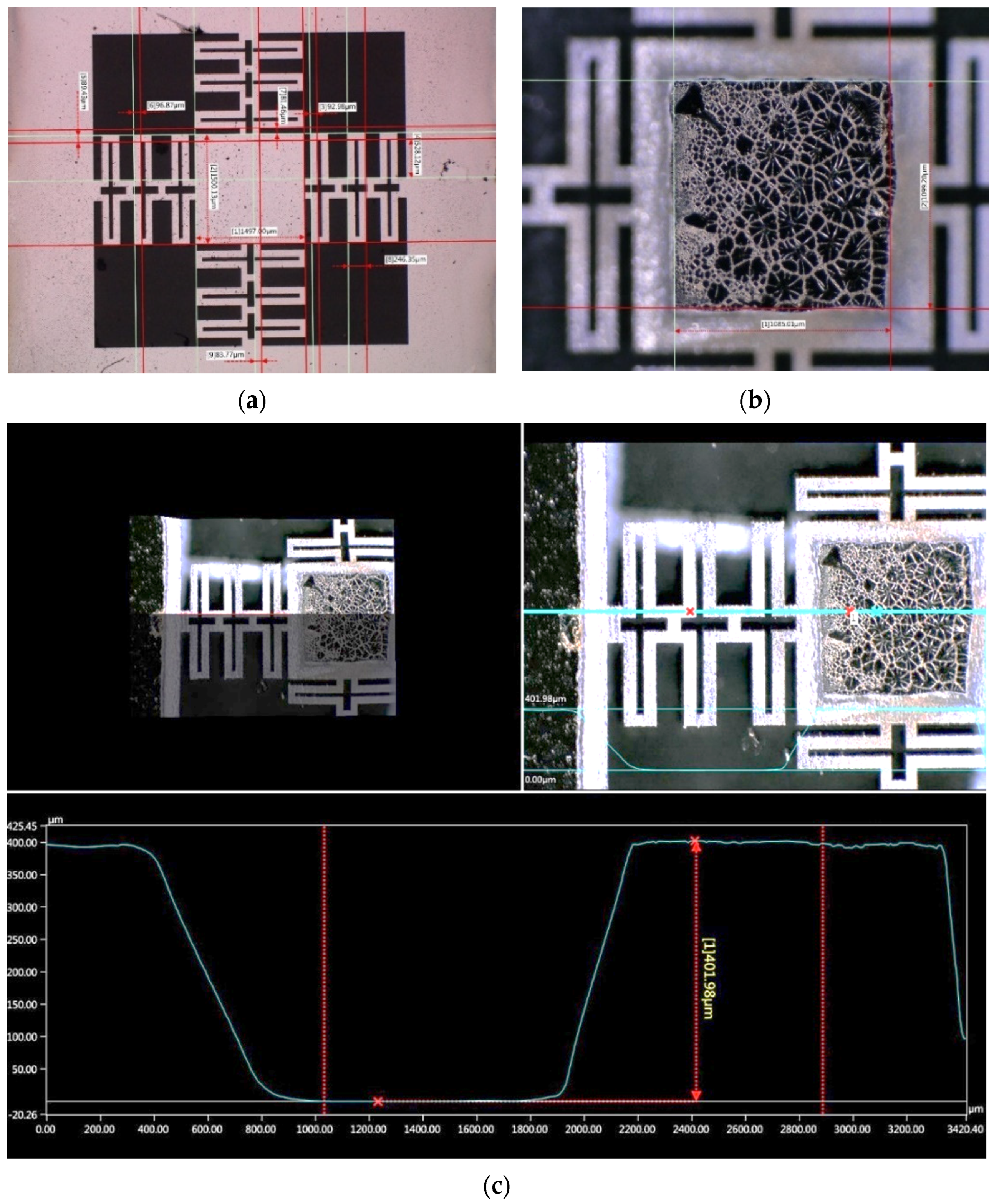
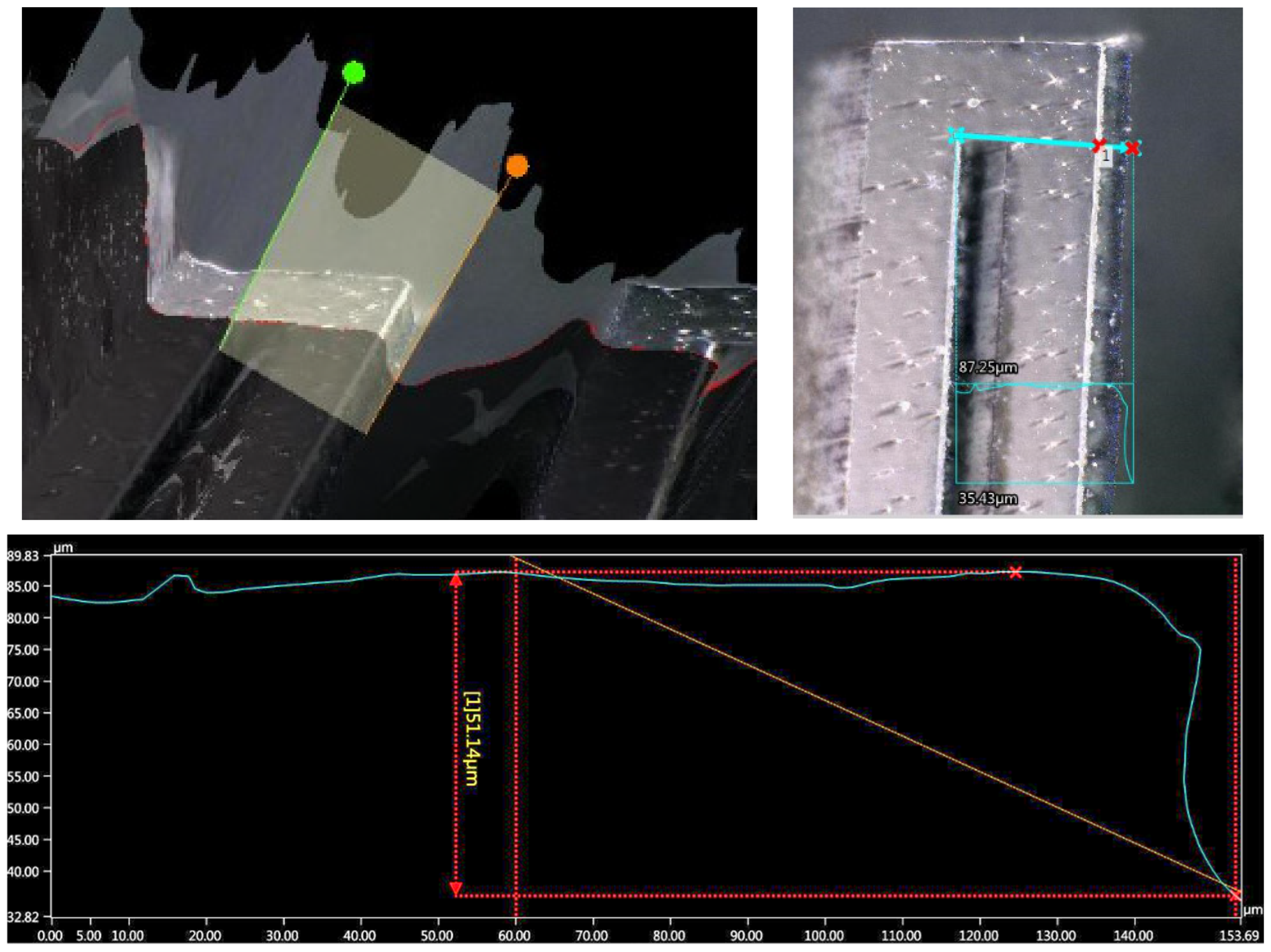
| Hm | Mass thickness | 490.36 | 401.98 | 18.02 |
| Lm | Mass length | 1500 × 1500 | 1500.13 × 1497 | 0.01 × 0.20 |
| W1 | Beam width | 86.02 | 89.43 | 3.96 |
| W2 | Joint width between supports and mass | 96.21 | 96.87 | 0.69 |
| L2 | Length of the joint between supports and mass | 86.6 | 81.46 | 5.94 |
| Hb | Beam thickness | 18.9 | 51.14 | 180.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Fraga, R.; Tecpoyotl-Torres, M.; Mejía, I.; Mañón, J.O.; Riestra, L.E.; Alcantar-Peña, J. Optical Sensor, Based on an Accelerometer, for Low-Frequency Mechanical Vibrations. Micromachines 2022, 13, 1462. https://doi.org/10.3390/mi13091462
Sánchez-Fraga R, Tecpoyotl-Torres M, Mejía I, Mañón JO, Riestra LE, Alcantar-Peña J. Optical Sensor, Based on an Accelerometer, for Low-Frequency Mechanical Vibrations. Micromachines. 2022; 13(9):1462. https://doi.org/10.3390/mi13091462
Chicago/Turabian StyleSánchez-Fraga, Rodolfo, Margarita Tecpoyotl-Torres, Israel Mejía, Jorge Omar Mañón, Luis Eduardo Riestra, and Jesús Alcantar-Peña. 2022. "Optical Sensor, Based on an Accelerometer, for Low-Frequency Mechanical Vibrations" Micromachines 13, no. 9: 1462. https://doi.org/10.3390/mi13091462
APA StyleSánchez-Fraga, R., Tecpoyotl-Torres, M., Mejía, I., Mañón, J. O., Riestra, L. E., & Alcantar-Peña, J. (2022). Optical Sensor, Based on an Accelerometer, for Low-Frequency Mechanical Vibrations. Micromachines, 13(9), 1462. https://doi.org/10.3390/mi13091462








