Extension of the Measurable Wavelength Range for a Near-Infrared Spectrometer Using a Plasmonic Au Grating on a Si Substrate
Abstract
1. Introduction
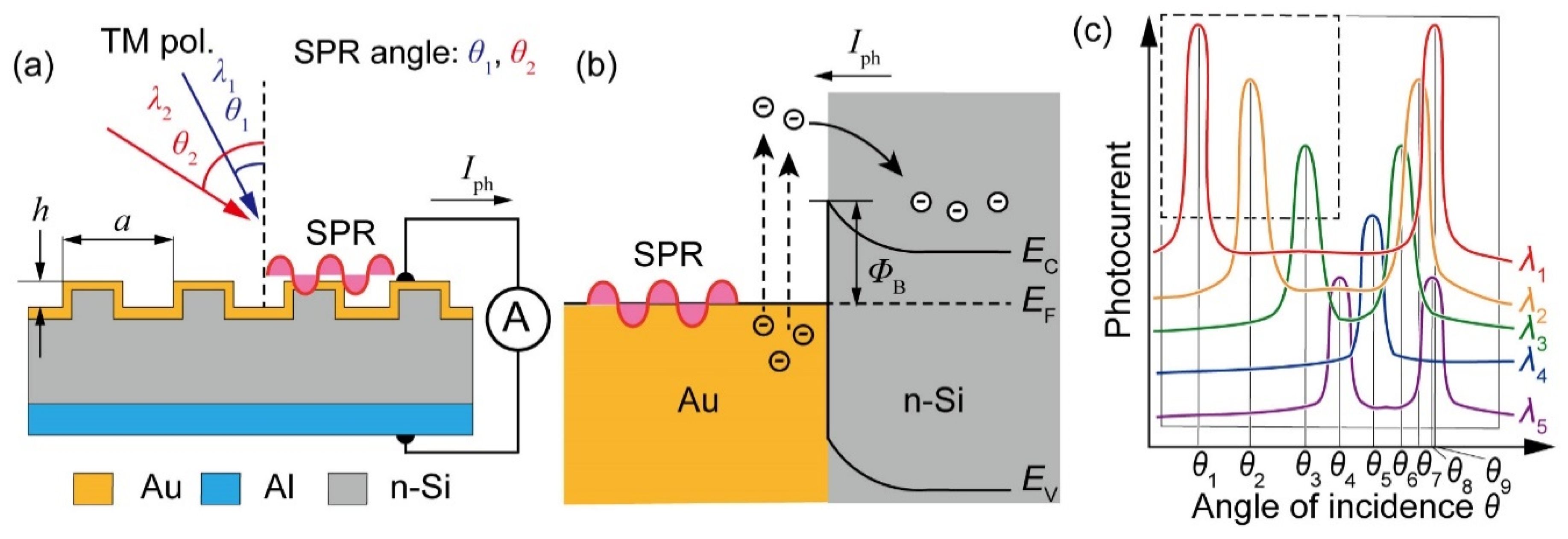
2. Principles of Light Detection Using Surface Plasmon Resonance (SPR)
3. Spectral Calculation Procedures
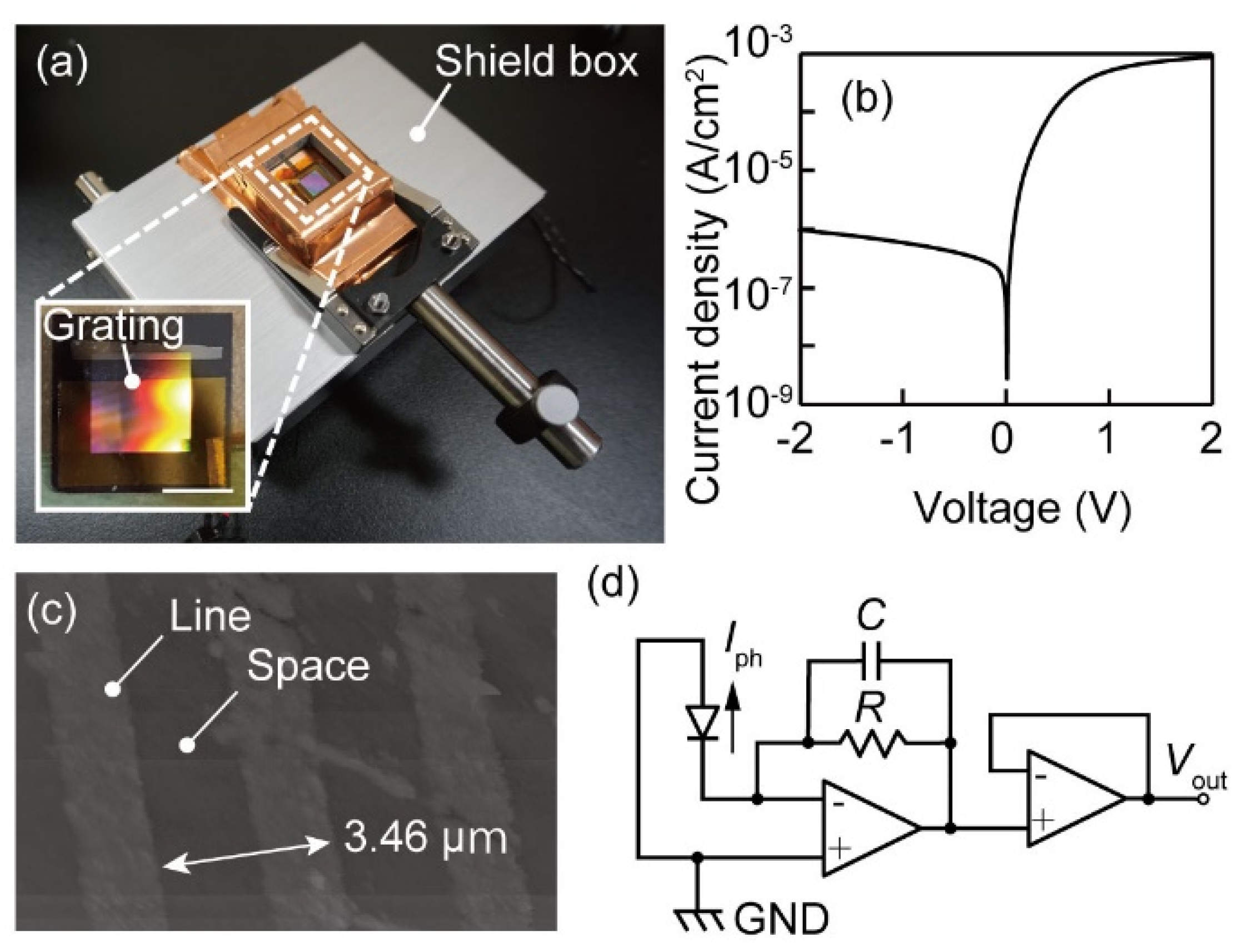
4. Materials and Methods
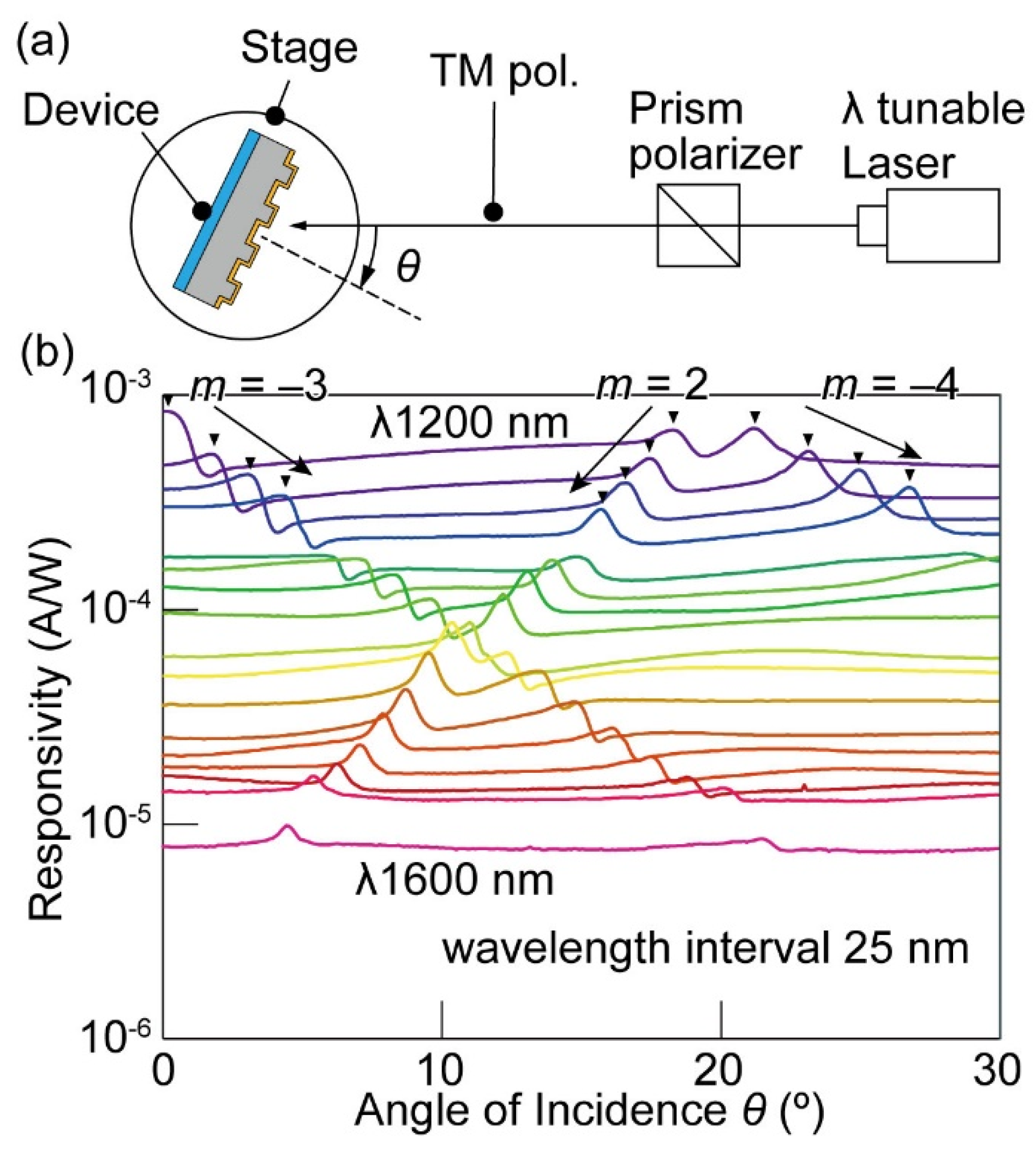
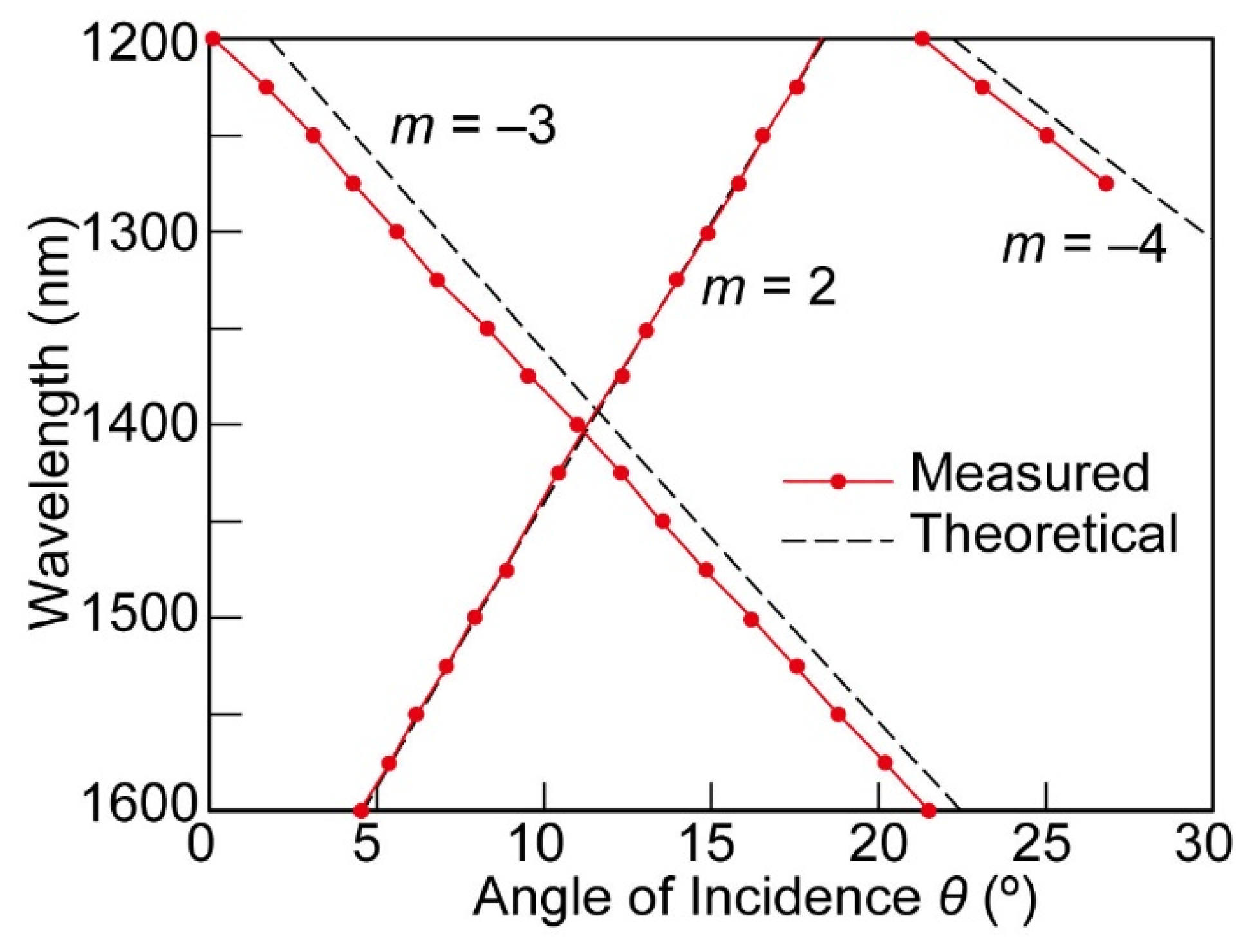
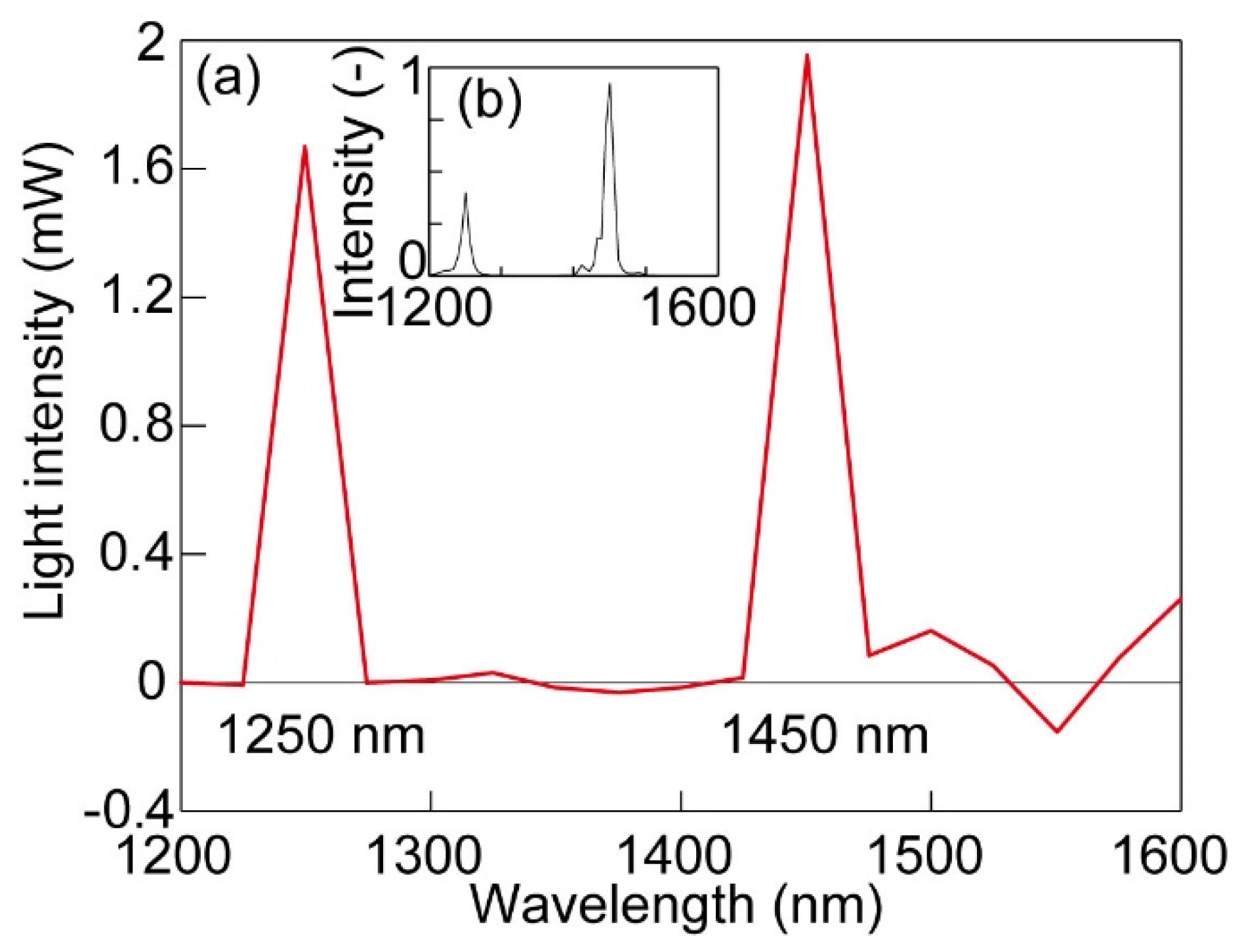
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Magwaza, L.S.; Opara, U.L.; Nieuwoudt, H.; Cronje, P.J.R.; Saeys, W.; Nicolaï, B. NIR Spectroscopy applications for internal and external quality analysis of citrus fruit—A review. Food Bioprocess. Technol. 2012, 5, 425–444. [Google Scholar] [CrossRef]
- Nicolaï, B.M.; Beullens, K.; Bobelyn, E.; Peirs, A.; Saeys, W.; Theron, K.I.; Lammertyn, J. Nondestructive measurement of fruit and vegetable quality by means of NIR spectroscopy: A review. Postharvest Biol. Technol. 2007, 46, 99–118. [Google Scholar] [CrossRef]
- Roggo, Y.; Chalus, P.; Maurer, L.; Lema-Martinez, C.; Edmond, A.; Jent, N. A review of near infrared spectroscopy and chemometrics in pharmaceutical technologies. J. Pharm. Biomed. Anal. 2007, 44, 683–700. [Google Scholar] [CrossRef]
- Villringer, A.; Chance, B. Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 1997, 20, 435–442. [Google Scholar] [CrossRef]
- Tsur, Y.; Arie, A. On-chip plasmonic spectrometer. Opt. Lett. 2016, 41, 3523. [Google Scholar] [CrossRef] [PubMed]
- Fleischman, D.; Sweatlock, L.A.; Murakami, H.; Atwater, H. Hyper-selective plasmonic color filters. Opt. Express 2017, 25, 27386. [Google Scholar] [CrossRef] [PubMed]
- Ema, D.; Kanamori, Y.; Sai, H.; Hane, K. Plasmonic color filters integrated on a photodiode array. Electron. Commun. Jpn. 2018, 101, 95–104. [Google Scholar] [CrossRef]
- Kim, S.; Lee, Y.; Kim, J.Y.; Yang, J.H.; Kwon, H.J.; Hwang, J.Y.; Moon, C.; Jang, J.E. Color-sensitive and spectrometer-free plasmonic sensor for biosensing applications. Biosens. Bioelectron. 2019, 126, 743–750. [Google Scholar] [CrossRef]
- Chen, W.; Kan, T.; Ajiki, Y.; Matsumoto, K.; Shimoyama, I. NIR spectrometer using a Schottky photodetector enhanced by grating-based SPR. Opt. Express 2016, 24, 25797. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer: Berlin, Germany, 1988; Volume 111. [Google Scholar]
- Kimata, M.; Denda, M.; Yutanj, N.; Iwade, S.; Tsubouchi, N. A 512 × 512-element PtSi Schottky-barrier infrared image sensor. IEEE J. Solid-State Circuits 1987, 22, 1124–1129. [Google Scholar] [CrossRef]
- Kosonocky, W.F.; Shallcross, F.V.; Villani, T.S.; Groppe, J.V. 160 × 244 element PtSi Schottky-barrier IR-CCD image sensor. IEEE Trans. Electron. Devices 1985, 32, 1564–1573. [Google Scholar] [CrossRef]
- Scales, C.; Berini, P. Thin-film Schottky barrier photodetector models. IEEE J. Quantum Electron. 2010, 46, 633–643. [Google Scholar] [CrossRef]
- Casalino, M.; Sirleto, L.; Moretti, L.; Gioffrè, M.; Coppola, G.; Rendina, I. Silicon resonant cavity enhanced photodetector based on the internal photoemission effect at 1.55 μm: Fabrication and characterization. Appl. Phys. Lett. 2008, 92, 251104. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Cheung, S.K.; Cheung, N.W. Extraction of Schottky diode parameters from forward current-voltage characteristics. Appl. Phys. Lett. 1986, 49, 85–87. [Google Scholar] [CrossRef]
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef] [PubMed]
- Cai, D.; Lu, Y.; Lin, K.; Wang, P.; Ming, H. Improving the sensitivity of SPR sensors based on gratings by double-dips method (DDM). Opt. Express 2008, 16, 14597. [Google Scholar] [CrossRef]
- Yoon, K.H.; Shuler, M.L.; Kim, S.J.; Jung, J.-M.; Shin, Y.-B.; Kim, M.-G.; Ro, H.-S.; Jung, H.-T.; Chung, B.H. Design optimization of nano-grating surface plasmon resonance sensors. J. Phys. Chem. B 2006, 14, 22351–22358. [Google Scholar] [CrossRef]
- Pi, S.; Zeng, X.; Zhang, N.; Ji, D.; Chen, B.; Song, H.; Cheney, A.; Xu, Y.; Jiang, S.; Sun, D.; et al. Dielectric-grating-coupled surface plasmon resonance from the back side of the metal film for ultrasensitive sensing. IEEE Photonics J. 2016, 8, 4800207. [Google Scholar]
- Li, W.; Valentine, J. Metamaterial perfect absorber based hot electron photodetection. Nano Lett. 2014, 14, 3510–3514. [Google Scholar] [CrossRef] [PubMed]
- Ford, J.E.; Aksyuk, V.A.; Bishop, D.J.; Walker, J.A. Wavelength add-drop switching using tilting micromirrors. J. Light. Technol. 1999, 17, 904–911. [Google Scholar] [CrossRef]
- Dickensheets, D.L.; Kino, G.S. Silicon-micromachined scanning confocal optical microscope. J. Microelectromech. Syst. 1998, 7, 38–47. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suido, Y.; Yamamoto, Y.; Thomas, G.; Ajiki, Y.; Kan, T. Extension of the Measurable Wavelength Range for a Near-Infrared Spectrometer Using a Plasmonic Au Grating on a Si Substrate. Micromachines 2019, 10, 403. https://doi.org/10.3390/mi10060403
Suido Y, Yamamoto Y, Thomas G, Ajiki Y, Kan T. Extension of the Measurable Wavelength Range for a Near-Infrared Spectrometer Using a Plasmonic Au Grating on a Si Substrate. Micromachines. 2019; 10(6):403. https://doi.org/10.3390/mi10060403
Chicago/Turabian StyleSuido, Yu, Yosuke Yamamoto, Gaulier Thomas, Yoshiharu Ajiki, and Tetsuo Kan. 2019. "Extension of the Measurable Wavelength Range for a Near-Infrared Spectrometer Using a Plasmonic Au Grating on a Si Substrate" Micromachines 10, no. 6: 403. https://doi.org/10.3390/mi10060403
APA StyleSuido, Y., Yamamoto, Y., Thomas, G., Ajiki, Y., & Kan, T. (2019). Extension of the Measurable Wavelength Range for a Near-Infrared Spectrometer Using a Plasmonic Au Grating on a Si Substrate. Micromachines, 10(6), 403. https://doi.org/10.3390/mi10060403



