Modeling and Experiment of the Critical Depth of Cut at the Ductile–Brittle Transition for a 4H-SiC Single Crystal
Abstract
1. Introduction
2. Modeling
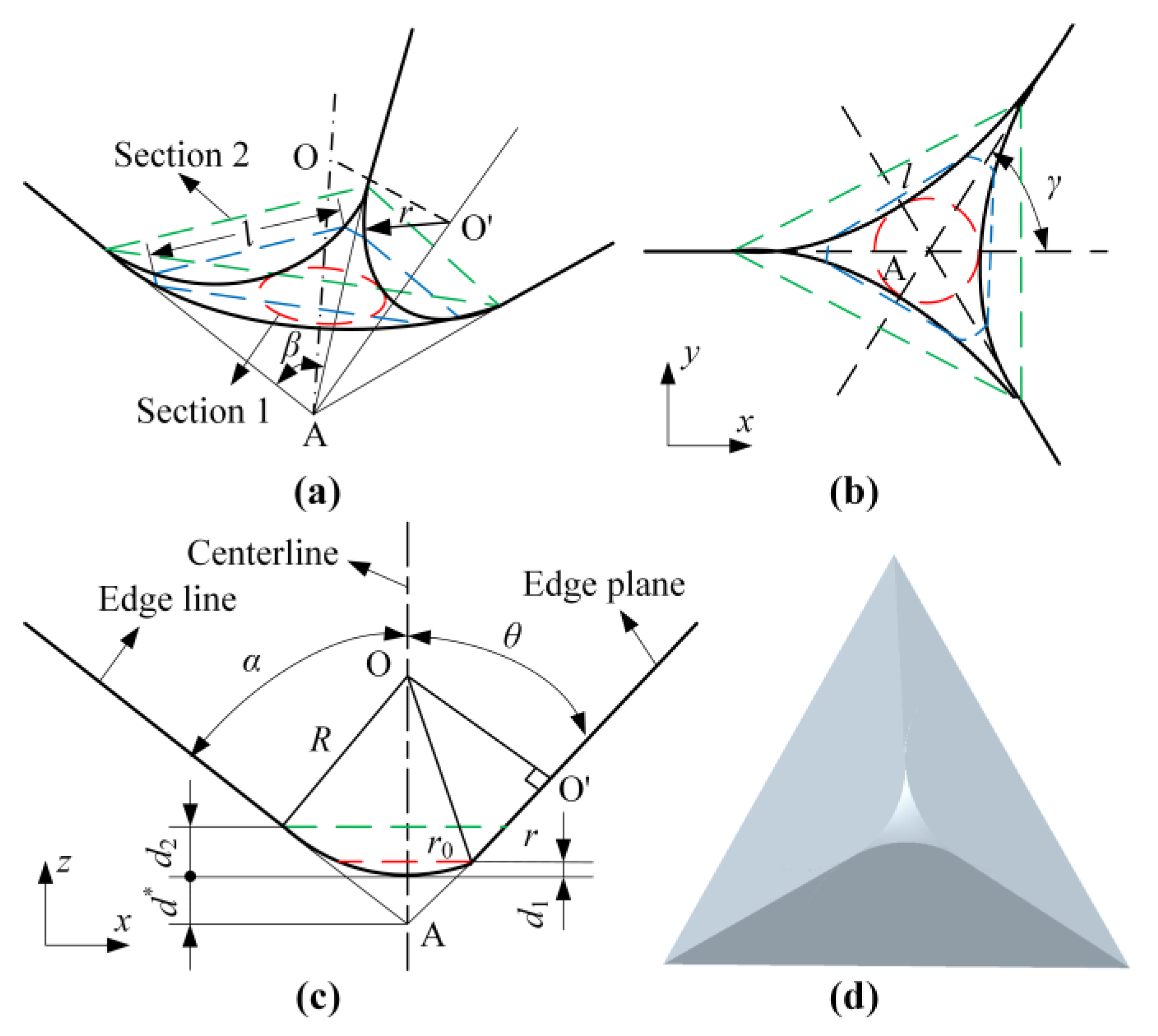
2.1. Modeling of the Indenter Structure
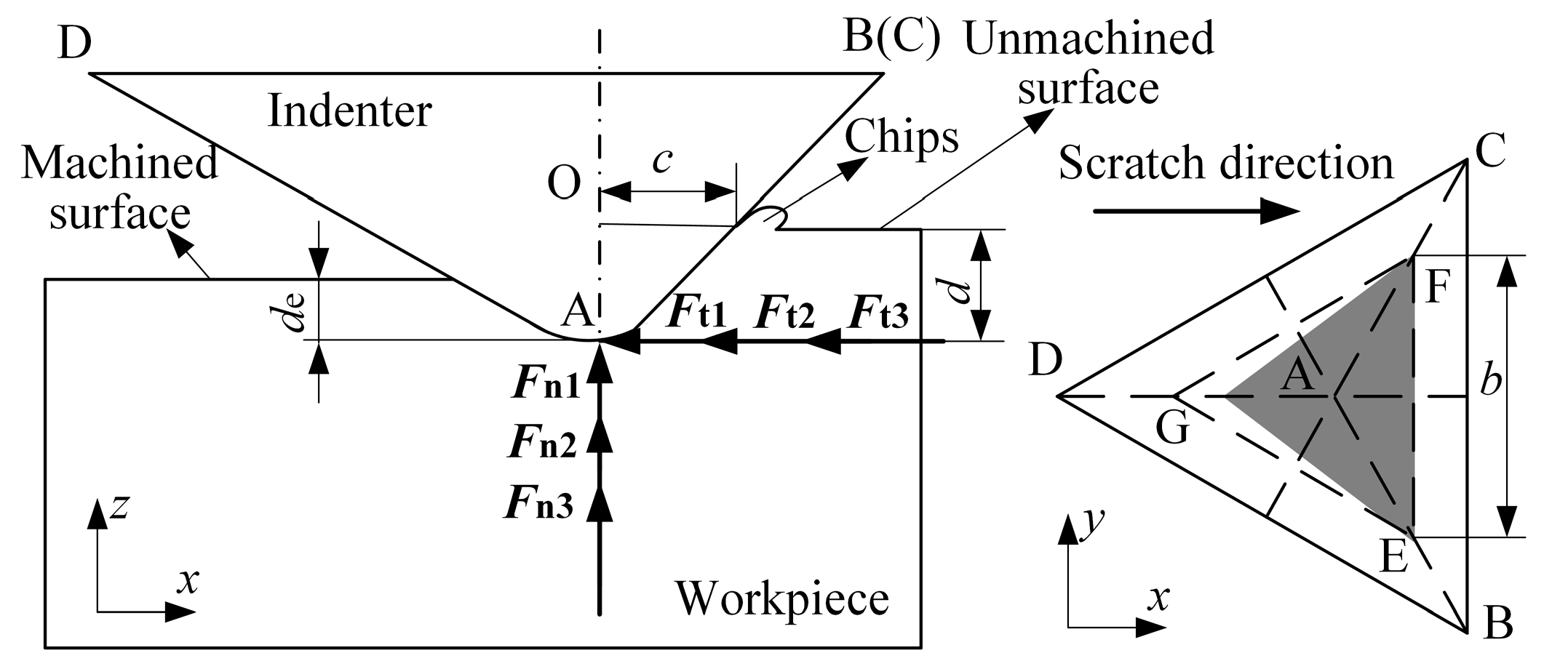
2.2. Modeling of the Critical Depth of Cut
3. Experimental Setup
4. Results, Analysis, and Discussion
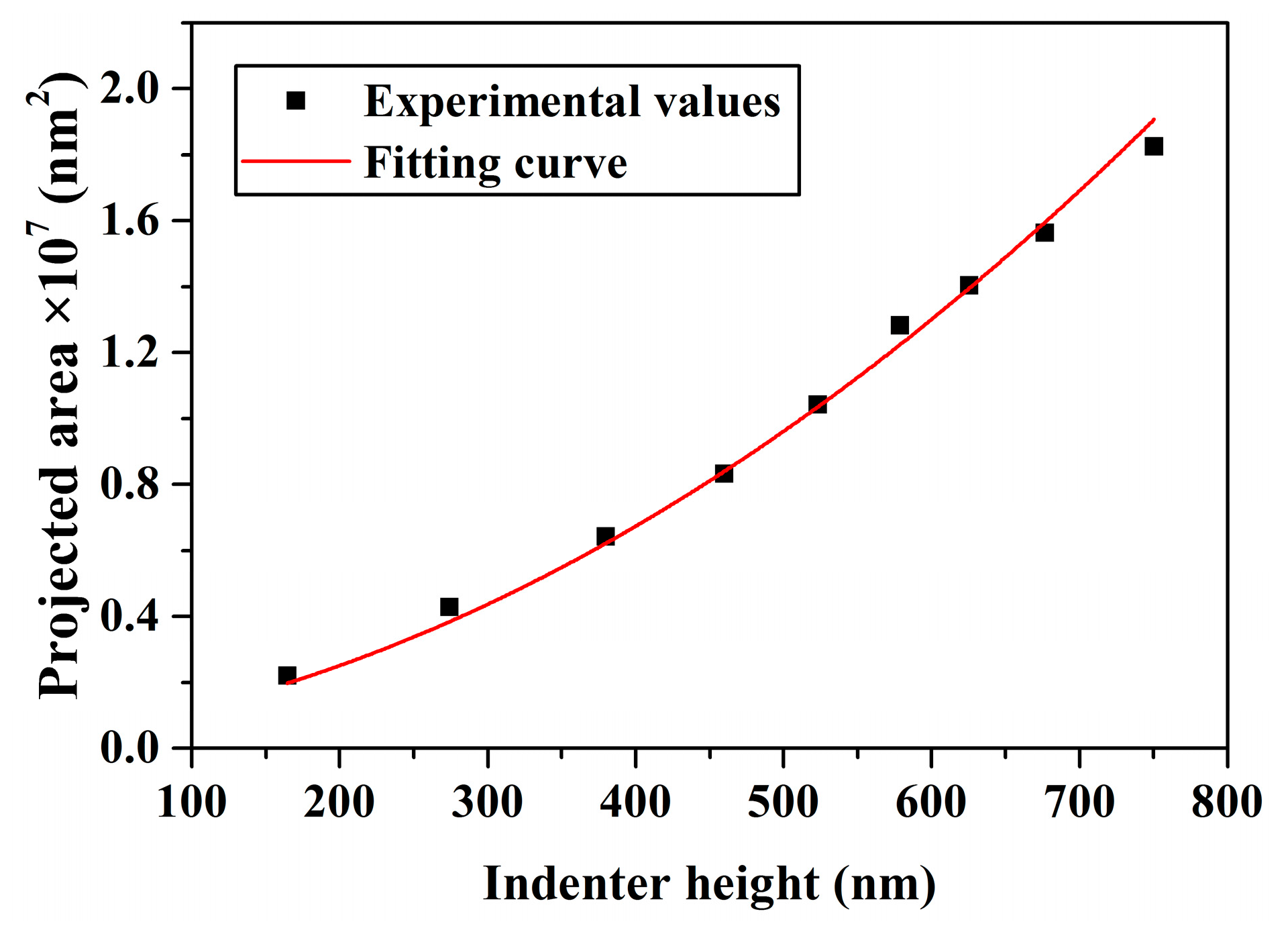
4.1. Determination of the Indenter Nose Radius
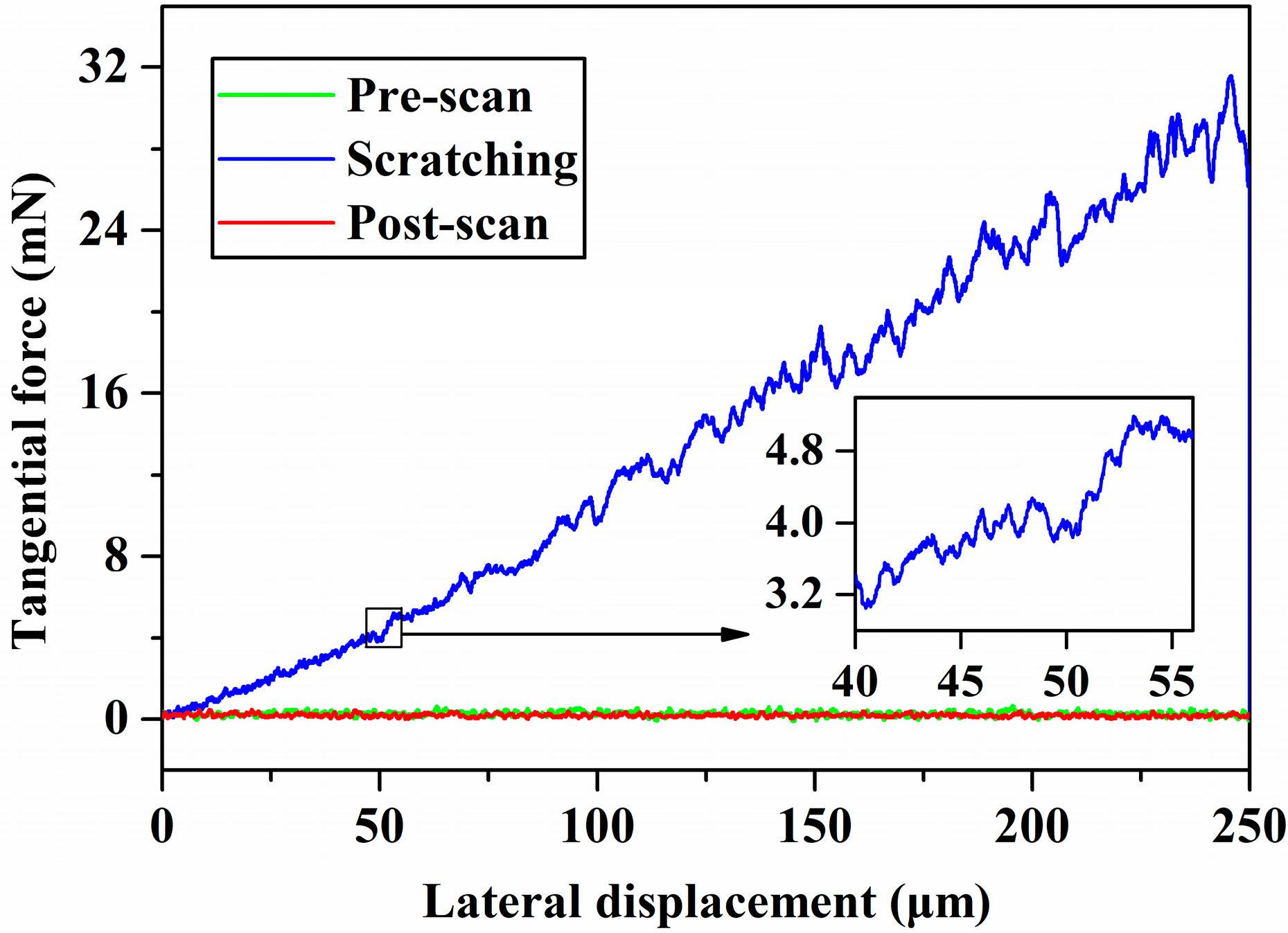
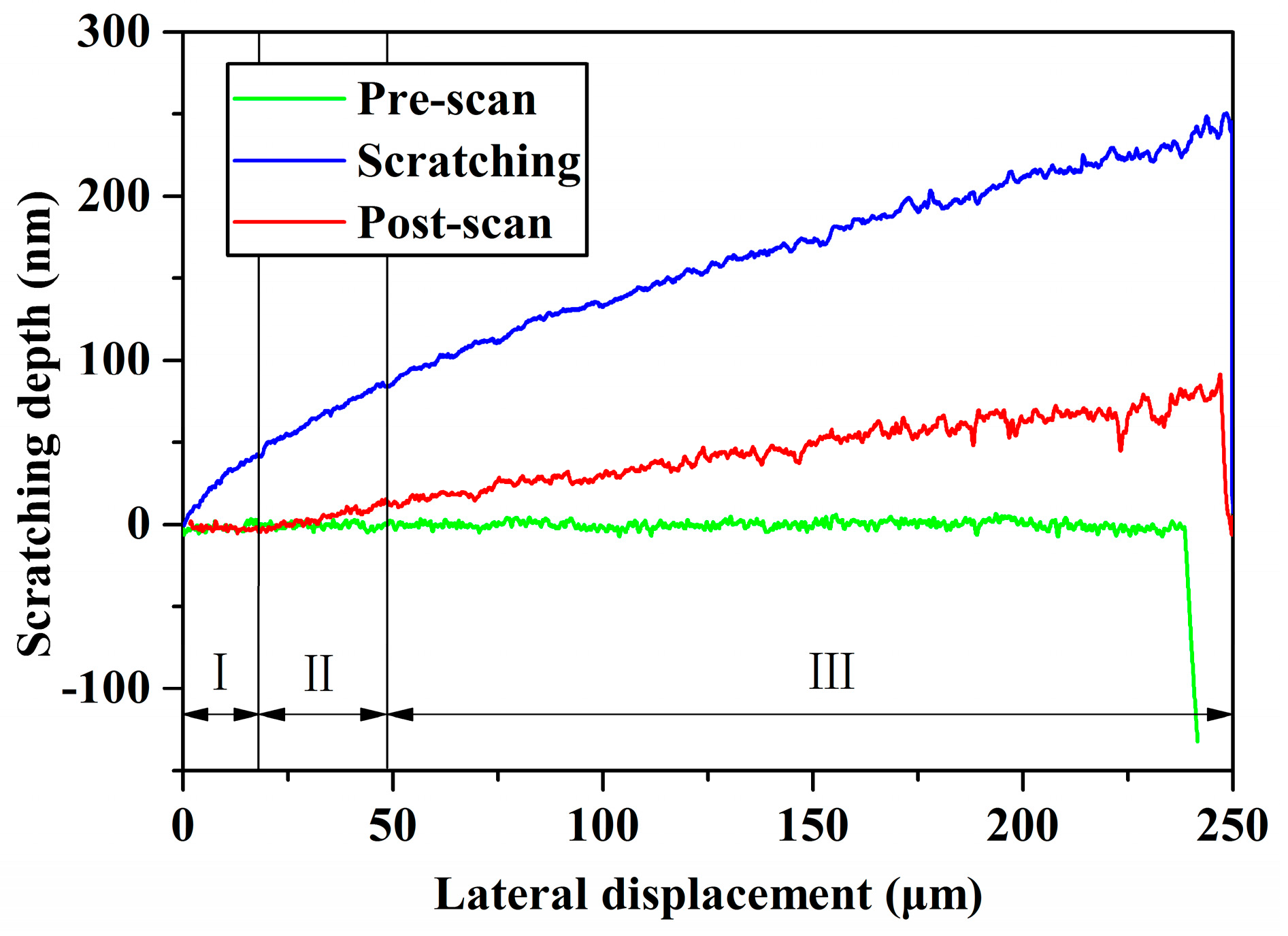
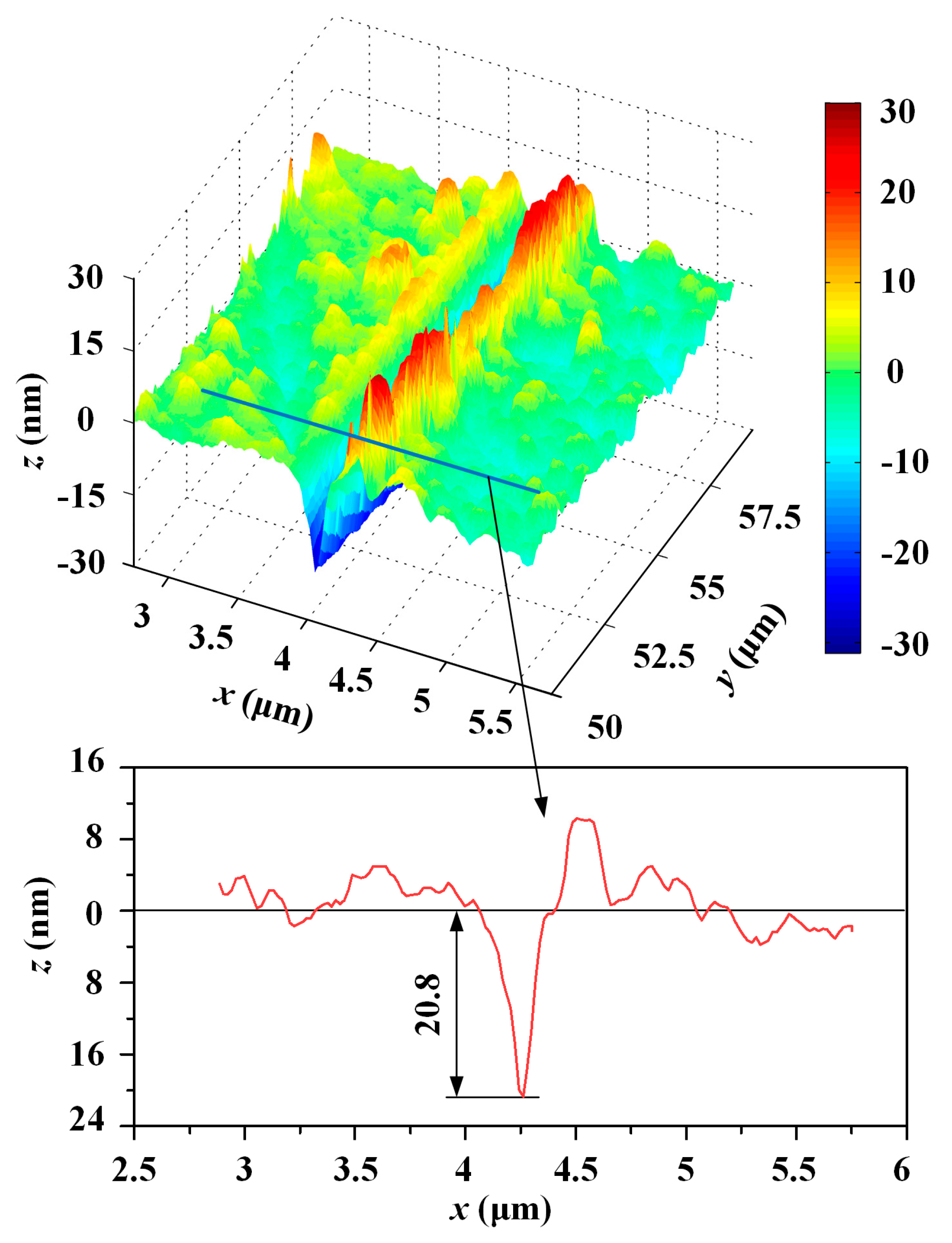
4.2. Analytic Surface Morphology
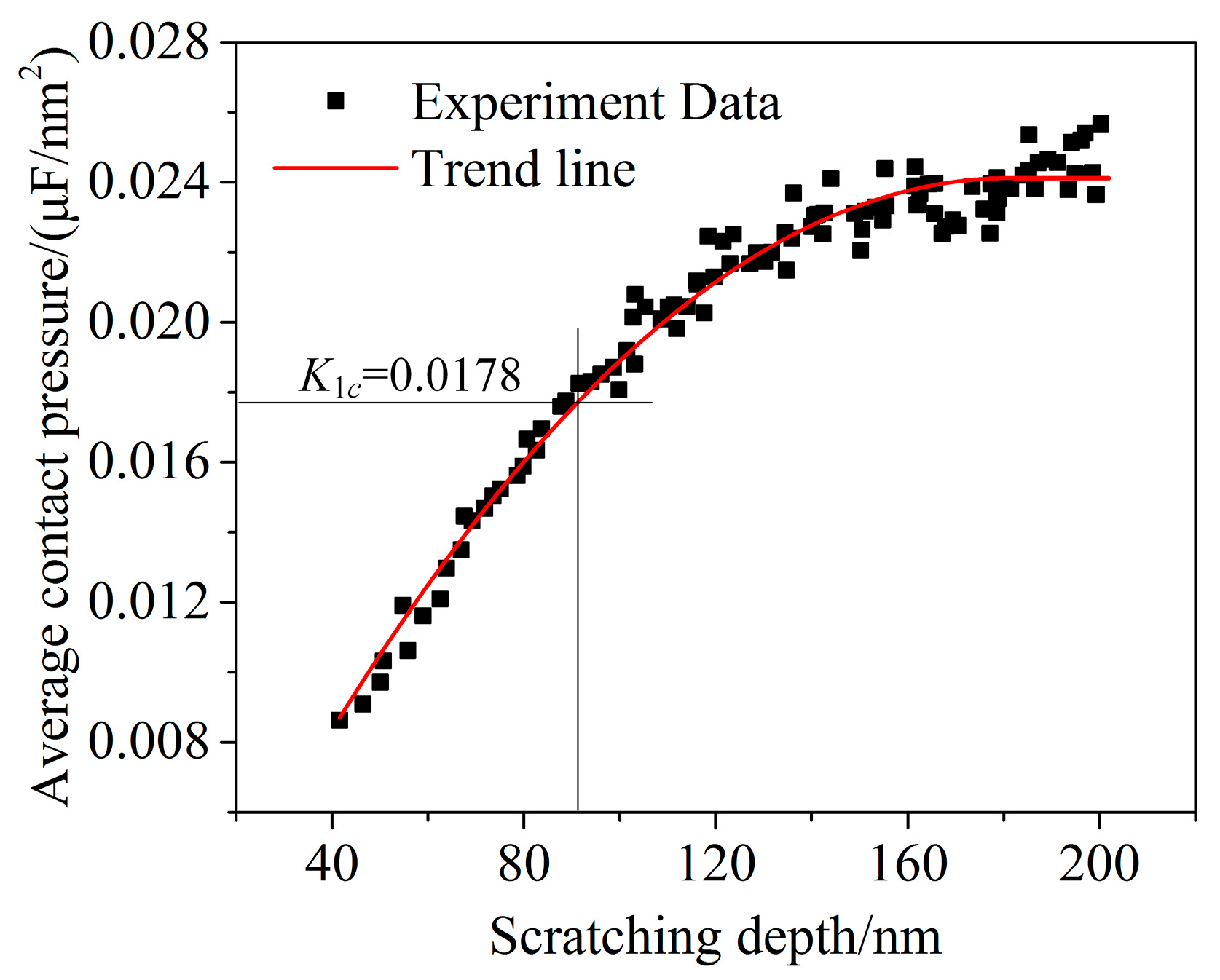
4.3. Comparison of the Critical Depth of Cut between Simulation and Experiments
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goel, S. The current understanding on the diamond machining of silicon carbide. J. Phys. D Appl. Phys. 2014, 47, 243001. [Google Scholar] [CrossRef]
- Choyke, W.J.; Pensl, G. Physical properties of SiC. MRS Bull. 1997, 22, 25–29. [Google Scholar] [CrossRef]
- Miyazaki, H.; Zhou, Y.; Iwakiri, S.; Hirotsuru, H.; Hirao, K.; Fukuda, S.; Izu, N.; Hyuga, H. Improved resistance to thermal fatigue of active metal brazing substrates for silicon carbide power modules using tough silicon nitrides with high thermal conductivity. Ceram. Int. 2018, 44, 8870–8876. [Google Scholar] [CrossRef]
- Han, D.; Mei, H.; Xiao, S.; Dassios, K.G.; Cheng, L. A review on the processing technologies of carbon nanotube/silicon carbide composites. J. Eur. Ceram. Soc. 2018, 38, 3695–3708. [Google Scholar] [CrossRef]
- Robichaud, J.; Guregian, J.J.; Schwalm, M. SiC optics for Earth observing applications. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 10 November 2003; Volume 5151, pp. 53–62. [Google Scholar] [CrossRef]
- Lee, H.S.; Kim, D.I.; An, J.H.; Lee, H.J.; Kim, K.H.; Jeong, H. Hybrid polishing mechanism of single crystal SiC using mixed abrasive slurry (MAS). CIRP Ann. 2010, 59, 333–336. [Google Scholar] [CrossRef]
- Yin, L.; Vancoille, E.Y.J.; Lee, L.C.; Huang, H.; Ramesh, K.; Liu, X.D. High-quality grinding of polycrystalline silicon carbide spherical surfaces. Wear 2004, 256, 197–207. [Google Scholar] [CrossRef]
- Gassilloud, R.; Ballif, C.; Gasser, P.; Buerki, G.; Michler, J. Deformation mechanisms of silicon during nanoscratching. Phys. Status Solidi 2010, 202, 2858–2869. [Google Scholar] [CrossRef]
- Nian, D.; Yiqing, Y.; Wenshan, W.; Xu, X. Analysis of grit interference mechanisms for the double scratching of monocrystalline silicon carbide by coupling the FEM and SPH. Int. J. Mach. Tool. Manuf. 2017, 120, 49–60. [Google Scholar] [CrossRef]
- Swain, M.V. Microfracture about scratches in brittle solids. Proc. Royal Soc. Lond. A Math. Phys. Sci. 1979, 366, 575–597. [Google Scholar] [CrossRef]
- Wasmer, K.; Ballif, C.; Gassilloud, R.; Pouvreau, C.; Rabe, R.; Michler, J.; Breguet, J.-M.; Solletti, J.-M.; Karimi, A.; Schulz, D. Cleavage Fracture of Brittle Semiconductors from the Nanometre to the Centimetre Scale. Adv. Eng. Mater. 2005, 7, 309–317. [Google Scholar] [CrossRef]
- Lawn, B.R.; Swain, M.V. Microfracture beneath point indentations in brittle solids. J. Mater. Sci. 1975, 10, 113–122. [Google Scholar] [CrossRef]
- Bondokov, R.T.; Lashkov, T.; Sudarshan, T.S. Influence of Structural Defects on the Polishing of Silicon Carbide Single Crystal Wafers. Jpn. J. Appl. Phys. 2004, 43, 43–49. [Google Scholar] [CrossRef]
- King, R.F.; Tabor, D. The Strength Properties and Frictional Behaviour of Brittle Solids. Proc. Royal Soc. Lond. A Math. Phys. Sci. 1954, 223, 225–238. [Google Scholar] [CrossRef]
- Agarwal, S.; Rao, P.V. Experimental investigation of surface/subsurface damage formation and material removal mechanisms in SiC grinding. Int. J. Mach. Tool. Manuf. 2008, 48, 698–710. [Google Scholar] [CrossRef]
- Virkar, S.R.; Patten, J.A. Numerical Simulations and Analysis of the Thermal Effects on Silicon Carbide During Ductile Mode Micro-Laser Assisted Machining. In Proceedings of the ASME 2009 International Manufacturing Science and Engineering Conference, West Lafayette, IN, USA, 4–7 October 2009; pp. 409–416. [Google Scholar] [CrossRef]
- Goel, S.; Luo, X.; Comley, P.; Reuben, R.L.; Cox, A. Brittle–ductile transition during diamond turning of single crystal silicon carbide. Int. J. Mach. Tool. Manuf. 2013, 65, 15–21. [Google Scholar] [CrossRef]
- Shujuan, L.; Aofei, T.; Yong, L.; Wang, J.; Cui, D.; Landers, R.G. Analytical Force Modeling of Fixed Abrasive Diamond Wire Saw Machining With Application to SiC Monocrystal Wafer Processing. J. Manuf. Sci. Eng. 2017, 139, 041003. [Google Scholar] [CrossRef]
- Cao, J.; Wu, Y.; Lu, D.; Fujimoto, M.; Nomura, M. Material removal behavior in ultrasonic-assisted scratching of sic ceramics with a single diamond tool. Int. J. Mach. Tool. Manuf. 2014, 79, 49–61. [Google Scholar] [CrossRef]
- Patten, J.; Gao, W.; Yasuto, K. Ductile regime nanomachining of single-crystal silicon carbide. J. Manuf. Sci. Eng. 2005, 127, 522–532. [Google Scholar] [CrossRef]
- Mussi, A.; Rabier, J.; Thilly, L.; Demenet, J.L. Plasticity and deformation microstructure of 4h-SiC below the brittle-to-ductile transition. Phys. Status Solidi C 2011, 4, 2929–2933. [Google Scholar] [CrossRef]
- Xie, J.; Li, Q.; Sun, J.X.; Li, Y.H. Study on ductile-mode mirror grinding of sic ceramic freeform surface using an elliptical torus-shaped diamond wheel. J. Mater. Process Tech. 2015, 222, 422–433. [Google Scholar] [CrossRef]
- Bifano, T.G.; Dow, T.A.; Scattergood, R.O. Ductile Regime Grinding A New Technology for Machining Brittle Materials. J. Eng. Ind. 1991, 113, 184–189. [Google Scholar] [CrossRef]
- Xiao, G.; To, S.; Zhang, G. The mechanism of ductile deformation in ductile regime machining of 6H SiC. Comput. Mater. Sci. 2015, 98, 178–188. [Google Scholar] [CrossRef]
- Wang, P.; Ge, P.; Li, Z.; Ge, M.; Gao, Y. A scratching force model of diamond abrasive particles in wire sawing of single crystal sic. Mater. Sci. Semicon. Proc. 2017, 68, 21–29. [Google Scholar] [CrossRef]
- Le Houérou, V.; Sangleboeuf, J.C.; Dériano, S.; Rouxel, T.; Duisit, G. Surface damage of soda–lime–silica glasses: Indentation scratch behavior. J. Non-Cryst. Solids. 2003, 316, 54–63. [Google Scholar] [CrossRef]
- Popov, V.L. Contact Mechanics and Friction: Physical Principles and Applications; Springer: Heidelberg/Dordrecht, Germany; London, UK; New York, NY, USA, 2010; pp. 56–62. [Google Scholar]
- Son, S.M.; Han, S.L.; Ahn, J.H. Effects of the friction coefficient on the minimum cutting thickness in micro cutting. Int. J. Mach. Tool. Manuf. 2005, 45, 529–535. [Google Scholar] [CrossRef]
- Rowe, W.B. Principles of Modern Grinding Technology; Elsevier Inc.: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Lawn, B.R. Fracture of Brittle Solids-Second Edition; Cambridge University Press: Cambridge, UK, 1993; pp. 71–86. [Google Scholar]
- Veld, A.J.G.O.H.; Veldkamp, J.D.B. Mechanical and microscopical investigation of SiC whiskers. Fibre Sci. Technol. 1970, 2, 269–281. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987; pp. 96–122. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Zhang, F.; Meng, B.; Geng, Y.; Zhang, Y.; Li, Z. Friction behavior in nanoscratching of reaction bonded silicon carbide ceramic with Berkovich and sphere indenters. Tribol. Int. 2016, 97, 21–30. [Google Scholar] [CrossRef]
- Zhao, X.; Langford, R.M.; Shapiro, I.P.; Xiao, P. Onset Plastic Deformation and Cracking Behavior of Silicon Carbide under Contact Load at Room Temperature. J. Am. Ceram. Soc. 2011, 94, 3509–3514. [Google Scholar] [CrossRef]
- Meng, B.; Zhang, F.; Li, Z. Deformation and removal characteristics in nanoscratching of 6H-SiC with berkovich indenter. Mater. Sci. Semicon. Proc. 2015, 31, 160–165. [Google Scholar] [CrossRef]
- Ravindra, D.; Virkar, S.; Patten, J. Ductile Mode Micro Laser Assisted Machining of Silicon Carbide. In Properties and Applications of Silicon Carbide; Gerhardt, R., Ed.; In Tech: London, UK, 2011. [Google Scholar]
- Bhattacharya, B.; Patten, J.A.; Jacob, J. Ductile Regime Nano-Machining of Polycrystalline Silicon Carbide(6H). In Proceedings of the 2005 Annual Meeting ASPE, Norfolk, VA, USA, 9–14 October 2005; Volume 37, pp. 403–406. [Google Scholar]
- Jacob, J.; Patten, J.A.; Bhattacharya, B.; Couey, J.A.; Marsh, E.R. Determination of the ductile to brittle transition and critical depth of cut in 6H-silicon carbide through fly cutting. In Proceedings of the 2005 Annual Meeting ASPE, Norfolk, VA, USA, 9–14 October 2005; Volume 37, pp. 472–475. [Google Scholar]
- Tanaka, H.; Shimada, S. Damage-free machining of monocrystalline silicon carbide. CIRP Ann. 2013, 62, 55–58. [Google Scholar] [CrossRef]
- Xu, N.; Han, W.; Wang, Y.; Li, J.; Shan, Z. Nanoscratching of copper surface by CeO2. Acta Mater. 2017, 124, 343–350. [Google Scholar] [CrossRef]


| Test Parameters | Unit | Values |
|---|---|---|
| Pre-scan/post-scan load | mN | 0.1 |
| Loading range | mN | 0.1–80 |
| Scratch length | μm | 250 |
| Scratch velocity | μm/s | 4 |
| Load (mN) | Indenter Height (nm) | Contact Area (nm2) |
|---|---|---|
| 20 | 164.5 | 2.2053 × 106 |
| 40 | 274.2 | 4.2905 × 106 |
| 60 | 379.6 | 6.4158 × 106 |
| 80 | 460.1 | 8.3211 × 106 |
| 100 | 522.9 | 1.0426 × 107 |
| 120 | 578.6 | 1.3032 × 107 |
| 140 | 625.4 | 1.4037 × 107 |
| 160 | 676.5 | 1.5642 × 107 |
| 180 | 750.4 | 1.8247 × 107 |
| Test Number | Critical Depth of Cut (nm) |
|---|---|
| 1 | 92 |
| 2 | 93 |
| 3 | 90 |
| Average value | 91.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, P.; Li, S.; Li, Y. Modeling and Experiment of the Critical Depth of Cut at the Ductile–Brittle Transition for a 4H-SiC Single Crystal. Micromachines 2019, 10, 382. https://doi.org/10.3390/mi10060382
Chai P, Li S, Li Y. Modeling and Experiment of the Critical Depth of Cut at the Ductile–Brittle Transition for a 4H-SiC Single Crystal. Micromachines. 2019; 10(6):382. https://doi.org/10.3390/mi10060382
Chicago/Turabian StyleChai, Peng, Shujuan Li, and Yan Li. 2019. "Modeling and Experiment of the Critical Depth of Cut at the Ductile–Brittle Transition for a 4H-SiC Single Crystal" Micromachines 10, no. 6: 382. https://doi.org/10.3390/mi10060382
APA StyleChai, P., Li, S., & Li, Y. (2019). Modeling and Experiment of the Critical Depth of Cut at the Ductile–Brittle Transition for a 4H-SiC Single Crystal. Micromachines, 10(6), 382. https://doi.org/10.3390/mi10060382





