Second-Order Vector Mode Propagation in Hollow-Core Antiresonant Fibers
Abstract
1. Introduction
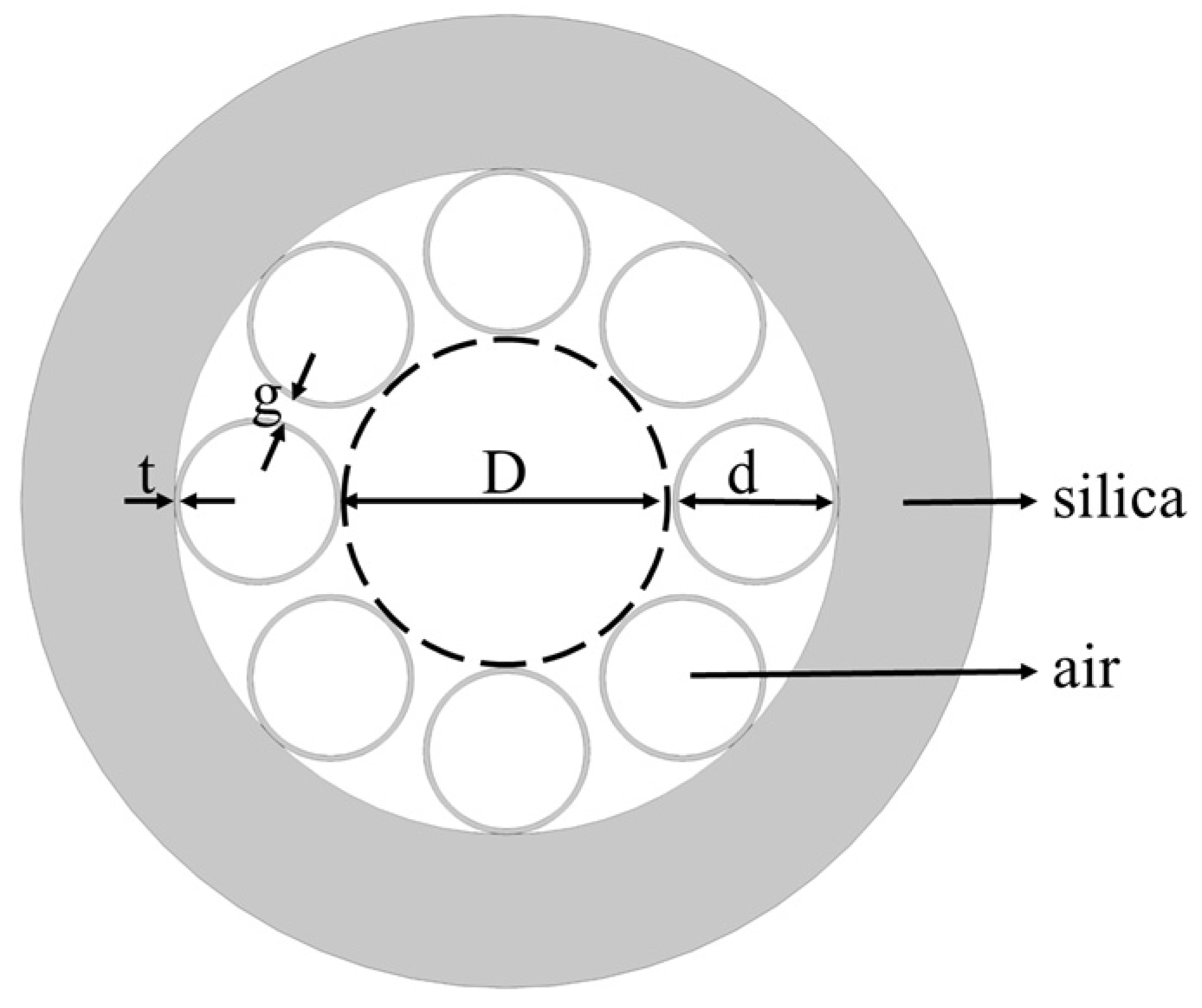
2. Fiber Structures and Modal Engineering Conception
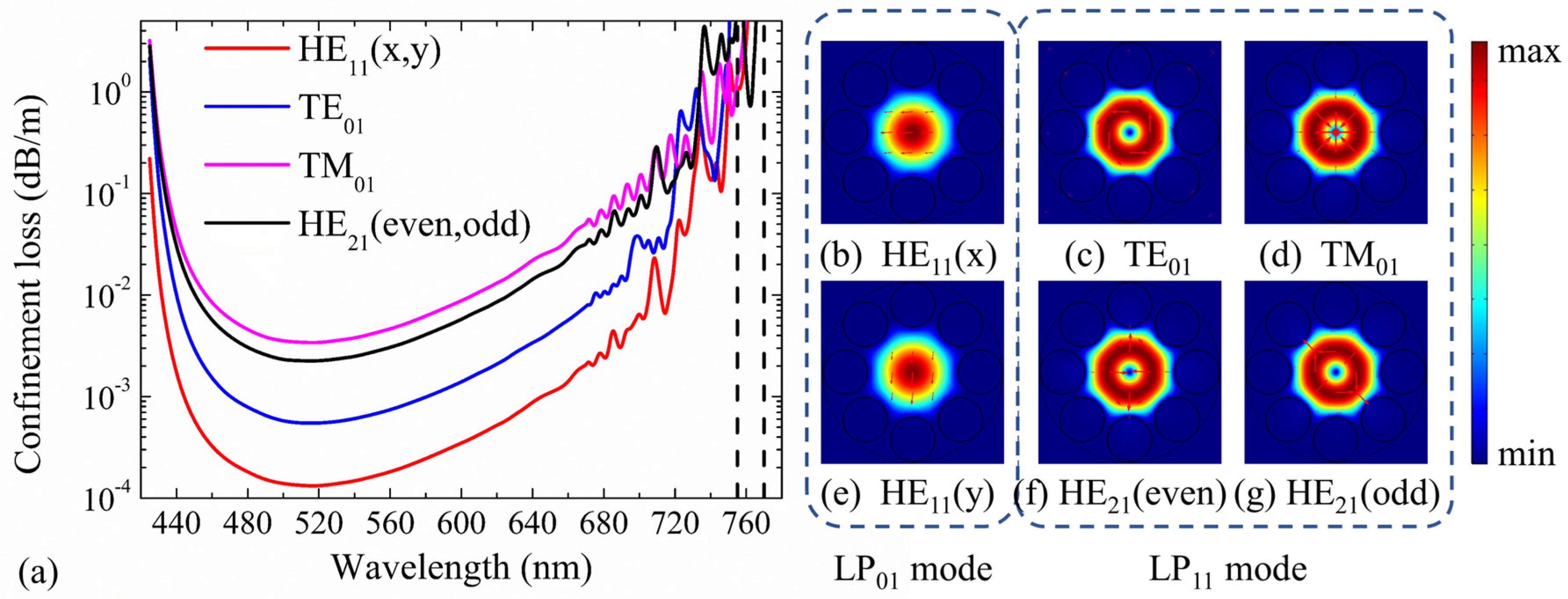
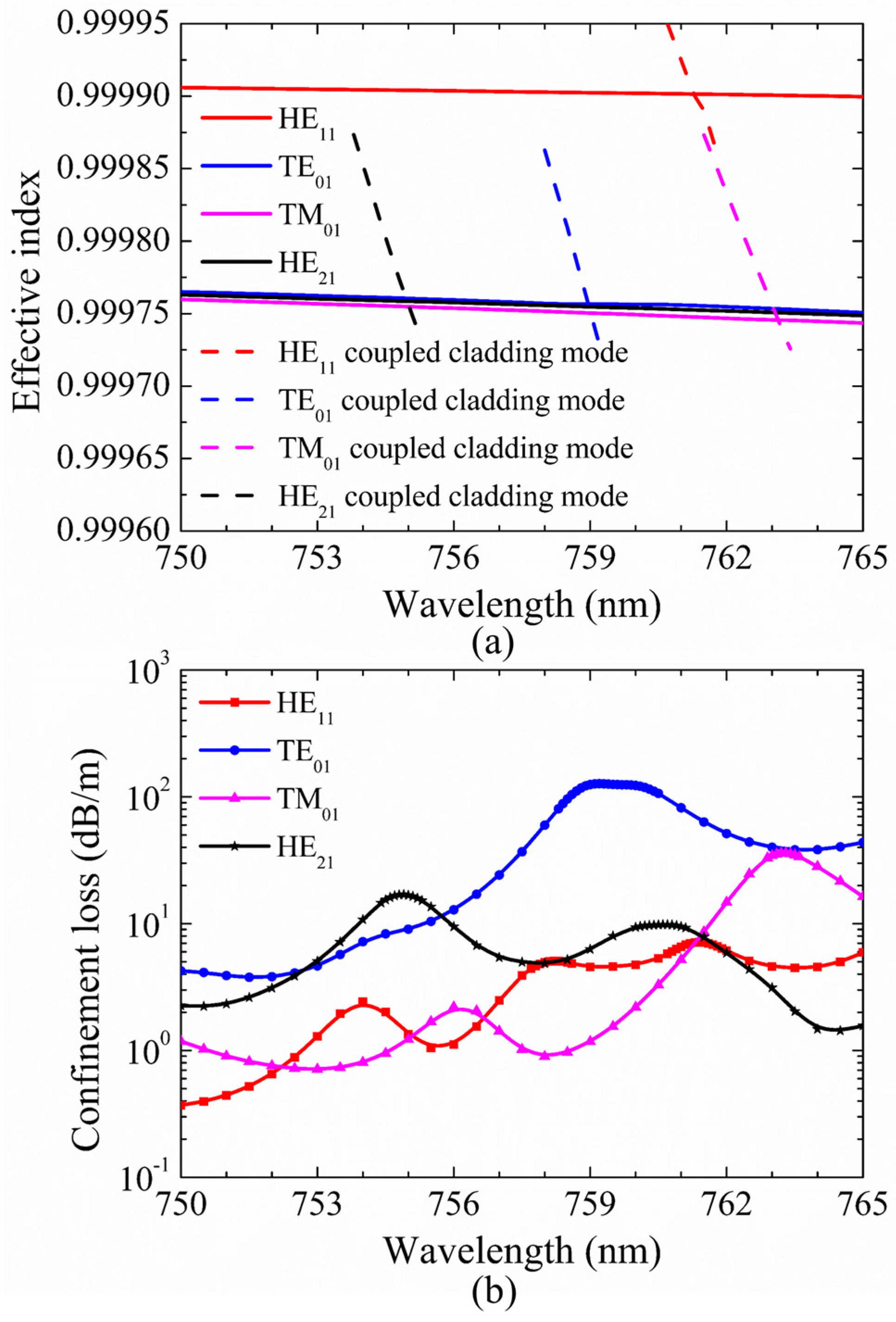
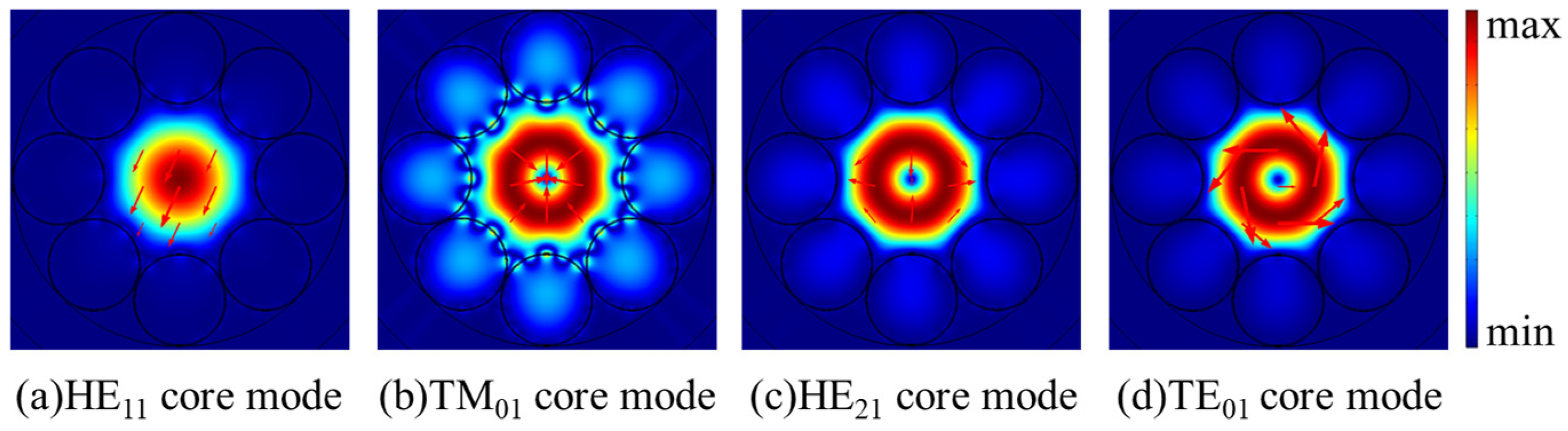
3. Characteristics of Second-Order Modes in HC-ARFs and Discussion
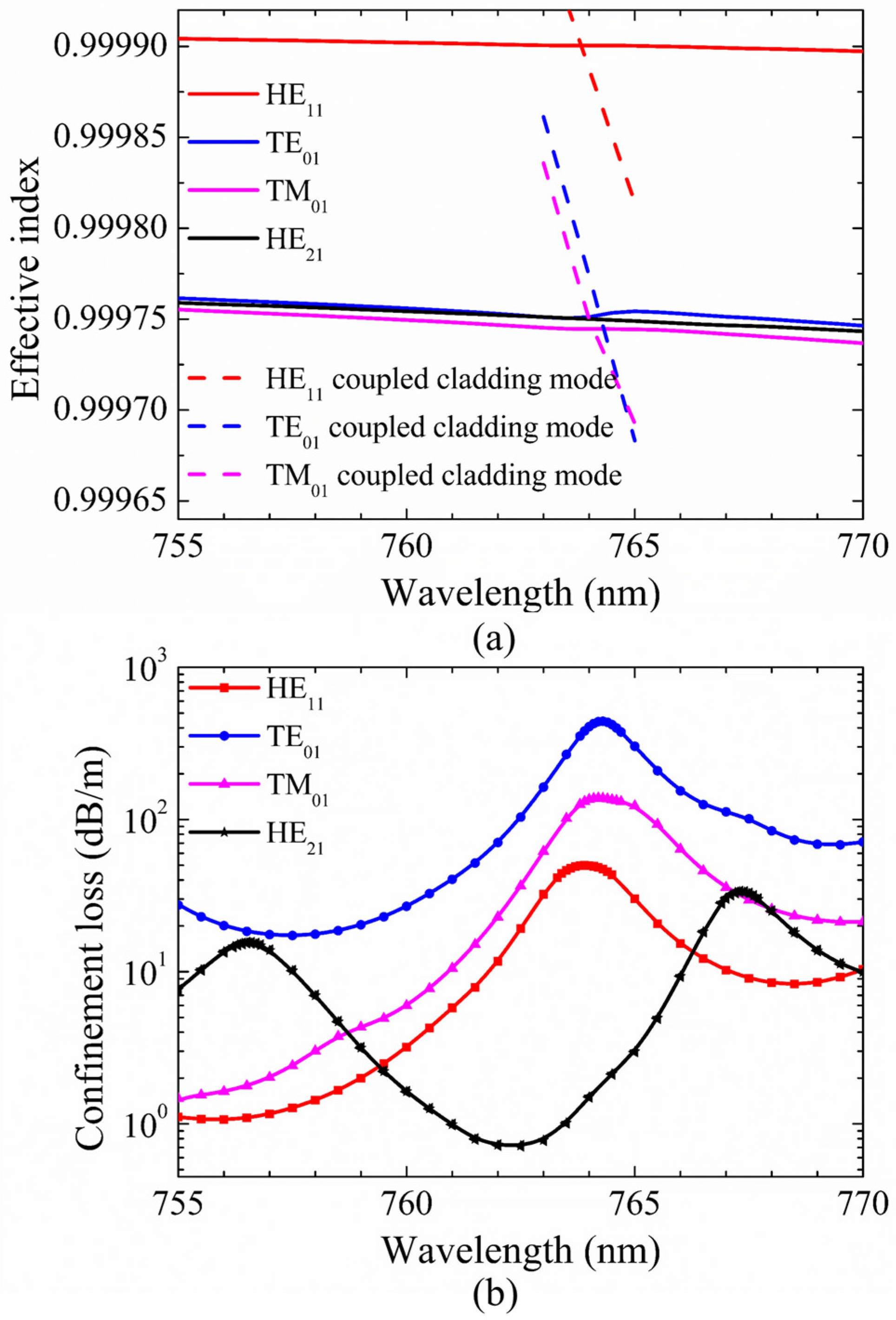
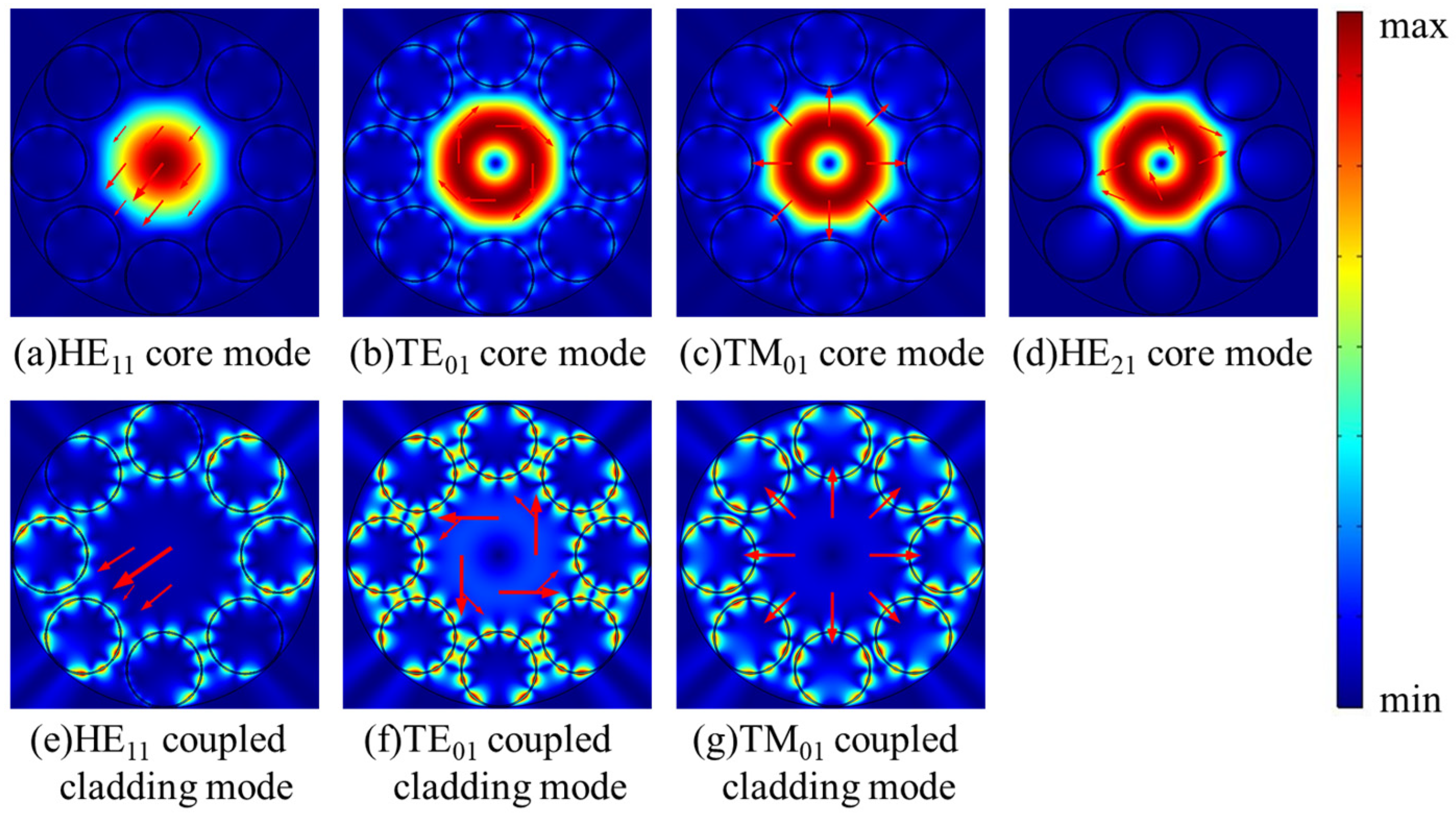
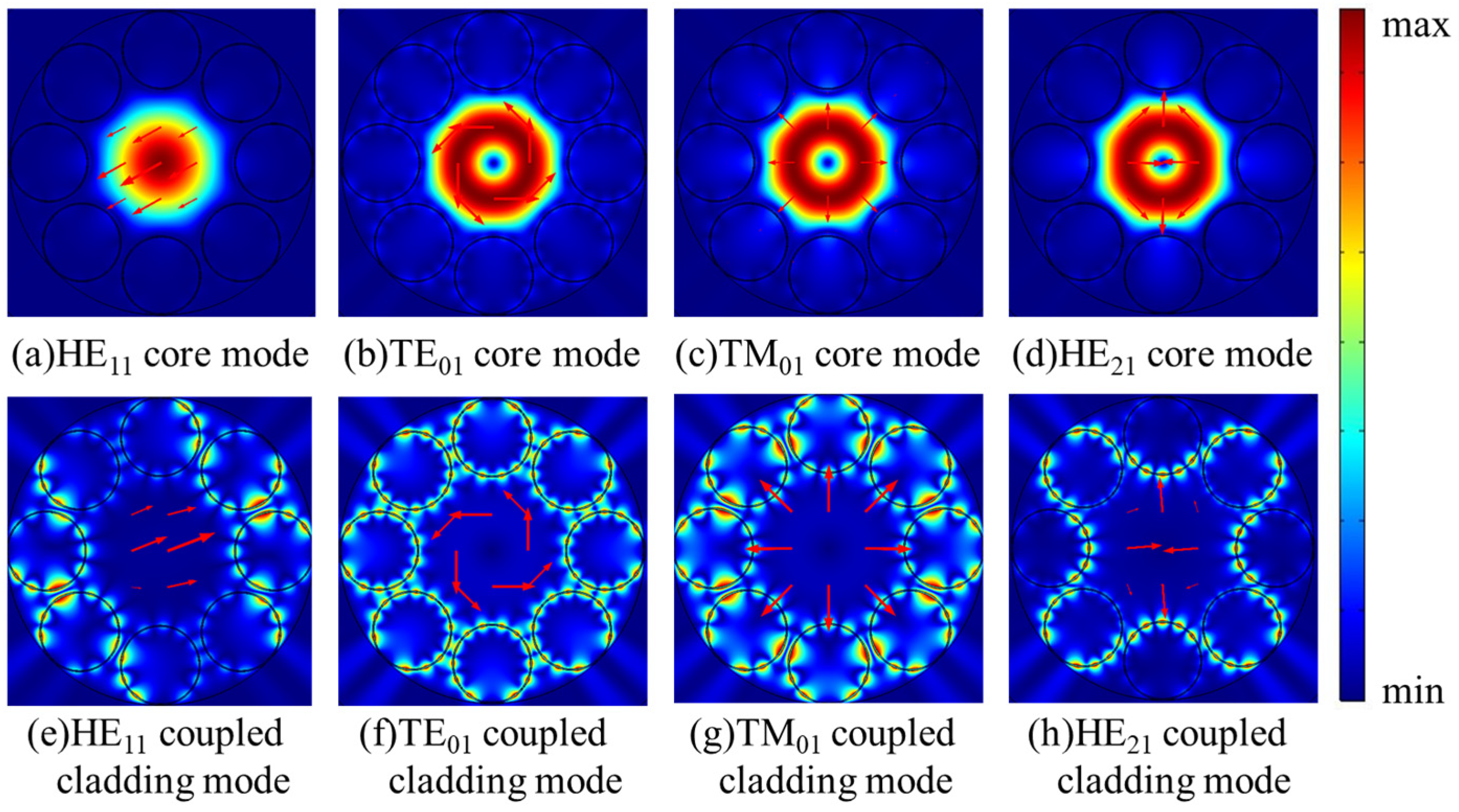
3.1. Characteristics of Only HE21 Mode Propagation
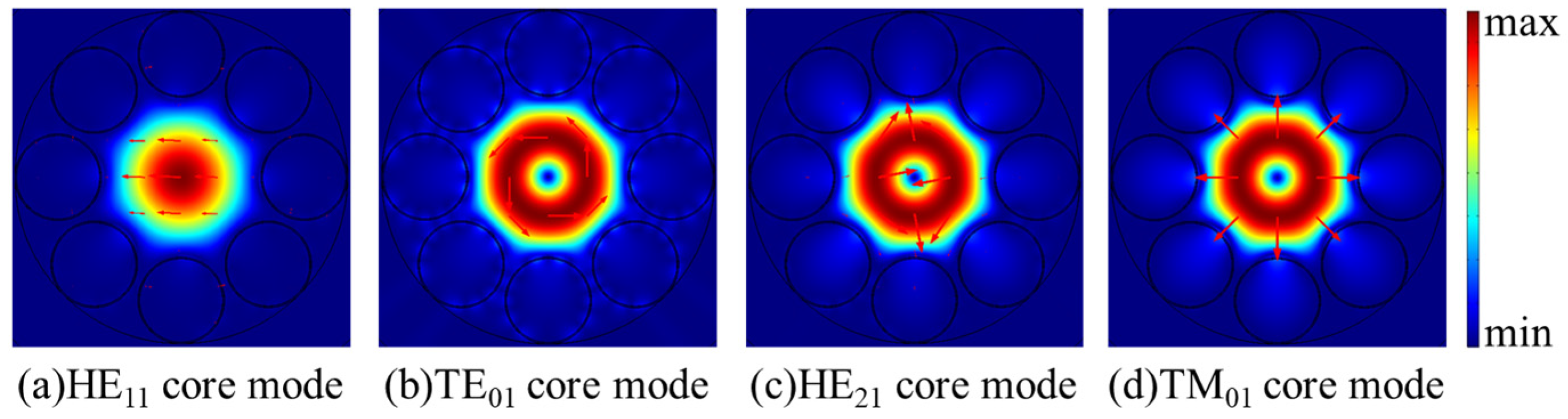
3.2. Characteristics of Only TM01 Mode Propagation
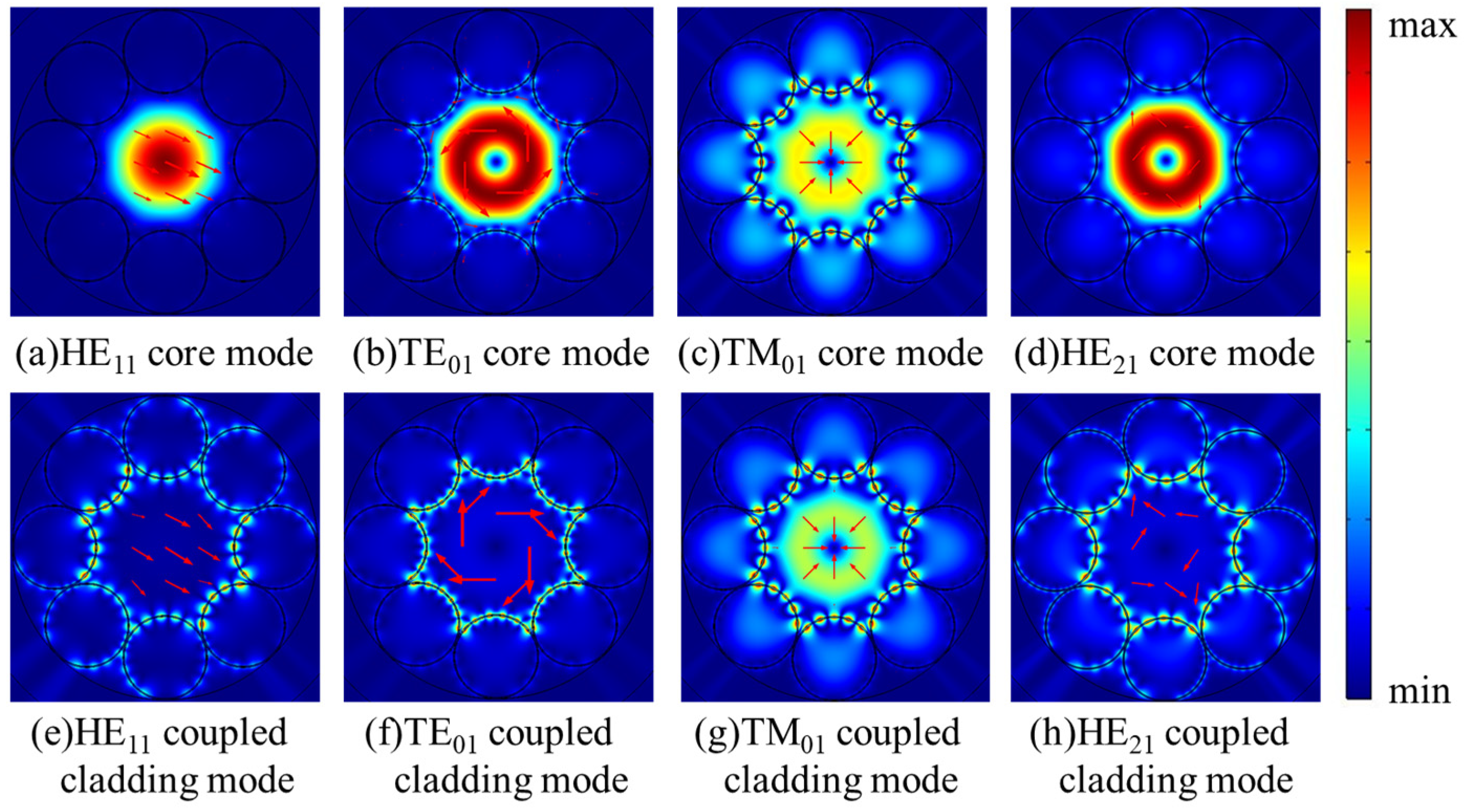
3.3. Characteristics of Only TE01 Mode Propagation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yu, F.; Knight, J.C. Negative curvature hollow-core optical fiber. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 4400610. [Google Scholar] [CrossRef]
- Wei, C.; Weiblen, R.J.; Menyuk, C.R.; Hu, J. Negative curvature fibers. Adv. Opt. Photonics 2017, 9, 504–561. [Google Scholar] [CrossRef]
- Poletti, F. Nested antiresonant nodeless hollow core fiber. Opt. Express 2014, 22, 23807–23828. [Google Scholar] [CrossRef] [PubMed]
- Hayes, J.R.; Sandoghchi, S.R.; Bradley, T.D.; Liu, Z.; Slavík, R.; Gouveia, M.A.; Wheeler, N.; Jasion, G.; Chen, Y.; Fokoua, E.N.; et al. Antiresonant hollow core fiber with an octave spanning bandwidth for short haul data communications. J. Lightwave Technol. 2017, 35, 437–442. [Google Scholar] [CrossRef]
- Jaworski, P.; Yu, F.; Maier, R.J.; Wadsworth, W.J.; Knight, J.C.; Shephard, J.D.; Hand, D.P. Picosecond and nanosecond pulse delivery through a hollow-core negative curvature fiber for micro-machining applications. Opt. Express 2013, 21, 22742–22753. [Google Scholar] [CrossRef] [PubMed]
- Urich, A.; Maier, R.R.J.; Yu, F.; Knight, J.C.; Hand, D.P.; Shephard, J.D. Flexible delivery of Er:YAG radiation at 2.94 µm with negative curvature silica glass fibers: A new solution for minimally invasive surgical procedures. Biomed. Opt. Express 2013, 4, 193–205. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Cann, M.; Brunton, A.; Wadsworth, W.; Knight, J. Single-mode solarization-free hollow-core fiber for ultraviolet pulse delivery. Opt. Express 2018, 26, 10879–10887. [Google Scholar] [CrossRef]
- Wang, Z.; Belardi, W.; Yu, F.; Wadsworth, W.J.; Knight, J.C. Efficient diode-pumped mid-infrared emission from acetylene-filled hollow-core fiber. Opt. Express 2014, 22, 21872–21878. [Google Scholar] [CrossRef]
- Hao, Y.; Xiao, L.; Benabid, F. Optimized design of unsymmetrical gap nodeless hollow core fibers for optofluidic applications. J. Lightwave Technol. 2018, 36, 3162–3168. [Google Scholar] [CrossRef]
- Monfared, Y.E. Transient dynamics of stimulated Raman scattering in gas-filled hollow-core photonic crystal fibers. Adv. Mater. Sci. Eng. 2018, 8951495. [Google Scholar] [CrossRef]
- Monfared, Y.E.; Ponomarenko, S.A. Non-Gaussian statistics of extreme events in stimulated Raman scattering: The role of coherent memory and source noise. Phys. Rev. A 2017, 96, 043817. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Abeeluck, A.K.; Headley, C.; Eggleton, B.J. Antiresonant reflecting photonic crystal optical waveguides. Opt. Lett. 2002, 27, 1592–1594. [Google Scholar] [CrossRef] [PubMed]
- Debord, B.; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.M.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gerome, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217. [Google Scholar] [CrossRef]
- Lee, E.; Luo, J.; Sun, B.; Ramalingam, V.; Zhang, Y.; Wang, Q.; Yu, F.; Yu, X. Flexible single-mode delivery of a high-power 2 μm pulsed laser using an antiresonant hollow-core fiber. Opt. Lett. 2018, 43, 2732–2735. [Google Scholar] [CrossRef]
- Bradley, T.D.; Hayes, J.R.; Chen, Y.; Jasion, G.T.; Sandoghchi, S.R.; Slavík, R.; Fokoua, E.N.; Bawn, S.; Sakr, H.; Davidson, I.A.; et al. Record low-loss 1.3 dB/km data transmitting antiresonant hollow core fibre. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Liu, X.; Ding, W.; Wang, Y.Y.; Gao, S.; Cao, L.; Feng, X.; Wang, P. Characterization of a liquid-filled nodeless anti-resonant fiber for biochemical sensing. Opt. Lett. 2017, 42, 863–866. [Google Scholar] [CrossRef] [PubMed]
- Uebel, P.; Günendi, M.C.; Frosz, M.H.; Ahmed, G.; Edavalath, N.N.; Ménard, J.-M.; Russell, P.S.J. Broadband robustly single-mode hollow-core PCF by resonant filtering of higher-order modes. Opt. Lett. 2016, 41, 1961–1964. [Google Scholar] [CrossRef]
- Wei, C.; Kuis, R.A.; Chenard, F.; Menyuk, C.R.; Hu, J. Higher-order mode suppression in chalcogenide negative curvature fibers. Opt. Express 2015, 23, 15824–15832. [Google Scholar] [CrossRef]
- Ge, A.; Meng, F.; Li, Y.; Liu, B.; Hu, M. Higher-order mode suppression in antiresonant nodeless hollow-core fibers. Micromachines 2019, 10, 128. [Google Scholar] [CrossRef]
- Lopez-Galmiche, G.; Eznaveh, Z.S.; Antonio-Lopez, J.E.; Benitez, A.M.V.; Asomoza, J.R.; Mondragon, J.S.; Gonnet, C.; Sillard, P.; Li, G.; Schülzgen, A.; et al. Few-mode erbium-doped fiber amplifier with photonic lantern for pump spatial mode control. Opt. Lett. 2016, 41, 2588–2591. [Google Scholar] [CrossRef]
- Sillard, P.; Bigot-Astruc, M.; Molin, D. Few-mode fibers for mode-division-multiplexed systems. J. Lightwave Technol. 2014, 32, 2824–2829. [Google Scholar] [CrossRef]
- Li, A.; Wang, Y.; Hu, Q.; Shieh, W. Few-mode fiber based optical sensors. Opt. Express 2015, 23, 1139–1150. [Google Scholar] [CrossRef]
- Larsen, S.H.M.; Rishøj, L.S.; Rottwitt, K. All-fiber Raman probe using higher order modes. In Proceedings of the Advanced Photonics Congress: Optical Sensors, Rio Grande, PR, USA, 14–17 July 2013. [Google Scholar]
- Ramachandran, S.; Fini, J.M.; Mermelstein, M.; Nicholson, J.W.; Ghalmi, S.; Yan, M.F. Ultra-large effective-area, higher-order mode fibers: A new strategy for high-power lasers. Laser Photonics Rev. 2008, 2, 429–448. [Google Scholar] [CrossRef]
- Van Howe, J.; Lee, J.H.; Zhou, S.; Wise, F.; Xu, C.; Ramachandran, S.; Ghalmi, S.; Yan, M.F. Demonstration of soliton self-frequency shift below 1300 nm in higher-order-mode, solid silica-based fiber. Opt. Lett. 2007, 32, 340–342. [Google Scholar] [CrossRef]
- Ramachandran, S.; Kristensen, P. Optical vortices in fiber. Nanophotonics 2013, 2, 455–474. [Google Scholar] [CrossRef]
- Gu, M.; Kang, H.; Li, X. Breaking the diffraction-limited resolution barrier in fiber-optical two-photon fluorescence endoscopy by an azimuthally-polarized beam. Sci. Rep. 2014, 4, 3627. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Shvedov, V.G.; Krolikowski, W. The role of light-induced nanostructures in femtosecond laser micromachining with vector and scalar pulses. Opt. Express 2013, 21, 12651–12656. [Google Scholar] [CrossRef]
- Peng, F.; Yao, B.; Yan, S.; Zhao, W.; Lei, M. Trapping of low-refractive-index particles with azimuthally polarized beam. J. Opt. Soc. Am. B. 2009, 26, 2242–2247. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.M.; Zhu, L.; Wang, A.D.; Chen, S.; Klitis, C.; Du, C.; Mo, Q.; Sorel, M.; Yu, S.; et al. Direct fiber vector eigenmode multiplexing transmission seeded by integrated optical vortex emitters. Light Sci. Appl. 2018, 7, 17148. [Google Scholar] [CrossRef]
- Yanai, A.; Levy, U. Plasmonic focusing with a coaxial structure illuminated by radially polarized light. Opt. Express 2009, 17, 924–932. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Yang, K.; Liu, Y.; Wang, Z.; Li, Y.; Han, Y.; Zhang, H. Twist sensor based on long period grating and tilted bragg grating written in few-mode fibers. IEEE Photonics J. 2018, 10, 7102708. [Google Scholar] [CrossRef]
- Pureur, V.; Knight, J.C.; Kuhlmey, B.T. Higher order guided mode propagation in solid-core photonic bandgap fibers. Opt. Express 2010, 18, 8906–8915. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, G.; Chen, Y.; Hou, Z.; Xia, C.; Yuan, J.; Zhang, W. Suppression of the fundamental mode in a dual-mode photonic crystal fiber. Opt. Commun. 2015, 336, 235–239. [Google Scholar] [CrossRef]
- Chen, M.Y.; Chiang, K.S. Mode-selective characteristics of an optical fiber with a high-index core and a photonic bandgap cladding. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 4900307. [Google Scholar] [CrossRef]
- Digonnet, M.J.F.; Kim, H.K.; Kino, G.S.; Fan, S. Understanding air-core photonic-bandgap fibers: Analogy to conventional fibers. J. Lightwave Technol. 2005, 23, 4169–4177. [Google Scholar] [CrossRef]
- Osório, J.H.; Chafer, M.; Debord, B.; Giovanardi, F.; Cordier, M.; Maurel, M.; Delahaye, F.; Amrani, F.; Vincetti, L.; Gérôme, F.; et al. Tailoring modal properties of inhibited-coupling guiding fibers by cladding modification. Sci. Rep. 2019, 9, 1376. [Google Scholar] [CrossRef]
- Meier, M.; Romano, V.; Feurer, T. Material processing with pulsed radially and azimuthally polarized laser radiation. Appl. Phys. A. 2007, 86, 329–334. [Google Scholar] [CrossRef]
- Zhan, Q. Radiation forces on a dielectric sphere produced by highly focused cylindrical vector beams. J. Opt. A Pure Appl. Opt. 2003, 5, 229–232. [Google Scholar] [CrossRef]
- Youngworth, K.S.; Brown, T.G. Focusing of high numerical aperture cylindrical vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef]
- Wei, C.; Menyuk, C.R.; Hu, J. Impact of cladding tubes in chalcogenide negative curvature fibers. IEEE Photonics J. 2016, 8, 2200509. [Google Scholar] [CrossRef]
- Malitson, I. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.; Chen, H. Two kinds of polarization filter based on photonic crystal fiber with nanoscale gold film. IEEE Photonics J. 2015, 7, 2700210. [Google Scholar] [CrossRef]
- Michieletto, M.; Lyngsø, J.K.; Jakobsen, C.; Lægsgaard, J.; Bang, O.; Alkeskjold, T.T. Hollow-core fibers for high power pulse delivery. Opt. Express 2016, 24, 7103–7119. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Xiao, L. Second-Order Vector Mode Propagation in Hollow-Core Antiresonant Fibers. Micromachines 2019, 10, 381. https://doi.org/10.3390/mi10060381
Li L, Xiao L. Second-Order Vector Mode Propagation in Hollow-Core Antiresonant Fibers. Micromachines. 2019; 10(6):381. https://doi.org/10.3390/mi10060381
Chicago/Turabian StyleLi, Lili, and Limin Xiao. 2019. "Second-Order Vector Mode Propagation in Hollow-Core Antiresonant Fibers" Micromachines 10, no. 6: 381. https://doi.org/10.3390/mi10060381
APA StyleLi, L., & Xiao, L. (2019). Second-Order Vector Mode Propagation in Hollow-Core Antiresonant Fibers. Micromachines, 10(6), 381. https://doi.org/10.3390/mi10060381




