3-D Design and Simulation of a Piezoelectric Micropump
Abstract
1. Introduction
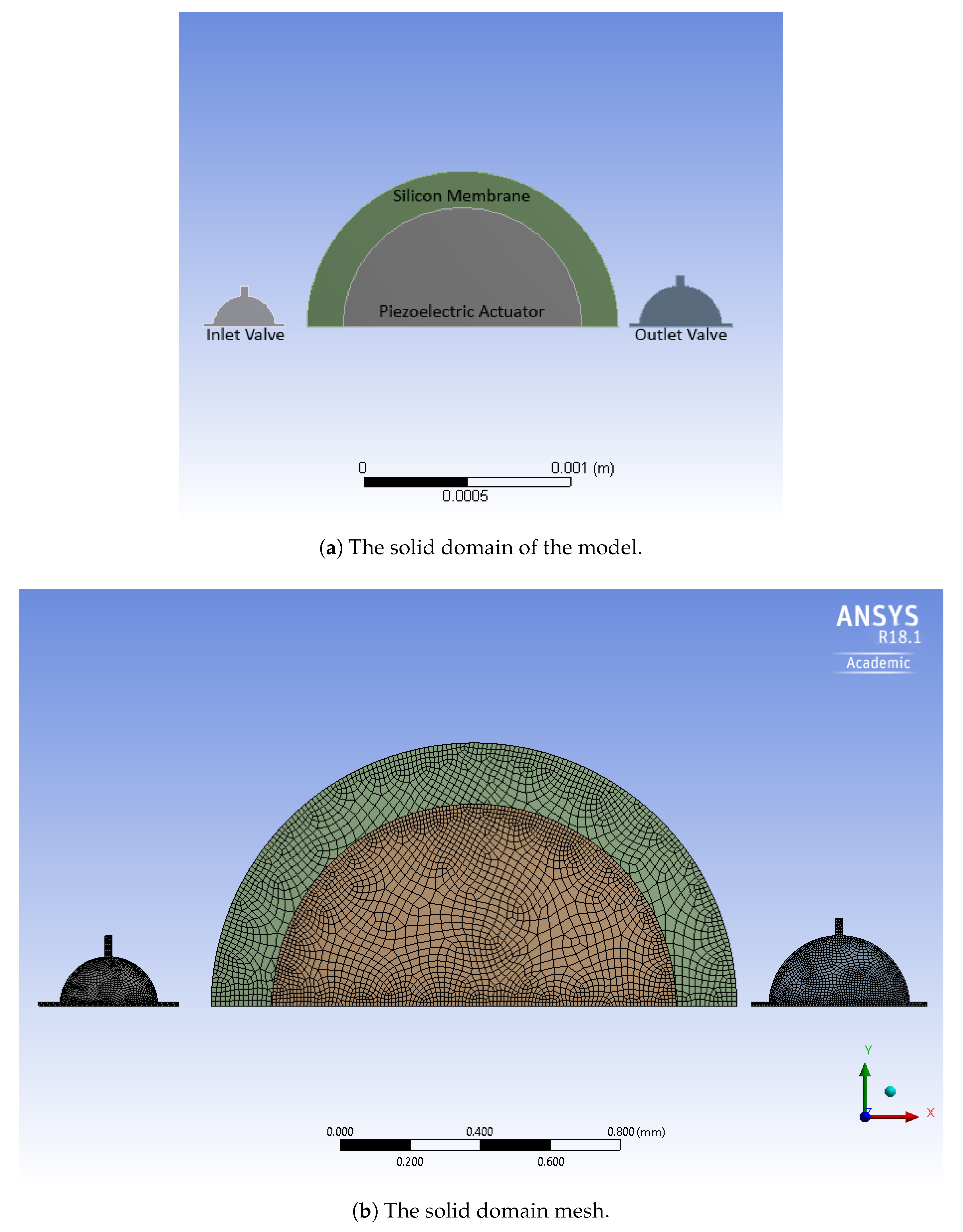
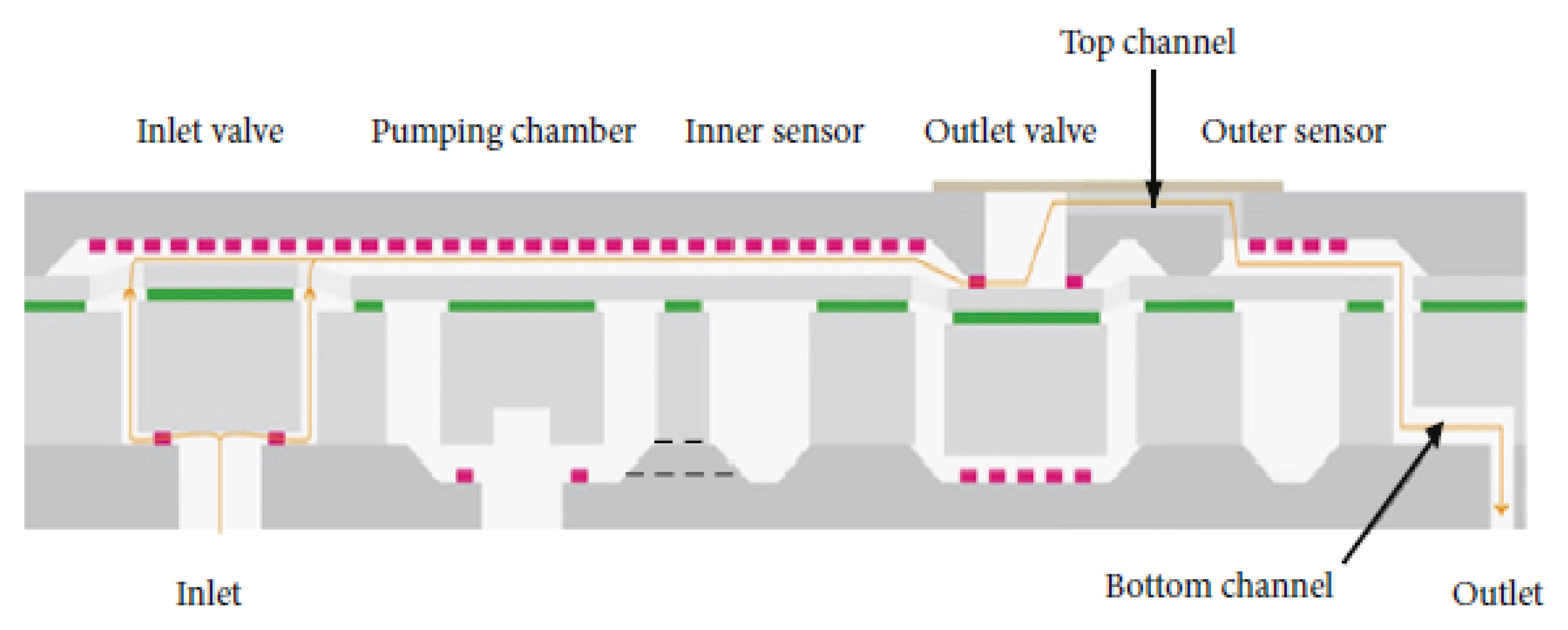
2. Description of the Proposed Layout
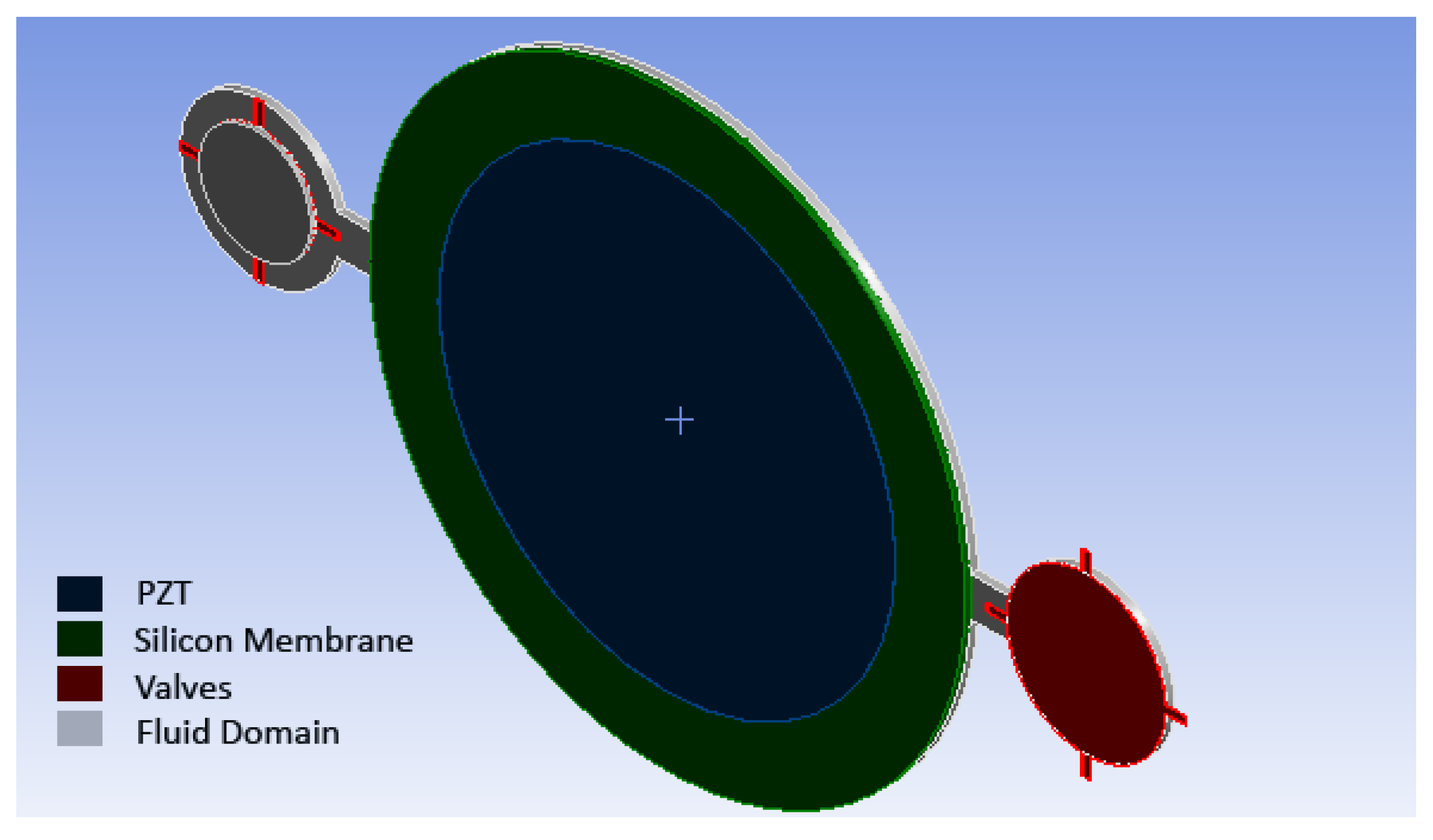
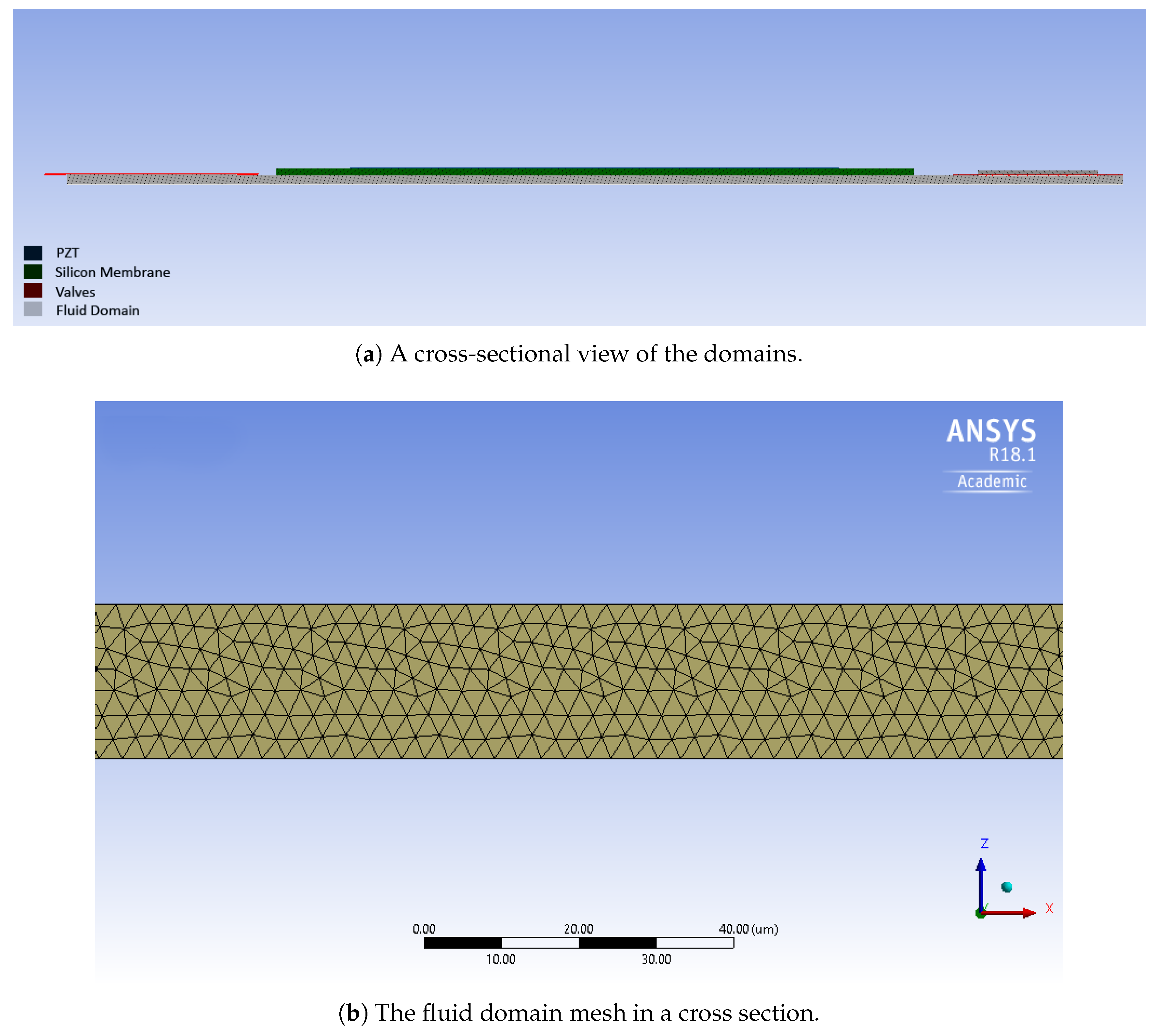
3. The Three-Dimensional Model
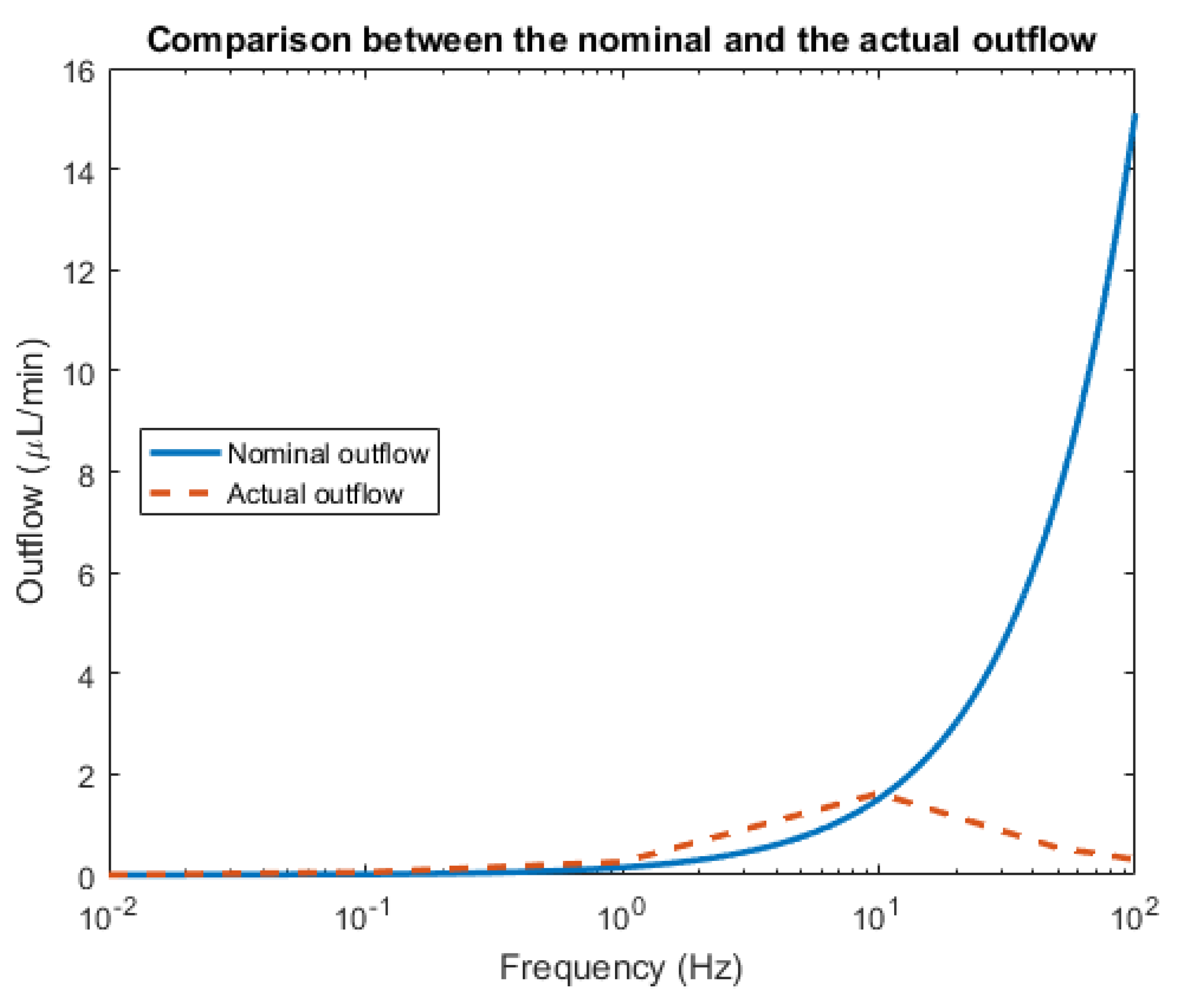
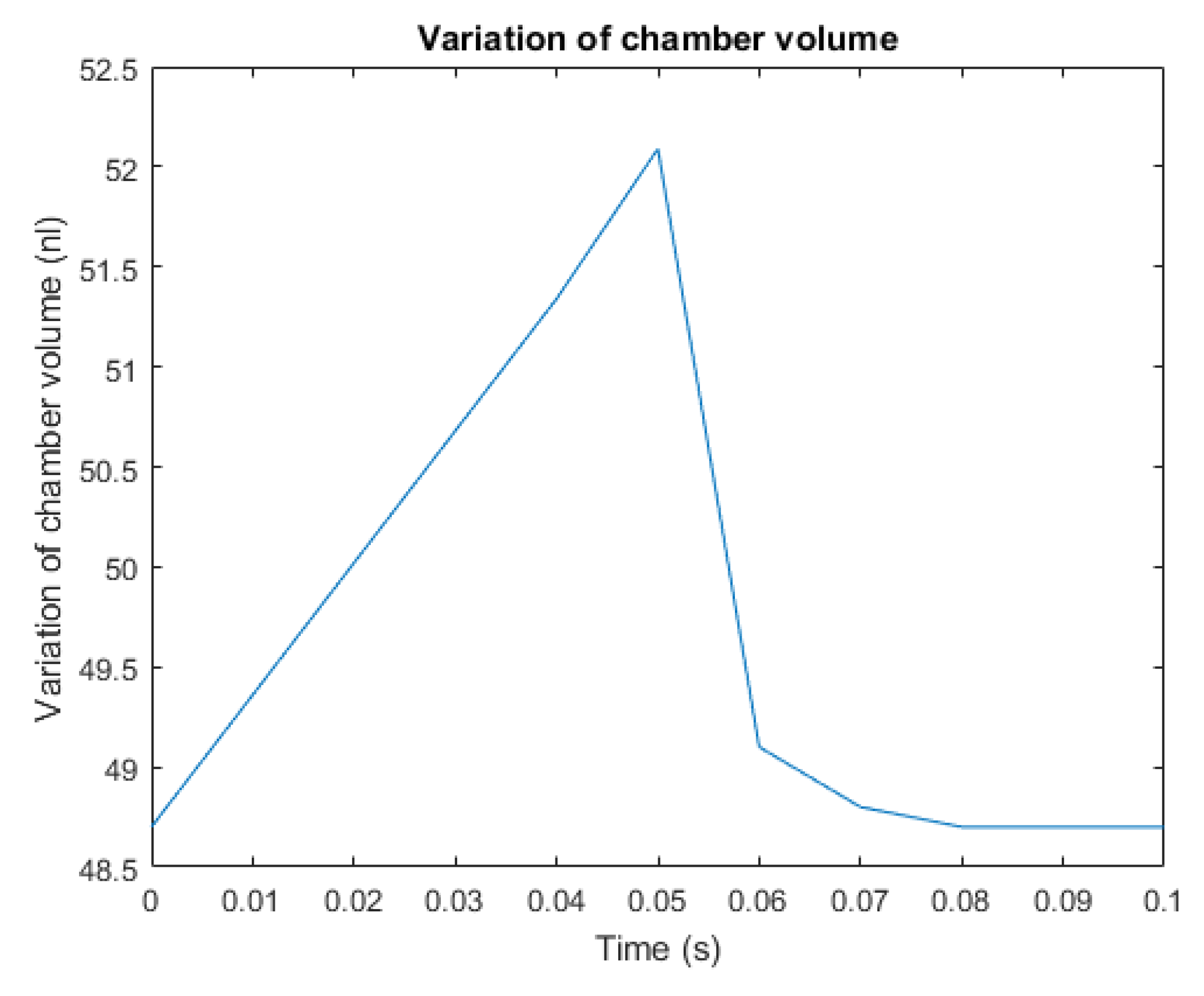
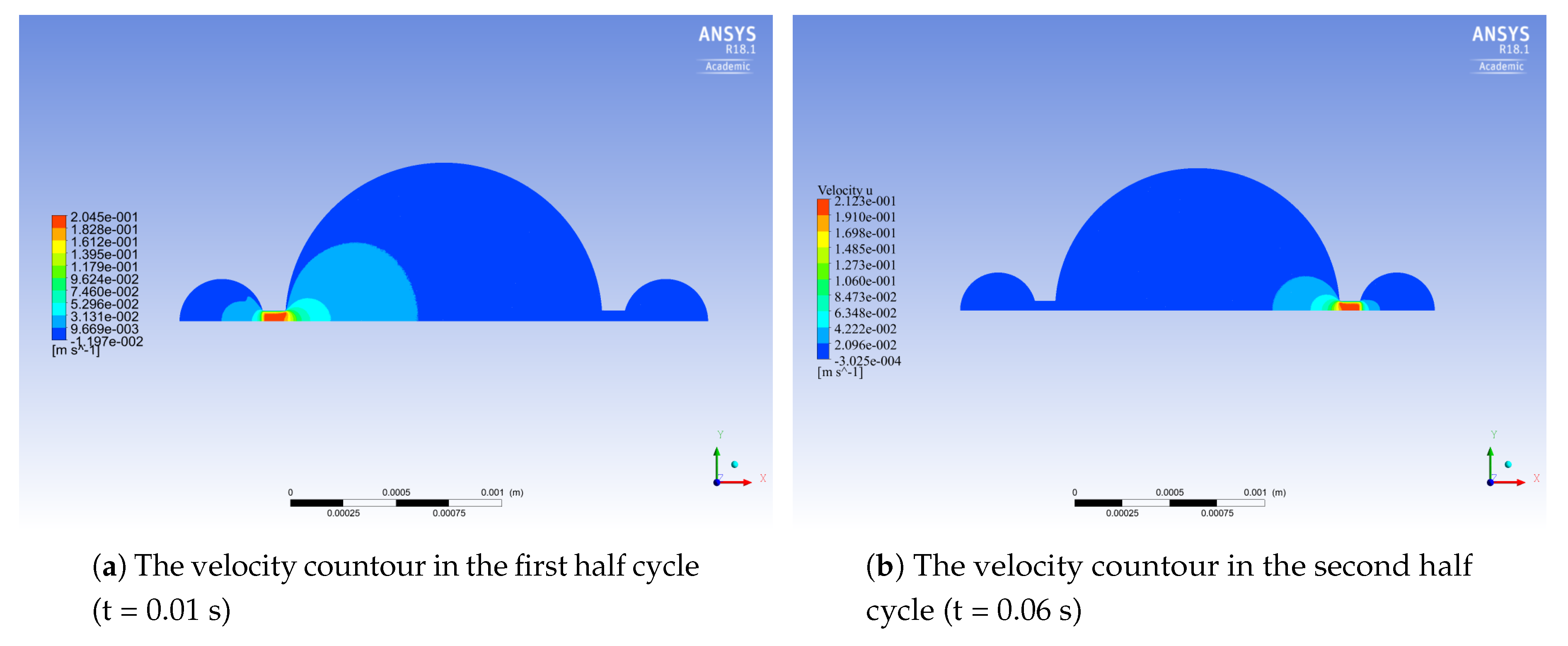
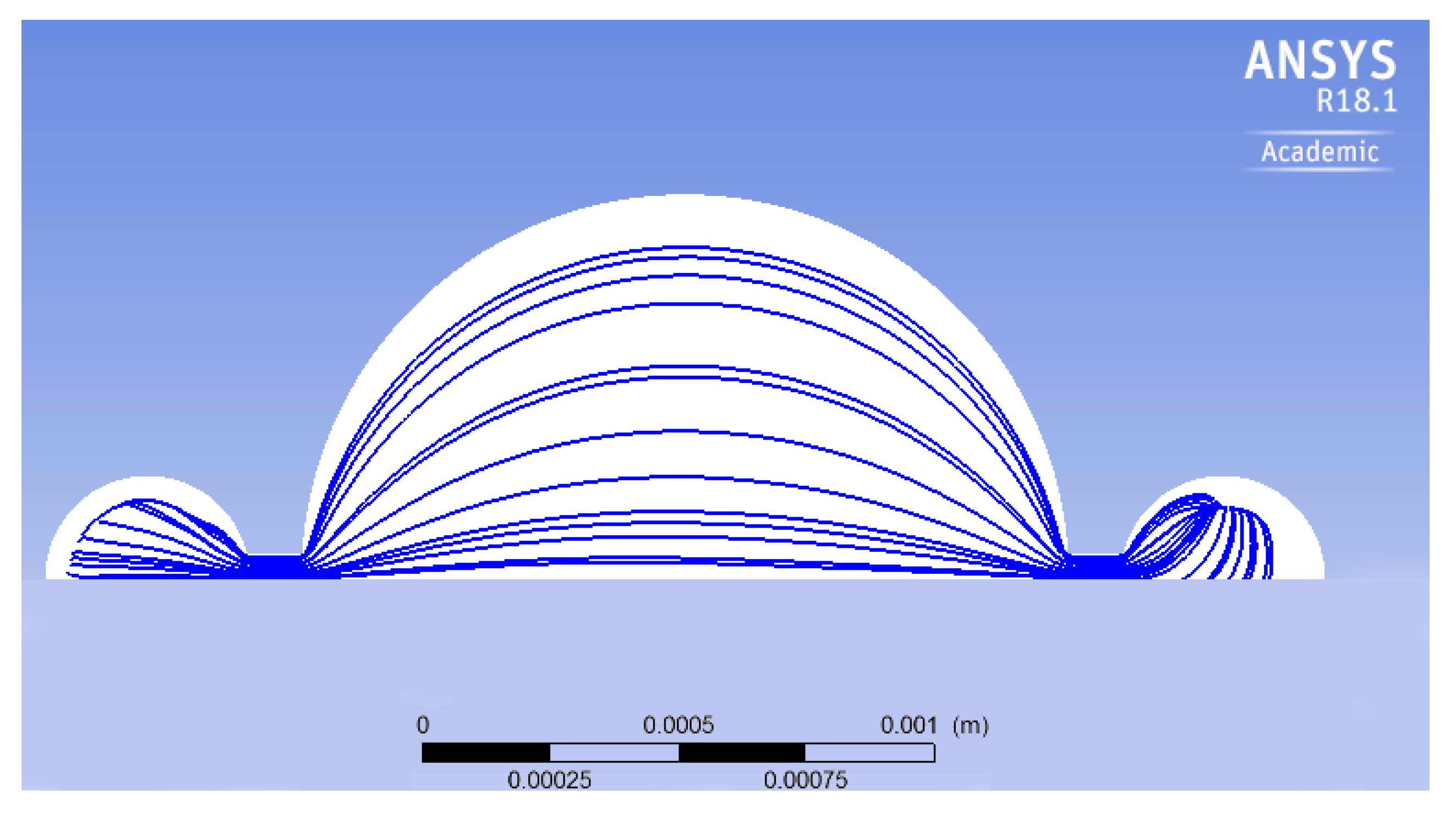
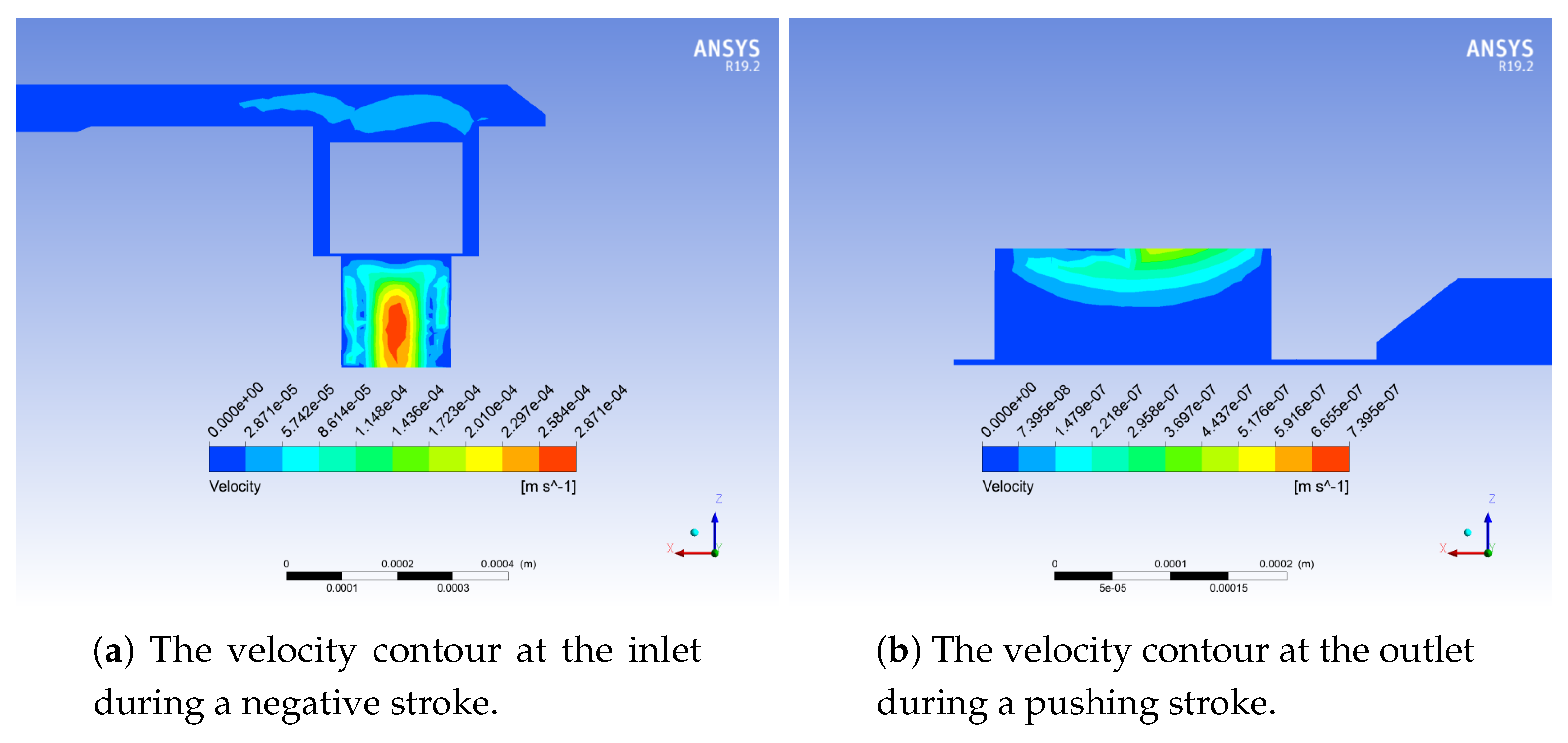
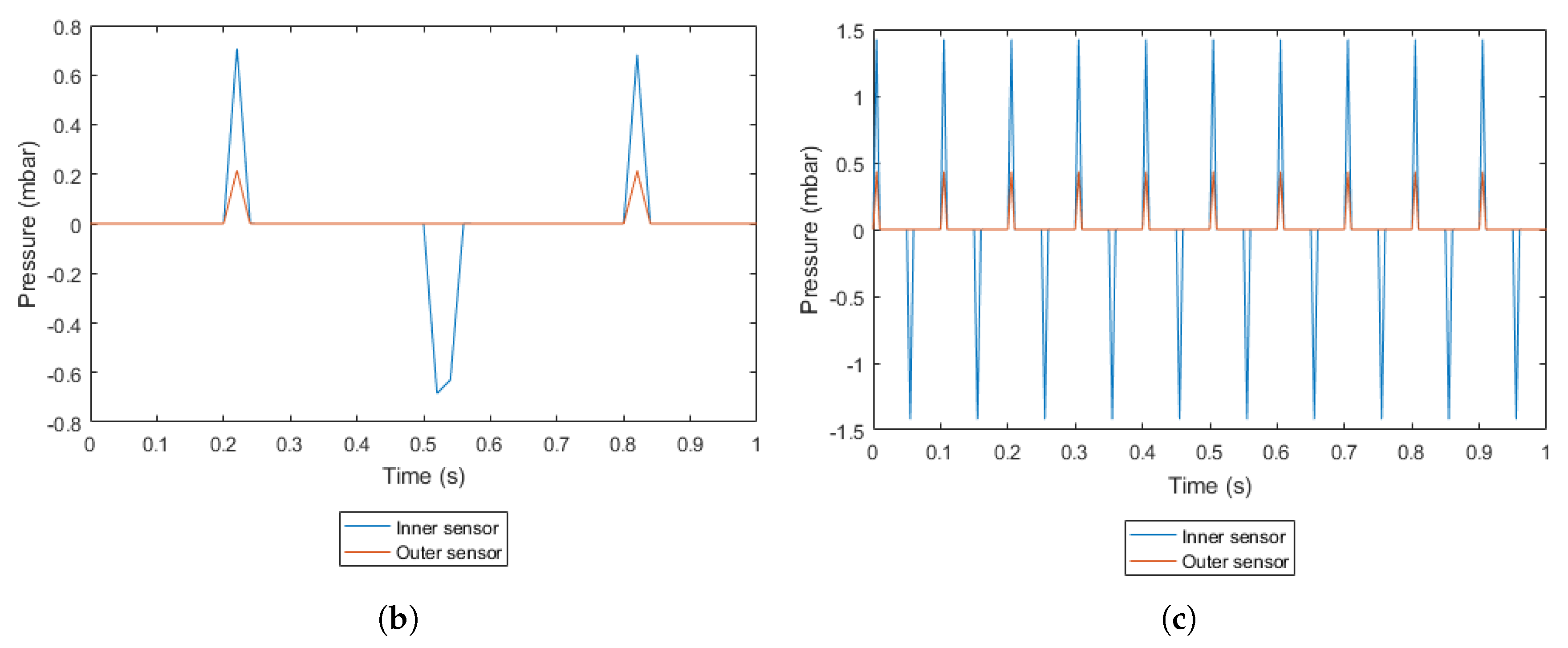
4. Preliminary Results
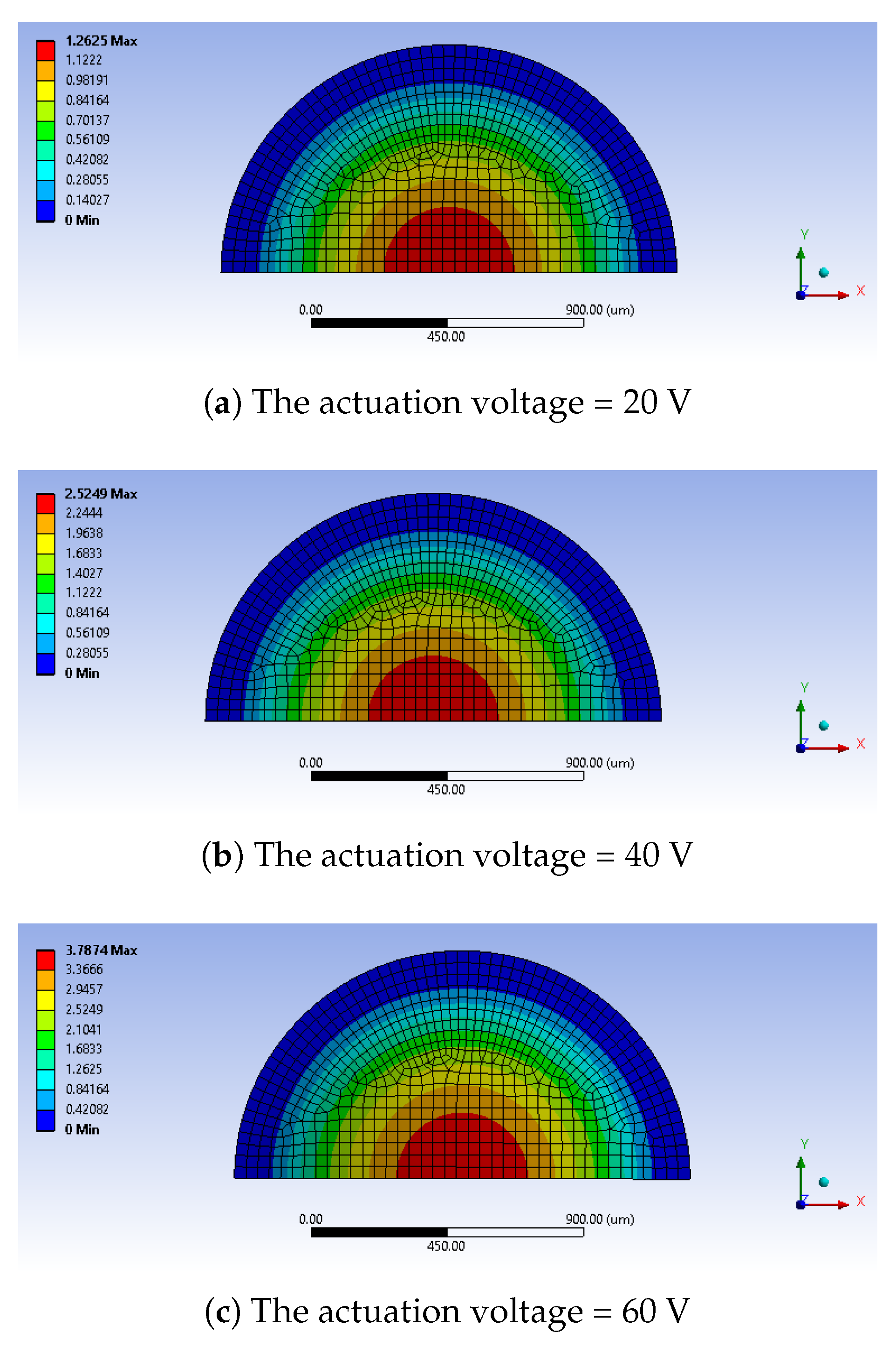
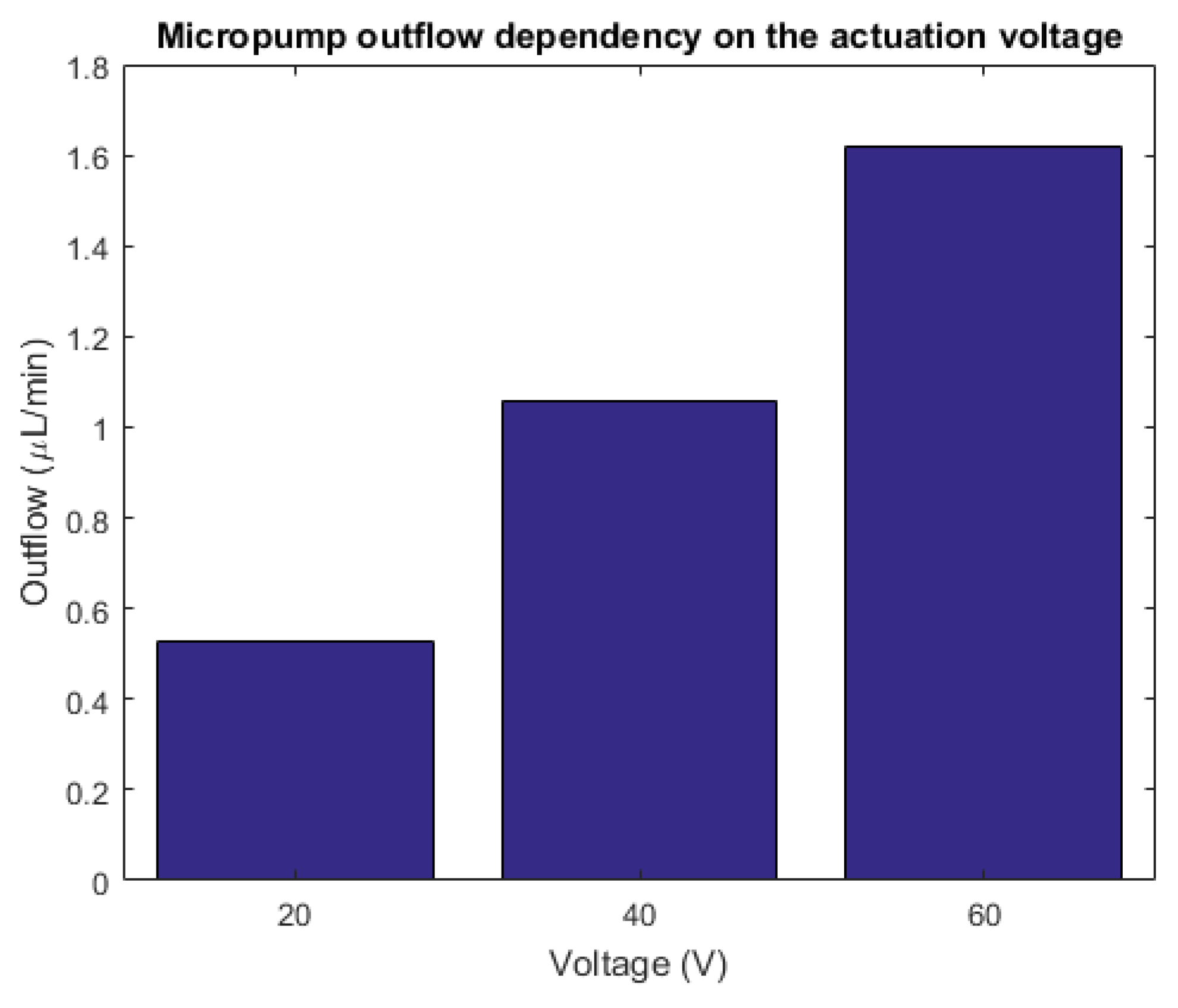
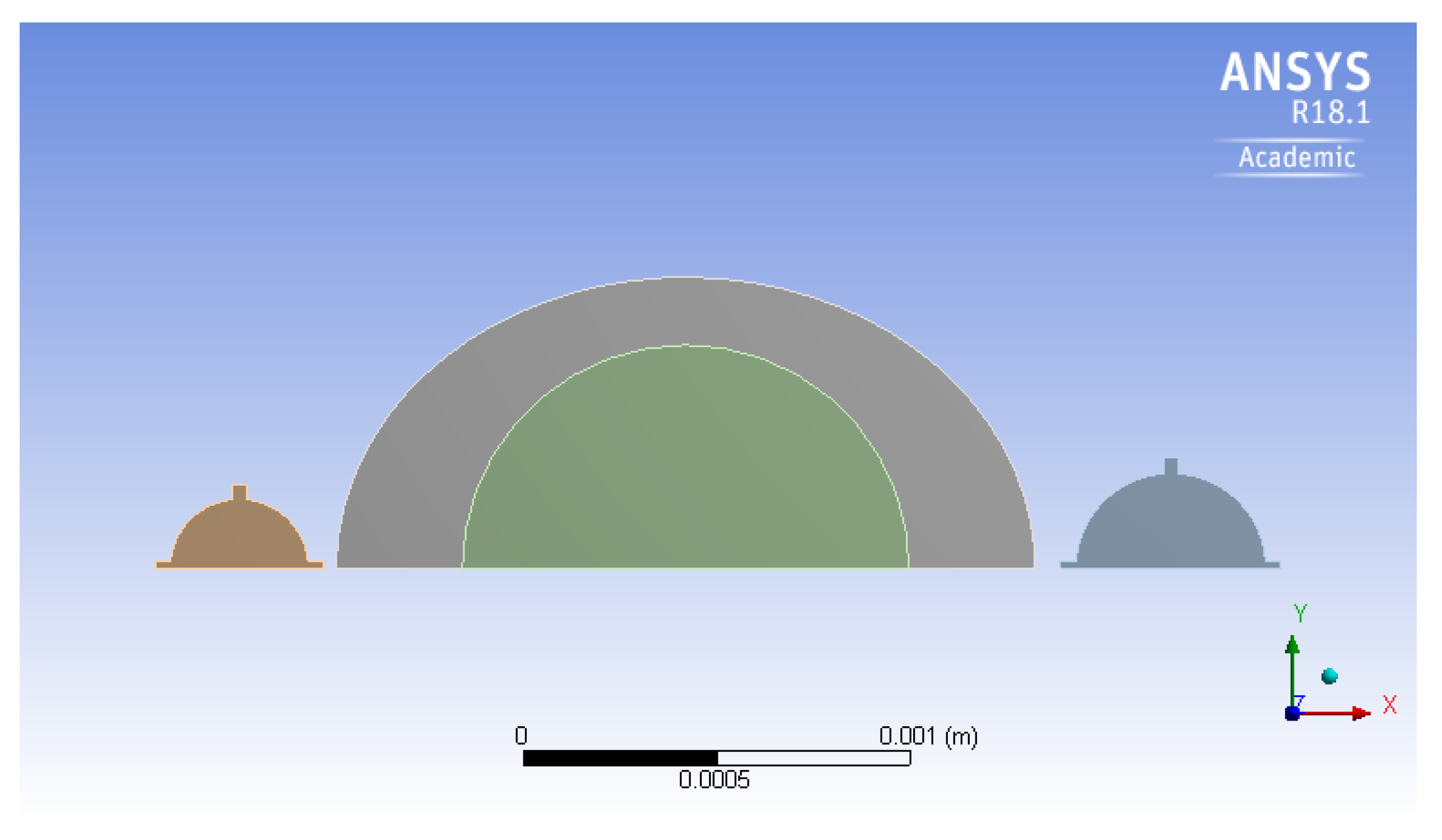
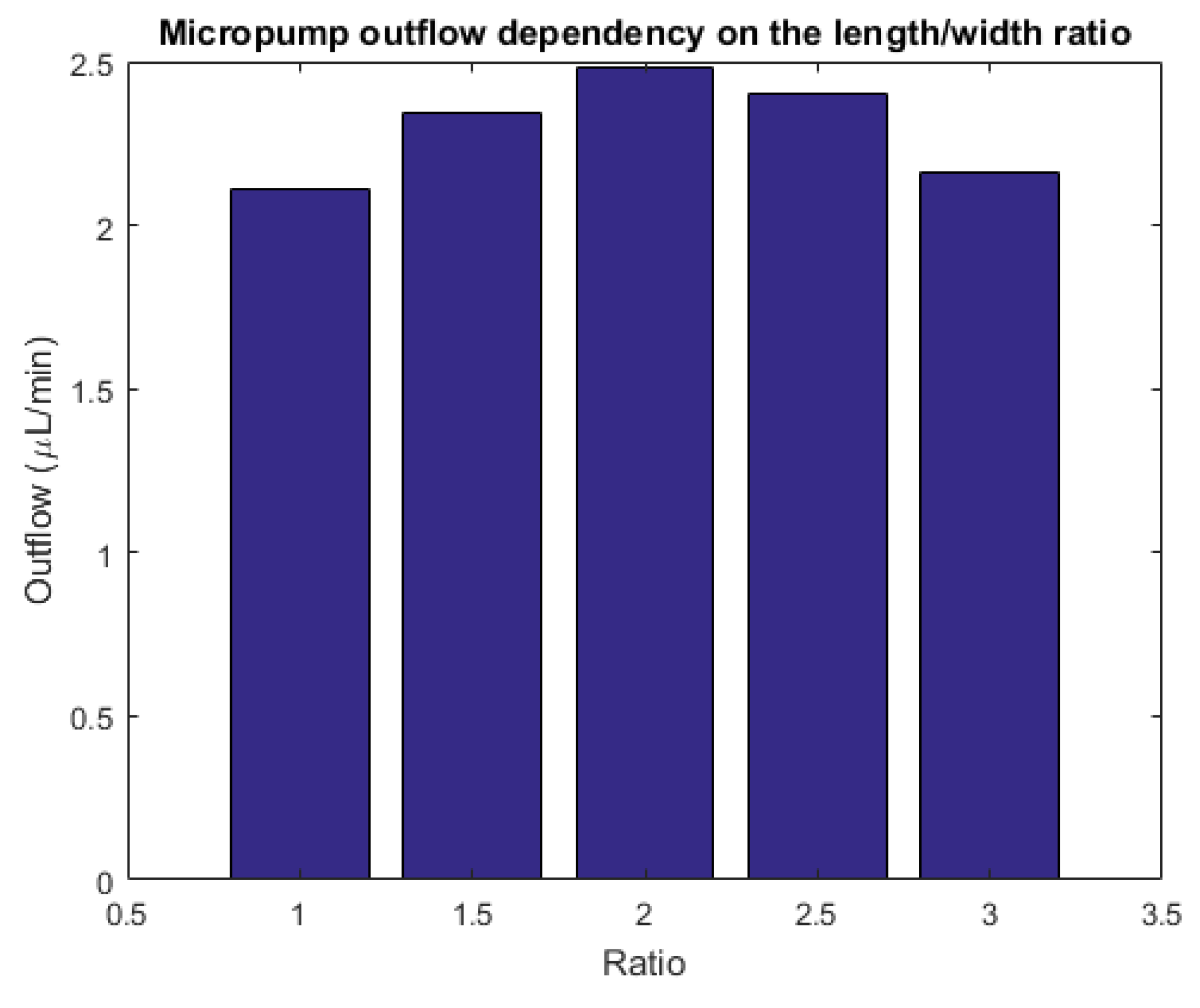
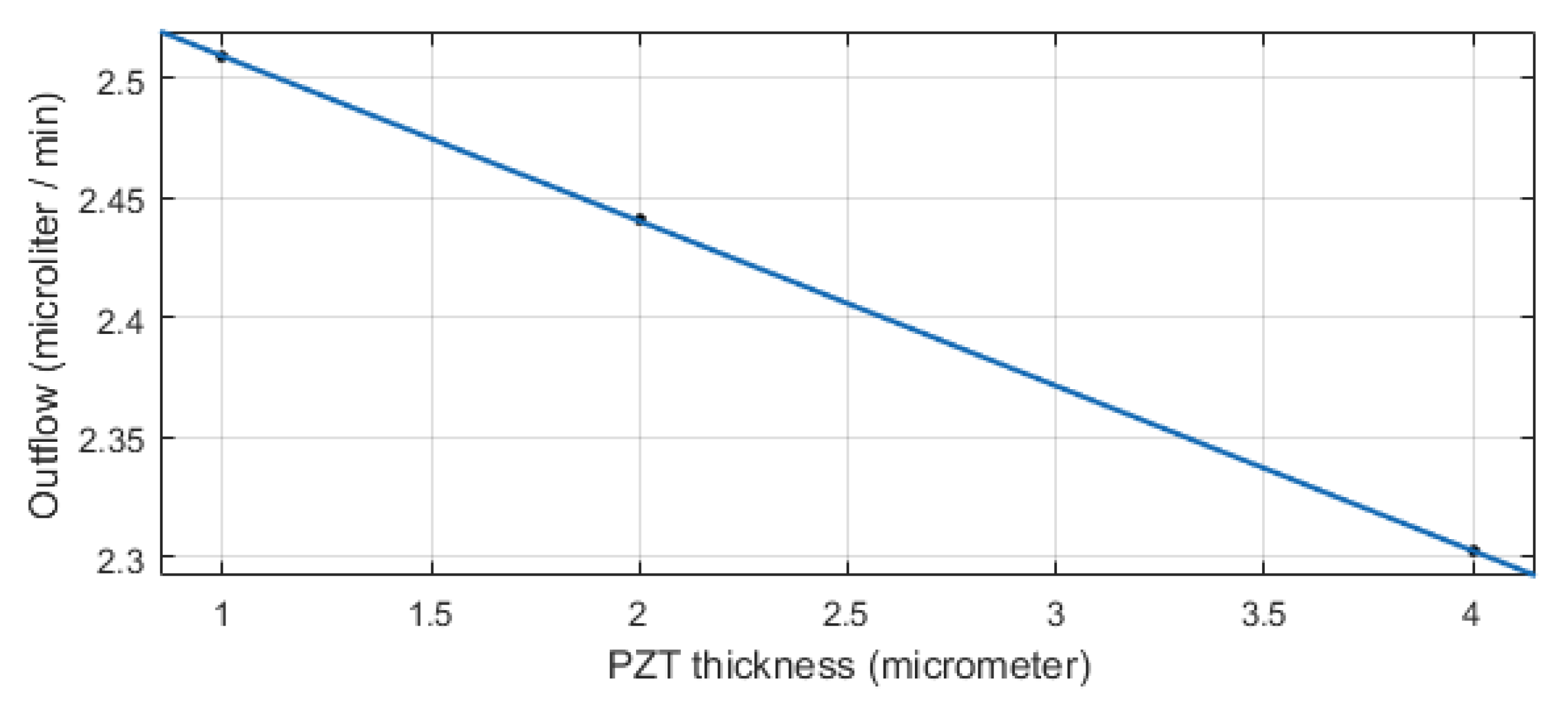
5. Geometrical Modifications
Geometry of the Chamber
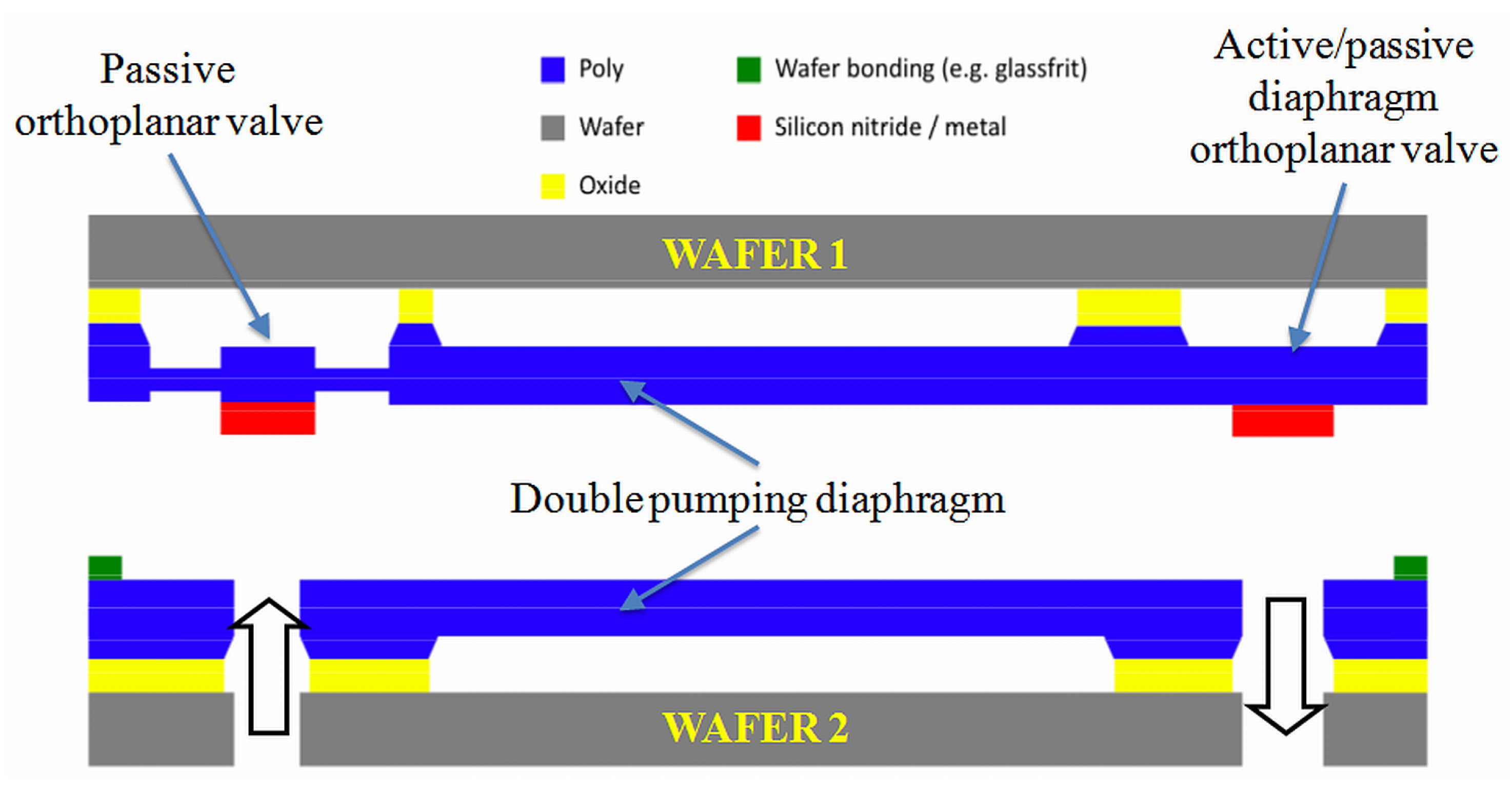
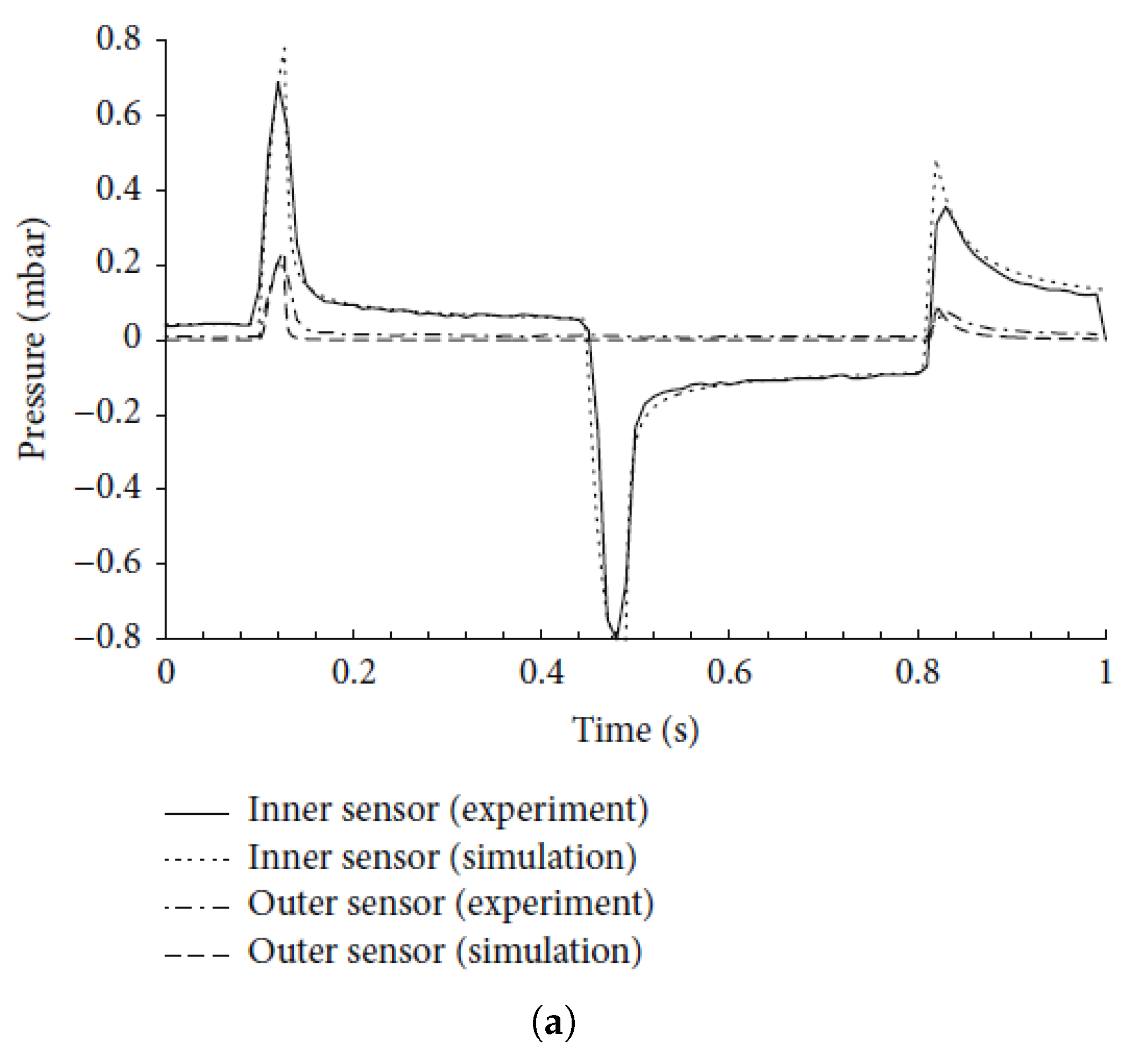
6. Comparison with a Commercial, Three-Wafer Micropump
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Corigliano, A.; Ardito, R.; Comi, C.; Frangi, A.; Ghisi, A.; Mariani, S. Mechanics of Microsystems; John Wiley & Sons: Hoboken, NJ, USA, 2018; Volume 7646. [Google Scholar]
- Shawgo, R.; Grayson, A.R.; Li, Y.; Cima, M. BioMEMS for drug delivery. Curr. Opin. Solid State Mater. Sci. 2002, 6, 329–334. [Google Scholar] [CrossRef]
- Woias, P. Micropumps—Past, progress and future prospects. Sens. Actuators B Chem. 2005, 105, 28–38. [Google Scholar] [CrossRef]
- Bertarelli, E.; Ardito, R.; Bianchi, E.; Laganà, K.; Procopio, F.; Baldo, L.; Corigliano, A.; Dubini, G.; Contro, R. A computational study for design optimization af an electrostatic micropump in stable and pull-in regime. AES Tech. Rev. Int. J. Ser. 2010, 1, 19–25. [Google Scholar]
- Bertarelli, E.; Ardito, R.; Corigliano, A.; Contro, R. A plate model for the evaluation of pull-in instability occurrence in electrostatic micropump diaphragms. Int. J. Appl. Mech. 2011, 3, 1–19. [Google Scholar] [CrossRef]
- Ardito, R.; Bertarelli, E.; Corigliano, A.; Gafforelli, G. On the application of piezolaminated composites to diaphragm micropumps. Compos. Struct. 2013, 99, 231–240. [Google Scholar] [CrossRef]
- Flynn, A.M.; Sanders, S.R. Fundamental limits on energy transfer and circuit considerations for piezoelectric transformers. IEEE Trans. Power Electron. 2002, 17, 8–14. [Google Scholar] [CrossRef]
- Cazorla, P.H.; Fuchs, O.; Cochet, M.; Maubert, S.; Le Rhun, G.; Fouillet, Y.; Defay, E. A low voltage silicon micro-pump based on piezoelectric thin films. Sens. Actuators A Phys. 2016, 250, 35–39. [Google Scholar] [CrossRef]
- Nisar, A.; Afzulpukar, N.; Mahisavariya, B.; Tuantranont, A. MEMS-based micropump in drug delivery and biomedical applications. Sens. Actuators B Chem. 2008, 130, 917–942. [Google Scholar] [CrossRef]
- Revathi, S.; Padmapriya, N.; Padmanabhan, R. A design analysis of piezoelectric-polymer composite-based valveless micropump. Int. J. Model. Simul. 2018. [Google Scholar] [CrossRef]
- Sateesh, J.; Sravani, K.G.; Kumar, R.A.; Guha, K.; Rao, K.S. Design and flow analysis of MEMS based piezo-electric micro pump. Microsyst. Technol. 2018, 24, 1609–1614. [Google Scholar] [CrossRef]
- Corigliano, A.; Ardito, R.; Bertarelli, E.; Ferrera, M. Micropump with Electrostatic Actuation. Patent PCT/IB2016/053985, 1 July 2016. [Google Scholar]
- Trolier-McKinstry, S.; Muralt, P. Thin film piezoelectrics for MEMS. J. Electroceram. 2004, 12, 7–17. [Google Scholar] [CrossRef]
- Jacobsen, H.; Prume, K.; Wagner, B.; Ortner, K.; Jung, T. High-rate sputtering of thick PZT thin films for MEMS. J. Electroceram. 2010, 25, 198–202. [Google Scholar] [CrossRef]
- Horwitz, J.; Grabowski, K.; Chrisey, D.; Leuchtner, R. In situ deposition of epitaxial PbZrxTi(1 − x)O3 thin films by pulsed laser deposition. Appl. Phys. Lett. 1991, 59, 1565–1567. [Google Scholar] [CrossRef]
- Schroth, A.; Lee, C.; Matsumoto, S.; Maeda, R. Application of sol-gel deposited thin PZT film for actuation of 1D and 2D scanners. Sens. Actuators A Phys. 1999, 73, 144–152. [Google Scholar] [CrossRef]
- ANSYS Academic Research Mechanical, Release 15, Help System, System Coupling User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2017.
- Liang, C.; Sun, F.; Rogers, C. Coupled electro-mechanical analysis of adaptive material systems-determination of the actuator power consumption and system energy transfer. J. Intell. Mater. Syst. Struct. 1997, 8, 335–343. [Google Scholar] [CrossRef]
- Wei, J.; Xie, H.; Nai, M.; Wong, C.; Lee, L. Low temperature wafer anodic bonding. J. Micromech. Microeng. 2003, 13, 217. [Google Scholar] [CrossRef]
- Tan, C.; Reif, R. Silicon multilayer stacking based on copper wafer bonding. Electrochem. Solid State Lett. 2005, 8, G147–G149. [Google Scholar] [CrossRef]
- Knechtel, R. Glass frit bonding: An universal technology for wafer level encapsulation and packaging. Microsyst. Technol. 2005, 12, 63–68. [Google Scholar] [CrossRef]
- Dumont-Fillon, D.; Tahriou, H.; Conan, C.; Chappel, E. Insulin micropump with embedded pressure sensors for failure detection and delivery of accurate monitoring. Micromachines 2014, 5, 1161–1172. [Google Scholar] [CrossRef]
- Fournier, S.; Chappel, E. Modeling of a piezoelectric MEMS micropump dedicated to insulin delivery and experimental validation using integrated pressure sensors: Application to partial occlusion management. J. Sens. 2017, 2017, 3719853. [Google Scholar] [CrossRef]
- Ashraf, M.W.; Tayyaba, S.; Afzulpurkar, N. Micro electromechanical systems (MEMS) based microfluidic devices for biomedical applications. Int. J. Mol. Sci. 2011, 12, 3648–3704. [Google Scholar] [CrossRef]
- Van Lintel, H.; Van de Pol, F.; Bouwstra, S. A piezoelectric micropump based on micromachining of silicon. Sens. Actuators 1988, 15, 153–167. [Google Scholar] [CrossRef]
- Esashi, M.; Shoji, S.; Nakano, A. Normally closed microvalve and mircopump fabricated on a silicon wafer. Sens. Actuators 1989, 20, 163–169. [Google Scholar] [CrossRef]
- Shoji, S.; Nakagawa, S.; Esashi, M. Micropump and sample-injector for integrated chemical analyzing systems. Sens. Actuators A Phys. 1990, 21, 189–192. [Google Scholar] [CrossRef]
- Matsumoto, S.; Klein, A.; Maeda, R. Development of bi-directional valve-less micropump for liquid. In Proceedings of the Twelfth IEEE International Conference on Micro Electro Mechanical Systems (MEMS’99), Orlando, FL, USA, 21 January 1999; pp. 141–146. [Google Scholar]
- Li, H.; Roberts, D.; Steyn, J.; Turner, K.; Carretero, J.; Yaglioglu, O.; Su, Y.; Saggere, L.; Hagood, N.; Spearing, S.; et al. A high frequency high flow rate piezoelectrically driven MEMS micropump. In Proceedings of the IEEE Solid State Sensors and Actuators Workshop, Hilton Head Island, SC, USA, 4–8 June 2000. [Google Scholar]
- MIP Implantable Product Information. Available online: www.debiotech.sa (accessed on 16 April 2019).
- Liu, G.; Shen, C.; Yang, Z.; Cai, X.; Zhang, H. A disposable piezoelectric micropump with high performance for closed-loop insulin therapy system. Sens. Actuators A Phys. 2010, 163, 291–296. [Google Scholar] [CrossRef]
- Luo, W.F.; Ma, H.K. Development of a Piezoelectric Micropump with Novel Separable Design. Appl. Mech. Mater. 2014, 670–671, 1426–1429. [Google Scholar] [CrossRef]



| Section | Geometrical Specifications | |||
|---|---|---|---|---|
| Radius (m) | Width (m) | Length (m) | Thickness (m) | |
| Chamber | 750 | - | - | 20 |
| Entrance/Exit Cylinders | 200 | - | - | 20 |
| Inlet | 140 | - | - | |
| Outlet | 250 | - | - | |
| Channels | - | 100 | 100 | 20 |
| Properties | Materials | ||
|---|---|---|---|
| Silicon | PZT-5A | Water | |
| E (MPa) | 169,000 | 70,000 | - |
| 0.23 | 0.3 | - | |
| (kg/m) | 2300 | 7700 | 999.97 |
| (N/V m) | - | −5.04 | - |
| (N/V m) | - | 19.7 | - |
| - | 1320 | - | |
| - | 1250 | - | |
| (cP) | - | - | 1 (20 C) |
| Part | Geometrical Specifications | |
|---|---|---|
| Radius (m) | Thickness (m) | |
| Membrane | 750 | 16 |
| Piezoelectric | 547.5 | 1 |
| Inlet Valve | 150 | 2 |
| Outlet Valve | 250 | 2 |
| Author and Year | Package Size (mm) | Frequency (Hz) | Max. Back Pressure (kPa) | (V) | q (L min) |
|---|---|---|---|---|---|
| Proposed micropump | 8 | 10 | 10.2 | 60 | 2.5 |
| Van Linten 1988 [25] | 4100 | 0.1 | 24 | NR | 0.6 |
| Esashi 1989 [26] | 800 | 30 | 6.4 | 90 | 15 |
| Shoji 1990 [27] | 4000 | 50 | NR | 100 | 22 |
| Matsumuto 1999 [28] | NR | 5 | NR | NR | 5.5 |
| Li et al. 2000 [29] | 4600 | 20 | 35 | 450 | 2500 |
| MIP Implantable 2003 [30] | 357 | 0.2 | 55 | 150 | 1.7 |
| Liu et al. 2010 [31] | 1413 | 200 | 22 | 36 | 747.6 |
| Luo et al. 2014 [32] | 628 | 120 | NR | 60 | 15030 |
| Debiotech 2014 [22] | 84 | 3.125 | NR | 200 | 41.67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farshchi Yazdi, S.A.F.; Corigliano, A.; Ardito, R. 3-D Design and Simulation of a Piezoelectric Micropump. Micromachines 2019, 10, 259. https://doi.org/10.3390/mi10040259
Farshchi Yazdi SAF, Corigliano A, Ardito R. 3-D Design and Simulation of a Piezoelectric Micropump. Micromachines. 2019; 10(4):259. https://doi.org/10.3390/mi10040259
Chicago/Turabian StyleFarshchi Yazdi, Seyed Amir Fouad, Alberto Corigliano, and Raffaele Ardito. 2019. "3-D Design and Simulation of a Piezoelectric Micropump" Micromachines 10, no. 4: 259. https://doi.org/10.3390/mi10040259
APA StyleFarshchi Yazdi, S. A. F., Corigliano, A., & Ardito, R. (2019). 3-D Design and Simulation of a Piezoelectric Micropump. Micromachines, 10(4), 259. https://doi.org/10.3390/mi10040259







