Investigation of the Young’s Modulus and the Residual Stress of 4H-SiC Circular Membranes on 4H-SiC Substrates
Abstract
1. Introduction
2. Materials and Methods
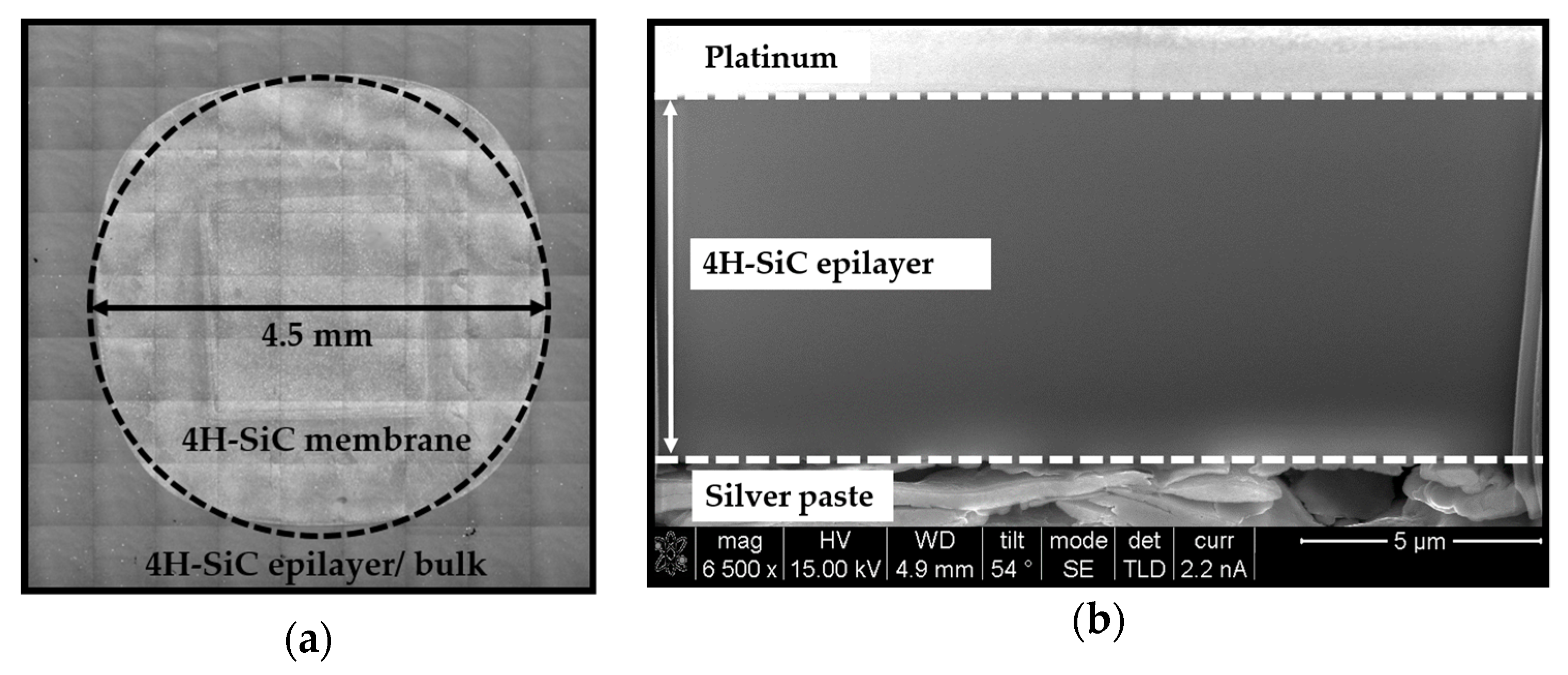
2.1. Sample Preparation
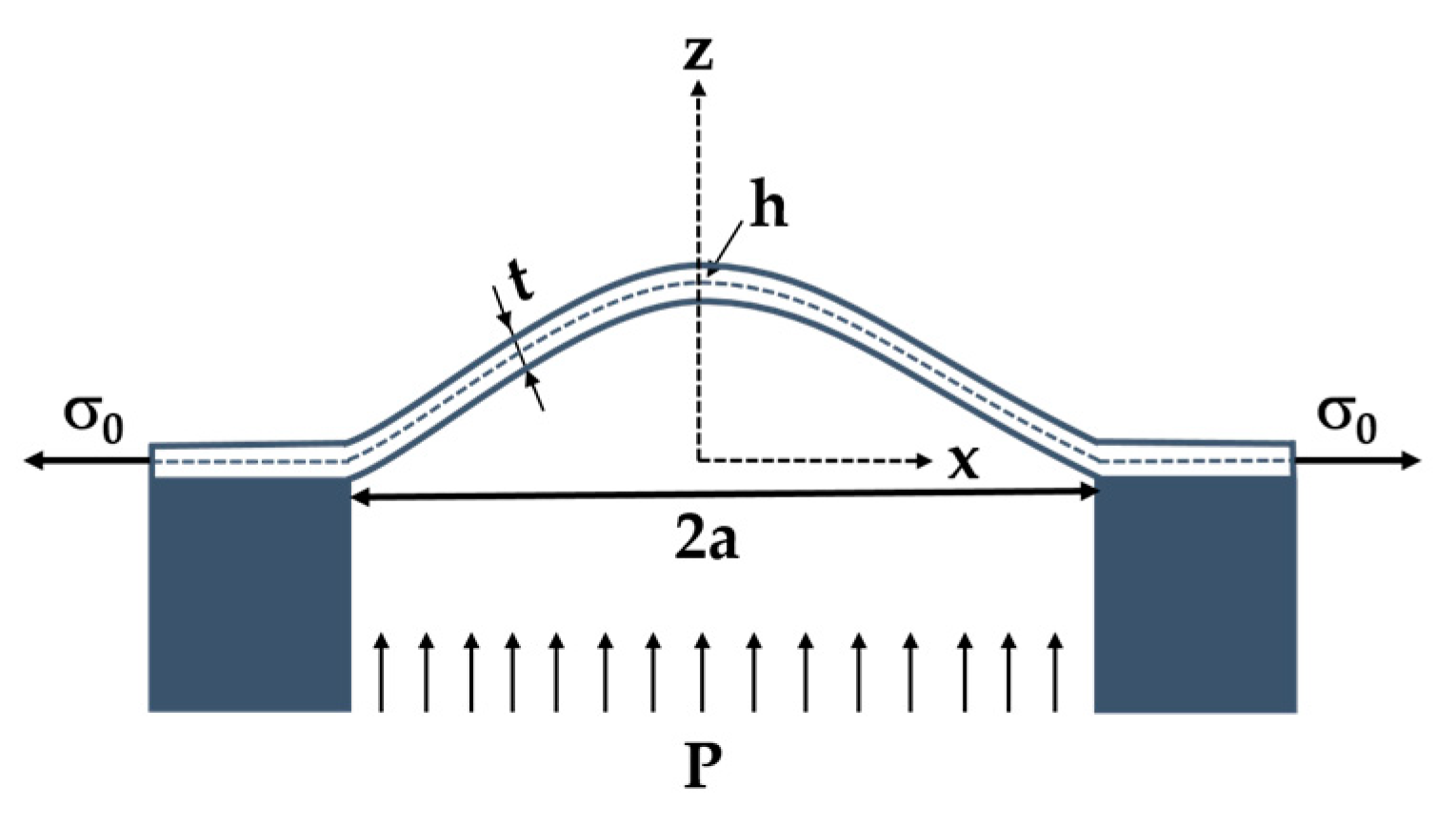
2.2. Circular Membrane Deflection under Uniform Pressure
2.3. Membrane Vibration
2.3.1. Analytical Description
2.3.2. Finite Element Method Approach
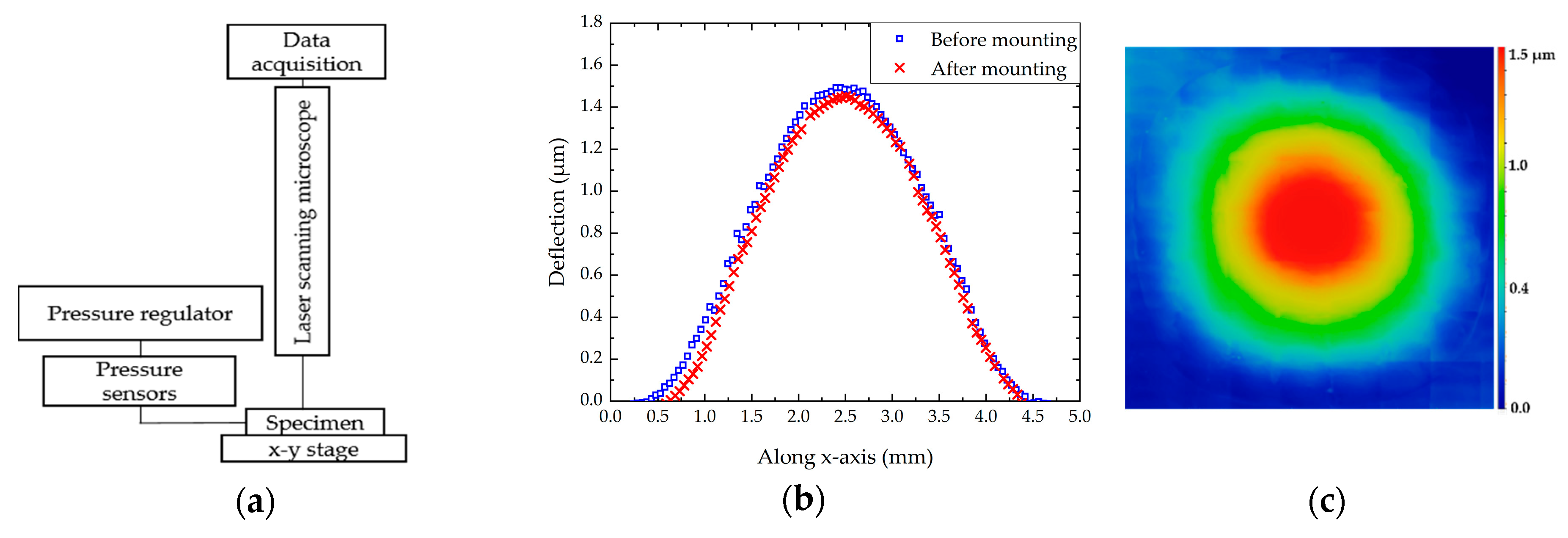
2.4. Load-Deflection Measurements
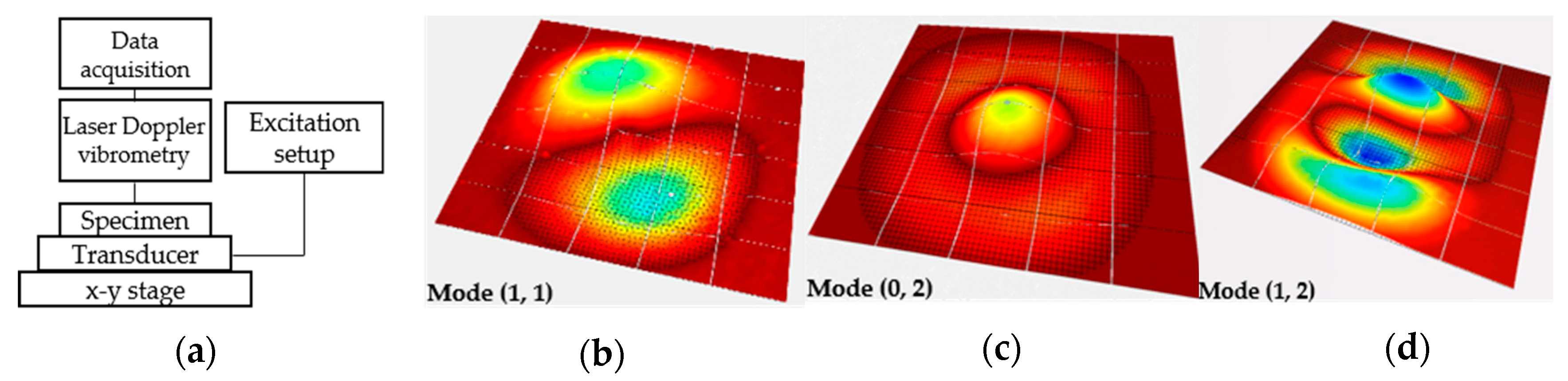
2.5. Dynamic Behavior Measurements
3. Results and Discussion
3.1. Bulge Test Results
3.2. Vibrometry Results
3.3. Finite Element Computations
3.4. Etching Profile Determination
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sarro, P.M. Silicon carbide as a new MEMS technology. Sens. Actuators A Phys. 2000, 82, 210–218. [Google Scholar] [CrossRef]
- Elyassi, B.; Sahimi, M.; Tsotsis, T.T. Silicon carbide membranes for gas separation applications. J. Membr. Sci. 2007, 288, 290–297. [Google Scholar] [CrossRef]
- Mehregany, M.; Zorman, C.A.; Rajan, N.; Wu, C.H. Silicon carbide MEMS for harsh environments. Proc. IEEE 1998, 86, 1594–1609. [Google Scholar] [CrossRef]
- Michaud, J.-F.; Portail, M.; Alquier, D. 3C-SiC—From Electronic to MEMS Devices. In Advanced Silicon Carbide Devices and Processing; InTech: Philadelphia, PA, USA, 2015; p. 33. ISBN 978-953-51-2168-8. [Google Scholar]
- Zielinski, M.; Leycuras, A.; Ndiaye, S.; Chassagne, T. Stress relaxation during the growth of 3C-SiC/Si thin films. Appl. Phys. Lett. 2006, 89, 2004–2007. [Google Scholar] [CrossRef]
- Nida, S.; Tsibizov, A.; Ziemann, T.; Woerle, J.; Moesch, A.; Schulze-Briese, C.; Pradervand, C.; Tudisco, S.; Sigg, H.; Bunk, O.; et al. Silicon carbide X-ray beam position monitors for synchrotron applications. J. Synchrotron Radiat. 2019, 26, 28–35. [Google Scholar] [CrossRef]
- Dahal, R.; Chowdhury, S.; Hitchcock, C.; Chow, T.P.; Bhat, I.B. Fabrication of thick free-standing lightly-doped n-type 4H- SiC wafers. Mater. Sci. Forum 2017, 897, 379–382. [Google Scholar] [CrossRef]
- Janssen, G.C.A.M.; Abdalla, M.M.; van Keulen, F.; Pujada, B.R.; van Venrooy, B. Celebrating the 100th anniversary of the Stoney equation for film stress: Developments from polycrystalline steel strips to single crystal silicon wafers. Thin Solid Films 2009, 517, 1858–1867. [Google Scholar] [CrossRef]
- Feng, X.; Huang, Y.; Rosakis, A.J. On the Stoney Formula for a thin film/substrate system with nonuniform substrate thickness. J. Appl. Mech. 2007, 74, 1276–1281. [Google Scholar] [CrossRef]
- Bazin, A.-E.; Chassagne, T.; Alquier, D.; Zielinski, M.; Jiao, S.; Michaud, J.-F.; Portail, M. Micromachining of thin 3C-SiC films for mechanical properties investigation. MRS Proc. 2010, 1246, 3–9. [Google Scholar] [CrossRef]
- Fang, W.; Wickert, J.A. Determining mean and gradient residual stresses in thin films using micromachined cantilevers. J. Micromech. Microeng. 1996, 6, 301–309. [Google Scholar] [CrossRef]
- Yang, S.; Miyagawa, R.; Miyake, H.; Hiramatsu, K.; Harima, H. Raman scattering spectroscopy of residual stresses in epitaxial AlN films. Appl. Phys. Express 2011, 4, 10–13. [Google Scholar] [CrossRef]
- Piluso, N.; Anzalone, R.; Camarda, M.; Severino, A.; D’Arrigo, G.; La Via, F. Stress fields analysis in 3C-SiC free-standing microstructures by micro-Raman spectroscopy. Thin Solid Films 2012, 522, 20–22. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Xiang, Y.; Chen, X.; Vlassak, J.J. Plane-strain bulge test for thin films. J. Mater. Res. 2005, 20, 2360–2370. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, J.; Sun, G.; Liu, X.; Yang, F.; Li, J. Fracture properties of silicon carbide thin films by bulge test of long rectangular membrane. J. Microelectromech. Syst. 2008, 17, 453–461. [Google Scholar] [CrossRef]
- Maden, M.A.; Jagota, A.; Mazur, S.; Farris, R.J. Vibrational technique for stress measurement in films: I, ideal membrane behavior. J. Am. Ceram. Soc. 1994, 77, 625–635. [Google Scholar] [CrossRef]
- Yaralioglu, G.G.; Ergun, A.S.; Bayram, B.; Marentis, T.; Khuri-Yakub, B.T. Residual stress and Young’s modulus measurement of capacitive micromachined ultrasonic transducer membranes. Proc. IEEE 2001, 2, 953–956. [Google Scholar] [CrossRef]
- Vlassak, J.J.; Nix, W.D. A new bulge test technique for the determination of Young’s modulus and Poisson’s ratio of thin films. J. Mater. Res. 1992, 7, 3242–3249. [Google Scholar] [CrossRef]
- Malhaire, C. Comparison of two experimental methods for the mechanical characterization of thin or thick films from the study of micromachined circular diaphragms. Rev. Sci. Instrum. 2012, 83, 055008. [Google Scholar] [CrossRef]
- Watanabe, N.; Kimoto, T.; Suda, J. Fabrication of electrostatic-actuated single-crystalline 4H-SiC bridge structures by photoelectrochemical etching. Proc. SPIE 2011, 7926, 79260B. [Google Scholar] [CrossRef]
- Gautier, G.; Biscarrat, J.; Valente, D.; Defforge, T.; Gary, A.; Cayrel, F. Systematic study of anodic etching of highly doped N-type 4H-SiC in various HF based electrolytes. J. Electrochem. Soc. 2013, 160, 372–379. [Google Scholar] [CrossRef]
- Gautier, G.; Cayrel, F.; Capelle, M.; Billoué, J.; Song, X.; Michaud, J.-F. Room light anodic etching of highly doped n-type 4H-SiC in high-concentration HF electrolytes: Difference between C and Si crystalline faces. Nanoscale Res. Lett. 2012, 7, 367. [Google Scholar] [CrossRef] [PubMed]
- Vinci, R.P.; Vlassak, J.J. Mechanical behavior of thin films. Annu. Rev. Mater. Sci. 1996, 26, 431–462. [Google Scholar] [CrossRef]
- Nádai, A. Die Elastischen Platten; Springer: Berlin/Heidelberg, Germany, 1925. [Google Scholar]
- Way, S. Bending of circular plates with large deflection. Trans. ASME 1934, 54, 627–636. [Google Scholar]
- Beams, J.W. Mechanical properties of thin films of silver. In Structure and Properties of Thin Films; John Wiley and Sons: New York, NY, USA, 1959; pp. 183–192. [Google Scholar]
- Lin, P. The In-Situ Measurement of Mechanical Properties of Multi-Layer Coatings. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1990. [Google Scholar]
- Small, M.K.; Nix, W.D. Analysis of the accuracy of the bulge test in determining the mechanical properties of thin films. J. Mater. Res. 1992, 7, 1553–1563. [Google Scholar] [CrossRef]
- Pan, J.Y.; Lin, P.; Maseeh, F.; Senturia, S.D. Verification of FEM analysis of load-deflection methods for measuring mechanical properties of thin films. In Proceedings of the IEEE 4th Technical Digest on Solid-State Sensor and Actuator Workshop, Hilton Head Island, SC, USA, 4–7 June 1990; pp. 70–73. [Google Scholar] [CrossRef]
- Hohlfelder, R.J.; Vlassak, J.J.; Nix, W.D.; Luo, H.; Christopher, E.D. Blister test analysis methods. Mater. Res. Soc. 1995, 356, 585–590. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Krieger, S.W. Theory of Plate and Shells, 2nd ed.; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Blevins, R.D. Formulas for Natural Frequency and Mode Shape; Van Nostrand Reinhold Company: New York, NY, USA, 1979. [Google Scholar]
- Mitchell, J.S.; Zorman, C.A.; Kicher, T.; Roy, S.; Mehregany, M. Examination of bulge test for determining residual stress, Young’s modulus, and Poisson’s ratio of 3C-SiC thin films. J. Aerosp. Eng. 2003, 16, 46–54. [Google Scholar] [CrossRef]
- Jayaraman, S.; Edwards, R.L.; Hemker, K.J. Relating mechanical testing and microstructural features of polysilicon thin films. J. Mater. Res. 1999, 14, 688–697. [Google Scholar] [CrossRef]
- Olympus. Available online: www.olympus-europa.com (accessed on 19 November 2019).
- Huang, H.; Liu, Y.; Dell, J.M. Determination of mechanical properties of PECVD silicon nitride thin films for tunable MEMS Fabry–Perot optical filters. J. Micromech. Microeng. 2005, 15, 608. [Google Scholar] [CrossRef]
- Hill, R.C. A theory of the plastic bulging of a metal diaphragm by lateral pressure. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1950, 41, 1133–1142. [Google Scholar] [CrossRef]
- Ma, S.; Wang, S.; Iacopi, F.; Huang, H. A resonant method for determining the residual stress and elastic modulus of a thin film. Appl. Phys. Lett. 2013, 103, 031603. [Google Scholar] [CrossRef]
- Deutsch, B.M.; Robinson, A.R.; Felce, R.J.; Moore, T.R. Nondegenerate normal-mode doublets in vibrating flat circular plates. Am. J. Phys. 2004, 72, 220–225. [Google Scholar] [CrossRef]
- Fartash, A.; Schuller, I.K.; Grimsditch, M. Thinfilm modeling for mechanical measurements: Should membranes be used or plates? J. Appl. Phys. 1992, 71, 4244–4248. [Google Scholar] [CrossRef]
- Biscarrat, J.; Michaud, J.F.; Collard, E.; Alquier, D. ICP Etching of 4H-SiC Substrates. Mater. Sci. Forum 2013, 740–742, 825–828. [Google Scholar] [CrossRef]
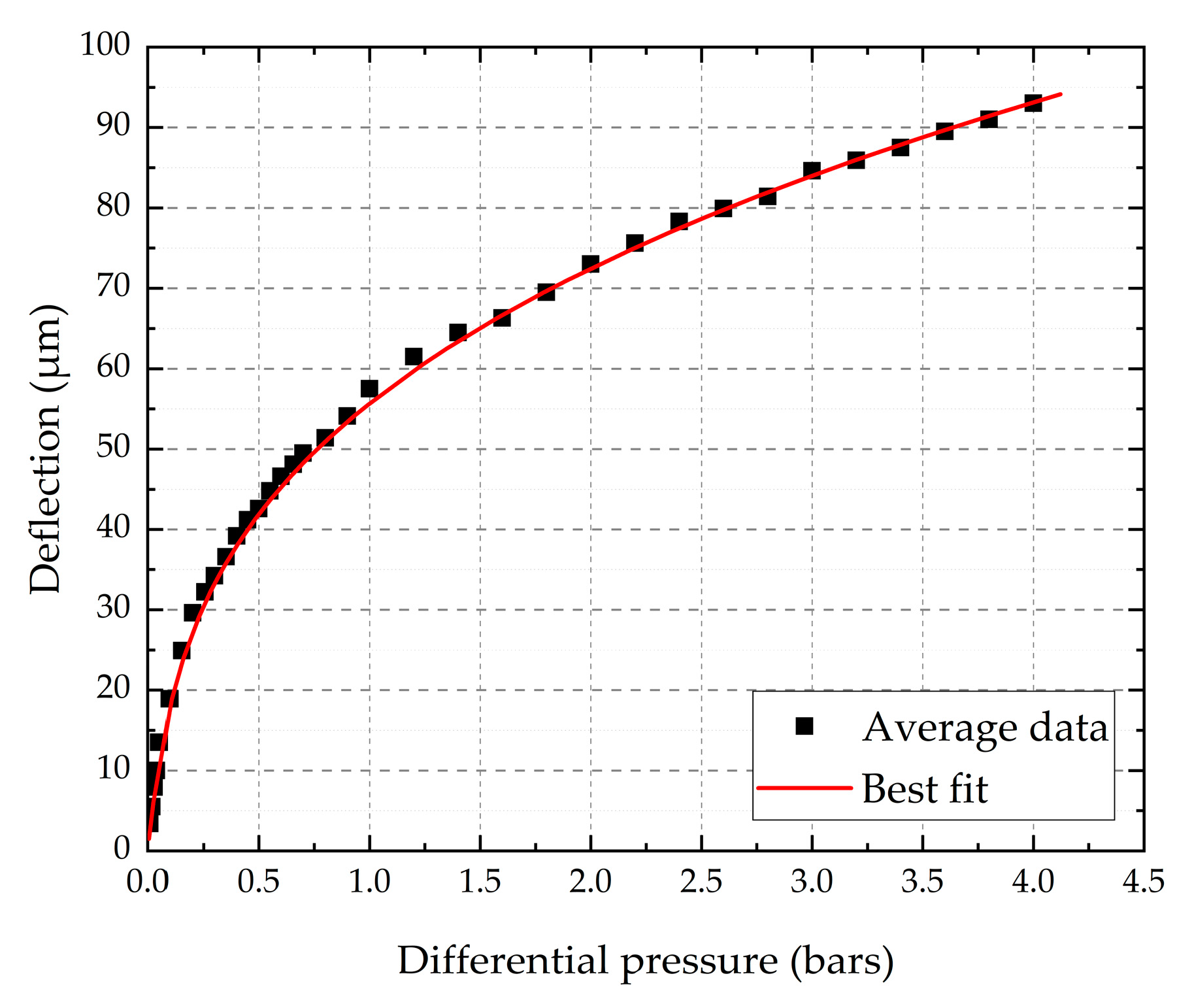
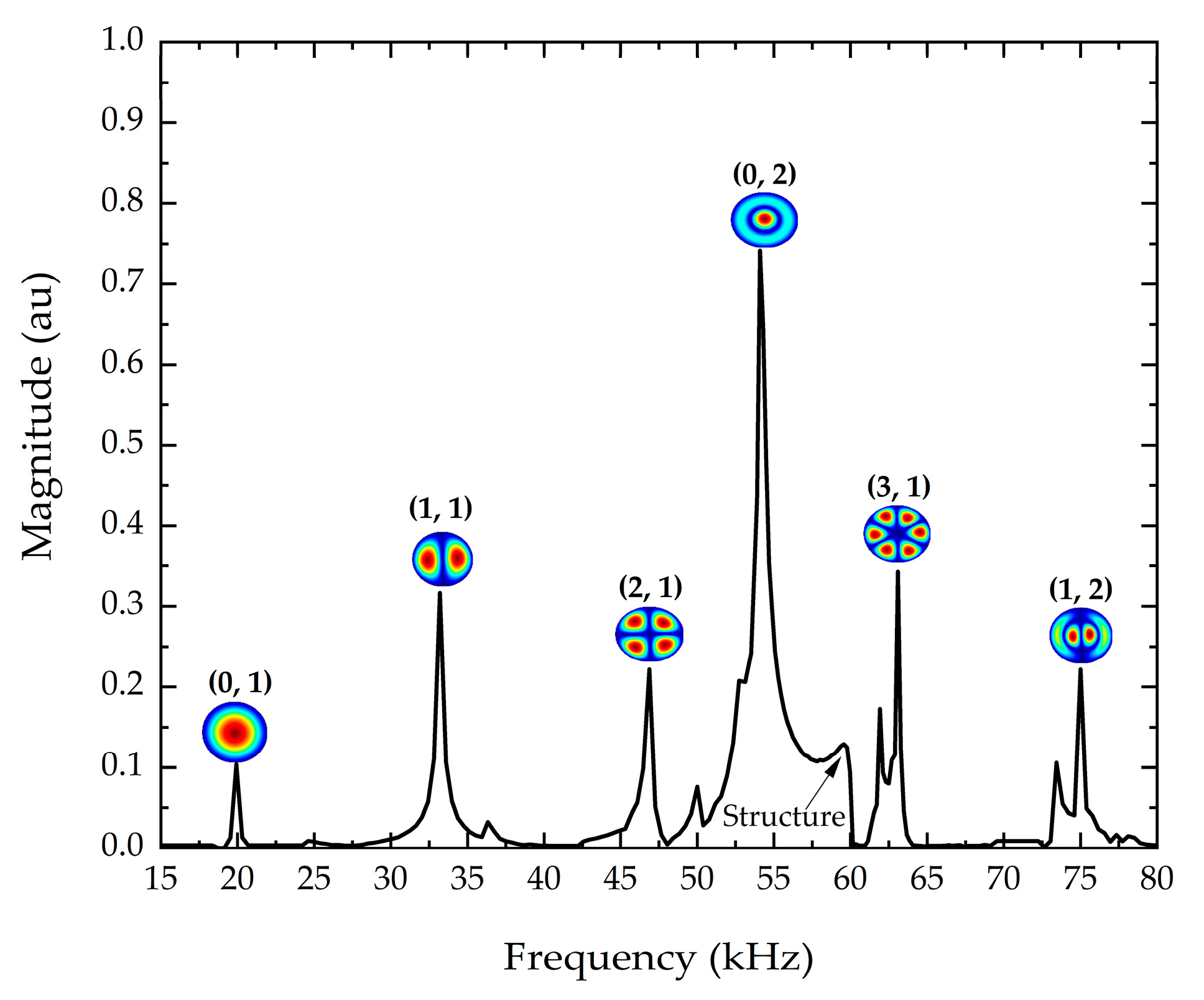
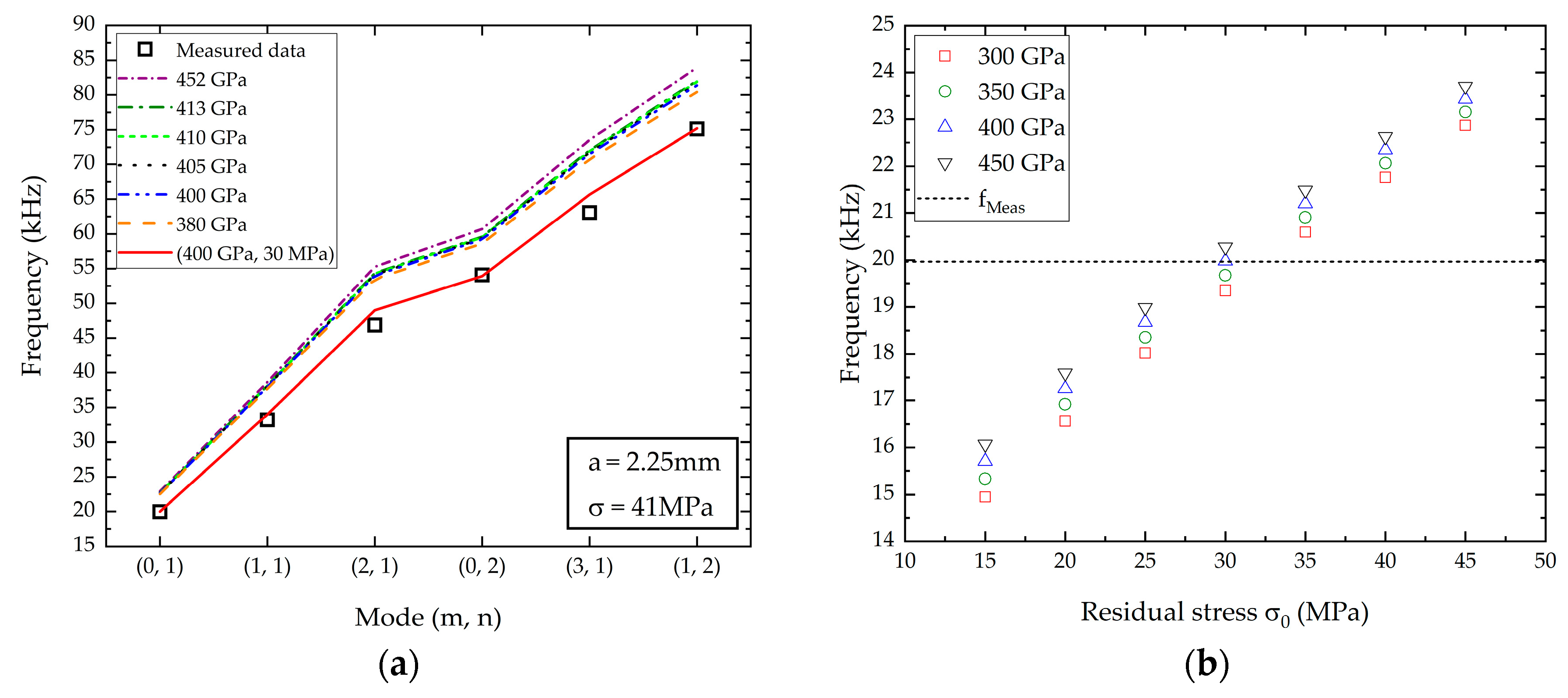

| Models | C1 | C2 | C2(υ = 0.25) | Approach |
|---|---|---|---|---|
| Lin [28] | 4.0 | (7 − υ)/3 | 2.25 | Energy minimization |
| Beams [27] | 4.0 | 8/3 | 2.67 | Spherical cap |
| Small et al. [29] | 4.0 | (8/3) × (1 − 0.241 × υ) | 2.51 | Finite Element Method |
| Pan et al. [30] | 4.0 | (8/3)/(1.026 + 0.233 × υ) | 2.46 | Finite Element Method |
| Hohlfelder et al. [31] | 4.0 | (8/3) × (1.015 − 0.247 × υ) | 2.54 | Number approximation |
| Timoshenko et al. [32] | - | (8/3) × 0.976/(1 + υ) | 2.08 | Energy minimization |
| Parameters | Values |
|---|---|
| A (Pa/m) | 3.0 × 108 |
| B (Pa/m3) | 4.6 × 1017 |
| Density (kg/m3) | 3210 |
| Poisson’s ratio | 0.25 |
| Membrane radius (µm) | 2250 |
| Membrane thickness (µm) | 8.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Messaoud, J.; Michaud, J.-F.; Certon, D.; Camarda, M.; Piluso, N.; Colin, L.; Barcella, F.; Alquier, D. Investigation of the Young’s Modulus and the Residual Stress of 4H-SiC Circular Membranes on 4H-SiC Substrates. Micromachines 2019, 10, 801. https://doi.org/10.3390/mi10120801
Ben Messaoud J, Michaud J-F, Certon D, Camarda M, Piluso N, Colin L, Barcella F, Alquier D. Investigation of the Young’s Modulus and the Residual Stress of 4H-SiC Circular Membranes on 4H-SiC Substrates. Micromachines. 2019; 10(12):801. https://doi.org/10.3390/mi10120801
Chicago/Turabian StyleBen Messaoud, Jaweb, Jean-François Michaud, Dominique Certon, Massimo Camarda, Nicolò Piluso, Laurent Colin, Flavien Barcella, and Daniel Alquier. 2019. "Investigation of the Young’s Modulus and the Residual Stress of 4H-SiC Circular Membranes on 4H-SiC Substrates" Micromachines 10, no. 12: 801. https://doi.org/10.3390/mi10120801
APA StyleBen Messaoud, J., Michaud, J.-F., Certon, D., Camarda, M., Piluso, N., Colin, L., Barcella, F., & Alquier, D. (2019). Investigation of the Young’s Modulus and the Residual Stress of 4H-SiC Circular Membranes on 4H-SiC Substrates. Micromachines, 10(12), 801. https://doi.org/10.3390/mi10120801





