A Study on the Trimming Effects on the Quality Factor of Micro-Shell Resonators Vibrating in Wineglass Modes
Abstract
:1. Introduction
2. Problem Characterization
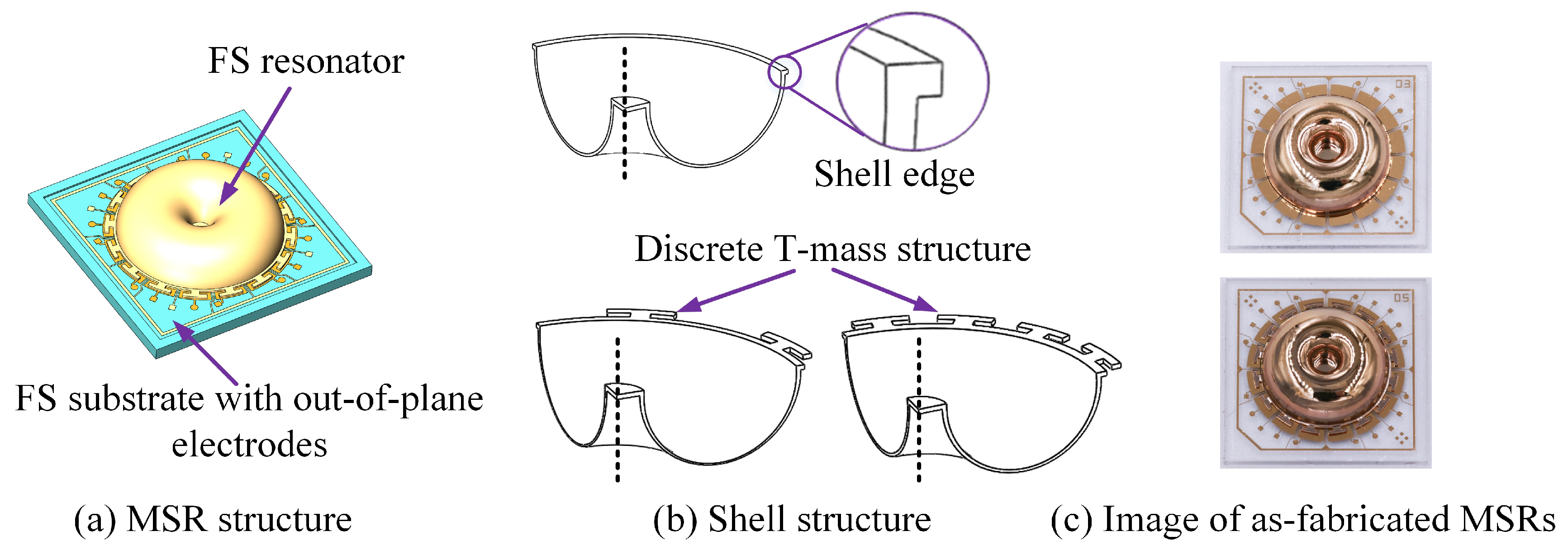
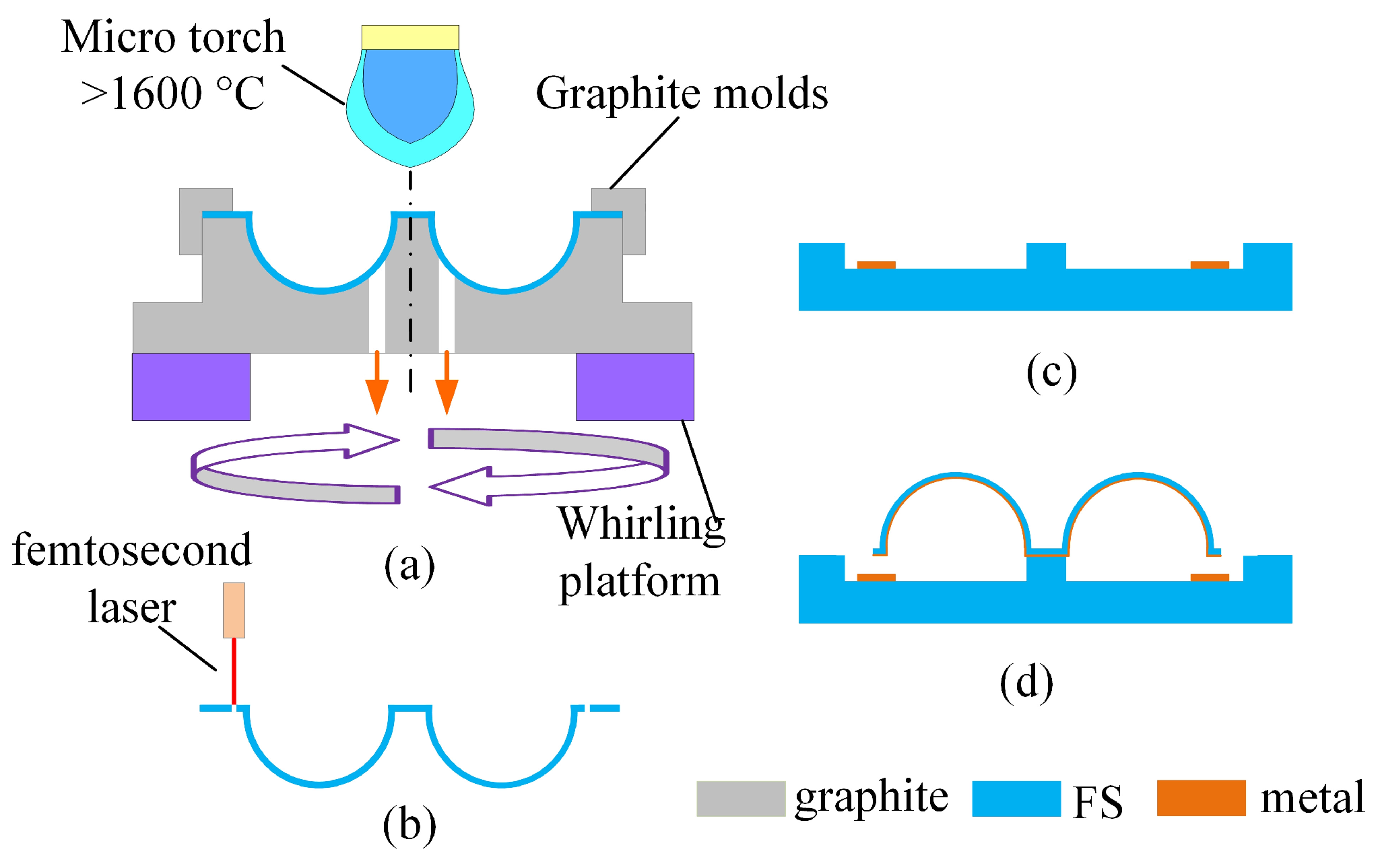
2.1. Structure Description
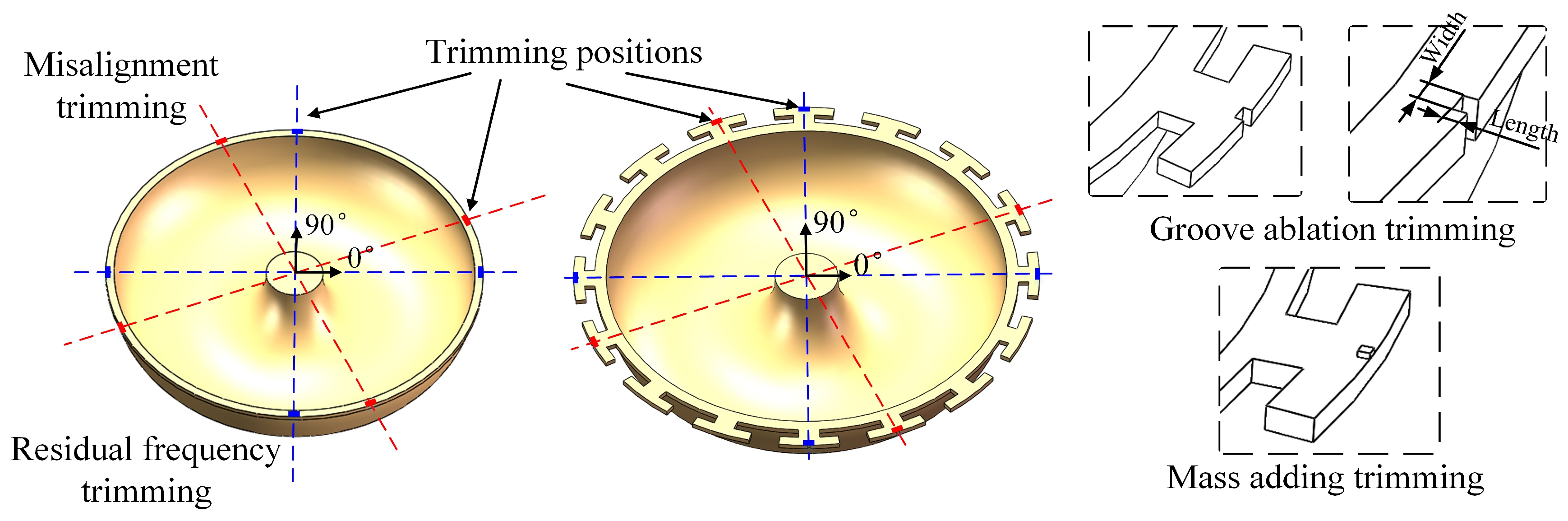
2.2. Trimming of FS MSRs
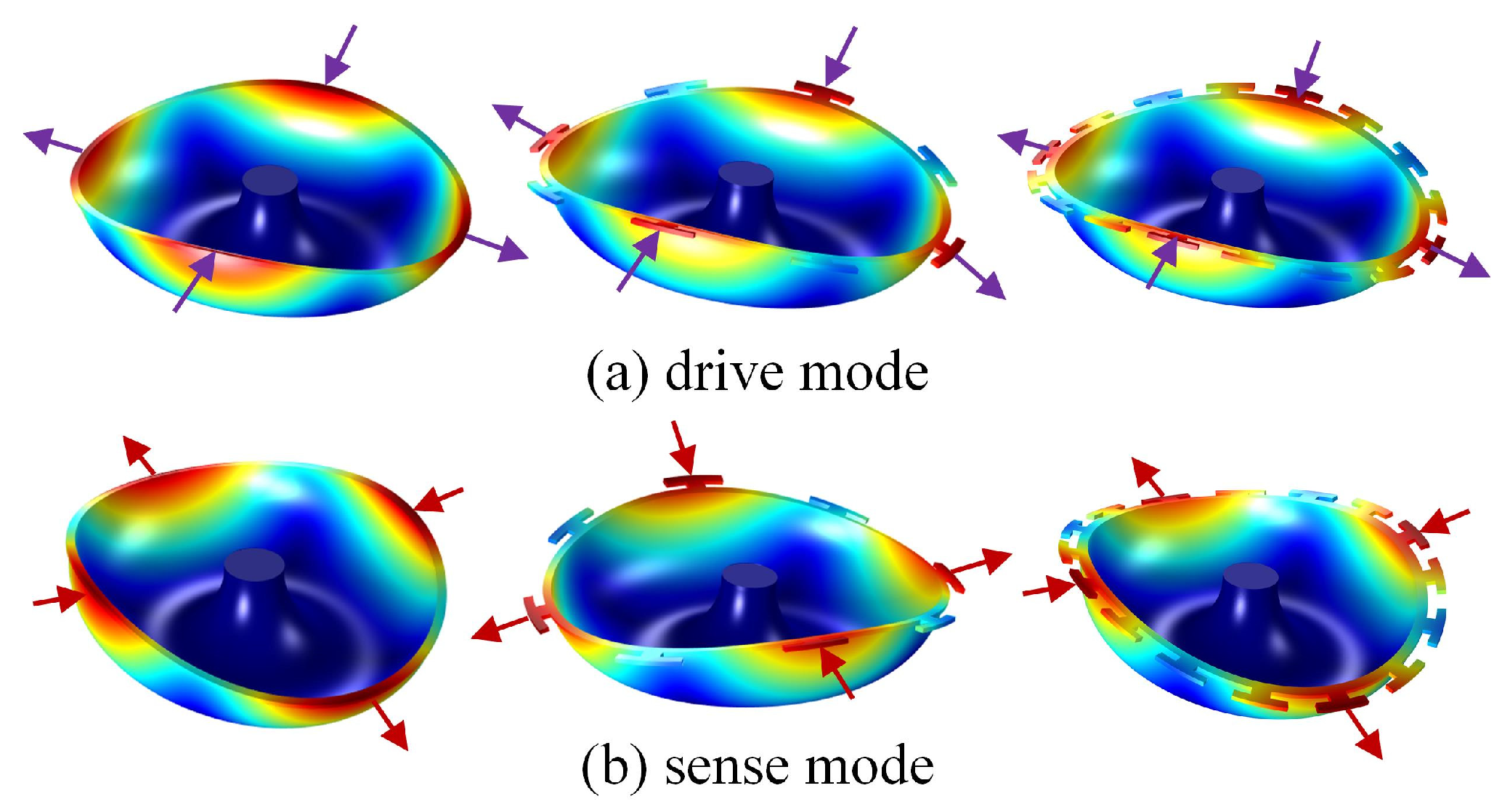
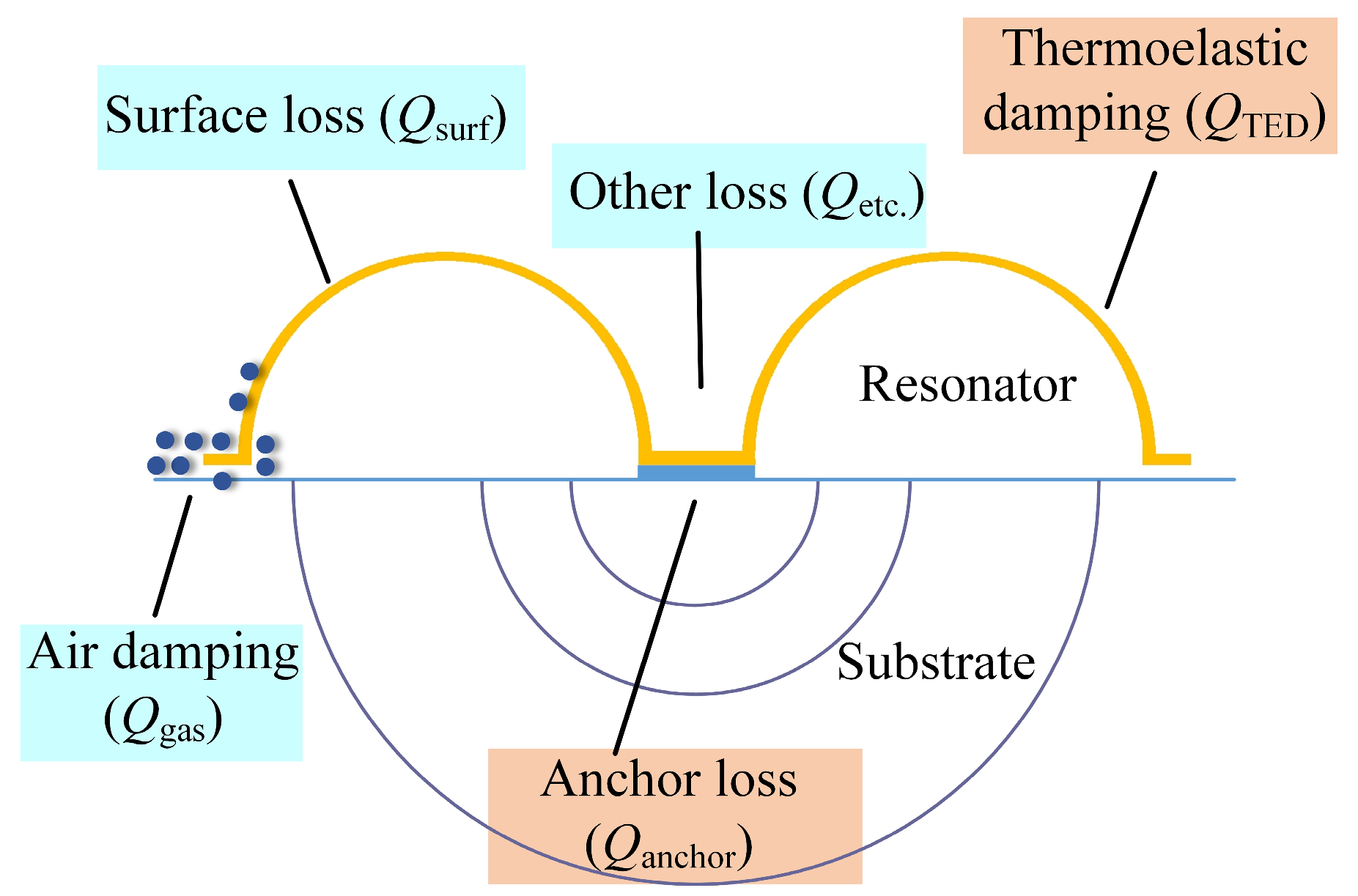
2.3. Quality Factor of the Trimmed Resonator
- Air damping is the most dominant factor when the resonator works at atmospheric conditions, including squeeze film damping and slide film damping. It can be eliminated by operating the resonator in a high vacuum condition. As for MSRs, the most concerned air damping is caused by the vibration of flat rim. Because the trimming process would not increase the area of the resonator rim, the Qgas could hardly change. Hence, the groove trimming process cannot increase air damping.
- Surface loss is often believed to be caused by defects, roughness, and other imperfections on the surface of the resonator [32]. At present, there is no analytical formula to calculate Qsurf, and modeling concerning Qsurf is still controversial. Besides, surface roughness is generally thought to be a main factor of the Qsurf. In our research, trimming grooves are ablated by a femtosecond laser, which uses the same process as the releasing of the shell structure. Thus, the effects of trimming on Qsurf are minimized through the femtosecond laser to achieve a smooth surface quality of the trimming grooves.
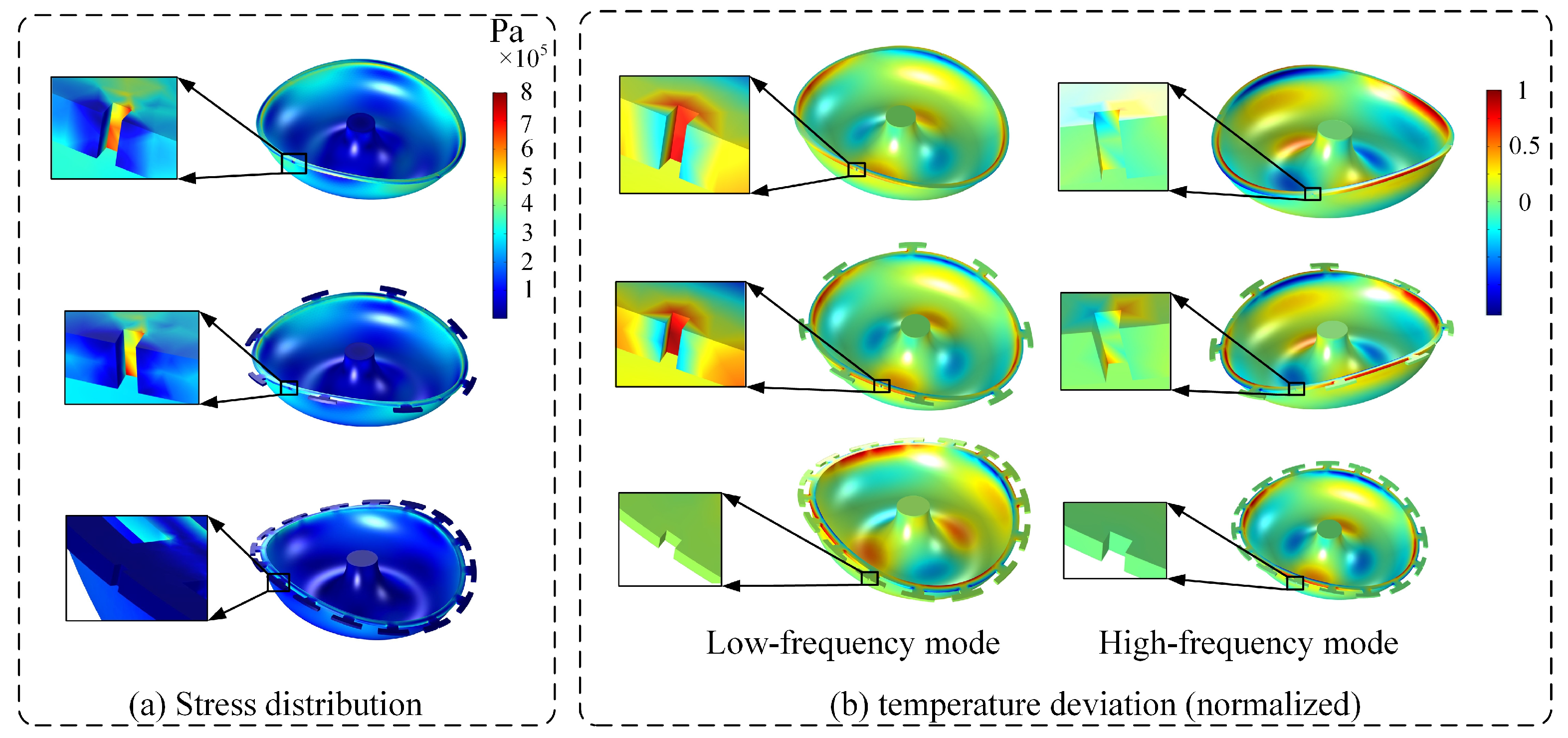
- Thermoelastic damping loss is caused by the interaction between elastic strain and thermal effects. When the MSR vibrates in the wineglass mode, some regions are under compression while others are under extension. In those conditions, irreversible heat flow occurs from the warmer parts of the structure to the cooler parts, and this heat flow is associated with energy loss [33]. Trimming grooves may have an impact on the stress distribution and elastic energy variation, resulting in more damping loss. Besides, the mass adding trimming method may cause a reduction of QTED because it could result in more heat generation and dissipation between the resonator and the added masses.
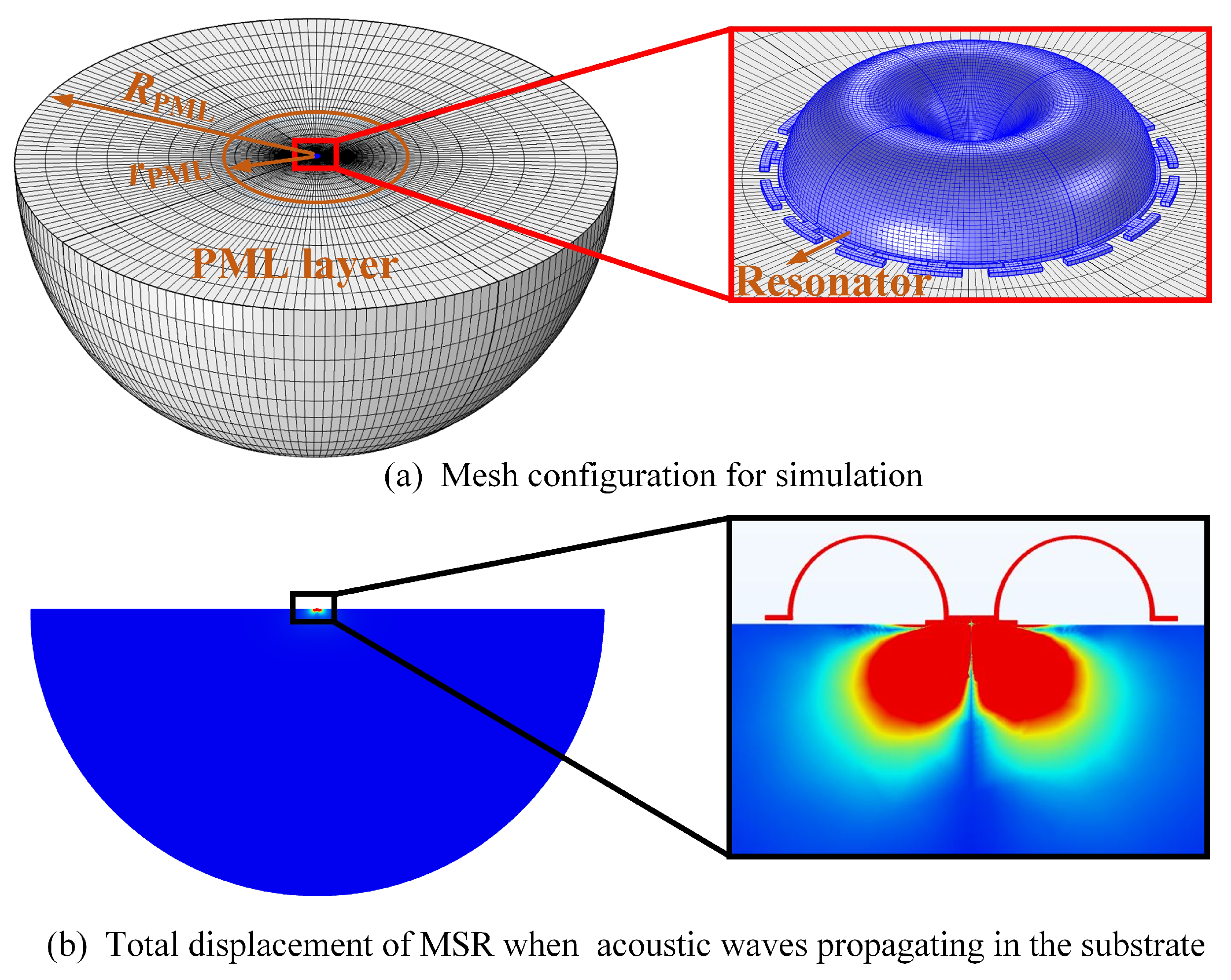
- Anchor losses occur when the vibration of the MSR and its supporting anchors excites acoustic waves propagating in the substrate [34]. These waves are radiated away from the resonator, resulting in a loss of mechanical energy. Trimming grooves may affect the coupling of the resonant mode to the substrate and result in more anchor loss.
3. FEM Simulation of Quality Factor
3.1. FEM Simulation of QTED of Trimmed MSRs
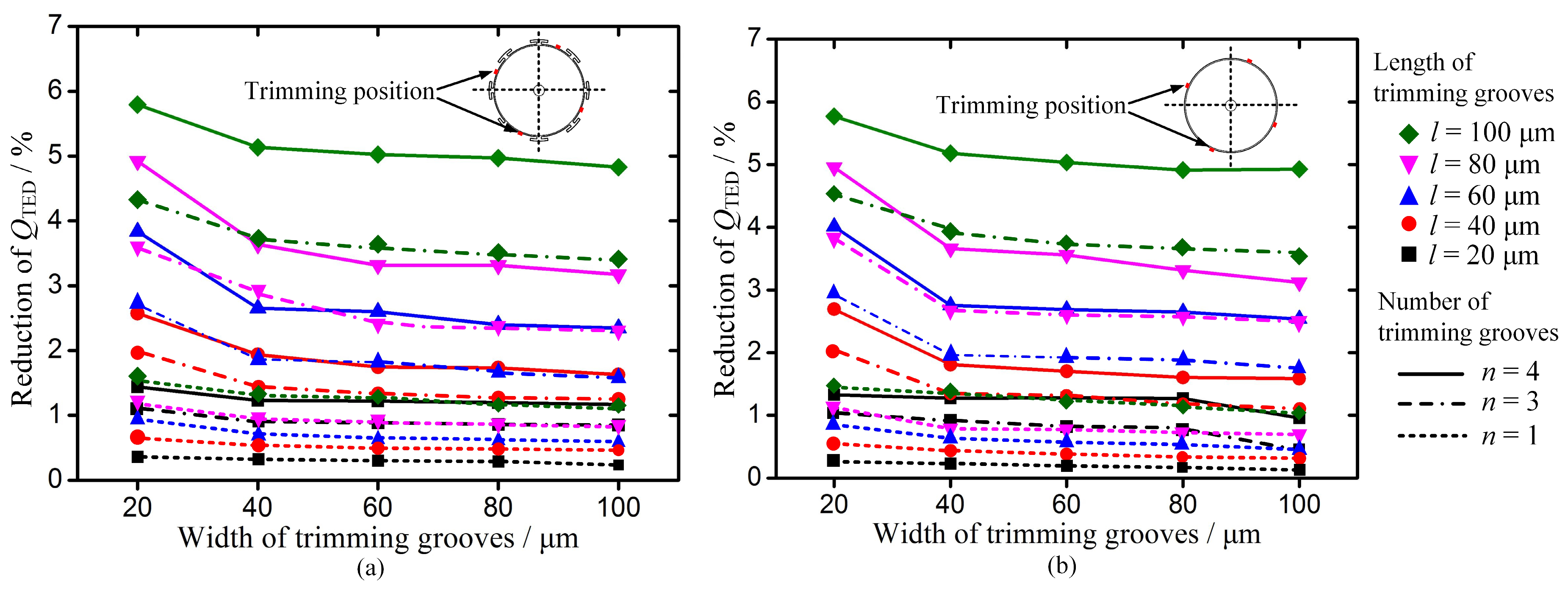
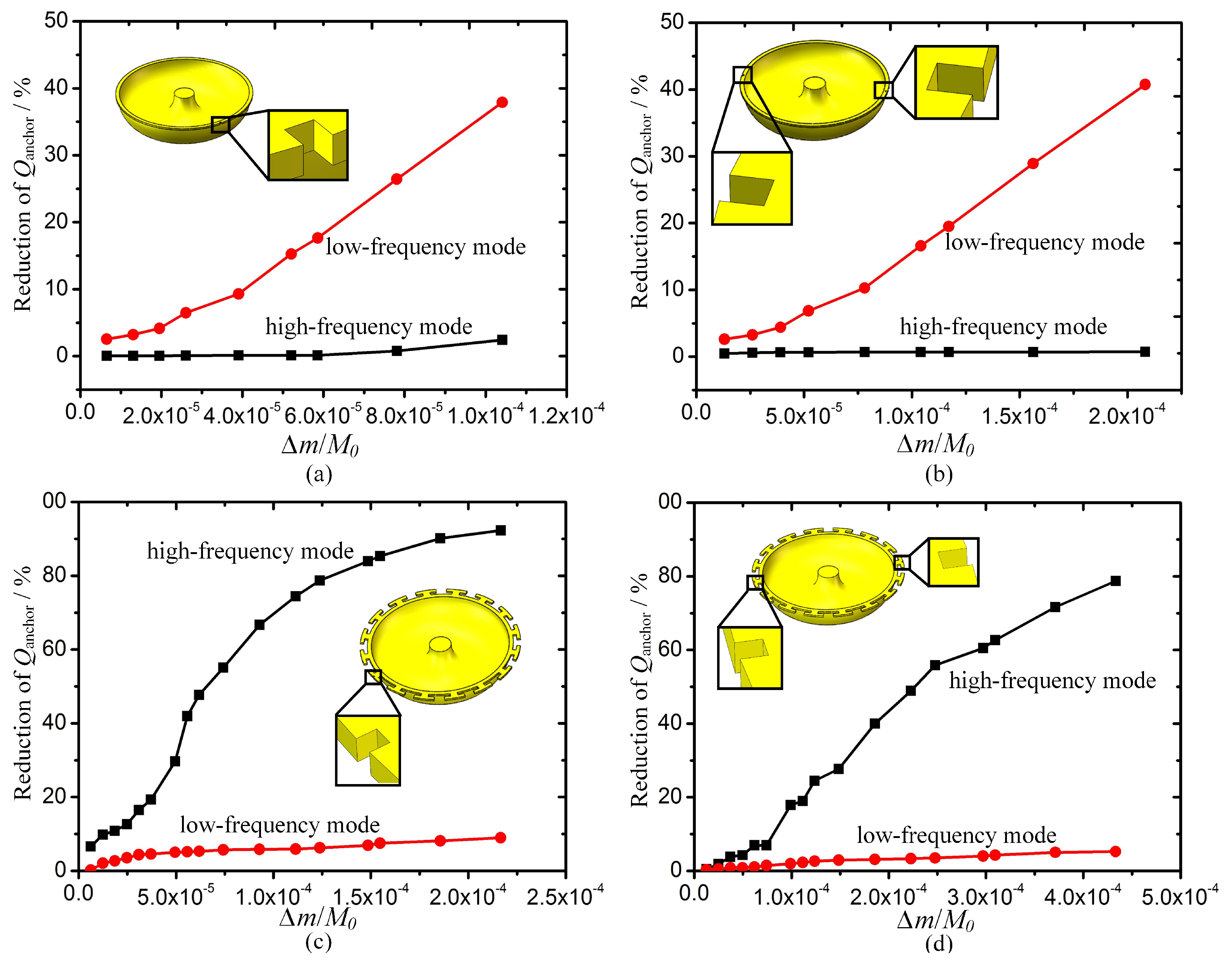
3.1.1. Effect of Removing Masses on QTED
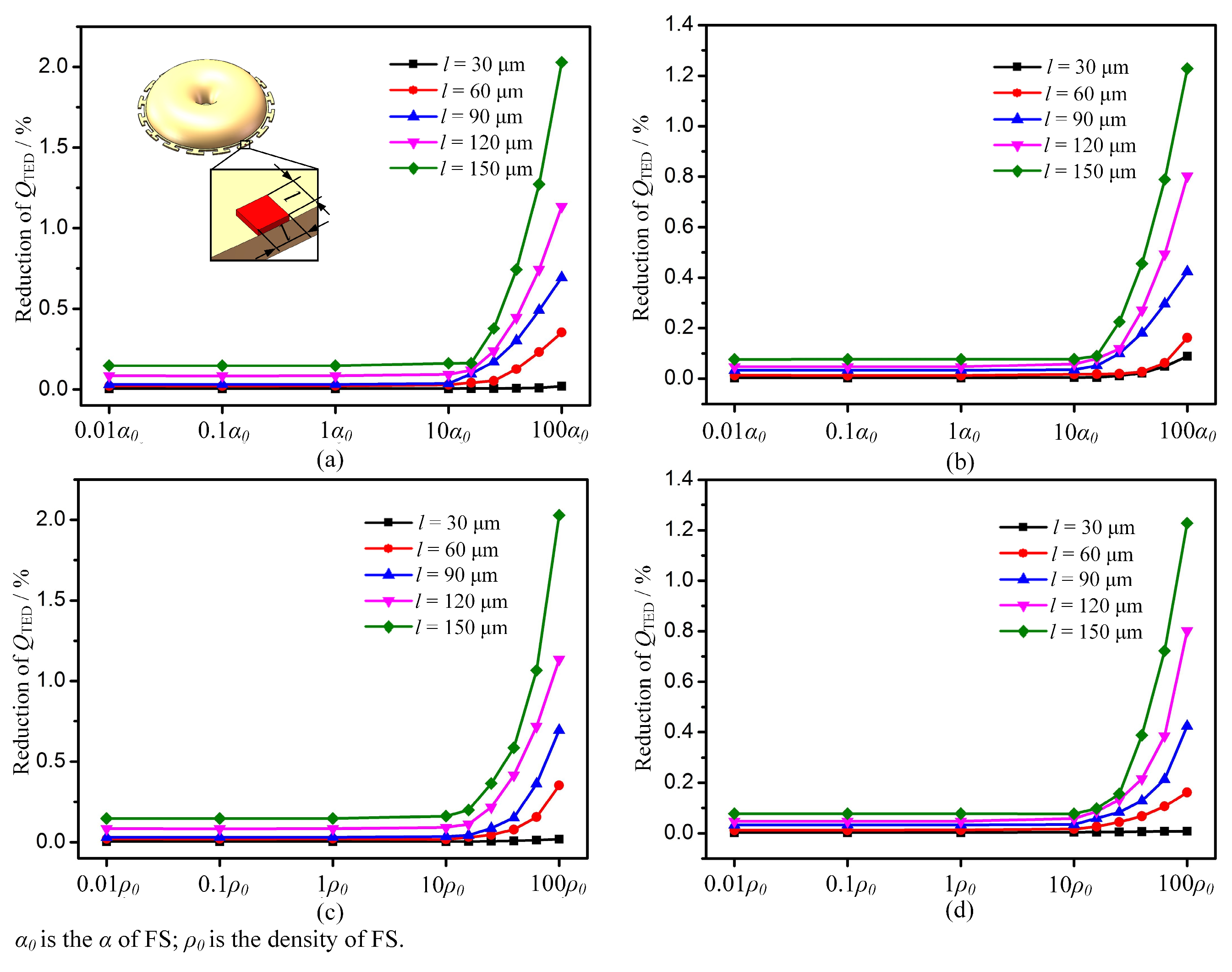
3.1.2. Effect of Added Masses on QTED
3.2. FEM Simulation of Qanchor of Trimmed MSRs
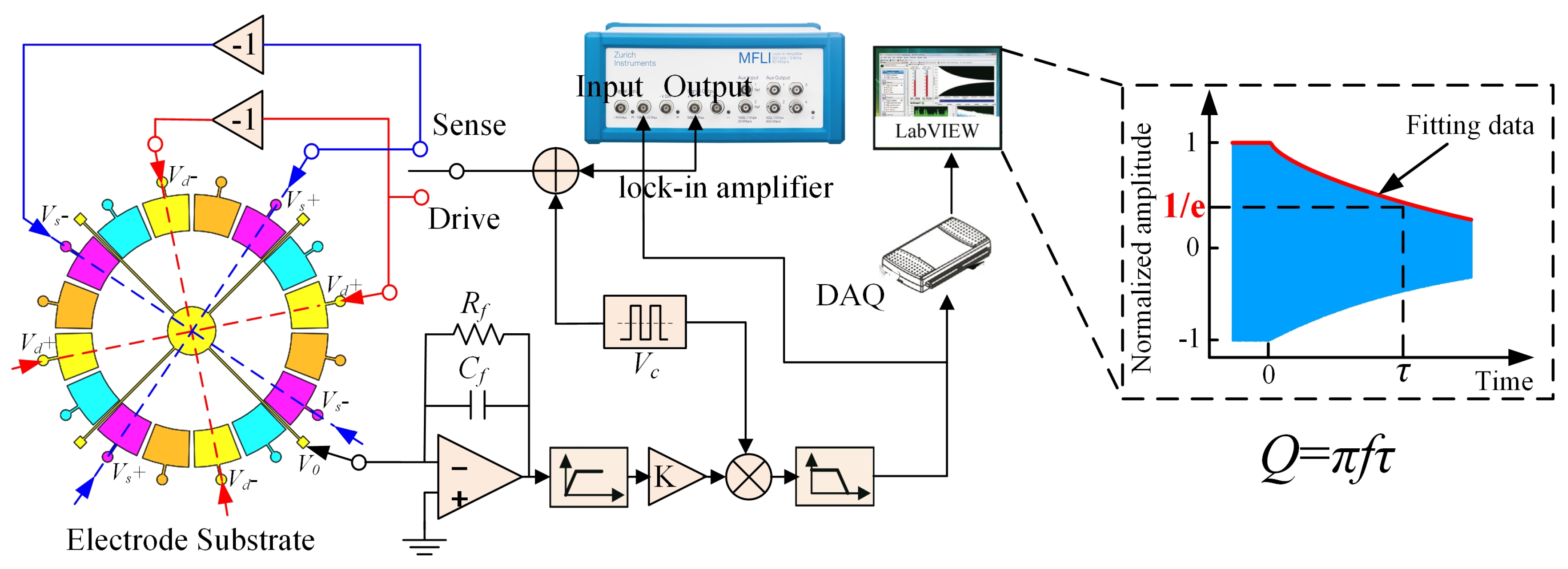
4. Experiments and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boyd, C.; Woo, J.K.; Cho, J.Y.; Nagourney, T.; Darvishian, A.; Shiari, B.; Najafi, K. Effect of drive-axis displacement on MEMS birdbath resonator gyroscope performance. In Proceedings of the 4th IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27 March 2017; pp. 175–176. [Google Scholar]
- Cho, J.Y.; Woo, J.K.; He, G.; Yang, D.; Boyd, C.; Singh, S.; Darvishian, A.; Shiari, B.; Najafi, K. 1.5-Million Q-factor vaccum-packaged birdbath resonator gyroscope (BRG). In Proceedings of the 32th IEEE International Conference on Micro Electro Mechanical Systems, Seoul, Korea, 27 January 2019; pp. 210–213. [Google Scholar]
- Bernstein, J.J.; Bancu, M.G.; Bauer, J.M.; Cook, E.H.; Kumar, P.; Newton, E.; Nyinjee, T.; Perlin, G.E.; Ricker, J.A.; Teynor, W.A.; et al. High Q diamond hemispherical resonators: Fabrication and energy loss mechanisms. J. Micromech. Microeng. 2015, 25, 085006. [Google Scholar] [CrossRef]
- Heidari, A.; Chan, M.; Yang, H.; Jaramillo, G.; Taheri, P.; Fonda, P.; Najar, H.; Yamazaki, K.; Lin, L.; Horsley, D.A. Hemispherical wineglass resonators fabricated from the microcrystalline diamond. J. Micromech. Microeng. 2013, 23, 571–596. [Google Scholar] [CrossRef]
- Shao, P.; Tavassoli, V.; Mayberry, C.L.; Ayazi, F. A 3D-HARPSS Polysilicon Microhemispherical Shell Resonating Gyroscope: Design, Fabrication, and Characterization. IEEE Sens. J. 2015, 15, 4974–4985. [Google Scholar] [CrossRef]
- Pai, P.; Chowdhruy, F.K.; Pourzand, H.; Tabib-Azar, M. Fabrication and testing of hemispherical MEMS wineglass resonators. In Proceedings of the 26th IEEE International Conference on Micro Electro Mechanical Systems, Taipei, Taiwan, 20 January 2013; pp. 677–680. [Google Scholar]
- Shiari, B.; Nagourney, T.; Darvishian, A.; Cho, J.Y.; Najafi, K. Simulation of blowtorch reflow of fused silica. J. Microelectromech. Syst. 2017, 26, 782–792. [Google Scholar] [CrossRef]
- Senkal, D.; Ahamed, M.J.; Trusov, A.A.; Shkel, A.M. High temperature micro-glassblowing process demonstrated on fused quartz and ULE TSG. Sens. Actuators A Phys. 2015, 201, 525–531. [Google Scholar] [CrossRef]
- Senkal, D.; Ahamed, M.J.; Trusov, A.A.; Shkel, A.M. Electrostatic and mechanical characterization of 3-D micro-wineglass resonators. Sens. Actuators A Phys. 2014, 215, 150–154. [Google Scholar] [CrossRef] [Green Version]
- Ghaffari, S.; Kenny, T.W. Thermoelastic dissipation in composite silicon MEMS resonators with thin film silicon dioxide coating. MRS Proc. 2012, 1426, 193–198. [Google Scholar] [CrossRef]
- Judge, J.A.; Photiadis, D.M.; Vignola, J.F.; Houston, B.H.; Jarzynski, J. Attachment loss of micromechanical and nanomechanical resonators in the limits of thick and thin support structures. J. Appl. Phys. 2007, 101, 013521. [Google Scholar] [CrossRef]
- Darvishian, A.; Shiari, B.; He, G.; Najafi, K. Effect of substrate thickness on quality factor of mechanical resonators. In Proceedings of the 2th IEEE International Symposium on Inertial Sensors & Systems, Hapuna Beach, HI, USA, 23 March 2015; pp. 1–4. [Google Scholar]
- Darvishian, A.; Shiari, B.; Cho, J.Y.; Nagourney, T.; Najafi, K. Anchor loss in hemispherical shell resonators. J. Microelectromech. Syst. 2017, 26, 51–66. [Google Scholar] [CrossRef]
- Darvishian, A.; Nagourney, T.; Cho, J.Y.; Shiari, B.; Najafi, K. Thermoelastic dissipation in micromachined birdbath shell resonators. J. Microelectromech. Syst. 2017, 26, 758–772. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Seshia, A.A. 5.4 MHz single-crystal silicon wine glass mode disk resonator with quality factor of 2 million. Sens. Actuators A Phys. 2009, 156, 28–35. [Google Scholar] [CrossRef]
- Khine, L.; Palaniapan, M.; Wong, W.K. 6 MHz bulk mode resonator with Q values exceeding one million. In Proceedings of the 14th International Conference on Solid-state Sensors, Actuators & Microsystems, Lyon, France, 10 June 2007; pp. 2445–2448. [Google Scholar]
- Elsayed, M.Y.; Nabki, F.; El-Gamal, M.N. A Combined Comb/ Bulk Mode Gyroscope Structure for Enhanced Sensitivity. In Proceedings of the 26th IEEE International Conference on Micro Electro Mechanical Systems, Taipei, Taiwan, 20 January 2013; pp. 649–652. [Google Scholar]
- Elsayed, M.Y.; Nabki, F. Piezoelectric Bulk Mode Disk Resonator Post-Processed for Enhanced Quality Factor Performance. J. Microelectromech. Syst. 2017, 26, 75–83. [Google Scholar] [CrossRef]
- Ahamed, M.J.; Senkal, D.; Shkel, A.M. Effect of Annealing on Mechanical Quality Factor of Fused Quartz Hemispherical Resonator. In Proceedings of the 1st IEEE International Symposium on Inertial Sensors and Systems(ISISS), Laguna Beach, CA, USA, 25 February 2014; pp. 59–62. [Google Scholar]
- Kanik, M.; Bordeenithikasem, P.; Kim, D.; Selden, N.; Desai, A.; M’Closkey, R. Metallic Glass Hemispherical Shell Resonators. J. Microelectromech. Syst. 2015, 24, 19–28. [Google Scholar] [CrossRef]
- Senkal, D.; Ahamed, M.J.; Trusov, A.A.; Shkel, A.M. Achieving Sub-Hz Frequency Symmetry in Micro-Glassblown Wineglass Resonators. J. Microelectromech. Syst. 2014, 23, 30–38. [Google Scholar] [CrossRef]
- Hamelin, B.; Tavassoli, V.; Ayazi, F. Localized Eutectic Trimming of Polysilicon Microhemispherical Resonating Gyroscopes. IEEE Sens. J. 2014, 24, 3498–3505. [Google Scholar] [CrossRef]
- Asadian, M.H.; Wang, Y.; Askari, S.; Shkel, A. Controlled capacitive gaps for electrostatic actuation and tuning of 3D fused quartz micro wineglass resonator gyroscope. In Proceedings of the 4th IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27 March 2017; pp. 19–22. [Google Scholar]
- Li, W.; Hou, Z.; Shi, Y.; Lu, K.; Xi, X.; Wu, Y.; Wu, X.; Xiao, D. Application of micro-blowtorching process with whirling platform for enhancing frequency symmetry of microshell structure. J. Micromech. Microeng. 2018, 28, 115004. [Google Scholar] [CrossRef]
- Lu, K.; Shi, Y.; Xiao, D.; Hou, Z.; Li, W.; Wu, X.; Wu, Y. Investigation on precise frequency trimming of a micro shell resonator with T-shape masses using low power femtosecond laser ablation. In Proceedings of the 5th IEEE International Symposium on Inertial Sensors & Systems, Lake Como, Italy, 26 March 2018; pp. 153–156. [Google Scholar]
- Lu, K.; Xi, X.; Li, W.; Shi, Y.; Hou, Z.; Zhuo, M.; Wu, X.; Wu, Y.; Xiao, D. Research on Precise Mechanical Trimming of a Micro Shell Resonator with T-shape Masses Using Femtosecond Laser Ablation. Sens. Actuators A Phys. 2019, 201, 525–531. [Google Scholar] [CrossRef]
- Xiao, D.; Li, W.; Hou, Z.; Lu, K.; Shi, Y.; Wu, Y. Fused Silica Micro Shell Resonator with T-masses for Gyroscopic Application. J. Microelectromech. Syst. 2017, 99, 1–12. [Google Scholar] [CrossRef]
- Li, W.; Hou, Z.; Xiao, D.; Lu, K.; Shi, Y.; Wu, Y.; Wu, X. Decoupling Design of Stiffness and Mass for Micro Shell Resonator with High Sensitivity. In Proceedings of the 31th IEEE International Conference on Micro Electro Mechanical Systems, Belfast, Ireland, 21 January 2018; pp. 988–991. [Google Scholar]
- Fox, C.H.J. A simple theory for the analysis and correction of frequency splitting in slightly imperfect rings. J. Sound Vib. 1990, 142, 227–243. [Google Scholar] [CrossRef]
- Ahn, C.H.; Ng, E.J.; Hong, V.A.; Yang, Y.; Lee, B.J.; Flader, I.; Kenny, T.W. Mode-Matching of Wineglass Mode Disk Resonator Gyroscope in (100) Single Crystal Silicon. J. Microelectromech. Syst. 2017, 24, 343–350. [Google Scholar] [CrossRef]
- Rourke, A.K.; Mcwilliam, S.; Fox, C.H.J. Multi-mode Trimming of Imperfect Ring. J. Sound Vib. 2001, 248, 695–724. [Google Scholar] [CrossRef]
- Kim, B. Temperature dependence of quality factor in MEMS. J. Microelectromech. Syst. 2008, 17, 755–766. [Google Scholar] [CrossRef]
- Zener, Z. Internal friction in solids II. General theory of thermoelastic internal friction. Phys. Rev. 1938, 53, 90–99. [Google Scholar] [CrossRef]
- Xia, D.; Huang, L.; Xu, L.; Gao, H. Structural Analysis of Disk Resonance Gyroscope. Micromachines 2017, 8, 296. [Google Scholar] [CrossRef] [PubMed]


| Type of MSRs | Initial Δf/Hz | Original Q | Q after Trimming | Reduction of Q | ||||
|---|---|---|---|---|---|---|---|---|
| Qdrive | Qsense | Qdrive | Qsense | Drive Mode | Sense Mode | |||
| MSR with 16 T-masses | No.1 | 13.3 | 168.5 k | 179.3 k | 165.5 k | 175.1 k | 1.78% | 2.34% |
| No.2 | 15.8 | 136.8 k | 125.9 k | 133.6 k | 121.9 k | 2.34% | 3.18% | |
| No.3 | 20.7 | 156.9 k | 150.2 k | 153.7 k | 145.5 k | 2.04% | 3.13% | |
| MSR with 8 T-masses | No.4 | 20.82 | 129.4 k | 134.3 k | 110.7 k | 118.2 k | 14.45% | 11.99% |
| No.5 | 35.5 | 135.5 k | 145.1 k | 113.8 k | 138.9 k | 16.01% | 4.27% | |
| No.6 | 46.07 | 122.2 k | 119.8 k | 101.2 k | 109.7 k | 17.18% | 8.43% | |
| MSR without T-masses | No.7 | 15.4 | 145.6 k | 147.2 k | 125.3 k | 138.2 k | 13.94% | 6.11% |
| No.8 | 19.7 | 149.7 k | 156.6 k | 128.1 k | 141.8 k | 14.43% | 9.45% | |
| No.9 | 22.5 | 161.3 k | 143.8 k | 139.7 k | 129.9 k | 13.39% | 9.66% | |
| Samples | Initial Δf/Hz | Diameter of Mass/μm | Original Q | Q after Trimming | Reduction of Q | |||
|---|---|---|---|---|---|---|---|---|
| Qdrive | Qsense | Qdrive | Qsense | Drive Mode | Sense Mode | |||
| No.10 | 20.7 | ~ ϕ 80 | 157.1 k | 168.4 k | 139.8 k | 155.6 k | 11.01% | 7.60% |
| No.11 | 23.5 | ~ ϕ 120 | 179.6 k | 171.5 k | 150.9 k | 158.1 k | 15.98% | 7.81% |
| No.12 | 18.2 | ~ ϕ 165 | 149.8 k | 155.7 k | 120.6 k | 138.3 k | 19.49% | 11.2% |
| Samples | Initial Δf/Hz | Original Q | Q after Trimming | Reduction of Q | |||
|---|---|---|---|---|---|---|---|
| Qdrive | Qsense | Qdrive | Qsense | Drive Mode | Sense Mode | ||
| No.13 | 12.8 | 175.9 k | 161.2 k | 171.1 k | 157.6 k | 2.73% | 2.23% |
| No.14 | 18.7 | 136.4 k | 150.1 k | 134.3 k | 147.1 k | 1.54% | 2.00% |
| No.15 | 21.6 | 167.3 k | 175.7 k | 164.5 k | 170.2 k | 1.67% | 3.13% |
| No.16 | 13.9 | 146.8 k | 161.9 k | 144.1 k | 157.6 k | 1.83% | 2.66% |
| No.17 | 16.4 | 131.9 k | 129.1 k | 128.2 k | 124.3 k | 2.81% | 3.72% |
| No.18 | 23.8 | 153.8 k | 162.7 k | 150.9 k | 157.1 k | 1.89% | 3.44% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.; Xi, X.; Xiao, D.; Shi, Y.; Zhuo, M.; Wu, X.; Wu, Y. A Study on the Trimming Effects on the Quality Factor of Micro-Shell Resonators Vibrating in Wineglass Modes. Micromachines 2019, 10, 695. https://doi.org/10.3390/mi10100695
Lu K, Xi X, Xiao D, Shi Y, Zhuo M, Wu X, Wu Y. A Study on the Trimming Effects on the Quality Factor of Micro-Shell Resonators Vibrating in Wineglass Modes. Micromachines. 2019; 10(10):695. https://doi.org/10.3390/mi10100695
Chicago/Turabian StyleLu, Kun, Xiang Xi, Dingbang Xiao, Yan Shi, Ming Zhuo, Xuezhong Wu, and Yulie Wu. 2019. "A Study on the Trimming Effects on the Quality Factor of Micro-Shell Resonators Vibrating in Wineglass Modes" Micromachines 10, no. 10: 695. https://doi.org/10.3390/mi10100695
APA StyleLu, K., Xi, X., Xiao, D., Shi, Y., Zhuo, M., Wu, X., & Wu, Y. (2019). A Study on the Trimming Effects on the Quality Factor of Micro-Shell Resonators Vibrating in Wineglass Modes. Micromachines, 10(10), 695. https://doi.org/10.3390/mi10100695




