Hybrid 3D Shape Measurement Using the MEMS Scanning Micromirror
Abstract
1. Introduction
2. Principles
2.1. Principle of 3D Shape Measurement with FPP and LSS
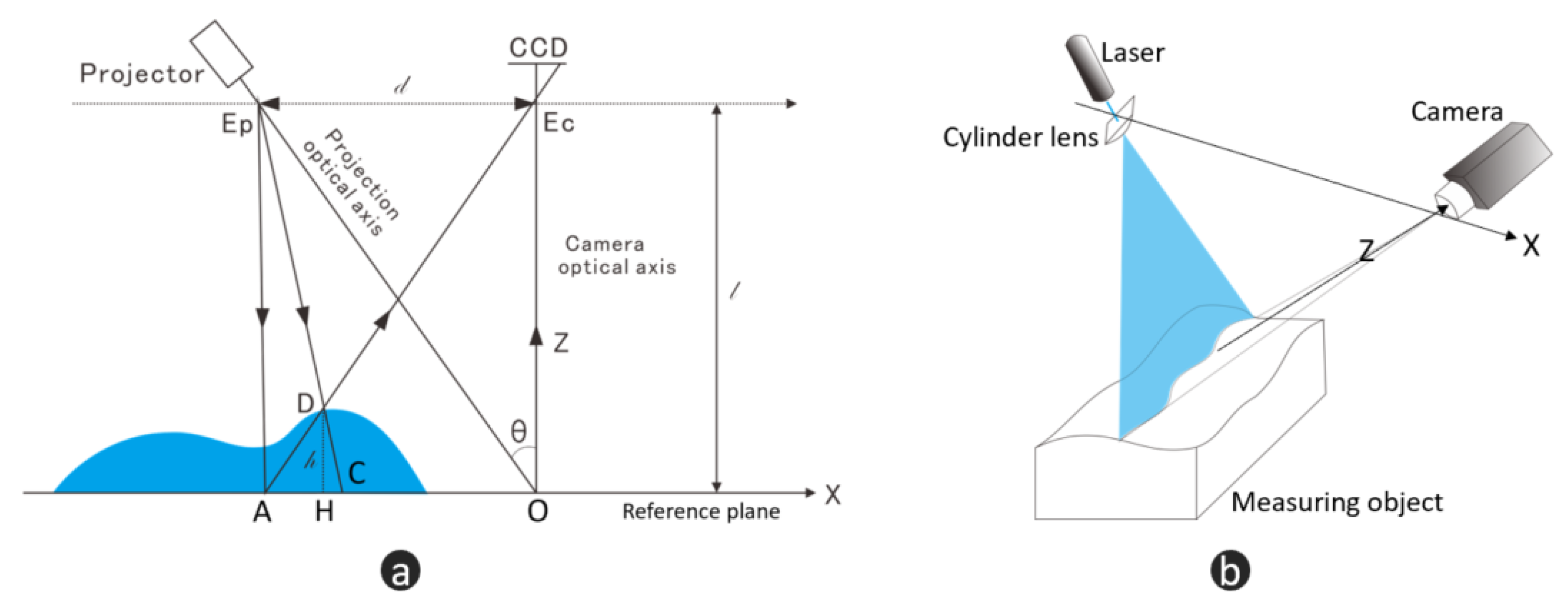
2.1.1. Principle of Fringe Projection Profilometry
2.1.2. Principle of Laser Stripe Scanning
2.2. Hybrid 3D Shape Measurement System
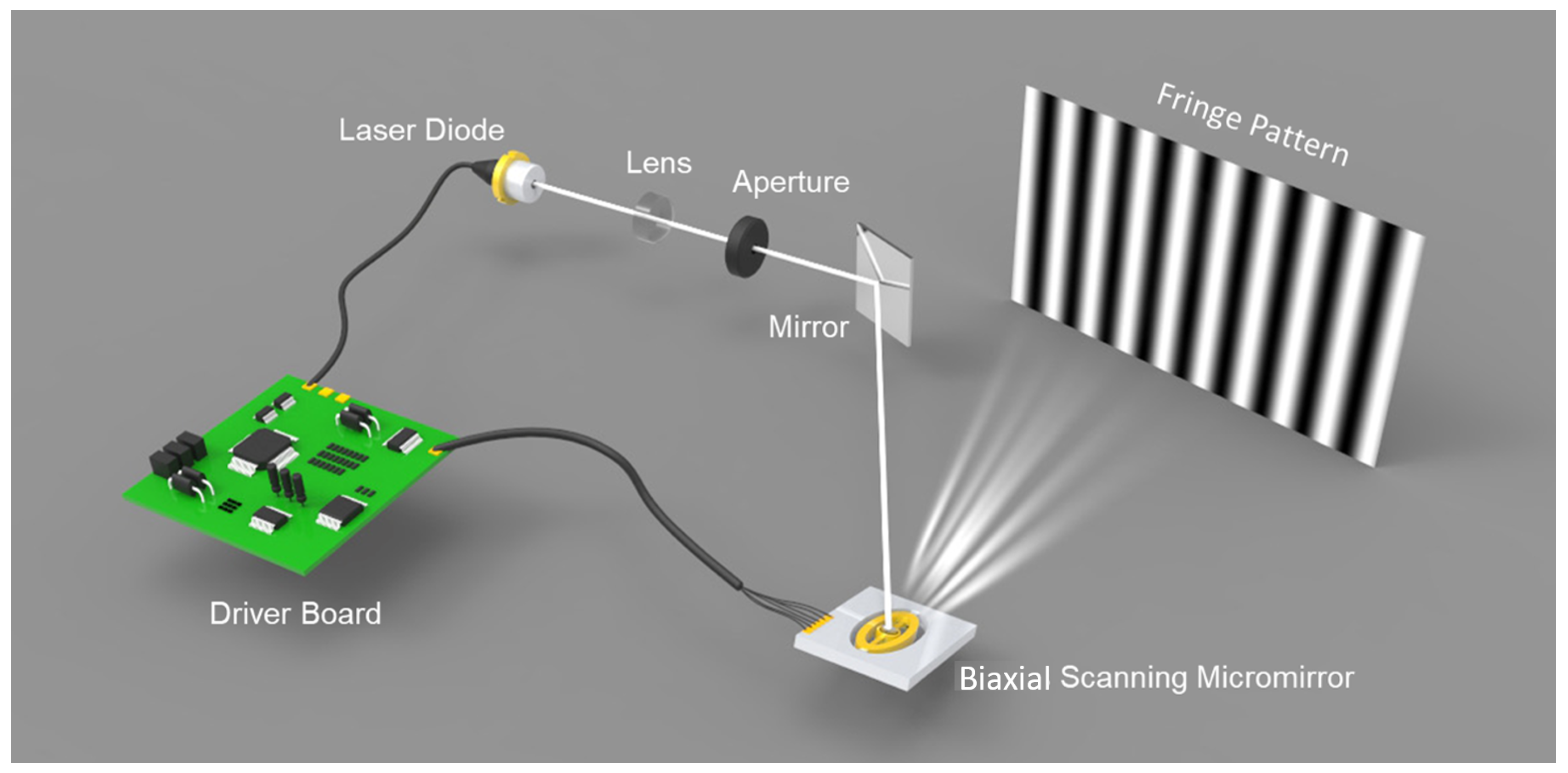
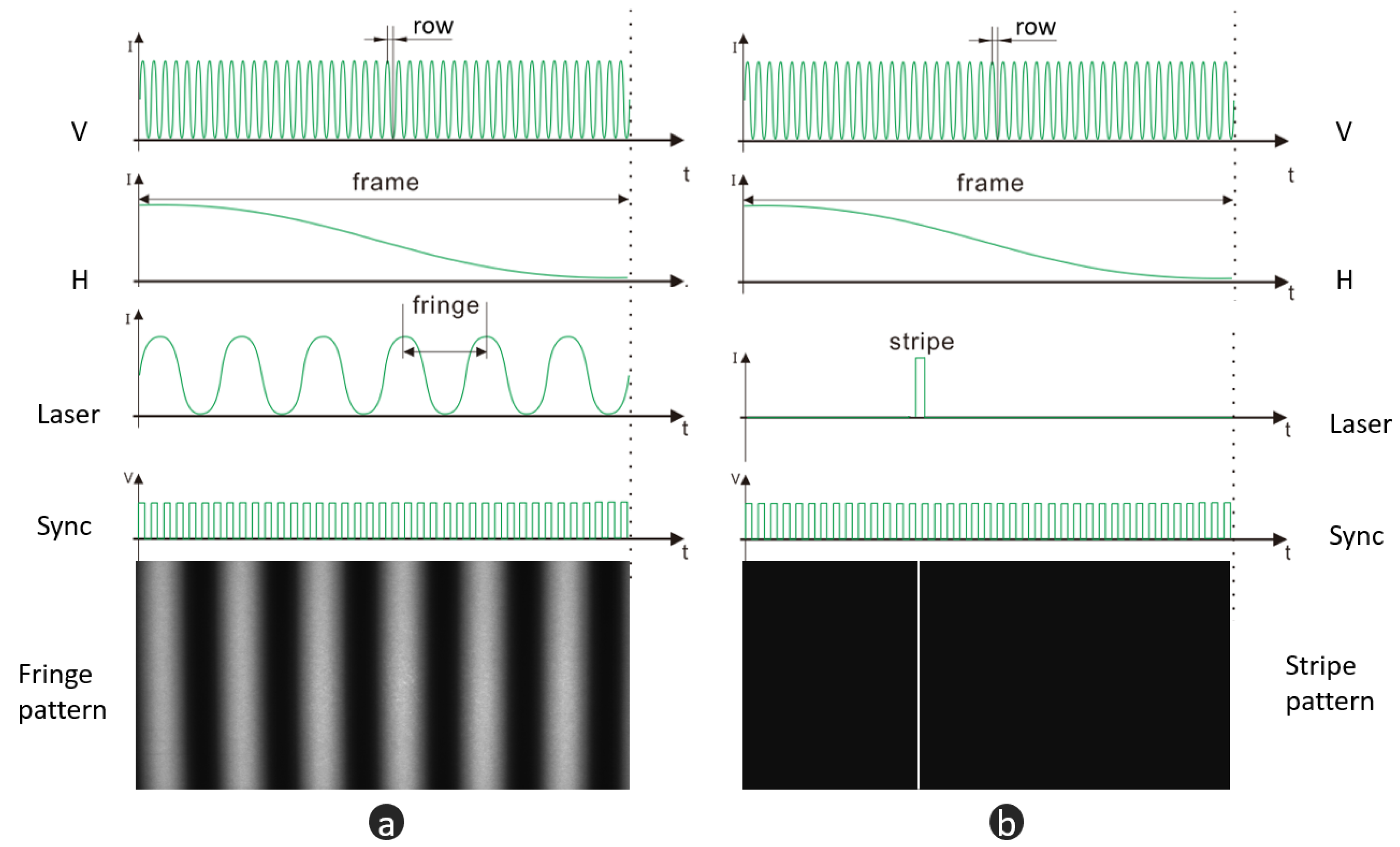
2.2.1. Biaxial MEMS Micromirror-Based Pattern Projection
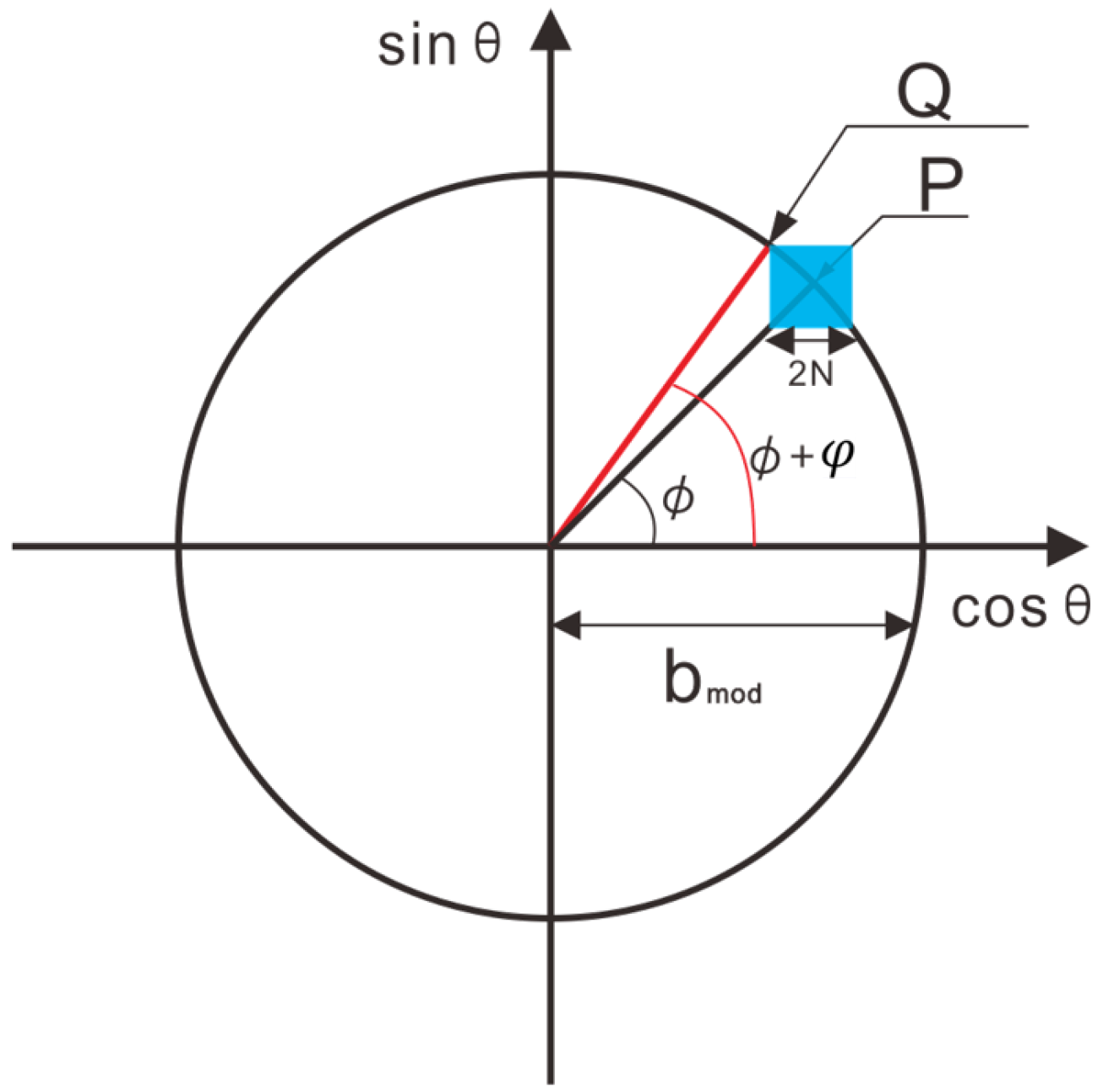
2.2.2. Quality Index in the Proposed Approach
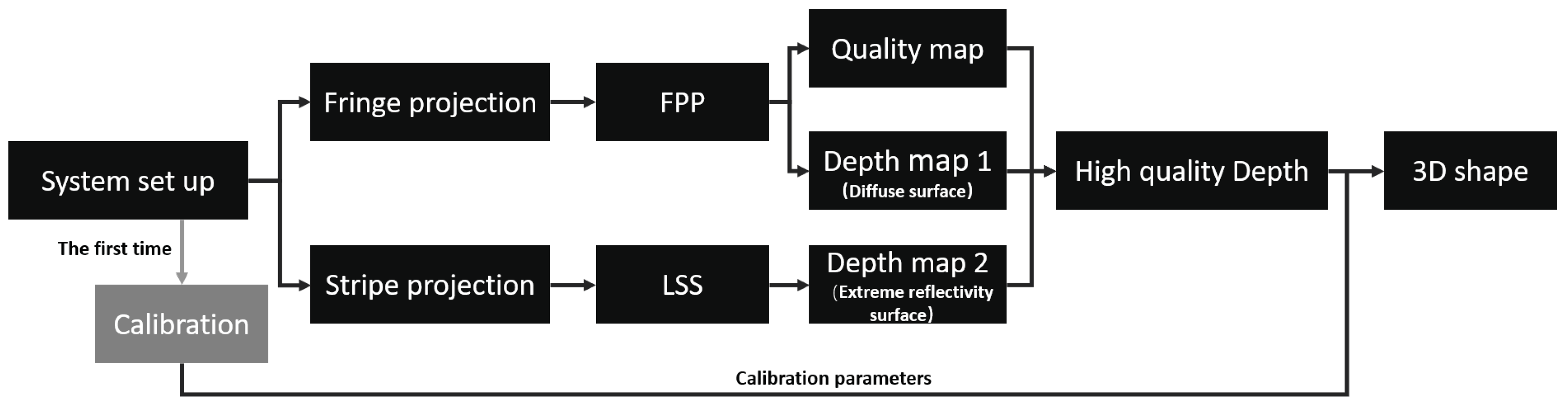
2.2.3. Hybrid 3D Shape Measurement Pipeline
3. Experiments
3.1. Linearity Test of Proposed Pattern Projection System
3.2. Experiments on the Quality Index
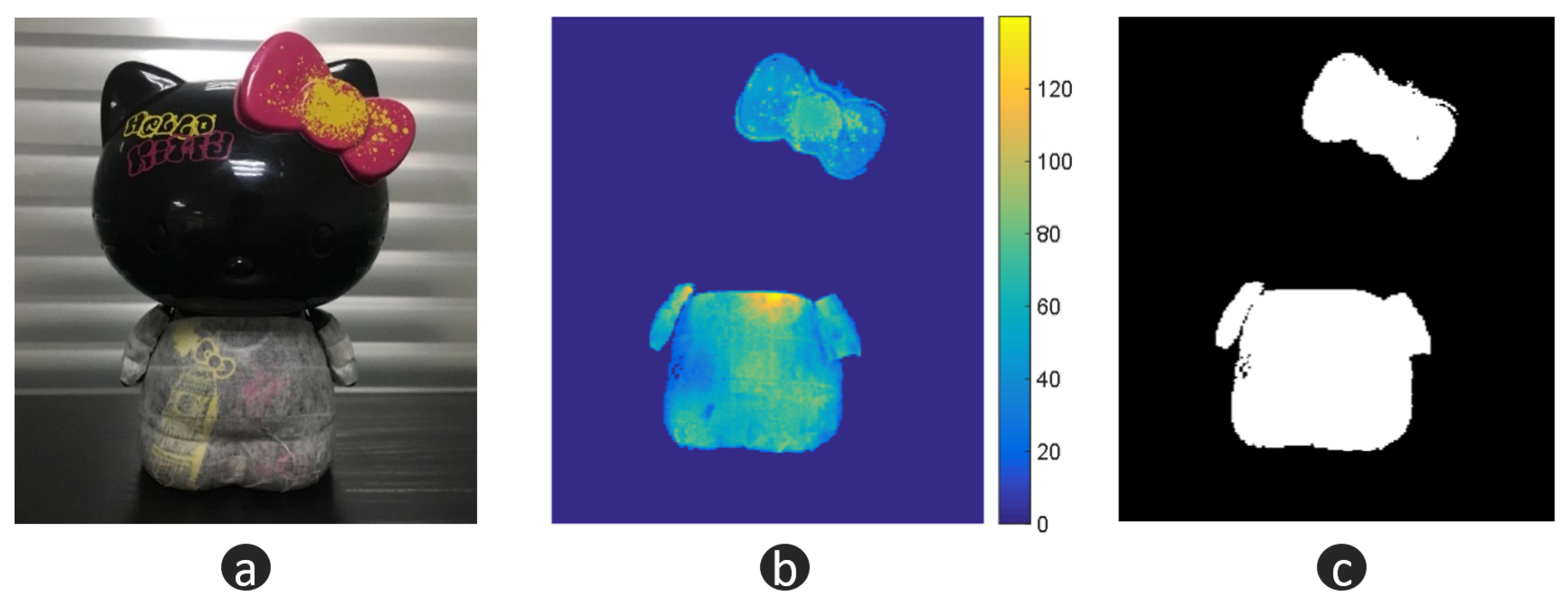
3.3. Hybrid 3D Shape Measurement
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rautaray, S.S.; Agrawal, A. Vision based hand gesture recognition for human computer interaction: A survey. Artif. Intell. Rev. 2015, 43, 1–54. [Google Scholar] [CrossRef]
- Raheja, J.L.; Chandra, M.; Chaudhary, A. 3D gesture based real-time object selection and recognition. Pattern Recognit. Lett. 2018, 115, 14–19. [Google Scholar] [CrossRef]
- Soltanpour, S.; Boufama, B.; Wu, Q.J. A survey of local feature methods for 3D face recognition. Pattern Recognit. 2017, 72, 391–406. [Google Scholar] [CrossRef]
- Zulqarnain Gilani, S.; Mian, A. Learning From Millions of 3D Scans for Large-Scale 3D Face Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1896–1905. [Google Scholar]
- Faessler, M.; Fontana, F.; Forster, C.; Mueggler, E.; Pizzoli, M.; Scaramuzza, D. Autonomous, vision-based flight and live dense 3d mapping with a quadrotor micro aerial vehicle. J. Field Robot. 2016, 33, 431–450. [Google Scholar] [CrossRef]
- Kim, H.; Leutenegger, S.; Davison, A.J. Real-time 3D reconstruction and 6-DoF tracking with an event camera. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 349–364. [Google Scholar]
- Sra, M.; Garrido-Jurado, S.; Schmandt, C.; Maes, P. Procedurally generated virtual reality from 3D reconstructed physical space. In Proceedings of the 22nd ACM Conference on Virtual Reality Software and Technology, Munich, Germany, 2–4 November 2016; pp. 191–200. [Google Scholar]
- Sra, M.; Garrido-Jurado, S.; Maes, P. Oasis: Procedurally Generated Social Virtual Spaces from 3D Scanned Real Spaces. IEEE Trans. Vis. Comput. Graph. 2018, 24, 3174–3187. [Google Scholar] [CrossRef]
- Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Gorthi, S.S.; Rastogi, P. Fringe projection techniques: Whither we are? Opt. Lasers Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Zhang, Z. Review of single-shot 3D shape measurement by phase calculation-based fringe projection techniques. Opt. Lasers Eng. 2012, 50, 1097–1106. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, L.; Zuo, C.; Tao, T.; Chen, Q.; Gu, G. High dynamic range 3-D measurements with fringe projection profilometry: A review. Meas. Sci. Technol. 2018, 29, 122001. [Google Scholar] [CrossRef]
- Jiang, H.; Zhao, H.; Li, X. High dynamic range fringe acquisition: A novel 3-D scanning technique for high-reflective surfaces. Opt. Lasers Eng. 2012, 50, 1484–1493. [Google Scholar] [CrossRef]
- Zhang, S.; Yau, S.T. High dynamic range scanning technique. Opt. Eng. 2009, 48, 033604. [Google Scholar]
- Salahieh, B.; Chen, Z.; Rodriguez, J.J.; Liang, R. Multi-polarization fringe projection imaging for high dynamic range objects. Opt. Express 2014, 22, 10064–10071. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, Y.; Chen, Q.; Zuo, C.; Li, R.; Shen, G. General solution for high dynamic range three-dimensional shape measurement using the fringe projection technique. Opt. Lasers Eng. 2014, 59, 56–71. [Google Scholar] [CrossRef]
- Liu, G.H.; Liu, X.Y.; Feng, Q.Y. 3D shape measurement of objects with high dynamic range of surface reflectivity. Appl. Opt. 2011, 50, 4557–4565. [Google Scholar] [CrossRef]
- Jiang, C.; Bell, T.; Zhang, S. High dynamic range real-time 3D shape measurement. Opt. Express 2016, 24, 7337–7346. [Google Scholar] [CrossRef]
- Lin, H.; Gao, J.; Mei, Q.; He, Y.; Liu, J. Adaptive digital fringe projection technique for high dynamic range three-dimensional shape measurement. Opt. Express 2016, 24, 7703–7718. [Google Scholar] [CrossRef]
- Waddington, C.J.; Kofman, J.D. Modified sinusoidal fringe-pattern projection for variable illuminance in phase-shifting three-dimensional surface-shape metrology. Opt. Eng. 2014, 53, 084109. [Google Scholar] [CrossRef]
- Sheng, H.; Xu, J.; Zhang, S. Dynamic projection theory for fringe projection profilometry. Appl. Opt. 2017, 56, 8452–8460. [Google Scholar] [CrossRef]
- Chen, C.; Gao, N.; Wang, X.; Zhang, Z. Adaptive pixel-to-pixel projection intensity adjustment for measuring a shiny surface using orthogonal color fringe pattern projection. Meas. Sci. Technol. 2018, 29, 055203. [Google Scholar] [CrossRef]
- Qi, Z.; Wang, Z.; Huang, J.; Xue, Q. Improving the quality of stripes in structured-light three-dimensional profile measurement. Opt. Eng. 2016, 56, 031208. [Google Scholar] [CrossRef]
- Haug, K.; Pritschow, G. Robust laser-stripe sensor for automated weld-seam-tracking in the shipbuilding industry. In Proceedings of the 24th Annual Conference of the IEEE Industrial Electronics Society, Aachen, Germany, 31 August–4 September 1998; Volume 2, pp. 1236–1241. [Google Scholar]
- Usamentiaga, R.; Molleda, J.; Garcia, D.F.; Bulnes, F.G. Removing vibrations in 3D reconstruction using multiple laser stripes. Opt. Lasers Eng. 2014, 53, 51–59. [Google Scholar] [CrossRef]
- Ye, Z.; Lianpo, W.; Gu, Y.; Chao, Z.; Jiang, B.; Ni, J. A Laser Triangulation-Based 3D Measurement System for Inner Surface of Deep Holes. In Proceedings of the ASME 2018 13th International Manufacturing Science and Engineering Conference, College Station, TX, USA, 18–22 June 2018. [Google Scholar]
- Usamentiaga, R.; Molleda, J.; Garcia, D.F. Structured-light sensor using two laser stripes for 3D reconstruction without vibrations. Sensors 2014, 14, 20041–20063. [Google Scholar] [CrossRef]
- Sun, Q.; Chen, J.; Li, C. A robust method to extract a laser stripe centre based on grey level moment. Opt. Lasers Eng. 2015, 67, 122–127. [Google Scholar] [CrossRef]
- Tian, Q.; Zhang, X.; Ma, Q.; Ge, B. Utilizing polygon segmentation technique to extract and optimize light stripe centerline in line-structured laser 3D scanner. Pattern Recognit. 2016, 55, 100–113. [Google Scholar]
- Usamentiaga, R.; Molleda, J.; García, D.F. Fast and robust laser stripe extraction for 3D reconstruction in industrial environments. Mach. Vis. Appl. 2012, 23, 179–196. [Google Scholar] [CrossRef]
- Zhang, S. High-Speed 3D Imaging with Digital Fringe Projection Techniques; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Huang, P.S.; Zhang, C.; Chiang, F.P. High-speed 3-D shape measurement based on digital fringe projection. Opt. Eng. 2003, 42, 163–169. [Google Scholar] [CrossRef]
- Holmstrom, S.T.; Baran, U.; Urey, H. MEMS laser scanners: A review. J. Microelectromech. Syst. 2014, 23, 259–275. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Zhang, X.; Xie, H. Thermal Reliability Study of an Electrothermal MEMS Mirror. IEEE Trans. Device Mater. Reliab. 2018, 18, 422–428. [Google Scholar] [CrossRef]
- Xie, H. Editorial for the Special Issue on MEMS Mirrors. Micromachines 2018, 9, 99. [Google Scholar] [CrossRef]
- Tanguy, Q.A.; Duan, C.; Wang, W.; Xie, H.; Bargiel, S.; Struk, P.; Lutz, P.; Gorecki, C. A 2-axis electrothermal MEMS micro-scanner with torsional beam. In Proceedings of the 2016 International Conference on Optical MEMS and Nanophotonics (OMN), Singapore, 31 July–4 August 2016; pp. 1–2. [Google Scholar]
- Yoshizawa, T.; Wakayama, T. Compact camera system for 3D profile measurement. In Proceedings of the 2009 International Conference on Optical Instruments and Technology: Optoelectronic Imaging and Process Technology, Shanghai, China, 19–22 October 2009; Volume 7513, p. 751304. [Google Scholar]
- Guo, H.; He, H.; Chen, M. Gamma correction for digital fringe projection profilometry. Appl. Opt. 2004, 43, 2906–2914. [Google Scholar] [CrossRef]
- Lu, J.; Mo, R.; Sun, H.; Chang, Z. Flexible calibration of phase-to-height conversion in fringe projection profilometry. Appl. Opt. 2016, 55, 6381–6388. [Google Scholar] [CrossRef]







| Items | Parameters and Description |
|---|---|
| Camera | Model: Charge-coupled Device (CCD), mono, global shutter. Resolution: 1920 × 1200. Max frames per second: 163 |
| Lens for camera | Focal length: 12 mm |
| MEMS scanner | Model: 2D electromagnetic actuation. Fast axis: 18 kHz, ±16°. Slow axis: 0.5 kHz, ±10° |
| Laser diode | Wavelength: 650 nm. Power consumption: 320 mW |
| Lens for LD | Model: aspheric lens. Focal length: 4.51 mm. Aspheric coefficient: −0.925. Distance from LD: 4.55 mm. Distance from MEMS scanner: 33 mm |
| USB hub | USB3.0 × 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Zhang, G.; Li, H.; Zhou, X. Hybrid 3D Shape Measurement Using the MEMS Scanning Micromirror. Micromachines 2019, 10, 47. https://doi.org/10.3390/mi10010047
Yang T, Zhang G, Li H, Zhou X. Hybrid 3D Shape Measurement Using the MEMS Scanning Micromirror. Micromachines. 2019; 10(1):47. https://doi.org/10.3390/mi10010047
Chicago/Turabian StyleYang, Tao, Guanliang Zhang, Huanhuan Li, and Xiang Zhou. 2019. "Hybrid 3D Shape Measurement Using the MEMS Scanning Micromirror" Micromachines 10, no. 1: 47. https://doi.org/10.3390/mi10010047
APA StyleYang, T., Zhang, G., Li, H., & Zhou, X. (2019). Hybrid 3D Shape Measurement Using the MEMS Scanning Micromirror. Micromachines, 10(1), 47. https://doi.org/10.3390/mi10010047




