Alpine Forest Drought Monitoring in South Tyrol: PCA Based Synergy between scPDSI Data and MODIS Derived NDVI and NDII7 Time Series

Abstract

Observed alternation of global and local meteorological patterns governs increasing drought impact, which puts at risk ecological balance and biodiversity of the alpine forest. Despite considerable attention, drought impact on forest ecosystems is still not entirely understood, and comprehensive forest drought monitoring has not been implemented. In this study, we proposed to bridge this gap exploiting a time-domain synergetic use of medium resolution MODSI NDVI (Normalized Difference Vegetation Index) and NDII7 (Normalized Difference Infrared Index band 7) time series as well as on-station temperature and precipitation measures combined in the scPDSI (self-calibrated Palmer Drought Severity Index) datasets. Analysis employed the S-mode Principal Component Analysis (PCA) examined under multiple method settings and data setups. The investigation performed for South Tyrol (2001–2012) indicated prolonged meteorological drought condition between 2003 and 2007, as well as general drying tendencies. Corresponding temporal variability was identified for local mountain forest. The former response was fostered more often by NDII7, which is related to foliage water content, whereas NDVI was more prone to report on an overall downturn and implied drop in forest photosynthetic activity. Among tested approaches, the covariance-matrix based S-mode PCA of z-score normalized vegetation season NDVI and NDII7 time series ensured the most prominent identification of drought impact. Consistency in recognized temporal patterns confirms integrity of the approach and aptness of used remote-sensed datasets, suggesting great potential for drought oriented environmental analyses.

1. Introduction

Drought is one of the most common environmental disasters nowadays. It affects an enormous number of people and the biggest area worldwide [1] drawing attention of scientists, economists, policy makers as well as the public [2]. Increasing, but not uniform drought threat is noted on local to global scale, and is driven by prolonged climatic anomaly [3,4] expressed in change in temperature, precipitation and insolation patterns (e.g., [5,6,7,8,9,10,11,12]).

Although drought is a “burning” issue, its understanding and defining in unified terms is biased due to region and environment dependent perception of the phenomenon [13], relative course and impact, as well as not well specified inception and end of an event [1]. Furthermore, drought is perceived through its manifestations such as precipitation shortfall, insufficient soil moisture or diminished vegetation status. Consequently, the majority of conceptual drought definitions describes a drought event through divergence from local long-term “normal” conditions of a selected environmental variable. Additionally, aridity impact is not only relative, but also non-discrete, which implies further difficulty in its monitoring and quantification.

Drought impact on vegetation is nowadays of particular interest in relation to global climate change modeling and carbon sink efficiency (e.g., [14,15,16]). Among others, complex drought influence on forest ecosystems [17,18] is especially crucial for comprehensive and holistic environmental monitoring [19] and has become a subject of numerous studies (e.g., [14,20,21,22]) and further projections [23,24]. Despite high importance, drought impact on forest ecosystems is still not entirely understood, particularly with respect to dry spell intensity, trees response under diverse local environmental conditions [22], uncertainty of long term change scenarios [16] as well as regional to global scale consequences. Although local dendrochronological surveys provide essential information on trees development under water stress conditions (e.g., [25,26,27,28,29]), they are limited to small sites or transects [30], restraining broader understanding of the forest environment.

Unlike field studies, remote sensing techniques allow spatial surveys at local to regional or even global scale, ensuring not only dense temporal sampling, but also generating relatively low costs. Although high spatial resolution of remotely sensed data is usually still compromised by low spatial and temporal coverage (and the other way round), remote sensing acquisitions provide reliable information for environmental monitoring, especially when complemented by in-situ data. Vegetation drought impact can be measured by an extensive suite of remote sensing indices, among which the red and near infrared spectra based NDVI (Normalized Difference Vegetation Index [31]), as well as near and short wave infrared based NDII (Normalized Difference Infrared Index [32]) and NBR (Normalized Burn Ratio [33], also known as NDII7 (Normalized Difference Infrared Index band 7) [34] which adopts MODIS band 7 short infrared information) gained high recognition. Despite some constraints due to saturation effect [35], sensitivity to soil information [36], species dependent value range and nonlinear correlation with precipitation (e.g., [37,38,39,40,41]), aforementioned metrics offer great simplicity and robustness in approximating photosynthetic plant activity and plant water content. Moreover, they ensure abundance of data, with some datasets and time series dating back even to the 1970s [42]. The latter provides an outstanding opportunity for comprehensive vegetation analyses in the context of ongoing climate alteration and increasing drought threat.

Although time series of remotely sensed vegetation indices allow an extensive examination, the four-dimensional character of datasets (latitude, longitude, index value and time) imposes a need for efficient spatio-temporal processing. Moreover, non-discrete character of changes and limited ground truth or reference information on vegetation drought impact present an additional challenge in the analyses. Among multiple statistical and mathematical methods for multidimensional analyses, particularly convenient to address these issues are variance oriented approaches that identify the dominant variability in space and/or time domain of data [43]. The Principal Component Analysis (PCA) [44] is probably the best known and most frequently applied multivariate decomposition method. Robustness and straightforward calculation spurred its use in environmental studies including analyses of remote sensed data (e.g., [44,45,46,47,48,49,50]). Despite its popularity, the approach is sometimes implemented as an exploratory analysis, without correct exploitation of various PCA decomposition modes [44,51,52]. Consequently, results might not be derived by the optimal PCA setup and next to general methodological constraints [52] they might be additionally affected by poor application.

Meeting the arising need for a comprehensive approach to large scale forest drought impact detection [19], we exploited in this paper the PCA decomposition of remotely sensed time series of vegetation indices. The analyses were carried out using the 2001–2012 time series of MODIS derived 16-day NDVI and NDII7 datasets, subjected to the S-mode PCA (time priority mode) and aimed at time-domain recognition of drought impact. Investigation examined multiple PCA decomposition settings and data setups, including correlation/covariance matrix based PCA convolution, data z-score normalization, diverse annual time-windows as well as two loadings (eigenvectors) rotation approaches (orthogonal Varimax [53] and oblique Promax [54] solutions). In order to assess robustness of the method, the study was conducted for a complex and diverse mountain forest of South Tyrol, which is known not only to have experienced 2003 heat-wave related disturbances [55], but also accelerated climate change [56]. Due to a shortage of available ground truth data on regional spatio-temporal drought development, PCA PCs (scores), representing herein the most dominant temporal evolution of forest status, were evaluated against regional meteorological conditions. The latter was approximated by the temperature and precipitation based scPDSI (self-calibrated Palmer Drought Severity Index [57]), which has been demonstrated to be well correlated with forest status [58,59,60]. The unified regional scPDSI responses were also identified through the S-mode PCA decomposition. Consequently, the applied coupling allowed recognizing regional temporal forest variability in response to meteorological conditions.

In this paper we: (i) present a synthesis of 2001–2012 meteorological drought conditions in South Tyrol; (ii) relatively evaluate the utility of the S-mode PCA of 16-day MODIS NDVI and NDII7 time series used for identification of short to medium term temporal vegetation variability, and propose the most suitable PCA setups for monitoring of drought impact in alpine forest; (iii) demonstrate efficiency of the applied scPDSI–NDVI/NDII7 synergy for reliable analysis of drought impact on temporal development of forest status in the complex and diverse alpine ecosystem; and (IV) discuss and interpret the most eminent time-domain variability of the South Tyrolean forest status governed by the identified 2001–2012 meteorological drought conditions.

2. Materials and Methods

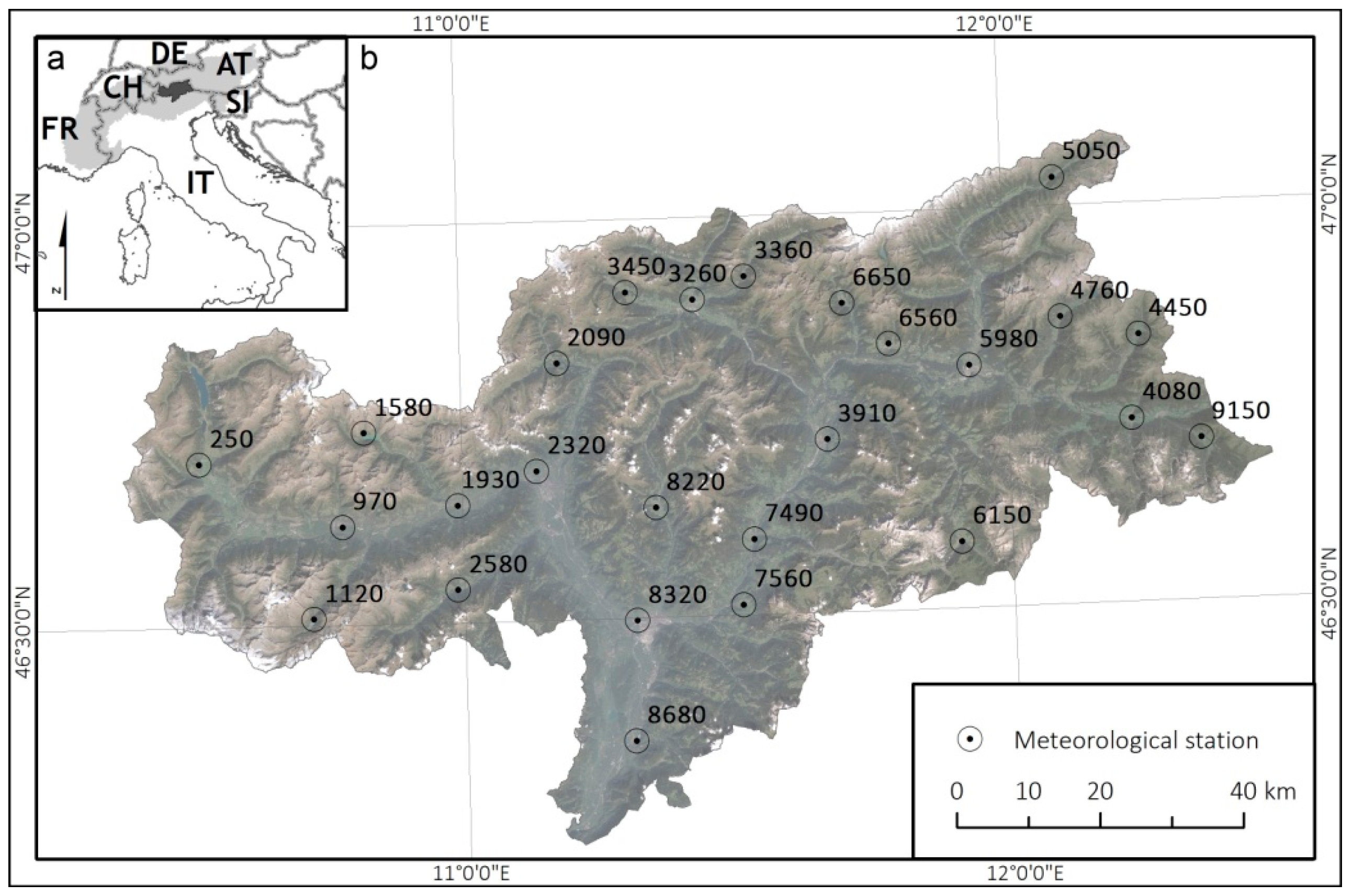
2.1. Study Area

South Tyrol (Autonome Provinz Bozen—Südtirol/Provincia Autonoma di Bolzano—Alto Adige), is the north most province of the Italian Republic, located in the central part of the Alps (Figure 1). It is a typical alpine region characterized by complex and diverse orography ranging from 190 m asl (southern Adige Valley) to 3905 m asl (Mount Ortler), where 86% of the area is placed above 1000 m asl, and over 40% above 2000 m asl [61]. Around 43% of the region (namely 3170.5 km² out of 7400 km²) is covered by forest, with its overall structure predominated by a coniferous woodland (90.1%) with an addition of mixed (7.3%) and broadleaved (2.6%) stands. Following the elevation gradient combined with regional climatic diversification, hardwood species are present in the valley floors and on lower elevations in the central part of the region.

2.2. Data

2.2.1. Meteorological Data and scPDSI

Monthly on-station cumulative precipitation and mean temperature records, essential for the scPDSI computation, were obtained from the WISKI database of the Hydrographic Office of the Autonomous Province of Bolzano-Südtirol. Only stations with minimum 25 years of uninterrupted coupled observations of both variables were considered [57] (taking December 2012 as a final record entry, meteorological observations had to date back to, at least, January 1988). This condition was fulfilled by 26 stations evenly spread around the province (Figure 1; information on selected stations and the length of available records are presented in Table S1). The scPDSI was calculated independently for each location using the code written within The GreenLeaf Project [62]. The computation was always based on the longest available time series of records (Table S1). In order to match the time-span of MODIS data, only the 2001–2012 scPDSI results were considered further (Figure 2).

2.2.2. MODIS Derived Time Series of Vegetation Indices

The study was based on a 16-day MOD13Q1 standard MODIS products of 250 m spatial resolution acquired for a h18v04 tile for the 2001–2012 period. For each of the 276 considered datasets, NDVI, QA (Quality Assessment) as well as bands 2 (NIR: 0.840–0.876 µm) and 7 (MIR: 2.105–2.155 µm) were extracted. Subsequently, NDII7 was computed according to the formula:

NDII7 = (NIR − MIR)/(NIR + MIR)

(1)

All pixels in the NDVI and NDII7 time series with QA-usefulness values below “acceptable” were masked out following the suggestion of Colditz et al. [63]. Next, outliers (confidence level 0.95 according to Chebyshev’s Theorem) and masked-out low quality pixels were replaced using a time-domain linear interpolation carried out in the TimeStats Software Tool [64]. To ensure the highest quality and limit amount of “artificial” values introduced to the time series, the interpolation was performed only for a single observation gap. Longer gaps were not revised. As a result, complete 2001–2012 NDII7 time series was available for 52,009 forest pixels (out of 52,394). NDVI spatial coverage was not affected. Finally, following the findings of Wang et al. [65], adjustment for MODIS sensor degradation was completed for both time series.

2.2.3. Ancillary Data—Forest Mask

Forest mask information for South Tyrol were adopted from a core forest product of the FP7 geoland2 project (EL-04a dataset; [66]). Information gaps present in the layer (in total 162 km² excluded due to cloud cover and shadowing) were filled in using the CORINE Land Cover 2006 dataset [67]. Resolution change from 20 m (native to the EL-04a and CORINE) to 250 m was based on a spatial averaging, where a new 250 m × 250 m pixel was assigned to a “forest” class only when at least 50% of its area was devoted to a forest within the core dataset.

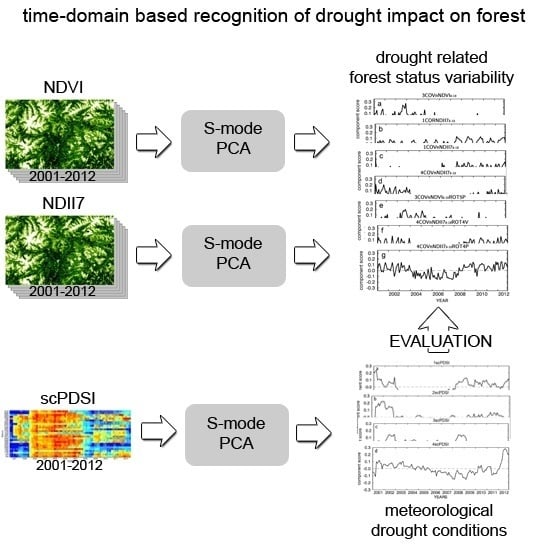
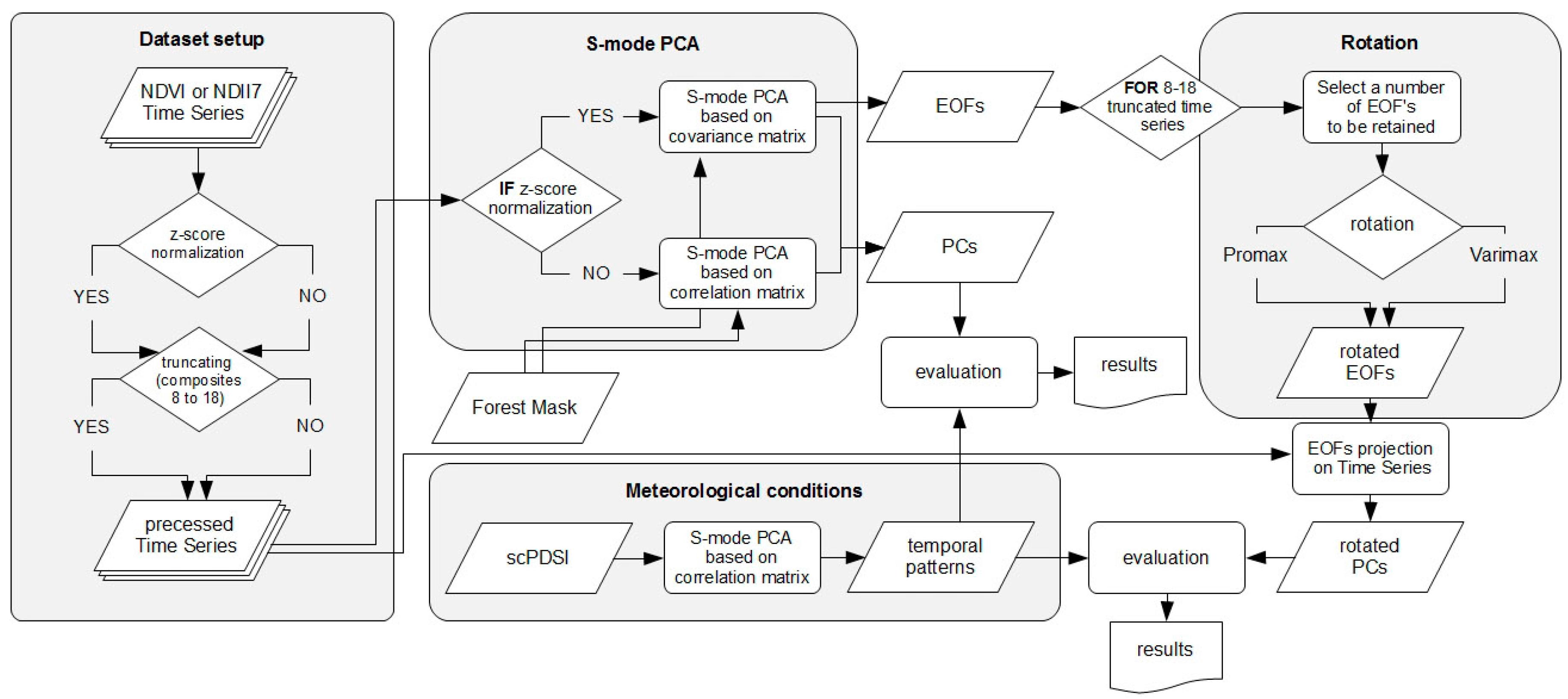
2.3. PCA Analyses Design

2.3.1. scPDSI Based Meteorological Variability

Interannual 2001–2012 meteorological variability in South Tyrol was identified applying the S-mode PCA on a data matrix combining 26 on-station scPDSI time series. In order to ensure equal impact of each time-step the decomposition was based on a correlation-matrix [52] (Scheme 1; for a detailed description of the S-mode PCA see Appendix A).

2.3.2. MODIS Derived NDVI and NDII7 Time Series

Analysis design (Scheme 1,

Table 1. Summary of the S-mode PCA design exploring utility of the NDVI and NDII7 time series, data z-score normalization, diverse annual time windows, correlation and covariance-matrix based PCA setting, as well as loading rotation for detection of drought related changes in forest status.

Index	z-Score Data Normalization	Annual Time Window (MODIS Composites)	Dataset Short Name	EOF Matrix	Rotation (Retained Scores)
NDVI	no	full year (1–23)	NDVI1–23	cor.	no
	no	veg. season (8–18)	NDVI8–18	cor.	no
	yes	full year (1–23)	nNDVI1–23	cov.	no
	yes	veg. season (8–18)	nNDVI8–18	cov.	yes (1–5)
NDII7	no	veg. season (8–18)	NDII78–18	cor.	no
	yes	veg. season (8–18)	nNDII78–18	cov.	yes (1–4)

Abbreviations: veg.—vegetation; cor.—correlation; cov.—covariance.

) aimed at exploring potential of the S-mode PCA for identifying vegetation dynamism and related drought impact. The following PCA settings and data setups were exploited:

• NDVI and NDII7 time series, where the former relates to the photosynthetic activity, while the latter approximates foliage water content;
• removal of seasonality through a per-pixel z-score normalization

  $$d=\frac{X_{ij}-{\mu }_{j-com}}{{\delta }_{j-com}}$$

  (2)

  where X_ij denotes a j-th composite ($j\in \left[1, 23\right]$) of an i-th year ($i\in \left[2001, 2012\right]$) of the complete 2001–2012 time series, µ_j-com stands for an average value for all j-th composites across all the years, and σ_j-com is a standard deviation for all the j-th composite in the time series;
• two different lengths of NDVI and NDII7 time series (applied to the original and z-score normalized datasets alike) where beside the complete MODIS time series comprising all 23 annual composites (1–23), a vegetation season time series focusing on a period between end of April and mid-October (corresponding with 8th to 18th MODIS annual composites (8–18)) were also exploited as time series restricted to vegetation season allow excluding dormancy state signal and potential impact of snow cover; and
• PCA decomposition based on a correlation and on a covariance matrix—following the suggestion of Eastman and Fulk [50], a covariance-matrix based PCA was applied to normalized time series, while not-normalized datasets were decomposed based on a correlation matrix (Scheme 1).

Each PCA setup (Table 1) was run independently where only pixels within the forest mask were considered.

The first four PCs (scores) resulting from each of the tested PCA setup (Table 1) and representing temporal profiles of changes in forest vegetation status were cross-compared against four identified scPDSI temporal patterns (Scheme 1). The process allowed recognizing scores with physical meaning of forest response following recognized drought conditions. Owing to inconsistent time steps (16-day vs. monthly) and annual windows, vegetation indices based PCs and scPDSI temporal profiles were correlated for yearly averages. Since a sign of a resulting PCA score function is arbitrary and originates from the data variance based rotation of the original dataset, when needed, a sign of emerging PCs was subsequently adjusted to fit the scPDSI approximated meteorological variability. This step simplified interpretation and comparison between results. The PCA resulting EOFs (loadings) were not evaluated due to unavailable ground-truth information on drought footprint in South Tyrol.

A limit to inspect only the first four resulting PCs of each PCA setup was governed by eigenvalues that indicate amount of dataset variance explained by a given loading and corresponding score. Since temporal and spatial patterns associated with higher variance are more likely to carry a physical meaning [43], we decided to focus only on most prominent PCs.

In order to enhance potential physical meaning of identified temporal profiles of changes in forest status, loadings rotation was performed (for more information see Appendix A). Since the approach is targeted at strengthening already recognized patterns exploring only a subset of the total data variance, rotation was applied only to those PCA setups that revealed sound drought related temporal variability in the first four resulting PCs (Table 1). Two rotation algorithms were tested: orthogonal Varimax [53] and oblique Promax [54] techniques, where a number of EOFs to be rotated was determined using the Cattell’s scree test [68]. In this case, a potential physical meaning was also sought within the first four emerging PCs and was evaluated, on a yearly bases, against the scPDSI identified meteorological variability (Scheme 1).

Since the yearly averages fail to address intra-annual data variability, performed correlation between vegetation indices based PCs and scPDSI temporal profiles ensured only a coarse similarity measure. Frequent single-value anomalies presented in the NDVI and NDII7 derived scores were not validated in relation to smooth scPDSI temporal variability. Consequently, despite high correlation values, yearly means could foster misleading impression of recognized forest response to drought. Therefore, statistical analyses were complemented by a visual evaluation of similarity between scPDSI temporal patterns and PCs they controlled. Although potentially subjective, this approach ensured straightforward comparison between time series of diverse time steps and annual length, where all erratic and “noisy” PCs were rejected despite high yearly based correlation to the scPDSI profiles.

PCs carrying the most eminent forest response to identified drought conditions were subsequently mutually compared in order to specify the information overlap.

3. Results

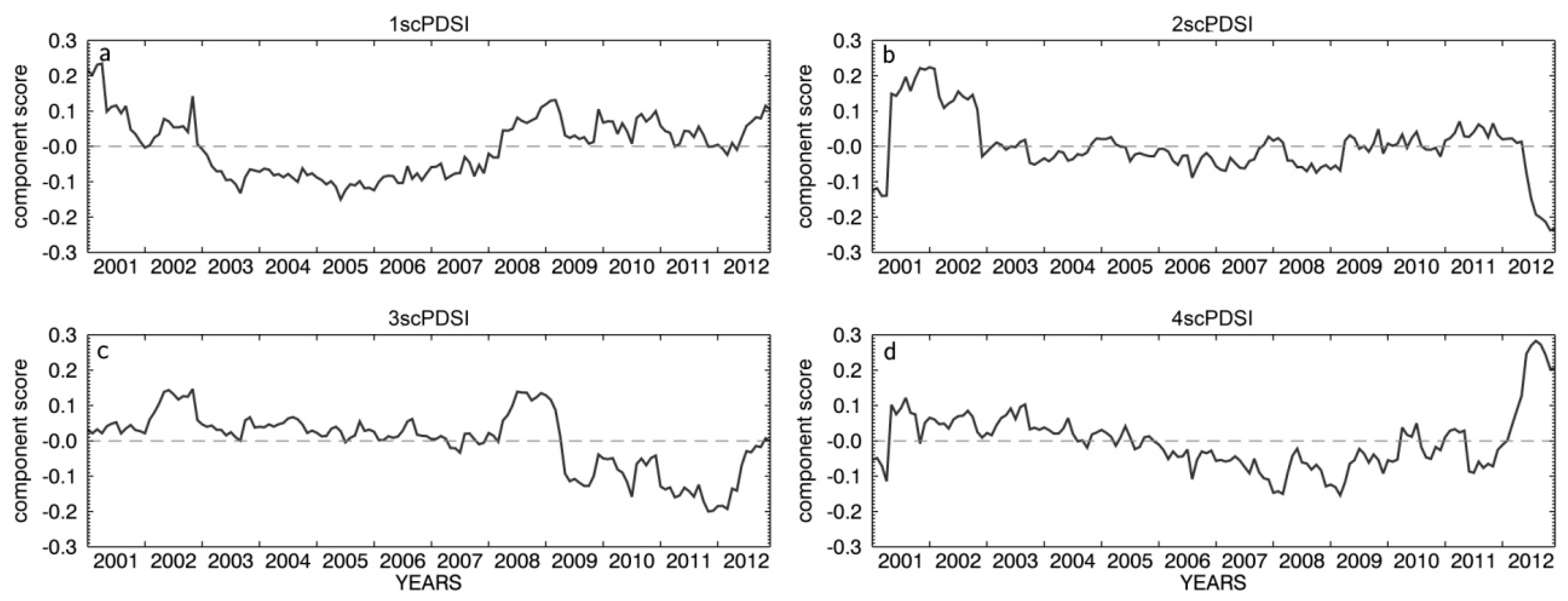
3.1. Meteorological Conditions in South Tyrol

The first PC (1scPDSI; Figure 3a) resulting from the correlation-matrix based S-mode PCA of the 2001–2012 monthly scPDSI time series indicated drought conditions between 2003 and 2007. This variability explained 63% of the total data variance. The second identified score (2scPDSI; Figure 3b) revealed leveled temporal response with positive anomalies in 2001 and 2002, which accounted for 9.95% of data variability. The third PC (3scPDSI; Figure 3c) demonstrated positive anomalies in 2002 and 2008 as well as drought conditions in 2009, 2011 and 2012. Furthermore, a subtle overall decreasing trend was revealed in this time evolution pattern. It explained 7.36% of the total variance present in the scPDSI time series. Finally, the fourth resulting score (4scPDSI; Figure 3d) showed gradual decrease between 2001 and 2008 followed by a strong positive anomaly in 2012. This temporal pattern was associated with 5.61% data variability.

The scPDSI PCA results provided an interesting and essential insight into meteorological variability in South Tyrol between 2001 and 2012. First, strong scPDSI drought condition was identified in the region between 2003 and 2007 with the most severe drop in 2005 (Figure 2 and Figure 3a). Second, a clear positive anomaly was observed in 2008 for all on-stations scPDSI time series (Figure 2), and was well singled out in the 1scPDSI, 3scPDSI and 4scPDSI scores (Figure 3a,c,d, respectively). Third, the 2scPDSI, as well as 1scPDSI and 3scPDSI scores (Figure 3a–c, respectively) highlighted above-average wet conditions for 2001 and 2002. Fourth the 3scPDSI indicated drought circumstances in 2009 and 2011 (Figure 3c), and overall subtle decreasing trend. Finally, the 4scPDSI temporal pattern revealed a fine linear downturn between 2003 and 2007. Neither decreasing tendency was obvious in the original scPDSI dataset.

3.2. Forest Photosynthetic Activity Captured by PCA of MODIS NDVI Time Series

The correlation-matrix based S-mode PCA of the complete NDVI time series (NDVI_1–23) revealed seasonality in all first four resulting PCs (Figure S1). This behavior was the most robust for the first score (herein 1CORNDVI_1–23; Figure S1a), which explained 63.23% of the total data variability. The following PCs (2CORNDVI_1–23, 3CORNDVI_1–23 and 4CORNDVI_1–23, respectively; Figure S1b–d) not only demonstrated more wobbly temporal profiles but also accounted for significantly smaller data variance (3.29%, 2.68% and 1.69%, respectively). All PCs showed limited forest ecosystem response to drought. Only the 2CORNDVI_1–23 and 3scPDSI, as well as the 3CORNDVI_1–23 and 1scPDSI demonstrated moderate mutual correlation (0.584 and 0.664, respectively; correlation was performed on a yearly basis due to non conforming time steps; Table S2a).

Covariance-matrix based S-mode PCA of the full year z-score normalized NDVI time series (nNDVI_1–23) revealed temporal patterns with intense changes in vegetation photosynthetic activity between consecutive observations (Figure S2). The first four PCs together accounted for 28% of the data variance with the first score explaining 18.55%. Correlation with the scPDSI temporal profiles, based on yearly averages, indicated strong relation between the second resulting PC (herein 2COVnNDVI_1–23: Figure S2b) and 1scPDSI as well as the third score (3COVnNDVI_1–23; Figure S2c) and 3scPDSI (0.712 and 0.731 respectively; Table S2b).

The correlation-matrix based PCA decomposition of the vegetation season (end of April–mid October) NDVI time series (NDVI_8–18) left some periodic fluctuations in the scores (Figure S3). This was especially strong in the first PC (herein 1CORNDVI_8–18; Figure S3a), which explained 41.94% of the total data variance. The leading score depicted potentially drought related diminished forest photosynthetic activity in 2006 and 2007 as well as subtle intra-annual NDVI irregularity in 2003 and 2011. Despite this, the 1CORNDVI_8–18 was not correlated to any of the scPDSI temporal profiles (Table S2c). NDVI_8–18 derived PCs of the higher order (Figure S3b–d) addressed much smaller amount of the data variability, namely 4.77%, 3.04% and 2.68% for the second to fourth scores, respectively (herein 2CORNDVI_8–18, 3CORNDVI_8–18 and 4CORNDVI_8–18, respectively). Correlating the 2CORNDVI_8–18 with the 1scPDSI (both aggregated on a yearly basis) revealed strong mutual relation (0.825; Table S2c). Despite positive correlation visual resemblance of both temporal patterns was obscured due to various single-value anomalies in the 2CORNDVI_8–18.

The z-score normalized vegetation season NDVI time series (nNDVI_8–18) convoluted with the covariance matrix S-mode PCA produced principal components showing in places intense isolated anomalies (Figure S4). Dominance of the first PC (herein 1COVnNDVI_8–18; Figure S4a) was not so strong comparing with the NDVI_8–18 results, with the leading score explaining 15.25% of the data variance. A potential physical meaning of forest drought impact was observed in the second PC (2COVnNDVI_8–18; Figure S4b) that significantly correlated on a yearly bases with the 1scPDSI and 2scPDSI (0.713 and 0.608, respectively; Table S2d). Furthermore, the third resulting score (3COVnNDVI_8–18; Figure S4d) depicted intense value increase in 2003 followed by decreasing tendency, and was found in accordance with the 3scPDSI (0.632; Table S2d). Both PCs explained 5.56% and 3.37% of the total data variance, respectively.

3.3. Forest Foliage Water Content Indicated by PCA of Vegetation Season MODIS NDII7 Time Series

The NDII7 PCA focused on the vegetation season (end of April–mid October) datasets. Initially, the NDII7_8–18 time series was decomposed with the correlation-matrix based S-mode PCA. The first PC (herein, 1CORNDII7_8–18; Figure S5a) revealed a potentially meaningful response to drought conditions, with diminished values in the seasonal envelope before 2008, and two local minima in 2003 and 2007. This temporal profile was strongly consistent on a yearly bases with the 1scPDSI (0.736; Table S2e) and represented 22.55% of the total data variance. The 1scPDSI correlated well with the third (3CORNDII7_8–18; Figure S5c; 0.660) and fourth (4CORNDII7_8–18; Figure S5d 0.702) PCs, which accounted for 4.40% and 2.68% of the total data variability, respectively. This relation was, however, visually concealed due to intensive value fluctuations in both temporal profiles.

The first PC of the covariance-matrix based decomposition of the z-score normalized vegetation season NDII7 (nNDII7_8–18) time series (herein 1COVnNDII7_8–18; Figure S6a) explained 11.98% of the data variance and showed strong correlation to the 1scPDSI (0.717; Table S2f). This score revealed diminished forest foliage water content in 2003, 2004 and 2007. Although the fourth resulting PC (4COVnNDII7_8–18; Figure S6d) accounted for only 1.66% of the total data variance, the score clearly resembled the 1scPDSI, which was supported by moderate correlation calculated on a yearly bases (0.608; Table S2f). NDII7 decrease revealed in the 4COVnNDII7_8–18 between 2003 and 2007 implied mild connection to the 4scPDSI temporal pattern (0.583; Table S2f).

3.4. Loadings Rotation

Rotations were performed on the eigenvectors of the z-score normalized vegetation season NDVI and NDII7 time series decomposed using covariance-matrix based S-mode PCA (Scheme 1; Table 1). This selection was motivated by the highest cumulative accordance between the first four PCs of each setup and the scPDSI temporal profiles. Decomposition results based on the NDII7_8–18 dataset were not considered due to the seasonal component, which dominated variability of the first four PCs and would further control rotated EOFs and their scores.

Following Cattell’s scree test, the first five eigenvectors were retained for the nNDVI_8–18 time series (Figure S7a). Rotation performed with the Varimax and Promax methods produced very similar sets of first four PCs (Figures S8 and S9, Table S3a). A pair of first PCs (herein 1COVnNDVI_8–18ROT5V and 1COVnNDVI_8–18ROT5P for the Varimax and Promax solutions respectively; Figures S8a and S9a) were moderately correlated on a yearly bases with the 2scPDSI (0.638 and 0.615, respectively; Table S4a), whereas both second principal components (herein 2COVnNDVI_8–18ROT5V and 2COVnNDVI_8–18ROT5P; Figures S8b and S9b) showed moderate negative relation to the 3scPDSI (−0.588 and −0.576, respectively; Table S4a). Moreover, the Promax rotation generated a third PC (herein 3COVnNDVI_8–18ROT5P; Figure S9c), which bore mild resemblance to the 3scPDSI (0.607), and secondary negative relation to the 1scPDSI (−0.590; Table S3a). Finally, the fourth Promax derived score (herein 4COVnNDVI_8–18ROT5P; Figure S9d) followed variability of the 4scPDSI temporal pattern (0.612; Table S3a).

The first four loadings were retained for the z-score normalized vegetation season NDII7 time series (nNDII7_8–18) based on Cattell’s scree test (Figure S7b). Temporal patterns constructed through the Varimax and Promax rotations (Figures S10 and S11 respectively) revealed very high mutual accordance (Table S3b), where the latter solution demonstrated less intense single-value abrupt irregularities in the envelope. In both cases, the fourth resulting scores (herein 4COVnNDII7_8–18ROT4V and 4COVnNDII7_8–18ROT4P for the Varimax and Promax rotation, respectively; Figure S10d and S11d) demonstrated diminished forest foliage water content between 2003 and 2007, and were found strongly correlated to the 1scPDSI (0.751 and 0.772 respectively; Table S4b). Significant relation was also identified on a yearly bases, between the 2scPDSI temporal pattern and a pair of the first PCs (herein 1COVnNDII7_8–18ROT4V and 1COVnNDII7_8–18ROT4P; Figures S10a and S11a; 0.614 and 0.689, respectively). Furthermore, beside the 1COVnNDII7_8–18ROT4V, the drought year of 2003 was also emphasized in the third PC resulting from the Varimax based convolution (3COVnNDII7_8–18ROT4V; Figure S10c).

3.5. Comparison of Identified Potential Forest Responses to Meteorological Drought Conditions

Among all sets of the first four PCs of multiple S-mode PCA setups, 22 scores were significantly correlated on a yearly bases with at least one out of four identified scPDSI temporal patterns. Visual comparison of each of these PCs with its controlling scPDSI profile allowed rejecting erratic scores with intense sequential fluctuations. All scores associated only with the 2cPDSI were excluded due to non-drought related variability of this temporal pattern.

Seven PCs with the most eminent relation between forest photosynthetic activity or foliage water content and meteorological drought conditions were singled out (Figure 4). Five of these scores were primary related to the 1scPDSI variability (

Table 2. Correlation among investigated drought related PCs (in columns, index letters correspond with Figure 4 and Table 3) and first four scPDSI temporal patterns approximating meteorological conditions.

	PCs
	a	b	c	d	e	f	g
1scPDSI	−0.310	0.736 *	0.717 *	0.608 *	−0.590 *	0.751 *	0.772 *
2scPDSI	0.360	−0.172	−0.199	0.502	0.186	0.301	0.241
3scPDSI	0.632 *	−0.576 *	−0.559	−0.023	0.607 *	−0.331	−0.397
4scPDSI	0.257	0.030	−0.010	0.583*	0.029	0.466	0.400

*—significant at the level p < 0.05.

, Figure 4b–d,f,g) with two PCs additionally influenced by the 3scPDSI and 4scPDSI temporal patterns (Table 2, Figure 4b and d respectively). Diminished forest foliage water content between 2003 and 2007 was particularly clear in the 4COVnNDII7_8–18ROT4V (Figure 4f, Table 2; abbreviation explained in

Table 3. Naming convention structure of seven PCs identified as carrying potential meaning of forest response to recognized meteorological drought conditions. Index letters correspond with Figure 4, whereas short names of datasets are explained in Table 1.

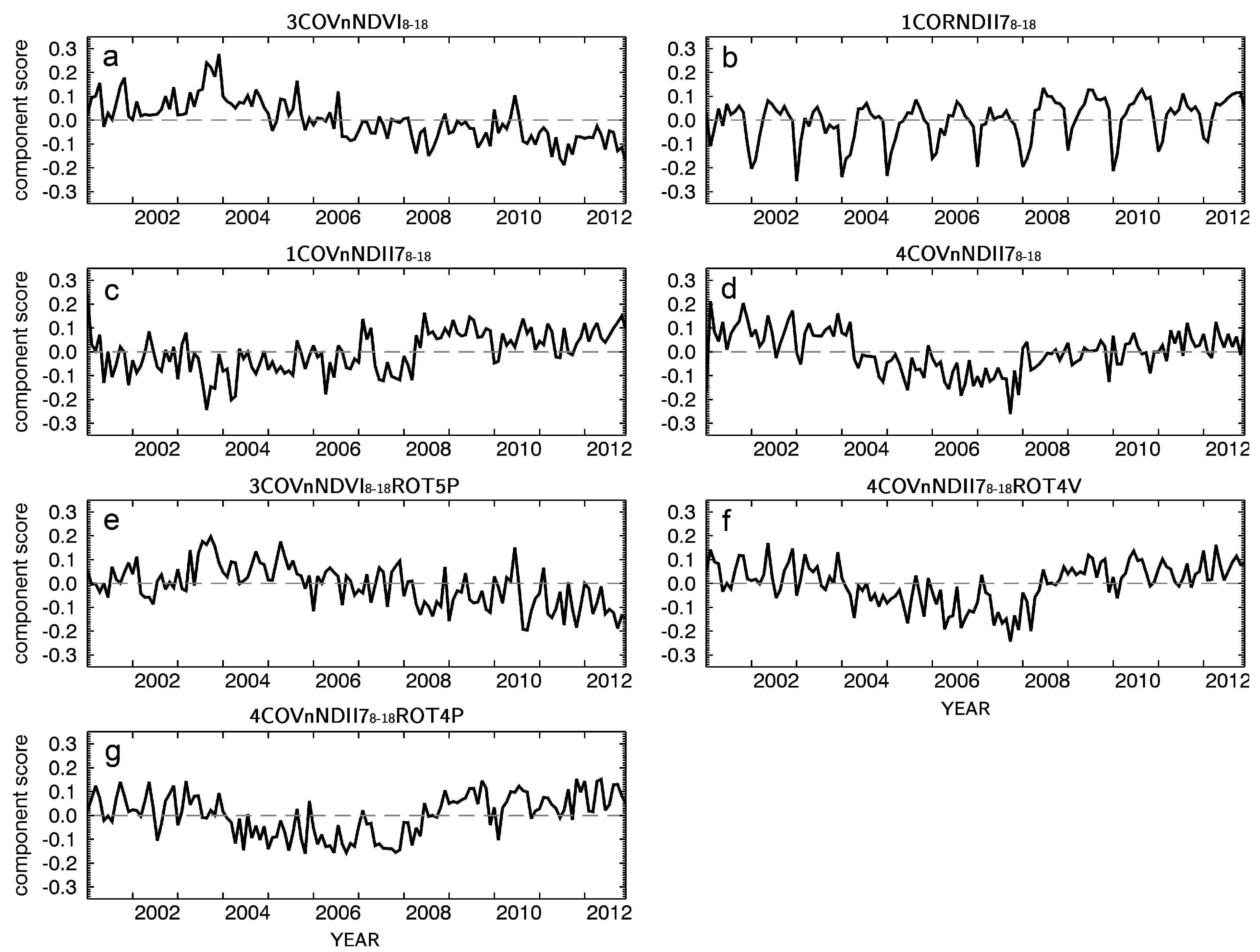
Index	PC Name	Score Order	EOF Matrix Rotation	Short Name of Original Dataset	Scores Retained for Rotation	Rotation Approach
a	3COVnNDVI8–18	3	cov.	nNDVI8–18	-	-
b	1CORNDII78–18	1	cor.	NDII78–18	-	-
c	1COVnNDII78–18	1	cov.	nNDII78–18	-	-
d	4COVnNDII78–18	4	cov.	nNDII78–18	-	-
e	3COVnNDVI8–18ROT5P	3	cov.	nNDVI8–18	(1–5)	Promax
f	4COVnNDII78–18ROT4V	4	cov.	nNDII78–18	(1–4)	Varimax
g	4COVnNDII78–18ROT4V	4	cov.	nNDII78–18	(1–4)	Promax

Abbreviations: cor.—correlation; cov.—covariance; “-”—not applicable.

) and 4COVnNDII7_8–18ROT4P (Figure 4g, Table 2 and Table 3). Both PCs were highly correlated (

Table 4. Mutual correlation among investigated drought related PCs. PCs index letters correspond with Figure 4 as well as Table 2 and Table 3.

Index	PC Name	PCs
		a	b	c	d	e	f	g
a	3COVnNDVI8–18	1.000 *
b	1CORNDII78–18	−0.207 *	1.000 *
c	1COVnNDII78–18	−0.422 *	0.487 *	1.000 *
d	4COVnNDII78–18	0.267 *	0.032	0.000	1.000 *
e	3COVnNDVI8–18ROT5P	0.714 *	−0.352 *	−0.674 *	−0.031 *	1.000 *
f	4COVnNDII78–18ROT4V	0.320 *	0.187 *	0.339 *	0.617 *	0.025	1.000 *
g	4COVnNDII78–18ROT4V	0.285 *	0.226 *	0.497 *	0.659 *	−0.051	0.924 *	1.000 *

*—significant at the level p < 0.05.

), and emerged from drought related variability detected in the 4COVnNDII7_8–18 (Figure 4d, Table 3) subsequently strengthened through the rotation. Mutual correlation among the original and rotated PCs was moderate (Table 4).

The 1CORNDII7_8–18 (Figure 4b; Table 3) as well as 1COVnNDII7_8–18 (Figure 4c; Table 3) PCs demonstrated, on a yearly bases, high correspondence with drought conditions approximated by the 1scPDSI (Table 2). Both temporal patterns rendered deteriorated forest foliage water content before 2008, with two stronger declines in 2003 and 2007. Moreover, the 1COVnNDII7_8–18 PC indicated additional drop in 2004, which was in line with similar anomaly observed in the 4COVnNDII7_8–18ROT4P (Figure 4f). Owing to phenology component, the 1CORNDII7_8–18 was weakly correlated with other scores (Table 4). The 1COVnNDII7_8–18 (Table 3) also revealed no substantial connection to other PCs, but for reverse moderate relation with the 3COVnNDVI_8–18ROT5P score (Figure 4e, Table 3 and Table 4).

Increasing aridity demonstrated through the overall scPDSI decline observed in the 3scPDSI temporal profile governed forest response identified in the 3COVnNDVI_8–18 (Figure 4a; Table 3) and 3COVnNDVI_8–18ROT5P PCs (Figure 4e; Table 3). The former was better correlated on a yearly bases with the controlling 3scPDSI pattern (Table 2) as well as showed smoother temporal variability. Since the 3COVnNDVI_8–18ROT5P score employed the 3COVnNDVI_8–18 related variance, both temporal profiles bore considerable resemblance (Table 4), including strong positive anomaly in 2003.

Gradual scPDSI decline between 2003 and 2007 depicted in the 4scPDSI temporal pattern was recognized as a secondary driver in the 4COVnNDII7_8–18 PC (Figure 4d).

4. Discussion

4.1. Drought Conditions in South Tyrol

Four temporal patterns of meteorological variability were identified for South Tyrol between 2001 and 2012. Three of them indicated drought conditions or tendency for increasing aridity.

The strongest and most persistent drought conditions were depicted by the 1scPDSI between 2003 and 2007 (Figure 3a). They initiated with a very hot and dry summer of 2003, which resulted from the pan-European summer heat wave of 2003 [69]. Consecutive year was also characterized by below-normal scPDSI values, which harmonized with drought conditions observed in Western Europe and the Mediterranean [70]. The 2005 drought circumstances comprised extremely arid spring culminated in a drought peak in May–June. These extreme conditions were attributed on exceptional setup of pressure system over Europe, and considerably affected the Iberian Peninsula and central Mediterranean Basin [71]. Impact of the heat-wave of 2006, associated by Rebetez et al. [72] mainly with Central and North Europe, was demonstrated in our analyses also for South Tyrol. Meteorological conditions showed here below-average rainfall sums and extreme temperatures from June onwards [73]. Finally, drought depicted in 2007 arose from averagely wet, but extremely hot spring and summer of 2007. These conditions were related to drought events observed in central Europe [3], Tyrol [74] as well as Mediterranean region [75]. Importantly, the extensive, five-year-long (2003–2007) persistent drought conditions identified in our study are in strong accordance with the drought response recognized for Central Europe by Ivits et al. [76]. An earlier ingress of drought marked in the 1scPDSI (Figure 3a) and perceived in the southern and eastern parts of South Tyrol (Figure 2) could be linked to the Mediterranean drought of 2001–2002 [76].

Drought conditions in 2009 and 2011–2012 depicted in the 3scPDSI (Figure 3c) were perceived in the central and eastern part of South Tyrol (Figure 2) as well as the most western outskirts of the province. They correspond well with drought alerts in Central Europe [3] and drought in western and central Mediterranean basin [70]. Moreover, subtle scPDSI decreasing trend identified within the 3scPDSI temporal profile likely captured an on-going climate transformation and increasing aridity in the region, suggested by Auer et al. [77]. A similar observation was made for the 4scPDSI which indicated scPDSI decrease between 2003 and 2007 (Figure 3d).

Beside aforementioned drought events, identified meteorological variability indicated several periods with precipitation surplus. The scPDSI increase in 2008, depicted in the 1scPDSI and 3scPDSI (Figure 3a,c respectively), corresponds with a timing of Tropical Cyclone “Emma”, which hit Europe in the spring of 2008 and preceded a hot but rainy summer. Moreover, the excess of rainfall observed mainly in the northern part of South Tyrol in 2001 through 2002, and depicted in the 2scPDSI and 3scPDSI (Figure 3b,c) is in strong accordance with the continental weather variability and flood events in Central Europe in 2002 [78]. In addition, wetter than average meteorological condition denoted by the 1scPDSI and 3scPDSI during 2012 are also aligned with humid European weather patterns of that year.

Four described temporal patterns comprised meteorological variability being strongly in line with documented pan-European weather conditions as well as regional events. Unlike in [79], time evolution patterns of the S-mode PCA decomposition explained high portion of the total scPDSI data variance, which supports their credibility. Therefore we assumed all four PCs to have physical meaning.

Potential shortcoming of the applied scPDSI model originates from the algorithm underlying assumption on a liquid phase of precipitation [80], which, in a case of the Alps, is not always fulfilled. This issue can be further addressed through a scPDSI-incorporated snowmelt model [81]. Nevertheless, since snowfall and concluding snow cover occur during vegetation dormancy and affect mostly alpine and subalpine zones, leaving the colline and mountain forest under limited snow impact, it was decided to keep the original assumption.

4.2. Evaluation of Multiple S-mode PCA Decomposition Approaches and Data Setups

Inspected S-mode PCA settings and data setups produced variety of NDVI and NDII7 based PCs, among which many scores demonstrated considerable accordance with drought conditions identified by the scPDSI temporal patterns. Vegetation season time series were more successful in this task than datasets comprising full year information. Applied truncating excluded vegetation dormancy state and snow cover impacts, hence targeted analysis at the most relevant and “drought sensitive” portion of data variance. Consequently, PCA decomposition of the vegetation season time series was more efficient in identifying coherent temporal profiles of subtle drought induced changes in forest photosynthetic activity and foliage water content. The z-score normalization combined with the covariance-matrix based S-mode PCA further enhanced correspondence between resulting PCs and scPDSI drought temporal patterns. Although the correlation matrix approach implies standardization of a time series, the process is based on a global mean, therefore is ineffective in removing a seasonal component from resulting PCs. On the contrary, adopted z-score normalizes each observation using a composite mean, which is calculated across all years only for a given annual time period (corresponding with only one MODIS 16-day composite). As a result, a z-score normalized time series carries more exact information on divergence from “average conditions”. This approach reduces total variance of a time series being introduced into PCA, hence allows on more efficient exploration of drought related signal. Moreover, time-specific expression of anomalies corresponds better with conceptual drought definitions as well as computation schemes of drought indices, including the scPDSI [1].

The advantage of loadings rotation on enhancing drought related forest vegetation response was not obvious. Although some principal components constructed through a rotation indicated higher correlations with the scPDSI temporal patterns, other cases showed deconstruction of drought related variability identified in unrotated PCs. Differences between orthogonal Varimax and oblique Promax solutions were limited, nevertheless the latter revealed slightly better correlation with the scPDSI temporal profiles.

Both NDVI and NDII7 datasets introduced into the S-mode PCA decomposition provided a selection of PCs with significant correlation to the scPDSI temporal profiles. Due to diverse design and properties, NDVI focuses on photosynthetic activity rendering a straightforward canopy status, whereas the NDII7 approximates tree foliage water content. Consequently, both indices captured different but complementary drought induced changes in forest status. We suggest to use them together, with a slight preferences for the NDII7, which has higher ability to capture forest recovery and regrowth [82]. Since resulting PCs were evaluated against the scPDSI temporal profiles, absolute assessment of identified drought impact was impossible.

4.3. Forest Drought Response Identified through PCA Decomposition of MODIS NDVI and NDII7 Time Series

Seven PCs showed prominent relation to the scPDSI temporal patterns approximating 2001–2012 meteorological drought conditions in South Tyrol. They depicted two particular drought related phenomena: a gradual decline and prolonged reduction in forest status between 2004 and 2007. While the latter was mainly recognized in the NDII7 based PCs (1CORNDII7_8–18, 4COVnNDII7_8–18, 4COVnNDII7_8–18ROT4V and 4COVnNDII7_8–18ROT4P), and represented drought coincident diminished foliage water content, identified downturn in forest status was fostered by two NDVI based PCs (3COVnNDVI_8–18 and 3COVnNDVI_8–18ROT5P) and corresponded with indicated increasing aridity of the alpine climate [77,83]. Since progressing dryness has been already reported to sway ecological balance in the Alps [24,84,85,86] leading to uphill shift of vegetation belts [18,87,88], alternation of phenological phases [89,90,91] and intensification of local dieback processes (e.g., Minerbi et al., 2006; Theurillat and Guisan, 2001), we assume that detected NDVI tendency depicts climate change governed decline of coniferous stands [23,24]. On the other hand, the 1COVnNDII7_8–18 score, as well as the 3COVnNDVI_8–18 and 3CONnNDVI_8–18ROT5P PCs considered with a reversed sign, suggested increasing forest foliage water content and photosynthetic activity, which could be explained by upturn of hardwood species being better adjusted to drought conditions [18,21]. Both interpretations supplement each other, since due to altitudinal distribution of forest, drought sensitive coniferous species grow at higher altitudes, whereas broadleaved trees are present mainly in the valley floors and on lower parts of slopes [92].

Beside seemingly apparent long-term tendencies, PCA results shed some light on complex short-term forest changes. Particularly interesting is diverse response to the heat wave of 2003. While a decrease in tree foliage water content corresponding with 2003 productivity decline demonstrated by Ciais et al. [93] was indicated in the 1COVnNDII7_8–18 and 1CORNDII7_8–18, the 3COVnNDVI_8–18 as well as 3COVnNDVI_8–18ROT5P PCs implied abrupt increment in forest photosynthetic activity. The latter is supported by results of Jolly et al. [94] who documented rise in alpine vegetation productivity at higher elevations in response to released elevation gradient constraint. Moreover, aforementioned upturn in forest photosynthetic activity depicted in the reversed 3COVnNDVI_8–18 and 3COVnNDVI_8–18ROT5P scores, commenced with intense drop in 2003. This outline is in strong agreement with drought induced local Scots Pine dieback in Eisack Valley followed by an intense growth of hardwood species of the understory [55]. Corresponding transitions have already been observed in the Alps [18]. Finally, the 4COVnNDII7_8–18, 4COVnNDII7_8–18ROT4V and 4COVnNDII7_8–18ROT4P demonstrated NDII7 decline not before 2004. This distinction could be, among others, attributed to different adaptation strategies to drought and persistent aridity stress, which are controlled by environmental conditions (e.g., [30,95]), tree species (e.g., [21,24,83]) or local tree competition (e.g., [18,27,29,96,97]). Furthermore, some tree species response to drought can be physiologically lagged [27,30]. Since the nature of presented analyses promotes the best correlation with the scPDSI pattern, delayed and more subtle forest responses [98] could be overlooked. Moreover, the presented approach determines adoption of scPDSI based definition of a drought event, including its inception and end. Identified drought related PCs, although relatively eminent, addressed only limited portion of variability composing NDVI and NDII7 time series. Consequently, comprehension of physical mechanisms governing other, non-drought related PCs would be valuable, but cannot be done without extensive ground truth information.

Despite the forest of South Tyrol is predominated by coniferous stands and all PCAs were conducted without forest type distinction, our results allowed to recognize forest type specific responses to stress conditions. Although this unspecific approach limits in-depth exploitation of differences between drought response of coniferous and hardwood species, obtained results imply considerable utility of the method, and encourage to test it further, including use of a more specific forest division. However, it should be kept in mind that complex structure of the South Tyrolean forest, combined with the coarse resolution of MODIS datasets make it challenging to identify homogeneous regions or pixels with pure signal. Furthermore, less than 10% share of broadleaved and mixed stands present an additional constraint for PCA.

We believe that despite adopted generalization, presented approach ensures a reliable approximation of forest drought response on a regional scale.

5. Conclusions

Constantly rising risk of drought events necessitates the advancement in drought monitoring. The task is especially important with respect to complex and diverse alpine forest ecosystems. This study addresses this need presenting PCA (Principal Component Analysis) based synergy between scPDSI (self-calibrated Palmer Drought Severity Index) data and remotely sensed time series of vegetation indices. Demonstrated approach ensures robust regional review of short to medium term meteorological conditions, and identification of complementary temporal profiles of forest status evolution. Exemplified case study of South Tyrol confirms effectiveness of the method, as well as sheds some light on regional drought conditions and resulting forest status.

The presented scPDSI S-mode PCA results provides an interesting insight and essential synthesis of meteorological variability in South Tyrol between 2001 and 2012. The identified drought conditions between 2003 and 2007, as well as increasing aridity trends are in strong accordance with other global and local studies, and confirm intense drought impact in the region.

Forest status analyzed with the S-mode PCA of MODIS derived 2001–2012 NDVI (Normalized Difference Vegetation Index) and NDII7 (Normalized Difference Infrared Index band 7) time series tend to follow recognized scPDSI temporal variability. The correlation between meteorological conditions and PCs derived for time series of vegetation indices gave robust results supported by acknowledged patterns of forest vegetation drought impacts and documented local case-studies. Despite differences in temporal resolution of coupled time series, combination of quantitative and qualitative evaluations allowed to identify the most prominent and meaningful temporal patterns of forest drought responses: (i) diminished foliage water content between 2004 and 2007, which was mainly supported by NDII7 based PCs; and (ii) decreasing (increasing) photosynthetic activity, which was most commonly detected in the NDVI based scores. Regardless of the diverse PCA setups, numerous PCs rendered similar information. This confirms robustness of the method in extracting both dominant and latent drought stress conditions, and in indicating vegetation feedback as well as the quality of applied vegetation related measures. Next to a general overview of climate change and drought impact within the South Tyrolean forest, derived results ensure also more specific short-term variability, which presumably originates from local differences in forest structure, species distribution and environmental conditions. Although further analyses are required to fully comprehend detected response, presented outcome is consistent with other studies.

Based on a comparison among multiple S-mode PCA setups we indicate the covariance-matrix based decomposition of z-score normalized vegetation time series as the most suitable analysis design for the alpine forest drought related temporal monitoring. Both NDVI and NDII7 MODIS derived datasets provided reliable and complementary estimation of forest condition ensuring detection of drought induced changes. Although no clear conclusion was drawn on the advantage of loadings rotation, we consider the oblique Promax solution to reveal higher potential.

We believe our study suggests the efficient method for temporal monitoring of drought impact on alpine mountain forest. Demonstrated robustness of the model facilitates its application for other, less complex regions. Moreover, aptness of derived temporal patterns encourage to advance the approach towards spatial recognition of identified drought evolution responses and further examination of phenology and productivity within drought affected forest sties. This step will ensure additional insight into recognized changes and allow on more detailed analyses that will conclusively broaden our understanding of subtle complexity of drought impact on alpine forest ecosystem.