An Off-Grid Compressive Sensing Algorithm Based on Sparse Bayesian Learning for RFPA Radar
Abstract
1. Introduction
2. Materials and Methods
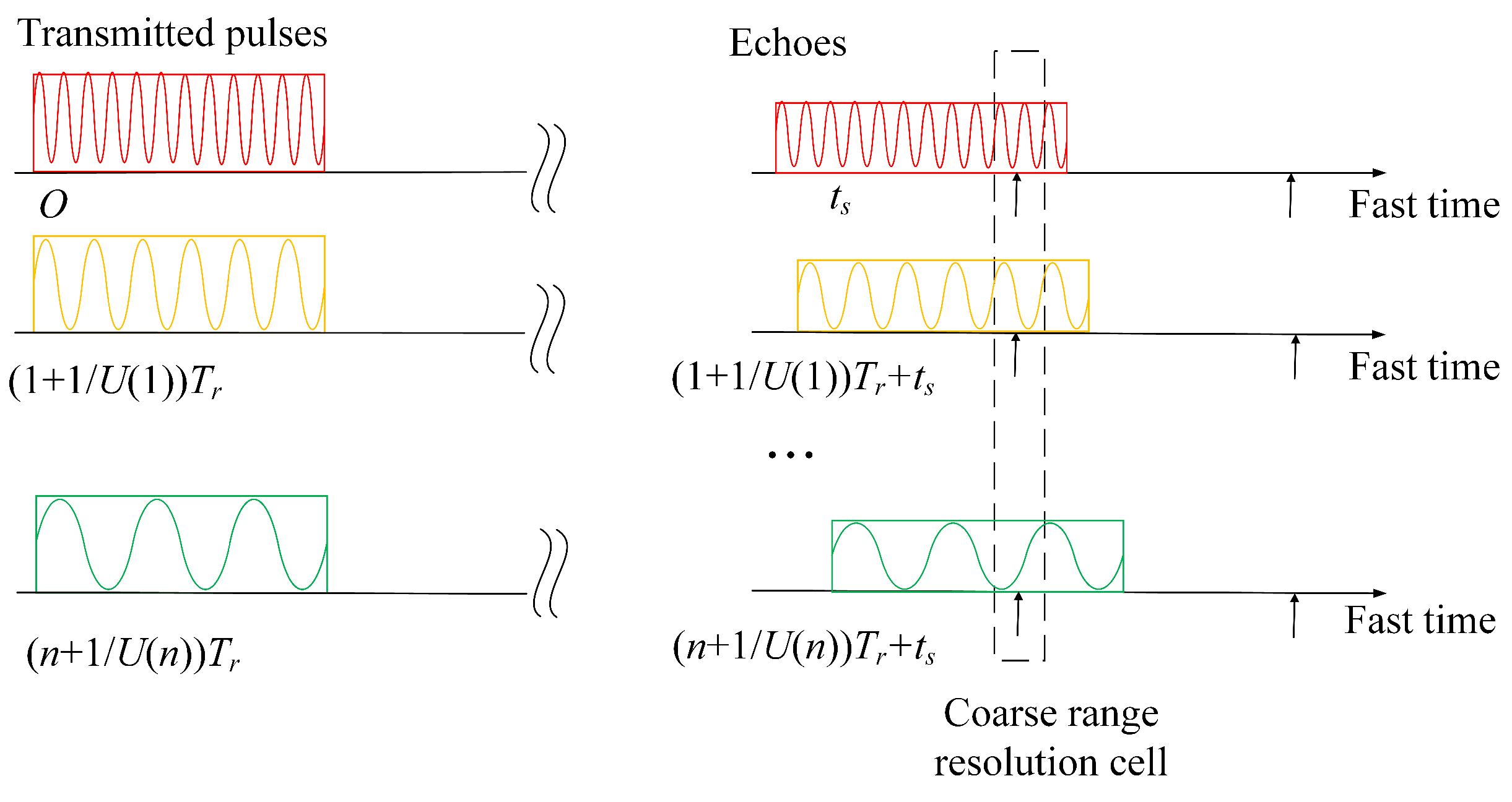
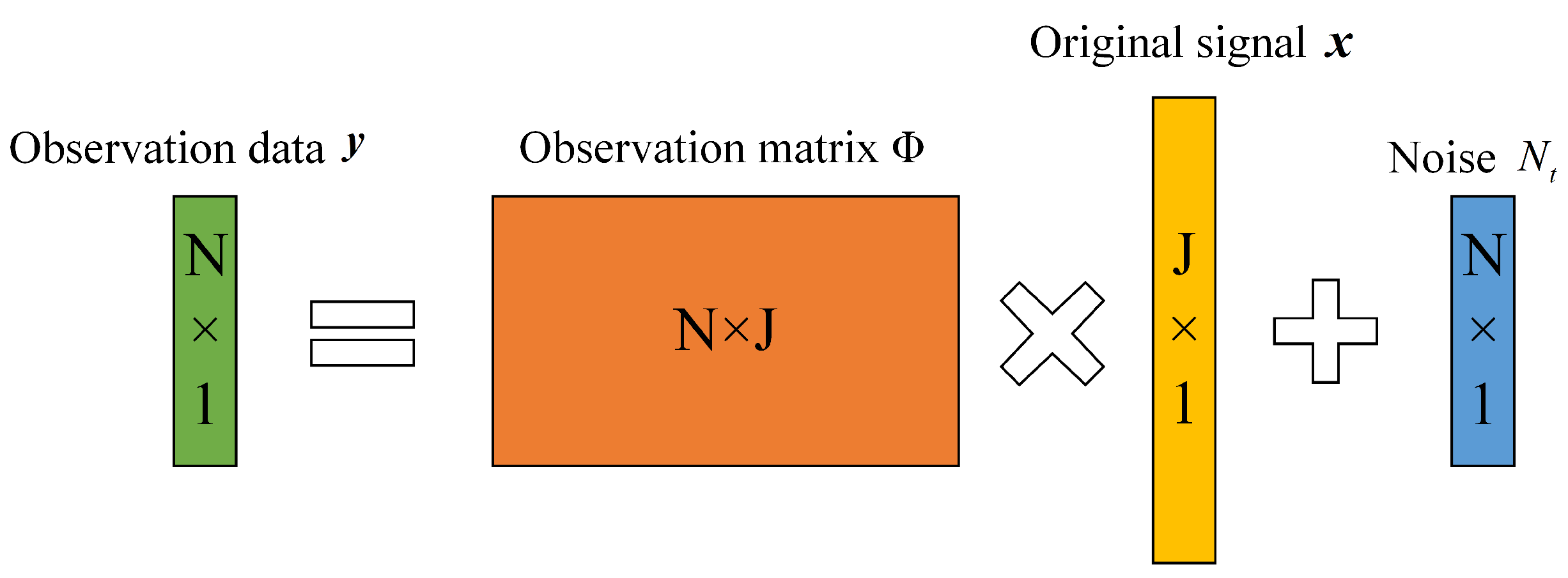
2.1. Signal Model
2.2. Prior Distribution Assumption for Signals
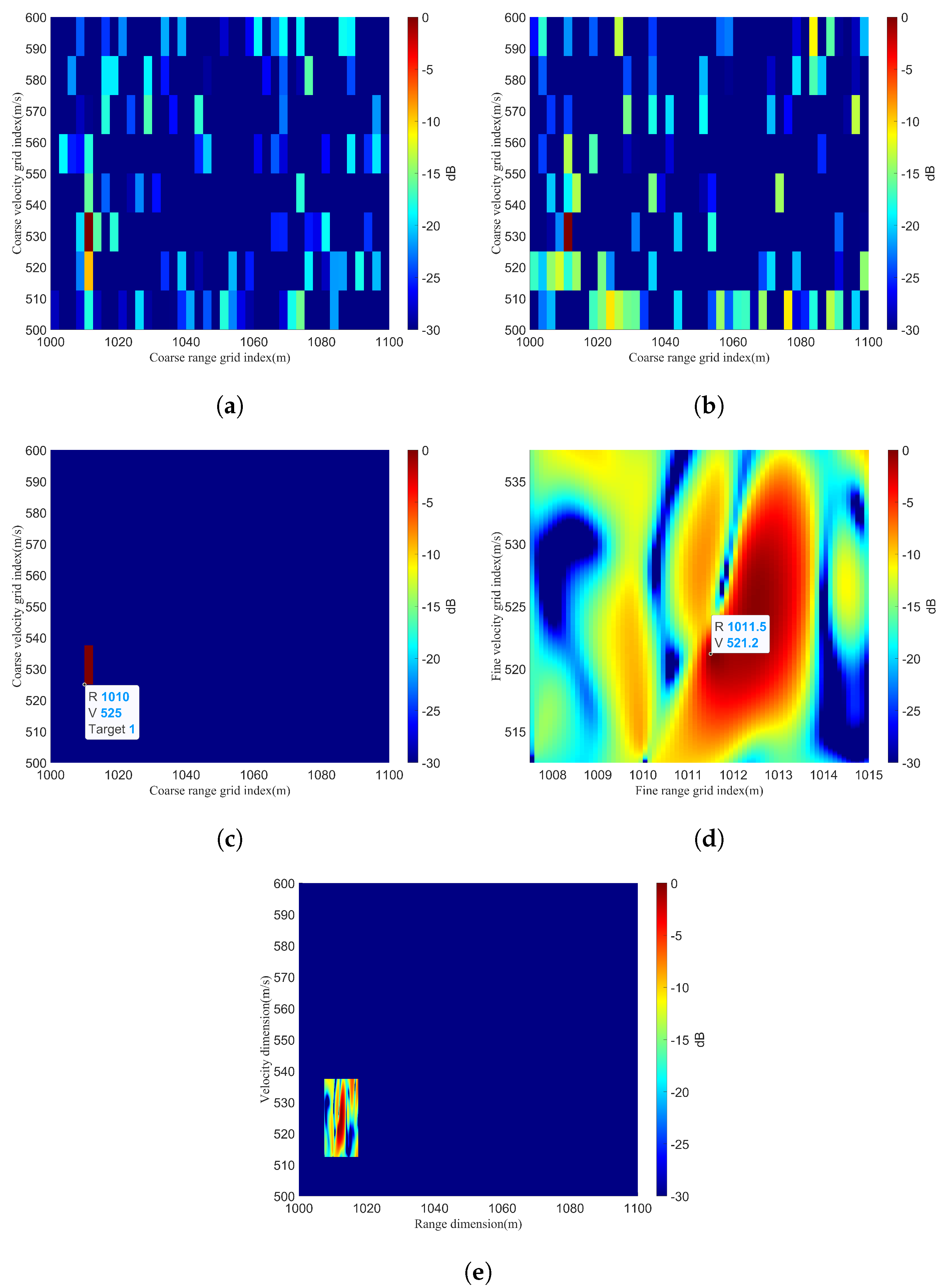
2.3. Coarse Search for RFPA Radar Targets
2.4. Fine Search for RFPA Radar Targets
| Algorithm 1: The Proposed RGDP−SBL Algorithm |
1: Input: observed data composed of echoes , error threshold , observation matrix , the number of snapshots L, the number of range−velocity grid points J, , pulse number N, parameter controlling the sparsity , 2: Initialization: , , , . 3: while do 4: . 5: Update and by Formulas (15) and (20). 6: Update and by Formulas (19) and (22). 7: Update by Formula (25). 8: if 9: break 10: end 11: end while 12: Find H largest peak clusters in . 13: for do 14: Update by Formula (28). 15: Update by Formula (27). 16: Update by Formula (29). 17: end for 18: Output: , , , converting the grid points yields the range and velocity of the target. |
3. Simulation Results
3.1. Simulation Setup
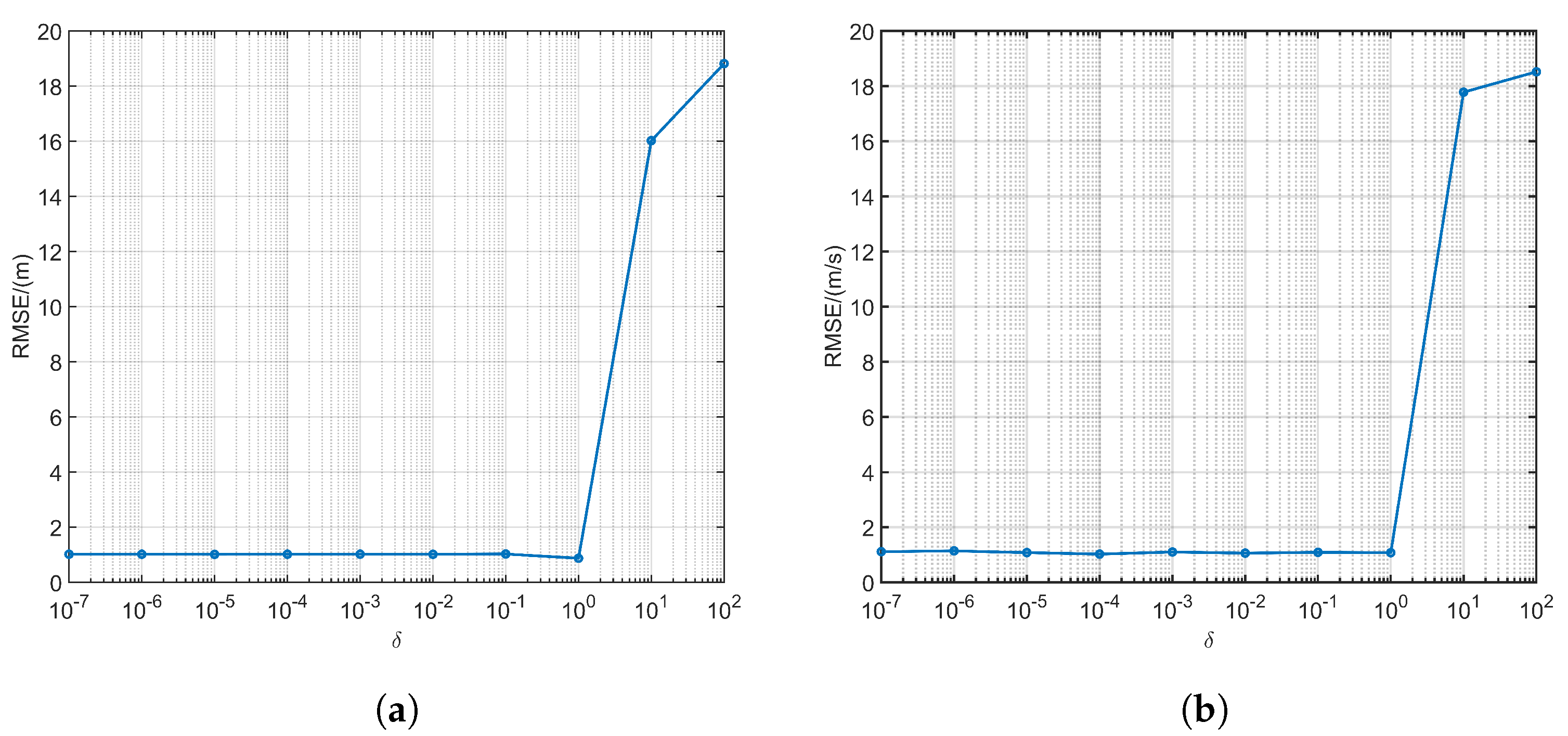
3.2. GDP Parameters Analysis
3.3. Performance Analysis under Off−Grid Conditions with On−Grid Assumption
3.3.1. Impact of Performance Due to Different Prior Distributions
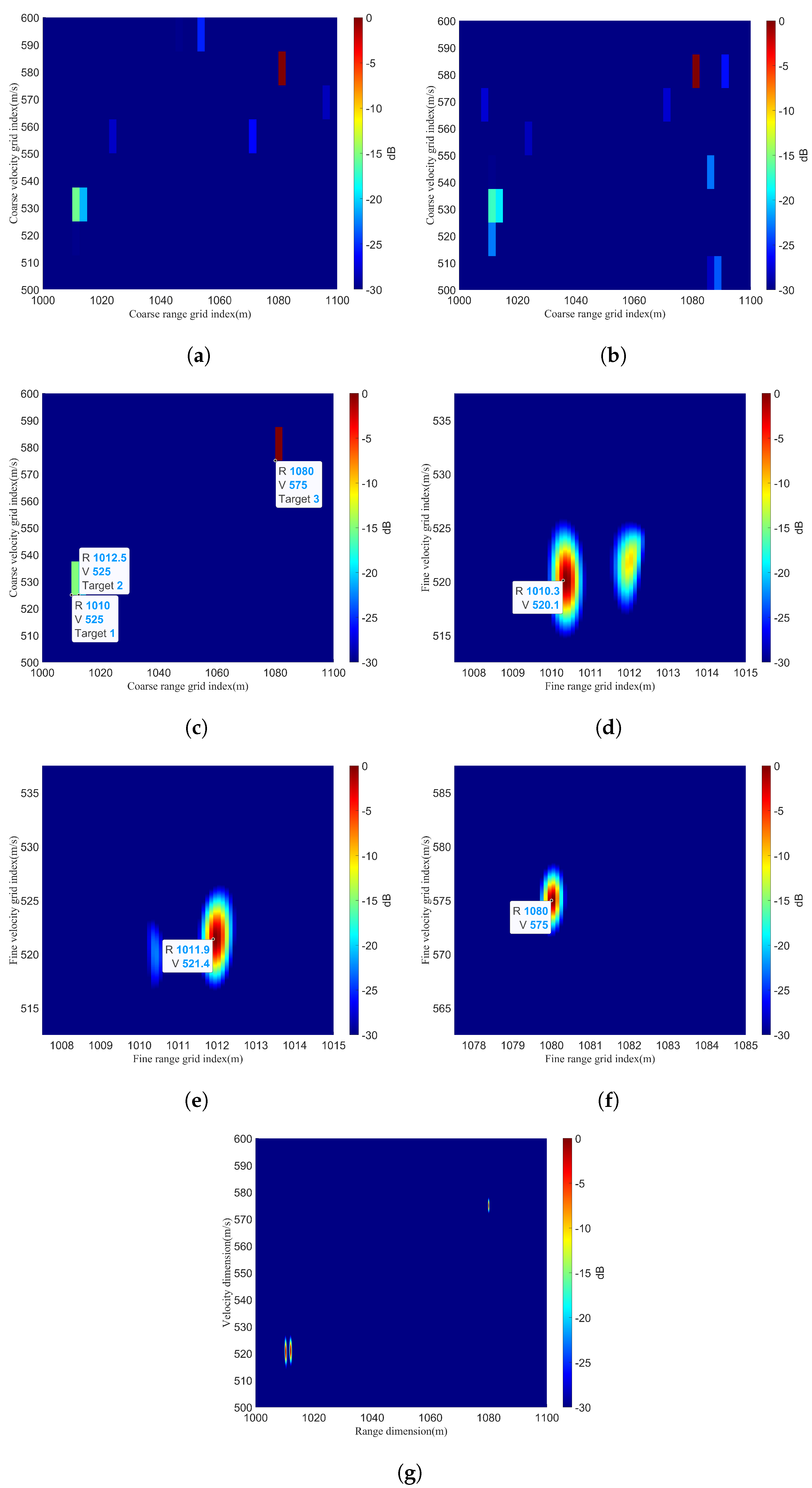
3.3.2. Performance of Algorithms with the Coarse Search Parts
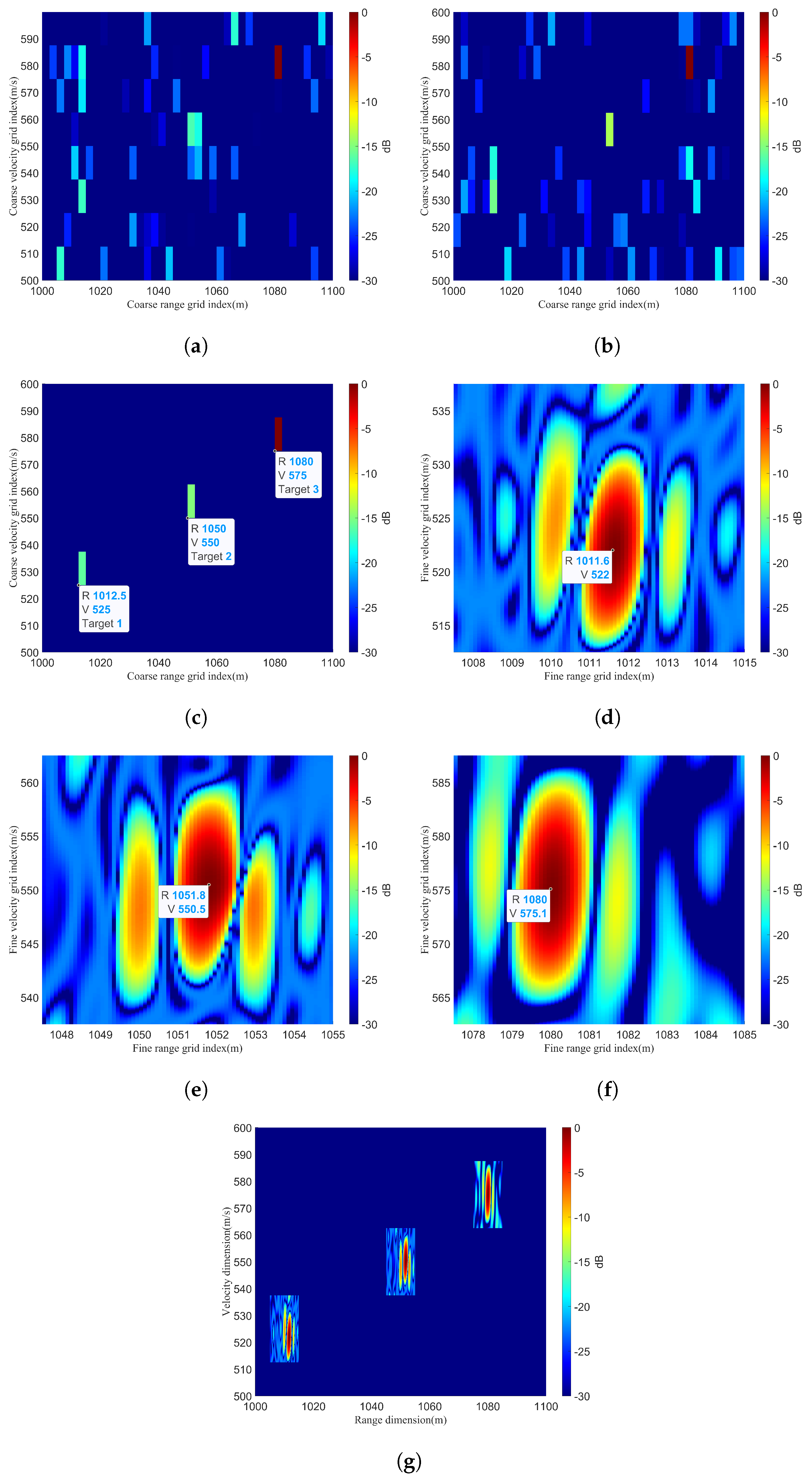
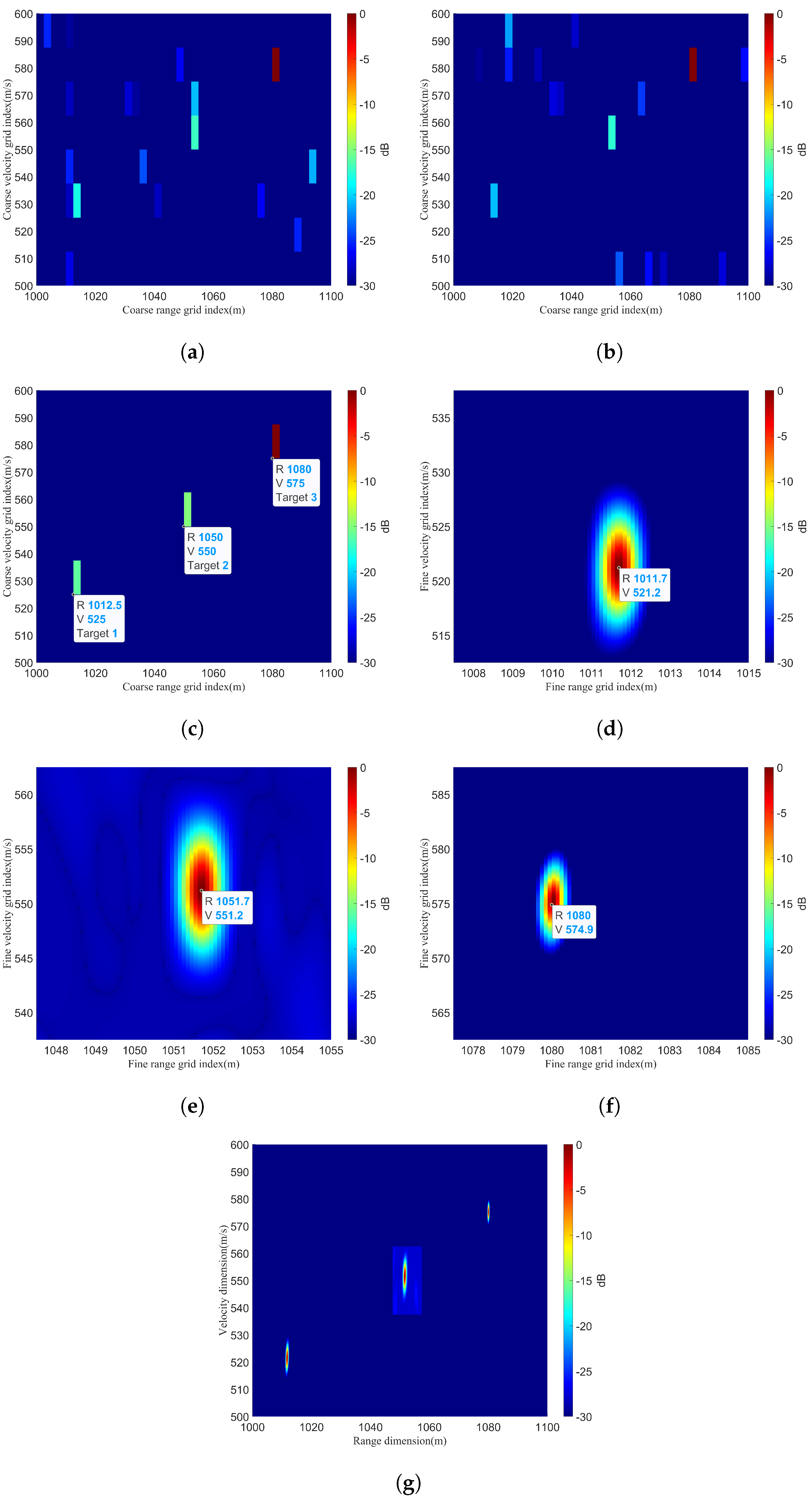
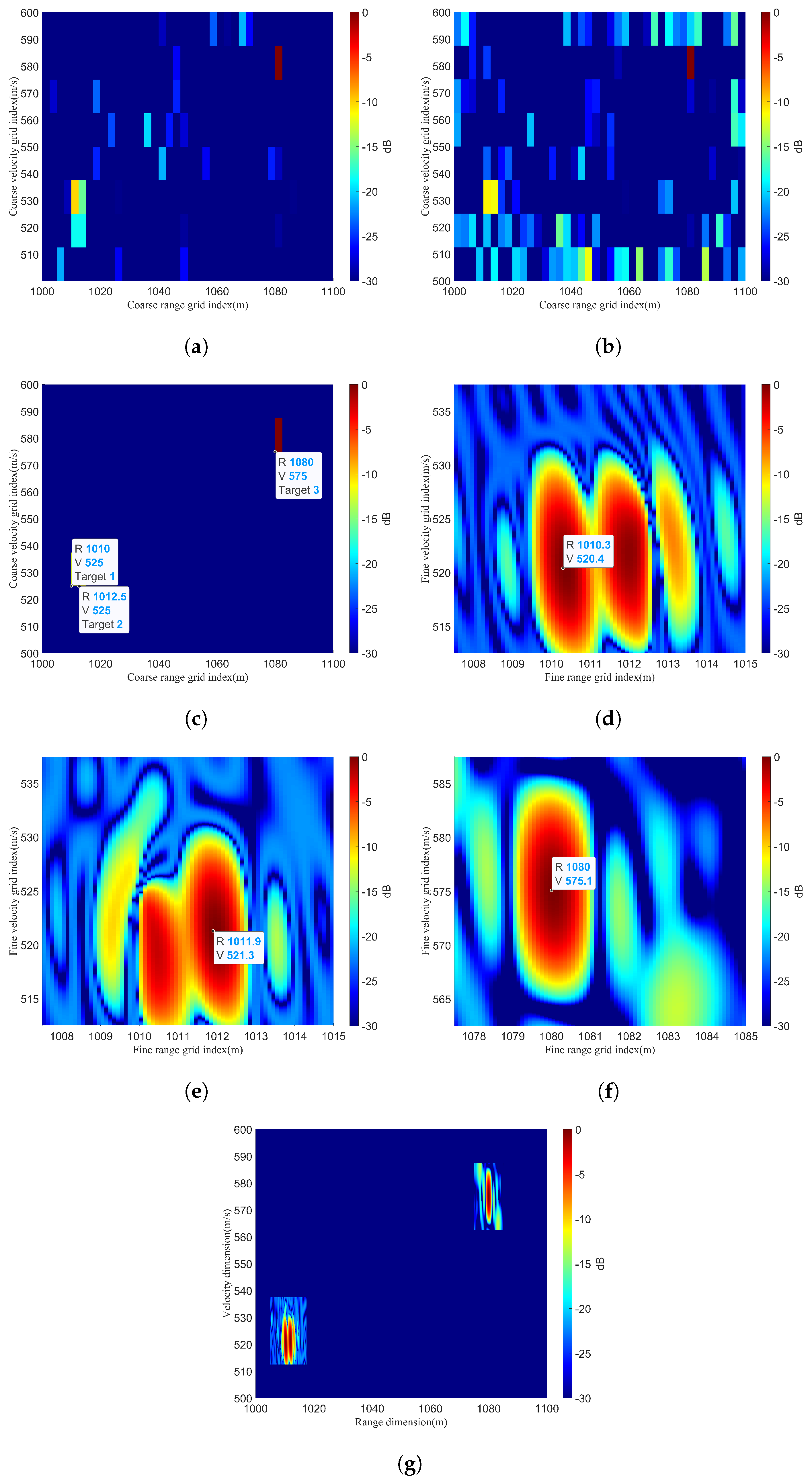
3.4. Performance Analysis under the Off−Grid Condition with Off−Grid Assumption
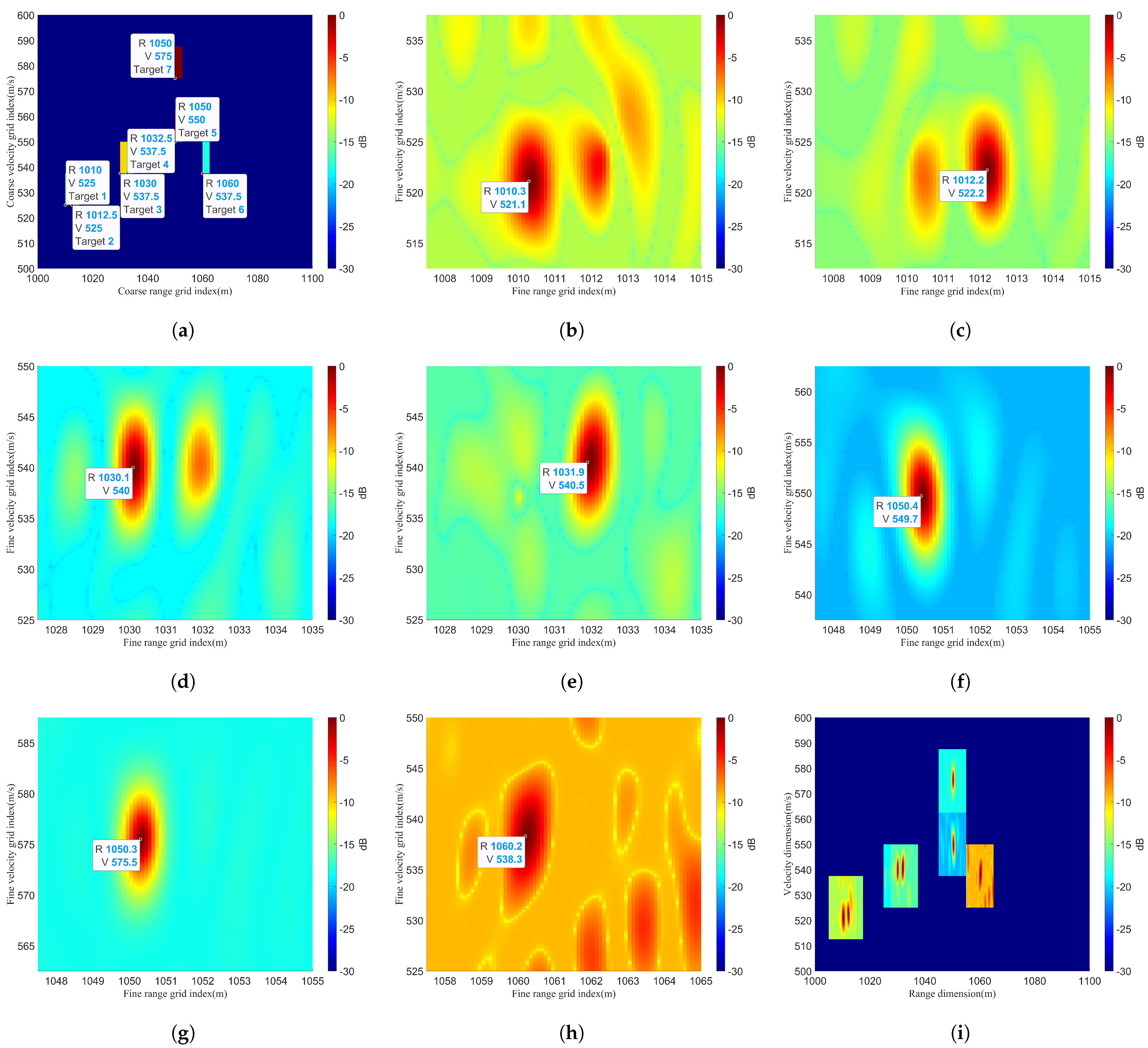
3.4.1. Impact of Performance Due to Different Scenarios
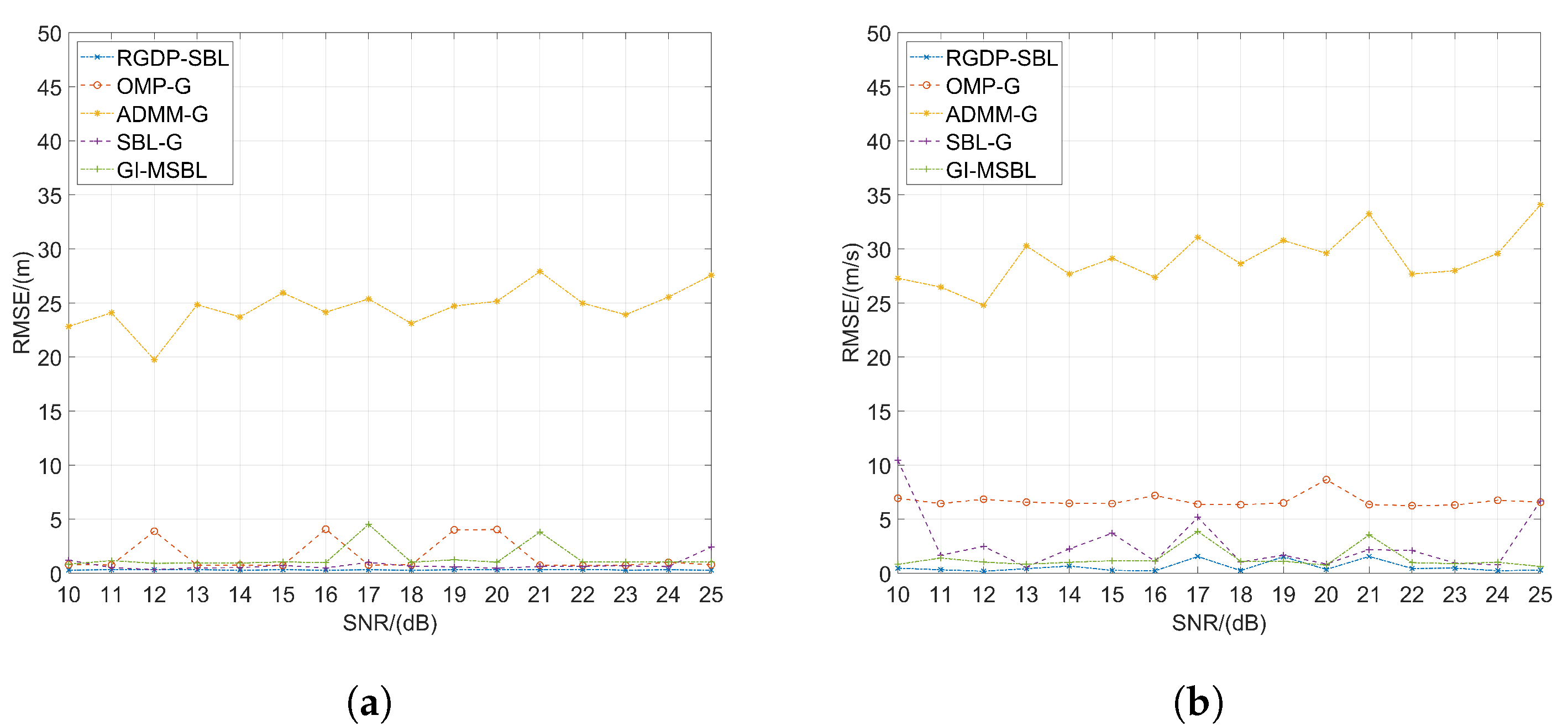
3.4.2. Impact of Performance Due to Different SNR Values
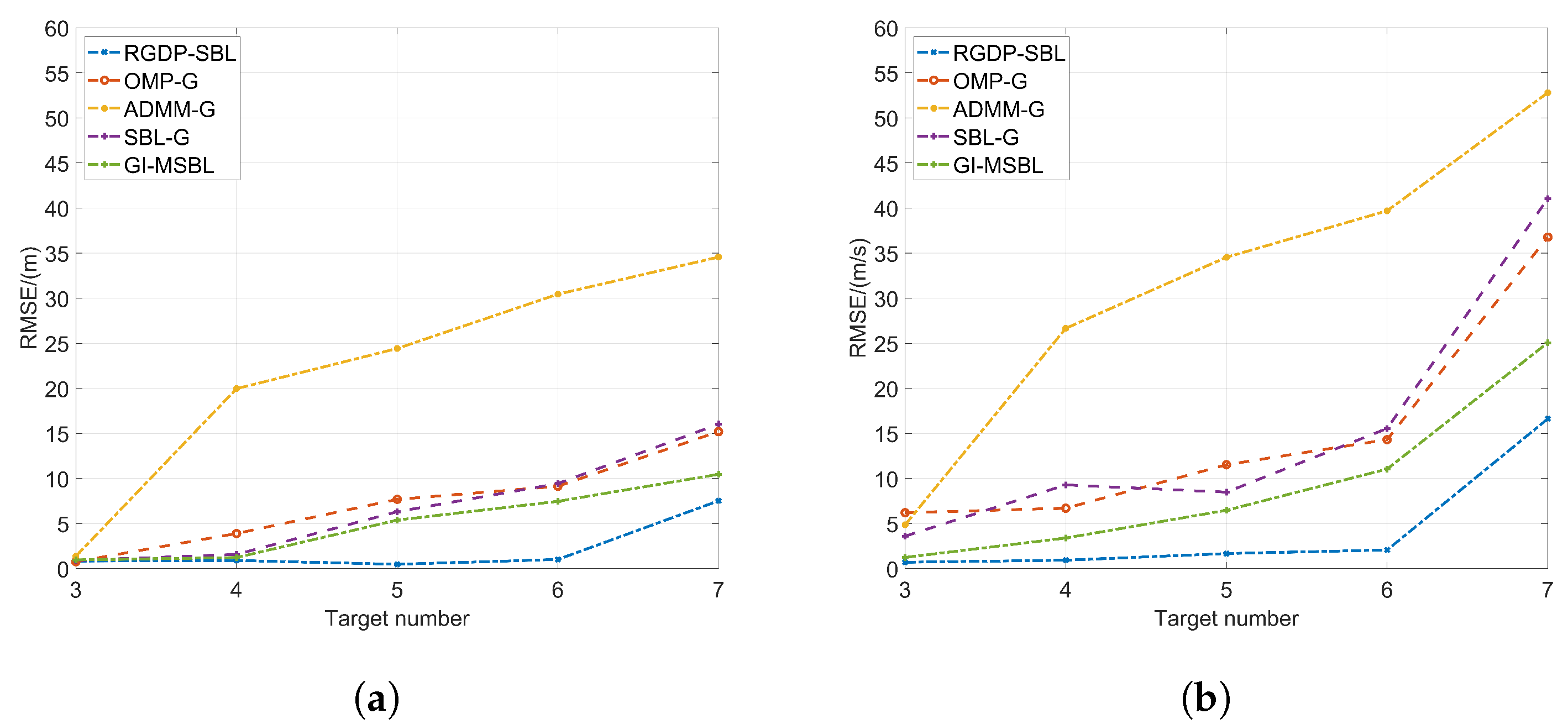
3.4.3. Impact of Performance Due to Different Target Numbers
4. Discussion
4.1. Discussion of Computational Complexity
4.2. Discussion of Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PRI | Pulse Repetition Interval |
| RFPA | Random Frequency and Pulse Repetition Interval Agile |
| CS | Compressed Sensing |
| SBL | Sparse Bayesian Learning |
| BP | Basis Pursuit |
| ADMM | Alternating Direction Method of Multipliers |
| NP | Nondeterministic Polynomial |
| OMP | Orthogonal Matching Pursuit |
| DOA | Direction of Arrive |
| MIMO | Multiple−Input Multiple−Output |
| CS−IGO | CS−Iterative Grid Optimization |
| AMP−CTLS | Adaptive Matching Pursuit with Constrained Total Least Squares |
| PSO | Particle Swarm Optimization |
| OGSBI | Off−Grid Sparse Bayesian Inference |
| GI−MSBL | Grid Interpolation-Multiple snapshot SBL |
| GDP | Generalized Double Pareto |
| RGDP−SBL | grid Refinement and GDP distribution based on SBL |
| CPI | Coherent Processing Interval |
| Probability Density Function | |
| EM | Expectation-Maximization |
| E−step | Expectation step |
| M−step | Maximization step |
| RMSE | Root Mean Square Error |
| SNR | signal−to−noise ratio |
References
- Long, X.W.; Li, K.; Tian, J.; Wang, J.; Wu, S.L. Ambiguity Function Analysis of Random Frequency and PRI Agile Signals. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 382–396. [Google Scholar] [CrossRef]
- Quan, Y.H.; Fang, W.; Gao, X.; Ruan, F.; Li, Y.C.; Xing, M.D. Review on Frequency Agile Radar Seeker. Aero Weapon. 2021, 28, 1–9. (In Chinese) [Google Scholar]
- Pace, P.E. Detecting and Classifying Low Probability of Intercept Radar, 2nd ed.; Artech: Morristown, NJ, USA, 2008. [Google Scholar]
- Blunt, S.D.; Mokole, E.L. Overview of radar waveform diversity. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 2–42. [Google Scholar] [CrossRef]
- Long, X.W.; Wu, W.H.; Li, K.; Wang, J.; Wu, S.L. Multi-Timeslot Wide-Gap Frequency-Hopping RFPA Signal and Its Sidelobe Suppression. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 634–649. [Google Scholar] [CrossRef]
- Axelsson, S.R.J. Analysis of Random Step Frequency Radar and Comparison With Experiments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 890–904. [Google Scholar] [CrossRef]
- Kulpa, J.S. Noise radar sidelobe suppression algorithm using mismatched filter approach. Int. J. Microw. Wirel. Technol. 2016, 8, 865–869. [Google Scholar] [CrossRef]
- Costas, J.P. A study of a class of detection waveforms having nearly ideal range-Doppler ambiguity properties. Proc. IEEE 1984, 72, 996–1009. [Google Scholar] [CrossRef]
- Maric, S.; Titlebaum, E.L. A class of frequency hop codes with nearly ideal characteristics for use in multiple-access spread-spectrum communications and radar and sonar systems. IEEE Trans. Commun. 1992, 40, 1442–1447. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Huang, T.Y. Coherent Frequency-Agile Radar Signal Processing by Solving an Inverse Problem with a Sparsity Constraint. Ph.D. Thesis, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Anitori, L.; Maleki, A.; Otten, M.; Baraniuk, R.G.; Hoogeboom, P. Design and Analysis of Compressed Sensing Radar Detectors. IEEE Trans. Signal Process. 2013, 61, 813–827. [Google Scholar] [CrossRef]
- Quan, Y.H.; Fang, W.; Sha, M.H.; Chen, X.D.; Ruan, F.; Li, X.H.; Meng, F.; Wu, Y.J.; Xing, M.D. Present situation and prospects of frequency agility radar waveform countermeasures. Syst. Eng. Electron. 2021, 43, 3126–3136. [Google Scholar]
- Yang, J.G. Research on Sparsity-Driven Regularization Radar Imaging Theory and Method. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Liu, Z.; Wei, X.Z.; Li, X. Low sidelobe robust imaging in random frequency-hopping wideband radar based on compressed sensing. J. Cent. South Univ. 2013, 20, 702–714. [Google Scholar] [CrossRef]
- Wang, W. A Study of Convex Relaxation Algorithms for Compressed Sensing Reconstruction Problem. Master’s Dissertation, Xidian University, Xi’an, China, 2014. [Google Scholar]
- Huang, T.Y.; Liu, Y.M.; Xu, X.Y.; Xu, X.Y.; Eldar, Y.C.; Wang, X.Q. Analysis of Frequency Agile Radar via Compressed Sensing. IEEE Trans. Signal Process. 2018, 66, 6228–6240. [Google Scholar] [CrossRef]
- Quan, Y.H.; Wu, Y.J.; Li, Y.C.; Sun, G.C.; Xing, M.D. Range-Doppler reconstruction for frequency agile and PRF-jittering radar. IET Radar, Sonar Navig 2017, 12, 348–352. [Google Scholar] [CrossRef]
- Wipf, D.; Palmer, J.; Rao, B. Perspectives on Sparse Bayesian Learning. Adv. Neural Inf. Process. Syst. 2003, 16, 249–256. [Google Scholar]
- Wipf, D.; Rao, B. Sparse Bayesian Learning for Basis Selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Tao, Y.J.; Zhang, G.; Tao, T.B.; Leng, Y.; Leung, H. Frequency-agile Coherent Radar Target Sidelobe Suppression Based on Sparse Bayesian Learning. In Proceedings of the 2019 IEEE MTT-S International Microwave Biomedical Conference (IMBioC), Nanjing, China, 6–8 May 2019; Volume 1, pp. 1–4. [Google Scholar]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Huang, Q.H.; Zhang, G.F.; Fang, Y. Real-valued DOA estimation for spherical arrays using sparse Bayesian learning. Signal Process. 2016, 125, 79–86. [Google Scholar] [CrossRef]
- Liu, H.C.; Jiu, B.; Liu, H.W.; Bao, Z. A novel ISAR imaging algorithm for micromotion targets based on multiple sparse Bayesian learning. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1772–1776. [Google Scholar]
- Liu, Z.X.; Zhu, S.Q.; Xu, J.W.; Lan, L. An Adaptive Range-Angle-Doppler Processing Approach for FDA-MIMO Radar Based on Sparse Reconstruction. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 1704–1708. [Google Scholar]
- Wipf, D. Sparse estimation with structured dictionaries. Adv. Neural Inf. Process. Syst. 2011, 24, 2016–2024. [Google Scholar]
- Chae, D.H.; Sadeghi, P.; Kennedy, R.A. Effects of basis-mismatch in compressive sampling of continuous sinusoidal signals. In Proceedings of the 2010 2nd International Conference on Future Computer and Communication, Wuhan, China, 21–24 May 2010; Volume 2, pp. V2-739–V2-743. [Google Scholar]
- Chi, Y.J.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to Basis Mismatch in Compressed Sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, X.Z.; Li, X. Adaptive clutter suppression for airborne random pulse repetition interval radar based on compressed sensing. Prog. Electromagn. Res. 2012, 128, 291–311. [Google Scholar] [CrossRef][Green Version]
- Huang, T.Y.; Liu, Y.M.; Meng, H.D.; Wang, X.Q. Adaptive Matching Pursuit for Off-Grid Compressed Sensing. arXiv 2013, arXiv:arXiv:13084273. [Google Scholar]
- Chen, Q.; Wu, X.J.; Liu, J.H. Adaptive compressed sensing based randomized step frequency radar with a weighted PSO. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 1751–1756. [Google Scholar]
- Zhang, G.B.; Huang, T.Y.; Liu, Y.M.; Eldar, Y.C.; Wang, X.Q. Frequency Agile Radar Using Atomic Norm Soft Thresholding with Modulations. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Yang, Z.; Xie, L.H.; Zhang, C.S. Off-Grid Direction of Arrival Estimation Using Sparse Bayesian Inference. IEEE Trans. Signal Process. 2013, 61, 38–43. [Google Scholar] [CrossRef]
- Dai, J.S.; Bao, X.; Xu, W.C.; Chang, C.Q. Root Sparse Bayesian Learning for Off-Grid DOA Estimation. IEEE Signal Process. Lett. 2017, 24, 46–50. [Google Scholar] [CrossRef]
- Wang, Q.S.; Yu, H.; Li, J.; Dong, C.; Ji, F.; Chen, Y.K. Sparse Bayesian Learning Based Algorithm for DOA Estimation of Closely Spaced Signals. J. Electron. Inf. Technol. 2021, 43, 708–716. [Google Scholar]
- Wipf, D.P. Bayesian Methods for Finding Sparse Representations; University of California: San Diego, CA, USA, 2006. [Google Scholar]
- Huang, T.Y.; Liu, Y.M.; Meng, H.D.; Wang, X.Q. Adaptive waveform design in random stepped frequency radar. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013; pp. 1–5. [Google Scholar]
- Gerstoft, P.; Mecklenbräuker, C.F.; Xenaki, A.; Nannuru, S. Multisnapshot Sparse Bayesian Learning for DOA. IEEE Signal Process. Lett. 2016, 23, 1469–1473. [Google Scholar] [CrossRef]
- Ji, S.H.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Armagan, A.; Dunson, D.B.; Lee, J. Generalized double Pareto shrinkage. Stat. Sin. 2011, 23, 119–143. [Google Scholar] [CrossRef]
- Wang, Q.S.; Yu, H.; Li, J.; Ji, F.; Chen, F.J. Sparse Bayesian Learning Using Generalized Double Pareto Prior for DOA Estimation. IEEE Signal Process. Lett. 2021, 28, 1744–1748. [Google Scholar] [CrossRef]
- Wipf, D.; Rao, B. An Empirical Bayesian Strategy for Solving the Simultaneous Sparse Approximation Problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef]
- Giri, R.; Rao, B. Type I and Type II Bayesian Methods for Sparse Signal Recovery Using Scale Mixtures. IEEE Trans. Signal Process. 2016, 64, 3418–3428. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Wang, A.P.; Zhang, G.Y.; Liu, F. Research and Application of EM Algorithm. Comput. Technol. Dev. 2009, 19, 108–110. (In Chinese) [Google Scholar]


| Parameters | Symbols | Values | Units |
|---|---|---|---|
| Central Carrier Frequency | 10 | GHz | |
| Average PRI | 10 | s | |
| Pulse Width | 1 | s | |
| Bandwidth of Frequency−Hopping Step | 1 | MHz | |
| Pulse Number | N | 128 | - |
| Frequency agility range | B | 128 | MHz |
| PRI agility range | 5 | s |
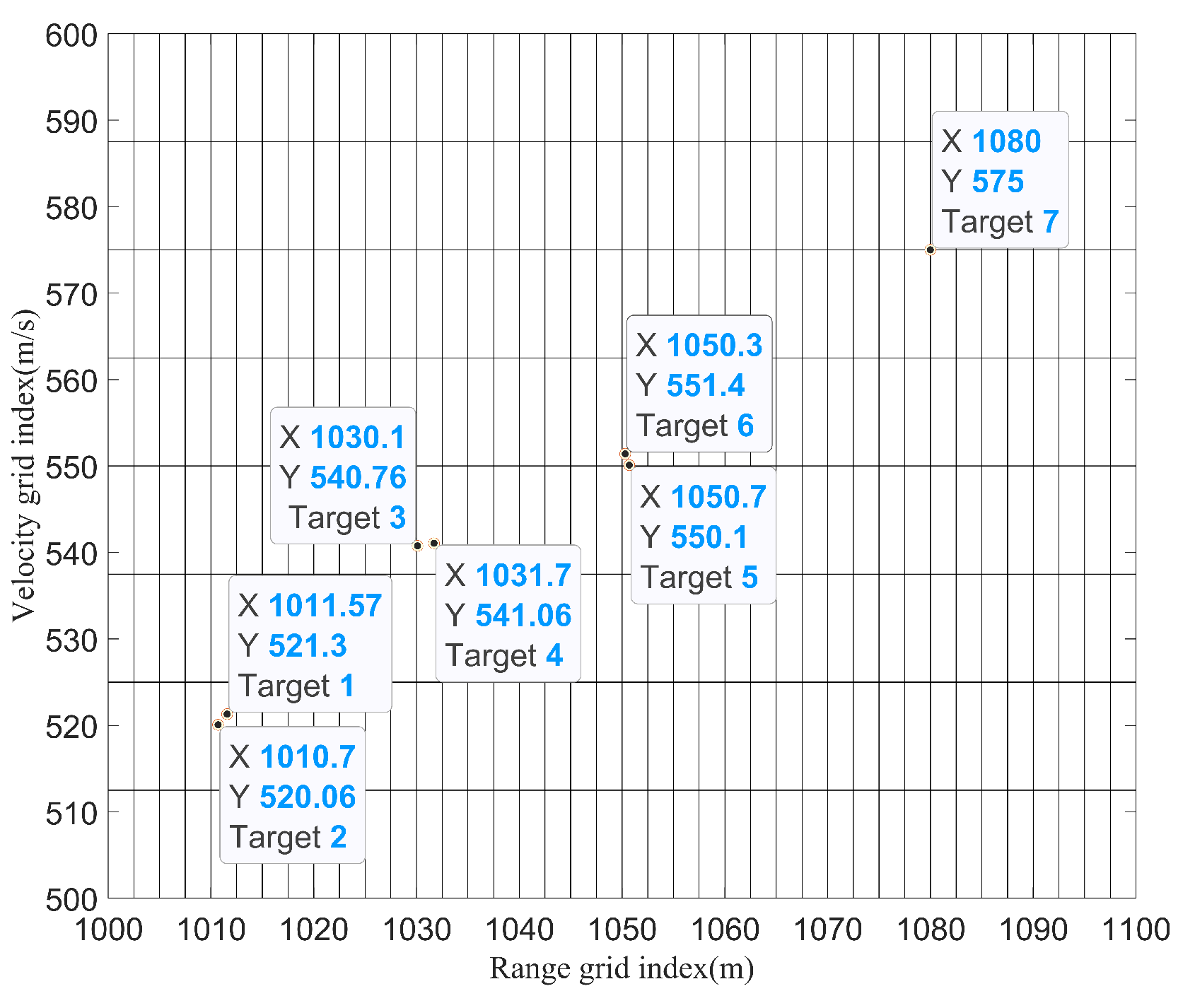
| Scenarios | Targets | Range (m) | Velocity (m/s) | SNR (dB) |
|---|---|---|---|---|
| Scenario 1 | Target 1 | 1011.57 | 521.3 | 20 |
| Scenario 2 | Target 1 | 1011.57 | 521.3 | 20 |
| Target 2 | 1051.7 | 551.06 | 20 | |
| Target 3 | 1080 | 575 | 30 | |
| Scenario 3 | Target 1 | 1011.57 | 521.3 | 20 |
| Target 2 | 1010.7 | 520.06 | 20 | |
| Target 3 | 1080 | 575 | 30 | |
| Scenario 4 | Target 1 | 1011.57 | 521.3 | 20 |
| Target 2 | 1010.7 | 520.06 | 20 | |
| Target 3 | 1030.1 | 540.76 | 20 | |
| Target 4 | 1080 | 575 | 30 | |
| Scenario 5 | Target 1 | 1011.57 | 521.3 | 20 |
| Target 2 | 1010.7 | 520.06 | 20 | |
| Target 3 | 1030.1 | 540.76 | 20 | |
| Target 4 | 1031.7 | 541.06 | 20 | |
| Target 5 | 1080 | 575 | 30 | |
| Scenario 6 | Target 1 | 1011.57 | 521.3 | 20 |
| Target 2 | 1010.7 | 520.06 | 20 | |
| Target 3 | 1030.1 | 540.76 | 20 | |
| Target 4 | 1031.7 | 541.06 | 20 | |
| Target 5 | 1050.7 | 550.1 | 20 | |
| Target 6 | 1080 | 575 | 30 | |
| Scenario 7 | Target 1 | 1011.57 | 521.3 | 20 |
| Target 2 | 1010.7 | 520.06 | 20 | |
| Target 3 | 1030.1 | 540.76 | 20 | |
| Target 4 | 1031.7 | 541.06 | 20 | |
| Target 5 | 1050.7 | 550.1 | 20 | |
| Target 6 | 1050.3 | 551.4 | 20 | |
| Target 7 | 1080 | 575 | 30 |
| Scenarios | Distribution | (m) | (m/s) |
|---|---|---|---|
| Scenario 1 | complex Gaussian | 0.93 | 3.70 |
| Laplace | 0.93 | 3.70 | |
| GDP | 0.67 | 3.70 | |
| Scenario 2 | complex Gaussian | 1.09 | 2.72 |
| Laplace | 0.72 | 2.70 | |
| GDP | 0.70 | 2.22 | |
| Scenario 3 | complex Gaussian | 2.51 | 4.01 |
| Laplace | 0.90 | 3.85 | |
| GDP | 0.72 | 3.97 |
| Scenarios | Algorithms | (m) | (m/s) |
|---|---|---|---|
| Scenario 1 | OMP−C | 0.81 | 6.10 |
| ADMM | 0.76 | 6.10 | |
| SBL | 0.93 | 3.70 | |
| GI−MSBL−C | 0.93 | 3.70 | |
| RGDP−SBL−C | 0.67 | 3.70 | |
| Scenario 2 | OMP−C | 0.71 | 2.11 |
| ADMM | 0.71 | 2.31 | |
| SBL | 1.01 | 2.22 | |
| GI−MSBL−C | 0.71 | 2.22 | |
| RGDP−SBL−C | 0.70 | 2.22 | |
| Scenario 3 | OMP−C | 1.38 | 3.78 |
| ADMM | 0.99 | 5.82 | |
| SBL | 2.51 | 4.18 | |
| GI−MSBL−C | 0.71 | 3.85 | |
| RGDP−SBL−C | 0.67 | 3.56 |
| Scenarios | Algorithms | (m) | (m/s) |
|---|---|---|---|
| Scenario 1 | OMP−G * | 0.57 | 0.70 |
| ADMM−G * | 0.42 | 0.66 | |
| SBL−G * | 0.05 | 0.45 | |
| GI−MSBL−G * | 0.03 | 0.10 | |
| RGDP−SBL ** | 0.03 | 0.06 | |
| Scenario 2 | OMP−G * | 0.45 | 1.89 |
| ADMM−G * | 0.71 | 2.23 | |
| SBL−G * | 0.46 | 0.71 | |
| GI−MSBL−G * | 0.11 | 0.23 | |
| RGDP−SBL ** | 0.04 | 0.14 | |
| Scenario 3 | OMP−G * | 1.37 | 3.56 |
| ADMM−G * | 0.97 | 4.85 | |
| SBL−G * | 1.37 | 3.56 | |
| GI−MSBL−G * | 1.02 | 1.13 | |
| RGDP−SBL ** | 0.41 | 0.96 |
| Algorithms | Target Scenarios | Running Time (s) | Computational Complexity |
|---|---|---|---|
| SBL * in [22] | Scenario 1 | 0.43058 | |
| Scenario 2 | 0.62564 | ||
| Scenario 3 | 1.25592 | ||
| RGDP−SBL−C ** | Scenario 1 | 0.0887 | |
| Scenario 2 | 0.11848 | ||
| Scenario 3 | 0.1267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Shan, B.; Duan, S.; Zhao, Y.; Zhong, Y. An Off-Grid Compressive Sensing Algorithm Based on Sparse Bayesian Learning for RFPA Radar. Remote Sens. 2024, 16, 403. https://doi.org/10.3390/rs16020403
Wang J, Shan B, Duan S, Zhao Y, Zhong Y. An Off-Grid Compressive Sensing Algorithm Based on Sparse Bayesian Learning for RFPA Radar. Remote Sensing. 2024; 16(2):403. https://doi.org/10.3390/rs16020403
Chicago/Turabian StyleWang, Ju, Bingqi Shan, Song Duan, Yi Zhao, and Yi Zhong. 2024. "An Off-Grid Compressive Sensing Algorithm Based on Sparse Bayesian Learning for RFPA Radar" Remote Sensing 16, no. 2: 403. https://doi.org/10.3390/rs16020403
APA StyleWang, J., Shan, B., Duan, S., Zhao, Y., & Zhong, Y. (2024). An Off-Grid Compressive Sensing Algorithm Based on Sparse Bayesian Learning for RFPA Radar. Remote Sensing, 16(2), 403. https://doi.org/10.3390/rs16020403






