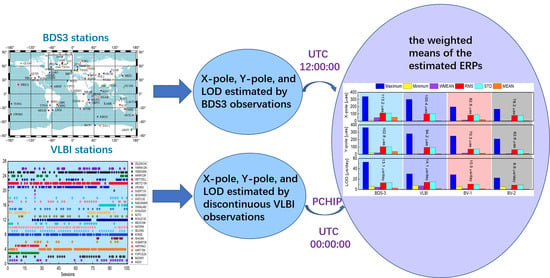
Estimation of Earth Rotation Parameters Based on BDS-3 and Discontinuous VLBI Observations
Abstract
1. Introduction
2. Materials and Methods
2.1. Estimating ERPs from BDS-3 Observations
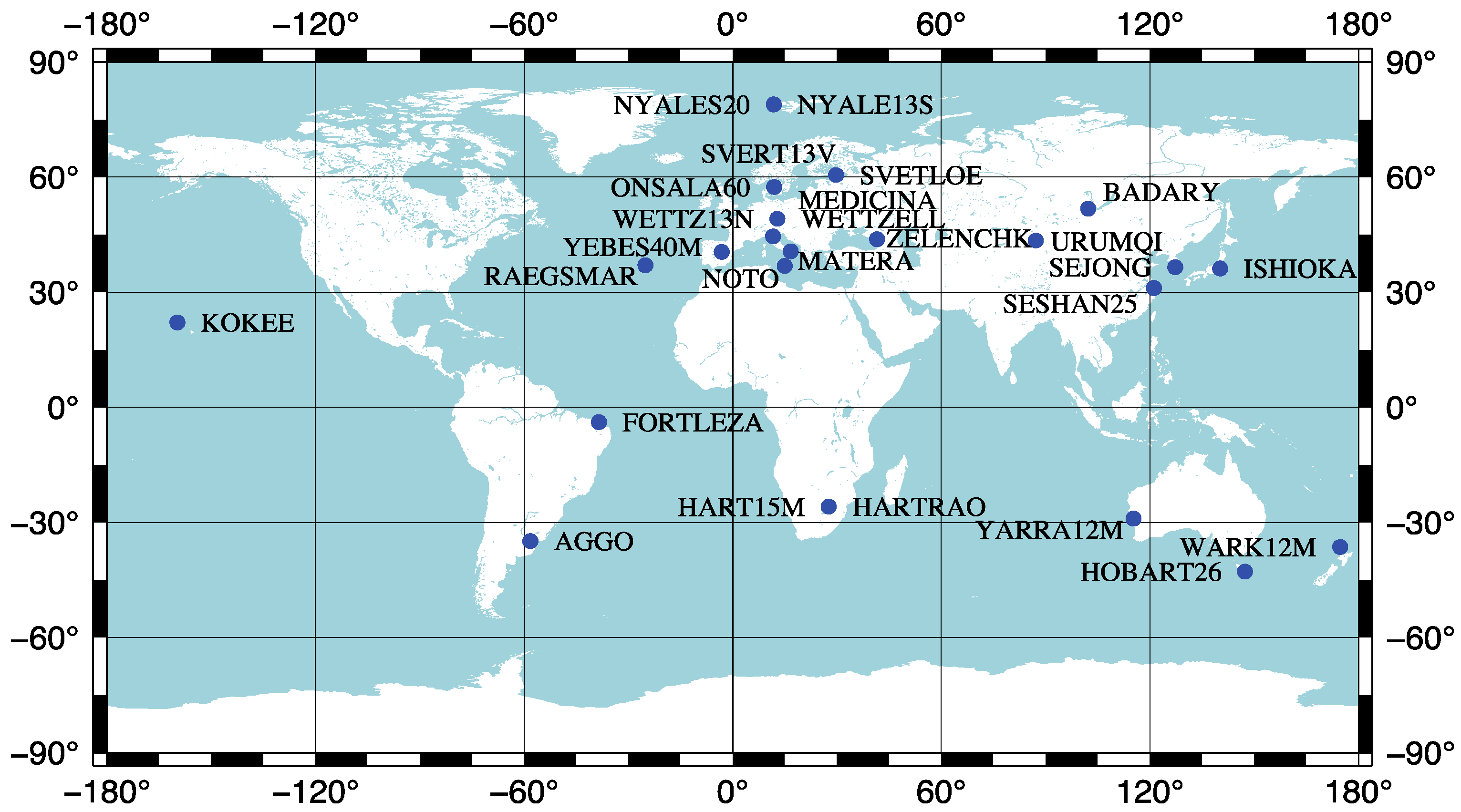
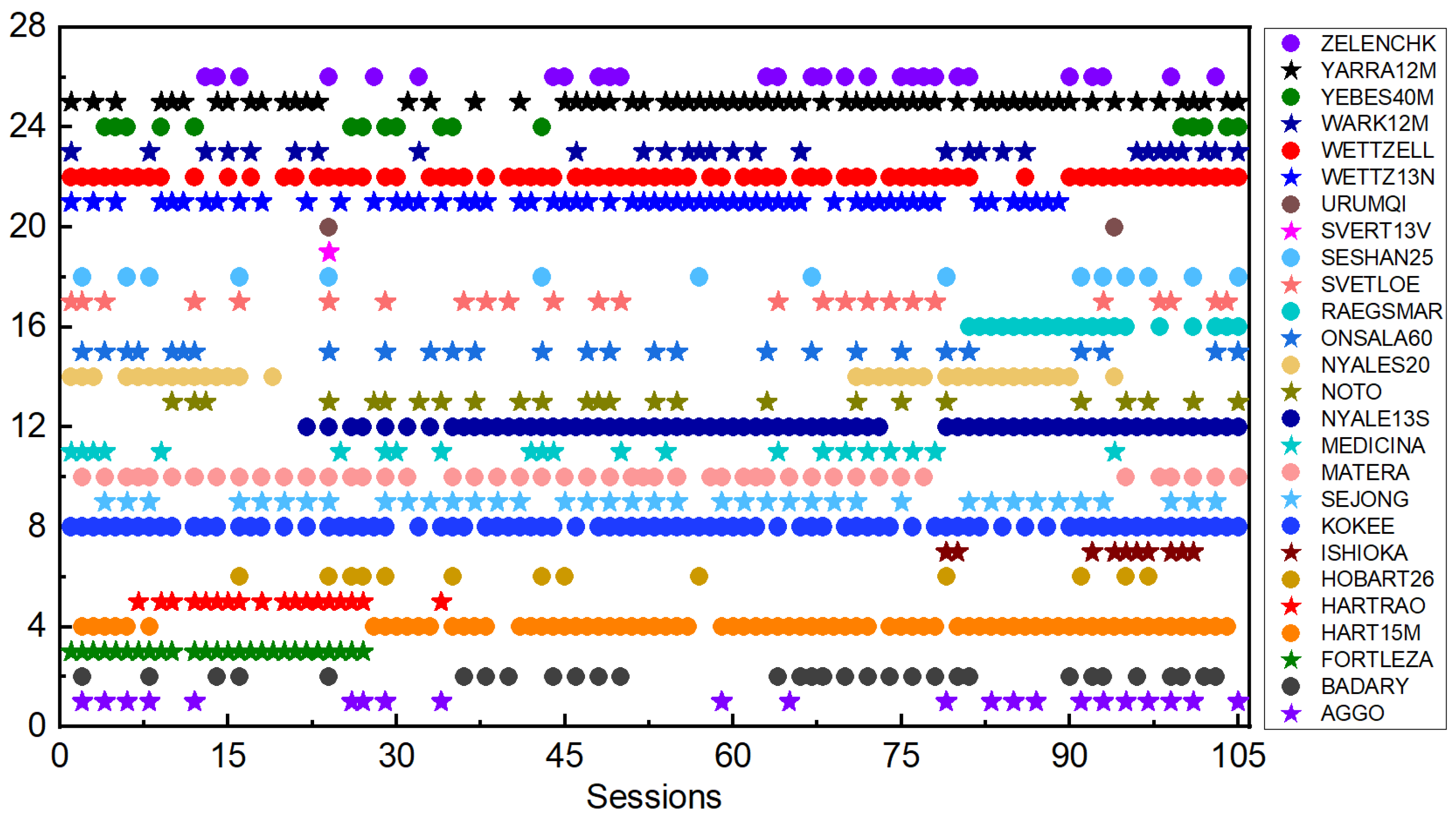
2.2. Estimating ERPs from VLBI Observations
| Items | Strategy |
|---|---|
| Method | Gauss-Markov least squares estimation |
| Weighting scheme | The stand approach (SA) [55] for EOP estimation |
| Clock offset | Estimated as piecewise linear offsets (60 min), one rate, and one quadratic term per clock |
| Troposphere | Corrected by the Saastamoinen model [56] and VMF3 mapping function [57], the zenith wet delay estimation interval is 60 min and the gradient parameters were not estimated |
| Ionosphere | Ionospheric free combination |
| ERPs | Bulletin A is used as a priori model, and the resolution for the estimated ERPs is 24 h. |
| Source coordinate | Estimated |
| Station coordinate | Estimated as one offset each session |
| ITRF/ICRF model | ITRF2020 [58], ICRF3 [59] |
| Solid Earth tides, pole tides | IERS Conventions 2010 |
| Ocean tides | FES2004 [45] |
| Earth Rotation Parameters | The X-pole, Y-pole, UT1-UTC are estimated, and their constraints: polar motion (2 mas); UT1-UTC (20 µs) |
| Other parameters | Using the default values provided by VieVS software version 3.2 (VieVS3.2) |
3. Results
3.1. Daily ERP Series Estimated Using BDS-3 Observations
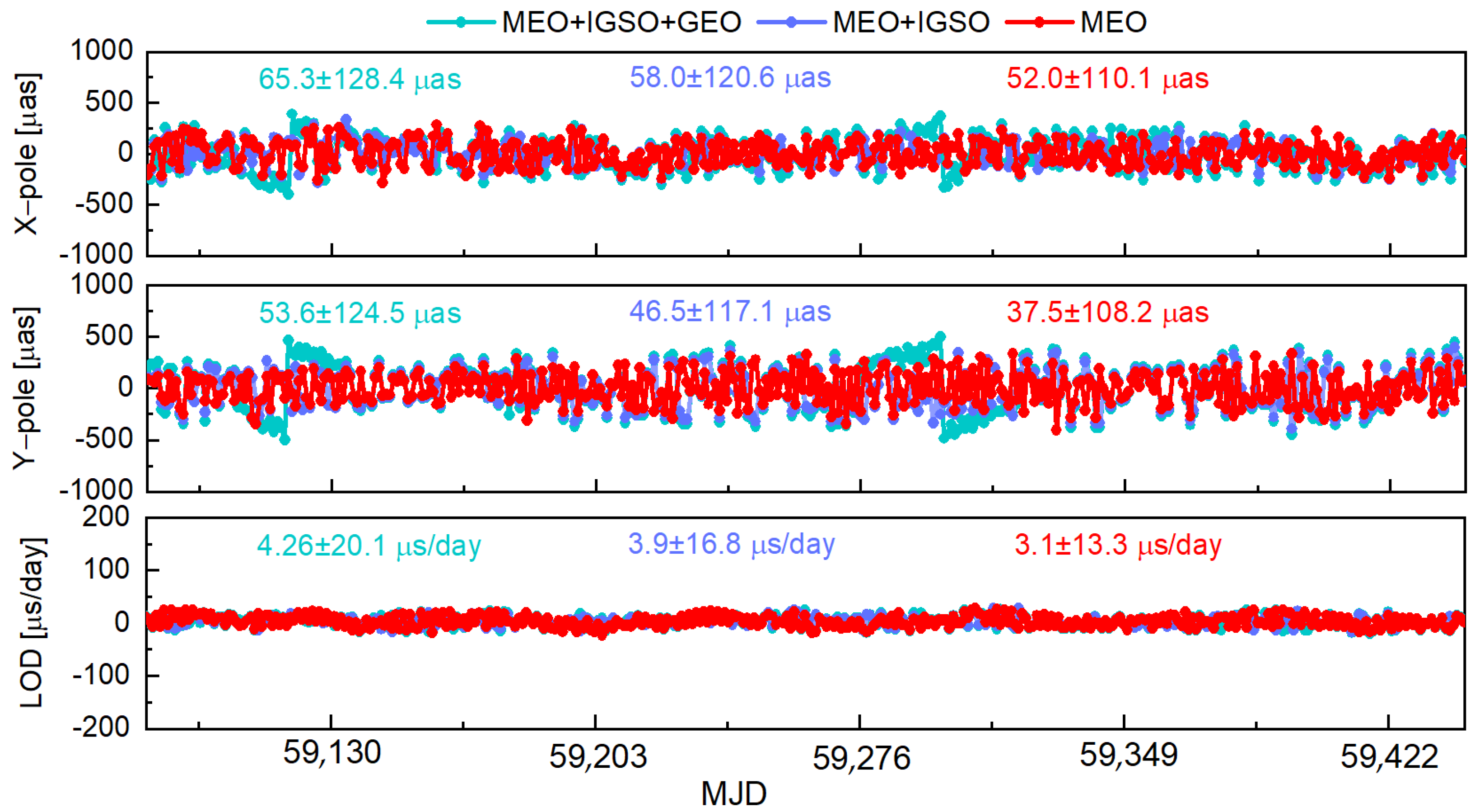
3.2. Analysis of Daily ERP Series Estimated by VLBI Observations
3.3. Analysis of the Daily ERP Series from the Combination of VLBI and BDS-3
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gambis, D. Monitoring Earth orientation using space-geodetic techniques: State-of-the-art and prospective. J. Geod. 2004, 78, 295–303. [Google Scholar] [CrossRef]
- Kalarus, M.; Schuh, H.; Kosek, W.; Akyilmaz, O.; Bizouard, C.; Gambis, D.; Gross, R.; Jovanović, B.; Kumakshev, S.; Kutterer, H.; et al. Achievements of the Earth orientation parameters prediction comparison campaign. J. Geod. 2010, 84, 587–596. [Google Scholar] [CrossRef]
- Kouba, J. Sub-daily earth rotation parameters and the international Gps service orbit clock solution products. Stud. Geophys. Geod. 2002, 46, 9–25. [Google Scholar] [CrossRef]
- Lutz, S.; Beutler, G.; Schaer, S.; Dach, R.; Jäggi, A. CODE’s new ultra-rapid orbit and ERP products for the IGS. GPS Solut. 2016, 20, 239–250. [Google Scholar] [CrossRef]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geod. 2019, 93, 621–633. [Google Scholar] [CrossRef]
- Seitz, M.; Angermann, D.; Bloßfeld, M.; Drewes, H.; Gerstl, M. The 2008 DGFI realization of the ITRS: DTRF2008. J. Geod. 2012, 86, 1097–1123. [Google Scholar] [CrossRef]
- Kern, M.; Schwarz, K.P.; Sneeuw, N. A study on the combination of satellite, airborne, and terrestrial gravity data. J. Geod. 2003, 77, 217–225. [Google Scholar] [CrossRef]
- Dettmering, D.; Schmidt, M.; Heinkelmann, R.; Seitz, M. Combination of different space-geodetic observations for regional ionosphere modeling. J. Geod. 2011, 85, 989–998. [Google Scholar] [CrossRef]
- Krügel, M.; Thaller, D.; Tesmer, V.; Rothacher, M.; Angermann, D.; Schmid, R. Tropospheric parameters: Combination studies based on homogeneous VLBI and GPS data. J. Geod. 2007, 81, 515–527. [Google Scholar] [CrossRef]
- Buetler, G.; Pearlman, M.; Plag, H.; Neilan, R.; Rummel, R. Global Geodetic Observing System: Meeting the Requirements of a Global Society on a Changing Planet in 2020; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Nilsson, T.; Böhm, J.; Schuh, H.; Schreiber, U.; Gebauer, A.; Klügel, T. Combining VLBI and ring laser observations for determination of high frequency Earth rotation variation. J. Geodyn. 2012, 62, 69–73. [Google Scholar] [CrossRef]
- Nilsson, T.; Heinkelmann, R.; Karbon, M.; Raposo-Pulido, V.; Soja, B.; Schuh, H. Earth orientation parameters estimated from VLBI during the CONT11 campaign. J. Geod. 2014, 88, 491–502. [Google Scholar] [CrossRef]
- Hobiger, T.; Rieck, C.; Haas, R.; Koyama, Y. Combining GPS and VLBI for iner-continental frequency transfer. Metrologia 2015, 52, 251. [Google Scholar] [CrossRef][Green Version]
- Nothnagel, A.; Artz, T.; Behrend, D.; Malkin, Z. International VLBI Service for Geodesy and Astrometry: Delivering high-quality products and embarking on observations of the next generation. J. Geod. 2016, 91, 711–721. [Google Scholar] [CrossRef]
- Nothnagel, A.; Anderson, J.; Behrend, D.; Böhm, J.; Charlot, P.; Colomer, F.; Witt, A.d.; John, G.; Haas, R.; Hall, D. IVS Infrastructure Development Plan 2030; 2021. Available online: http://hdl.handle.net/20.500.12708/40332 (accessed on 3 January 2023).
- Dow, J.M.; Neilan, R.E.; Rizos, C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Ferland, R.; Piraszewski, M. The IGS-combined station coordinates, earth rotation parameters and apparent geocenter. J. Geod. 2009, 83, 385–392. [Google Scholar] [CrossRef]
- Ray, J.; Rebischung, P.; Griffiths, J. IGS polar motion measurement accuracy. Geod. Geodyn. 2017, 8, 413–420. [Google Scholar] [CrossRef]
- Ray, J.; Altamimi, Z. Evaluation of co-location ties relating the VLBI and GPS reference frames. J. Geod. 2005, 79, 189–195. [Google Scholar] [CrossRef]
- Ray, J.; Kouba, J.; Altamimi, Z. Is there utility in rigorous combinations of VLBI and GPS Earth orientation parameters? J. Geod. 2005, 79, 505–511. [Google Scholar] [CrossRef]
- Wang, J.; Ge, M.; Glaser, S.; Balidakis, K.; Heinkelmann, R.; Schuh, H. Impact of Tropospheric Ties on UT1-UTC in GNSS and VLBI Integrated Solution of Intensive Sessions. J. Geophys. Res. Solid Earth 2022, 127, e2022JB025228. [Google Scholar] [CrossRef]
- Wang, J.; Ge, M.; Glaser, S.; Balidakis, K.; Heinkelmann, R.; Schuh, H. Improving VLBI analysis by tropospheric ties in GNSS and VLBI integrated processing. J. Geod. 2022, 96, 32. [Google Scholar] [CrossRef]
- Thaller, D.; Krügel, M.; Rothacher, M.; Tesmer, V.; Schmid, R.; Angermann, D. Combined Earth orientation parameters based on homogeneous and continuous VLBI and GPS data. J. Geod. 2007, 81, 529–541. [Google Scholar] [CrossRef]
- Bourda, G.; Charlot, P.; Biancale, R. VLBI analyses with the GINS software for multi-technique combination at the observation level. In Proceedings of the SF2A-2008: Annual Meeting of the French Society of Astronomy and Astrophysics, Paris, France, 30 June–4 July 2008. [Google Scholar]
- Hobiger, T.; Otsubo, T.; Sekido, M. Observation level combination of SLR and VLBI with c5++: A case study for TIGO. Adv. Space Res. 2014, 53, 119–129. [Google Scholar] [CrossRef]
- CSNO. BeiDou Navigation Satelite System B2a, Version 1.0; CSNO China Satellite Navigation Office: Beijing, China, 2017. [Google Scholar]
- CSNO. BeiDou Navigation Satellite System Signal In Space Interface Control Document Open Service Signal B3I, Version 1.0; CSNO China Satellite Navigation Office: Beijing, China, 2018. [Google Scholar]
- CSNO. Development of the BeiDou Navigaton Satelite System, Version 4.0; CSNO China Satellite Navigation Office: Beijing, China, 2019. [Google Scholar]
- CSNO. BeiDou Navigation Satellite System Open Service Performance Standard, Version 3.0; CSNO China Satellite Navigation Office: Beijing, China, 2021. [Google Scholar]
- Tianhe, X.; Sumei, Y.; Jianjin, L. Earth Rotation Parameters Determination Using BDS and GPS Data Based on MGEX Network. In China Satellite Navigation Conference (CSNC) 2014 Proceddings; Springer: Berlin/Heidelberg, Germany, 2014; pp. 289–299. [Google Scholar]
- Li, M.; Xu, T. Research on the Combination of IGS Analysis-Center Solution for station Coordinates and ERPs. In Proceedings of the China Satellite Navigation Conference (CSNC), Nanjing, China, 21–23 May 2014; pp. 15–30. [Google Scholar]
- Fang, X.; Fan, L.; Guo, S.; Zhou, L.; Shi, C. Earth Rotation Parameters Determination with BDS-3/LEO Simulations under Small-Scale Ground Networks. In Proceedings of the China Satellite Navigation Conference (CSNC 2022) Proceedings; Springer: Singapore, 2022; Volume III, pp. 102–112. [Google Scholar]
- Johnston, G.; Riddell, A.; Hausler, G. The international GNSS service. In Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 967–982. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U.; Selmke, I.; Marz, S.; Killian, M.; Rott, M. BeiDou Satellite Radiation Force Models for Precise Orbit Determination and Geodetic Applications. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2823–2836. [Google Scholar] [CrossRef]
- Zajdel, R.; Sośnica, K.; Bury, G.; Dach, R.; Prange, L. System-specific systematic errors in earth rotation parameters derived from GPS, GLONASS, and Galileo. GPS Solut. 2020, 24, 74. [Google Scholar] [CrossRef]
- Peng, Y.; Lou, Y.; Dai, X.; Guo, J.; Shi, C. Impact of solar radiation pressure models on earth rotation parameters derived from BDS. GPS Solut. 2022, 26, 126. [Google Scholar] [CrossRef]
- He, Z.; Wei, E.; Zhang, Q.; Wang, L.; Li, Y.; Liu, J. Earth rotation parameters from BDS, GPS, and Galileo data: An accuracy analysis. Adv. Space Res. 2023, 71, 3968–3980. [Google Scholar] [CrossRef]
- Liu, J.; Ge, M. PANDA Software and its Preliminary Result of Positioning and Orbit Determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar] [CrossRef]
- Liu, Y.; Ge, M.; Shi, C.; Lou, Y.; Wickert, J.; Schuh, H. Improving integer ambiguity resolution for GLONASS precise orbit determination. J. Geod. 2016, 90, 715–726. [Google Scholar] [CrossRef]
- Standish, E.M. JPL Planetary and Lunar Ephemerides, DE405/LE405. JPL IOM 1998, 312, F-98-048. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B4. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Zhao, Q.; Liu, J. Yaw attitude modeling for BeiDou I06 and BeiDou-3 satellites. GPS Solut. 2018, 22, 117. [Google Scholar] [CrossRef]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sośnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010); IERS Technical Note 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Vincent, C.; Seago, J.H.; Vallado, D.A. The IAU 2000A and IAU 2006 precession-nutation theories and their implementation. Adv. Astronaut. Sci. 2009, 919–938. Available online: https://www.researchgate.net/publication/289753602 (accessed on 10 January 2023).
- Böhm, J.; Böhm, S.; Nilsson, T.; Pany, A.; Plank, L.; Spicakova, H.; Teke, K.; Schuh, H. The New Vienna VLBI Software VieVS. In Geodesy for Planet Earth: Proceedings of the 2009 IAG Symposium, Buenos Aires, Argentina, 31 August–4 September 2009; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1007–1011. [Google Scholar]
- Schuh, H.; Behrend, D. VLBI: A fascinating technique for geodesy and astrometry. J. Geodyn. 2012, 61, 68–80. [Google Scholar] [CrossRef]
- Madzak, M.; Böhm, S.; Krásná, H.; Plank, L.; Mayer, D. Vinna VLBI Software (VieVS), Version 2.2; Department of Geodesy and Geoinformation, Vienna University of Technology: Vienna, Austria, 2014. [Google Scholar]
- Bolotin, S.; Baver, K.; Gipson, J.; Gordon, D.; MacMillan, D. Transition to the vgosDb Format. In Proceedings of the IVS 2016 general Meeting Proceedings, Johannesburg, South Africa, 13–17 March 2016; pp. 222–224. Available online: https://ui.adsabs.harvard.edu/abs/2016ivs..conf..222B/abstract (accessed on 10 January 2023).
- Böhm, J.; Böhm, S.; Boisits, J.; Girdiuk, A.; Gruber, J.; Hellerschmied, A.; Krásná, H.; Landskron, D.; Madzak, M.; Mayer, D.; et al. Vienna VLBI and Satellite Software (VieVS) for Geodesy and Astrometry. Pub. Astron. Soc. Pac. 2018, 130, 044503. [Google Scholar] [CrossRef]
- Koch, K.R. Parameter Estimation and Hypothesis Testing in Linear Models; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Wu, Y.; Shen, W.B. Simulation experiments on high-precision VGOS time transfer for future geopotential difference determination. Adv. Space Res. 2021, 68, 2453–2469. [Google Scholar] [CrossRef]
- Böhm, S. Tidal Excitation of Earth Rotation Observed by VLBI and GNSS. Ph.D. Thesis, Technische Universität Wien, Wien, Germany, 2012. [Google Scholar]
- Wielgosz, A.; Tercjak, M.; Brzeziński, A. Testing impact of the strategy of VLBI data analysis on the estimation of Earth Orientation Parameters and station coordinates. Rep. Geod. Geoinform. 2016, 101, 1–15. [Google Scholar] [CrossRef]
- Saastamoinen, J. Introduction to practical computation of astronomical refraction. Bull. Géodésique 1972, 106, 383–397. [Google Scholar] [CrossRef]
- Landskron, D.; Bohm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Collilieux, X.; Métivier, L.; Chanard, K. ITRF2020: An augmented reference frame refining the modeling of nonlinear station motions. J. Geod. 2023, 97, 47. [Google Scholar] [CrossRef]
- Jacobs, C.; Arias, F.; Boboltz, D.; Boehm, J.; Bolotin, S.; Bourda, G.; Charlot, P.; De Witt, A.; Fey, A.; Gaume, R. ICRF-3: Roadmap to the next generation ICRF. In Proceedings of the Journées, Paris, France, 16–18 September 2013; pp. 51–56. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential code bias estimation using multi GNSS ovservations and global iomosphere maps. Navigation 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y.; Zhu, Y.; Huang, J.; Wu, J.; Xiong, Y.; Zhang, X.; Li, X. Precise orbit determination for BDS3 experimental satellites using iGMAS and MGEX tracking networks. J. Geod. 2018, 93, 103–117. [Google Scholar] [CrossRef]
- Joe, B. GEOMPACK a software package for the generation of meshes using geometric algorithms. Adv. Eng. Softw. 1991, 13, 325–331. [Google Scholar] [CrossRef]
- Rabbath, C.A.; Corriveau, D. A comparison of piecewise cubic Hermite interpolating polynomials, cubic splines and piecewise linear functions for the approximation of projectile aerodynamics. Def. Technol. 2019, 15, 741–757. [Google Scholar] [CrossRef]
- Malkin, Z. On comparison of the Earth orientation parameters obtained from different VLBI networks and observing programs. J. Geod. 2009, 83, 547–556. [Google Scholar] [CrossRef]
- Lytvyn, M.O. Method for obtaining the combined solution for geodynamical parameters from modern space geodesy technique observation. Kinemat. Phys. Celest. Bodies 2009, 25, 198–205. [Google Scholar] [CrossRef]
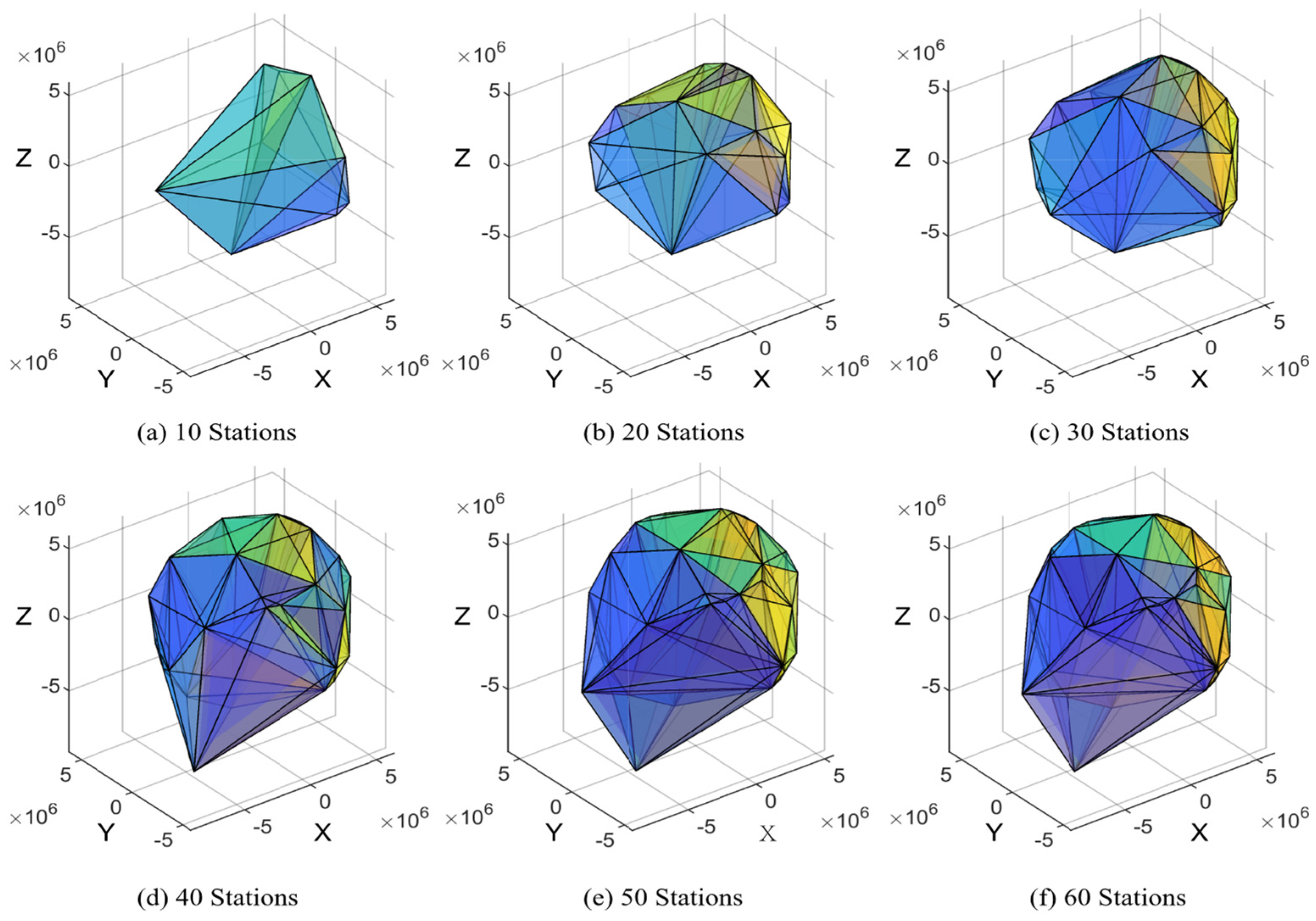
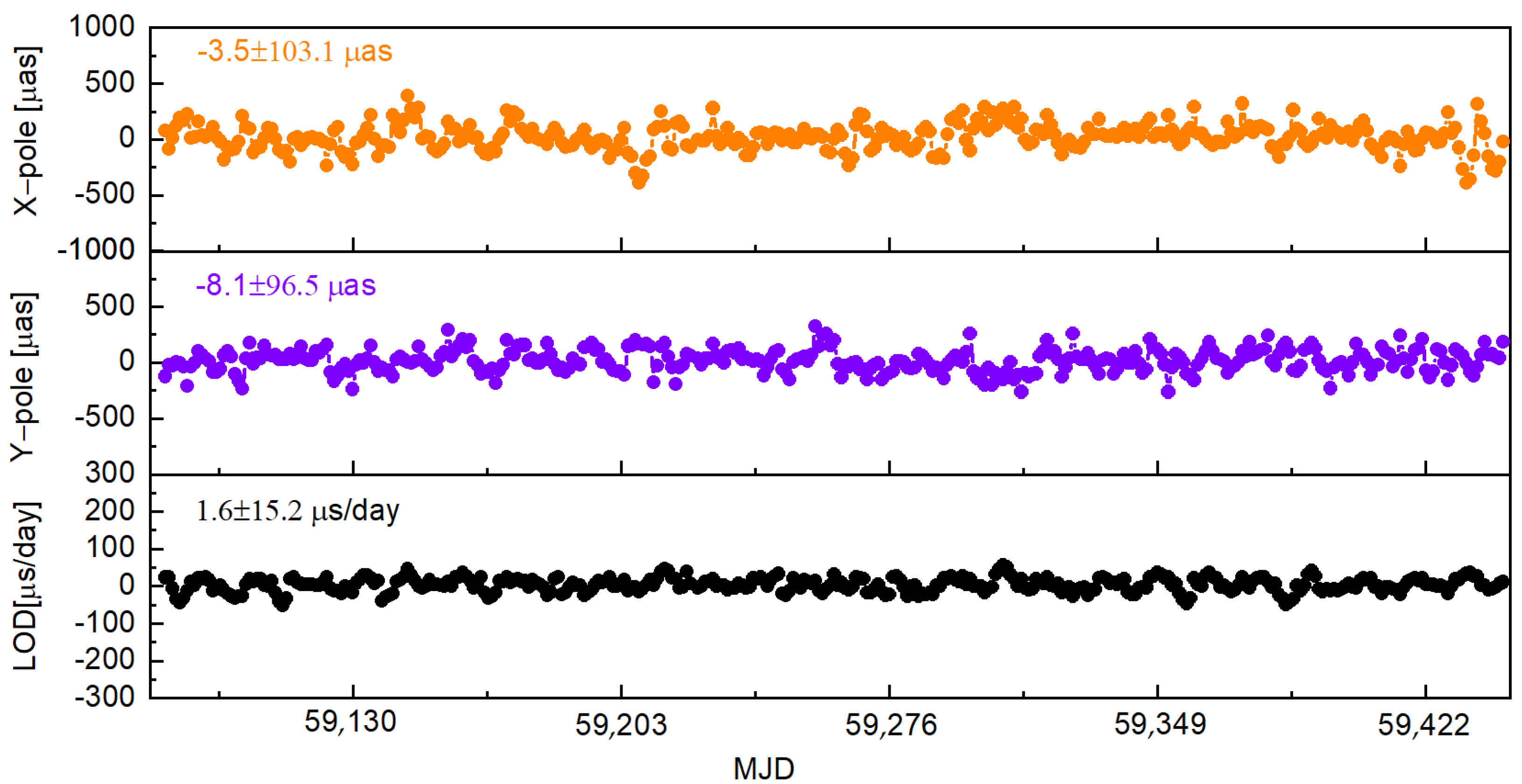
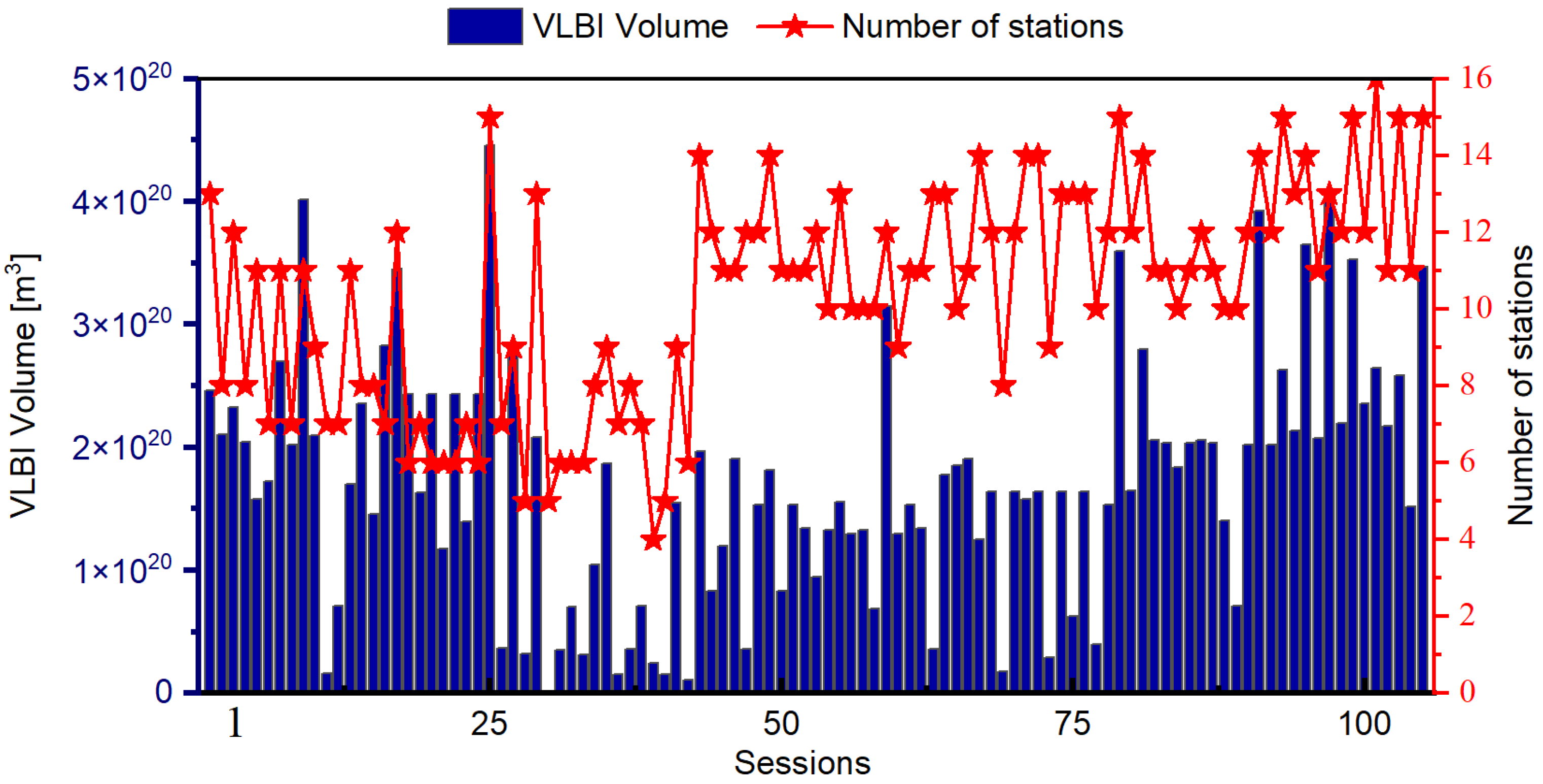
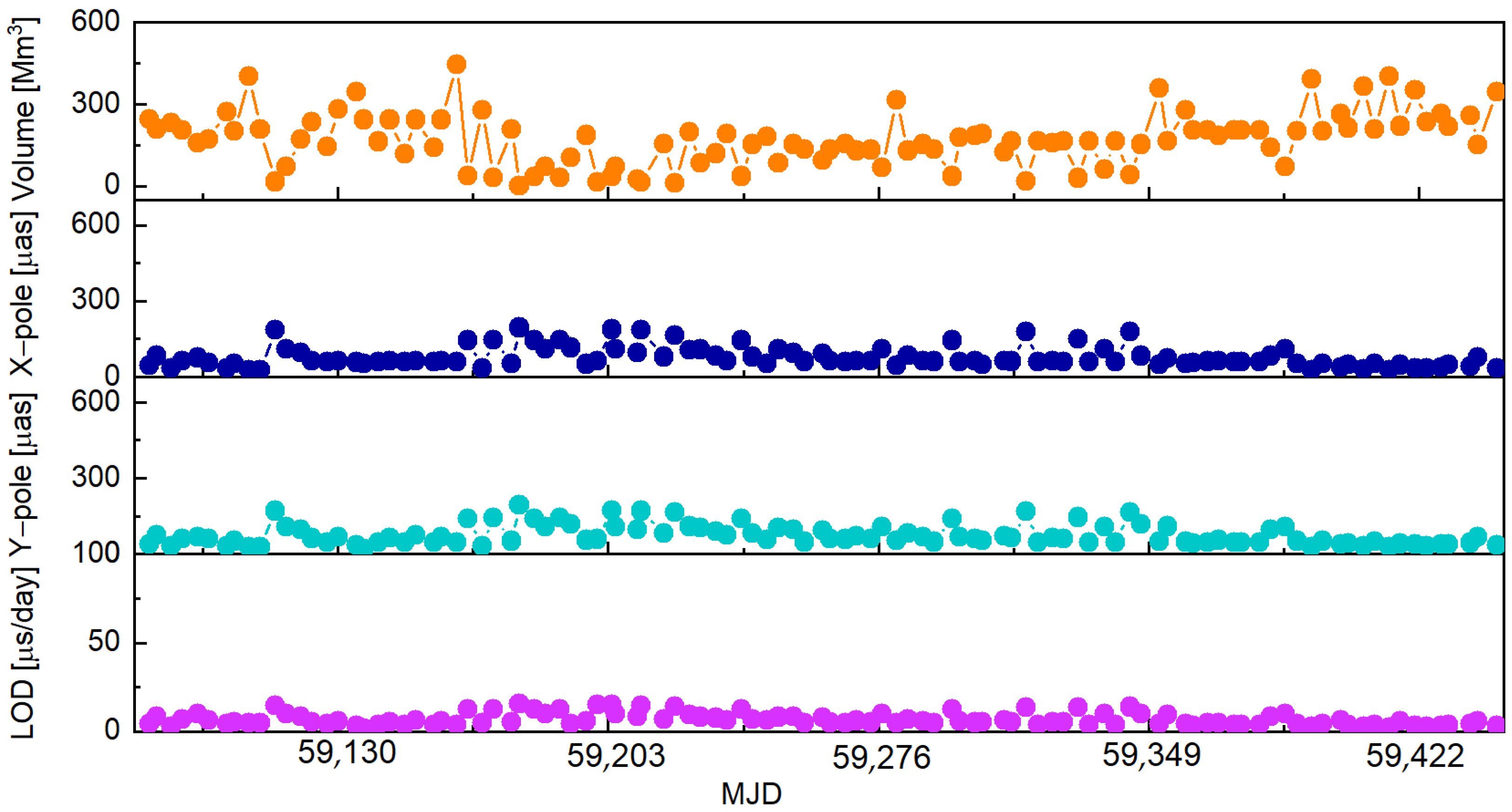
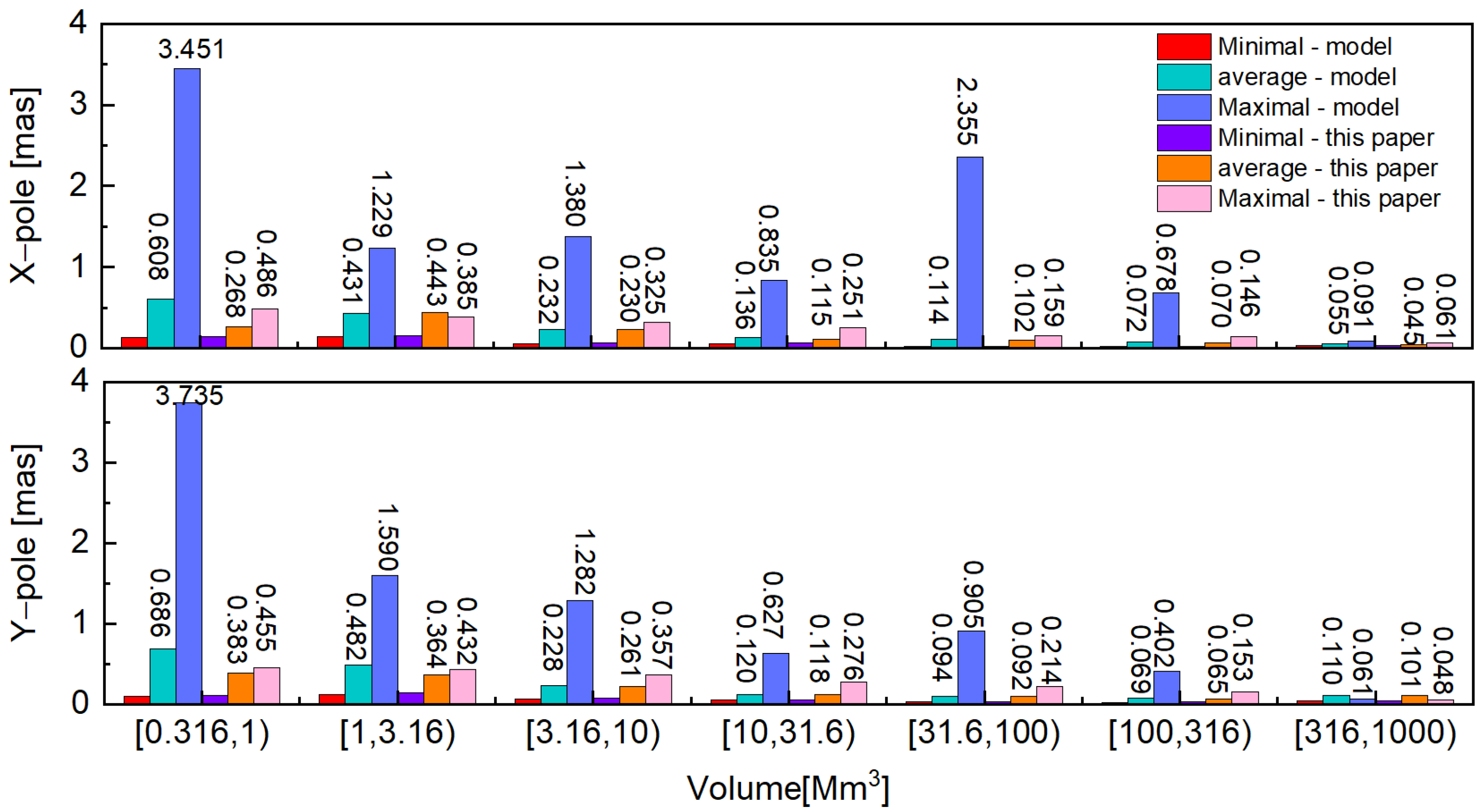
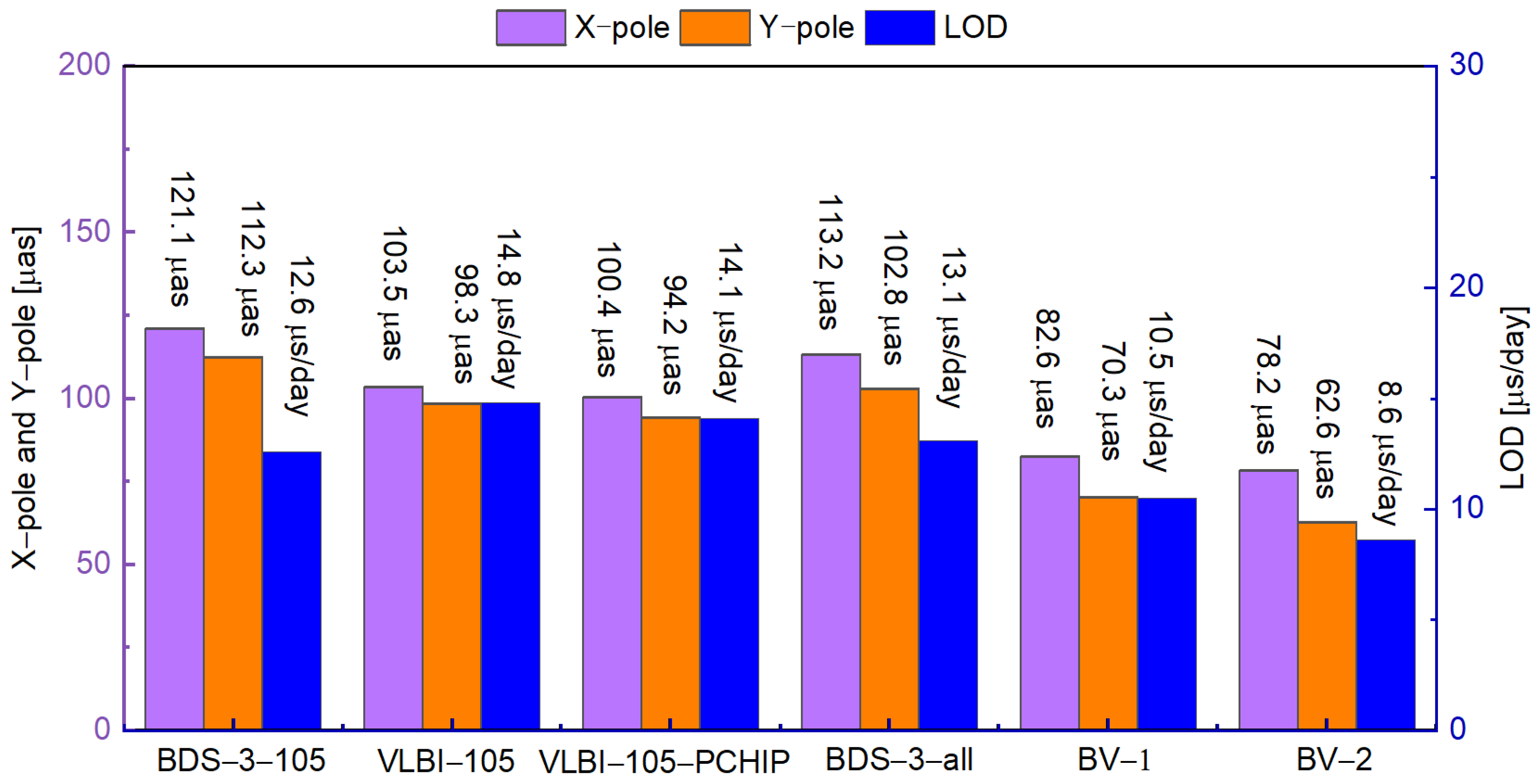
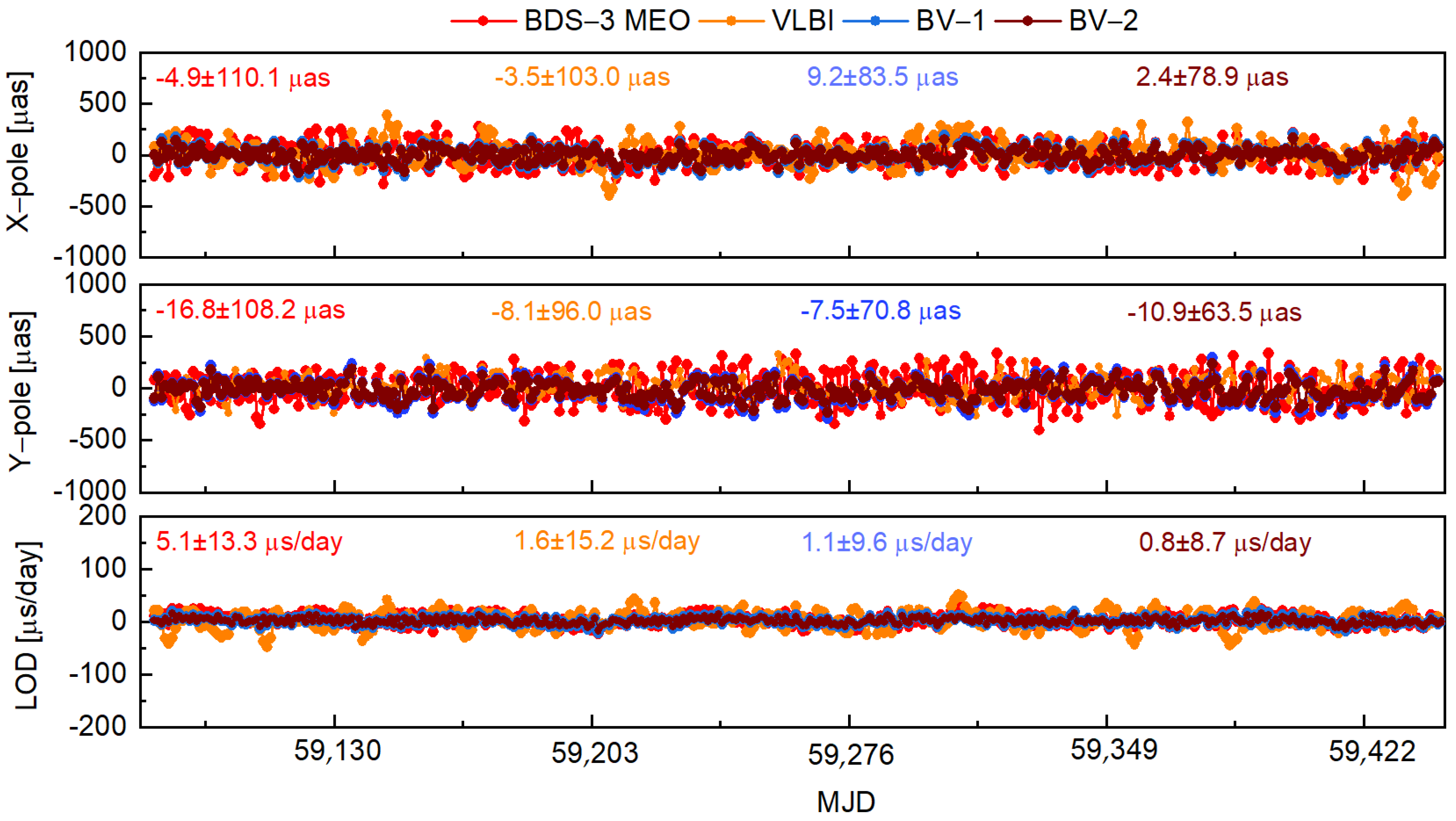
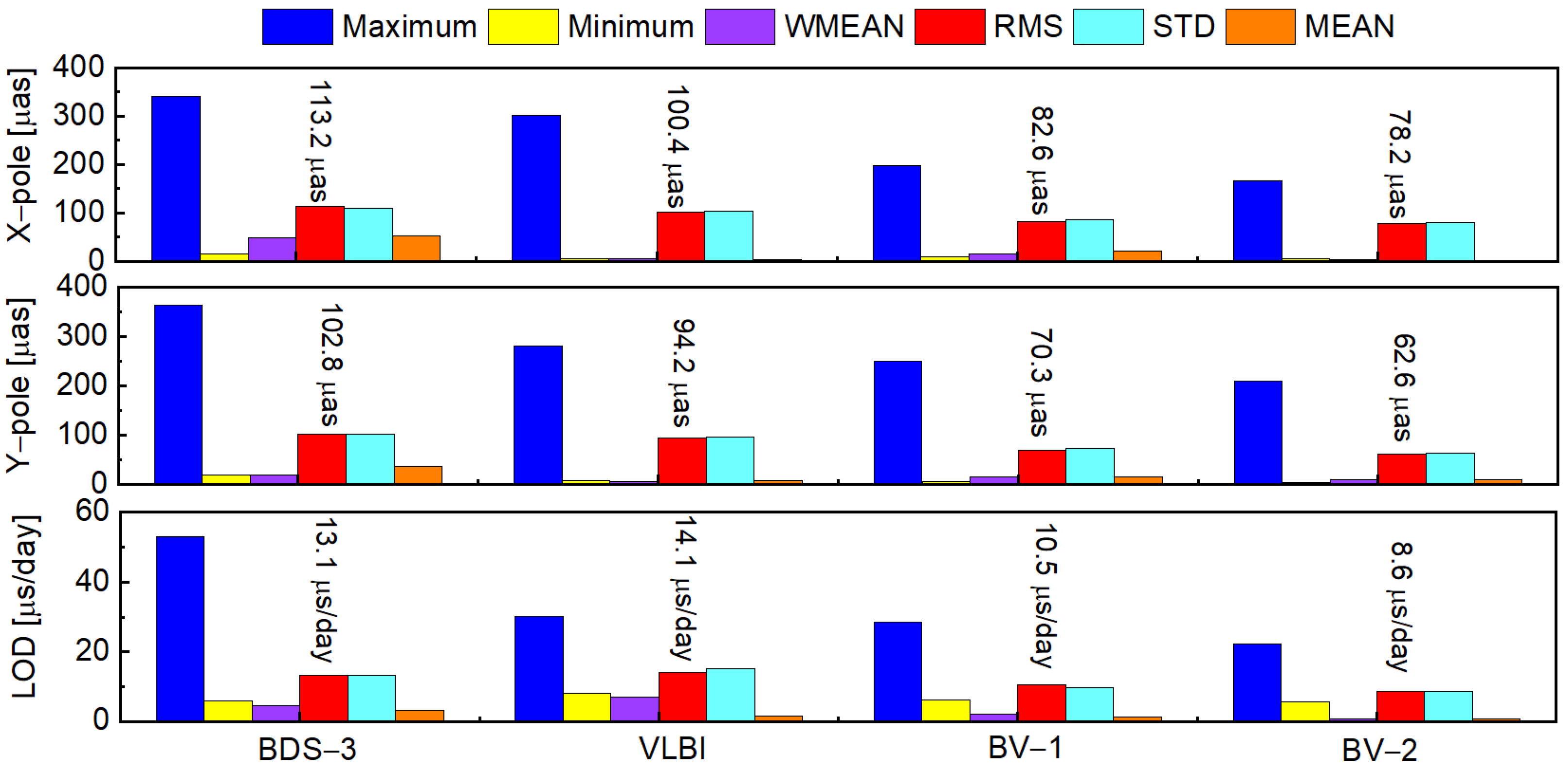
| Items | Strategy |
|---|---|
| Basic observables | BDS-3: B1I and B3I |
| Observation weight | Elevation (E)-dependent with a cutoff of 7 degrees. The weight is 1 if E > 30 deg, otherwise 2 sin(E) |
| N-body gravitation | Jet Propulsion Laboratory (JPL) DE405 [40] |
| Estimator | LSQ in batch mode |
| Geopotential | 12 × 12 EGM2008 model [41] |
| Sampling rate and arc length | 300 s sampling, 1 day OD arc length |
| Attitude mode | Yaw-steering model for BDS3 [42] |
| Solar radiation | The 5-parameter ECOM model [43] |
| Satellite antenna PCO/PCV | PCO values according to CSNO/TARC (https://www.csno-tarc.cn, accessed on 3 January 2023); ignoring PCVs |
| A priori reference frame | IGS20 (https://lists.igs.org/pipermail/igsmail/2022/008234.html, accessed on 3 January 2023) |
| Receiver antenna PCO/PCV | igs20.atx corrected for BDS3 |
| Solid earth ties, Pole ties | IERS conventions 2010 [44] |
| Ocean tides | FES2004 [45] for ocean tides |
| Tropospheric delay | Zenith troposphere delay and gradient parameters are estimated as piecewise constant with 2-h and 24-h intervals, respectively. |
| Earth Rotation Parameters | Precession and Nutation: IAU2006A [46]; A priori ERPs: Bulletin A (https://garner.ucsd.edu/pub/gamit/tables/finals.data, accessed on 3 January 2023). A priori-constraints: polar motion (3 as); polar motion rates (0.3 as/day); UT1-UTC (20 µs); ΔLOD (20 ms/day). |
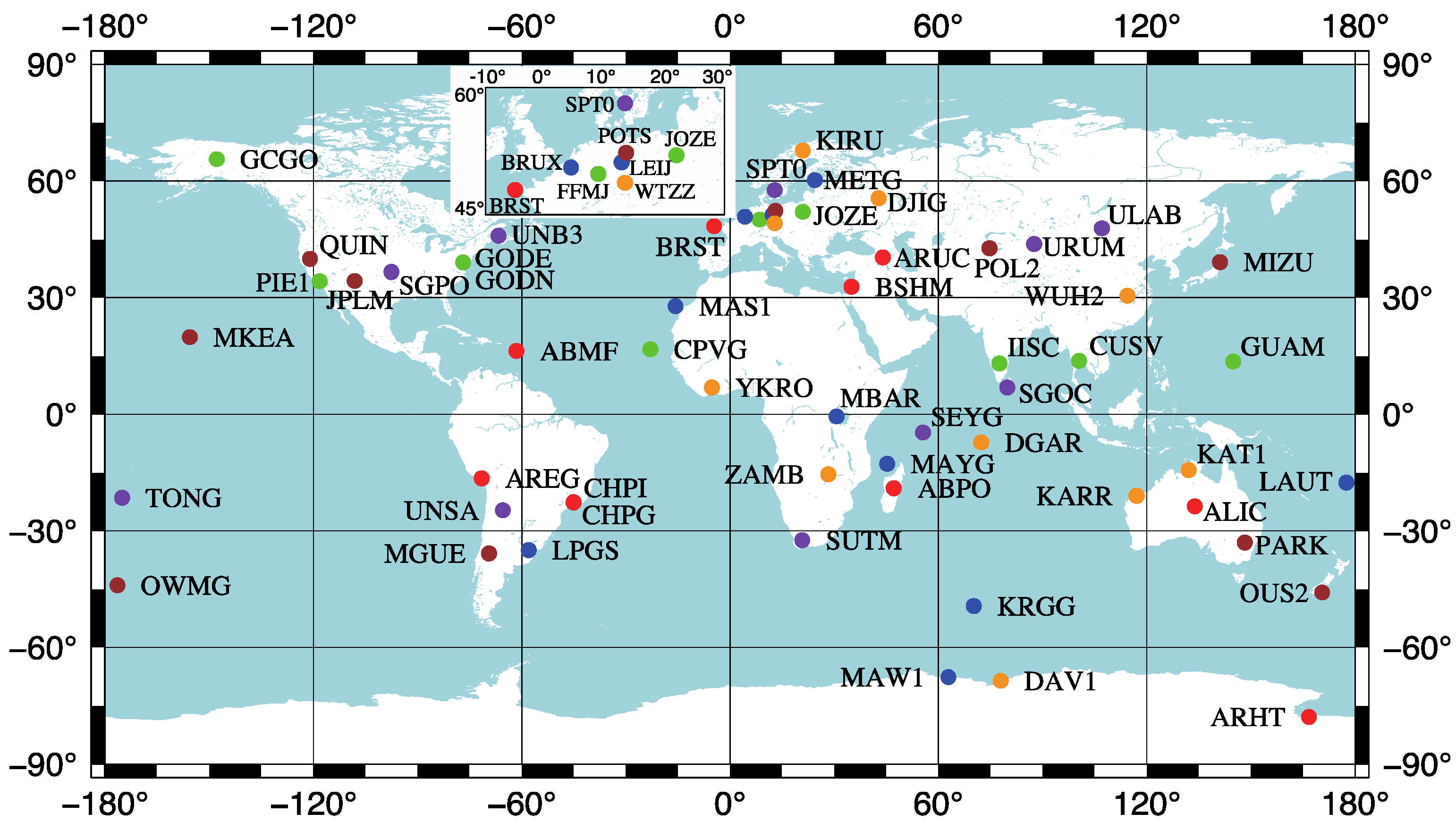
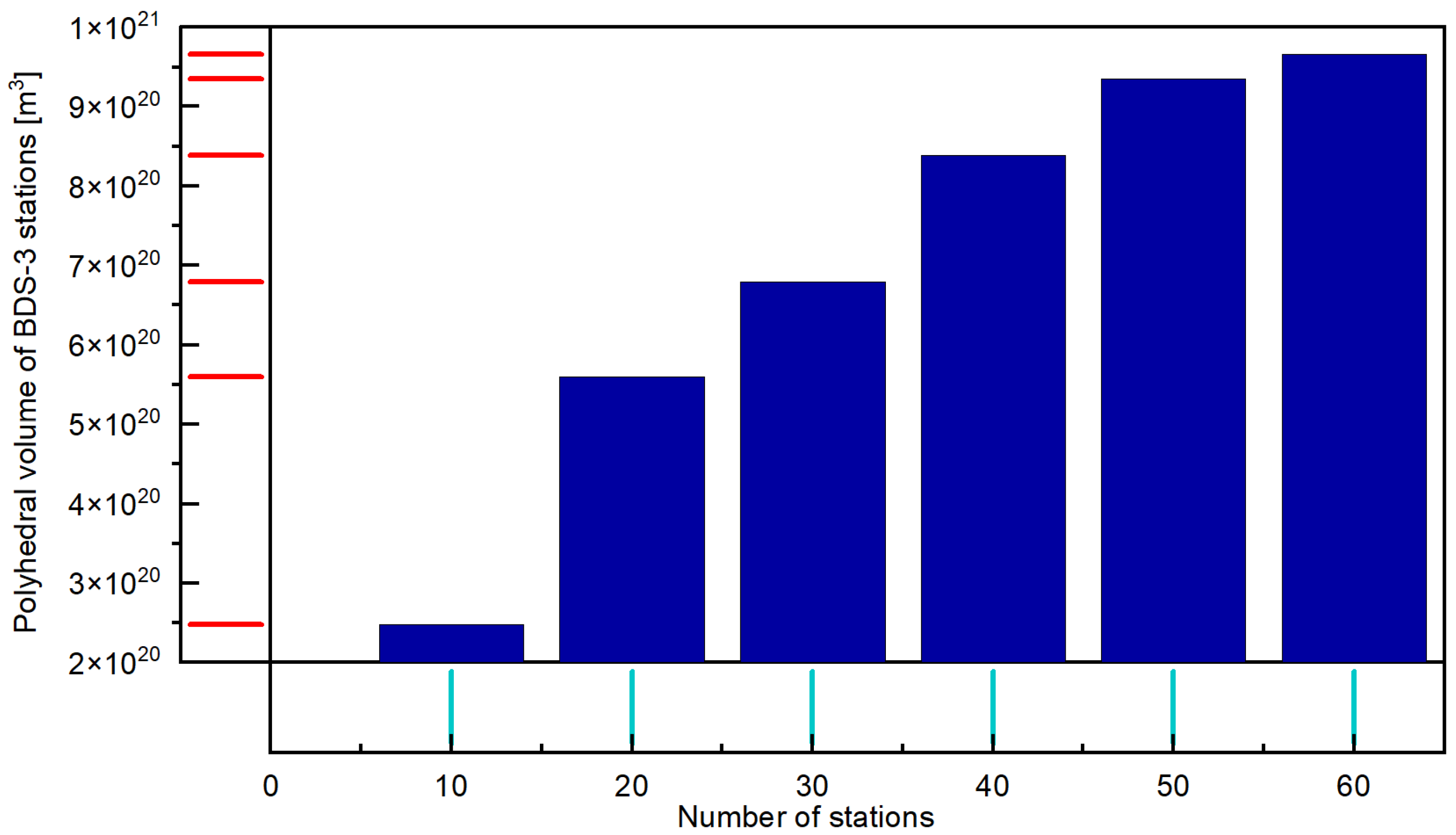
| Group | Stations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 | ABMF | ABPO | ALIC | AREG | ARHT | ARUC | BRST | BSHM | CHPG | CHPI | |
| Group 2 | CPVG | CUSV | FFMJ | GCGO | GODE | GODN | GUAM | IISC | JOZE | JPLM | plus Group 1 |
| Group 3 | KRGG | LAUT | LEIJ | BRUX | LPGS | MAS1 | MAW1 | MAYG | MBAR | METG | plus Group 2 |
| Group 4 | MGUM | MIZU | MKEA | OUS2 | OWMG | PARK | PIE1 | POL2 | POTS | QUIN | plus Group 3 |
| Group 5 | SEYG | SGOC | SGPO | SPT0 | SUTM | TONG | ULAB | UNB3 | UNSA | URUM | plus Group 4 |
| Group 6 | WTZZ | DGAR | WUH2 | YKRO | ZAMB | DJIG | DAV1 | KIRU | KAT1 | KARR | plus Group 5 |
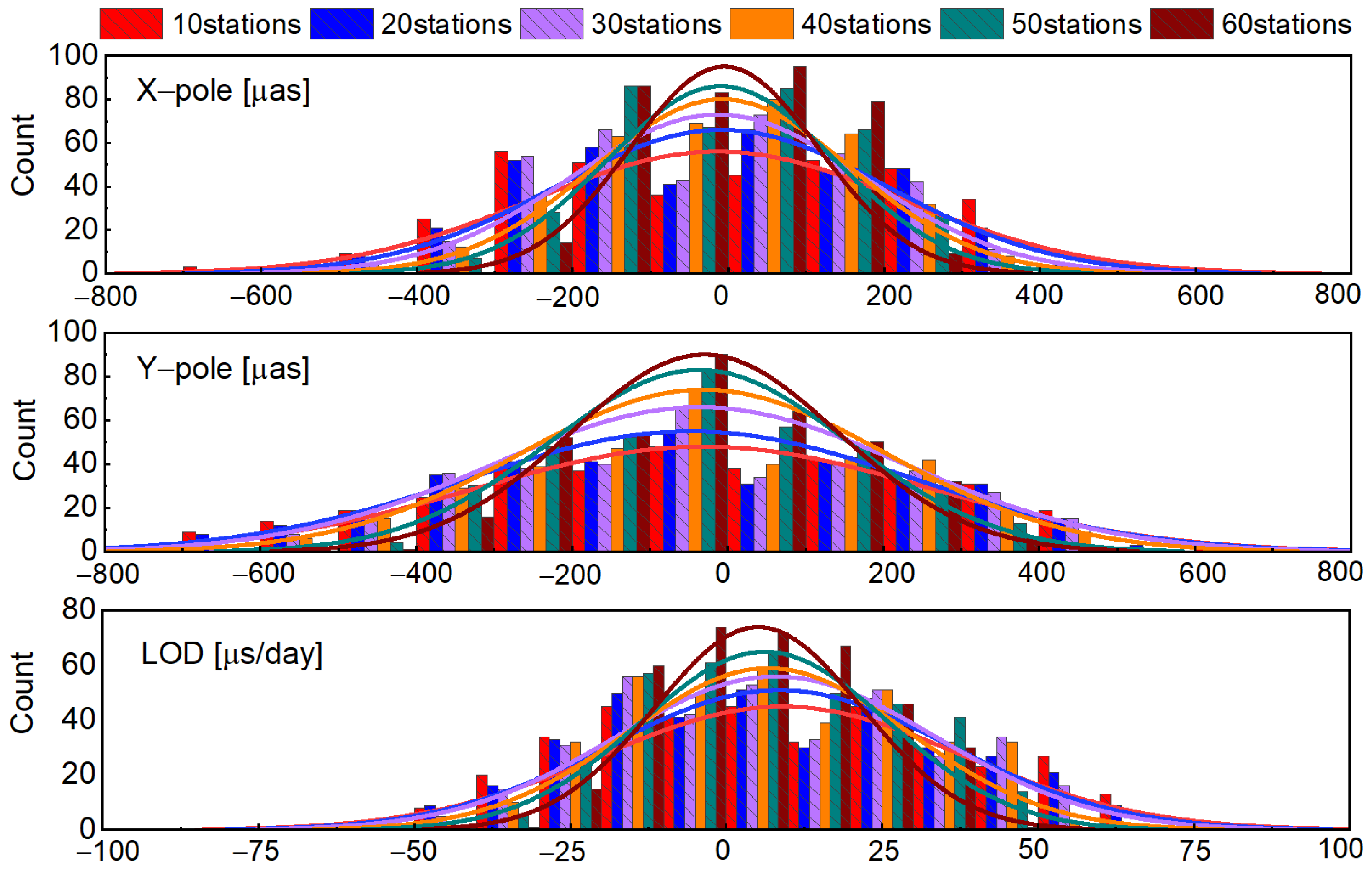
| Statistics Stations | X-Pole [µas] | Y-Pole [µas] | LOD [µs] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMS | STD | MEAN | RMS | STD | MEAN | RMS | STD | MEAN | |
| 10 | 170.2 | 170.1 | −13.0 | 160.1 | 161.5 | −21.3 | 18.3 | 18.4 | 8.9 |
| 20 | 161.0 | 160.4 | −8.4 | 148.3 | 150.2 | −29.5 | 17.2 | 17.3 | 8.5 |
| 30 | 143.3 | 145.3 | −13.5 | 135.6 | 136.7 | −22.6 | 16.2 | 16.1 | 7.9 |
| 40 | 130.2 | 130.6 | −7.6 | 120.4 | 120.5 | −17.4 | 14.8 | 14.9 | 6.8 |
| 50 | 122.3 | 122.4 | −8.9 | 117.5 | 113.5 | −18.7 | 14.1 | 14.1 | 6.2 |
| 60 | 113.2 | 110.1 | −4.9 | 102.8 | 102.3 | −16.8 | 13.1 | 13.3 | 5.1 |
| ERPs | BDS-3-105 | VLBI-105 | VLBI-105-PCHP | BDS-3-all | BV-1 |
|---|---|---|---|---|---|
| X-pole | 35.4% | 24.4% | 22.1% | 30.9% | 5.3% |
| Y-pole | 44.3% | 36.3% | 33.5% | 39.1% | 11.0% |
| LOD | 31.7% | 41.9% | 39.0% | 34.4% | 18.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Sang, J.; Li, X.; Zhang, P. Estimation of Earth Rotation Parameters Based on BDS-3 and Discontinuous VLBI Observations. Remote Sens. 2024, 16, 333. https://doi.org/10.3390/rs16020333
Wang C, Sang J, Li X, Zhang P. Estimation of Earth Rotation Parameters Based on BDS-3 and Discontinuous VLBI Observations. Remote Sensing. 2024; 16(2):333. https://doi.org/10.3390/rs16020333
Chicago/Turabian StyleWang, Chenxiang, Jizhang Sang, Xingxing Li, and Pengfei Zhang. 2024. "Estimation of Earth Rotation Parameters Based on BDS-3 and Discontinuous VLBI Observations" Remote Sensing 16, no. 2: 333. https://doi.org/10.3390/rs16020333
APA StyleWang, C., Sang, J., Li, X., & Zhang, P. (2024). Estimation of Earth Rotation Parameters Based on BDS-3 and Discontinuous VLBI Observations. Remote Sensing, 16(2), 333. https://doi.org/10.3390/rs16020333