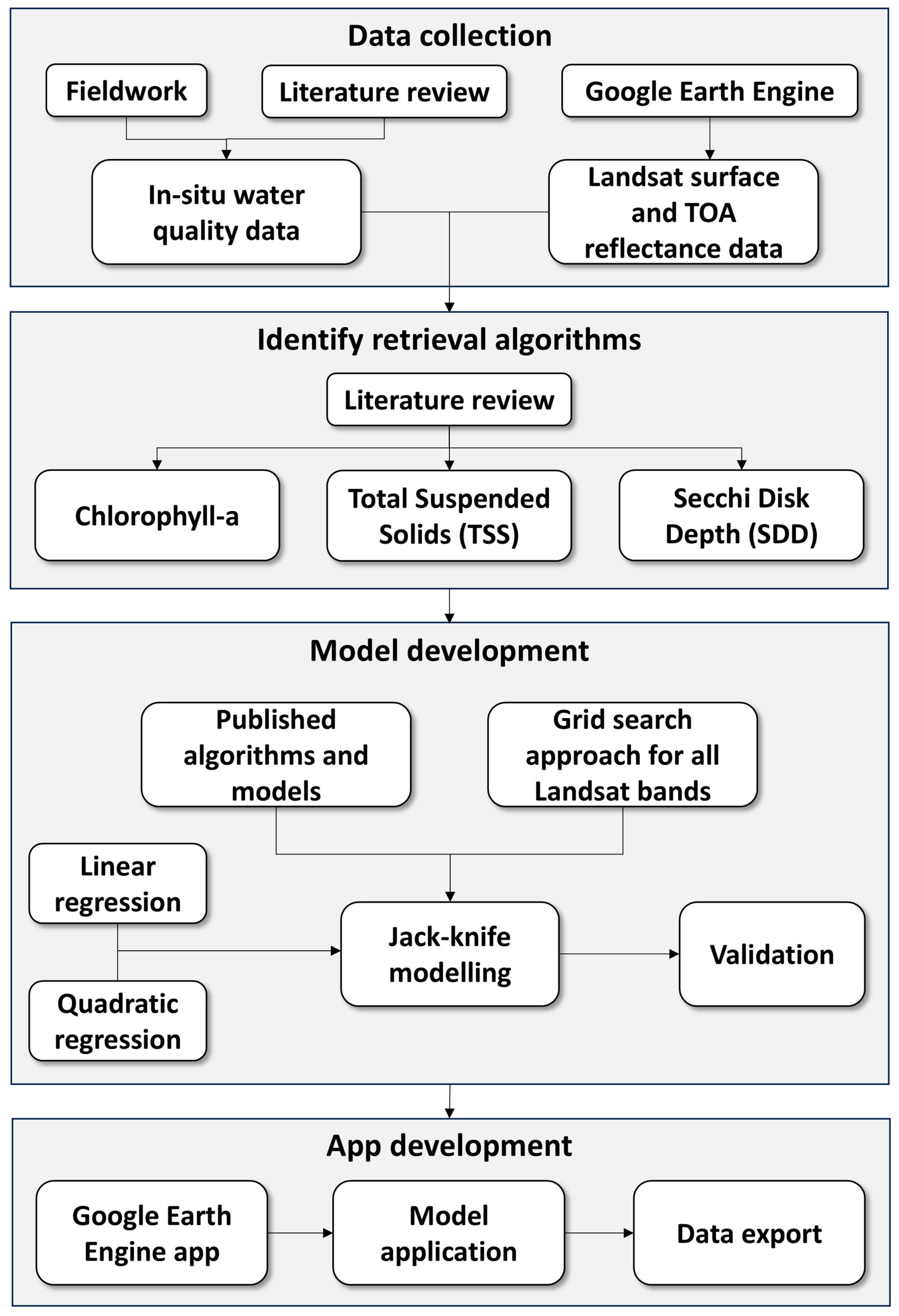
LAQUA: a LAndsat water QUality retrieval tool for east African lakes
Abstract
1. Introduction
- Compile a ground truth database of water quality observations and Landsat satellite match-ups for East African lakes from existing studies supplemented by newly collected data.
- Identify existing Landsat water quality retrieval algorithms for chlorophyll-a, TSS, and SDD and assess their accuracy for East African lakes.
- Develop region-specific models where no suitable global models were available.
- Develop an easy-to-use Google Earth Engine application incorporating the best performing models for each parameter.
2. Methods
2.1. Study Lakes
2.2. In Situ Data
2.3. Satellite Imagery
2.4. Water Quality Retrieval Algorithms
- Band algorithms (also known as spectral indices): mathematical equations comprising combinations of Landsat reflectance bands.
- Fully parameterised models: band algorithms that have been calibrated against ground-based observations to estimate model coefficients.
2.5. Model Development and Validation
2.6. App Development and Model Application
3. Results
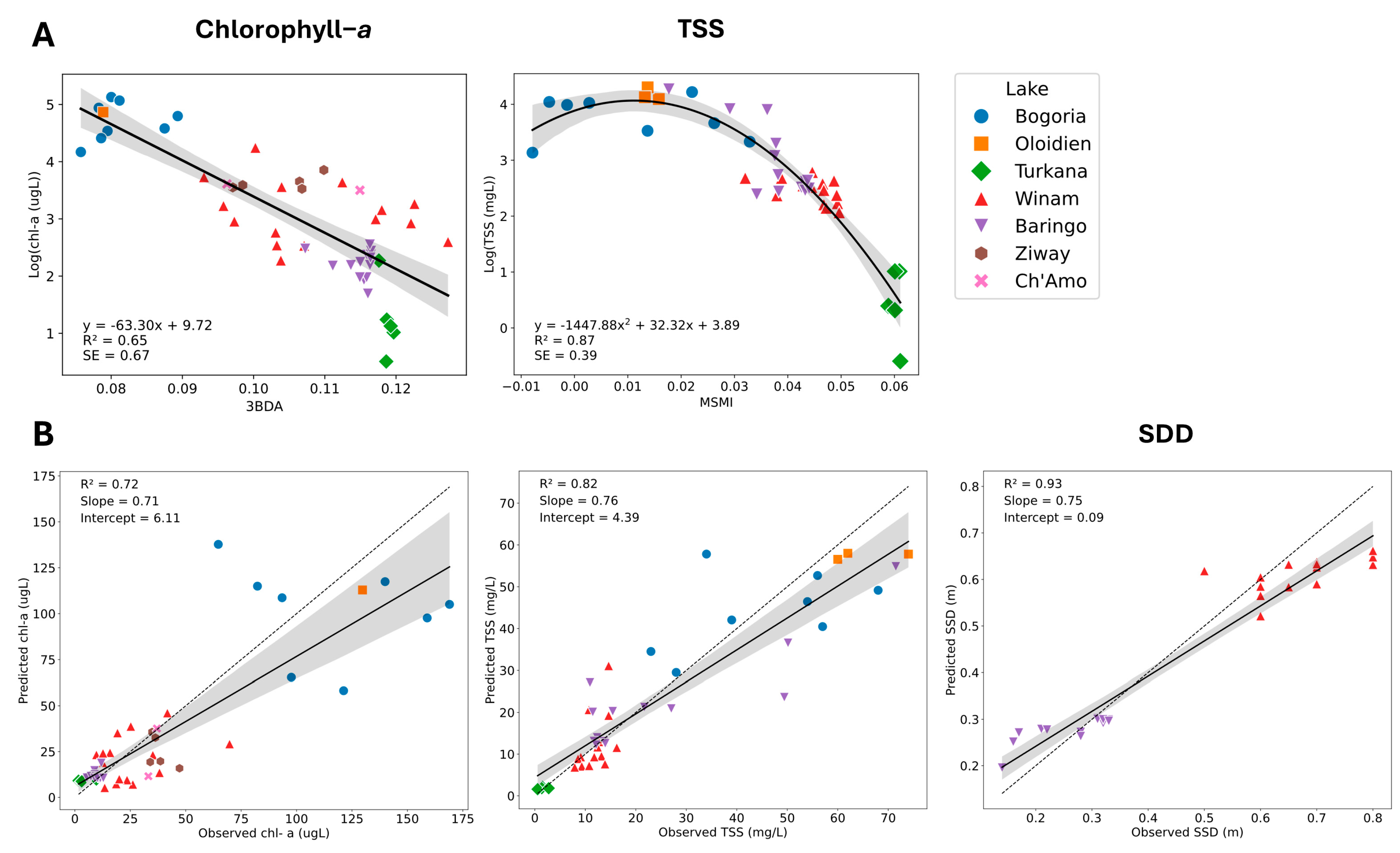
3.1. Chlorophyll-a
3.2. Total Suspended Solids
3.3. Secchi Disk Depth
3.4. Google Earth Engine App and Validation
4. Discussion
- For chlorophyll-a: a parameterised version of the three-band algorithm (3BDA).
- For total suspended solids (TSS): a modified version of the Suspended Matter Index (SMI) developed in this study with an additional blue band.
- For Secchi disk depth (SDD): an existing global model developed by Song et al. (2022).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lehner, B.; Messager, M.L.; Korver, M.C.; Linke, S. Global Hydro-Environmental Lake Characteristics at High Spatial Resolution. Sci. Data 2022, 9, 351. [Google Scholar] [CrossRef]
- Fazi, S.; Butturini, A.; Tassi, F.; Amalfitano, S.; Venturi, S.; Vazquez, E.; Clokie, M.; Wanjala, S.W.; Pacini, N.; Harper, D.M. Biogeochemistry and Biodiversity in a Network of Saline–Alkaline Lakes: Implications of Ecohydrological Connectivity in the Kenyan Rift Valley. Ecohydrol. Hydrobiol. 2018, 18, 96–106. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Monitoring the Water Balance of Lake Victoria, East Africa, from Space. J. Hydrol. 2009, 370, 163–176. [Google Scholar] [CrossRef]
- Musie, M.; Momblanch, A.; Sen, S. Exploring Future Global Change-Induced Water Imbalances in the Central Rift Valley Basin, Ethiopia. Clim. Chang. 2021, 164, 47. [Google Scholar] [CrossRef]
- Walker, D.; Shutler, J.D.; Morrison, E.H.J.; Harper, D.M.; Hoedjes, J.C.B.; Laing, C.G. Quantifying Water Storage within the North of Lake Naivasha Using Sonar Remote Sensing and Landsat Satellite Data. Ecohydrol. Hydrobiol. 2022, 22, 12–20. [Google Scholar] [CrossRef]
- Morara, G.; Omondi, R.; Obegi, B.; Getabu, A.; Njiru, J.; Rindoria, N. Water Level Fluctuations and Fish Yield Variations in Lake Naivasha, Kenya: The Trends and Relationship. J. Fish. Environ. 2022, 46, 13–27. [Google Scholar]
- Plisnier, P.D.; Kayanda, R.; MacIntyre, S.; Obiero, K.; Okello, W.; Vodacek, A.; Cocquyt, C.; Abegaz, H.; Achieng, A.; Akonkwa, B.; et al. Need for Harmonized Long-Term Multi-Lake Monitoring of African Great Lakes. J. Great Lakes Res. 2023, 49, 101988. [Google Scholar] [CrossRef]
- Wegman, M.; Leutner, B.; Dech, S. Remote Sensing and GIS for Ecologists; Pelagic Publishing Ltd.: London, UK, 2016. [Google Scholar]
- Tebbs, E.; Byrne, A.; Lomeo, D.; Thompson, H.; Owoko, W.; Nyaga, J.; Ongore, C.; Last, J.; Migeni, Z.; Everitt, L. Satellite Earth Observation for the Sustainable Management of the African Great Lakes; King’s College: London, UK, 2023. [Google Scholar]
- Ermida, S.L.; Mantas, V.; Göttsche, F. Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series. Remote Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Tebbs, E.J.; Remedios, J.J.; Harper, D.M. Remote Sensing of Chlorophyll-a as a Measure of Cyanobacterial Biomass in Lake Bogoria, a Hypertrophic, Saline—Alkaline, Flamingo Lake, Using Landsat ETM+. Remote Sens. Environ. 2013, 135, 92–106. [Google Scholar] [CrossRef]
- Wang, C.; Chen, S.; Li, D.; Wang, D.; Liu, W.; Yang, J. A Landsat-Based Model for Retrieving Total Suspended Solids Concentration of Estuaries and Coasts in China. Geosci. Model Dev. 2017, 10, 4347–4365. [Google Scholar] [CrossRef]
- Harrington, J.A.; Schiebe, F.R.; Nix, J.E. Remote Sensing of Lake Chicot, Arkansas: Monitoring Suspended Sediments, Turbidity, and Secchi Depth with Landsat MSS Data. Remote Sens. Environ. 1992, 39, 15–27. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized Difference Chlorophyll Index: A Novel Model for Remote Estimation of Chlorophyll-a Concentration in Turbid Productive Waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Tavora, J.; Jiang, B.; Kiffney, T.; Bourdin, G.; Gray, P.C.; de Carvalho, L.S.; Hesketh, G.; Schild, K.M.; de Souza, L.F.; Brady, D.C.; et al. Recipes for the Derivation of Water Quality Parameters Using the High-Spatial-Resolution Data from Sensors on Board Sentinel-2A, Sentinel-2B, Landsat-5, Landsat-7, Landsat-8, and Landsat-9 Satellites. J. Remote Sens. 2023, 3, 0049. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, J.; Xu, Y.; Guo, S.; Nie, X.; Guo, Y.; Li, X.; Hao, F.; Fu, Y.H. Monitoring of Chlorophyll-a and Suspended Sediment Concentrations in Optically Complex Inland Rivers Using Multisource Remote Sensing Measurements. Ecol. Indic. 2023, 155, 111041. [Google Scholar] [CrossRef]
- Kiage, L.M.; Douglas, P. Linkages between Land Cover Change, Lake Shrinkage, and Sublacustrine Influence Determined from Remote Sensing of Select Rift Valley Lakes in Kenya. Sci. Total Environ. 2020, 709, 136022. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, S.V.; Pahlevan, N.; Smith, B.; Binding, C.; Schalles, J.; Loisel, H.; Gurlin, D.; Greb, S.; Alikas, K.; Randla, M.; et al. Robust Algorithm for Estimating Total Suspended Solids (TSS) in Inland and Nearshore Coastal Waters. Remote Sens. Environ. 2020, 246, 111768. [Google Scholar] [CrossRef]
- Turner, A.; Millward, G.E. Suspended Particles: Their Role in Estuarine Biogeochemical Cycles. Estuar. Coast. Shelf Sci. 2002, 55, 857–883. [Google Scholar] [CrossRef]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Measurement of Total Dissolved Solids and Total Suspended Solids in Water Systems: A Review of the Issues, Conventional, and Remote Sensing Techniques. Remote Sens. 2023, 15, 3534. [Google Scholar] [CrossRef]
- Song, K.; Li, L.; Wang, Z.; Liu, D.; Zhang, B.; Xu, J.; Du, J.; Li, L.; Li, S.; Wang, Y. Retrieval of Total Suspended Matter (TSM) and Chlorophyll-a (Chl-a) Concentration from Remote-Sensing Data for Drinking Water Resources. Environ. Monit. Assess. 2012, 184, 1449–1470. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Shi, K.; Zhou, Y.; Li, N. Remote Sensing Estimation of Water Clarity for Various Lakes in China. Water Res. 2021, 192, 116844. [Google Scholar] [CrossRef] [PubMed]
- Alba, A.C.G.; Anabella, B.C.F.; Marcelo, C.S.; Andrea, D.G.A.; Ivana, E.T.; Iba, E.; Sandra, E.T.; Michal, F.S.; Pascal, U.B.; Paz, L.; et al. Spectral Monitoring of Algal Blooms in an Eutrophic Lake Using Sentinel-2A. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 306–309. [Google Scholar]
- Buma, W.G.; Lee, S. Il Evaluation of Sentinel-2 and Landsat 8 Images for Estimating Chlorophyll-a Concentrations in Lake Chad, Africa. Remote Sens. 2020, 12, 2437. [Google Scholar] [CrossRef]
- Smith, B.; Pahlevan, N.; Schalles, J.; Ruberg, S.; Errera, R.; Ma, R.; Giardino, C.; Bresciani, M.; Barbosa, C.; Moore, T.; et al. A Chlorophyll-a Algorithm for Landsat-8 Based on Mixture Density Networks. Front. Remote Sens. 2021, 1, 623678. [Google Scholar] [CrossRef]
- Singh, R.; Saritha, V.; Pande, C.B. Monitoring of Wetland Turbidity Using Multi-Temporal Landsat-8 and Landsat-9 Satellite Imagery in the Bisalpur Wetland, Rajasthan, India. Environ. Res. 2024, 241, 117638. [Google Scholar] [CrossRef] [PubMed]
- Byrne, A.; Tebbs, E.J.; Njoroge, P.; Nkwabi, A.; Chadwick, M.A.; Freeman, R.; Harper, D.; Norris, K. Productivity Declines Threaten East African Soda Lakes and the Iconic Lesser Flamingo. Curr. Biol. 2024, 34, 1786–1793.e4. [Google Scholar] [CrossRef] [PubMed]
- Ballatore, T.J.; Bradt, S.R.; Olaka, L.; Cózar, A.; Loiselle, S.A. Remote Sensing of African Lakes: A Review. In Remote Sensing of the African Seas; Springer: Dordrecht, The Netherlands, 2014; pp. 403–422. [Google Scholar]
- UNEP. The Global Water Quality Database; GEMStat: Koblenz, Germany, 2020. [Google Scholar]
- Lehmann, M.K.; Gurlin, D.; Pahlevan, N.; Alikas, K.; Anstee, J.; Balasubramanian, S.V.; Barbosa, C.C.F.; Binding, C.; Bracher, A.; Bresciani, M.; et al. GLORIA—A Globally Representative Hyperspectral in Situ Dataset for Optical Sensing of Water Quality. Sci. Data 2023, 10, 100. [Google Scholar] [CrossRef] [PubMed]
- Arias-Rodriguez, L.F.; Tüzün, U.F.; Duan, Z.; Huang, J.; Tuo, Y.; Disse, M. Global Water Quality of Inland Waters with Harmonized Landsat-8 and Sentinel-2 Using Cloud-Computed Machine Learning. Remote Sens. 2023, 15, 1390. [Google Scholar] [CrossRef]
- Kaufman, Y.J. Atmospheric Effects on Remote Sensing of Surface Reflectance. Remote Sens. Crit. Rev. Technol. 1984, 475, 20–33. [Google Scholar] [CrossRef]
- Majozi, N.P.; Salama, M.S.; Bernard, S.; Harper, D.M.; Habte, M.G. Remote Sensing of Euphotic Depth in Shallow Tropical Inland Waters of Lake Naivasha Using MERIS Data. Remote Sens. Environ. 2014, 148, 178–189. [Google Scholar] [CrossRef]
- Kneubühler, M.; Frank, T.; Kellenberger, T.; Pasche, N.; Schmid, M. Mapping Chlorophyll-a in Lake Kivu with Remote Sensing Methods. In Proceedings of the Envisat Symposium 2007, Montreux, Switzerland, 23–27 April 2007. [Google Scholar] [CrossRef]
- Ndungu, J.; Monger, B.C.; Augustijn, D.C.M.; Hulscher, S.J.M.H.; Kitaka, N.; Mathooko, J.M. Evaluation of Spatio-Temporal Variations in Chlorophyll-a in Lake Naivasha, Kenya: Remote-Sensing Approach. Int. J. Remote Sens. 2013, 34, 8142–8155. [Google Scholar] [CrossRef]
- Nicholson, S.E. Climate and Climatic Variability of Rainfall over Eastern Africa. Rev. Geophys. 2017, 55, 590–635. [Google Scholar] [CrossRef]
- Ogega, O.M.; Mbugua, J.; Misiani, H.O.; Nyadawa, M.; Scoccimarro, E.; Endris, H.S. Detection and Attribution of Lake Victoria’s Water-Level Fluctuations in a Changing Climate. Preprints 2021, 2021070575. [Google Scholar] [CrossRef]
- Tarits, C.; Renaut, R.W.; Tiercelin, J.J.; Le Hérissé, A.; Cotten, J.; Cabon, J.Y. Geochemical Evidence of Hydrothermal Recharge in Lake Baringo, Central Kenya Rift Valley. Hydrol. Process. 2006, 20, 2027–2055. [Google Scholar] [CrossRef]
- Seka, A.M.; Zhang, J.; Ayele, G.T.; Demeke, Y.G.; Han, J.; Prodhan, F.A. Spatio-Temporal Analysis of Water Storage Variation and Temporal Correlations in the East Africa Lake Basins. J. Hydrol. Reg. Stud. 2022, 41, 101094. [Google Scholar] [CrossRef]
- WWF. Climate Change Impacts on East Africa. 2006. Available online: https://www.wwf.or.jp/activities/lib/pdf_climate/environment/east_africa_climate_change_impacts_final.pdf (accessed on 2 February 2024).
- Schagerl, M. Soda Lakes of East Africa; Springer: Cham, Switzerland, 2016; ISBN 9783319286204. [Google Scholar]
- Tilahun, G.; Ahlgren, G. Seasonal Variations in Phytoplankton Biomass and Primary Production in the Ethiopian Rift Valley Lakes Ziway, Awassa and Chamo—The Basis for Fish Production. Limnologica 2010, 40, 330–342. [Google Scholar] [CrossRef]
- Tebbs, E.J.; Remedios, J.J.; Avery, S.T.; Rowland, C.S.; Harper, D.M. Regional Assessment of Lake Ecological States Using Landsat: A Classification Scheme for Alkaline-Saline, Flamingo Lakes in the East African Rift Valley. Int. J. Appl. Earth Obs. Geoinf. 2015, 40, 100–108. [Google Scholar] [CrossRef]
- Kahru, M.; Kudela, R.M.; Anderson, C.R.; Manzano-Sarabia, M.; Mitchell, B.G. Evaluation of Satellite Retrievals of Ocean Chlorophyll-a in the California Current. Remote Sens. 2014, 6, 8524–8540. [Google Scholar] [CrossRef]
- Baird, R.; Bridgewater, L. Standard Methods for the Examination of Water and Wastewater, 23rd ed.; American Public Health Association: Washington, DC, USA, 2017. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- USGS. Landsat Collection 2 Level-1 Product Courtesy of the U.S. Geological Survey. Available online: https://www.usgs.gov/landsat-missions/landsat-collection-2-level-1-data (accessed on 15 January 2024).
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Joseph Hughes, M.; Laue, B. Cloud Detection Algorithm Comparison and Validation for Operational Landsat Data Products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- Johansen, R.; Beck, R.; Nowosad, J.; Nietch, C.; Xu, M.; Shu, S.; Yang, B.; Liu, H.; Emery, E.; Reif, M.; et al. Evaluating the Portability of Satellite Derived Chlorophyll-a Algorithms for Temperate Inland Lakes Using Airborne Hyperspectral Imagery and Dense Surface Observations. Harmful Algae 2018, 76, 35–46. [Google Scholar] [CrossRef]
- Boucher, J.; Weathers, K.C.; Norouzi, H.; Steele, B. Assessing the Effectiveness of Landsat 8 Chlorophyll a Retrieval Algorithms for Regional Freshwater Monitoring. Ecol. Appl. 2018, 28, 1044–1054. [Google Scholar] [CrossRef] [PubMed]
- Dallosch, M.A.; Creed, I.F. Optimization of Landsat Chl-a Retrieval Algorithms in Freshwater Lakes through Classification of Optical Water Types. Remote Sens. 2021, 13, 4607. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, Q.; Liu, G.; Jacinthe, P.A.; Wang, X.; Lyu, L.; Tao, H.; Ma, Y.; Duan, H.; Shang, Y.; et al. Remote Sensing of Total Suspended Matter Concentration in Lakes across China Using Landsat Images and Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2022, 187, 61–78. [Google Scholar] [CrossRef]
- Lymburner, L.; Botha, E.; Hestir, E.; Anstee, J.; Sagar, S.; Dekker, A.; Malthus, T. Landsat 8: Providing Continuity and Increased Precision for Measuring Multi-Decadal Time Series of Total Suspended Matter. Remote Sens. Environ. 2016, 185, 108–118. [Google Scholar] [CrossRef]
- Kloiber, S.M.; Brezonik, P.L.; Bauer, M.E. Application of Landsat Imagery to Regional-Scale Assessments of Lake Clarity. Water Res. 2002, 36, 4330–4340. [Google Scholar] [CrossRef] [PubMed]
- Lathrop, R.G., Jr.; Lillesand, T.M. Use of Thematic Mapper Data to Assess Water Quality in Green Bay and Central Lake Michigan. Photogramm. Eng. Remote Sens. 1986, 52, 671–680. [Google Scholar]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-Year Landsat Water Clarity Census of Minnesota’s 10,000 Lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Lu, S.; Bian, Y.; Chen, F.; Lin, J.; Lyu, H.; Li, Y.; Liu, H.; Zhao, Y.; Zheng, Y.; Lyu, L. An Operational Approach for Large-Scale Mapping of Water Clarity Levels in Inland Lakes Using Landsat Images Based on Optical Classification. Environ. Res. 2023, 237, 116898. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Wang, Q.; Liu, G.; Jacinthe, P.A.; Li, S.; Tao, H.; Du, Y.; Wen, Z.; Wang, X.; Guo, W.; et al. A Unified Model for High Resolution Mapping of Global Lake (>1 Ha) Clarity Using Landsat Imagery Data. Sci. Total Environ. 2022, 810, 151188. [Google Scholar] [CrossRef]
- Kutser, T. Quantitative Detection of Chlorophyll in Cyanobacterial Blooms by Satellite Remote Sensing. Limnol. Oceanogr. 2004, 49, 2179–2189. [Google Scholar] [CrossRef]
- Sinharay, S. Jackknife Methods. In International Encyclopedia of Education; Academic Press: Oxford, UK, 2010; Volume 7, pp. 229–231. [Google Scholar]
- Volpe, V.; Silvestri, S.; Marani, M. Remote Sensing Retrieval of Suspended Sediment Concentration in Shallow Waters. Remote Sens. Environ. 2011, 115, 44–54. [Google Scholar] [CrossRef]
- Zhai, K.; Wu, X.; Qin, Y.; Du, P. Comparison of Surface Water Extraction Performances of Different Classic Water Indices Using OLI and TM Imageries in Different Situations. Geo-Spat. Inf. Sci. 2015, 18, 32–42. [Google Scholar] [CrossRef]
- Hickley, P.; Boar, R.R.; Mavuti, K.M. Bathymetry of Lake Bogoria, Kenya. J. East Afr. Nat. Hist. 2003, 92, 107–117. [Google Scholar] [CrossRef]
- Okech, E.O.; Kitaka, N.; Oduor, S.O.; Verschuren, D. Trophic State and Nutrient Limitation in Lake Baringo, Kenya. Afr. J. Aquat. Sci. 2018, 43, 169–173. [Google Scholar] [CrossRef]
- Huan, Y.; Sun, D.; Wang, S.; Zhang, H.; Li, Z.; Zhang, Y.; He, Y. Phytoplankton Package Effect in Oceanic Waters: Influence of Chlorophyll-a and Cell Size. Sci. Total Environ. 2022, 838, 155876. [Google Scholar] [CrossRef] [PubMed]
- Alvado, B.; Sòria-Perpinyà, X.; Vicente, E.; Delegido, J.; Urrego, P.; Ruíz-Verdú, A.; Soria, J.M.; Moreno, J. Estimating Organic and Inorganic Part of Suspended Solids from Sentinel 2 in Different Inland Waters. Water 2021, 13, 2453. [Google Scholar] [CrossRef]
- Maciel, D.A.; Pahlevan, N.; Barbosa, C.C.F.; de Novo, E.M.L.D.M.; Paulino, R.S.; Martins, V.S.; Vermote, E.; Crawford, C.J. Validity of the Landsat Surface Reflectance Archive for Aquatic Science: Implications for Cloud-Based Analysis. Limnol. Oceanogr. Lett. 2023, 8, 850–858. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A Global Assessment of Atmospheric Correction Methods for Landsat-8 and Sentinel-2 over Lakes, Rivers, and Coastal Waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]



| Lake | Country | Freshwater or Saline | Average Surface Area (km2) | Average Depth (m) | Elevation (m asl) | Watershed Area (km2) |
|---|---|---|---|---|---|---|
| Ziway | Ethiopia | Freshwater | 411.96 | 13.9 | 1636 | 7296.3 |
| Chamo | Ethiopia | Freshwater | 312.04 | 26.9 | 1109 | 1940.6 |
| Turkana | Ethiopia/Kenya | Saline | 7473.43 | 31.8 | 361 | 149,329.0 |
| Baringo | Kenya | Freshwater | 125.43 | 14.5 | 968 | 6604.4 |
| Bogoria | Kenya | Saline | 36.25 | 23.2 | 990 | 760.7 |
| Oloidien | Kenya | Saline | 5.21 | 8.9 | 1883 | 144.7 |
| Victoria | Kenya/Uganda/ Tanzania | Freshwater | 67,166.2 | 41.1 | 1134 | 265,373.0 |
| Lake | Date | Parameters | Number of In Situ Samples | Source |
|---|---|---|---|---|
| Ziway | 24 January 2005– 4 January 2006 | Chl-a | 12 | [42] |
| Chamo | 25 March 2006– 8 February 2007 | Chl-a | 12 | [42] |
| Turkana | 1 September 2016– 4 September 2016 | Chl-a, TSS, SDD | 12 | This study |
| Baringo | 18 September 2023, 19 September 2023 | Chl-a, TSS, SDD | 15 | This study |
| Bogoria | 21 April 2010– 26 April 2010, 1 April 2012– 11 April 2012 | Chl-a, TSS, SDD | 39 | [11,43] |
| Oloidien | 31 March 2011– 1 April 2011 | Chl-a, TSS, SDD | 10 | [43] |
| Victoria | 13 September 2023 | Chl-a, TSS, SDD | 15 | This study |
| Parameter | Index | Band Combination | Example Reference |
|---|---|---|---|
| Chl-a | Normalised Difference Chlorophyll Index (NDCI) | [25,27] | |
| 2-Band Algorithm (2BDA) | [25] | ||
| 3-Band algorithm (3BDA) | [50] | ||
| Fluorescence Line Height Blue (FLH BLUE) | [50] | ||
| Surface Algal Bloom Index (SABI) | [50,51] | ||
| 3BDA-like (KIVU) | [50] | ||
| NRVI | [52] | ||
| Tebbs et al. (2013) | [11] | ||
| TSS | Suspended Matter Index (SMI) | [53] | |
| Total Suspended Matter Index (TSMI) | [54] | ||
| Normalised Suspended Material Index (NSMI) | [21] | ||
| Normalised Difference Suspended Sediment Index (NDSSI) | [21] | ||
| 2-Band Algorithm 1 (2BDA1) | [17] | ||
| 2-Band Algorithm 2 (2BDA2) | [17] | ||
| Normalised Difference Turbidity Index (NDTI) | [27] | ||
| SDD | Kloiber | [55] | |
| Lathrop | [56] | ||
| Normalised Difference Turbidity Index (NDTI) | [27] | ||
| Empirical Band Ratio (EBR) | [57] | ||
| Lu2023T2 | [58] | ||
| Song et al. (2022) | [59] |
| Site | Parameter | Mean | Median | Min | Max | n |
|---|---|---|---|---|---|---|
| Baringo | Chl-a (μg/L) | 9.44 | 9.44 | 5.43 | 12.8 | 15 |
| TSS (mg/L) | 23.3 | 14.0 | 10.9 | 71.5 | 15 | |
| SDD (m) | 0.265 | 0.280 | 0.140 | 0.330 | 15 | |
| Bogoria | Chl-a (μg/L) | 115.9 | 109.4 | 64.7 | 169.0 | 8 |
| TSS (mg/L) | 44.8 | 46.5 | 23.0 | 68.0 | 8 | |
| SDD (m) | - | - | - | - | - | |
| Chamo | Chl-a (μg/L) | 35.1 | 35.1 | 33.2 | 37.0 | 2 |
| TSS (mg/L) | - | - | - | - | - | |
| SDD (m) | - | - | - | - | - | |
| Oloidien | Chl-a (μg/L) | 129.8 | 129.8 | 129.8 | 129.8 | 1 |
| TSS (mg/L) | 65.3 | 62.0 | 60.0 | 74.0 | 3 | |
| SDD (m) | - | - | - | - | - | |
| Turkana | Chl-a (μg/L) | 4.13 | 3.09 | 1.66 | 9.69 | 5 |
| TSS (mg/L) | 1.78 | 1.48 | 0.552 | 2.75 | 5 | |
| SDD (m) | - | - | - | - | - | |
| Victoria | Chl-a (μg/L) | 25.5 | 20.0 | 9.72 | 69.8 | 15 |
| TSS (mg/L) | 12.0 | 12.4 | 7.90 | 16.2 | 15 | |
| SDD (m) | 0.673 | 0.700 | 0.500 | 0.800 | 15 | |
| Ziway | Chl-a (μg/L) | 38.2 | 36.3 | 34.0 | 47.2 | 5 |
| TSS (mg/L) | - | - | - | - | - | |
| SDD (m) | - | - | - | - | - | |
| All sites | Chl-a (μg/L) | 36.5 | 18.6 | 1.66 | 169.0 | 51 |
| TSS (mg/L) | 24.1 | 13.9 | 0.552 | 74.0 | 46 | |
| SDD (m) | 0.469 | 0.415 | 0.140 | 0.800 | 30 |
| Parameter | Algorithm | Model Type | Reflectance | Intercept | R2 | p-Value | RMSE | MAE | MAPE | Bias |
|---|---|---|---|---|---|---|---|---|---|---|
| Chl-a (μg/L) | NDCI | Linear | SR | 6.13 | 0.520 | 0.000 | 31.6 | 19.2 | 64.8 | −4.44 |
| 2BDA | Quadratic | SR | 6.09 | 0.540 | 0.000 | 30.2 | 18.1 | 59.9 | −5.84 | |
| 3BDA | Linear | TOA | 6.11 | 0.717 | 0.000 | 22.9 | 14.7 | 59.9 | −4.61 | |
| FLH BLUE | Quadratic | SR | 19.0 | 0.105 | 0.020 | 43.2 | 25.9 | 118.6 | −15.42 | |
| SABI | Quadratic | SR | 9.43 | 0.589 | 0.000 | 28.5 | 18.3 | 62.7 | −8.22 | |
| KIVU | Quadratic | TOA | 12.2 | 0.385 | 0.000 | 34.7 | 21.1 | 95.1 | −10.50 | |
| NRVI | Linear | TOA | 8.10 | 0.470 | 0.000 | 32.4 | 19.8 | 67.5 | −6.59 | |
| Tebbs et al. (2013) | Linear | TOA | 77.9 | 0.551 | 0.000 | 150.1 | 118.4 | 293.2 | 108.24 | |
| This study—NDCI-SABI ratio | Linear | SR | 6.49 | 0.578 | 0.000 | 28.9 | 17.3 | 56.8 | −3.29 | |
| TSS (mg/L) | SMI | Quadratic | TOA | 14.8 | 0.043 | 0.169 | 21.9 | 14.4 | 102.4 | −7.67 |
| TSMI | Quadratic | TOA | 11.7 | 0.253 | 0.000 | 18.8 | 12.1 | 84.8 | −4.85 | |
| NSMI | Quadratic | TOA | 13.5 | 0.147 | 0.008 | 20.4 | 12.9 | 100.3 | −6.49 | |
| NDSSI | Linear | TOA | 15.7 | 0.352 | 0.000 | 16.9 | 12.9 | 58.2 | −0.36 | |
| 2BDA1 | Quadratic | TOA | 15.8 | 0.005 | 0.658 | 22.5 | 14.6 | 112.9 | −7.55 | |
| 2BDA2 | Quadratic | TOA | 11.9 | 0.232 | 0.001 | 19.3 | 12.3 | 89.2 | −6.03 | |
| NDTI | Quadratic | TOA | 9.8 | 0.187 | 0.003 | 21.2 | 12.9 | 78.3 | −5.64 | |
| This study—MSMI | Quadratic | TOA | 4.39 | 0.822 | 0.000 | 9.00 | 5.91 | 28.3 | −1.25 | |
| SDD (m) | Kloiber | Quadratic | TOA | 0.025 | 0.913 | 0.000 | 0.065 | 0.050 | 12.6 | −0.003 |
| Lathrop | Quadratic | SR | 0.070 | 0.850 | 0.000 | 0.084 | 0.066 | 17.1 | −0.000 | |
| Song et al. (2022) | Linear | TOA | 0.091 | 0.933 | 0.000 | 0.073 | 0.058 | 13.3 | −0.025 | |
| NDTI | Quadratic | TOA | 0.043 | 0.889 | 0.000 | 0.073 | 0.051 | 12.8 | −0.006 | |
| EBR | Quadratic | TOA | 0.024 | 0.904 | 0.000 | 0.068 | 0.054 | 13.8 | −0.004 | |
| Lu2023T2 | Quadratic | TOA | 0.035 | 0.875 | 0.000 | 0.077 | 0.056 | 12.6 | −0.004 | |
| This study—Red-Blue ratio | Quadratic | TOA | 0.025 | 0.921 | 0.000 | 0.061 | 0.046 | 11.3 | −0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Byrne, A.; Lomeo, D.; Owoko, W.; Aura, C.M.; Nyakeya, K.; Odoli, C.; Mugo, J.; Barongo, C.; Kiplagat, J.; Mwirigi, N.; et al. LAQUA: a LAndsat water QUality retrieval tool for east African lakes. Remote Sens. 2024, 16, 2903. https://doi.org/10.3390/rs16162903
Byrne A, Lomeo D, Owoko W, Aura CM, Nyakeya K, Odoli C, Mugo J, Barongo C, Kiplagat J, Mwirigi N, et al. LAQUA: a LAndsat water QUality retrieval tool for east African lakes. Remote Sensing. 2024; 16(16):2903. https://doi.org/10.3390/rs16162903
Chicago/Turabian StyleByrne, Aidan, Davide Lomeo, Winnie Owoko, Christopher Mulanda Aura, Kobingi Nyakeya, Cyprian Odoli, James Mugo, Conland Barongo, Julius Kiplagat, Naftaly Mwirigi, and et al. 2024. "LAQUA: a LAndsat water QUality retrieval tool for east African lakes" Remote Sensing 16, no. 16: 2903. https://doi.org/10.3390/rs16162903
APA StyleByrne, A., Lomeo, D., Owoko, W., Aura, C. M., Nyakeya, K., Odoli, C., Mugo, J., Barongo, C., Kiplagat, J., Mwirigi, N., Avery, S., Chadwick, M. A., Norris, K., Tebbs, E. J., & on behalf of the NSF-IRES Lake Victoria Research Consortium. (2024). LAQUA: a LAndsat water QUality retrieval tool for east African lakes. Remote Sensing, 16(16), 2903. https://doi.org/10.3390/rs16162903







