Optimizing Temporal Weighting Functions to Improve Rainfall Prediction Accuracy in Merged Numerical Weather Prediction Models for the Korean Peninsula
Abstract
1. Introduction
2. Data and Methodology
2.1. NWP Model and Radar Observation Data
- (1)
- Event 1: 3 August 2020, 00:00 LST to 4 August 2020, 00:00 LST;
- (2)
- Event 2: 1 August 2021, 00:00 LST to 2 August 2021, 00:00 LST;
- (3)
- Event 3: 21 August 2021, 00:00 LST to 22 August 2021, 00:00 LST.
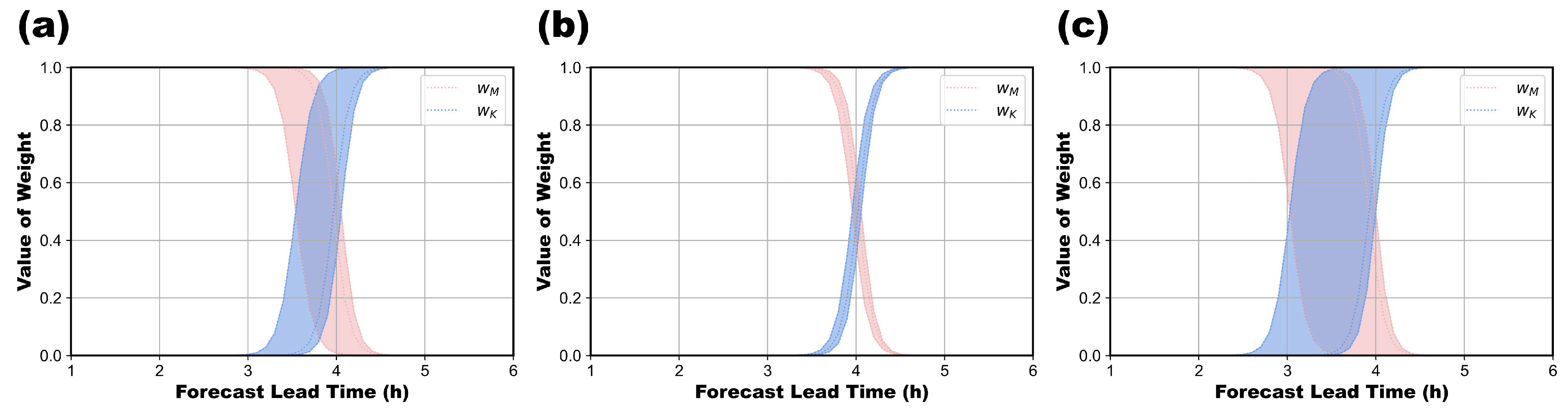
2.2. Temporal Weighting Function
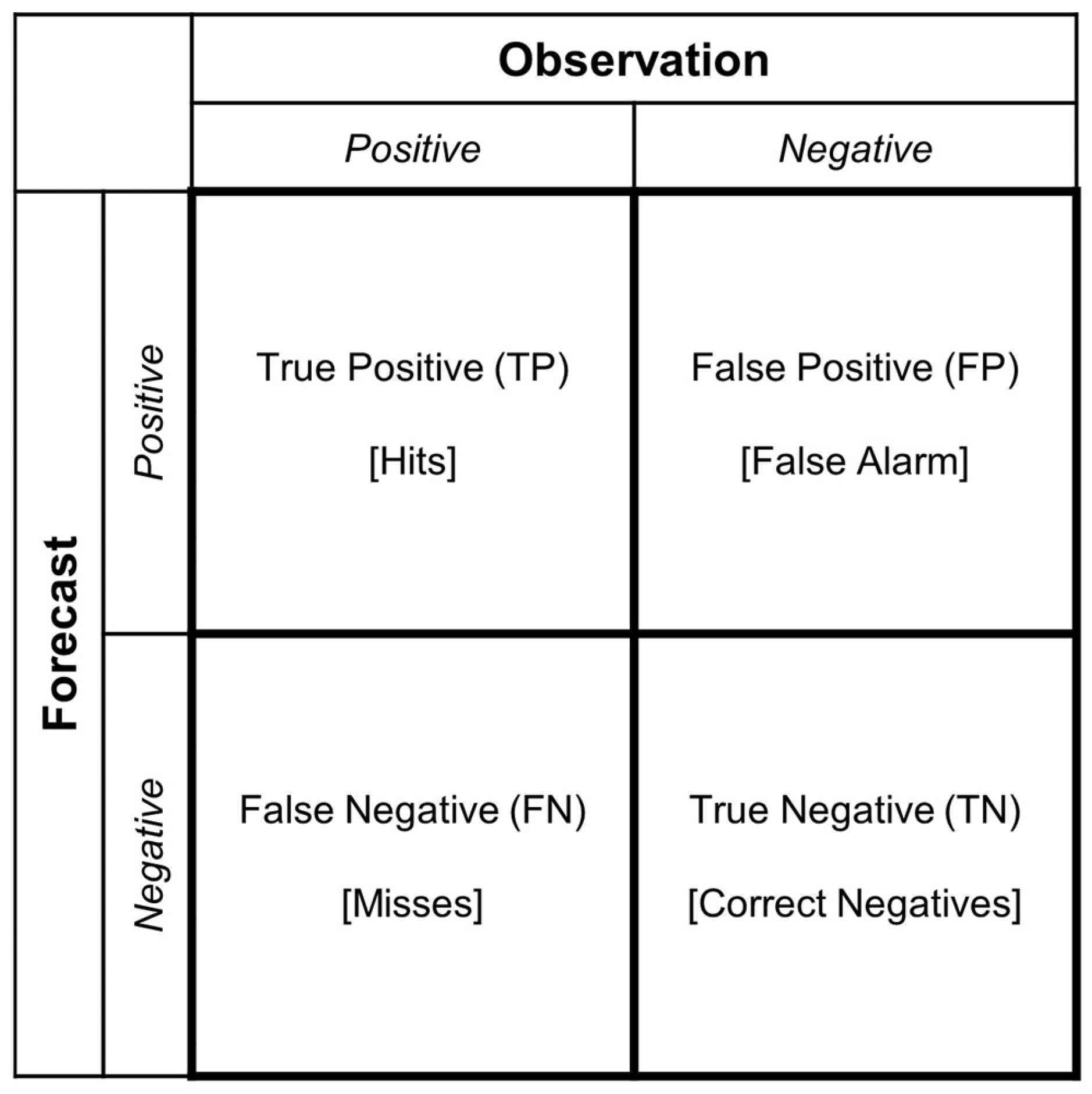
2.3. Performance Index
- (1)
- Probability of Detection (POD) quantifies the proportion of reference observations correctly identified via the simulation. It can be calculated using Equation (5), with values ranging from 0 to 1, with 0 denoting no skill, while 1 represents a perfect score;
- (2)
- False Alarm Ratio (FAR) indicates the fraction of events identified via the simulation but not confirmed with reference observations. It can be calculated using Equation (6), with values ranging from 0 to 1, with 0 denoting a perfect score;
- (3)
- Critical Success Index (CSI), also referred to as the Threat Score, integrates various aspects of POD and FAR, providing an overall assessment of the simulation performance relative to reference observation. It can be calculated using Equation (7), with values ranging from 0 to 1, with 0 indicating no skill, while 1 signifies a perfect score;
- (4)
- True Positive Rate (TPR), also known as Sensitivity or Recall, represents the proportion of positive events correctly identified via the simulation among all actual positive events. It can be calculated using Equation (8), with values ranging from 0 to 1, with 0 indicating no true positives detected, while 1 denotes perfect identification of positive events;
- (5)
- False Positive Rate (FPR), also referred to as the Fall-out, quantifies the fraction of negative events incorrectly identified as positive via the simulation out of all actual negative events. It can be computed using Equation (9), with values ranging from 0 to 1, with 0 denoting a perfect score, indicating no false positives, while 1 signifies all negative events being falsely identified as positive;
- (6)
- Root Mean Squared Error (RMSE) measures the average magnitude of errors between predicted and observed values, indicating the model performance in capturing the data variability. It is computed using Equation (10), where N represents the total number of observations, denotes the predicted value, and represents the observed value for the ith observation. The RMSE ranges from 0 to positive infinity, with lower values indicating better model performance.
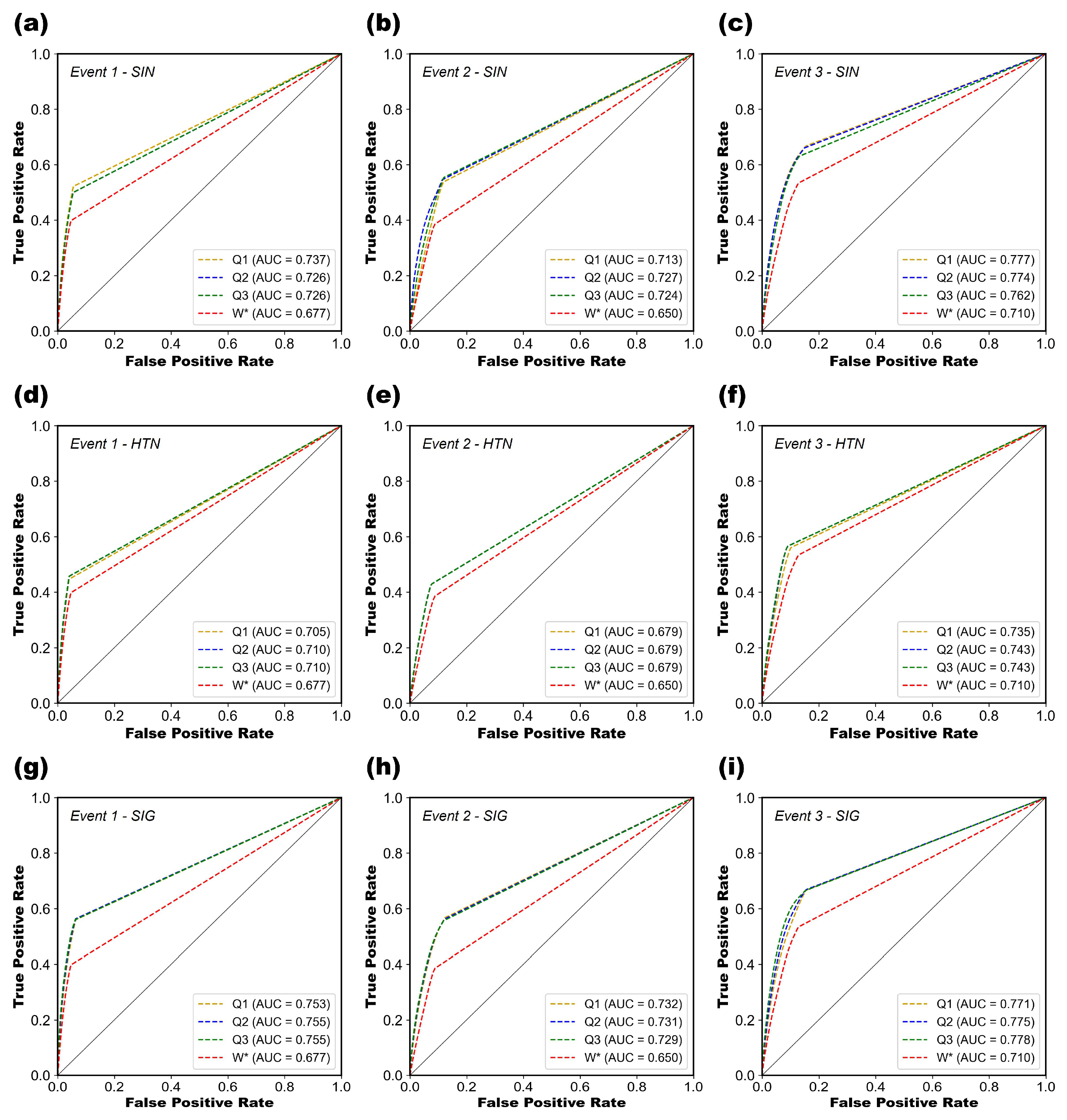
2.4. Receiver Operating Characteristic (ROC) Curve
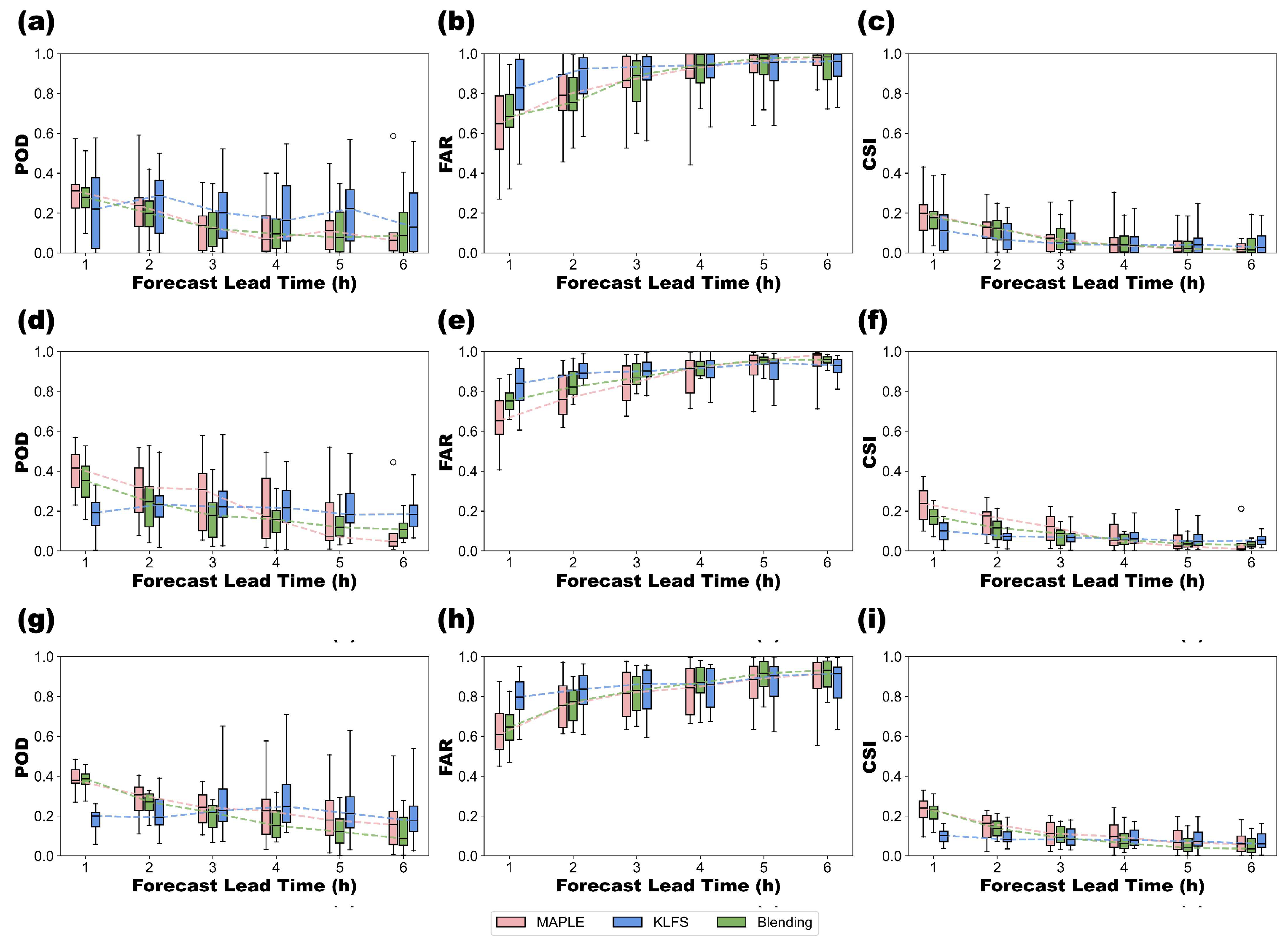
3. Results
3.1. Performance Results of Temporal Weighting Function
3.1.1. Parameter Results across Different Quartiles
3.1.2. Comparison of Performance Results with Previous Studies
3.2. Blending Results with Performance Index
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arnell, N.W.; Lowe, J.A.; Challinor, A.J.; Osborn, T.J. Global and Regional Impacts of Climate Change at Different Levels of Global Temperature Increase. Clim. Chang. 2019, 155, 377–391. [Google Scholar] [CrossRef]
- Lindsey, R.; Dahlman, L. Climate Change: Global Temperature. Climate.gov 2020, 16. Available online: https://www.climate.gov/news-features/understanding-climate/climate-change-global-temperature (accessed on 5 August 2024).
- Crowley, T.J. Causes of Climate Change over the Past 1000 Years. Science 2000, 289, 270–277. [Google Scholar] [CrossRef] [PubMed]
- Etukudoh, E.A.; Ilojianya, V.I.; Ayorinde, O.B.; Daudu, C.D.; Adefemi, A.; Hamdan, A. Review of Climate Change Impact on Water Availability in the USA and Africa. Int. J. Sci. Res. Arch. 2024, 11, 942–951. [Google Scholar] [CrossRef]
- Radha, S.V.V.D.; Sabarathinam, C.; Al Otaibi, F.; Al-Sabti, B.T. Variation of Centennial Precipitation Patterns in Kuwait and Their Relation to Climate Change. Environ. Monit. Assess. 2023, 195, 20. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, F.; Fattahi, M.H. Climate Change-Induced Influences on the Nonlinear Dynamic Patterns of Precipitation and Temperatures (Case Study: Central England). Theor. Appl. Climatol. 2023, 152, 1147–1158. [Google Scholar] [CrossRef]
- Bindoff, N.L.; Willebrand, J.; Artale, V.; Cazenave, A.; Gregory, J.M.; Gulev, S.; Hanawa, K.; Le Quere, C.; Levitus, S.; Nojiri, Y. Observations: Oceanic Climate Change and Sea Level. 2007. Available online: https://nora.nerc.ac.uk/id/eprint/15400/ (accessed on 5 August 2024).
- Nerem, R.S.; Beckley, B.D.; Fasullo, J.T.; Hamlington, B.D.; Masters, D.; Mitchum, G.T. Climate-Change–Driven Accelerated Sea-Level Rise Detected in the Altimeter Era. Proc. Natl. Acad. Sci. USA 2018, 115, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Roy, P.; Pal, S.C.; Chakrabortty, R.; Chowdhuri, I.; Saha, A.; Shit, M. Effects of Climate Change and Sea-Level Rise on Coastal Habitat: Vulnerability Assessment, Adaptation Strategies and Policy Recommendations. J. Environ. Manag. 2023, 330, 117187. [Google Scholar] [CrossRef] [PubMed]
- Yum, S.-G.; Song, M.-S.; Adhikari, M. Das Assessing Typhoon Soulik-Induced Morphodynamics over the Mokpo Coastal Region in South Korea Based on a Geospatial Approach. Nat. Hazards Earth Syst. Sci. 2023, 23, 2449–2474. [Google Scholar] [CrossRef]
- Om, K.; Ren, G.; Jong, S.; Ham, Y.; Hong, C.; Kang-Chol, O.; Tysa, S.K. Spatial and Temporal Patterns in Observed Extreme Precipitation Change over Northern Part of the Korean Peninsula. J. Geophys. Res. Atmos. 2024, 129, e2023JD039305. [Google Scholar] [CrossRef]
- Lee, M.; Min, S.-K.; Cha, D.-H. Convection-Permitting Simulations Reveal Expanded Rainfall Extremes of Tropical Cyclones Affecting South Korea due to Anthropogenic Warming. npj Clim. Atmos. Sci. 2023, 6, 176. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W.; Hlaing, P.T.; Wangwongchai, A.; Dechpichai, P. Advancements in Daily Precipitation Forecasting: A Deep Dive into Daily Precipitation Forecasting Hybrid Methods in the Tropical Climate of Thailand. MethodsX 2024, 12, 102757. [Google Scholar] [CrossRef]
- Bansal, K.; Tripathi, A.K.; Pandey, A.C.; Sharma, V. RfGanNet: An Efficient Rainfall Prediction Method for India and Its Clustered Regions Using RfGan and Deep Convolutional Neural Networks. Expert Syst. Appl. 2024, 235, 121191. [Google Scholar] [CrossRef]
- Anuradha, T.; Formal, P.S.G.A.S.; RamaDevi, J. Hybrid Model for Rainfall Prediction with Statistical and Technical Indicator Feature Set. Expert Syst. Appl. 2024, 249, 123260. [Google Scholar] [CrossRef]
- Fan, P.; Yang, J.; Chen, Z.; Zhao, J.; Zang, N.; Feng, G. Neural Network-Based Climate Index: Advancing Rainfall Prediction in EI Niño Contexts. Atmos. Res. 2024, 300, 107216. [Google Scholar] [CrossRef]
- Byun, J.; Jun, C.; Kim, J.; Cha, J.; Narimani, R. Deep Learning-Based Rainfall Prediction Using Cloud Image Analysis. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Lee, J.; Byun, J.; Baik, J.; Jun, C.; Kim, H.J. Estimation of Raindrop Size Distribution and Rain Rate with Infrared Surveillance Camera in Dark Conditions. Atmos. Meas. Tech. 2023, 16, 707–725. [Google Scholar] [CrossRef]
- Hwang, S.; Jun, C.; De Michele, C.; Kim, H.-J.; Lee, J. Rainfall Observation Leveraging Raindrop Sounds Acquired Using Waterproof Enclosure: Exploring Optimal Length of Sounds for Frequency Analysis. Sensors 2024, 24, 4281. [Google Scholar] [CrossRef] [PubMed]
- Suemitsu, K.; Endo, S.; Sato, S. Classification of Rainfall Intensity and Cloud Type from Dash Cam Images Using Feature Removal by Masking. Climate 2024, 12, 70. [Google Scholar] [CrossRef]
- Wang, B. Rainy Season of the Asian–Pacific Summer Monsoon. J. Clim. 2002, 15, 386–398. [Google Scholar] [CrossRef]
- Om, K.-C.; Ren, G.; Li, S.; Kang-Chol, O. Climatological Characteristics and Long-Term Variation of Rainy Season and Torrential Rain over DPR Korea. Weather Clim. Extrem. 2018, 22, 48–58. [Google Scholar] [CrossRef]
- Oh, J.-H.; Kwon, W.-T.; Ryoo, S.-B. Review of the Researches on Changma and Future Observational Study (KORMEX). Adv. Atmos. Sci. 1997, 14, 207–222. [Google Scholar] [CrossRef]
- Saito, N. Quasi-Stationary Waves in Mid-Latitudes and the Baiu in Japan. J. Meteorol. Soc. Japan. Ser. II 1985, 63, 983–995. [Google Scholar] [CrossRef]
- TAO, S.-Y. A Review of Recent Research on the East Asian Summer Monsoon in China. Monsoon Meteorol. 1987, 60–92. [Google Scholar]
- Chen, G.T.-J. Observational Aspects of the Mei-Yu Phenomenon in Subtropical China. J. Meteorol. Soc. Japan. Ser. II 1983, 61, 306–312. [Google Scholar] [CrossRef]
- Chung, Y.S.; Kim, H.S. Observations on Changes in Korean Changma Rain Associated with Climate Warming in 2017 and 2018. Air Qual. Atmos. Health 2019, 12, 197–215. [Google Scholar] [CrossRef]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global Increasing Trends in Annual Maximum Daily Precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Shepherd, T.G. Attribution of Climate Extreme Events. Nat. Clim. Chang. 2015, 5, 725–730. [Google Scholar] [CrossRef]
- Messner, F.; Meyer, V. Flood Damage, Vulnerability and Risk Perception–Challenges for Flood Damage Research. In Flood Risk Management: Hazards, Vulnerability and Mitigation Measures; Springer: Dordrecht, The Netherlands, 2006; pp. 149–167. [Google Scholar]
- Razavi, S.; Gober, P.; Maier, H.R.; Brouwer, R.; Wheater, H. Anthropocene Flooding: Challenges for Science and Society. Hydrol. Process. 2020, 34. [Google Scholar] [CrossRef]
- Knox, J.C. Large Increases in Flood Magnitude in Response to Modest Changes in Climate. Nature 1993, 361, 430–432. [Google Scholar] [CrossRef]
- Poduje, A.C.C.; Haberlandt, U. Short Time Step Continuous Rainfall Modeling and Simulation of Extreme Events. J. Hydrol. 2017, 552, 182–197. [Google Scholar] [CrossRef]
- Iliadis, C.; Galiatsatou, P.; Glenis, V.; Prinos, P.; Kilsby, C. Urban Flood Modelling under Extreme Rainfall Conditions for Building-Level Flood Exposure Analysis. Hydrology 2023, 10, 172. [Google Scholar] [CrossRef]
- Jun, C.; Qin, X.; Gan, T.Y.; Tung, Y.-K.; De Michele, C. Bivariate Frequency Analysis of Rainfall Intensity and Duration for Urban Stormwater Infrastructure Design. J. Hydrol. 2017, 553, 374–383. [Google Scholar] [CrossRef]
- Li, P.; Yu, Z.; Jiang, P.; Wu, C. Spatiotemporal Characteristics of Regional Extreme Precipitation in Yangtze River Basin. J. Hydrol. 2021, 603, 126910. [Google Scholar] [CrossRef]
- Bowler, N.E.; Pierce, C.E.; Seed, A.W. STEPS: A Probabilistic Precipitation Forecasting Scheme Which Merges an Extrapolation Nowcast with Downscaled NWP. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2006, 132, 2127–2155. [Google Scholar] [CrossRef]
- Sokol, Z. Nowcasting of 1-h Precipitation Using Radar and NWP Data. J. Hydrol. 2006, 328, 200–211. [Google Scholar] [CrossRef]
- Sokol, Z.; Pešice, P. Comparing Nowcastings of Three Severe Convective Events by Statistical and NWP Models. Atmos. Res. 2009, 93, 397–407. [Google Scholar] [CrossRef]
- Huang, L.X.; Isaac, G.A.; Sheng, G. Integrating NWP Forecasts and Observation Data to Improve Nowcasting Accuracy. Weather Forecast. 2012, 27, 938–953. [Google Scholar] [CrossRef]
- Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.M.; Li, P.-W.; Golding, B. Use of NWP for Nowcasting Convective Precipitation: Recent Progress and Challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Buizza, R.; Milleer, M.; Palmer, T.N. Stochastic Representation of Model Uncertainties in the ECMWF Ensemble Prediction System. Q. J. R. Meteorol. Soc. 1999, 125, 2887–2908. [Google Scholar] [CrossRef]
- Demeritt, D.; Cloke, H.; Pappenberger, F.; Thielen, J.; Bartholmes, J.; Ramos, M.-H. Ensemble Predictions and Perceptions of Risk, Uncertainty, and Error in Flood Forecasting. Environ. Hazards 2007, 7, 115–127. [Google Scholar] [CrossRef]
- Cuo, L.; Pagano, T.C.; Wang, Q.J. A Review of Quantitative Precipitation Forecasts and Their Use in Short-to Medium-Range Streamflow Forecasting. J. Hydrometeorol. 2011, 12, 713–728. [Google Scholar] [CrossRef]
- Toth, Z.; Buizza, R. Weather Forecasting: What Sets the Forecast Skill Horizon? In Sub-Seasonal to Seasonal Prediction; Elsevier: Amsterdam, The Netherlands, 2019; pp. 17–45. [Google Scholar]
- Spiridonov, V.; Ćurić, M. Fundamentals of Meteorology; Springer: Cham, Switzerland, 2021; ISBN 3030526542. [Google Scholar]
- Polavarapu, S.; Shepherd, T.G.; Rochon, Y.; Ren, S. Some Challenges of Middle Atmosphere Data Assimilation. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2005, 131, 3513–3527. [Google Scholar] [CrossRef]
- Bock, O.; Nuret, M. Verification of NWP Model Analyses and Radiosonde Humidity Data with GPS Precipitable Water Vapor Estimates during AMMA. Weather Forecast. 2009, 24, 1085–1101. [Google Scholar] [CrossRef]
- Eyre, J.R. Observation Bias Correction Schemes in Data Assimilation Systems: A Theoretical Study of Some of Their Properties. Q. J. R. Meteorol. Soc. 2016, 142, 2284–2291. [Google Scholar] [CrossRef]
- Caya, A.; Sun, J.; Snyder, C. A Comparison between the 4DVAR and the Ensemble Kalman Filter Techniques for Radar Data Assimilation. Mon. Weather Rev. 2005, 133, 3081–3094. [Google Scholar] [CrossRef]
- Sokol, Z.; Pesice, P. Nowcasting of Precipitation–Advective Statistical Forecast Model (SAM) for the Czech Republic. Atmos. Res. 2012, 103, 70–79. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chiang, Y.-M.; Tsai, M.-J.; Shieh, M.-C.; Hsu, K.-L.; Sorooshian, S. Watershed Rainfall Forecasting Using Neuro-Fuzzy Networks with the Assimilation of Multi-Sensor Information. J. Hydrol. 2014, 508, 374–384. [Google Scholar] [CrossRef]
- Liu, Y.; Xi, D.-G.; Li, Z.-L.; Hong, Y. A New Methodology for Pixel-Quantitative Precipitation Nowcasting Using a Pyramid Lucas Kanade Optical Flow Approach. J. Hydrol. 2015, 529, 354–364. [Google Scholar] [CrossRef]
- Austin, G.L.; Bellon, A. The Use of Digital Weather Radar Records for Short-term Precipitation Forecasting. Q. J. R. Meteorol. Soc. 1974, 100, 658–664. [Google Scholar]
- Browning, K.A.; Collier, C. Nowcasting of Precipitation Systems. Rev. Geophys. 1989, 27, 345–370. [Google Scholar] [CrossRef]
- Lin, C.; Vasić, S.; Kilambi, A.; Turner, B.; Zawadzki, I. Precipitation Forecast Skill of Numerical Weather Prediction Models and Radar Nowcasts. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Pierce, C.; Bowler, N.; Seed, A.; Jones, A.; Jones, D.; Moore, R. Use of a Stochastic Precipitation Nowcast Scheme for Fluvial Flood Forecasting and Warning. Atmos. Sci. Lett. 2005, 6, 78–83. [Google Scholar] [CrossRef]
- Turner, B.J.; Zawadzki, I.; Germann, U. Predictability of Precipitation from Continental Radar Images. Part III: Operational Nowcasting Implementation (MAPLE). J. Appl. Meteorol. Climatol. 2004, 43, 231–248. [Google Scholar] [CrossRef]
- Germann, U.; Zawadzki, I. Scale-Dependence of the Predictability of Precipitation from Continental Radar Images. Part I: Description of the Methodology. Mon. Weather Rev. 2002, 130, 2859–2873. [Google Scholar] [CrossRef]
- Ruzanski, E.; Chandrasekar, V. An Investigation of the Short-Term Predictability of Precipitation Using High-Resolution Composite Radar Observations. J. Appl. Meteorol. Climatol. 2012, 51, 912–925. [Google Scholar] [CrossRef]
- Sokol, Z.; Kitzmiller, D.; Pesice, P.; Mejsnar, J. Comparison of Precipitation Nowcasting by Extrapolation and Statistical-Advection Methods. Atmos. Res. 2013, 123, 17–30. [Google Scholar] [CrossRef]
- Wang, C.; Wang, P.; Wang, P.; Xue, B.; Wang, D. Using Conditional Generative Adversarial 3-D Convolutional Neural Network for Precise Radar Extrapolation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5735–5749. [Google Scholar] [CrossRef]
- Zhang, Z.; He, Z.; Yang, J.; Liu, Y.; Bao, R.; Gao, S. A 3-D Storm Motion Estimation Method Based on Point Cloud Learning and Doppler Weather Radar Data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Dixon, M.; Wiener, G. TITAN: Thunderstorm Identification, Tracking, Analysis, and Nowcasting—A Radar-Based Methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Sorooshian, S.; Gao, X. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- Zahraei, A.; Hsu, K.; Sorooshian, S.; Gourley, J.J.; Hong, Y.; Behrangi, A. Short-Term Quantitative Precipitation Forecasting Using an Object-Based Approach. J. Hydrol. 2013, 483, 1–15. [Google Scholar] [CrossRef]
- Matyas, C.J.; Zick, S.E.; Tang, J. Using an Object-Based Approach to Quantify the Spatial Structure of Reflectivity Regions in Hurricane Isabel (2003). Part I: Comparisons between Radar Observations and Model Simulations. Mon. Weather Rev. 2018, 146, 1319–1340. [Google Scholar] [CrossRef]
- Duda, J.D.; Turner, D.D. Large-Sample Application of Radar Reflectivity Object-Based Verification to Evaluate HRRR Warm-Season Forecasts. Weather Forecast. 2021, 36, 805–821. [Google Scholar] [CrossRef]
- Privé, N.C.; Errico, R.M. The Role of Model and Initial Condition Error in Numerical Weather Forecasting Investigated with an Observing System Simulation Experiment. Tellus A Dyn. Meteorol. Oceanogr. 2013, 65, 21740. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Arpe, B.K.; Hollingsworth, A.; Tracton, M.S.; Lorenc, A.C.; Uppala, S.; Kållberg, P. The Response of Numerical Weather Prediction Systems to FGGE Level IIb Data. Part II: Forecast Verifications and Implications for Predictability. Q. J. R. Meteorol. Soc. 1985, 111, 67–101. [Google Scholar] [CrossRef]
- Conway, B.J.; Browning, K.A. Weather Forecasting by Interactive Analysis of Radar and Satellite Imagery. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1988, 324, 299–315. [Google Scholar]
- Pierce, C.E.; Hardaker, P.J.; Collier, C.G.; Haggett, C.M. GANDOLF: A System for Generating Automated Nowcasts of Convective Precipitation. Meteorol. Appl. 2000, 7, 341–360. [Google Scholar] [CrossRef]
- Wong, W.K.; Lai, E.S.T. RAPIDS–Operational Blending of Nowcast and NWP QPF. In Proceedings of the 2nd International Symposium on Quantitative Precipitation Forecasting and Hydrology, Boulder, CO, USA, 4–8 June 2006; pp. 4–8. [Google Scholar]
- Golding, B.W. Nimrod: A System for Generating Automated Very Short Range Forecasts. Meteorol. Appl. 1998, 5, 1–16. [Google Scholar] [CrossRef]
- Wong, W.K.; Yeung, L.H.Y.; Wang, Y.C.; Chen, M. Towards the Blending of NWP with Nowcast—Operation Experience in B08FDP. In Proceedings of the WMO Symposium on Nowcasting, Whistler, BC, Canada, 30 August–4 September 2009; Volume 30, p. 24. [Google Scholar]
- Wilson, J.; Xu, M. Experiments in Blending Radar Echo Extrapolation and NWP for Nowcasting Convective Storms. In Proceedings of the Fourth European Conference on Radar in Meteorology and Hydrology, Barcelona, Spain, 18–22 September 2006; pp. 519–522. [Google Scholar]
- Kober, K.; Craig, G.C.; Keil, C.; Dörnbrack, A. Blending a Probabilistic Nowcasting Method with a High-resolution Numerical Weather Prediction Ensemble for Convective Precipitation Forecasts. Q. J. R. Meteorol. Soc. 2012, 138, 755–768. [Google Scholar] [CrossRef]
- Sokol, Z. Assimilation of Extrapolated Radar Reflectivity into a NWP Model and Its Impact on a Precipitation Forecast at High Resolution. Atmos. Res. 2011, 100, 201–212. [Google Scholar] [CrossRef]
- Radhakrishnan, C.; Chandrasekar, V. CASA Prediction System over Dallas–Fort Worth Urban Network: Blending of Nowcasting and High-Resolution Numerical Weather Prediction Model. J. Atmos. Ocean. Technol. 2020, 37, 211–228. [Google Scholar] [CrossRef]
- Ashesh, A.; Chang, C.-T.; Chen, B.-F.; Lin, H.-T.; Chen, B.; Huang, T.-S. Accurate and Clear Quantitative Precipitation Nowcasting Based on a Deep Learning Model with Consecutive Attention and Rain-Map Discrimination. Artif. Intell. Earth Syst. 2022, 1, e210005. [Google Scholar] [CrossRef]
- Yao, S.; Chen, H.; Thompson, E.J.; Cifelli, R. An Improved Deep Learning Model for High-Impact Weather Nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7400–7413. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, M.; Chen, K.; Xing, L.; Jin, R.; Jordan, M.I.; Wang, J. Skilful Nowcasting of Extreme Precipitation with NowcastNet. Nature 2023, 619, 526–532. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.C.; Lee, Y.H.; Ha, J.-C.; Chang, D.-E.; Bellon, A.; Zawadzki, I.; Lee, G. McGill Algorithm for Precipitation Nowcasting by Lagrangian Extrapolation (MAPLE) Applied to the South Korean Radar Network. Part II: Real-Time Verification for the Summer Season. Asia-Pac. J. Atmos. Sci. 2010, 46, 383–391. [Google Scholar] [CrossRef]
- Chung, K.-S.; Yao, I.-A. Improving Radar Echo Lagrangian Extrapolation Nowcasting by Blending Numerical Model Wind Information: Statistical Performance of 16 Typhoon Cases. Mon. Weather Rev. 2020, 148, 1099–1120. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Kim, J.-B.; Bae, D.-H. Improving Radar-Based Rainfall Forecasts by Long Short-Term Memory Network in Urban Basins. Water 2021, 13, 776. [Google Scholar] [CrossRef]
- Kim, Y.; Hong, S. Very Short-Term Prediction of Weather Radar-Based Rainfall Distribution and Intensity over the Korean Peninsula Using Convolutional Long Short-Term Memory Network. Asia-Pac. J. Atmos. Sci. 2022, 58, 489–506. [Google Scholar] [CrossRef]
- Ahn, M.-H.; Won, H.Y.; Han, D.; Kim, Y.-H.; Ha, J.-C. Characterization of Downwelling Radiance Measured from a Ground-Based Microwave Radiometer Using Numerical Weather Prediction Model Data. Atmos. Meas. Tech. 2016, 9, 281–293. [Google Scholar] [CrossRef]
- Song, H.; Roh, S. Improved Weather Forecasting Using Neural Network Emulation for Radiation Parameterization. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002609. [Google Scholar] [CrossRef]
- Shin, H.-C.; Ha, J.-H.; Ahn, K.D.; Lee, E.H.; Kim, C.H.; Lee, Y.H.; Clayton, A. An Overview of KMA’s Operational NWP Data Assimilation Systems. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. IV); Springer: Cham, Switzerland, 2022; pp. 665–687. [Google Scholar]
- Oh, S.-G.; Son, S.-W.; Kim, Y.-H.; Park, C.; Ko, J.; Shin, K.; Ha, J.-H.; Lee, H. Deep Learning Model for Heavy Rainfall Nowcasting in South Korea. Weather Clim. Extrem. 2024, 44, 100652. [Google Scholar] [CrossRef]
- Kwon, S.; Jung, S.-H.; Lee, G. Inter-Comparison of Radar Rainfall Rate Using Constant Altitude Plan Position Indicator and Hybrid Surface Rainfall Maps. J. Hydrol. 2015, 531, 234–247. [Google Scholar] [CrossRef]
- Kim, Y.; Hong, S. Hypothetical Ground Radar-like Rain Rate Generation of Geostationary Weather Satellite Using Data-to-Data Translation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Song, J.J.; Innerst, M.; Shin, K.; Ye, B.-Y.; Kim, M.; Yeom, D.; Lee, G. Estimation of Precipitation Area Using S-Band Dual-Polarization Radar Measurements. Remote Sens. 2021, 13, 2039. [Google Scholar] [CrossRef]
- So, B.-J.; Kim, H.-S.; Kwon, H.-H. Spatial Pattern of Bias in Areal Rainfall Estimations and Its Impact on Hydrological Modeling: A Comparative Analysis of Estimating Areal Rainfall Based on Radar and Weather Station Networks in South Korea. Stoch. Environ. Res. Risk Assess. 2024, 38, 2797–2813. [Google Scholar] [CrossRef]
- Laroche, S.; Zawadzki, I. Retrievals of Horizontal Winds from Single-Doppler Clear-Air Data by Methods of Cross Correlation and Variational Analysis. J. Atmos. Ocean. Technol. 1995, 12, 721–738. [Google Scholar] [CrossRef]
- Bellon, A.; Zawadzki, I.; Kilambi, A.; Lee, H.C.; Lee, Y.H.; Lee, G. McGill Algorithm for Precipitation Nowcasting by Lagrangian Extrapolation (MAPLE) Applied to the South Korean Radar Network. Part I: Sensitivity Studies of the Variational Echo Tracking (VET) Technique. Asia-Pac. J. Atmos. Sci. 2010, 46, 369–381. [Google Scholar] [CrossRef]
- Albers, S.C. The LAPS Wind Analysis. Weather Forecast. 1995, 10, 342–352. [Google Scholar] [CrossRef]
- Albers, S.C.; McGinley, J.A.; Birkenheuer, D.L.; Smart, J.R. The Local Analysis and Prediction System (LAPS): Analyses of Clouds, Precipitation, and Temperature. Weather Forecast. 1996, 11, 273–287. [Google Scholar] [CrossRef]
- Hiemstra, C.A.; Liston, G.E.; Pielke, R.A.; Birkenheuer, D.L.; Albers, S.C. Comparing Local Analysis and Prediction System (LAPS) Assimilations with Independent Observations. Weather Forecast. 2006, 21, 1024–1040. [Google Scholar] [CrossRef]
- Song, H.-J.; Roh, S. Impact of Horizontal Resolution on the Robustness of Radiation Emulators in a Numerical Weather Prediction Model. Remote Sens. 2023, 15, 2637. [Google Scholar] [CrossRef]
- He, Z.; Xie, Y.; Li, W.; Li, D.; Han, G.; Liu, K.; Ma, J. Application of the Sequential Three-Dimensional Variational Method to Assimilating SST in a Global Ocean Model. J. Atmos. Ocean. Technol. 2008, 25, 1018–1033. [Google Scholar] [CrossRef]
- Lyu, G.; Jung, S.-H.; Nam, K.-Y.; Kwon, S.; Lee, C.-R.; Lee, G. Improvement of Radar Rainfall Estimation Using Radar Reflectivity Data from the Hybrid Lowest Elevation Angles. J. Korean Earth Sci. Soc. 2015, 36, 109–124. [Google Scholar] [CrossRef]
- Choi, Y.; Cha, K.; Back, M.; Choi, H.; Jeon, T. RAIN-F+: The Data-Driven Precipitation Prediction Model for Integrated Weather Observations. Remote Sens. 2021, 13, 3627. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Anagnostou, M.N.; Krajewski, W.F.; Kruger, A.; Miriovsky, B.J. High-Resolution Rainfall Estimation from X-Band Polarimetric Radar Measurements. J. Hydrometeorol. 2004, 5, 110–128. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Review of the Different Sources of Uncertainty in Single Polarization Radar-Based Estimates of Rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The Distribution of Raindrops with Size. J. Atmos. Sci. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Zhang, G.; Vivekanandan, J.; Brandes, E. A Method for Estimating Rain Rate and Drop Size Distribution from Polarimetric Radar Measurements. IEEE Trans. Geosci. Remote Sens. 2001, 39, 830–841. [Google Scholar] [CrossRef]
- Chen, B.; Yang, J.; Pu, J. Statistical Characteristics of Raindrop Size Distribution in the Meiyu Season Observed in Eastern China. J. Meteorol. Soc. Japan. Ser. II 2013, 91, 215–227. [Google Scholar] [CrossRef]
- Kim, H.-J.; Lee, K.-O.; You, C.-H.; Uyeda, H.; Lee, D.-I. Microphysical Characteristics of a Convective Precipitation System Observed on July 04, 2012, over Mt. Halla in South Korea. Atmos. Res. 2019, 222, 74–87. [Google Scholar] [CrossRef]
- Yoo, C.; Yoon, J.; Kim, J.; Ro, Y. Evaluation of the Gap Filler Radar as an Implementation of the 1.5 Km CAPPI Data in Korea. Meteorol. Appl. 2016, 23, 76–88. [Google Scholar] [CrossRef]
- Aghdaii, N.; Younesy, H.; Zhang, H. 5–6–7 Meshes: Remeshing and Analysis. Comput. Graph. 2012, 36, 1072–1083. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A. Quantitative Assessment of Short-term Rainfall Forecasts from Radar Nowcasts and MM5 Forecasts. Hydrol. Process. 2012, 26, 3842–3857. [Google Scholar] [CrossRef]
- Valldecabres, L.; Nygaard, N.G.; Vera-Tudela, L.; Von Bremen, L.; Kühn, M. On the Use of Dual-Doppler Radar Measurements for Very Short-Term Wind Power Forecasts. Remote Sens. 2018, 10, 1701. [Google Scholar] [CrossRef]
- Prudden, R.; Adams, S.; Kangin, D.; Robinson, N.; Ravuri, S.; Mohamed, S.; Arribas, A. A Review of Radar-Based Nowcasting of Precipitation and Applicable Machine Learning Techniques. arXiv 2020, arXiv:2005.04988. [Google Scholar]
- Stern, H.; Davidson, N.E. Trends in the Skill of Weather Prediction at Lead Times of 1–14 Days. Q. J. R. Meteorol. Soc. 2015, 141, 2726–2736. [Google Scholar] [CrossRef]
- Wang, G.; Wang, D.; Yang, J.; Liu, L. Evaluation and Correction of Quantitative Precipitation Forecast by Storm-Scale NWP Model in Jiangsu, China. Adv. Meteorol. 2016, 2016, 8476720. [Google Scholar] [CrossRef]
- Giebel, G.; Kariniotakis, G. Wind Power Forecasting—A Review of the State of the Art. Renew. Energy Forecast. 2017, 59–109. [Google Scholar] [CrossRef]
- Austin, G.L.; Bellon, A.; Dionne, P.; Roch, M. On the Interaction between Radar and Satellite Image Nowcasting Systems and Mesoscale Numerical Models. In Proceedings of the Mesoscale Analysis and Forecasting, Vancouver, BC, Canada, 17–19 August 1987; pp. 225–228. [Google Scholar]
- Wilson, J.W.; Crook, N.A.; Mueller, C.K.; Sun, J.; Dixon, M. Nowcasting Thunderstorms: A Status Report. Bull. Am. Meteorol. Soc. 1998, 79, 2079–2100. [Google Scholar] [CrossRef]
- Zahraei, A.; Hsu, K.; Sorooshian, S.; Gourley, J.J.; Lakshmanan, V.; Hong, Y.; Bellerby, T. Quantitative Precipitation Nowcasting: A Lagrangian Pixel-Based Approach. Atmos. Res. 2012, 118, 418–434. [Google Scholar] [CrossRef]
- Ganguly, A.R.; Bras, R.L. Distributed Quantitative Precipitation Forecasting Using Information from Radar and Numerical Weather Prediction Models. J. Hydrometeorol. 2003, 4, 1168–1180. [Google Scholar] [CrossRef]
- Haiden, T.; Kann, A.; Wittmann, C.; Pistotnik, G.; Bica, B.; Gruber, C. The Integrated Nowcasting through Comprehensive Analysis (INCA) System and Its Validation over the Eastern Alpine Region. Weather Forecast. 2011, 26, 166–183. [Google Scholar] [CrossRef]
- Isaac, G.A.; Joe, P.I.; Mailhot, J.; Bailey, M.; Bélair, S.; Boudala, F.S.; Brugman, M.; Campos, E.; Carpenter, R.L.; Crawford, R.W. Science of Nowcasting Olympic Weather for Vancouver 2010 (SNOW-V10): A World Weather Research Programme Project. Pure Appl. Geophys. 2014, 171, 1–24. [Google Scholar] [CrossRef]
- Gultepe, I.; Sharman, R.; Williams, P.D.; Zhou, B.; Ellrod, G.; Minnis, P.; Trier, S.; Griffin, S.; Yum, S.S.; Gharabaghi, B. A Review of High Impact Weather for Aviation Meteorology. Pure Appl. Geophys. 2019, 176, 1869–1921. [Google Scholar] [CrossRef]
- Wolfson, M.M.; Dupree, W.J.; Rasmussen, R.M.; Steiner, M.; Benjamin, S.G.; Weygandt, S.S. Consolidated Storm Prediction for Aviation (CoSPA). In Proceedings of the 2008 Integrated Communications, Navigation and Surveillance Conference, Bethesda, MD, USA, 5–7 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–19. [Google Scholar]
- Yang, D.; Shen, S.; Shao, L. A Study on Blending Radar and Numerical Weather Prediction Model Products in Very Short-Range Forecast and Nowcasting. In Proceedings of the MIPPR 2009: Remote Sensing and GIS Data Processing and Other Applications, Yichang, China, 30 October–1 November 2009; SPIE: Bellingham, WA, USA, 2009; Volume 7498, pp. 595–602. [Google Scholar]
- Wang, G.; Wong, W.-K.; Hong, Y.; Liu, L.; Dong, J.; Xue, M. Improvement of Forecast Skill for Severe Weather by Merging Radar-Based Extrapolation and Storm-Scale NWP Corrected Forecast. Atmos. Res. 2015, 154, 14–24. [Google Scholar] [CrossRef]
- Elfwing, S.; Uchibe, E.; Doya, K. Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning. Neural Netw. 2018, 107, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Daunizeau, J. Semi-Analytical Approximations to Statistical Moments of Sigmoid and Softmax Mappings of Normal Variables. arXiv 2017, arXiv:1703.00091. [Google Scholar]
- Sharma, N.; Singh, M.K.; Low, S.Y.; Kumar, A. Weighted Sigmoid-Based Frequency-Selective Noise Filtering for Speech Denoising. Circuits Syst. Signal Process. 2021, 40, 276–295. [Google Scholar] [CrossRef]
- Mason, I. A Model for Assessment of Weather Forecasts. Aust. Meteor. Mag. 1982, 30, 291–303. [Google Scholar]
- Gelpi, I.R.; Gaztelumendi, S.; Carreño, S.; Hernández, R.; Egaña, J. Study of NWP Parameterizations on Extreme Precipitation Events over Basque Country. Adv. Sci. Res. 2016, 13, 137–144. [Google Scholar] [CrossRef]
- Done, J.; Davis, C.A.; Weisman, M. The next Generation of NWP: Explicit Forecasts of Convection Using the Weather Research and Forecasting (WRF) Model. Atmos. Sci. Lett. 2004, 5, 110–117. [Google Scholar] [CrossRef]
- Ghelli, A.; Primo, C. On the Use of the Extreme Dependency Score to Investigate the Performance of an NWP Model for Rare Events. Meteorol. Appl. A J. Forecast. Pract. Appl. Train. Tech. Model. 2009, 16, 537–544. [Google Scholar] [CrossRef]
- Ebert, E.E. Fuzzy Verification of High-resolution Gridded Forecasts: A Review and Proposed Framework. Meteorol. Appl. A J. Forecast. Pract. Appl. Train. Tech. Model. 2008, 15, 51–64. [Google Scholar] [CrossRef]
- Gold, S.; White, E.; Roeder, W.; McAleenan, M.; Kabban, C.S.; Ahner, D. Probabilistic Contingency Tables: An Improvement to Verify Probability Forecasts. Weather Forecast. 2020, 35, 609–621. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Mehran, A. Extended Contingency Table: Performance Metrics for Satellite Observations and Climate Model Simulations. Water Resour. Res. 2013, 49, 7144–7149. [Google Scholar] [CrossRef]
- Madrigal, J.; Solera, A.; Suárez-Almiñana, S.; Paredes-Arquiola, J.; Andreu, J.; Sanchez-Quispe, S.T. Skill Assessment of a Seasonal Forecast Model to Predict Drought Events for Water Resource Systems. J. Hydrol. 2018, 564, 574–587. [Google Scholar] [CrossRef]
- Colli, M.; Lanza, L.G.; La Barbera, P.; Chan, P.W. Measurement Accuracy of Weighing and Tipping-Bucket Rainfall Intensity Gauges under Dynamic Laboratory Testing. Atmos. Res. 2014, 144, 186–194. [Google Scholar] [CrossRef]
- Saha, R.; Testik, F.Y.; Testik, M.C. Assessment of OTT Pluvio 2 Rain Intensity Measurements. J. Atmos. Ocean. Technol. 2021, 38, 897–908. [Google Scholar] [CrossRef]
- Krüger, R.; Karrasch, P.; Eltner, A. Calibrating Low-Cost Rain Gauge Sensors for Their Applications in Internet of Things (IoT) Infrastructures to Densify Environmental Monitoring Networks. Geosci. Instrum. Methods Data Syst. 2024, 13, 163–176. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100, ISBN 0123850223. [Google Scholar]
- Andronache, C. Estimated Variability of Below-Cloud Aerosol Removal by Rainfall for Observed Aerosol Size Distributions. Atmos. Chem. Phys. 2003, 3, 131–143. [Google Scholar] [CrossRef]
- Kwarteng, A.Y.; Dorvlo, A.S.; Vijaya Kumar, G.T. Analysis of a 27-Year Rainfall Data (1977–2003) in the Sultanate of Oman. Int. J. Climatol. 2009, 29, 605. [Google Scholar] [CrossRef]
- Guo, Y.; Shao, C.; Su, A. Comparative Evaluation of Rainfall Forecasts during the Summer of 2020 over Central East China. Atmosphere 2023, 14, 992. [Google Scholar] [CrossRef]
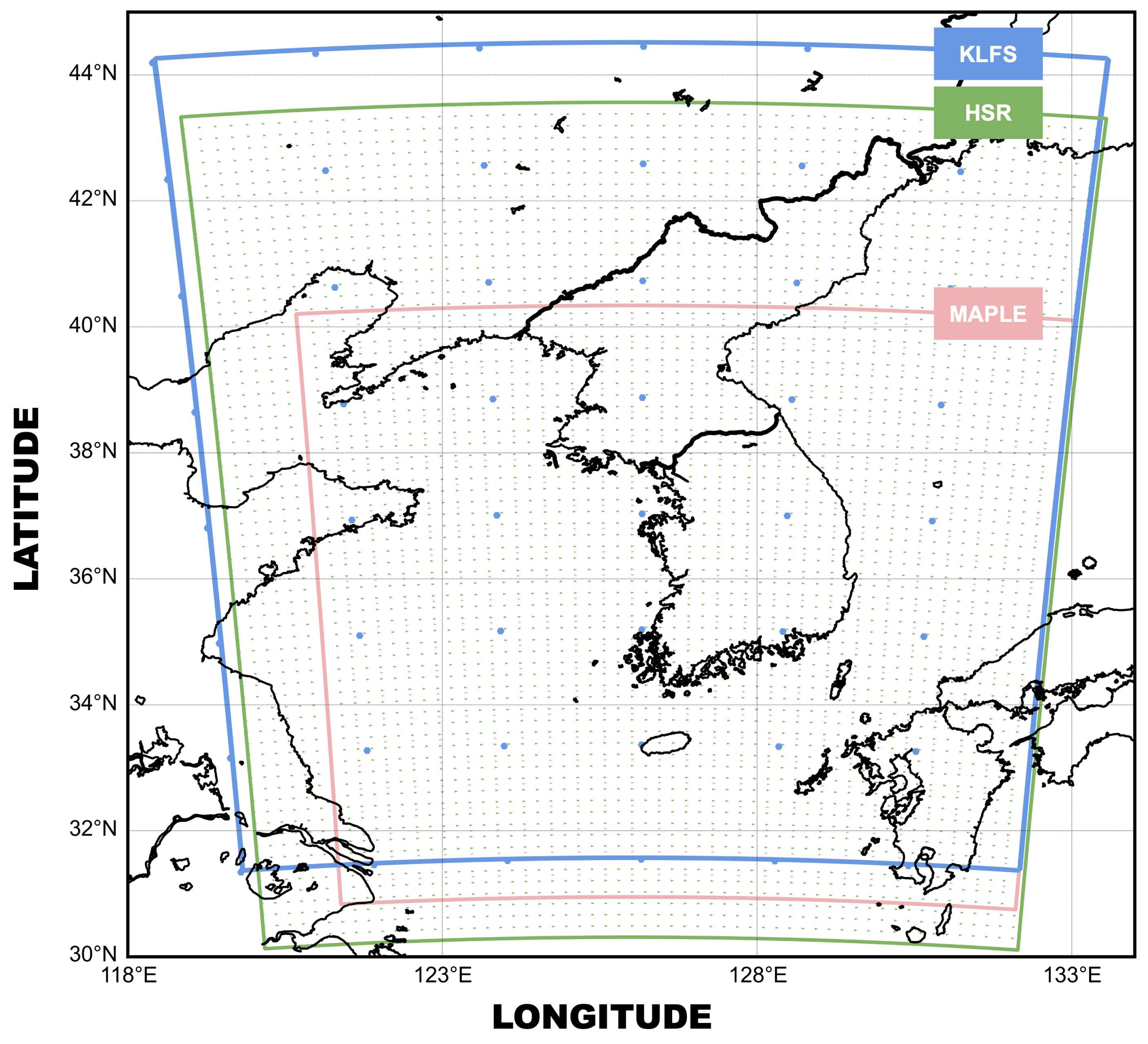



| Dataset | Number of Grids | Spatial Resolution | Temporal Resolution | Forecast Lead Time |
|---|---|---|---|---|
| MAPLE | 1024 × 1024 | 1 km | 10 min | 6 h |
| KLFS | 234 × 282 | 5 km | 1 h | 12 h |
| HSR | 2305 × 2881 | 0.5 km | 5 min | - |
| Weight Function | Rainfall Event | Parameter Quartile | |||||
|---|---|---|---|---|---|---|---|
| Q1 (25%) | Q2 (50%) | Q3 (75%) | |||||
| a | b | a | b | a | b | ||
| SIN | Event 1 | −0.314 | 2.827 | 0.314 | 14.451 | 0.314 | 96.133 |
| Event 2 | −0.314 | 0.340 | 0.031 | 16.000 | 0.314 | 64.560 | |
| Event 3 | 0.185 | 0.000 | 0.314 | 7.728 | 0.314 | 16.022 | |
| HTN | Event 1 | 5.221 | 3.539 | 5.565 | 3.968 | 5.949 | 4.053 |
| Event 2 | 5.501 | 3.957 | 5.689 | 4.020 | 6.024 | 4.059 | |
| Event 3 | 5.332 | 3.028 | 5.667 | 3.924 | 6.156 | 4.000 | |
| SIG | Event 1 | 1.000 | 3.572 | 1.000 | 4.650 | 1.000 | 5.602 |
| Event 2 | 1.000 | 4.757 | 1.000 | 5.475 | 1.000 | 5.982 | |
| Event 3 | 1.000 | 2.885 | 1.000 | 3.696 | 1.000 | 4.833 | |
| Rainfall Event | Data Type | Forecast Lead Time | |||||
|---|---|---|---|---|---|---|---|
| 1 h | 2 h | 3 h | 4 h | 5 h | 6 h | ||
| Event 1 | Blending | 12.064 | 14.915 | 14.231 | 13.283 | 12.687 | 12.329 |
| W* | 11.431 | 13.881 | 14.608 | 13.864 | 14.798 | 14.703 | |
| KLFS | 12.623 | 14.078 | 14.925 | 14.345 | 14.901 | 15.234 | |
| MAPLE | 11.869 | 13.457 | 13.723 | 14.867 | 14.590 | 15.205 | |
| Event 2 | Blending | 11.436 | 14.299 | 12.126 | 12.043 | 11.638 | 13.770 |
| W* | 11.944 | 14.466 | 15.552 | 11.790 | 13.388 | 13.220 | |
| KLFS | 12.554 | 14.706 | 16.319 | 15.207 | 15.078 | 14.210 | |
| MAPLE | 12.428 | 13.414 | 14.654 | 15.332 | 15.561 | 15.132 | |
| Event 3 | Blending | 11.436 | 14.299 | 12.126 | 12.043 | 11.638 | 13.770 |
| W* | 11.362 | 15.565 | 15.609 | 14.083 | 12.052 | 16.539 | |
| KLFS | 11.981 | 14.581 | 14.966 | 14.169 | 15.053 | 14.745 | |
| MAPLE | 12.057 | 14.449 | 15.446 | 15.558 | 15.139 | 14.764 | |
| Total | Blending | 11.524 | 14.885 | 13.788 | 12.974 | 12.052 | 12.974 |
| W* | 11.838 | 14.413 | 14.932 | 13.864 | 14.232 | 14.703 | |
| KLFS | 12.323 | 14.525 | 15.523 | 15.094 | 15.028 | 14.764 | |
| MAPLE | 12.033 | 14.001 | 14.324 | 15.197 | 15.249 | 15.286 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Byun, J.; Kim, H.-J.; Kang, N.; Yoon, J.; Hwang, S.; Jun, C. Optimizing Temporal Weighting Functions to Improve Rainfall Prediction Accuracy in Merged Numerical Weather Prediction Models for the Korean Peninsula. Remote Sens. 2024, 16, 2904. https://doi.org/10.3390/rs16162904
Byun J, Kim H-J, Kang N, Yoon J, Hwang S, Jun C. Optimizing Temporal Weighting Functions to Improve Rainfall Prediction Accuracy in Merged Numerical Weather Prediction Models for the Korean Peninsula. Remote Sensing. 2024; 16(16):2904. https://doi.org/10.3390/rs16162904
Chicago/Turabian StyleByun, Jongyun, Hyeon-Joon Kim, Narae Kang, Jungsoo Yoon, Seokhwan Hwang, and Changhyun Jun. 2024. "Optimizing Temporal Weighting Functions to Improve Rainfall Prediction Accuracy in Merged Numerical Weather Prediction Models for the Korean Peninsula" Remote Sensing 16, no. 16: 2904. https://doi.org/10.3390/rs16162904
APA StyleByun, J., Kim, H.-J., Kang, N., Yoon, J., Hwang, S., & Jun, C. (2024). Optimizing Temporal Weighting Functions to Improve Rainfall Prediction Accuracy in Merged Numerical Weather Prediction Models for the Korean Peninsula. Remote Sensing, 16(16), 2904. https://doi.org/10.3390/rs16162904











