Temporal Transferability of Tree Species Classification in Temperate Forests with Sentinel-2 Time Series
Abstract
1. Introduction
- (1)
- What is the predictive performance of models based on the spectral information of a single year?
- (2)
- How does the predictive performance of models change when a model trained on a single year is applied to the spectral information of another year?
- (3)
- What is the impact of multi-year training data on temporal transferability?
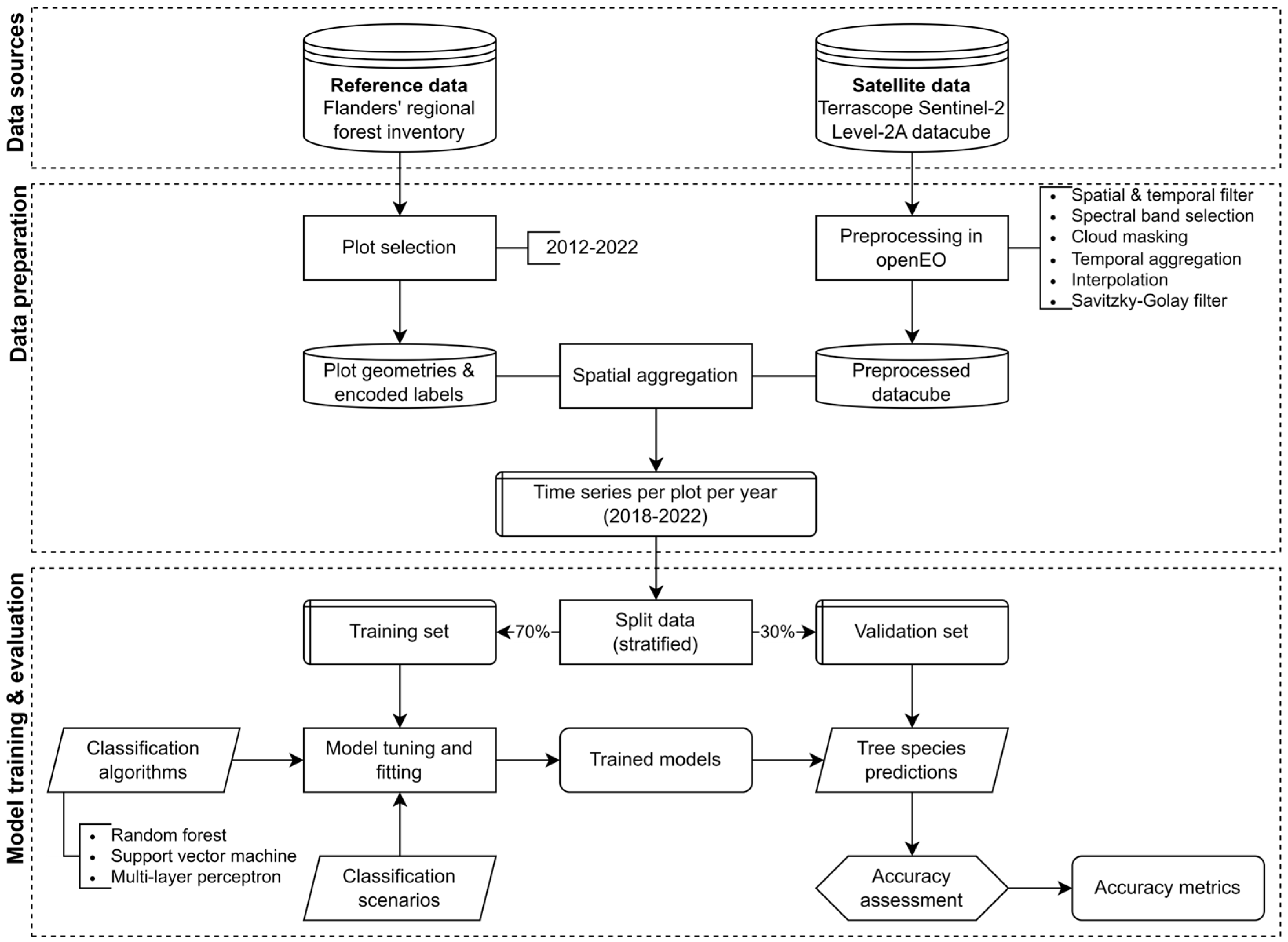
2. Methodology
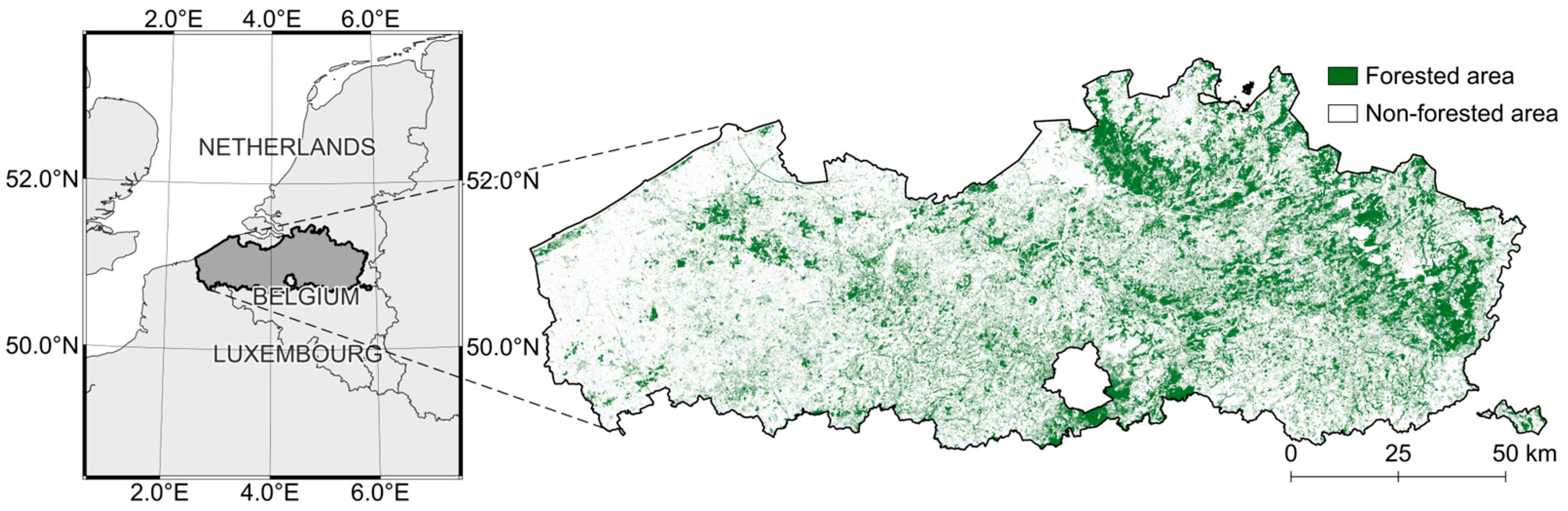
2.1. Study Area
2.2. Data Sources and Data Preparation
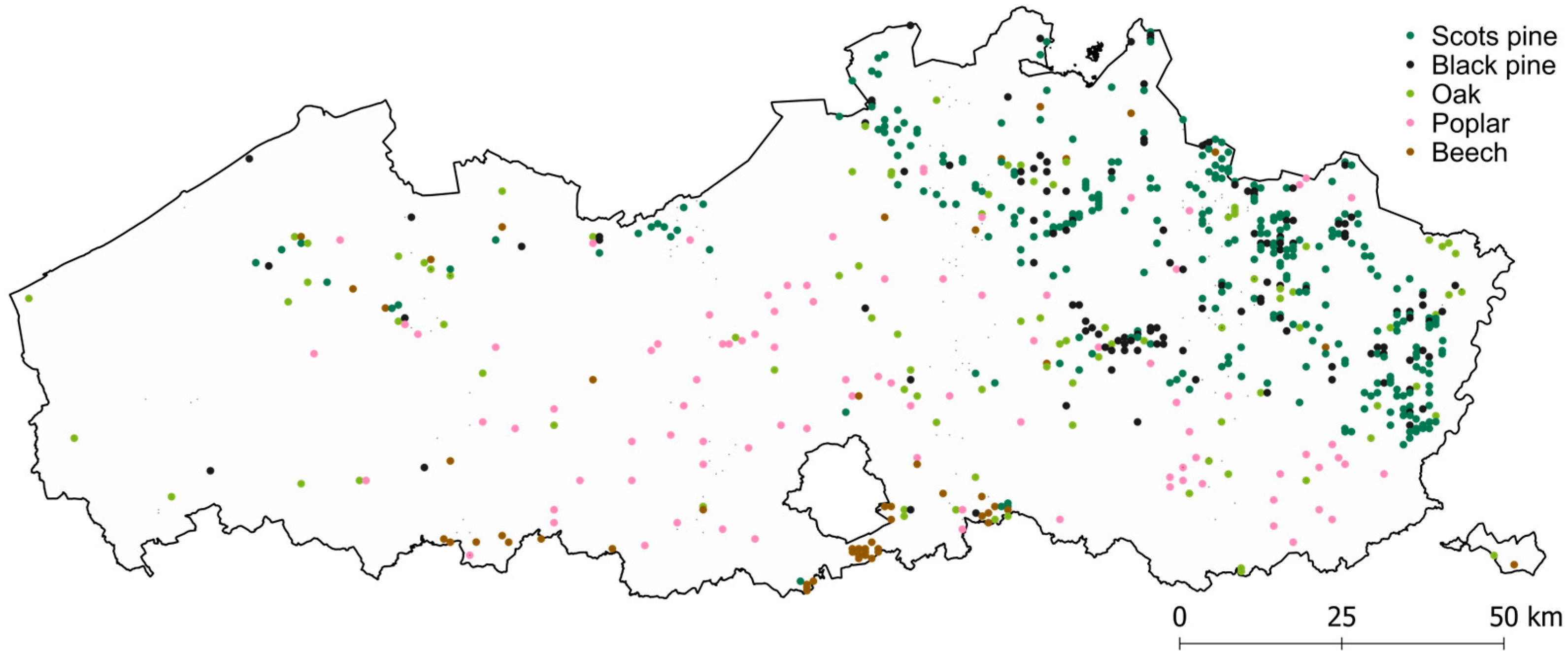
2.2.1. Reference Data
2.2.2. Satellite Data
2.3. Model Training and Evaluation
2.3.1. Classification Algorithms
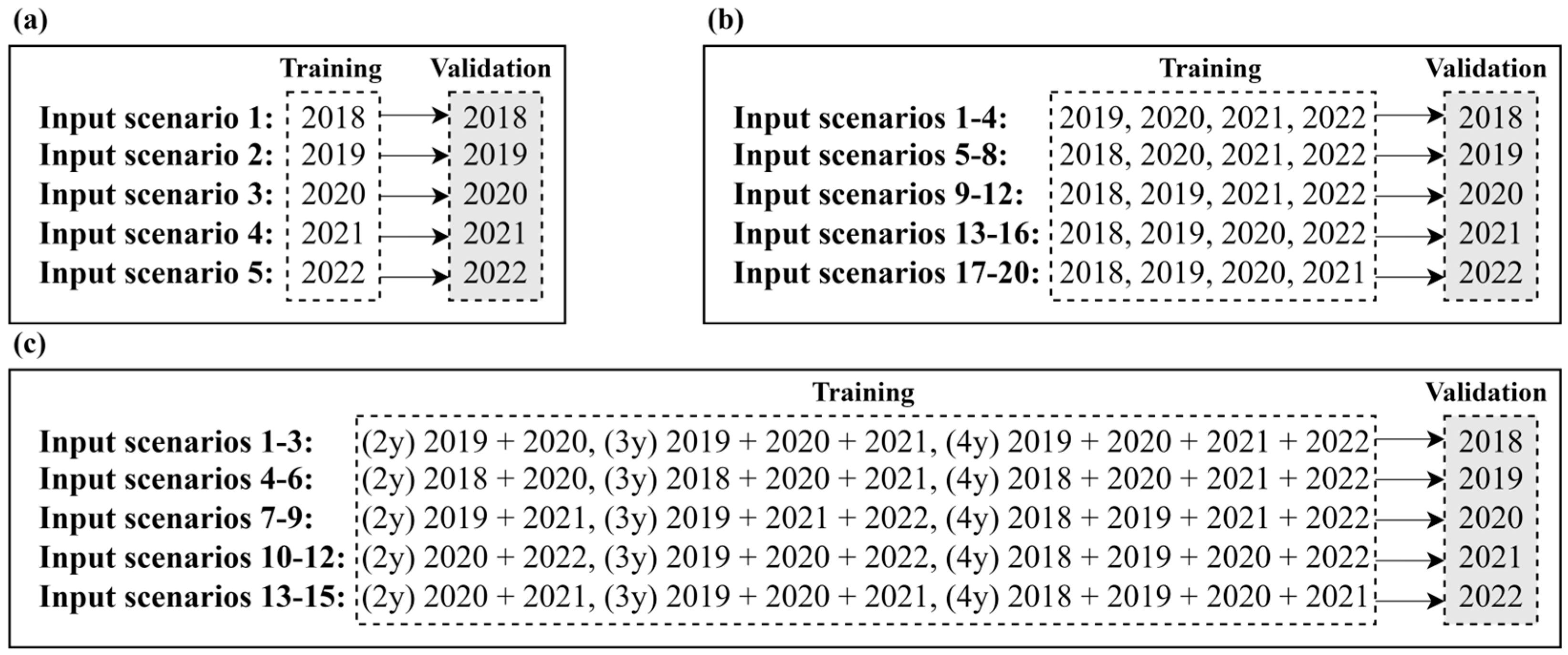
2.3.2. Training and Validation Sampling Design
2.3.3. Tree Species Classification
2.3.4. Accuracy Assessment
3. Results
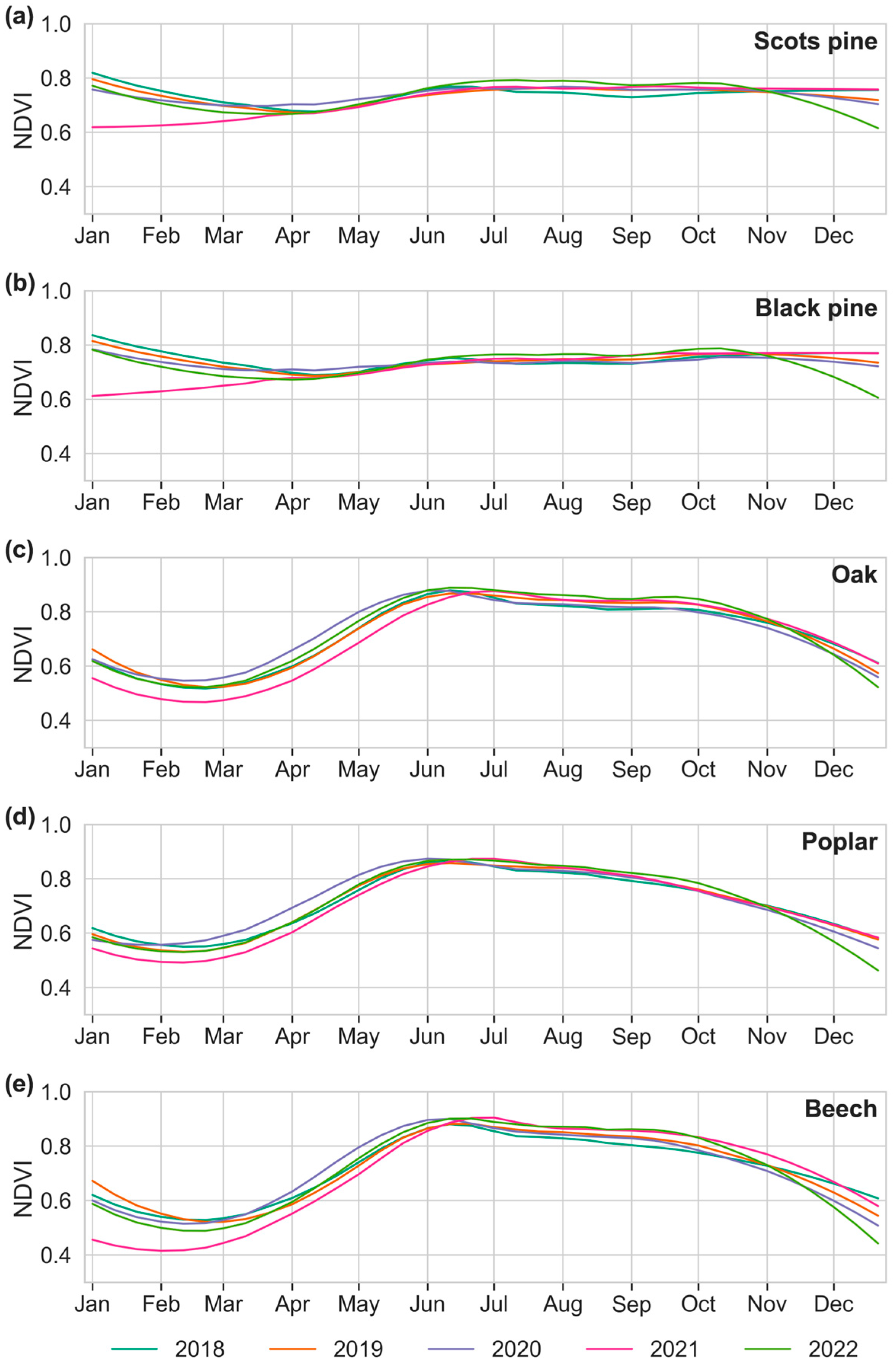
3.1. Species-Specific Phenology
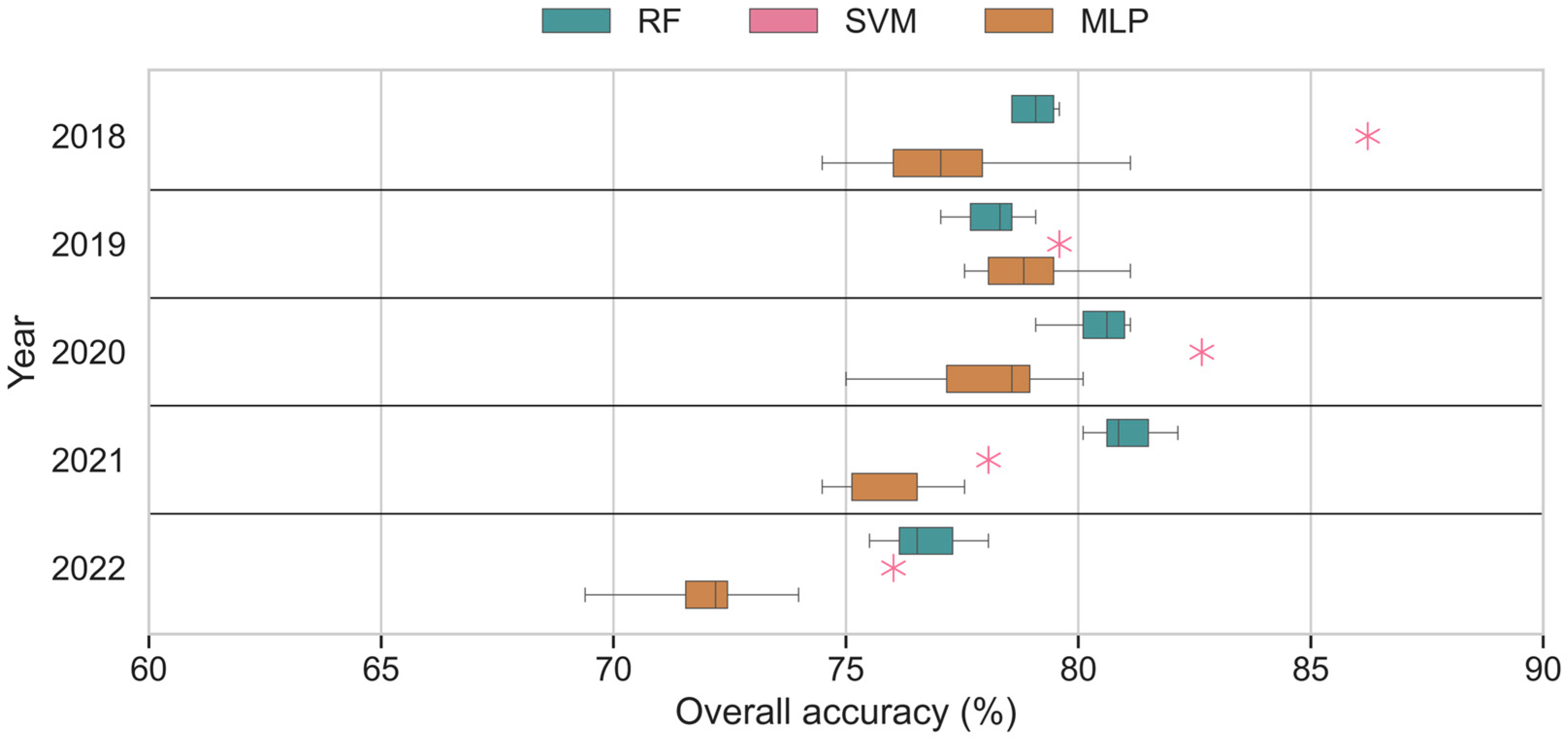
3.2. Same-Year Single-Year Input Scenarios
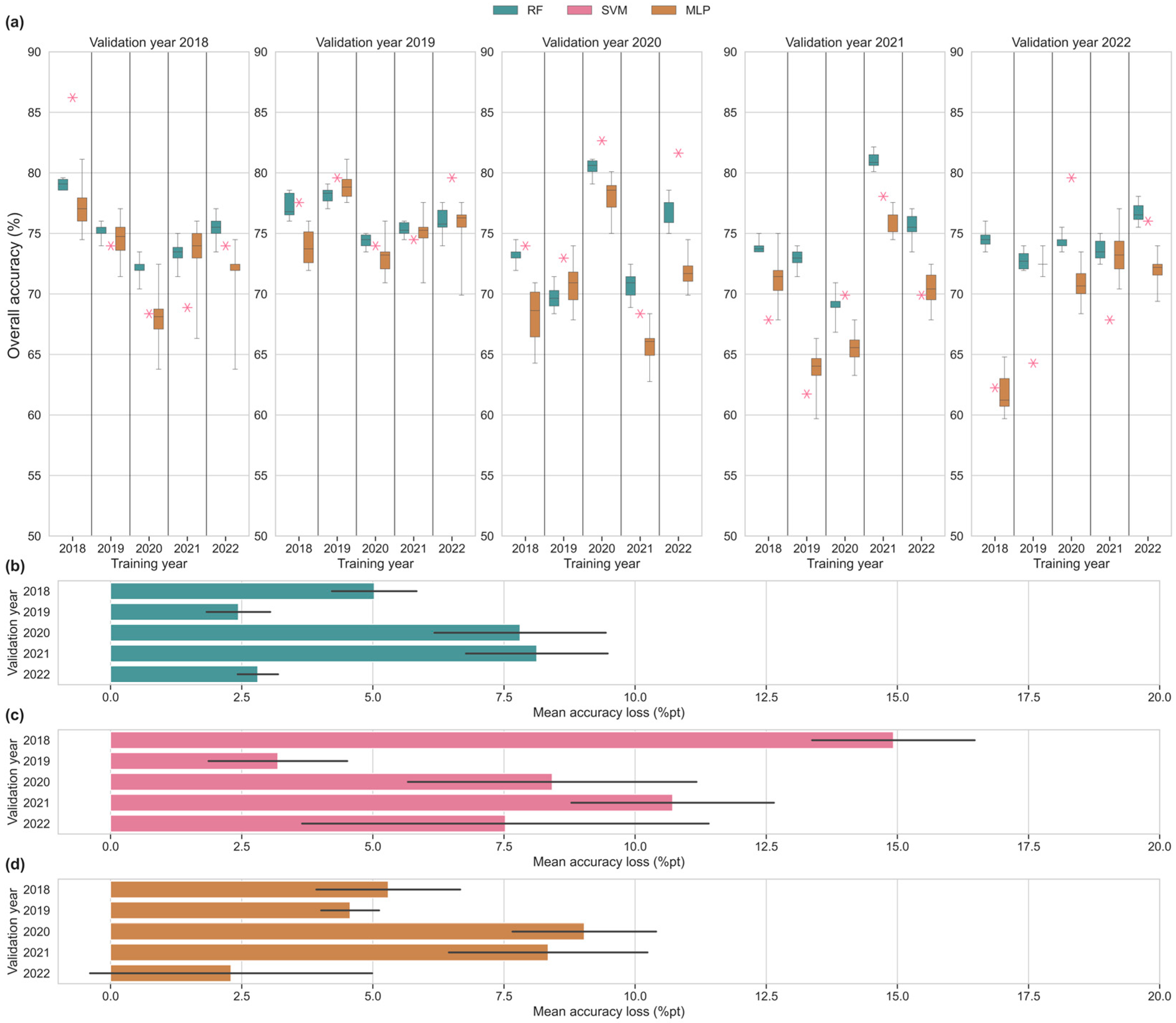
3.3. Cross-Year Single-Year Input Scenarios
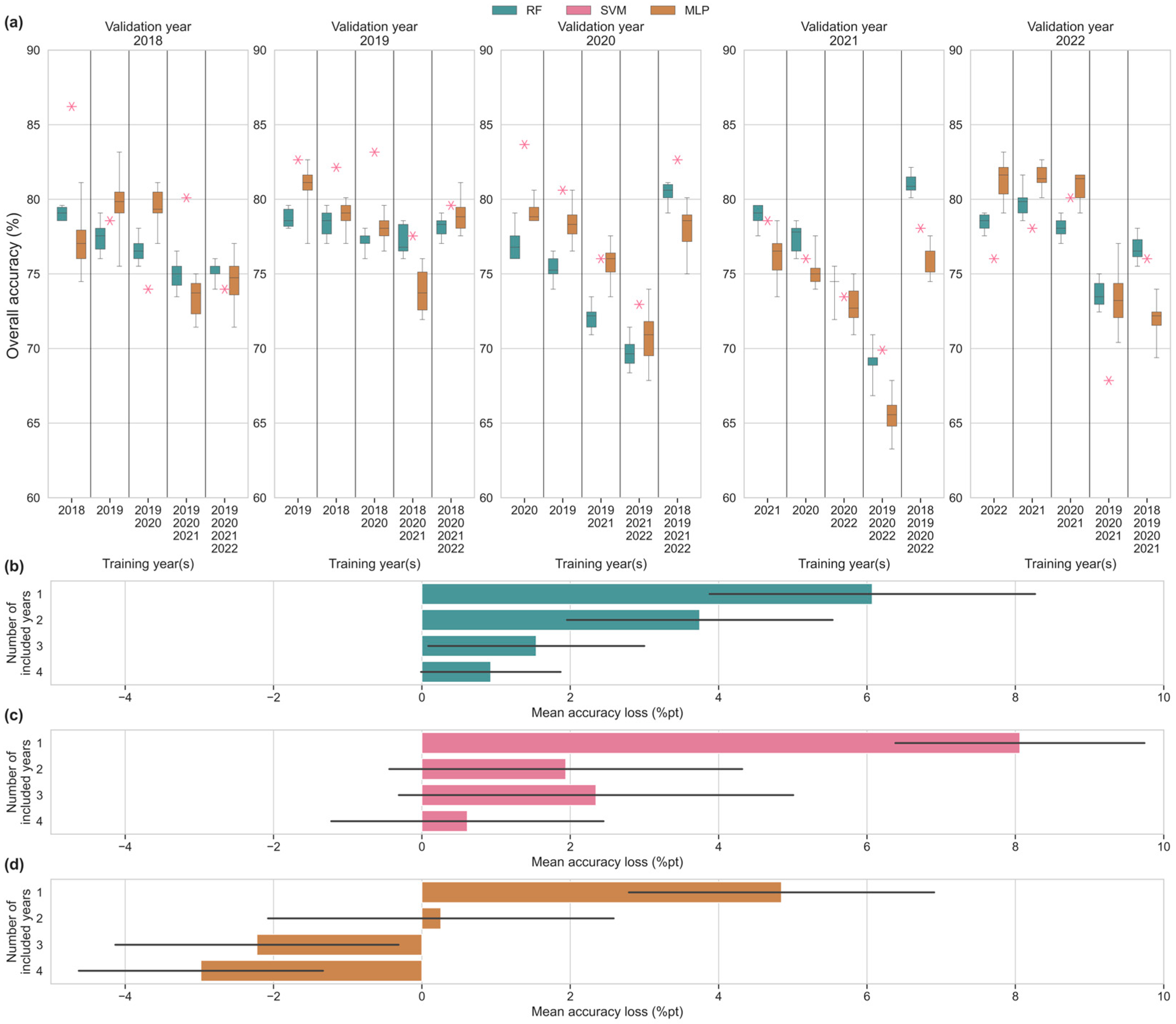
3.4. Multi-Year Input Scenarios
4. Discussion
4.1. Baseline Model Performances
4.2. Assessment of Temporal Transferability
4.3. Impact Multi-Year Training Data
4.4. Data Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brockerhoff, E.G.; Barbaro, L.; Castagneyrol, B.; Forrester, D.I.; Gardiner, B.; González-Olabarria, J.R.; Lyver, P.O.B.; Meurisse, N.; Oxbrough, A.; Taki, H.; et al. Forest Biodiversity, Ecosystem Functioning and the Provision of Ecosystem Services. Biodivers. Conserv. 2017, 26, 3005–3035. [Google Scholar] [CrossRef]
- Gamfeldt, L.; Snäll, T.; Bagchi, R.; Jonsson, M.; Gustafsson, L.; Kjellander, P.; Ruiz-Jaen, M.C.; Fröberg, M.; Stendahl, J.; Philipson, C.D.; et al. Higher Levels of Multiple Ecosystem Services Are Found in Forests with More Tree Species. Nat. Commun. 2013, 4, 1340. [Google Scholar] [CrossRef] [PubMed]
- Rogers, P.C. Disturbance Ecology; Wohlgemuth, T., Jentsch, A., Seidl, R., Eds.; Landscape Series; Springer: Cham, Switzerland, 2022; Volume 32, ISBN 978-3-030-98755-8. [Google Scholar]
- Boisvenue, C.; White, J. Information Needs of Next-Generation Forest Carbon Models: Opportunities for Remote Sensing Science. Remote Sens. 2019, 11, 463. [Google Scholar] [CrossRef]
- Shaw, C.H.; Bona, K.A.; Kurz, W.A.; Fyles, J.W. The Importance of Tree Species and Soil Taxonomy to Modeling Forest Soil Carbon Stocks in Canada. Geoderma Reg. 2015, 4, 114–125. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of Studies on Tree Species Classification from Remotely Sensed Data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Pu, R. Mapping Tree Species Using Advanced Remote Sensing Technologies: A State-of-the-Art Review and Perspective. J. Remote Sens. 2021, 2021, 9812624. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree Species Classification with Random Forest Using Very High Spatial Resolution 8-Band WorldView-2 Satellite Data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers. Remote Sens. 2016, 8, 445. [Google Scholar] [CrossRef]
- Dalponte, M.; Orka, H.O.; Gobakken, T.; Gianelle, D.; Naesset, E. Tree Species Classification in Boreal Forests with Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2632–2645. [Google Scholar] [CrossRef]
- Michałowska, M.; Rapiński, J. A Review of Tree Species Classification Based on Airborne LiDAR Data and Applied Classifiers. Remote Sens. 2021, 13, 353. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Ørka, H.O.; Hauglin, M. Use of Remote Sensing for Mapping of Non-Native Conifer Species. Ina Fagrapp. 2016, 33, 1–76. [Google Scholar]
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free Access to Landsat Imagery. Science 2008, 320, 1011. [Google Scholar] [CrossRef] [PubMed]
- Aschbacher, J.; Milagro-Pérez, M.P. The European Earth Monitoring (GMES) Programme: Status and Perspectives. Remote Sens. Environ. 2012, 120, 3–8. [Google Scholar] [CrossRef]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First Experience with Sentinel-2 Data for Crop and Tree Species Classifications in Central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Neumann, C.; Forster, M.; Buddenbaum, H.; Ghosh, A.; Clasen, A.; Joshi, P.K.; Koch, B. Comparison of Feature Reduction Algorithms for Classifying Tree Species with Hyperspectral Data on Three Central European Test Sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2547–2561. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree Species Classification in the Southern Alps Based on the Fusion of Very High Geometrical Resolution Multispectral/Hyperspectral Images and LiDAR Data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
- Heikkinen, V.; Tokola, T.; Parkkinen, J.; Korpela, I.; Jaaskelainen, T. Simulated Multispectral Imagery for Tree Species Classification Using Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1355–1364. [Google Scholar] [CrossRef]
- Bolyn, C.; Michez, A.; Gaucher, P.; Lejeune, P.; Bonnet, S. Forest Mapping and Species Composition Using Supervised per Pixel Classification of Sentinel-2 Imagery. BASE 2018, 22, 172–187. [Google Scholar] [CrossRef]
- Breidenbach, J.; Waser, L.T.; Debella-Gilo, M.; Schumacher, J.; Rahlf, J.; Hauglin, M.; Puliti, S.; Astrup, R. National Mapping and Estimation of Forest Area by Dominant Tree Species Using Sentinel-2 Data. Can. J. For. Res. 2021, 51, 365–379. [Google Scholar] [CrossRef]
- Wessel, M.; Brandmeier, M.; Tiede, D. Evaluation of Different Machine Learning Algorithms for Scalable Classification of Tree Types and Tree Species Based on Sentinel-2 Data. Remote Sens. 2018, 10, 1419. [Google Scholar] [CrossRef]
- Grabska, E.; Frantz, D.; Ostapowicz, K. Evaluation of Machine Learning Algorithms for Forest Stand Species Mapping Using Sentinel-2 Imagery and Environmental Data in the Polish Carpathians. Remote Sens. Environ. 2020, 251, 112103. [Google Scholar] [CrossRef]
- Hemmerling, J.; Pflugmacher, D.; Hostert, P. Mapping Temperate Forest Tree Species Using Dense Sentinel-2 Time Series. Remote Sens. Environ. 2021, 267, 112743. [Google Scholar] [CrossRef]
- Grabska, E.; Hostert, P.; Pflugmacher, D.; Ostapowicz, K. Forest Stand Species Mapping Using the Sentinel-2 Time Series. Remote Sens. 2019, 11, 1197. [Google Scholar] [CrossRef]
- Hościło, A.; Lewandowska, A. Mapping Forest Type and Tree Species on a Regional Scale Using Multi-Temporal Sentinel-2 Data. Remote Sens. 2019, 11, 929. [Google Scholar] [CrossRef]
- Immitzer, M.; Neuwirth, M.; Böck, S.; Brenner, H.; Vuolo, F.; Atzberger, C. Optimal Input Features for Tree Species Classification in Central Europe Based on Multi-Temporal Sentinel-2 Data. Remote Sens. 2019, 11, 2599. [Google Scholar] [CrossRef]
- Karasiak, N.; Fauvel, M.; Dejoux, J.-F.; Monteil, C.; Sheeren, D. Optimal dates for deciduous tree species mapping using full years Sentinel-2 time series in south west France. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 3, 469–476. [Google Scholar] [CrossRef]
- Persson, M.; Lindberg, E.; Reese, H. Tree Species Classification with Multi-Temporal Sentinel-2 Data. Remote Sens. 2018, 10, 1794. [Google Scholar] [CrossRef]
- Kollert, A.; Bremer, M.; Löw, M.; Rutzinger, M. Exploring the Potential of Land Surface Phenology and Seasonal Cloud Free Composites of One Year of Sentinel-2 Imagery for Tree Species Mapping in a Mountainous Region. Int. J. Appl. Earth Obs. Geoinf. 2021, 94, 102208. [Google Scholar] [CrossRef]
- Zagajewski, B.; Kluczek, M.; Raczko, E.; Njegovec, A.; Dabija, A.; Kycko, M. Comparison of Random Forest, Support Vector Machines, and Neural Networks for Post-Disaster Forest Species Mapping of the Krkonoše/Karkonosze Transboundary Biosphere Reserve. Remote Sens. 2021, 13, 2581. [Google Scholar] [CrossRef]
- Grabska-Szwagrzyk, E.; Tymińska-Czabańska, L. Sentinel-2 Time Series: A Promising Tool in Monitoring Temperate Species Spring Phenology. For. An Int. J. For. Res. 2023, 97, 267–281. [Google Scholar] [CrossRef]
- Hill, R.A.; Wilson, A.K.; George, M.; Hinsley, S.A. Mapping Tree Species in Temperate Deciduous Woodland Using Time-Series Multi-Spectral Data. Appl. Veg. Sci. 2010, 13, 86–99. [Google Scholar] [CrossRef]
- Sheeren, D.; Fauvel, M.; Josipovíc, V.; Lopes, M.; Planque, C.; Willm, J.; Dejoux, J.F. Tree Species Classification in Temperate Forests Using Formosat-2 Satellite Image Time Series. Remote Sens. 2016, 8, 734. [Google Scholar] [CrossRef]
- Gray, P.C.; Chamorro, D.F.; Ridge, J.T.; Kerner, H.R.; Ury, E.A.; Johnston, D.W. Temporally Generalizable Land Cover Classification: A Recurrent Convolutional Neural Network Unveils Major Coastal Change through Time. Remote Sens. 2021, 13, 3953. [Google Scholar] [CrossRef]
- Wijesingha, J.; Dzene, I.; Wachendorf, M. Evaluating the Spatial–Temporal Transferability of Models for Agricultural Land Cover Mapping Using Landsat Archive. ISPRS J. Photogramm. Remote Sens. 2024, 213, 72–86. [Google Scholar] [CrossRef]
- Kyere, I.; Astor, T.; Graß, R.; Wachendorf, M. Multi-Temporal Agricultural Land-Cover Mapping Using Single-Year and Multi-Year Models Based on Landsat Imagery and IACS Data. Agronomy 2019, 9, 309. [Google Scholar] [CrossRef]
- Momm, H.G.; ElKadiri, R.; Porter, W. Crop-Type Classification for Long-Term Modeling: An Integrated Remote Sensing and Machine Learning Approach. Remote Sens. 2020, 12, 449. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Gao, S.; Hu, T.; Liu, J.; Guo, Q. The Transferability of Random Forest in Canopy Height Estimation from Multi-Source Remote Sensing Data. Remote Sens. 2018, 10, 1183. [Google Scholar] [CrossRef]
- Domingo, D.; Alonso, R.; Lamelas, M.T.; Montealegre, A.L.; Rodríguez, F.; de la Riva, J. Temporal Transferability of Pine Forest Attributes Modeling Using Low-Density Airborne Laser Scanning Data. Remote Sens. 2019, 11, 261. [Google Scholar] [CrossRef]
- Fekety, P.A.; Falkowski, M.J.; Hudak, A.T. Temporal Transferability of LiDAR-Based Imputation of Forest Inventory Attributes. Can. J. For. Res. 2015, 45, 422–435. [Google Scholar] [CrossRef]
- de Lera Garrido, A.; Gobakken, T.; Ørka, H.O.; Næsset, E.; Bollandsås, O.M. Reuse of Field Data in Als-Assisted Forest Inventory. Silva Fenn. 2020, 54, 10272. [Google Scholar] [CrossRef]
- Tuia, D.; Persello, C.; Bruzzone, L. Domain Adaptation for the Classification of Remote Sensing Data: An Overview of Recent Advances. IEEE Geosci. Remote Sens. Mag. 2016, 4, 41–57. [Google Scholar] [CrossRef]
- Estrella, N.; Menzel, A. Responses of Leaf Colouring in Four Deciduous Tree Species to Climate and Weather in Germany. Clim. Res. 2006, 32, 253–267. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, X.; Wilson, A.M.; Silander, J.A. Predicting Autumn Phenology: How Deciduous Tree Species Respond to Weather Stressors. Agric. For. Meteorol. 2018, 250–251, 127–137. [Google Scholar] [CrossRef]
- Meier, M.; Vitasse, Y.; Bugmann, H.; Bigler, C. Phenological Shifts Induced by Climate Change Amplify Drought for Broad-Leaved Trees at Low Elevations in Switzerland. Agric. For. Meteorol. 2021, 307, 108485. [Google Scholar] [CrossRef]
- Duan, S.; He, H.S.; Spetich, M. Effects of Growing-Season Drought on Phenology and Productivity in Thewest Region of Central Hardwood Forests, USA. Forests 2018, 9, 377. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, X.; Silander, J.A. Deciduous Forest Responses to Temperature, Precipitation, and Drought Imply Complex Climate Change Impacts. Proc. Natl. Acad. Sci. USA 2015, 112, 13585–13590. [Google Scholar] [CrossRef]
- Govaere, L.; Leyman, A. Vlaamse Bosinventarisatie Agentschap Natuur En Bos (VBI1: 1997-1999; VBI2: 2009–2018; VBI3: 2019–2021). Available online: https://www.natuurenbos.be/vlaamse-bosinventaris/Website_BosAreaal.html (accessed on 8 December 2023).
- Forest Europe. State of Europe’s Forests 2020; Forest Europe: Bonn, Germany, 2020. [Google Scholar]
- Schneiders, A.; Alaerts, K.; Michels, H.; Stevens, M.; Van Gossum, P.; Van Reeth, W.; Vught, I. Natuurrapport 2020: Feiten En Cijfers Voor Een Nieuw Biodiversiteitsbeleid; Research Institute Nature and Forest: Brussels, Belgium, 2020. [Google Scholar]
- Vandekerkhove, K. Integration of Nature Protection in Forest Policy in Flanders (Belgium); European Forest Institute: Freiburg, Germany, 2013. [Google Scholar]
- Govaere, L. Een Blik Op de Kenmerken van Bos in Vlaanderen–Eerste Resultaten van Twee Opeenvolgende Vlaamse Bosinventarisaties. Bosrevue 2020, 83, 1–14. [Google Scholar]
- Zanaga, D.; Van De Kerchove, R.; Daems, D.; De Keersmaecker, W.; Brockmann, C.; Kirches, G.; Wevers, J.; Cartus, O.; Santoro, M.; Fritz, S.; et al. ESA WorldCover 10 m 2021 V200 2022; Zenodo: Geneva, Switzerland. [CrossRef]
- ANF Bosinventaris. Available online: https://www.natuurenbos.be/beleid-wetgeving/natuurbeheer/bosinventaris (accessed on 13 November 2023).
- Govaere, L.; Van de Kerckhove, P.; Roelandt, B.; Sannen, P.; Schrey, L. Handleiding Tweede Bosinventarisatie Vlaams Gewest; Agency for Nature and Forests: Brussels, Belgium, 2009. [Google Scholar]
- Govaere, L. Protocol En Handleiding Derde Bosinventarisatie Vlaams Gewest; Agency for Nature and Forests: Brussels, Belgium, 2019. [Google Scholar]
- Dumortier, M.; Van Gossum, P.; Van Calster, H.; Adriaens, D.; Adriaenssens, V.; Alaerts, K.; Brys, R.; Cools, N.; De Knijf, G.; Denys, L.; et al. Voorstel Voor Een Meetnet Biodiversiteit Agrarisch Gebied; Nr. INBO.A.4387; Adviezen van Het Instituut Voor Natuur-En Bosonderzoek; Research Institute Nature and Forest: Brussels, Belgium, 2022; pp. 1–51. [Google Scholar]
- Schramm, M.; Pebesma, E.; Milenković, M.; Foresta, L.; Dries, J.; Jacob, A.; Wagner, W.; Mohr, M.; Neteler, M.; Kadunc, M.; et al. The Openeo Api–Harmonising the Use of Earth Observation Cloud Services Using Virtual Data Cube Functionalities. Remote Sens. 2021, 13, 1125. [Google Scholar] [CrossRef]
- Dries, J.; Lippens, S. openeo-python-client (Version 0.22.0). Available online: https://github.com/Open-EO/openeo-python-client (accessed on 15 July 2024).
- Terrascope Terrascope. Available online: https://terrascope.be/en (accessed on 14 September 2023).
- Swinnen, E.; De Keukelaere, L. Terrascope Sentinel-2-Quality Assessment Report; Flemish Institute for Technological Research (VITO): Mol, Belgium, 2020; pp. 1–42. [Google Scholar]
- Richter, R.; Louis, J.; Müller-Wilm, U. Sentinel-2 MSI–Level 2A Products Algorithm Theoretical Basis Document; S2PAD-ATBD-0001, Issue 2.0; Telespazio VEGA Deutschland GmbH: Darmstadt, Germany, 2012. [Google Scholar]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Hermosilla, T.; Bastyr, A.; Coops, N.C.; White, J.C.; Wulder, M.A. Mapping the Presence and Distribution of Tree Species in Canada’s Forested Ecosystems. Remote Sens. Environ. 2022, 282, 113276. [Google Scholar] [CrossRef]
- Stas, M.; Van Orshoven, J.; Dong, Q.; Heremans, S.; Zhang, B. A Comparison of Machine Learning Algorithms for Regional Wheat Yield Prediction Using NDVI Time Series of SPOT-VGT. In Proceedings of the 2016 Fifth International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Tianjin, China, 18–20 July 2016; IEEE: Piscartway, NJ, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oates, T. Time Series Classification from Scratch with Deep Neural Networks: A Strong Baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 4–9 June 2017; IEEE: Piscartway, NJ, USA, 2017; Volume 2017-May, pp. 1578–1585. [Google Scholar] [CrossRef]
- Zhong, L.; Hu, L.; Zhou, H. Deep Learning Based Multi-Temporal Crop Classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Akbani, R.; Kwek, S.; Japkowicz, N. Applying Support Vector Machines to Imbalanced Datasets. In European Conference on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2004; pp. 39–50. [Google Scholar] [CrossRef]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data; Department of Statistics, University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- Zhong, L.; Gong, P.; Biging, G.S. Efficient Corn and Soybean Mapping with Temporal Extendability: A Multi-Year Experiment Using Landsat Imagery. Remote Sens. Environ. 2014, 140, 1–13. [Google Scholar] [CrossRef]
- Hao, X.; Liu, L.; Yang, R.; Yin, L.; Zhang, L.; Li, X. A Review of Data Augmentation Methods of Remote Sensing Image Target Recognition. Remote Sens. 2023, 15, 827. [Google Scholar] [CrossRef]
- Yang, S.; Xiao, W.; Zhang, M.; Guo, S.; Zhao, J.; Shen, F. Image Data Augmentation for Deep Learning: A Survey. arXiv 2022, arXiv:2204.08610. [Google Scholar]
- Iwana, B.K.; Uchida, S. An Empirical Survey of Data Augmentation for Time Series Classification with Neural Networks. PLoS ONE 2021, 16, e0254841. [Google Scholar] [CrossRef]
- Iglesias, G.; Talavera, E.; González-Prieto, Á.; Mozo, A.; Gómez-Canaval, S. Data Augmentation Techniques in Time Series Domain: A Survey and Taxonomy. Neural Comput. Appl. 2023, 35, 10123–10145. [Google Scholar] [CrossRef]
- Westra, T.; Verschelde, P.; Van Calster, H.; Lommelen, E.; Onkelinx, T.; Quataert, P.; Govaere, L. Opmaak van Een Analysestramien Voor de Gegevens van de Vlaamse Bosinventarisatie. Rapporten van het Instituu voor Natuur- en Bosonderzoek 2015; Research Institute for Nature and Forest: Brussels, Belgium, 2015. [Google Scholar]
| Parameter | Tested Values | |||
|---|---|---|---|---|
| RF | n_estimators | 50; 100; 250; 500; 1000 | ||
| max_depth | 3; 5; 7; 9; 30; None | |||
| SVM | class_weight | balanced; None | ||
| kernel | linear | C | 0.1; 1; 10; 100; 1000 | |
| class_weight | balanced; None | |||
| kernel | poly | C | 0.1; 1; 10; 100; 1000 | |
| gamma | 0.0001; 0.001; 0.01; 0.1; 1 | |||
| degree | 0, 1, 2, 3, 4, 5, 6 | |||
| class_weight | balanced; None | |||
| kernel | rbf | C | 0.1; 1; 10; 100; 1000 | |
| gamma | 0.0001; 0.001; 0.01; 0.1; 1 | |||
| class_weight | balanced; None | |||
| kernel | sigmoid | C | 0.1; 1; 10; 100; 1000 | |
| gamma | 0.0001; 0.001; 0.01; 0.1; 1 | |||
| class_weight | balanced; None | |||
| MLP | hidden_layer_sizes | (50, 50, 50); (50, 100, 50); (100,) | ||
| activation | tanh; relu | |||
| solver | sgd; adam | |||
| alpha | 0.0001; 0.001; 0.01; 0.1; 1 | |||
| learning_rate | constant; adaptive | |||
| Target Class | Training Sample Size | Validation Sample Size |
|---|---|---|
| Scots pine | 204 | 88 |
| Black pine | 88 | 37 |
| Oak | 64 | 28 |
| Poplar | 64 | 27 |
| Beech | 37 | 16 |
| Total | 457 | 196 |
| Total sample size | 653 | |
| Validation Year | ||||||
|---|---|---|---|---|---|---|
| 2018 | 2019 | 2020 | 2021 | 2022 | ||
| RF | Scots pine | 87.60 ± 0.56 | 85.43 ± 0.48 | 86.50 ± 0.48 | 87.06 ± 0.61 | 81.87 ± 0.36 |
| Black pine | 65.91 ± 1.14 | 61.59 ± 1.70 | 71.26 ± 1.70 | 70.71 ± 1.51 | 57.18 ± 1.37 | |
| Oak | 78.50 ± 1.22 | 78.56 ± 1.68 | 83.14 ± 1.68 | 84.16 ± 1.61 | 87.30 ± 2.20 | |
| Poplar | 77.27 ± 1.96 | 79.59 ± 1.31 | 73.23 ± 1.31 | 80.00 ± 0.00 | 82.11 ± 1.61 | |
| Beech | 64.44 ± 1.74 | 70.98 ± 1.47 | 73.89 ± 1.47 | 71.17 ± 1.77 | 64.95 ± 2.41 | |
| SVM | Scots pine | 89.41 ± 0.00 | 82.84 ± 0.00 | 87.72 ± 0.00 | 79.53 ± 0.00 | 75.15 ± 0.00 |
| Black pine | 79.01 ± 0.00 | 68.24 ± 0.00 | 79.01 ± 0.00 | 68.24 ± 0.00 | 62.22 ± 0.00 | |
| Oak | 88.89 ± 0.00 | 85.19 ± 0.00 | 87.27 ± 0.00 | 84.00 ± 0.00 | 87.27 ± 0.00 | |
| Poplar | 82.76 ± 0.00 | 86.67 ± 0.00 | 71.43 ± 0.00 | 83.87 ± 0.00 | 87.50 ± 0.00 | |
| Beech | 86.21 ± 0.00 | 77.78 ± 0.00 | 73.68 ± 0.00 | 80.00 ± 0.00 | 84.00 ± 0.00 | |
| MLP | Scots pine | 87.41 ± 1.37 | 85.23 ± 0.94 | 87.07 ± 0.94 | 84.17 ± 0.99 | 79.78 ± 1.61 |
| Black pine | 63.22 ± 9.74 | 58.75 ± 3.22 | 60.00 ± 3.22 | 55.32 ± 8.05 | 30.91 ± 13.37 | |
| Oak | 79.79 ± 2.88 | 90.23 ± 2.35 | 83.02 ± 2.35 | 82.23 ± 1.92 | 79.52 ± 2.84 | |
| Poplar | 40.77 ± 14.43 | 66.49 ± 5.17 | 54.88 ± 5.17 | 65.60 ± 4.59 | 73.80 ± 10.25 | |
| Beech | 68.17 ± 2.97 | 73.28 ± 1.97 | 72.91 ± 1.97 | 67.55 ± 1.41 | 68.89 ± 3.49 | |
| Validation Year | ||||||
|---|---|---|---|---|---|---|
| 2018 | 2019 | 2020 | 2021 | 2022 | ||
| RF | Scots pine | 4.47 ± 2.55 | 1.15 ± 1.01 | 2.16 ± 1.30 | 5.37 ± 1.66 | −0.07 ± 1.63 |
| Black pine | −0.82 ± 5.99 | 4.24 ± 4.83 | 6.62 ± 3.96 | 9.82 ± 8.75 | 9.11 ± 4.19 | |
| Oak | 7.06 ± 5.24 | −0.11 ± 4.49 | 11.84 ± 7.13 | 8.84 ± 6.59 | 6.97 ± 4.09 | |
| Poplar | 20.25 ± 24.68 | 8.57 ± 8.76 | 19.59 ± 15.95 | 25.85 ± 22.90 | 11.00 ± 10.49 | |
| Beech | 3.40 ± 4.48 | 7.64 ± 4.00 | 28.04 ± 12.43 | 11.29 ± 5.70 | −1.17 ± 4.72 | |
| SVM | Scots pine | 12.96 ± 2.97 | −0.68 ± 2.22 | 3.53 ± 3.93 | 1.08 ± 6.2 | 5.15 ± 10.40 |
| Black pine | 12.62 ± 5.25 | 6.12 ± 8.15 | 11.22 ± 6.71 | 10.20 ± 9.01 | 7.54 ± 5.03 | |
| Oak | 10.25 ± 10.44 | −0.48 ± 12.10 | 14.43 ± 5.16 | 16.98 ± 10.27 | 5.90 ± 10.54 | |
| Poplar | 21.09 ± 6.80 | 20.52 ± 7.93 | 4.85 ± 5.55 | 39.22 ± 3.66 | 17.96 ± 12.51 | |
| Beech | 25.05 ± 11.38 | 11.86 ± 8.34 | 24.25 ± 18.68 | 31.43 ± 9.16 | 14.14 ± 8.84 | |
| MLP | Scots pine | 1.57 ± 1.37 | 0.62 ± 0.87 | 3.04 ± 0.49 | 3.94 ± 4.08 | −0.96 ± 4.92 |
| Black pine | 0.09 ± 2.69 | 8.62 ± 7.04 | 8.00 ± 8.31 | 9.60 ± 12.01 | −14.73 ± 3.62 | |
| Oak | 16.90 ± 14.81 | 10.34 ± 8.02 | 17.84 ± 6.30 | 17.41 ± 13.18 | 8.43 ± 5.20 | |
| Poplar | 28.57 ± 10.76 | 10.02 ± 3.82 | 21.36 ± 12.45 | 28.59 ± 16.65 | 20.14 ± 13.40 | |
| Beech | 7.51 ± 1.93 | 10.48 ± 2.96 | 34.12 ± 19.68 | 9.64 ± 2.71 | 11.57 ± 7.42 | |
| Number of Years Included | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| RF | Scots pine | 2.97 ± 2.92 | 3.22 ± 3.50 | 2.33 ± 2.65 | 1.57 ± 2.16 |
| Black pine | 7.99 ± 5.83 | 2.88 ± 3.74 | −0.03 ± 4.07 | −0.34 ± 2.59 | |
| Oak | 8.63 ± 7.60 | 4.99 ± 6.88 | −2.03 ± 5.23 | −1.87 ± 4.74 | |
| Poplar | 16.44 ± 17.52 | 3.74 ± 6.94 | 3.75 ± 4.46 | 1.90 ± 4.78 | |
| Beech | 9.61 ± 9.52 | 5.07 ± 11.17 | 1.00 ± 10.0 | 0.28 ± 8.31 | |
| SVM | Scots pine | 3.12 ± 5.23 | −1.07 ± 4.86 | 0.70 ± 6.97 | −0.52 ± 5.07 |
| Black pine | 8.35 ± 5.28 | 2.85 ± 3.12 | 3.23 ± 5.64 | 1.15 ± 3.32 | |
| Oak | 7.79 ± 12.35 | 3.89 ± 8.82 | 1.09 ± 7.67 | −1.68 ± 5.34 | |
| Poplar | 23.72 ± 13.39 | 3.16 ± 4.74 | 5.34 ± 11.46 | 3.32 ± 7.41 | |
| Beech | 20.05 ± 11.29 | 12.01 ± 15.37 | 7.86 ± 10.17 | 6.79 ± 5.24 | |
| MLP | Scots pine | 0.55 ± 3.12 | −0.73 ± 3.04 | −1.15 ± 2.31 | −1.51 ± 1.80 |
| Black pine | −0.26 ± 11.73 | −5.04 ± 12.99 | −7.60 ± 11.88 | −9.33 ± 9.71 | |
| Oak | 13.11 ± 10.28 | 4.80 ± 8.97 | −3.00 ± 7.08 | −4.81 ± 6.10 | |
| Poplar | 23.92 ± 13.63 | 1.69 ± 12.31 | −4.28 ± 12.90 | −5.46 ± 13.08 | |
| Beech | 14.19 ± 8.74 | 4.44 ± 14.44 | −0.86 ± 9.86 | −1.17 ± 9.80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verhulst, M.; Heremans, S.; Blaschko, M.B.; Somers, B. Temporal Transferability of Tree Species Classification in Temperate Forests with Sentinel-2 Time Series. Remote Sens. 2024, 16, 2653. https://doi.org/10.3390/rs16142653
Verhulst M, Heremans S, Blaschko MB, Somers B. Temporal Transferability of Tree Species Classification in Temperate Forests with Sentinel-2 Time Series. Remote Sensing. 2024; 16(14):2653. https://doi.org/10.3390/rs16142653
Chicago/Turabian StyleVerhulst, Margot, Stien Heremans, Matthew B. Blaschko, and Ben Somers. 2024. "Temporal Transferability of Tree Species Classification in Temperate Forests with Sentinel-2 Time Series" Remote Sensing 16, no. 14: 2653. https://doi.org/10.3390/rs16142653
APA StyleVerhulst, M., Heremans, S., Blaschko, M. B., & Somers, B. (2024). Temporal Transferability of Tree Species Classification in Temperate Forests with Sentinel-2 Time Series. Remote Sensing, 16(14), 2653. https://doi.org/10.3390/rs16142653








