An Improved Gap-Filling Method for Reconstructing Dense Time-Series Images from LANDSAT 7 SLC-Off Data
Abstract
1. Introduction
2. Study Region and Data
3. Methodology
3.1. The Neighborhood Similar Pixel (NSPI) Interpolation Method
3.2. The ROBOT Algorithm
3.3. The Improved ROBOT (IROBOT) Algorithm
3.4. Experimental Design
3.5. Evaluation Metrics
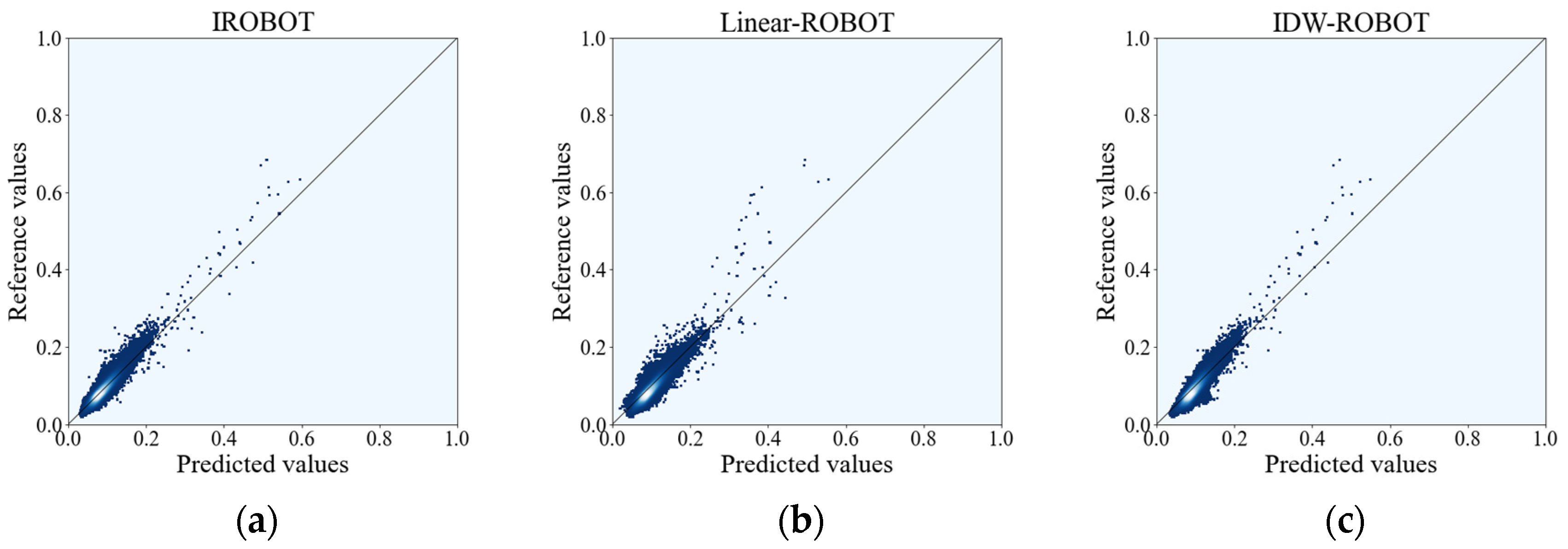
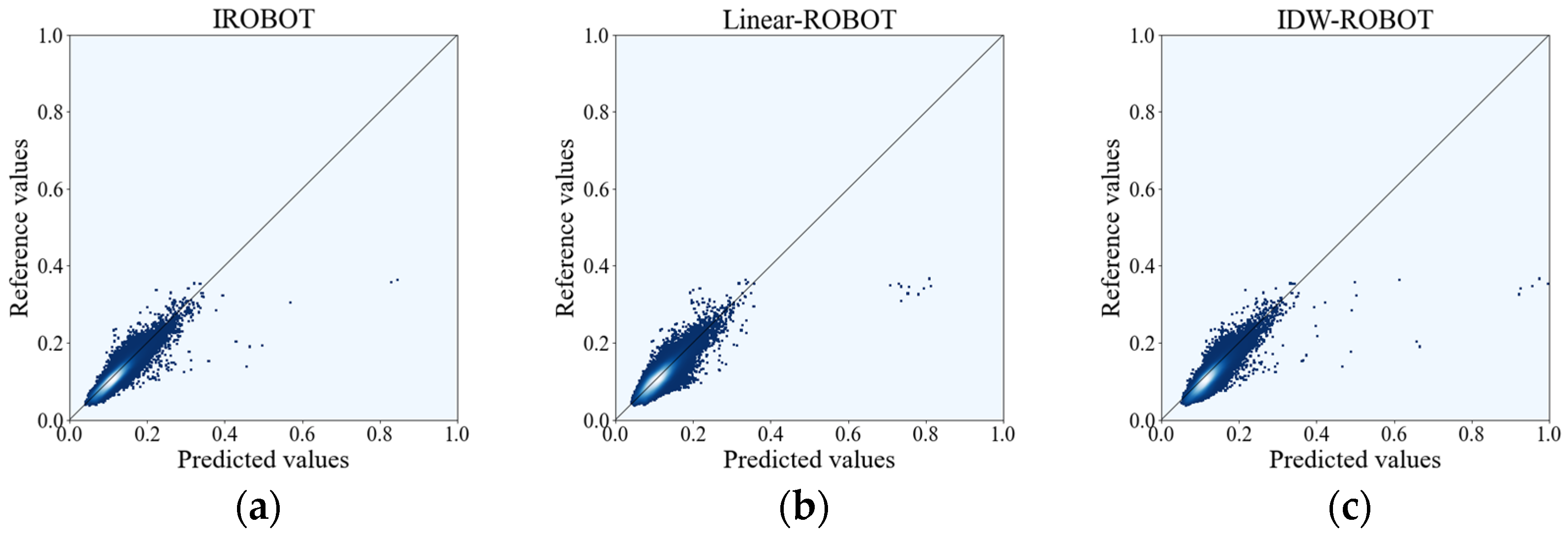
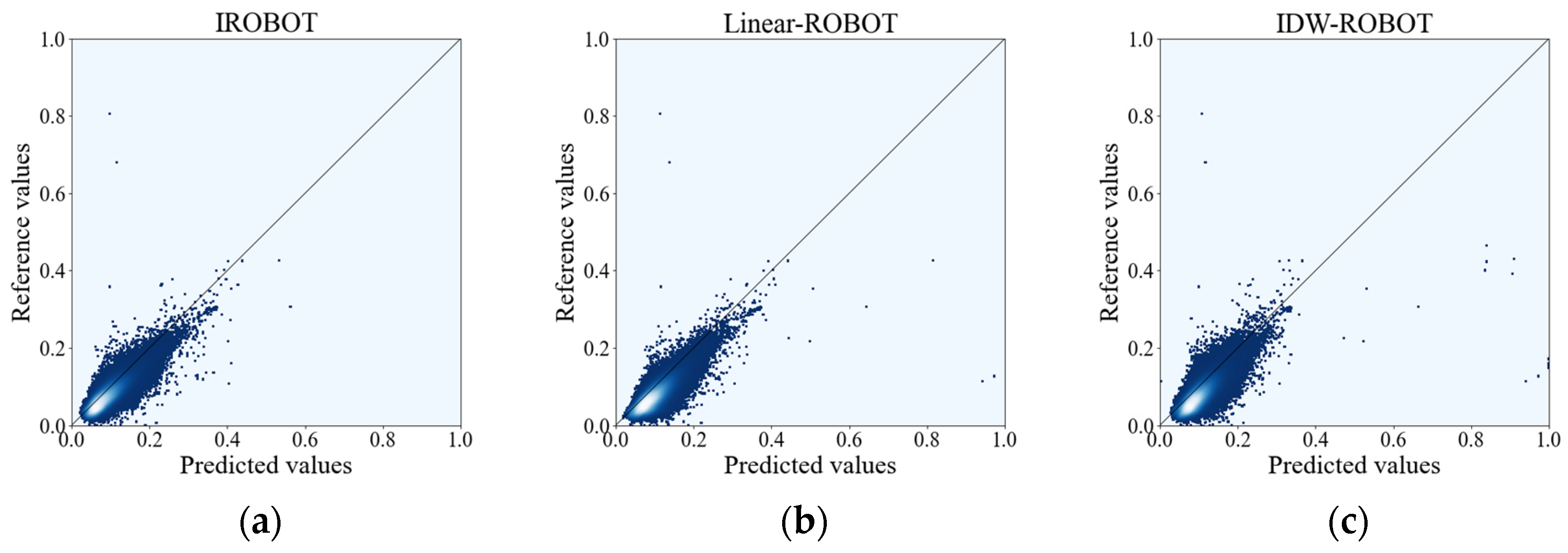
4. Results and Analysis
4.1. Experiment I: Evaluation of the Reconstruction Results with Landsat 5 Images
4.2. Experiment II: Evaluation of the Reconstruction Results with Landsat 8 Images
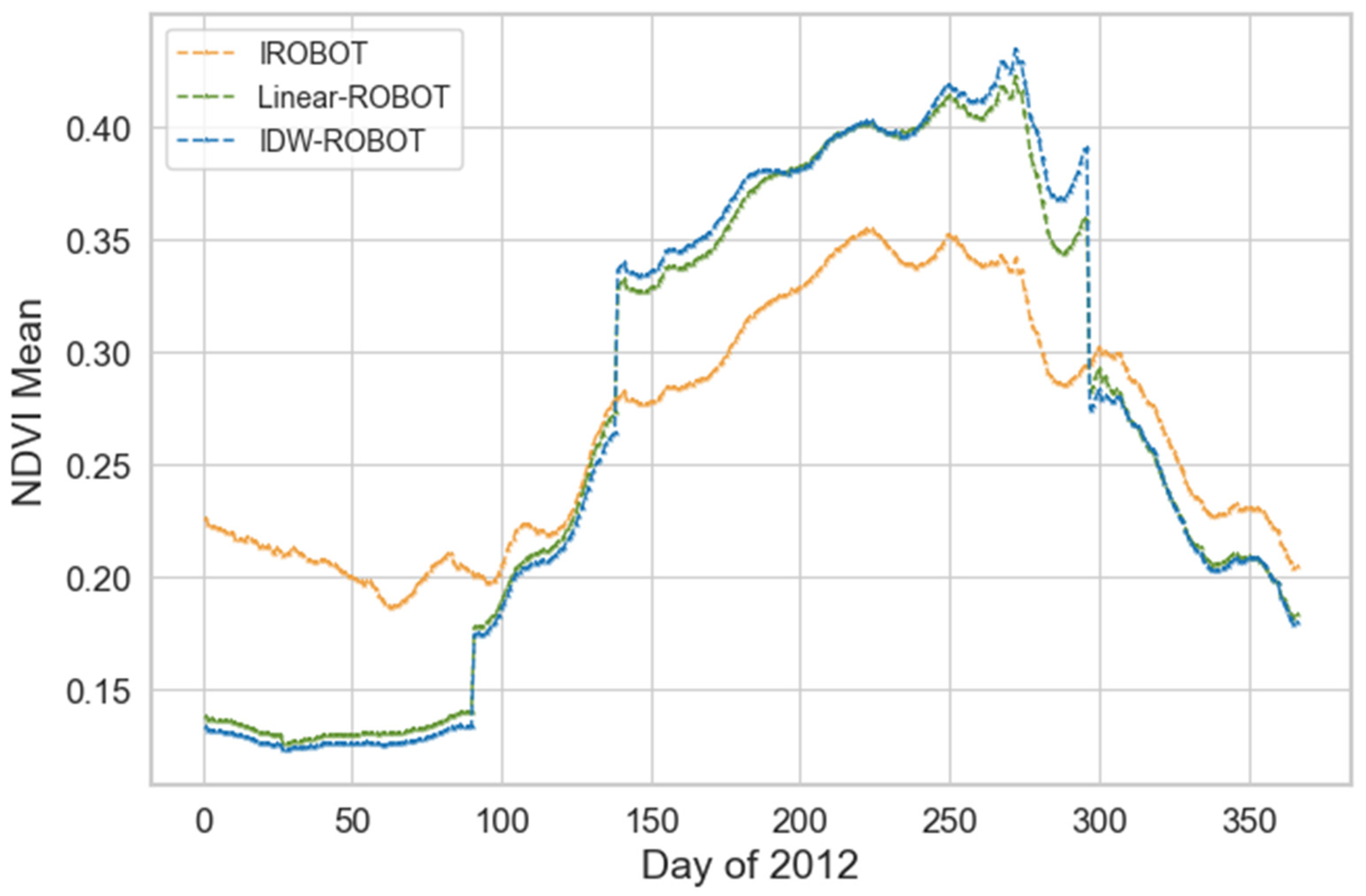
4.3. Experiment III: Reconstruction of the Dense and Continuous Time-Series NDVI
4.4. Temporal Continuity Analysis with Varying Numbers of Input Images
4.5. Comparative Analysis of the Reconstruction Results Using RMA and OLS Regression Coefficients
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A




Appendix B

| Evaluation Metrics | 31 January 2011 | 7 May 2011 | ||||||
|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Blue | Green | Red | NIR | |
| MAE | 0.0110 | 0.0195 | 0.0161 | 0.0122 | 0.0095 | 0.0135 | 0.0103 | 0.0198 |
| BIAS | 0.0097 | 0.0192 | 0.0152 | 0.0075 | 0.0082 | 0.0124 | 0.0055 | 0.0170 |
| CC | 0.9196 | 0.9364 | 0.9491 | 0.9553 | 0.9284 | 0.9225 | 0.9113 | 0.8860 |
| SSIM | 0.9281 | 0.9301 | 0.9401 | 0.9318 | 0.9765 | 0.9695 | 0.9618 | 0.9412 |
References
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current status of Landsat program, science, and applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Kline, K.; Scaramuzza, P.L.; Kovalskyy, V.; Hansen, M.; Loveland, T.R.; Vermote, E.; Zhang, C. Web-enabled Landsat Data (WELD): Landsat ETM+ composited mosaics of the conterminous United States. Remote Sens. Environ. 2010, 114, 35–49. [Google Scholar] [CrossRef]
- Loveland, T.R.; Dwyer, J.L. Landsat: Building a strong future. Remote Sens. Environ. 2012, 122, 22–29. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Suliman, S.I. Locally Linear Manifold Model for Gap-Filling Algorithms of Hyperspectral Imagery: Proposed Algorithms and a Comparative Study. Master’s Thesis, Michigan State University, East Lansing, MI, USA, 2016. [Google Scholar]
- Maxwell, S.K.; Schmidt, G.L.; Storey, J.C. A multi-scale segmentation approach to filling gaps in Landsat ETM+ SLC-off images. Int. J. Remote Sens. 2007, 28, 5339–5356. [Google Scholar] [CrossRef]
- United States Geological Survey (USGS). Preliminary Assessment of Landsat 7 ETM+ Data following Scan Line Corrector Malfunction. Available online: https://www.usgs.gov/media/files/preliminary-assessment-value-landsat-7-etm-slc-data.pdf (accessed on 20 December 2018).
- Wulder, M.A.; Coops, N.C.; Roy, D.P.; White, J.C.; Hermosilla, T. Land cover 2.0. Int. J. Remote Sens. 2018, 39, 4254–4284. [Google Scholar] [CrossRef]
- Graesser, J.; Stanimirova, R.; Friedl, M.A. Reconstruction of Satellite Time Series With a Dynamic Smoother. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1803–1813. [Google Scholar] [CrossRef]
- Farhat, L.; Manakos, I.; Sylaios, G.; Kalaitzidis, C. A Modified Version of the Direct Sampling Method for Filling Gaps in Landsat 7 and Sentinel 2 Satellite Imagery in the Coastal Area of Rhone River. Remote Sens. 2023, 15, 5122. [Google Scholar] [CrossRef]
- Case, N.; Vitti, A. Reconstruction of Multi-Temporal Satellite Imagery by Coupling Variational Segmentation and Radiometric Analysis. ISPRS Int. J. Geo-Inf. 2021, 10, 17. [Google Scholar] [CrossRef]
- Ali, S.M.; Mohammed, M.J. Gap-Filling Restoration Methods for ETM+ Sensor Images. Iraqi J. Sci. 2013, 54, 206–214. [Google Scholar]
- Olivier, R.; Hanqiang, C. Nearest Neighbor Value Interpolation. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2012, 3, 25–30. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Zhang, J. A region-based bi-cubic image interpolation algorithm. Comput. Eng. 2010, 36, 216–218. [Google Scholar]
- Zhang, C.; Li, W.; Travis, D. Gaps-fill of SLC-off Landsat ETM plus satellite image using a geostatistical approach. Int. J. Remote Sens. 2007, 28, 5103–5122. [Google Scholar] [CrossRef]
- Pringle, M.J.; Schmidt, M.; Muir, J.S. Geostatistical interpolation of SLC-off Landsat ETM+ images. ISPRS J. Photogramm. Remote Sens. 2009, 64, 654–664. [Google Scholar] [CrossRef]
- Boloorani, A.D.; Erasmi, S.; Kappas, M. Multi-Source Remotely Sensed Data Combination: Projection Transformation Gap-Fill Procedure. Sensors 2008, 8, 4429–4440. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D.; Chen, J. A new geostatistical approach for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2012, 124, 49–60. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.; Zhang, L. Recovering missing pixels for Landsat ETM+ SLC-off imagery using multi-temporal regression analysis and a regularization method. Remote Sens. Environ. 2013, 131, 182–194. [Google Scholar] [CrossRef]
- Maxwell, S.K. Filling Landsat ETM+ SLC-off gaps using a segmentation model approach. Photogramm. Eng. Remote Sens. 2004, 70, 1109–1111. [Google Scholar]
- Marujo, R.F.B.; Fonseca, L.M.G.; Körting, T.S.; Bendini, H.N. A multi-scale segmentation approach to filling gaps in landsat ETM+ SLC-off images through pixel weighting. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLII-3, 79–84. [Google Scholar] [CrossRef]
- SLC Gap-Filled Products Phase One Methodology. Available online: https://www.usgs.gov/media/files/landsat-7-slc-gap-filled-products-phase-one-methodology (accessed on 2 August 2019).
- Phase 2 Gap-Fill Algorithm: SLC-Off Gap-Filled Products Gap-Filled Algorithm Methodology. Available online: https://www.usgs.gov/media/files/landsat-7-slc-gap-filled-products-phase-two-methodology (accessed on 20 December 2018).
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Zhu, X.; Gao, F.; Liu, D.; Chen, J. Modified Neighborhood Similar Pixel Interpolator Approach for Removing Thick Clouds in Landsat Images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 521–525. [Google Scholar] [CrossRef]
- Liu, H.; Gong, P.; Wang, J.; Wang, X.; Ning, G.; Xu, B. Production of global daily seamless data cubes and quantification of global land cover change from 1985 to 2020—iMap World 1.0. Remote Sens. Environ. 2021, 258, 112364. [Google Scholar] [CrossRef]
- Zhang, H.K.; Roy, D.P. Using the 500 m MODIS land cover product to derive a consistent continental scale 30 m Landsat land cover classification. Remote Sens. Environ. 2017, 197, 15–34. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Zhu, X.; Cai, F.; Tian, J.; Williams, T.K.-A. Spatiotemporal Fusion of Multisource Remote Sensing Data: Literature Survey, Taxonomy, Principles, Applications, and Future Directions. Remote Sens. 2018, 10, 527. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Wang, Q.; Atkinson, P.M. Spatio-temporal fusion for daily Sentinel-2 images. Remote Sens. Environ. 2018, 204, 31–42. [Google Scholar] [CrossRef]
- Zhukov, B.; Oertel, D.; Lanzl, F.; Reinhackel, G. Unmixing-based multisensor multiresolution image fusion. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1212–1226. [Google Scholar] [CrossRef]
- Wu, M.; Niu, Z.; Wang, C.; Wu, C.; Wang, L. Use of MODIS and Landsat time series data to generate high-resolution temporal synthetic Landsat data using a spatial and temporal reflectance fusion model. J. Appl. Remote Sens. 2012, 6, 063507. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, H.K. Spatio-temporal reflectance fusion via unmixing: Accounting for both phenological and land-cover changes. Int. J. Remote Sens. 2014, 35, 6213–6233. [Google Scholar] [CrossRef]
- Lu, M.; Chen, J.; Tang, H.; Rao, Y.; Yang, P.; Wu, W. Land cover change detection by integrating object-based data blending model of Landsat and MODIS. Remote Sens. Environ. 2016, 184, 374–386. [Google Scholar] [CrossRef]
- Huang, B.; Song, H. Spatiotemporal Reflectance Fusion via Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Wei, J.; Wang, L.; Liu, P.; Chen, X.; Li, W.; Zomaya, A.Y. Spatiotemporal Fusion of MODIS and Landsat-7 Reflectance Images via Compressed Sensing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7126–7139. [Google Scholar] [CrossRef]
- Ke, Y.; Im, J.; Park, S.; Gong, H. Downscaling of MODIS One Kilometer Evapotranspiration Using Landsat-8 Data and Machine Learning Approaches. Remote Sens. 2016, 8, 215. [Google Scholar] [CrossRef]
- Boyte, S.P.; Wylie, B.K.; Rigge, M.B.; Dahal, D. Fusing MODIS with Landsat 8 data to downscale weekly normalized difference vegetation index estimates for central Great Basin rangelands, USA. GISci. Remote Sens. 2018, 55, 376–399. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Feng, R.; Liu, P.; Han, W.; Chen, X. CycleGAN-STF: Spatiotemporal Fusion via CycleGAN-Based Image Generation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5851–5865. [Google Scholar] [CrossRef]
- Song, H.; Liu, Q.; Wang, G.; Hang, R.; Huang, B. Spatiotemporal Satellite Image Fusion Using Deep Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
- Xue, J.; Leung, Y.; Fung, T. A Bayesian Data Fusion Approach to Spatio-Temporal Fusion of Remotely Sensed Images. Remote Sens. 2017, 9, 1310. [Google Scholar] [CrossRef]
- Li, A.; Bo, Y.; Zhu, Y.; Guo, P.; Bi, J.; He, Y. Blending multi-resolution satellite sea surface temperature (SST) products using Bayesian maximum entropy method. Remote Sens. Environ. 2013, 135, 52–63. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, Y.; Tong, X.; Atkinson, P.M. Virtual image pair-based spatio-temporal fusion. Remote Sens. Environ. 2020, 249, 112009. [Google Scholar] [CrossRef]
- Gevaert, C.M.; García-Haro, F.J. A comparison of STARFM and an unmixing-based algorithm for Landsat and MODIS data fusion. Remote Sens. Environ. 2015, 156, 34–44. [Google Scholar] [CrossRef]
- Xie, D.; Zhang, J.; Zhu, X.; Pan, Y.; Liu, H.; Yuan, Z.; Yun, Y. An Improved STARFM with Help of an Unmixing-Based Method to Generate High Spatial and Temporal Resolution Remote Sensing Data in Complex Heterogeneous Regions. Sensors 2016, 16, 207. [Google Scholar] [CrossRef]
- Chen, S.; Wang, J.; Gong, P. ROBOT: A spatiotemporal fusion model toward seamless data cube for global remote sensing applications. Remote Sens. Environ. 2023, 294, 113616. [Google Scholar] [CrossRef]
- Liu, H.; Gong, P. 21st century daily seamless data cube reconstruction and seasonal to annual land cover and land use dynamics mapping-iMap (China) 1.0. Natl. Remote Sens. Bull. 2021, 25, 126–147. [Google Scholar] [CrossRef]
- Dwyer, J.L.; Roy, D.P.; Sauer, B.; Jenkerson, C.B.; Zhang, H.K.; Lymburner, L. Analysis Ready Data: Enabling Analysis of the Landsat Archive. Remote Sens. 2018, 10, 1363. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Q.; Wang, J.; Chen, S.; Gong, P. Global 500 m seamless dataset (2000–2022) of land surface reflectance generated from MODIS products. Earth Syst. Sci. Data 2024, 16, 177–200. [Google Scholar] [CrossRef]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 reflective wavelength and normalized difference vegetation index continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A general method to normalize Landsat reflectance data to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef]
- Chastain, R.; Housman, I.; Goldstein, J.; Finco, M.; Tenneson, K. Empirical cross sensor comparison of Sentinel-2A and 2B MSI, Landsat-8 OLI, and Landsat-7 ETM+ top of atmosphere spectral characteristics over the conterminous United States. Remote Sens. Environ. 2019, 221, 274–285. [Google Scholar] [CrossRef]
- Nguyen, M.; Baez-Villanueva, O.; Bui, D.; Nguyen, P.; Ribbe, L. Harmonization of Landsat and Sentinel 2 for Crop Monitoring in Drought Prone Areas: Case Studies of Ninh Thuan (Vietnam) and Bekaa (Lebanon). Remote Sens. 2020, 12, 281. [Google Scholar] [CrossRef]
- Emelyanova, I.V.; McVicar, T.R.; Van Niel, T.G.; Li, L.T.; van Dijk, A.I.J.M. Assessing the accuracy of blending Landsat–MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sens. Environ. 2013, 133, 193–209. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; He, L.; Chen, J.; Plaza, A. Spatio-temporal fusion for remote sensing data: An overview and new benchmark. Sci. China Inf. Sci. 2020, 63, 140301. [Google Scholar] [CrossRef]












| Satellite | Available Images Start Time | Available Images End Time | Sensors Type | Resolution (m) | Cycle (Day) |
|---|---|---|---|---|---|
| Landsat 1 | 26 July 1972 | 6 January 1978 | MSS | 60 | 18 |
| Landsat 2 | 31 January 1975 | 3 February 1982 | MSS | 60 | 18 |
| Landsat 3 | 3 June 1978 | 23 February 1983 | MSS | 60 | 18 |
| Landsat 4 | 22 August 1982 | 24 June 1993 | MSS/TM | 60/30 | 16 |
| Landsat 5 | 16 March 1984 | 18 November 2011 | MSS/TM | 60/30 | 16 |
| Landsat 7 | 28 May 1999 | 31 May 2003 | ETM+ (SLC-on) | 30 | 16 |
| 1 June 2003 | 19 January 2024 | ETM+ (SLC-off) | |||
| Landsat 8 | 18 March 2013 | present | OLI/TIRS | 30 | 16 |
| Landsat 9 | 31 October 2021 | present | OLI2/TIRS2 | 30 | 16 |
| 2011 | 2012 | 2013 | ||
|---|---|---|---|---|
| 7 January 2011 | 15 May 2011 | 26 January 2012 | 1 March 2013 | 4 November 2013 |
| 23 January 2011 | 20 September 2011 | 14 March 2012 | 18 April 2013 | 12 November 2013 |
| 31 January 2011 | 6 October 2011 | 30 March 2012 | 20 May 2013 | 28 November 2013 |
| 8 February 2011 | 23 November 2011 | 17 May 2012 | 1 September 2013 | 14 December 2013 |
| 28 March 2011 | 9 December 2011 | 21 August 2012 | 25 September 2013 | 30 December 2013 |
| 7 May 2011 | 25 December 2011 | 24 December 2012 | 11 October 2013 | |
| Band | Regression Type | Between Sensors OLS and RMA Transformation Functions |
|---|---|---|
| Blue | OLS | OLI = 0.0003 + 0.8474 ETM+ |
| RMA | OLI = −0.0095 + 0.9785 ETM | |
| Green | OLS | OLI = 0.0088 + 0.8483 ETM+ |
| RMA | OLI = −0.0016 + 0.9542 ETM | |
| Red | OLS | OLI = 0.0061 + 0.9047 ETM+ |
| RMA | OLI = −0.0022 + 0.9825 ETM | |
| NIR | OLS | OLI = 0.0412 + 0.8462 ETM+ |
| RMA | OLI = −0.0021 + 1.0073 ETM |
| Evaluation Metrics | IROBOT | Linear-ROBOT | IDW-ROBOT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Blue | Green | Red | NIR | Blue | Green | Red | NIR | |
| MAE | 0.0069 | 0.0108 | 0.0090 | 0.0098 | 0.0110 | 0.0196 | 0.0176 | 0.0175 | 0.0104 | 0.0168 | 0.0141 | 0.0119 |
| BIAS | 0.0014 | 0.0093 | 0.0052 | 0.0023 | 0.0091 | 0.0189 | 0.0161 | 0.0151 | 0.0081 | 0.0160 | 0.0122 | 0.0040 |
| CC | 0.9288 | 0.9429 | 0.9543 | 0.9617 | 0.9127 | 0.9213 | 0.9282 | 0.9445 | 0.9110 | 0.9274 | 0.9410 | 0.9480 |
| SSIM | 0.9363 | 0.9441 | 0.9499 | 0.9407 | 0.9157 | 0.9129 | 0.9186 | 0.9161 | 0.9197 | 0.9231 | 0.9312 | 0.9210 |
| Evaluation Metrics | IROBOT | Linear-ROBOT | IDW-ROBOT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Blue | Green | Red | NIR | Blue | Green | Red | NIR | |
| MAE | 0.0089 | 0.0082 | 0.0126 | 0.0156 | 0.0106 | 0.0121 | 0.0153 | 0.0277 | 0.0145 | 0.0121 | 0.0181 | 0.0163 |
| BIAS | 0.0063 | 0.0026 | 0.0096 | 0.0124 | 0.0038 | −0.0048 | −0.0074 | 0.0239 | 0.0131 | 0.0088 | 0.0164 | 0.0122 |
| CC | 0.9209 | 0.9177 | 0.9186 | 0.9334 | 0.8659 | 0.8689 | 0.8699 | 0.8102 | 0.8863 | 0.8981 | 0.9081 | 0.9139 |
| SSIM | 0.9796 | 0.9763 | 0.9664 | 0.9599 | 0.9670 | 0.9575 | 0.9409 | 0.8966 | 0.9692 | 0.9691 | 0.9563 | 0.9526 |
| Evaluation Metrics | IROBOT | Linear-ROBOT | IDW-ROBOT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Blue | Green | Red | NIR | Blue | Green | Red | NIR | |
| MAE | 0.0190 | 0.0235 | 0.0299 | 0.0294 | 0.0257 | 0.0309 | 0.0398 | 0.0313 | 0.0268 | 0.0325 | 0.0406 | 0.0367 |
| BIAS | 0.0160 | 0.0215 | 0.0279 | 0.0157 | 0.0245 | 0.0300 | 0.0389 | 0.0141 | 0.0250 | 0.0310 | 0.0390 | 0.0243 |
| CC | 0.8306 | 0.8370 | 0.8643 | 0.8584 | 0.8064 | 0.8104 | 0.8289 | 0.8328 | 0.7917 | 0.7932 | 0.8326 | 0.8194 |
| SSIM | 0.9018 | 0.9301 | 0.8980 | 0.8584 | 0.8718 | 0.9089 | 0.8622 | 0.8469 | 0.8629 | 0.9003 | 0.8552 | 0.8239 |
| Evaluation Metrics | IROBOT | Linear-ROBOT | IDW-ROBOT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Blue | Green | Red | NIR | Blue | Green | Red | NIR | |
| MAE | 0.0132 | 0.0123 | 0.0115 | 0.0183 | 0.0158 | 0.0145 | 0.0133 | 0.0186 | 0.0170 | 0.0158 | 0.0149 | 0.0198 |
| BIAS | −0.0114 | −0.0102 | −0.0067 | 0.0145 | −0.0146 | −0.0132 | −0.0100 | 0.0140 | −0.0159 | −0.0145 | −0.0117 | 0.0143 |
| CC | 0.9031 | 0.9246 | 0.9345 | 0.9377 | 0.8961 | 0.9202 | 0.9300 | 0.9314 | 0.8877 | 0.9105 | 0.9214 | 0.9203 |
| SSIM | 0.9035 | 0.9215 | 0.9235 | 0.9315 | 0.8836 | 0.9126 | 0.9161 | 0.9277 | 0.8633 | 0.8922 | 0.8961 | 0.9096 |
| Evaluation Metrics | IROBOT | Linear-ROBOT | IDW-ROBOT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Blue | Green | Red | NIR | Blue | Green | Red | NIR | |
| MAE | 0.0183 | 0.0226 | 0.0287 | 0.0352 | 0.0247 | 0.0298 | 0.0384 | 0.0375 | 0.0262 | 0.0318 | 0.0396 | 0.0436 |
| BIAS | 0.0147 | 0.0200 | 0.0262 | 0.0243 | 0.0230 | 0.0286 | 0.0372 | 0.0246 | 0.0240 | 0.0300 | 0.0378 | 0.0338 |
| CC | 0.8173 | 0.8259 | 0.8604 | 0.8485 | 0.7942 | 0.8010 | 0.8263 | 0.8219 | 0.7806 | 0.7857 | 0.8331 | 0.8071 |
| SSIM | 0.9012 | 0.9304 | 0.8975 | 0.8357 | 0.8727 | 0.9100 | 0.8631 | 0.8257 | 0.8580 | 0.8981 | 0.8532 | 0.7992 |
| Evaluation Metrics | IROBOT | Linear-ROBOT | IDW-ROBOT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Blue | Green | Red | NIR | Blue | Green | Red | NIR | |
| MAE | 0.0142 | 0.0129 | 0.0124 | 0.0160 | 0.0150 | 0.0135 | 0.0128 | 0.0165 | 0.0159 | 0.0146 | 0.0141 | 0.0178 |
| BIAS | −0.0126 | −0.0108 | −0.0076 | 0.0007 | −0.0136 | −0.0116 | −0.0086 | 0.0021 | −0.0146 | −0.0126 | −0.0099 | 0.0019 |
| CC | 0.9017 | 0.9232 | 0.9341 | 0.9338 | 0.8931 | 0.9181 | 0.9295 | 0.9288 | 0.8850 | 0.9090 | 0.9214 | 0.9178 |
| SSIM | 0.8889 | 0.9069 | 0.9130 | 0.9087 | 0.8846 | 0.9057 | 0.9115 | 0.9084 | 0.8657 | 0.8852 | 0.8912 | 0.8887 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, Q.; Chen, S.; Zhang, X. An Improved Gap-Filling Method for Reconstructing Dense Time-Series Images from LANDSAT 7 SLC-Off Data. Remote Sens. 2024, 16, 2064. https://doi.org/10.3390/rs16122064
Li Y, Liu Q, Chen S, Zhang X. An Improved Gap-Filling Method for Reconstructing Dense Time-Series Images from LANDSAT 7 SLC-Off Data. Remote Sensing. 2024; 16(12):2064. https://doi.org/10.3390/rs16122064
Chicago/Turabian StyleLi, Yue, Qiang Liu, Shuang Chen, and Xiaotong Zhang. 2024. "An Improved Gap-Filling Method for Reconstructing Dense Time-Series Images from LANDSAT 7 SLC-Off Data" Remote Sensing 16, no. 12: 2064. https://doi.org/10.3390/rs16122064
APA StyleLi, Y., Liu, Q., Chen, S., & Zhang, X. (2024). An Improved Gap-Filling Method for Reconstructing Dense Time-Series Images from LANDSAT 7 SLC-Off Data. Remote Sensing, 16(12), 2064. https://doi.org/10.3390/rs16122064







