Satellite-Based PT-SinRH Evapotranspiration Model: Development and Validation from AmeriFlux Data
Abstract
1. Introduction
2. Methods
2.1. PT-JPL Model
2.2. PT-SinRH Model
3. Study Domain and Data
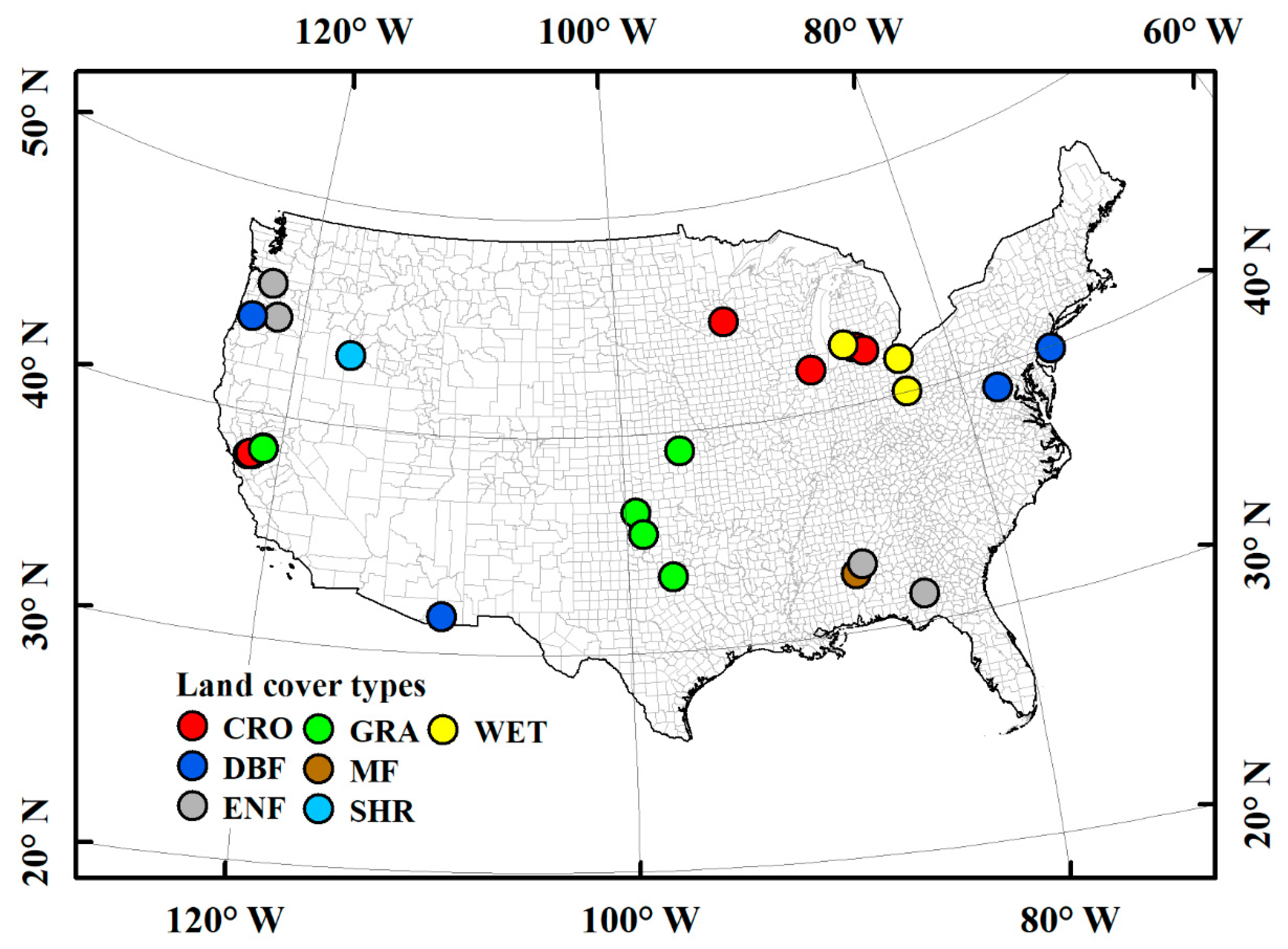
3.1. Study Domain
3.2. Data
3.2.1. Eddy Covariance Measurements
3.2.2. Satellite and Reanalysis Data
4. Model Evaluation
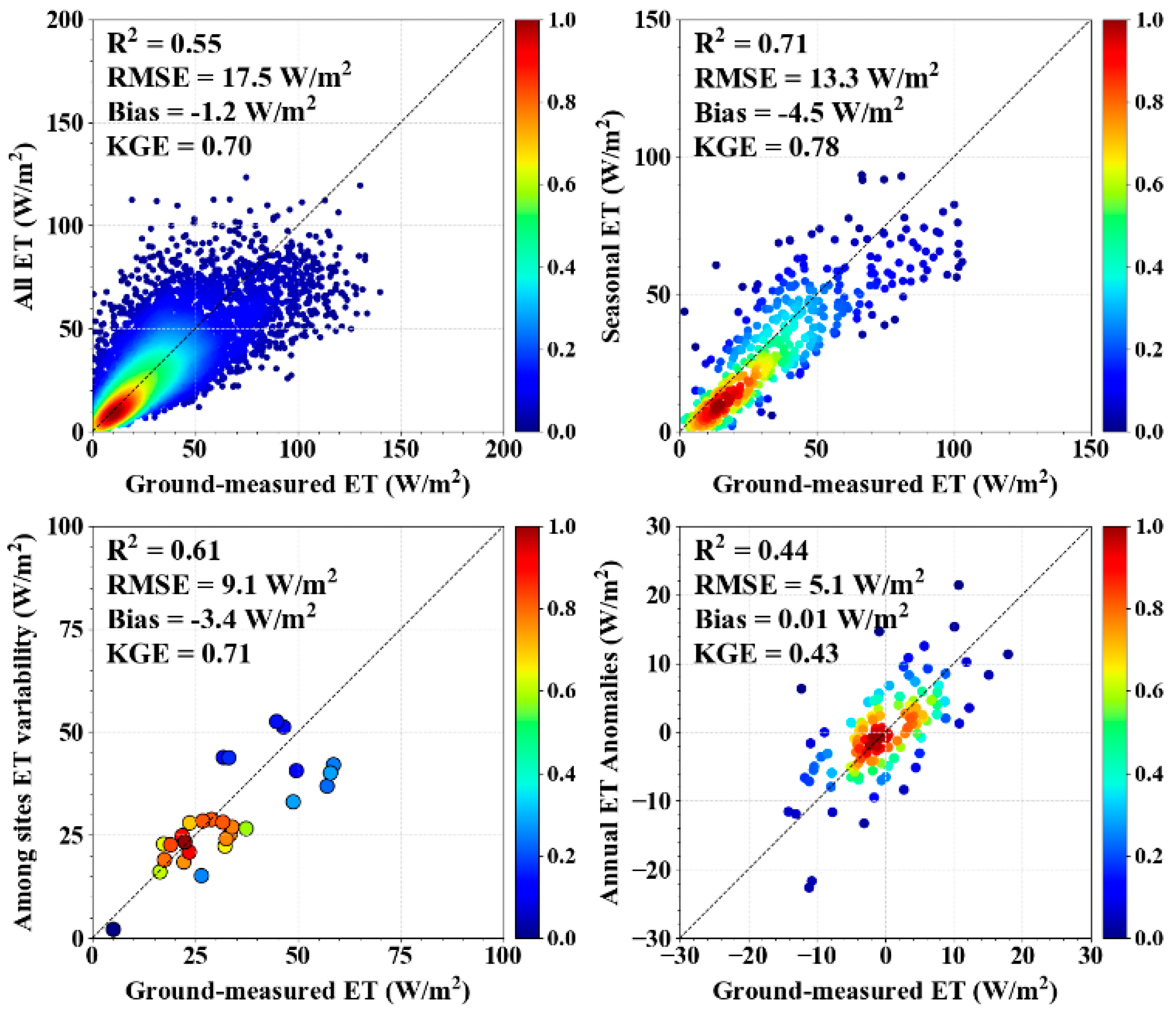
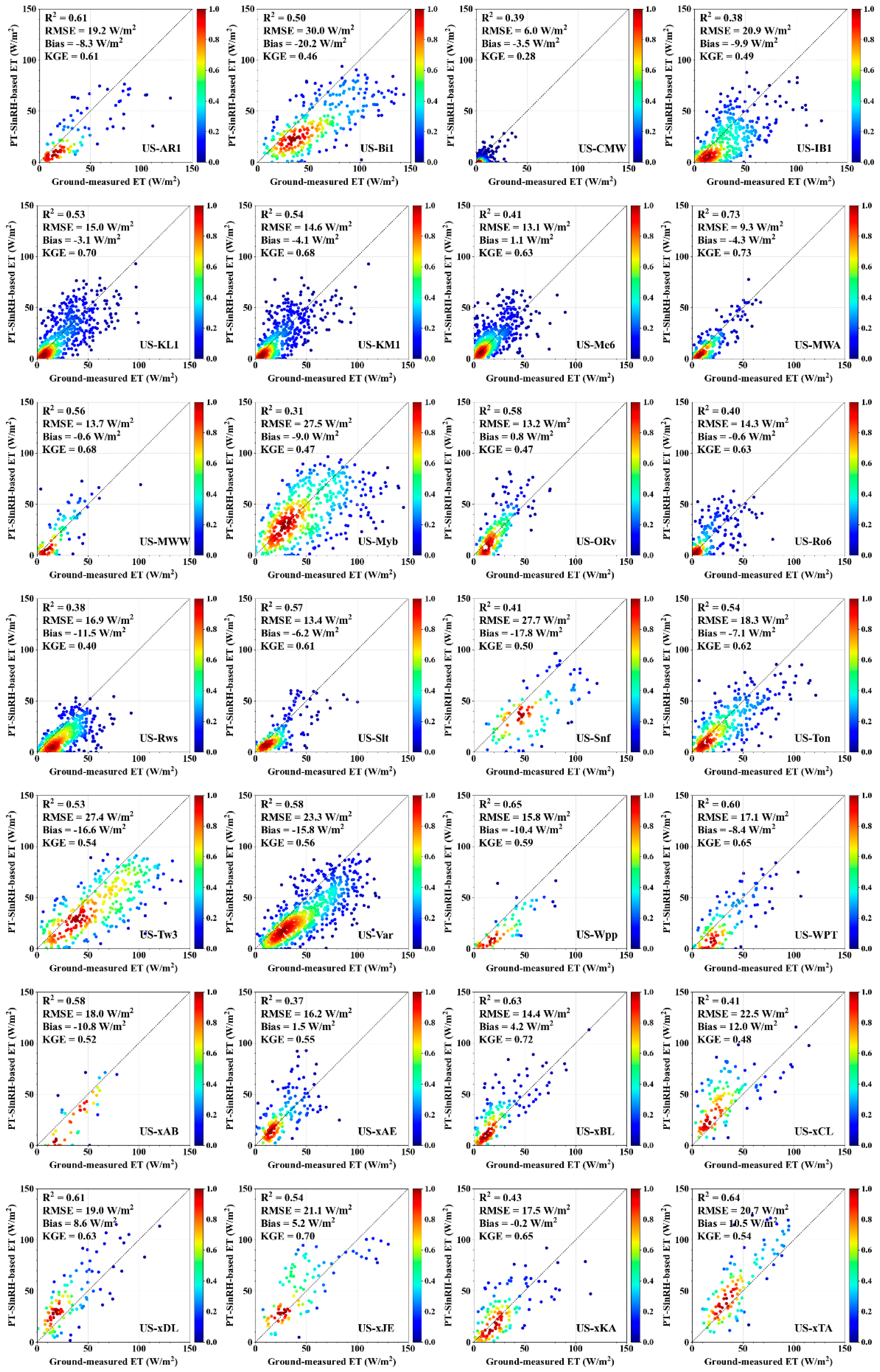
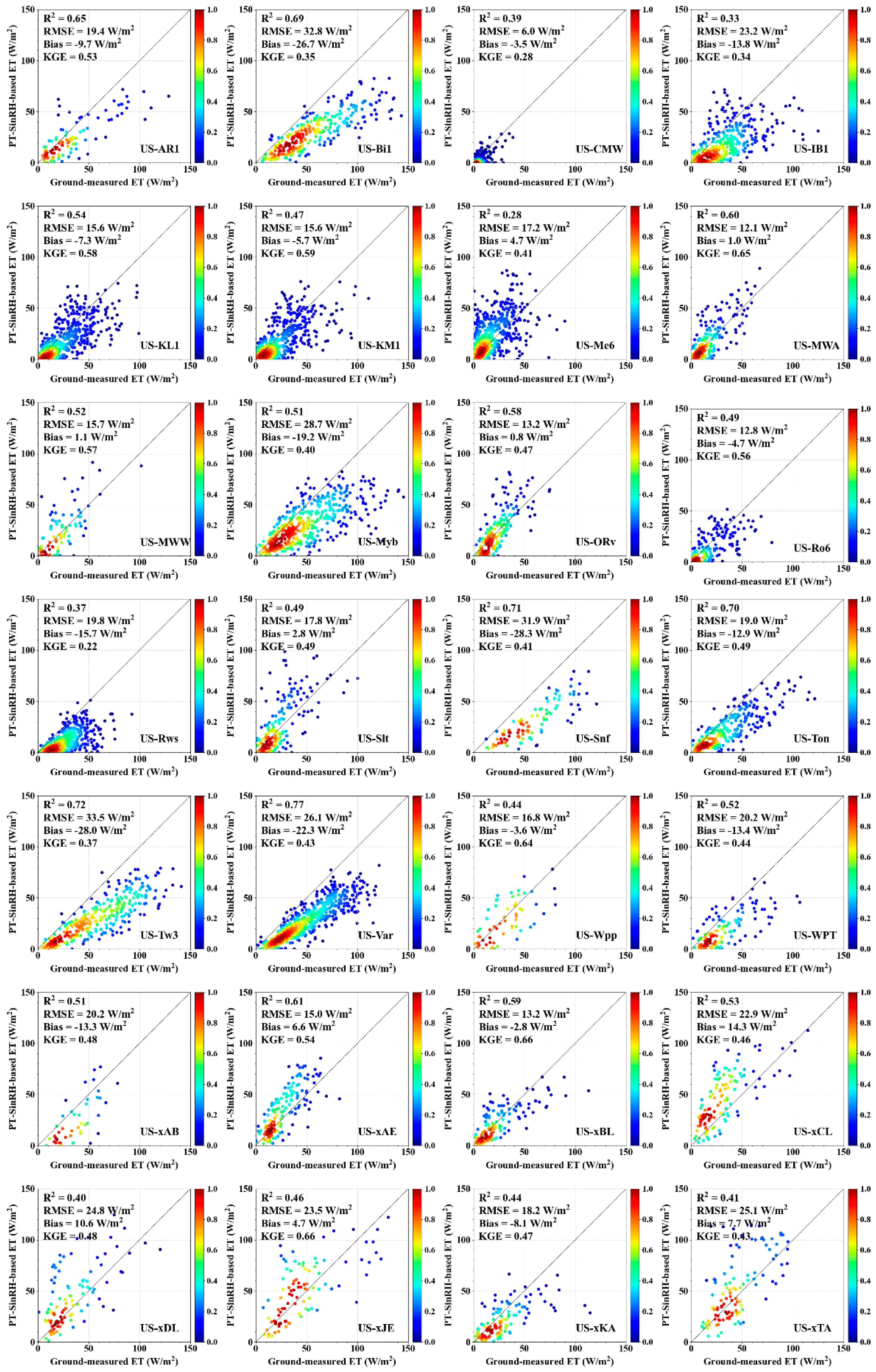
4.1. Model Validation Based on Site-Measured and Satellite Data Inputs
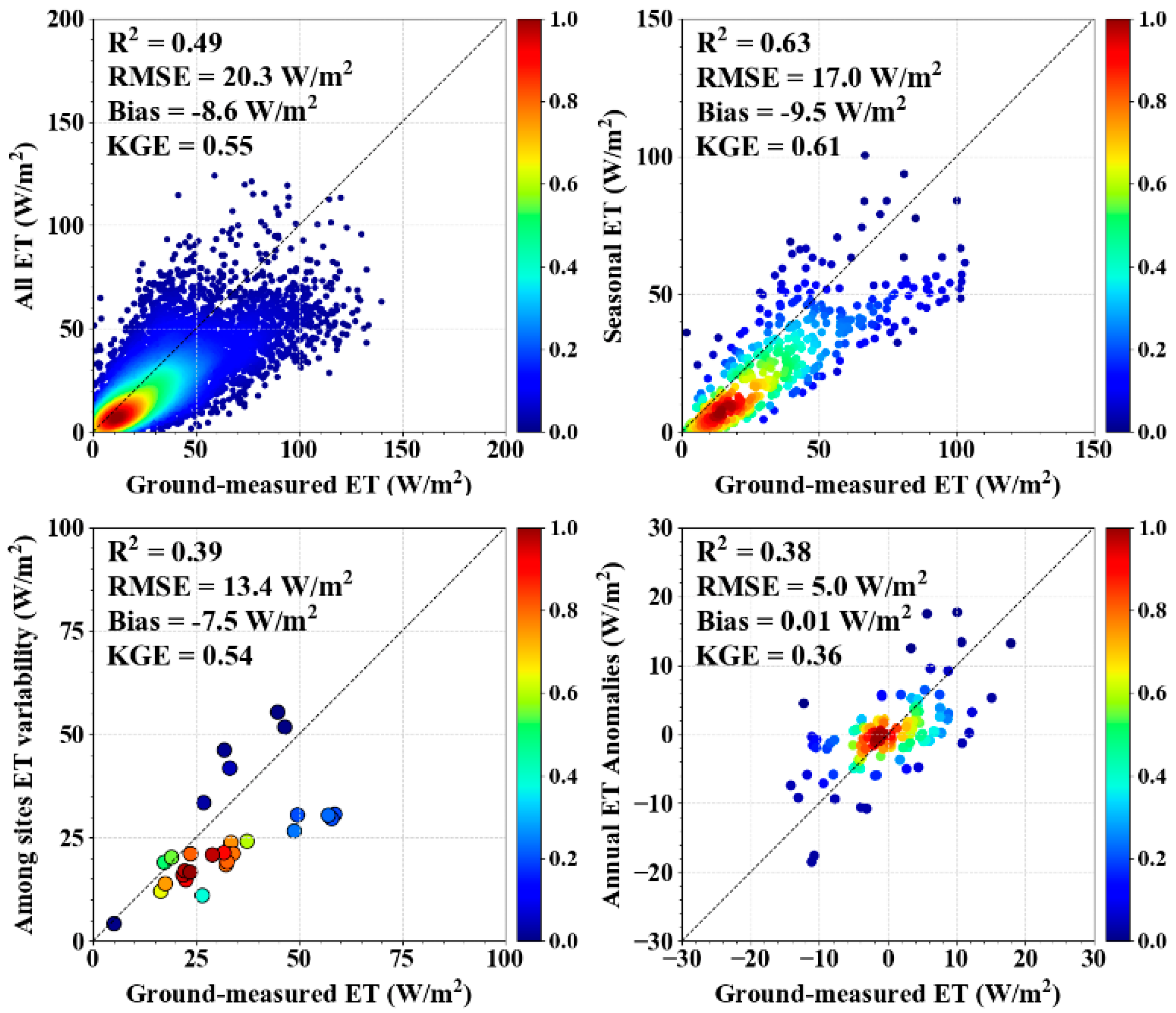
4.2. Model Validation Based on Reanalysis and Satellite Data Inputs
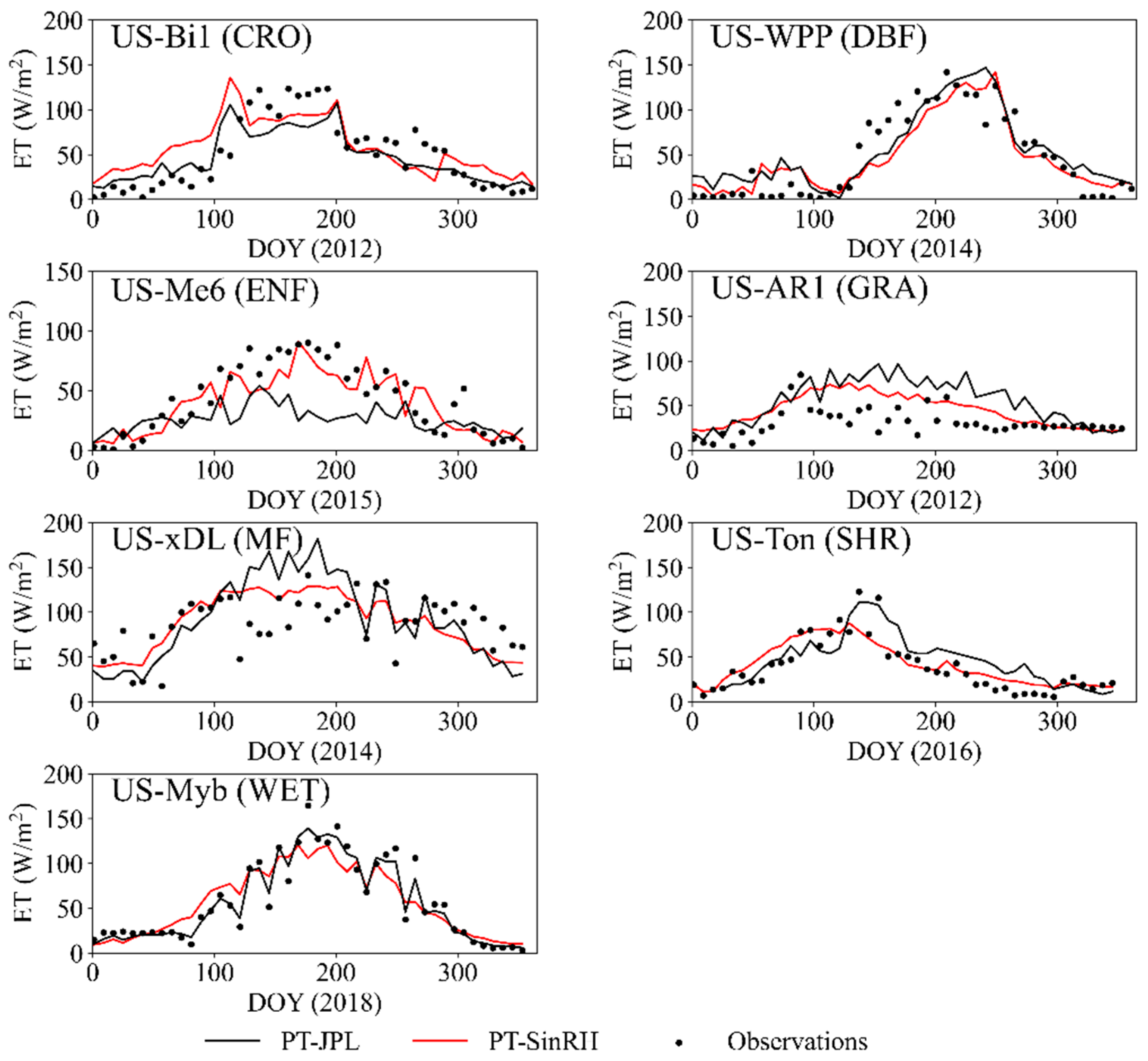
4.3. Comparison with the PT-JPL Model
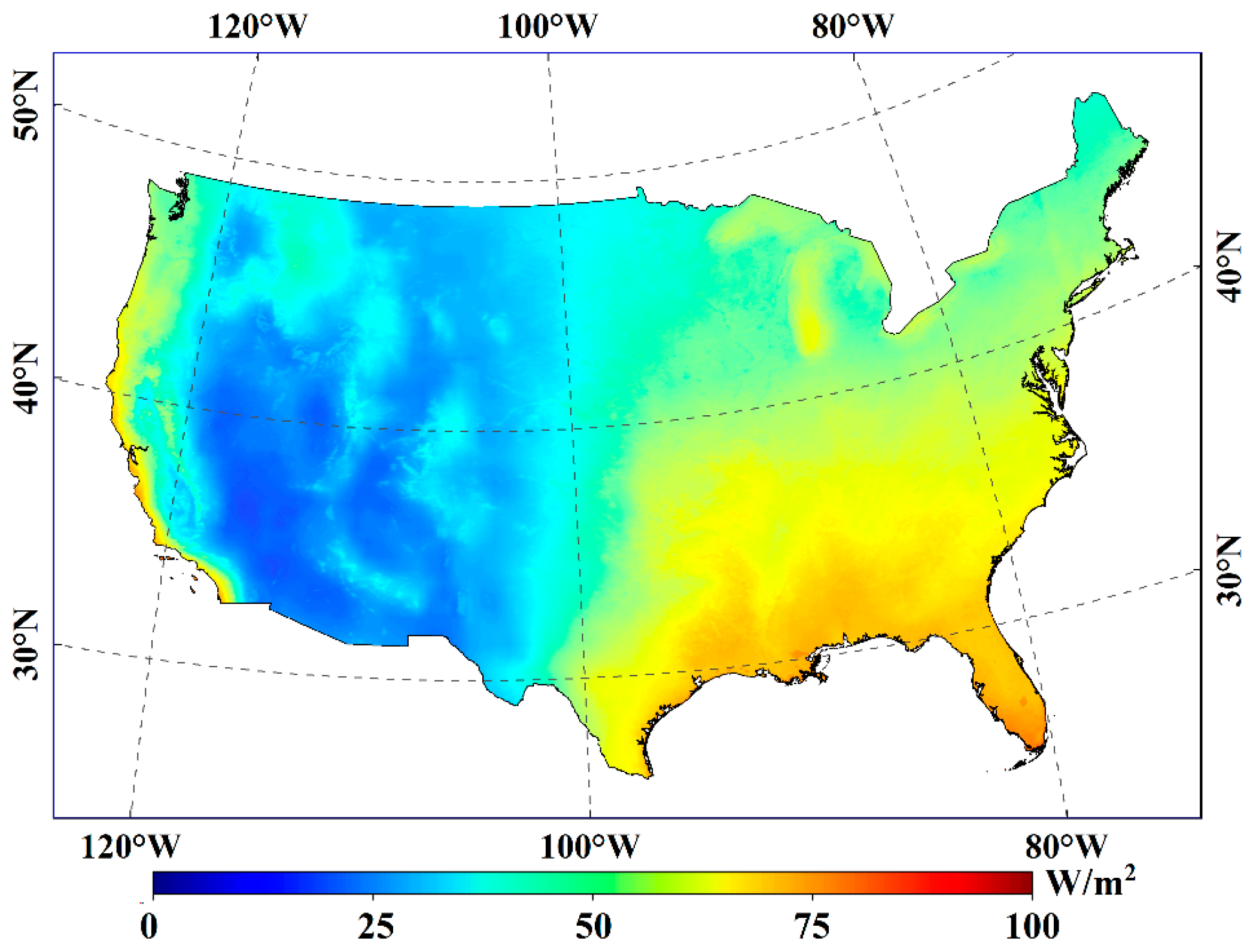
4.4. Mapping of PT-SinRH-Based Terrestrial ET Over CONUS
5. Discussion
5.1. Model Performance
5.1.1. Ability of the PT-SinRH Model to Simulate ET
5.1.2. Uncertainty in the PT-SinRH Estimates
5.2. Merits and Limitations of the PT-SinRH Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Liang, S.L.; Wang, K.C.; Zhang, X.T.; Wild, M. Review on estimation of land surface radiation and energy budgets from ground measurement, remote sensing and model simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Xu, Z.W.; Liu, S.M.; Zhu, Z.L.; Zhou, J.; Shi, W.J.; Xu, T.R.; Yang, X.F.; Zhang, Y.; He, X.L. Exploring evapotranspiration changes in a typical endorheic basin through the integrated observatory network. Agric. For. Meteorol. 2020, 290, 108010. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Yao, Y.J.; Liang, S.L.; Li, X.L.; Chen, J.Q.; Wang, K.C.; Jia, K.; Cheng, J.; Jiang, B.; Fisher, J.B.; Mu, Q.Z.; et al. A satellite-based hybrid algorithm to determine the Priestley-Taylor parameter for global terrestrial latent heat flux estimation across multiple biomes. Remote Sens. Environ. 2015, 165, 216. [Google Scholar] [CrossRef]
- Condon, L.E.; Atchley, A.L.; Maxwell, R.M. Evapotranspiration depletes groundwater under warming over the contiguous United States. Nat. Commun. 2020, 11, 873. [Google Scholar] [CrossRef] [PubMed]
- Fisher, J.B.; Lee, B.; Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A.; et al. ECOSTRESS: NASA’s next generation mission to measure evapotranspiration from the International Space Station. Water Resour. Res. 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
- Brust, C.; Kimball, J.S.; Maneta, M.P.; Jencso, K.; He, M.Z.; Reichle, R.H. Using SMAP Level-4 soil moisture to constrain MOD16 evapotranspiration over the contiguous USA. Remote Sens. Environ. 2021, 255, 112277. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Yao, Y.J.; Liang, S.L.; Yu, J.; Chen, J.Q.; Liu, S.M.; Lin, Y.; Fisher, J.B.; McVicar, T.R.; Cheng, J.; Jia, K.; et al. A simple temperature domain two-source model for estimating agricultural field surface energy fluxes from Landsat images. J. Geophys. Res.-Atmos. 2017, 122, 5211–5236. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Mu, Q.Z.; Zhao, M.S.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from Sparse Crops—An Energy Combination Theory. Q. J. R. Meteor. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Monteith, J.I.L. Evaporation and Environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Jung, M.; Koirala, S.; Weber, U.; Ichii, K.; Gans, F.; Camps-Valls, G.; Papale, D.; Schwalm, C.; Tramontana, G.; Reichstein, M. The FLUXCOM ensemble of global land-atmosphere energy fluxes. Sci. Data 2019, 6, 74. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.M.; Li, H.X.; Ma, Y.F.; Wang, J.H.; Zhang, Y.; Xu, Z.W.; Xu, T.R.; Song, L.S.; Yang, X.F.; et al. Intercomparison of Six Upscaling Evapotranspiration Methods: From Site to the Satellite Pixel. J. Geophys. Res.-Atmos. 2018, 123, 6777–6803. [Google Scholar] [CrossRef]
- Bateni, S.M.; Entekhabi, D.; Jeng, D.S. Variational assimilation of land surface temperature and the estimation of surface energy balance components. J. Hydrol. 2013, 481, 143–156. [Google Scholar] [CrossRef]
- Pipunic, R.C.; Walker, J.P.; Western, A. Assimilation of remotely sensed data for improved latent and sensible heat flux prediction: A comparative synthetic study. Remote Sens. Environ. 2008, 112, 1295–1305. [Google Scholar] [CrossRef]
- Mao, J.F.; Fu, W.T.; Shi, X.Y.; Ricciuto, D.M.; Fisher, J.B.; Dickinson, R.E.; Wei, Y.X.; Shem, W.; Piao, S.L.; Wang, K.C.; et al. Disentangling climatic and anthropogenic controls on global terrestrial evapotranspiration trends. Environ. Res. Lett. 2015, 10, 094008. [Google Scholar] [CrossRef]
- Talsma, C.J.; Good, S.P.; Jimenez, C.; Martens, B.; Fisher, J.B.; Miralles, D.G.; McCabe, M.F.; Purdy, A.J. Partitioning of evapotranspiration in remote sensing-based models. Agric. For. Meteorol. 2018, 260, 131–143. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Anderson, M.C.; Yang, Y.; Xue, J.; Knipper, K.R.; Yang, Y.; Gao, F.; Hain, C.R.; Kustas, W.P.; Cawse-Nicholson, K.; Hulley, G.; et al. Interoperability of ECOSTRESS and Landsat for mapping evapotranspiration time series at sub-field scales. Remote Sens. Environ. 2021, 252, 112189. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar] [CrossRef]
- Purdy, A.J.; Fisher, J.B.; Goulden, M.L.; Colliander, A.; Halverson, G.; Tu, K.; Farniglietti, J.S. SMAP soil moisture improves global evapotranspiration. Remote Sens. Environ. 2018, 219, 1–14. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Xie, Z.J.; Yao, Y.J.; Zhang, X.T.; Liang, S.L.; Fisher, J.B.; Chen, J.Q.; Jia, K.; Shang, K.; Yang, J.M.; Yu, R.Y.; et al. The Global LAnd Surface Satellite (GLASS) evapotranspiration product Version 5.0: Algorithm development and preliminary validation. J. Hydrol. 2022, 610, 127990. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Y.; Zhao, S.; Li, X.; Jia, K. Evaluation of three satellite-based latent heat flux algorithms over forest ecosystems using eddy covariance data. Environ. Monit. Assess. 2015, 187, 382. [Google Scholar] [CrossRef] [PubMed]
- Bai, P. Comparison of remote sensing evapotranspiration models: Consistency, merits, and pitfalls. J. Hydrol. 2023, 617, 128856. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Cheng, J.; Liu, S.; Fisher, J.B.; Zhang, X.; Jia, K.; Zhao, X.; Qin, Q.; Zhao, B. MODIS-driven estimation of terrestrial latent heat flux in China based on a modified Priestley–Taylor algorithm. Agric. For. Meteorol. 2013, 171, 187–202. [Google Scholar] [CrossRef]
- García, M.; Sandholt, I.; Ceccato, P.; Ridler, M.; Mougin, E.; Kergoat, L.; Morillas, L.; Timouk, F.; Fensholt, R.; Domingo, F. Actual evapotranspiration in drylands derived from in-situ and satellite data: Assessing biophysical constraints. Remote Sens. Environ. 2013, 131, 103–118. [Google Scholar] [CrossRef]
- Bouchet, R. Evapotranspiration reelle at potentielle, signification climatique. Int. Assoc. Sci. Hydro. Pub. 1963, 62, 134–142. [Google Scholar]
- Zhang, H.; Wu, B.; Yan, N. Remote sensing estimates of vapor pressure deficit: An overview. Adv. Earth Sci. 2014, 29, 559. [Google Scholar]
- Zhang, L.; Marshall, M.; Nelson, A.; Vrieling, A. A global assessment of PT-JPL soil evaporation in agroecosystems with optical, thermal, and microwave satellite data. Agric. For. Meteorol. 2021, 306, 108455. [Google Scholar] [CrossRef]
- Mahrt, L. Computing turbulent fluxes near the surface: Needed improvements. Agric. For. Meteorol. 2010, 150, 501–509. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.; Norman, J.; Cook, D.; Houser, P.; Meyers, T.; Prueger, J.; Starks, P.; Wesely, M. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Clement, R.; Malhi, Y.; Leuning, R.; Cleugh, H. A re-evaluation of long-term flux measurement techniques part I: Averaging and coordinate rotation. Bound.-Layer Meteorol. 2003, 107, 1–48. [Google Scholar] [CrossRef]
- Badgley, G.; Fisher, J.B.; Jiménez, C.; Tu, K.P.; Vinukollu, R. On uncertainty in global terrestrial evapotranspiration estimates from choice of input forcing datasets. J. Hydrometeorol. 2015, 16, 1449–1455. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W.; Nemani, R.R. Sensitivity of Moderate Resolution Imaging Spectroradiometer (MODIS) terrestrial primary production to the accuracy of meteorological reanalyses. J. Geophys. Res. Biogeosci. 2006, 111. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Zhang, Y.; Chen, J.; Jia, K.; Zhang, X.; Fisher, J.B.; Wang, X.; Zhang, L. Estimation of high-resolution terrestrial evapotranspiration from Landsat data using a simple Taylor skill fusion method. J. Hydrol. 2017, 553, 508–526. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Zhao, M.; Running, S.W.; Wofsy, S.C.; Urbanski, S.; Dunn, A.L.; Munger, J. Scaling gross primary production (GPP) over boreal and deciduous forest landscapes in support of MODIS GPP product validation. Remote Sens. Environ. 2003, 88, 256–270. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Bai, P.; Cai, C. Applicability evaluation of soil moisture constraint algorithms in remote sensing evapotranspiration models. J. Hydrol. 2023, 623, 129870. [Google Scholar] [CrossRef]
- Marshall, M.; Tu, K.; Andreo, V. On parameterizing soil evaporation in a direct remote sensing model of ET: PT-JPL. Water Resour. Res. 2020, 56, e2019WR026290. [Google Scholar] [CrossRef]
- Schenk, H.J.; Jackson, R.B. Rooting depths, lateral root spreads and below-ground/above-ground allometries of plants in water-limited ecosystems. J. Ecol. 2002, 90, 480–494. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Hashimoto, H.; Dungan, J.L.; White, M.A.; Yang, F.; Michaelis, A.R.; Running, S.W.; Nemani, R.R. Satellite-based estimation of surface vapor pressure deficits using MODIS land surface temperature data. Remote Sens. Environ. 2008, 112, 142–155. [Google Scholar] [CrossRef]
- Mallick, K.; Bhattacharya, B.K.; Patel, N.K. Estimating volumetric surface moisture content for cropped soils using a soil wetness index based on surface temperature and NDVI. Agric. For. Meteorol. 2009, 149, 1327–1342. [Google Scholar] [CrossRef]
- McNaughton, K.; Spriggs, T.W. An evaluation of the Priestley and Taylor equation and the complementary relationship using results from a mixed-layer model of the convective boundary layer. Estim. Areal Evapotranspiration 1989, 177, 89–104. [Google Scholar]
- Brutsaert, W. A generalized complementary principle with physical constraints for land-surface evaporation. Water Resour. Res. 2015, 51, 8087–8093. [Google Scholar] [CrossRef]
- Kustas, W.P.; Moran, M.S.; Humes, K.S.; Stannard, D.I.; Pinter, P.J.; Hipps, L.E.; Swiatek, E.; Goodrich, D.C. Surface-Energy Balance Estimates at Local and Regional Scales Using Optical Remote-Sensing from an Aircraft Platform and Atmospheric Data Collected over Semiarid Rangelands. Water Resour. Res. 1994, 30, 1241–1259. [Google Scholar] [CrossRef]
- Pitman, A.J. Assessing the Sensitivity of a Land-Surface Scheme to the Parameter Values Using a Single-Column Model. J. Clim. 1994, 7, 1856–1869. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Sun, X.M.; Zhu, Z.L.; Zhang, R.H.; Tian, J.; Liu, Y.F.; Guan, D.X.; Yuan, G.F. Surface roughness length dynamic over several different surfaces and its effects on modeling fluxes. Sci. China Ser. D 2006, 49, 262–272. [Google Scholar] [CrossRef]



| Parameter | Description | Formula |
|---|---|---|
| Evapotranspiration | ||
| Canopy transpiration | ||
| Soil evaporation | ||
| Interception evaporation | ||
| Relative surface wetness | ||
| Green canopy fraction | ||
| Plant temperature constraint | ||
| Plant moisture constraint | ||
| Soil moisture constraint | ||
| Fraction of PAR absorbed by green vegetation cover | ||
| Fraction of PAR intercepted by total vegetation cover | ||
| Fractional total vegetation cover | ||
| Optimum plant growth temperature |
| ID | Site Name | Lat (N), Long (E) | IGBP | ID | Site Name | Lat (N), Long (E) | IGBP |
|---|---|---|---|---|---|---|---|
| 1 | US-AR1 | 36.4267, −99.4200 | GRA | 15 | US-Snf | 38.0402, −121.7272 | GRA |
| 2 | US-Bi1 | 38.0992, −121.4993 | CRO | 16 | US-Ton | 38.4309, −120.9660 | SHR |
| 3 | US-CMW | 31.6637, −110.1777 | DBF | 17 | US-Tw3 | 38.1152, −121.6469 | CRO |
| 4 | US-IB1 | 41.8593, −88.2227 | CRO | 18 | US-Var | 38.4133, −120.9508 | GRA |
| 5 | US-KL1 | 42.4847, −85.4422 | CRO | 19 | US-Wpp | 44.1369, −123.1824 | DBF |
| 6 | US-KM1 | 42.4376, −85.3287 | CRO | 20 | US-WPT | 41.4646, −82.9962 | WET |
| 7 | US-Me6 | 44.3233, −121.6078 | ENF | 21 | US-xAB | 45.7624, −122.3303 | ENF |
| 8 | US-MWA | 42.2143, −84.8539 | CRO | 22 | US-xAE | 35.4106, −99.0588 | GRA |
| 9 | US-MWW | 42.6689, −86.0229 | WET | 23 | US-xBL | 39.0603, −78.0716 | DBF |
| 10 | US-Myb | 38.0503, −121.7652 | WET | 24 | US-xCL | 33.4012, −97.5700 | GRA |
| 11 | US-ORv | 40.0201, −83.0183 | WET | 25 | US-xDL | 32.5417, −87.8039 | MF |
| 12 | US-Ro6 | 44.6946, −93.0578 | CRO | 26 | US-xJE | 31.1948, −84.4686 | ENF |
| 13 | US-Rws | 43.1675, −116.7132 | SHR | 27 | US-xKA | 39.1104, −96.6129 | GRA |
| 14 | US-Slt | 39.9138, −74.5960 | DBF | 28 | US-xTA | 32.9505, −87.3933 | ENF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Yao, Y.; Li, Y.; Liu, L.; Ning, J.; Yu, R.; Fan, J.; Kan, Y.; Zhang, L.; Xu, J.; et al. Satellite-Based PT-SinRH Evapotranspiration Model: Development and Validation from AmeriFlux Data. Remote Sens. 2024, 16, 2783. https://doi.org/10.3390/rs16152783
Xie Z, Yao Y, Li Y, Liu L, Ning J, Yu R, Fan J, Kan Y, Zhang L, Xu J, et al. Satellite-Based PT-SinRH Evapotranspiration Model: Development and Validation from AmeriFlux Data. Remote Sensing. 2024; 16(15):2783. https://doi.org/10.3390/rs16152783
Chicago/Turabian StyleXie, Zijing, Yunjun Yao, Yufu Li, Lu Liu, Jing Ning, Ruiyang Yu, Jiahui Fan, Yixi Kan, Luna Zhang, Jia Xu, and et al. 2024. "Satellite-Based PT-SinRH Evapotranspiration Model: Development and Validation from AmeriFlux Data" Remote Sensing 16, no. 15: 2783. https://doi.org/10.3390/rs16152783
APA StyleXie, Z., Yao, Y., Li, Y., Liu, L., Ning, J., Yu, R., Fan, J., Kan, Y., Zhang, L., Xu, J., Jia, K., & Zhang, X. (2024). Satellite-Based PT-SinRH Evapotranspiration Model: Development and Validation from AmeriFlux Data. Remote Sensing, 16(15), 2783. https://doi.org/10.3390/rs16152783









