Abstract
Sun-induced chlorophyll fluorescence (SIF) has proven to be advantageous in estimating gross primary production, despite the lack of a stable relationship. Satellite-based SIF measurements at Level 2 offer comprehensive global coverage and are available in near real time. However, these measurements are often limited by spatial and temporal sparsity, as well as discontinuities. These limitations primarily arise from incomplete satellite trajectories. Additionally, variability in cloud cover and periodic issues specific to the instruments can compromise data quality. Two families of methods have been developed to address data discontinuity: (1) machine learning-based gap-filling techniques and (2) geostatistical techniques (various forms of kriging). The former techniques utilize the relationships between ancillary data and SIF, while the latter usually rely on the available SIF data recordings and their covariance structure to provide estimates at unsampled locations. In this study, we create a synthetic approach for SIF gap filling by hybridizing the two approaches under the umbrella of kriging with external drift. We performed leave-one-out cross-validation of the OCO-2 SIF retrieval aggregates for the entire year of 2019, comparing three methods: ordinary kriging, ML-based estimation using ancillary data, and kriging with external drift. The Mean Absolute Error (MAE) for ML, ordinary kriging, and the hybrid approach was found to be 0.1399, 0.1318, and 0.1183 mW m2 sr−1 nm−1, respectively. We demonstrate that the performance of the hybrid approach exceeds both parent techniques due to the incorporation of information from multiple resources. This use of multiple datasets enriches the hybrid model, making it more robust and accurate in handling the spatio-temporal variability and discontinuity of SIF data. The developed framework is portable and can be applied to SIF retrievals at various resolutions and from various sources (satellites), as well as extended to other satellite-measured variables.
1. Introduction
Without the ability to precisely define CO2 dynamics, understanding ecosystem–climate interactions is very difficult [1,2]. Gross primary production (GPP) is the primary driver of land CO2 sink, removing approximately one-quarter of annual anthropogenic CO2 emissions [3]. The signal of sun-induced chlorophyll fluorescence (SIF) is a promising predictor of vegetation function [4]. It directly reflects the photosynthetic activity of plants and can be used as a remote sensing index for estimating photosynthetic energy conversion and carbon absorption [1,5]. Using multiple available platforms, global spatio-temporal patterns of SIF can be easily monitored from space [6,7,8,9,10,11,12,13]. While SIF can be used as a proxy for intra- and inter-annual global and regional patterns in GPP [7,14,15,16], its relationship to GPP is biome- [5,13] and scale-dependent [1,13].
Despite the promising potential of SIF as a proxy for GPP, limitations in the current satellite SIF Level 2 data hinder our understanding of the GPP-SIF relationship at various scales. For clarity, ‘SIF Level 2 data’ refers to satellite-retrieved SIF data that retain the original satellite viewing geometry and have undergone basic quality control and calibration but lack global coverage due to the satellite’s orbital path and cloud cover. Ideally, these data would be available at high resolutions and provide global, contiguous coverage, which, unfortunately, is seldom the case. As a result, a variety of methodologies have been developed to generate contiguous Level 3 SIF data, sometimes at resolutions different from the native Level 2 data, thereby addressing some of the shortcomings mentioned above. Level 2 data represent a higher level of processed information compared to Level 1 data, which typically include raw or minimally processed sensor data. Level 2 SIF satellite data undergo additional processing steps, such as radiometric and geometric corrections, atmospheric corrections, and calibration. These processes aim to remove various artifacts and correct for known errors or biases in the raw data, resulting in more accurate and usable information. Typically, Level 3 processing refers to the aggregation and averaging of satellite data over larger spatial and temporal scales, which implies coarser resolution of the Level 3 datasets, usually gap-free. This aggregation helps to reduce noise and improve the overall accuracy and reliability of the data. Geostatistics and multiple machine learning techniques [17] used so far for this purpose demonstrated the possibility of creating Level 3 datasets matching or even exceeding the spatio-temporal supports of the Level 2 datasets. An example of such a high-resolution dataset is GOSIF, derived from OCO-2 satellite observations, Moderate Resolution Imaging Spectroradiometer (MODIS), and meteorological reanalysis data, which significantly enhances our ability to monitor global photosynthesis and assess ecosystem health and functionality, as in a study by [18].
Broadly, the spectrum of the created approaches can be divided into two groups: (1) ML-based approaches and (2) geostatistical approaches. The former group of methods exploits the relationships between SIF and ancillary data, which broadly represent various covariates informative of the SIF value (e.g., NDVI), aiming to reconstruct the SIF value at unsampled locations, while the latter group leverages the observed/modeled autocovariance structure within available data and then utilizes measurements and modeled covariance structure to reconstruct the data at unsampled locations. Both approaches have been successfully deployed so far to improve, downscale, or fill gaps in SIF satellite SIF measurements. For example, refs. [19,20] recently used a convolutional neural network (CNN) and Extreme Gradient Boosting (XGBoost), together with high-resolution ancillary data, to downscale SIF retrievals from a TROPOspheric Monitoring Instrument (TROPOMI) on board the satellite Sentinel-5P by a factor of up to 500 m and 0.05°, respectively. Refs. [21,22] harmonized GOME-2 and SCIAMACHY SIF datasets using ML with a moderate-resolution imaging spectroradiometer (MODIS) to downscale SIF products. Ref. [23] created a high-resolution OCO-2 Level 3 SIF dataset using ML constrained by physiological understandings, and ref. [24] did the same using high-resolution ancillary data. Ref. [22] recently downscaled the GOME-2 SIF Level 2 dataset using the Random Forest (RF) model. Ref. [25] downscaled OCO-2 SIF data to a super-fine resolution of 0.0005° using convolutional neural networks. Examples of the application of geostatistics to improve Level 2 satellite data are numerous, and some of the previous efforts were focused on SIF Level 2 data. In our previous studies [26,27], we gap filled GOME-2 SIF Level 2 data and provided a framework for upscaling and harmonizing the data to a higher resolution to create contiguous Level 3 datasets. The approach was based on modeling the covariance structure of Level 2 SIF data and employing spatial [27] or spatio-temporal covariance models [26] to estimate SIF at unsampled locations using the block kriging methodology. This methodology allows for the estimation of SIF values at locations not covered by genuine Level 2 data while also accounting for the change in support compared to the original Level 2 data. In a recent study, we further improved the modeling approach that can be used to process SIF data [28]. Interestingly, despite the common goals and similar outputs, these two groups of methods have never been directly compared or evaluated together, nor has the potential of creating a synthetic approach been exploited.
In this study, we venture beyond the existing methods and explore the potential of a hybrid model that integrates kriging and machine learning-based approaches. Our goal is to assess whether this hybridization could yield superior accuracy in SIF estimates by capitalizing on the strengths of both methodologies. Before the study, we expected that the hybrid technique’s accuracy would outperform both approaches separately due to synergy, given that the two techniques rely on different types of inputs, namely the relationship of the primary variable with ancillary data and the spatio-temporal covariance structure of the primary variable, in this case, SIF data. We chose universal kriging, also known as kriging with external drift, as the geostatistical component of our hybridization framework. This choice was inspired by its successful use in a similar context, where it helped reconstruct the spatial distribution pattern of the CO2 mixing ratio [29]. For the machine learning component, instead of creating a model and dataset from scratch, we opted to use a publicly available, recently created contiguous Level 3 OCO-2 SIF dataset created using neural networks [24] as a covariate in the hybrid approach; thus, the properties of the used dataset, including the SIF bands used, spatio-temporal resolution, etc., match the ones from that study. These resources, we believe, provide a solid foundation for our hybrid model due to their proven effectiveness in similar applications. We deployed the moving window ordinary kriging technique as a paradigmatic geostatistical approach, mimicking the approach from [27]. This method has already been used to estimate GOME-2 SIF at native and upscaled resolution. To evaluate the accuracy of both the parent techniques and the newly created hybrid, we employed a validation method known as ‘leave-one-out cross-validation’. In simpler terms, this method involves using one data point from the dataset as a ‘test’ case and the rest of the dataset for ‘training’. This process is repeated for each data point in our dataset, which consists of the entire 2019 year of OCO-2 SIF retrieval aggregates, containing over 400,000 data points (see Section 2.2).
2. Methods
Our research is underpinned by the assumption that both geostatistical and machine learning (ML) methodologies for quantifying solar-induced chlorophyll fluorescence (SIF) can achieve enhanced effectiveness when synergistically combined within a hybrid model. To test this hypothesis, we use a combination of aggregated SIF retrieval data and ML-based SIF estimates as inputs to the hybrid technique, which are built within the kriging with the external drift framework. The ML-based estimates are derived from a continuous SIF (CSIF) dataset published by [24], where the authors introduced a novel application of a multi-layer perceptron (MLP) type of ANN for generating a spatio-temporally continuous Level 3 SIF dataset based on ancillary data obtained from the Moderate Resolution Imaging Spectroradiometer (MODIS) instrument. The resulting CSIF product has a spatial resolution of 0.05 degrees (equivalent to approximately 5.6 km × 5.6 km at the equator) and a temporal resolution of four days, which aligns with the MODIS climate model grid (CMG) resolution and the resolution of the ancillary variables used in the original ML technique. The SIF estimates generated by this method will be validated with the aggregated SIF measurements from the Orbiting Carbon Observatory-2 (OCO-2) satellite at the corresponding geolocations (grid cells) of the CMG, where both the target SIF measurements and the ancillary variable measurements were recorded.
2.1. Data
OCO-2 is a NASA satellite that was launched in July 2014. The instrument possesses a three-channel grating spectrometer, with a spectral resolving power of [6,30], centered around the oxygen A band at 0.765 µm and carbon dioxide bands at 1.61 and 2.06 µm. The instrument conducts eight measurements across tracks, with swath widths of ~10 km. Its spatial resolution at the nadir is 1.3 km × 2.25 km. It has a 98.8 min orbit, with a 13:36 nodal crossing time and a 16 d ground-track repeat cycle [31]. OCO-2 SIF retrievals were validated by comparison to airborne measurements using the Chlorophyll Fluorescence Imaging Spectrometer [13,32]. Figure 1 shows the flight trajectory of the OCO-2 satellite on the world map and the measured SIF values.
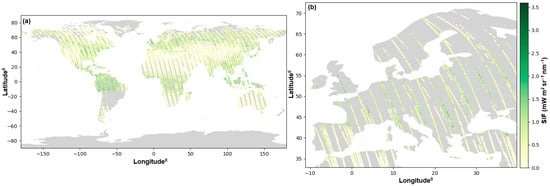
Figure 1.
(a) Global OCO-2 SIF retrievals (mW m2 sr−1 nm−1; at 740 nm) and (b) the same for Europe, collected over the entire year 2019, showing the degree of sparsity of the Level 2 OCO-2 SIF data.
When utilizing data as inputs for a hybrid data analysis technique like kriging with external drift, the spatial resolution must be carefully considered. In this study, the main variable (SIF retrievals) and the support variable (ML-based estimates) must have the same spatial resolution to produce accurate results. The optimal resolution is determined by the lower resolution of the two inputs, which, in this case, is the resolution of the CMG. Therefore, the support of the main variable must be spatially aligned with the grid cells to maintain consistency. To ensure this consistency, the Level 2 OCO-2 SIF retrievals were brought to a uniform 0.05-degree resolution using the process of aggregation. This involved selecting all SIF soundings within the bounds of a specific grid cell, as well as choosing only recoveries classified as clear-sky in the OCO-2 dataset. The remaining retrievals were then aggregated by calculating their mean, following the approach outlined by [33]. As a final step, grid cells containing less than five clear-sky retrievals were removed from the pseudo-retrieval SIF dataset.
The measured values of solar-induced fluorescence (SIF) are subject to variations that are primarily influenced by several factors, each of which contributes differently based on the environment and context of observation. The challenges of upscaling SIF measurement to daily average values are discussed in detail in a recent study [34]. The impacts of solar-view geometry and canopy structure were analyzed in [35] and the impact of growth and environmental factors in [36]. In addition, vegetation physiology and stress can cause variations ranging from 5% in controlled agricultural settings to more than 50% in natural ecosystems under environmental stress [36,37]. Additionally, the viewing geometry of the satellite and its orbital characteristics can introduce variability in SIF measurements by 5–20%, depending on the sensor and orbit specifics [38].
2.2. Generating Continuous SIF Estimates by Using an ML Model
In a study by [24], a neural network architecture composed of five input variables and one output variable was used to precisely estimate clear-sky solar-induced chlorophyll fluorescence (SIF) values at specific coordinates. The input variables, which were selected based on their informative value, were obtained from the Nadir Bidirectional reflectance distribution Adjust Reflectance (NBAR) product of the MODIS (Moderate Resolution Imaging Spectroradiometer) dataset (MCD43C4 V006). In particular, the first four bands of MODIS were utilized to extract the reflectance data, which center at wavelengths of 645 nm, 858 nm, 469 nm, and 555 nm, as previously suggested [39]. These particular bands were chosen due to their known influence on the variation in SIF and their inclusion of significant vegetation-related information [40]. It is important to highlight that the selection, rationale, and justification, as well as any potential constraints, regarding the training data utilized in the development of the machine learning (ML) model by [24], were beyond the control of the authors of the current study. While it could be argued that the incorporation of additional variables, such as supplementary vegetation indices or meteorological data, might alter or enhance the performance of the ML model, it is pertinent to note that the neural network-generated dataset is publicly available and serves an as input for our study. Therefore, providing an extensive elaboration on the decisions made during the development of that dataset is beyond the scope of this study. The output variables used for training the neural network were derived from the OCO-2 dataset and consisted of sounding-based SIF retrievals at 757 nm. The output data were subsequently processed by averaging and filtering, and the CMG resolution was adjusted to align with the resolution of the input data.
To accurately estimate the values of solar-induced chlorophyll fluorescence (SIF) using a hybrid method, data were collected from the OCO-2 SIF dataset for the entirety of 2019. This period was selected to account for any intra-annual and seasonal variations in the SIF signal and any potential correlations between SIF and other variables. This study is confined to 2019, despite the availability of data beyond this timeframe, as its primary focus lies in method development rather than providing updated or expanded datasets. The resulting dataset served as a reference, against which the performance of the machine learning (ML), geostatistical, and hybrid approaches was compared using the leave-one-out cross-validation scheme (detailed in Section 2.5). The fraction of the CSIF product used for the development of the hybrid method also includes data from the entire year of 2019. This specific year was chosen due to the availability of the most recent version of the CSIF product, with a full year’s data. This allows for the alignment of the collection of the ground truth data with the best-available ML-based SIF estimates in support of the hybrid method. An R2 analysis was performed on the CSIF and OCO-2 data, specifically for the year 2019, to ensure the data’s validity. The OCO-2 data were initially aggregated for each grid cell, creating pseudo-retrievals, a term referred to in the subsequent sections, following the methodology introduced by [24]. This approach considers only clear-sky values and grid cells with more than 5 clear-sky observations. The resulting plot is illustrated in Figure 1a. The achieved R2 score is 0.80, comparable to values reported in the original study.
2.3. Moving Window Ordinary Kriging
The ordinary kriging method used in the present study builds on the previous work of [27,41]. We perform the three-step mapping for each estimation location using observations collected on the same day. These steps are as follows: (1) subsampling of the observations, (2) characterization of the local spatial covariance structure, and (3) interpolation at the native spatial resolution. The kriging scheme that does not allow for the change of support is chosen because the supports for the pseudo-retrievals and ML-derived estimates have been previously harmonized. The goal of the subsampling strategy is to put more weight on the observations in the vicinity of a given estimation location, for both the characterization of the local spatial covariance structure and interpolation step, so that the mapped value and the associated uncertainty are representative of local values and variability. This is accomplished by selecting the minimum number of observations (N) that need to be present within the distance (‘moving window’; D) from the estimation location for the mapping to be performed. N is selected to be large enough to yield a representative sample. We do not constrain the upper bound of N, because all Ns encountered in this use case were computationally feasible to process. For the present study, N was set to 20 and D to 500 km. The preliminary step of the modeling is variography. For each estimation grid cell, a raw variogram is calculated based on the subsampled observations:
where γ is the raw variogram value for a given pair of observations y(xi) and y(xj), and h is the great circle distance between the locations and ) of these observations. The exponential theoretical variogram model with a nugget effect is fitted to the raw variogram using non-linear least squares, mimicking [27]:
where σ2 and are the variance and correlation length of the quantity mapped quantity, and σ2nug is the nugget variance, typically representative of retrieval errors.
The variogram parameters are used to define a corresponding local spatial covariance structure:
The matrix representing the measurement and retrieval error covariance structure (the nugget effect) is:
After modeling covariance parameters for each estimation location, the linear system of equations is solved to obtain the N weights λ assigned to the subsampled observations:
where Q is an N × N covariance matrix among the N subsampled observations, as defined in Equation (3), R is an N × N diagonal retrieval error covariance matrix among the N observations, as defined in Equation (4), 1 is an N × 1 unity vector, T denotes the vector transpose operation, and q is an N × 1 vector of the spatial covariances between the estimation location and the N observation locations.
λ and the Lagrange multiplier are obtained by solving the system in Equation (5). They are subsequently used to define the estimate (ẑ) and estimation uncertainty variance (σ2ẑ):
where y is the N × 1 vector of subsampled observations, and σ is the variance in the SIF, as shown in Equation (3).
ẑ = λTy
σ2ẑ = σ2 − λT q + ν
2.4. Hybrid Approach: Kriging with External Drift
Universal kriging, also known as kriging with external drift, is a technique used for data with a significant trend [42]. The mathematical machinery of universal kriging is very similar to that of ordinary kriging (see Equations (5)–(7) in [43]). In many cases encountered in environmental sciences, the trend is described as a function of spatial or spatio-temporal coordinates. However, the universal kriging framework is indifferent to the origins of the trend component, which allows for the use of machine learning (ML) SIF estimates as the source of the trend. The resulting approach combines kriging, which relies on spatial covariance structure analysis, with ML, which relies on the relationship between the primary variable (SIF) and ancillary data. It is generally accepted that the inclusion of secondary variables improves the accuracy of the kriging-based predictions [43], and this method also allows for the inclusion of non-linearities in kriging through the use of ML SIF covariates, making the hybrid technique more flexible. Alternatively, instead of introducing ML predictions as covariates into kriging machinery, one could use a regression kriging approach, i.e., first, ML predictions are used as the model of the trend, followed by kriging the residuals using ordinary kriging. However, these two approaches are mathematically equivalent and produce identical results [44].
Furthermore, the ML-based SIF estimates are employed as ancillary data (1) in the universal kriging scheme (2), along with the Level 2 SIF data (4) and covariance model parameters (6) derived through variography based on the Level 2 SIF data (5), Figure 2. These three inputs undergo universal kriging to generate hybrid SIF estimates, which exhibit superior performance compared to both ML-based estimates and purely geostatistical estimates without ancillary data.
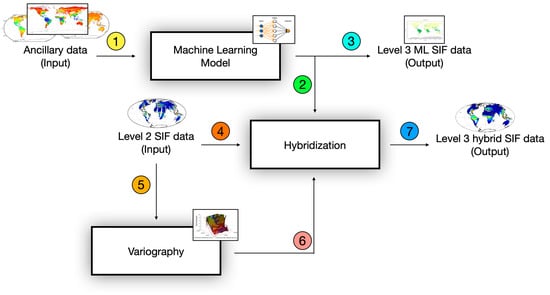
Figure 2.
The dataflow flowchart illustrates the hybrid approach incorporating kriging with external drift. Ancillary data are acquired as an output from the pure machine learning module for solar-induced fluorescence (SIF) prediction. On the left side, we depict the inputs for both parent techniques, in the form of ancillary data and Level 2 SIF data. On the right side, we present the final outputs from the ML-based approach (‘Level 3 ML SIF data’) and the hybrid approach (‘Level 3 hybrid SIF data’). The output from the ML-based approach serves as input for the hybrid approach. The ML-based SIF estimates are employed as ancillary data (1) in the universal kriging scheme (2), along with the Level 2 SIF data (4) and covariance model parameters (6) derived through variography based on the Level 2 SIF data (5), to produce final outputs (7).
By incorporating both ML-based and geostatistical techniques, the hybrid method leverages the strengths of each approach, leading to improved SIF estimates. The utilization of ancillary data, including ML-based estimates and Level 2 SIF data, contributes to the enhanced accuracy and reliability of the hybrid SIF estimates.
This hybrid approach utilizes machine learning (ML)-derived solar-induced fluorescence (SIF) estimates as an external drift in the kriging with external drift model, effectively exploiting the detailed spatial patterns and relationships captured by ML together with the spatial interpolation strength of kriging. The methodological integration aims to mitigate the limitations inherent in each approach when used independently, thereby offering a more robust and accurate estimation of SIF.
Combining machine learning models with geostatistical methods, this hybrid approach leverages the strengths of both methodologies: the capacity of machine learning to handle complex, non-linear relationships within large datasets, and the efficacy of geostatistical methods in incorporating spatial autocorrelation and addressing spatial data anomalies. Through this integration, our objective is to enhance prediction accuracy and reliability beyond what could be achieved using individual methods, particularly in spatial contexts where environmental variables exhibit strong spatial dependencies.
While SIF measurements and predictions were utilized to illustrate the current approach, it is essential to note that the applicability of this methodology is not limited to SIF alone. We aim to establish a potential general framework for the hybridization of ML and geostatistical approaches in other domains.
2.5. Method Evaluation: Leave-One-Out Cross-Validation
The performance of the mapping method was tested in terms of (1) accuracy (the difference between estimates and true values) and (2) bias (the mean of the difference between estimates and true values). Leave-one-out cross-validation technique on the entire dataset was used for the assessment. Estimates were given at satellite native supports, allowing for direct comparison of estimates and retrievals. Model data mismatch was assessed for every extracted coordinate using all retrievals within that same day (except the one obtained at the actual estimation location). Mapping steps were repeated ab initio for every cross-validation location. The statistics were built upon a comparison of estimates and measurements (retrievals).
3. Results
3.1. Performance Comparison
Figure 3 shows the degree of correlation between OCO-2 SIF pseudo-retrievals and SIF generated using three different methodologies: the original ML-based approach [24], SIF generated using moving window ordinary kriging, and SIF values generated by the newly developed hybrid approach. The highest correlation was found in the case of the hybrid approach (R2 = 0.8523), followed by ordinary kriging (R2 = 0.8111) and the machine learning approach (R2 = 0.7981). There are two notable features in Figure 3a: (1) there is a drop in the correlations between ML-generated SIF values and pseudo-retrievals for SIF values larger than 2 (mW m2 sr−1 nm−1), and (2) there is a lack of variability around ML-generated SIF values close to zero, resulting in the formation of a vertical line pattern. ML-generated predictions may have different origins and properties, but they do not necessarily represent artifacts. The noise from the pseudo-retrievals affects both moving window ordinary kriging and the hybrid approach and can artificially increase the predictions above the realistic values limited by the maximum density of plant biomass (chlorophyll) that can be packed on the Earth’s surface at multiple points. The ML-based approach could effectively filter out such cases and limit the SIF values by imposing a cut-off threshold around a value of 2, acting as an anchor and reinforcing the hypothesis that the hybrid approach could benefit from both parent methods. The second feature can be explained by analyzing the distribution of SIF per biome type, as shown in Figure 4a. For three biome types, barren or sparsely vegetated (BSV), bare ground tundra (BGT), and snow or ice (SOI), the ML-generated SIF values show a reduced variability compared to pseudo-retrievals, in addition to being close to zero. The three types of biomes are unlikely to exhibit significant plant activity due to their distinct characteristics. We argue that the ML-generated predictions are more aligned with common sense and that the artificial variability in pseudo-retrievals (which is propagated both in ordinary kriging and in predictions based on a hybrid approach) is likely due to retrieval errors and represents an artifact. Biome distribution is presented in Figure 4b; the image was generated based on data from MODIS Land Cover Type/Dynamics [45].
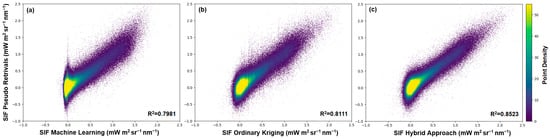
Figure 3.
The correlation plots and corresponding R2 between annual SIF pseudo-retrievals and predicted SIF values, given in mW m2 sr−1 nm−1: (a) SIF pseudo-retrievals vs. ML-derived values [24], (b) SIF pseudo-retrievals vs. ordinary kriging, (c) SIF pseudo-retrievals vs. SIF from the newly developed hybrid method.
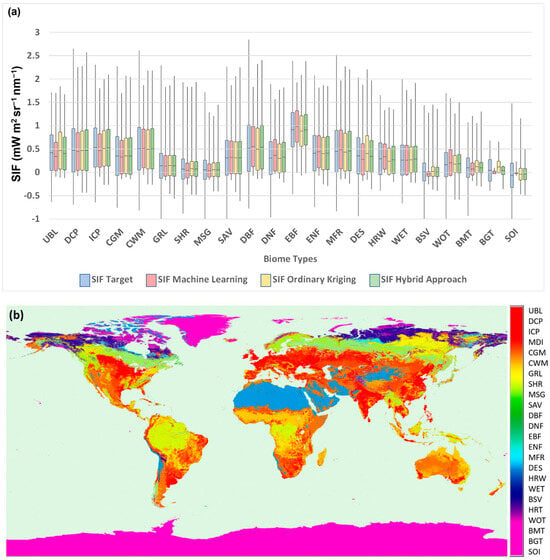
Figure 4.
(a) Box plot showing 2019 OCO-2 SIF pseudo-retrievals, ML-generated SIF, and SIF obtained from ordinary kriging and hybrid approach (mW m2 sr−1 nm−1), broken down by biome type. (b) Biome distribution on the world map. UBL = Urban and Built-Up Land, DCP = Dryland Cropland and Pasture, ICP = Irrigated Cropland and Pasture, MDI = Mixed Dryland/Irrigated Cropland and Pasture, CGM = Cropland/Grassland Mosaic, CWM = Cropland/Woodland Mosaic, GRL = Grassland, SHR = Shrubland, MSG = Mixed Shrubland/Grassland, SAV = Savanna, DBF = Deciduous Broadleaf Forest, DNF = Deciduous Needleleaf Forest, EBF = Evergreen Broadleaf Forest, ENF = Evergreen Needleleaf Forest, MFR = Mixed Forest, DES = Desert, HRW = Herbaceous Wetland, WET = Wooded Wetland, BSV = Barren or Sparsely Vegetated, HRT = Herbaceous Tundra, WOT = Wooded Tundra, BMT = Mixed Tundra, BGT = Bare Ground Tundra, SOI = Snow or Ice.
3.2. Prediction Accuracy and Bias
In Table 1, we present several performance measures of the three analyzed methods. The accuracy of the three mapping approaches was checked by calculating the average (a) Mean Absolute Error (MAE) and (b) Root Mean Squared Error (RMSE) in leave-one-out cross-validation.

Table 1.
The cross-validation results of the SIF dataset using multiple performance measures for all three predictive methodologies: Mean Absolute Error (MAE), Mean Square Error (MSE), Root Mean Square Error (RMSE), R2, and bias. The performance measures for SIF are given in (mW m2 sr−1 nm−1).
Based on the error statistics calculated and presented in Table 1, the hybrid approach outperformed all four performance measures, with the lowest errors, the highest percentage of variance explained (R2), and the smallest bias.
The synergy between geostatistical and ML-based approaches is apparent in Figure 5, which shows the bias values. Within the cross-validation framework, the bias of all three methods was calculated as the average difference between estimates and measurements. Perfectly unbiased estimates would have zero bias. The average daily biases, shown in Table 1, were 0.0103, −0.0003, and −0.0002 mW m2 sr−1 nm−1 for the ML-based approach, ordinary kriging, and hybrid approach, respectively. These values show that the estimates are virtually unbiased. Although all three approaches were shown to be unbiased, the hybrid approach outperformed the others. Error histograms for the two parent methods and the hybrid approach are shown in Figure 5. All three methods provide virtually unbiased estimates, but the magnitude of the model data mismatches, as represented by the histogram, is lowest for the hybrid approach, although the variances in the model data mismatch values for the two parent methods are similar, even though they rely on substantially different estimation frameworks.
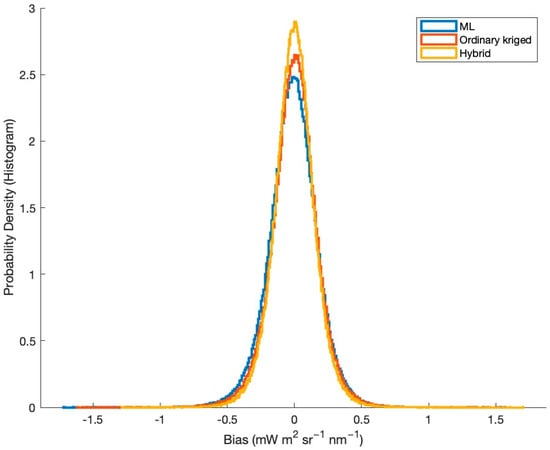
Figure 5.
Bias in differences between modeled values and pseudo-retrievals is represented by histograms (mW m2 sr−1 nm−1). The yellow histogram (hybrid approach) exhibits the highest probability density around zero, compared to the other two histograms.
4. Discussion
The limitations of the presented approaches are evident in the discrepancies observed in error statistics and correlation coefficients among the three methods. A notable decline in correlation is observed in machine learning (ML)-generated solar-induced fluorescence (SIF) values beyond a certain threshold, along with a reduction in variability, a phenomenon known as a loss of variance, particularly evident in low SIF values. This phenomenon points to intrinsic constraints in the ML approach in handling extremes, well recognized beyond the boundaries of this study. Specifically, the machine learning model tends to compress the range of predicted SIF values, resulting in a vertical line pattern for low values and a cut-off effect for high values. This behavior implies a potential underestimation of variability in areas with minimal vegetation and an artificial cap on SIF predictions, which may fail to capture the highest levels of photosynthetic activity adequately. While the hybrid approach partially mitigates these issues by incorporating geostatistical methods, acknowledging and addressing these limitations in machine learning predictions are essential for enhancing the accuracy and reliability of SIF estimation across diverse vegetation types and conditions.
In light of the observed properties of the hybrid method and indications suggesting its relative outperformance compared to both parent methods, we posit that further enhancements in the absolute performance of both the hybrid and parent methods are conceivable. The inherent accuracy of machine learning (ML)-derived predictions fundamentally depends on two factors: the nature and quality of ancillary data inputs and the efficacy of the specific ML model architecture tailored to the current use case. While the selection of ancillary data is contingent upon the specific use case, potentially unrelated to solar-induced fluorescence (SIF) specifically, ML model architectures remain subject to ongoing evolution. We foresee that the adoption of convolutional network-based approaches, expanding the scope of ancillary data inputs to encompass a broader spatio-temporal neighborhood, holds promise for enhancing the accuracy of ML-based techniques and their resulting predictions [19]. On the geostatistical front, sophisticated hyperdimensional approaches exploiting spatio-temporal correlation fields and data from a wider spatio-temporal neighborhood have demonstrated superior performance over traditional spatial kriging methods [28]. Additionally, the proposed hybridization scheme employing kriging with external drift represents merely one feasible approach. Alternatively, geostatistical predictions, combined with ancillary data, could serve as inputs for an ML model, potentially yielding even greater accuracy. We advocate for the exploration of these possibilities in future research endeavors.
5. Conclusions
In this research, we successfully developed and assessed a novel hybrid methodology for estimating solar-induced chlorophyll fluorescence (SIF) at locations where direct samples are not available. This methodology integrates two foundational approaches—ordinary kriging within a moving window and machine learning—into a cohesive framework using kriging with external drift.
Our evaluation, conducted through leave-one-out cross-validation on the global OCO-2 SIF dataset from 2019, reveals that our hybrid method consistently matches or surpasses the parent techniques in terms of accuracy, variance explained, and bias reduction. A distinctive advantage of our hybrid approach is its adaptive weighting mechanism, which intelligently allocates more weight to proximal sampled locations and increasingly leans on machine learning covariates as the distance to the nearest sample extends beyond the decorrelation length. Additionally, we offer a quantification of SIF estimate uncertainty, which is inherent to kriging methodologies.
The chosen resolution in our study aligns with the spatial support of the employed datasets, showcasing the adaptability of our method to meet the resolution requirements of various applications. This adaptability, combined with the assumption of stationarity in the relationship between ancillary data and solar-induced fluorescence (SIF) values, suggests the potential extension of our methodology into a downscaling technique within the geostatistical domain. The methodological groundwork for this extension has already been laid out; as previously mentioned, machine learning (ML) has been successfully employed for downscaling SIF data [25], and a geostatistical framework for downscaling SIF and other data is provided in the area-to-point subset of methods within the kriging family [46]. Our results are promising and indicate that the developed hybrid approach is not confined to SIF estimation but is applicable to a broader range of satellite datasets that exhibit similar characteristics. Furthermore, the machine learning component of our framework is flexible, allowing for the future integration of more comprehensive ancillary data or alternative model architectures, with no fundamental alterations to the method.
Expanding upon this innovative hybrid methodology for solar-induced fluorescence (SIF) estimation, several practical applications emerge, underscoring its versatility across diverse fields. For instance, in precision agriculture, this approach can accurately map spatial variability in crop health at a resolution sufficient for informing targeted intervention strategies, ultimately boosting yields and reducing input costs. Similarly, in forest management, the methodology’s capability to integrate and analyze satellite datasets can aid in the early detection of areas under stress from drought or disease, facilitating timely conservation efforts and mitigating potential losses. Urban planners could utilize the refined SIF data to monitor the health of urban green spaces, contributing to strategies aimed at improving air quality and enhancing the urban environment for residents. Additionally, in climate research, the framework’s ability to provide accurate and high-resolution SIF estimation enables more precise modeling of carbon fluxes, offering insights into the impacts of climate change on terrestrial ecosystems and informing global carbon management policies. These examples underscore the broad applicability and potential impact of the developed hybrid methodology on environmental management and sustainability efforts worldwide.
The versatility and robustness of the proposed framework mark a significant advancement in the field of remote sensing and geospatial analysis. We anticipate that the methodology will not only enhance the precision of SIF estimation but also serve as a template for the development of similar hybrid models in related domains. Future research will focus on exploring the potential application of this framework to various types of satellite data. Specifically, in reference to solar-induced fluorescence (SIF), we target data obtained from the Fluorescence Explorer (FLEX) mission. The high resolution and specificity of FLEX’s fluorescence measurements are expected to provide detailed and accurate SIF estimations. This will enable the enhancement of predictive models and the investigation of subtle photosynthetic dynamics across diverse vegetation types. The proposed method facilitates a straightforward implementation of advanced and emerging machine learning techniques, thereby fostering the development of more robust and versatile models.
Author Contributions
Conceptualization, J.M.T.; Methodology, J.M.T.; Software, V.I. and S.I.; Validation, V.I.; Formal analysis, J.M.T.; Resources, V.I. and M.P.; Data curation, S.I. and M.P.; Writing—original draft, J.M.T., S.I. and M.P.; Visualization, S.I.; Supervision, S.I.; Project administration, V.T.; Funding acquisition, V.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this study are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bai, Y.; Liang, S.; Yuan, W. Estimating global gross primary production from sun-induced chlorophyll fluorescence data and auxiliary information using machine learning methods. Remote Sens. 2021, 13, 963. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef]
- Spielmann, F.M.; Wohlfahrt, G.; Hammerle, A.; Kitz, F.; Migliavacca, M.; Alberti, G.; Ibrom, A.; El-Madany, T.S.; Gerdel, K.; Moreno, G.; et al. Gross Primary Productivity of Four European Ecosystems Constrained by Joint CO2 and COS Flux Measurements. Geophys. Res. Lett. 2019, 46, 5284–5293. [Google Scholar] [CrossRef]
- Mohammed, G.H.; Colombo, R.; Middleton, E.M.; Rascher, U.; van der Tol, C.; Nedbal, L.; Goulas, Y.; Pérez-Priego, O.; Damm, A.; Meroni, M.; et al. Remote sensing of solar-induced chlorophyll fluorescence (SIF) in vegetation: 50 years of progress. Remote Sens. Environ. 2019, 231, 111177. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M.E. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- Doughty, R.; Kurosu, T.P.; Parazoo, N.; Köhler, P.; Wang, Y.; Sun, Y.; Frankenberg, C. Global GOSAT, OCO-2, and OCO-3 solar-induced chlorophyll fluorescence datasets. Earth Syst. Sci. Data 2022, 14, 1513–1529. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Guanter, L.; Frankenberg, C.; Dudhia, A.; Lewis, P.E.; Gómez-Dans, J.; Kuze, A.; Suto, H.; Grainger, R.G. Retrieval and global assessment of terrestrial chlorophyll fluorescence from GOSAT space measurements. Remote Sens. Environ. 2012, 121, 236–251. [Google Scholar] [CrossRef]
- Joiner, J.; Guanter, L.; Lindstrot, R.; Voigt, M.; Vasilkov, A.P.; Middleton, E.M.; Huemmrich, K.F.; Yoshida, Y.; Frankenberg, C. Global monitoring of terrestrial chlorophyll fluorescence from moderate-spectral-resolution near-infrared satellite measurements: Methodology, simulations, and application to GOME-2. Atmos. Meas. Tech. 2013, 6, 2803–2823. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Yoshida, Y.; Corp, L.A.; Middleton, E.M. First observations of global and seasonal terrestrial chlorophyll fluorescence from space. Biogeosciences 2011, 8, 637–651. [Google Scholar] [CrossRef]
- Köhler, P.; Frankenberg, C.; Magney, T.S.; Guanter, L.; Joiner, J.; Landgraf, J. Global Retrievals of Solar-Induced Chlorophyll Fluorescence With TROPOMI: First Results and Intersensor Comparison to OCO-2. Geophys. Res. Lett. 2018, 45, 10456–10463. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Gao, M.; Li, Z.L. Retrieving sun-induced chlorophyll fluorescence from hyperspectral data with tansat satellite. Sensors 2021, 21, 4886. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Frankenberg, C.; Wood, J.D.; Schimel, D.S.; Jung, M.; Guanter, L.; Drewry, D.T.; Verma, M.; Porcar-Castell, A.; Griffis, T.J.; et al. OCO-2 advances photosynthesis observation from space via solar-induced chlorophyll fluorescence. Science 2017, 358, eaam5747. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xiao, J.; He, B.; Altaf Arain, M.; Beringer, J.; Desai, A.R.; Emmel, C.; Hollinger, D.Y.; Krasnova, A.; Mammarella, I.; et al. Solar-induced chlorophyll fluorescence is strongly correlated with terrestrial photosynthesis for a wide variety of biomes: First global analysis based on OCO-2 and flux tower observations. Glob. Chang. Biol. 2018, 24, 3990–4008. [Google Scholar] [CrossRef] [PubMed]
- Luus, K.A.; Commane, R.; Parazoo, N.C.; Benmergui, J.; Euskirchen, E.S.; Frankenberg, C.; Joiner, J.; Lindaas, J.; Miller, C.E.; Oechel, W.C.; et al. Tundra photosynthesis captured by satellite-observed solar-induced chlorophyll fluorescence. Geophys. Res. Lett. 2017, 44, 1564–1573. [Google Scholar] [CrossRef]
- Smith, W.K.; Biederman, J.A.; Scott, R.L.; Moore, D.J.P.; He, M.; Kimball, J.S.; Yan, D.; Hudson, A.; Barnes, M.L.; MacBean, N.; et al. Chlorophyll Fluorescence Better Captures Seasonal and Interannual Gross Primary Productivity Dynamics Across Dryland Ecosystems of Southwestern North America. Geophys. Res. Lett. 2018, 45, 748–757. [Google Scholar] [CrossRef]
- Kostić, S.; Stojković, M.; Ilić, V.; Trivan, J. Deep Neural Network Model for Determination of Coal Cutting Resistance and Performance of Bucket-Wheel Excavator Based on the Environmental Properties and Excavation Parameters. Process. Coal Min. Unconv. Oil Explor. 2023, 11, 3067. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J. A global, 0.05-degree product of solar-induced chlorophyll fluorescence derived from OCO-2, MODIS, and reanalysis data. Remote Sens. 2019, 11, 517. [Google Scholar] [CrossRef]
- Gensheimer, J.; Turner, A.J.; Köhler, P.; Frankenberg, C.; Chen, J. A convolutional neural network for spatial downscaling of satellite-based solar-induced chlorophyll fluorescence (SIFnet). Biogeosciences 2022, 19, 1777–1793. [Google Scholar] [CrossRef]
- Chen, X.; Huang, Y.; Nie, C.; Zhang, S.; Wang, G.; Chen, S.; Chen, Z. A long-term reconstructed TROPOMI solar-induced fluorescence dataset using machine learning algorithms. Sci. Data 2022, 9, 427. [Google Scholar] [CrossRef]
- Wen, J.; Köhler, P.; Duveiller, G.; Parazoo, N.C.; Magney, T.S.; Hooker, G.; Yu, L.; Chang, C.Y.; Sun, Y. A framework for harmonizing multiple satellite instruments to generate a long-term global high spatial-resolution solar-induced chlorophyll fluorescence (SIF). Remote Sens. Environ. 2020, 239, 111644. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, L.; Liu, X.; Chen, J. An improved downscaled sun-induced chlorophyll fluorescence (DSIF) product of GOME-2 dataset. Eur. J. Remote Sens. 2022, 55, 1564–1573. [Google Scholar] [CrossRef]
- Yu, L.; Wen, J.; Chang, C.Y.; Frankenberg, C.; Sun, Y. High-Resolution Global Contiguous SIF of OCO-2. Geophys. Res. Lett. 2019, 46, 1449–1458. [Google Scholar] [CrossRef]
- Zhang, Y.; Joiner, J.; Hamed Alemohammad, S.; Zhou, S.; Gentine, P. A global spatially contiguous solar-induced fluorescence (CSIF) dataset using neural networks. Biogeosciences 2018, 15, 5779–5800. [Google Scholar] [CrossRef]
- Kang, X.; Huang, C.; Zhang, L.; Zhang, Z.; Lv, X. Downscaling solar-induced chlorophyll fluorescence for field-scale cotton yield estimation by a two-step convolutional neural network. Comput. Electron. Agric. 2022, 201, 107260. [Google Scholar] [CrossRef]
- Tadić, J.M.; Qiu, X.; Miller, S.; Michalak, A.M. Spatio-temporal approach to moving window block kriging of satellite data v1.0. Geosci. Model. Dev. 2017, 10, 709–720. [Google Scholar] [CrossRef]
- Tadić, J.M.; Qiu, X.; Yadav, V.; Michalak, A.M. Mapping of satellite Earth observations using moving window block kriging. Geosci. Model. Dev. 2015, 8, 709–720. [Google Scholar] [CrossRef]
- Tadić, J.M.; Williams, I.N.; Tadić, V.M.; Biraud, S.C. Towards hyper-dimensional variography using the product-sum covariance model. Atmosphere 2019, 10, 148. [Google Scholar] [CrossRef]
- Ilić, V.; Tadić, J.; Imširagić, A. Kriging with machine learning covariates in environmental sciences: A hybrid approach. GeoMLA Geostat. Mach. Learn. Appl. Clim. Environ. Sci. 2016. Available online: https://www.researchgate.net/publication/319205953_Kriging_with_machine_learning_covariates_in_environmental_sciences_A_hybrid_approach (accessed on 6 May 2024).
- Crisp, D.; Pollock, H.; Rosenberg, R.; Chapsky, L.; Lee, R.; Oyafuso, F.; Frankenberg, C.; Dell, C.; Bruegge, C.; Doran, G.; et al. The on-orbit performance of the Orbiting Carbon Observatory-2 (OCO-2) instrument and its radiometrically calibrated products. Atmos. Meas. Tech. 2017, 10, 59–81. [Google Scholar] [CrossRef]
- Crisp, D. Measuring atmospheric carbon dioxide from space with the Orbiting Carbon Observatory-2 (OCO-2). In Earth Observing Systems XX; 2015; Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/browse/SPIE-Optics-Photonics/SPIE-Optical-Engineering-Applications/2015#_=_ (accessed on 6 May 2024).
- Frankenberg, C.; Köhler, P.; Magney, T.S.; Geier, S.; Lawson, P.; Schwochert, M.; McDuffie, J.; Drewry, D.T.; Pavlick, R.; Kuhnert, A. The Chlorophyll Fluorescence Imaging Spectrometer (CFIS), mapping far red fluorescence from aircraft. Remote Sens. Environ. 2018, 217, 523–536. [Google Scholar] [CrossRef]
- Frankenberg, C.; O’Dell, C.; Berry, J.; Guanter, L.; Joiner, J.; Köhler, P.; Pollock, R.; Taylor, T.E. Prospects for chlorophyll fluorescence remote sensing from the Orbiting Carbon Observatory-2. Remote Sens. Environ. 2014, 147, 1–12. [Google Scholar] [CrossRef]
- Cheng, R.; Köhler, P.; Frankenberg, C. Impact of radiation variations on temporal upscaling of instantaneous solar-induced chlorophyll fluorescence. Agric. For. Meteorol. 2022, 327, 109197. [Google Scholar] [CrossRef]
- Biriukova, K.; Celesti, M.; Evdokimov, A.; Pacheco-Labrador, J.; Julitta, T.; Migliavacca, M.; Giardino, C.; Miglietta, F.; Colombo, R.; Panigada, C.; et al. Effects of varying solar-view geometry and canopy structure on solar-induced chlorophyll fluorescence and PRI. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102069. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, W.; Wu, J.; Liu, S.; Teng, Y.; Yang, J.; Han, X. The impacts of growth and environmental parameters on solar-induced chlorophyll fluorescence at seasonal and diurnal scales. Remote Sens. 2019, 11, 2002. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Lin, X.; Zhang, H. Solar-induced chlorophyll fluorescence as an indicator for determining the end date of the vegetation growing season. Ecol. Indic. 2020, 109, 105755. [Google Scholar] [CrossRef]
- Sun, Y.; Frankenberg, C.; Jung, M.; Joiner, J.; Guanter, L.; Köhler, P.; Magney, T. Overview of Solar-Induced chlorophyll Fluorescence (SIF) from the Orbiting Carbon Observatory-2: Retrieval, cross-mission comparison, and global monitoring for GPP. Remote Sens. Environ. 2018, 209, 808–823. [Google Scholar] [CrossRef]
- Hamed Alemohammad, S.; Fang, B.; Konings, A.G.; Aires, F.; Green, J.K.; Kolassa, J.; Miralles, D.; Prigent, C.; Gentine, P. Water, Energy, and Carbon with Artificial Neural Networks (WECANN): A statistically based estimate of global surface turbulent fluxes and gross primary productivity using solar-induced fluorescence. Biogeosciences 2017, 14, 4101–4124. [Google Scholar] [CrossRef] [PubMed]
- Verrelst, J.; Rivera, J.P.; van der Tol, C.; Magnani, F.; Mohammed, G.; Moreno, J. Global sensitivity analysis of the SCOPE model: What drives simulated canopy-leaving sun-induced fluorescence? Remote Sens. Environ. 2015, 166, 8–21. [Google Scholar] [CrossRef]
- Hammerling, D.M.; Michalak, A.M.; Kawa, S.R. Mapping of CO2 at high spatiotemporal resolution using satellite observations: Global distributions from OCO-2. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Chilès, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; Wiley: Chichester, UK, 2012. [Google Scholar] [CrossRef]
- Hengl, T. A Practical Guide to Geostatistical Mapping; Scientific and Technical Research Series; University of Amsterdam: Amsterdam, The Netherland, 2009. [Google Scholar]
- Hengl, T.; Heuvelink, G.; Stein, A. Comparison of kriging with external drift and simple linear regression for predicting soil horizon thickness with different sample densities. Geoderma 2000, 97, 255–271. [Google Scholar] [CrossRef]
- Friedl, M. MODIS Land Cover Type/Dynamics. Available online: https://modis.gsfc.nasa.gov/data/dataprod/mod12.php (accessed on 6 May 2024).
- Jin, Y.; Ge, Y.; Wang, J.; Heuvelink, G.B.; Wang, L. Geographically weighted area-to-point regression kriging for spatial downscaling in remote sensing. Remote Sens. 2018, 10, 579. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).