Abstract
This paper presents a statistical analysis of intensity wavelength-resolution synthetic aperture radar (SAR) difference images. In this analysis, Anderson Darling goodness-of-fit tests are performed, considering two different statistical distributions as candidates for modeling the clutter-plus-noise, i.e., the background statistics. The results show that the Gamma distribution is a good fit for the background of the tested SAR images, especially when compared with the Exponential distribution. Based on the results of this statistical analysis, a change detection application for the detection of concealed targets is presented. The adequate selection of the background distribution allows for the evaluated change detection method to achieve a better performance in terms of probability of detection and false alarm rate, even when compared with competitive performance change detection methods in the literature. For instance, in an experimental evaluation considering a data set obtained by the Coherent All Radio Band Sensing (CARABAS) II UWB SAR system, the evaluated change detection method reached a detection probability of 0.981 for a false alarm rate of 1/km2.
1. Introduction
In recent decades, many civil and military applications have considered radar systems, e.g., forest area imagery [1], weather monitoring [2], vehicle traffic [3], remote areas imaging [4], air traffic control [5], and defense applications [6]. Given the efficiency of radar systems, some variants have been proposed aiming to monitor larger areas, highlighting the synthetic aperture radar (SAR) [7]. Such systems exploit the relative movement between the platform and the target to synthesize a larger antenna aperture. Thus, it is possible to obtain high-resolution images, similar to other systems with larger effective antenna apertures [8].
SAR systems have other advantages when compared to optical systems, which justifies their use in different monitoring applications [9,10,11]. Among them, their low sensitivity to weather conditions and the possibility of penetration into some structures to obtain specific frequencies stand out, e.g., SAR systems operating at frequencies below 1 GHz are capable of detecting concealed targets in forest regions. The systems used for this type of application are known as foliage-penetration (FOPEN) radars [12].
A widely used FOPEN SAR system is the Coherent All Radio Band Sensing (CARABAS) II SAR system [13,14,15,16,17], which operates in the lower range of the very high-frequency band (VHF). It is characterized by its large fractional bandwidth, e.g., ultra-wideband (UWB) and wide antenna bandwidth [18]; such characteristics make the CARABAS-II a wavelength-resolution SAR system, since the resolution of the system is of the order of the wavelength of the radar signal [19].
Since SAR images with wavelength resolution generally have a single scatter in the resolution cell of the system, these images tend not to suffer significantly from speckle noise [20]. Furthermore, during its scattering process, the dimension of the scatterer is related to the dimensions of the signal’s wavelength. Therefore, objects detected in these images mainly relate to large scatterers, such as trunks and human-made structures. These unique characteristics make wavelength-resolution SAR images suitable for FOPEN applications, especially for target detection [20].
Change detection (CD) methods are one of the most-used techniques in applications using wavelength-resolution SAR images [14,16,17,21]. Traditionally, change detection methods consider the use of SAR amplitude images [13,18]. Even when high performances are obtained in terms of probability of detection and low occurrence of false alarms [15,22,23], the mitigation of false alarms in such applications remains a research problem [24,25,26]. This problem can be solved based on the intensity of the SAR image, which results in a higher differentiation between target-related pixels and background-related pixels [27]. This feature transforms the statistical characteristics of the original amplitude SAR images [28]. Intensity SAR images are often used in traditional SAR systems operating in microwave frequency bands [29,30,31]. However, the study of VHF wavelength-resolution intensity SAR images for FOPEN applications is lacking.
A common type of CD used in FOPEN applications is based on the likelihood-ratio test (LRT) [15,32,33]. These methods consist of a hypothesis test based on the ratio between the target statistics plus background and the background statistics. For CD applications, little information about the targets is generally expected, which leads to targets usually being modeled as a constant [15,32,33]. Thus, background statistics play an essential role in the performance of the CD method, as stated in [32]. Different background statistics have been evaluated using wavelength-resolution SAR amplitude images, e.g., Gaussian distribution [32], Rayleigh distribution [15], K-distribution [15], and Gamma distribution [33]. However, to the best of our knowledge, there is no published study related to the study and evaluation of background statistics for wavelength-resolution intensity SAR images.
Motivated by the possible performance gains that could be obtained with the use of wavelength-resolution intensity SAR images in detecting concealed targets in forestry areas, this work presents a statistical analysis of these images. The statistical analysis is based on goodness-of-fit (GoF) testing using the Anderson Darling (AD) [34,35,36,37] test under the assumption of different distribution candidates. This paper considers the bivariate gamma distribution and bivariate exponential distribution. Considering the time stability of VHF wavelength-resolution intensity SAR images, difference images are used in our analysis to reduce the heterogeneity of the background of the evaluated scenarios. Finally, a change detection method based on the likelihood ratio test is presented and assessed, considering CARABAS-II data to exemplify the impact of the background statistics. The studied CD method is compared with other recently published results in terms of the probability of detection and the false alarm rate.
The remainder of this paper is organized as follows. The UWB wavelength-resolution SAR image characteristics and the data set used in this paper are presented in Section 2. Section 3 exhibits the statistical test performed over difference-intensity SAR images using the Anderson–Darling GoF test. Section 4 provides the CD algorithm using difference-intensity SAR images as input and the bivariate gamma distribution on the likelihood-ratio test. Section 4 presents an experimental evaluation of the studied change detection method. The performance of the evaluated technique is compared with amplitude change detection methods from the literature with a good performance. Section 5 discusses bivariate gamma distribution on the difference-intensity SAR images’ scheme. Finally, Section 6 presents some concluding remarks.
2. Materials and Methods
In this article, we focus on VHF UWB wavelength-resolution SAR systems with a resolution in the order of a few meters, herein denoted as low-frequency wavelength-resolution SAR systems. We describe in detail the wavelength-resolution SAR images. Our aim is to express some unique characteristics of this type of image, paying extra attention to their background and statistical aspects. The data set used in this paper is also presented.
2.1. Wavelength-Resolution SAR Images
Low-frequency wavelength-resolution SAR systems are not very sensitive to small scatterers present in the area of interest on the ground [8]. Thus, the scattering process in wavelength-resolution images is mainly related to scatterers with dimensions in the order of the signal wavelengths. Based on this backscattering phenomenology, it is very likely that the resolution cell contains a single scatter, resulting in images containing very little speckle noise, which usually degrades the quality of traditional microwave SAR images.
Another relevant characteristic of this kind of image is that large scatterers tend to be stable over time and less affected by weather conditions. This characteristic results in high similarity between images from the same ground scene when the same flight geometry is considered. Thus, wavelength-resolution SAR images can be used in change detection methods without clutter-reduction techniques [20]. One example of a system capable of generating low-frequency wavelength-resolution SAR images is CARABAS-II. This paper validates the statistical analyses and discussions using the available public CARABAS-II SAR images data set, made public by Air Force Research Laboratory (AFRL) [38]. A discussion regarding the CARABAS-II data set is presented in Section 2.2.
2.2. CARABAS-II System
The CARABAS-II is a VHF UWB SAR system developed by the Swedish Defence Research Agency (FOI) and the Swedish company SAAB. The CARABAS-II operates on the 20–90 MHz frequency band, resulting in a 15–3.3 m wavelength range [39], obtaining resolution cells of approximately 3 × 3 m. The data set comprises 24 incoherent amplitude SAR images, which are already calibrated, pre-processed, and geocoded. Those images cover the same ground area of 6 km2 (2 × 3 km), with a pixel size of 1 × 1 m. The data set was divided into four target deployments (Missions), measured using six flight geometries (passes). Each target deployment contains 25 testing targets in different configurations. Figure 1 presents one example of an image of each mission. For the sake of simplicity, an image classification similar to the one used in the FOI challenge paper [18] was considered. Additionally, more information related to the data set can be found in [18]. The intensity images studied in this paper were obtained using the original amplitude SAR data [38].
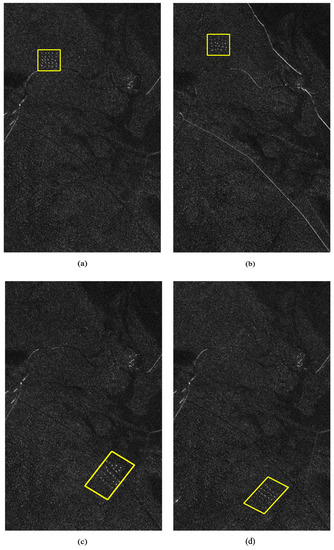
Figure 1.
CARABAS-II image samples for (a) Mission 2 and Pass 1 (b) Mission 3 and Pass 2 (c) Mission 4 and Pass 5 (d) Mission 5 and Pass 1. The target deployments of each image are highlighted.
3. Statistical Test
An analysis based on GoF tests is presented to study the statistical characteristics of intensity wavelength-resolution SAR images. As target amplitudes tend to be stronger than background amplitudes, wavelength-resolution SAR images are known to have a heavy-tailed amplitude distribution pattern [18]. Considering that the AD GoF is well-suited to analyzing tailed distributions compared to other GoF tests [40], this paper uses the AD GoF test to investigate whether a given probability distribution null hypothesis () should be rejected for a given data sample [41].
The AD test is based on the distance between the empirical distribution function () and cumulative distribution function () of . The distance is defined by [40] and can be described by
where for the n tested samples and is a weight function defined for . By sorting the observations in ascending order, it is possible to simplify (1) as
where .
The AD test consists of a comparison between and a critical value , where the critical value can be selected based on the following criterion
where is the significance level. The Anderson–Darling rejects the null hypothesis If ; Otherwise, the AD test fails to reject the null hypothesis.
In our analysis, the exact solution for the test presented in (3) is not achievable since the distribution is unknown. However, for , a good approximation for this unknown distribution is given by [42]
Finally, we use the numerical approximation for (4) presented in [42] to perform the AD test. This approximation is used to reduce the test’s computational complexity.
As previously mentioned, the selection of the clutter-plus-noise statistical model greatly influences the performance of several applications using wavelength-resolution SAR images [15,32,33]. The association of a better-matched clutter-plus-noise statistical model with better CD performances was previously observed in [32]. In [15,32,33], different clutter-plus-noise statistical models were used for amplitude low-frequency wavelength-resolution SAR images, e.g., Gaussian distribution, Rayleigh distribution, K-distribution, and Gamma distribution. However, in [15,32,33], the clutter-plus-noise statistical models were selected based on the simplicity of the statistical models and a visual inspection between the model and the data histogram. This selection does not consider the background heterogeneity that this type of SAR image may contain. This leads to a mismatch between the data and model, which can jeopardize the performance of applications using this information, e.g., change detection applications [32].
An alternative approach to achieve a better performance in terms of probability of detection is analyzed using intensity images [43]. In this scenario, the targets tend to be highlighted due to the intensity image’s nature. Usually, the clutter-plus-noise statistics for traditional microwave SAR images are modeled by an exponential distribution [43]. However, this selection may be inaccurate due to the scattering characteristics of the low-frequency wavelength-resolution SAR images due to the expected background heterogeneity of low-frequency wavelength-resolution SAR images.
Due to the time stability of low-frequency wavelength-resolution intensity images, it is possible to analyze only one image in the data set and extend this analysis to the others. For this initial evaluation, we performed the AD test considering an exponential distribution as the null hypothesis for , which is a typical significance level value for this kind of test [44]. Additionally, the tested image was divided into multiple cells of 50 × 50 pixels, aiming to obtain a good analysis of the statistical test. This selection was made to guarantee a better visualization, an equal division in the whole image, and a window covering a much higher region than a target footprint. The AD test results for this initial evaluation are presented in Figure 2.
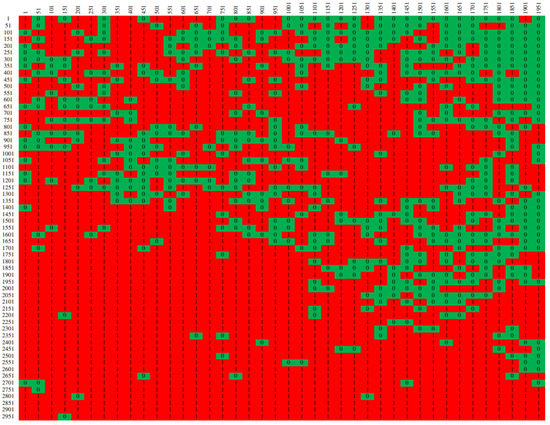
Figure 2.
Anderson–Darling test results for the exponential distribution null hypothesis. The cells in red represent samples where the AD rejects the exponential distribution, and the green cells represent samples where the AD fails to reject the exponential distribution.
Each cell of the matrix represented in Figure 2 represents a block of 50 × 50 pixels. The cells highlighted in green indicate that the AD test fails to reject the null hypothesis, i.e., the exponential distribution yields a good fit for the tested sample. Otherwise, the cells highlighted by the red color indicate that the AD test rejects the null hypothesis, i.e., the exponential distribution does not yield a good fit for the tested sample. As seen in Figure 2, the exponential distribution does not fit most of the tested cells well. This can mainly be observed in the lower fraction of the image, characterized by a forest area.
As previously mentioned, low-frequency wavelength-resolution SAR images present some unique characteristics compared to traditional microwave SAR images. More specifically, CARABAS-II intensity images tend to have a heterogeneous background. We used the following considerations to better select an adequate clutter-plus-noise statistical model. According to [20], the clutter-plus-noise statistical distribution of images obtained from the difference between two low-frequency wavelength-resolution amplitude SAR images with the same flight characteristics can be modeled as Gaussian. Additionally, the absolute value of a Gaussian random variable with non-zero mean has a folded normal distribution [45]. In the case of zero mean (), this can be modeled by a half-normal distribution [46]. Based on these considerations, the absolute value of the difference between two CARABAS-II images can be described with a half-normal distribution, assuming that the resulting image has zero mean. Finally, if a random variable described by a half-normal distribution is squared, this variable turns into a Chi-squared distribution with one degree of freedom, i.e., Gamma distribution [47]. Thus, based on this analysis, the intensity difference images from the CARABAS-II system can be modeled using a Gamma distribution.
To evaluate the selection of the Gamma distribution for modeling the clutter-plus-noise of low-frequency wavelength-resolution intensity SAR difference images, we performed a similar analysis considering the previous AD test but a different input type, i.e., difference images. For the study, the difference intensity image was obtained using a pair of CARABAS-II amplitude images with the same flight geometries, named Image 1 and Image 3. A simple subtraction in each pixel was performed to create the difference amplitude image, i.e., Images 1–3. Then, this difference amplitude image was submitted to a simple modulus-square operation, i.e., . The experimental evaluation was performed using the AD test under the assumption of the Gamma distribution null hypothesis. The results of this experimental evaluation are presented in Figure 3, where the same color system shown in Figure 2 is used.

Figure 3.
Anderson–Darling test results for the Gamma distribution null hypothesis. The cells in red represent samples where the AD rejects the Gamma distribution, and the green cells represent samples where the AD fails to reject the Gamma distribution.
As shown in Figure 3, the Gamma distribution yields a good fit for most of the evaluated cells. It is possible to observe that the cells in which the AD test rejects the Gamma null hypothesis are mainly related to isolated cells or changes, i.e., targets. The rejection of isolated cells may be related to false negatives, since no Type I error control technique was used in this initial evaluation. The option of not using this type of technique is based on the same considerations as made in [22] and can be evaluated in future studies. Additionally, it is observable that, for a pair of regions, the AD test rejects the Gamma null hypothesis. The upper region is the target region related to Image 1, and the other is the target region related to Image 3.
A CD algorithm is presented and evaluated in the next section to assess the Gamma distribution for the clutter-plus-noise statistical model. Further discussions can be found in Section 5.
4. Change Detection
The change detection method for low-frequency difference intensity wavelength-resolution SAR images studied in this paper consists of a hypothesis test to evaluate whether a pixel position is target-related or background-related. Thus, the test determines if a target is present or absent in the evaluated pixel position. The hypothesis considered in the test can be expressed as
where is the hypothesis that the pixel under test is background-related, is the hypothesis that the pixel under test is target-related, is the target signal vector, and , in which and represent the clutter vector and noise vector, respectively, and indexes and refer to the surveillance and reference SAR images. Generally, no target is expected in the reference image; thus, it is reasonable to assume that . The evaluated change detection method is the LRT presented in the next section.
4.1. Likelihood-Ratio Test
The development of a likelihood-ratio test with bivariate Gamma distribution for intensity SAR images is similar to the one investigated for amplitude SAR images in [33], where a CD method is proposed for VHF UWB SAR amplitude images considering the Bivariate Gamma distribution.
The probability density function (pdf) of the Bivariate Gamma distribution can be written as [33]
where denotes the modified Bessel function of the first kind, and are the shape and scale parameter, respectively, where , and is the association parameter between and under the assumption of , obtained as
where is the Pearson’s product-moment correlation coefficient. If , the association parameter between and can be calculated by
The correlation coefficient is estimated from the original sample data by
where and are the means and standard deviations of random variables, respectively.
The likelihood-ratio test can be written as
where both and are modeled as Bivariate Gamma distributions, , and x and y are the pixel intensity in the pixel position under test, respectively, in the reference and surveillance images. In our evaluation, the reference image is used to compute the shape parameter under the condition .
The method chosen to estimate the shape and scale parameters is the maximum likelihood estimator, for the sake of simplicity. These parameters are estimated as [33]
where
and
These estimations can be computed using MATLAB’s gamfit(.) function with the Newton–Raphson update.
The statistical hypothesis test under the assumption is derived in the following form [33]
where is the signal intensity from the interest image, is the sum , and , which can be approximated as [33]
Otherwise, i.e., if , then the statistical hypothesis test can be written as
4.2. Implementation Aspects
The chain processing used to evaluate the proposed CD method is performed in three steps. First, the difference images are obtained by two subtractions using three intensity SAR images. Then, the described LRT is realized. Finally, as an optional step, morphological operations can be performed. The output of this processing chain is a binary image named the detection image. A basic block diagram of the described processing chain is presented in Figure 4, where Image 1 represents the original surveillance image, Image 2 represents the original reference image, and Image 3 represents a common image to both subtractions. These difference-intensity images are obtained, respectively, by using the operations |Images 1–3|2 and |Images 2–3|2 in each pixel position of the original amplitude images. Based on (5) and (6), it is not possible that a target-related pixel contains a negative pixel amplitude after the subtraction Images 1–3. Thus, if the difference Images 1–3 is positive, then the proposed test performs a thresholding operation that consists of assigning 1 when and assigning 0 when , resulting in a binary image; otherwise, the output pixel is always assigned to 0. To ensure a fair comparison with other published results, the statistics were obtained considering a window of 100 × 100 pixels with a step of 10 pixels [48].
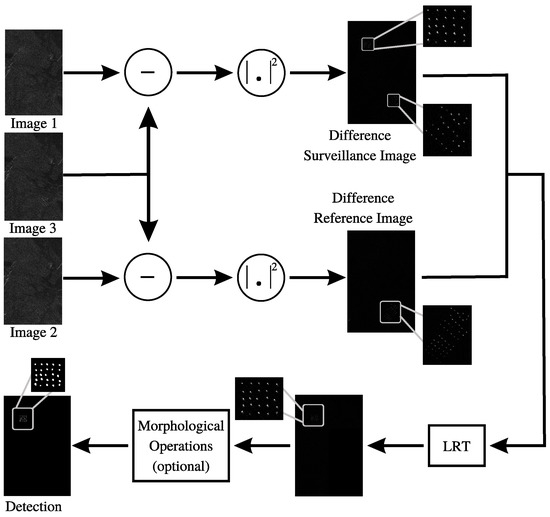
Figure 4.
Block diagram of the proposed change detection method. All SAR images illustrated in the block diagram are part of the CARABAS-II data set.
This paper uses morphological operations similar to those considered in [14,49], i.e., one erosion a 3 × 3 m erosion cell and one dilatation, using square structuring elements whose sizes enable the merging of any detected samples that are separated by 10 m or less. It is essential to highlight that these operations should be selected according to the method’s application specificity.
In our study, several combinations of the intensity constant and the threshold have been empirically evaluated. The experimental tests were performed considering the CD method using all 24 images provided in the CARABAS-II data set. This method is assessed in terms of the probability of detection () and false-alarm rate (FAR), i.e., the number of false alarms per square kilometer. In our evaluation, detection is defined as any detected object on the binary output matrix after morphological operations. Thus, correct target detection is any detected object lying in a range of, at maximum, 10 m from the original target position. Any other detected object is declared as a false alarm.
4.3. CD Results
Table 1 and Table 2 present the and FAR performances obtained by the CD method for two different thresholds and a fixed-intensity constant . In Table 1, the threshold value was empirically established to obtain a high performance, i.e., . In this scenario, the chosen threshold value is . Additionally, in Table 2, the threshold value selection was empirically established to obtain a high FAR performance, i.e., . For simplicity, the name of the images was shortened using the notation , where means mission x, where , and represents pass y, where .

Table 1.
Performance results of the proposed method for a threshold and . Herein, the images are represented using the notation , where means mission x, where , and represents pass y, where .

Table 2.
Performance results of the proposed method for a Threshold and . Herein, the images are represented using the notation where means mission x, where , and represents pass y, where .
From the results presented in Table 1 and Table 2, it is observable that experiment 18 has a significant impact on the performance of the studied technique, i.e., the majority of the non-detections and false alarms results from this experiment. This pattern was also observed in several other methods proposed in the literature [14,32,33,48]. To extend our discussion, Figure 5 and Figure 6 present the output detection image of the studied technique for experiments 1 and 18, considering the parameters from Table 1 and Table 2, respectively. It is important to highlight that the ground truth from experiment 1 comes from the target deployment presented in Figure 1a. In contrast, the ground truth from experiment 18 comes from the target deployment shown in Figure 1b.

Figure 5.
Output detection binary image for experiments 1 and 18 presented in (a,b), respectively, for and . The original target deployments for the evaluated experiments are presented in Figure 1a,b, respectively.
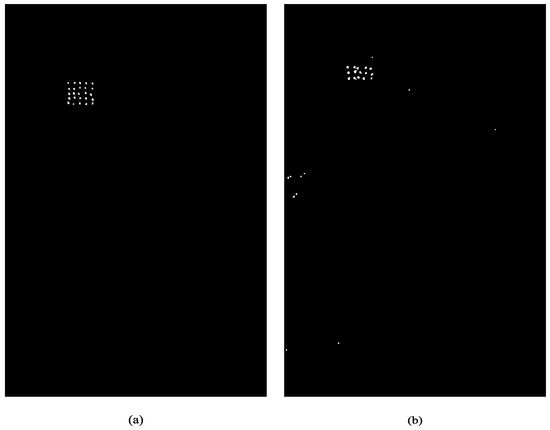
Figure 6.
Output detection binary image for experiments 1 and 18 presented in (a,b), respectively, for and . The original target deployments for the evaluated experiments are presented in Figure 1a,b, respectively.
As can be observed in Figure 5a and Figure 6a, the proposed method performs well for both scenarios, resulting in the detection of all targets in both cases. Note that the false alarms observed in Figure 5a mainly derive from the small threshold value, which was an expected pattern. However, the results observed in Figure 5b and Figure 6b show that several false alarms are observed for a low threshold scenario, and several non-detections are present in the case with a higher threshold value, which is an expected pattern. However, the proposed method detects an unexpected structure on the left side of the image in both evaluated cases. This structure is generated from some image-formation issues observed in the images used in experiment 18. Additional processing techniques are required to improve the detection performance for this type of evaluated scenario, as demonstrated in [23]. However, to guarantee a fair comparison with the other methods discussed throughout this section, these additional processing steps are not considered.
To conclude the performance analysis based on Table 1 and Table 2, a comparison with the LRT-based methods shown in [15] is presented. In [15], the authors proposed two LRT change detection methods based on Rayleigh and K-distributed background statistics, where points with are highlighted. For the evaluated CARABAS-II data set, the Rayleigh-based method detected 568 targets with 3594 false alarms, i.e., . The K-distributed-based technique detected 570 targets with 100 false alarms, i.e., . These results show that a better-selected background statistics distribution improves the change detection performance of the application. From Table 2, the method using the Gamma background statistics for difference intensity images detected 571 targets with 22 false alarms, i.e., , which corroborates the analysis regarding the background statistics’ distribution fit provided in Section 3.
The second presented evaluation is based on the variation in the intensity constant , and presented in terms of Receiver Operating Characteristic (ROC) curves in Figure 7. Additionally, Figure 7 shows ROC curves from other change detection methods in the literature, i.e., [32,33], which are used for performance comparison and further discussed throughout this section. For this evaluation, different values of were considered when evaluating several different threshold values, e.g., . The analysis related to the influence of the selection of can be carried out in a very high-detection-probability scenario, i.e., , and for a low-FAR scenario, i.e., FAR . Considering the high-detection-probability scenario, for instance, when FAR , the following detection probabilities are observed: for , for , and for . Thus, for low values, the proposed method tends to perform better. Additionally, it is possible to observe that, for , it is not possible to detect some targets, resulting in a saturation pattern in the ROC curve. When considering the low-FAR scenario, a different behavior is observed. Using low values of tends to produce false alarms related to objects with an almost target-like statistical behavior. These false alarm detections are directly related to the specificities of the data set. Frequently, these detections are mitigated by amplitude constraints [14,33]. Thus, the criterion selection of is directly related to the specificities of the application, prioritizing lower values for situations where a very high is required and prioritizing higher values of for situations where a low false alarm occurrence is needed.
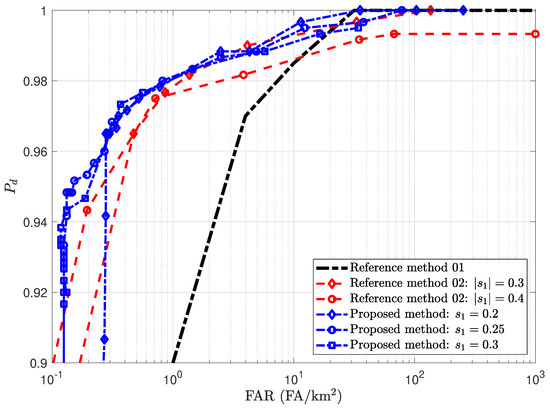
Figure 7.
ROC curves performance comparison of the performances obtained from the studied change detection method under different intensity constraints and reference methods from the literature. The compared performances were the best ROC curves extracted from [32,33], referred to as reference methods 01 and 02, respectively.
To conclude our experimental evaluation, the studied change detection performance is compared with other published change detection methods from the literature. This analysis is also based on the ROC curves in Figure 7. The assessment compares the proposed intensity-target detection method and other LRT-based techniques using amplitude SAR images. The first method, presented in [32], was one of the first LRT-based change detection methods using the CARABAS-II data. In this technique, the background statistics are modeled as Gaussian-distributed. The second method from the literature used in our performance comparison is presented in [33]. To the best of the authors’ knowledge, this technique is the LRT-based change detection method that provides the best performance for amplitude pairs using this data set and adopting similar constraints. The notation used in the original articles was maintained. Analyzing the results, considering an FAR , for the reference method [32], the following probability of detection is observed: . For the reference method [33], the following probabilities of detection are observed: using and using . For the proposed method, the following probabilities of detection are observed: for , for , and for . Similarly, considering an FAR , for the reference method [32], the following probability of detection is observable: . For the reference method [33], the following probabilities of detection are observable: using and using . For the proposed method, the following probabilities of detection are observed: for the three evaluated values of . As shown in Figure 7, the proposed method outperforms the other LRT-based change detection methods for most of the evaluated points presented in the ROC curve. It is suitable to relate these performance gains to the better selection of the clutter-plus-noise statistics, i.e., background statistics. Further discussion regarding these observations is presented in Section 5.
5. Discussions
The results presented in Figure 2 show that the exponential distribution does not provide a good fit for the background statistics of low-frequency difference intensity wavelength-resolution SAR images. Different conclusions can be derived from the results presented in Figure 3, which provided a good fit for most of the evaluated regions. The regions where the AD test rejected the Gamma distribution are mainly related to the target regions from the original images. Additionally, the isolated rejected cells could possibly be associated with isolated target-like patterns from the background, showing high-intensity pixels or Type I error, as discussed in [22]. Thus, according to the AD GoF test, the Gamma distribution provides a better statistical fit for the clutter-plus-noise of low-frequency difference intensity wavelength-resolution SAR images.
Two main patterns could be verified from the results observed in Table 1 and Table 2 from the visual inspection made considering Figure 5 and Figure 6 and the comparison with the LRT methods presented in [15]. The first pattern was verified when the target-related pixels showed an amplitude signature with high differentiation of the background-related pixels. This situation is observed in Figure 6a. Since intensity images tend to increase this differentiation, fewer false alarms are expected in this scenario than when using amplitude images. The second pattern is verified when the target-related pixels have an amplitude signature with low differentiation from the background-related pixels. This situation is observed in Figure 6b. In this scenario, these targets become more difficult to detect when using intensity images than when using amplitude images. Thus, fewer false alarms are expected in change detection methods using low-frequency difference intensity wavelength-resolution SAR images than in the amplitude ones. However, some targets tend to be more challenging to detect. Finally, these two patterns can also be verified using Figure 7, where low FAR values are observed for . However, a larger FAR increase was observed to detect all targets in the low-frequency difference-intensity wavelength-resolution SAR images than the increase noted for the amplitude techniques.
The results presented in Figure 7 show that the studied technique provides better results regarding the probability of detection of an FAR for most of the evaluated cases, i.e., for lower levels of FAR, the Gamma distribution for low-frequency difference-intensity wavelength-resolution SAR images yields to a higher probability of detection. Thus, based on these results, we observe that using intensity-difference wavelength-resolution SAR images in CD applications with an adequate background statistics model tends to provide gains in both and FAR compared with other methods in the literature.
6. Conclusions
Statistical analysis for difference wavelength-resolution intensity SAR images was presented in this article. Two statistical distributions were evaluated. The first considered distribution was the bivariate Exponential distribution, frequently used for microwave intensity SAR images. The second distribution was the bivariate Gamma distribution, selected based on previous observations on amplitude VHF wavelength-resolution SAR images. The results of the goodness-of-fit tests show that the bivariate Gamma distribution provides a better fit for the background statistics for low-frequency difference intensity wavelength-resolution SAR images.
A CD method for detecting concealed targets in forestry areas was evaluated considering the background statistics of difference intensity VHF wavelength-resolution SAR images, modeled as Gamma distribution. The good fit of the Gamma distribution for the background statistics in low-frequency wavelength-resolution SAR images results in good performances in the experimental evaluation using the CD technique. Additionally, the CD under evaluation presents a competitive performance compared to other recently published approaches.
Author Contributions
Conceptualization, G.H.M.V., D.I.A. and C.M.; methodology, G.H.M.V. and D.I.A.; software, G.H.M.V.; validation, G.H.M.V., D.I.A. and C.M.; formal analysis, G.H.M.V.; investigation, G.H.M.V. and D.I.A.; resources, D.I.A.; data curation, D.I.A.; writing—original draft preparation, G.H.M.V.; writing—review and editing, D.I.A., C.M., R.M., L.P.R., V.T.V. and M.I.P.; visualization, G.H.M.V.; supervision, R.M., V.T.V. and M.I.P.; project administration, R.M.; funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Brazilian Agencies National Council for Scientific and Technological Development (CNPq), Coordination for the Improvement of Higher Education Personnel (CAPES) – Finance Code 001 (Pró-Defesa IV), and São Paulo Research Foundation (FAPESP) under grant #2020/09838-0 (BI0S-Brazilian Institute of Data Science).
Data Availability Statement
The wavelength-resolution SAR images acquired by CARABAS-II system were obtained from AFRL Sensor Data Management System (SDMS) (https://www.sdms.afrl.af.mil/, accessed on 10 September 2019).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AD | Anderson-Darling |
| AFRL | Air Force Research Laboratory |
| CARABAS | Coherent All Radio Band Sensing |
| CD | Change Detection |
| FAR | False-Alarm Rate |
| FOI | Swedish Defence Research Agency |
| FOPEN | Foliage-Penetrating |
| GoF | Goodness-on-Fit |
| LRT | Likelihood-Ratio Test |
| ROC | Receiver Operating Characteristic |
| SAR | Synthetic Aperture Radar |
| UWB | Ultra-Wide-Band |
| VHF | Very-High Frequency |
References
- Fransson, J.E.; Walter, F.; Ulander, L.M. Estimation of forest parameters using CARABAS-II VHF SAR data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 720–727. [Google Scholar] [CrossRef]
- Vesecky, J.F.; Stewart, R.H. The observation of ocean surface phenomena using imagery from the SEASAT synthetic aperture radar: An assessment. J. Geophys. Res. Ocean. 1982, 87, 3397–3430. [Google Scholar] [CrossRef]
- Vu, V.T.; Sjögren, T.K.; Pettersson, M.I.; Marques, P.A. Application of the moving target detection by focusing technique in civil traffic monitoring. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; IEEE: New York, NY, USA, 2010; pp. 4118–4121. [Google Scholar]
- Tsai, Y.L.S.; Dietz, A.; Oppelt, N.; Kuenzer, C. Remote sensing of snow cover using spaceborne SAR: A review. Remote Sens. 2019, 11, 1456. [Google Scholar] [CrossRef]
- Galati, G.; Perrotta, G.; Di Girolamo, S.; Mura, R. Space-based SSR constellation for global air traffic control. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1088–1106. [Google Scholar] [CrossRef]
- Parker, D. Microwave industry outlook-defense applications. IEEE Trans. Microw. Theory Tech. 2002, 50, 1039–1041. [Google Scholar] [CrossRef]
- Davidson, M.; Iannini, L.; Torres, R.; Geudtner, D. New Perspectives for Applications and Services Provided by Future Spaceborne SAR Missions at the European Space Agency. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: New York, NY, USA, 2022; pp. 4720–4723. [Google Scholar]
- Richards, M.A.; Scheer, J.; Holm, W.A.; Melvin, W.L. Principles of Modern Radar, 1st ed.; Citeseer: Princeton, NJ, USA, 2010. [Google Scholar]
- Nagler, T.; Rott, H.; Ossowska, J.; Schwaizer, G.; Small, D.; Malnes, E.; Luojus, K.; Metsämäki, S.; Pinnock, S. Snow cover monitoring by synergistic use of Sentinel-3 Slstr and Sentinel-L Sar data. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: New York, NY, USA, 2018; pp. 8727–8730. [Google Scholar]
- Wang, Y.; Zhang, Z.; Li, N.; Hong, F.; Fan, H.; Wang, X. Maritime surveillance with undersampled SAR. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1423–1427. [Google Scholar] [CrossRef]
- Yan, H.; Wang, R.; Li, F.; Deng, Y.; Liu, Y. Ground moving target extraction in a multichannel wide-area surveillance SAR/GMTI system via the relaxed PCP. IEEE Geosci. Remote Sens. Lett. 2012, 10, 617–621. [Google Scholar] [CrossRef]
- Melvin, W.L.; Scheer, J.A. Principles of Modern Radar: Volume III—Radar Applications, 1st ed.; SciTech Publishing: Edison, NJ, USA, 2014. [Google Scholar]
- Ulander, L.M.H. VHF-Band SAR for Detection of Concealed Ground Targets. In RTO SCI Symposium on Sensors and Sensor Denial by Camouflage, Concealment and Deception; NATO: Brussels, Belgium, 2004; pp. 1–11. [Google Scholar]
- Alves, D.I.; Palm, B.G.; Hellsten, H.; Vu, V.T.; Pettersson, M.I.; Machado, R.; Uchôa-Filho, B.F.; Dammert, P. Wavelength-Resolution SAR Change Detection Using Bayes’ Theorem. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5560–5568. [Google Scholar] [CrossRef]
- Gomes, N.R.; Dammert, P.; Pettersson, M.I.; Vu, V.T.; Hellsten, H. Comparison of the Rayleigh and K-Distributions for Application in Incoherent Change Detection. IEEE Geosci. Remote Sens. Lett. 2019, 16, 756–760. [Google Scholar] [CrossRef]
- Vu, V.T. Wavelength-Resolution SAR Incoherent Change Detection Based on Image Stack. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1012–1016. [Google Scholar] [CrossRef]
- Voigt, G.H.M.; Alves, D.I.; Müller, C.; Machado, R.; Vu, V.T.; Pettersson, M.I. Change detection method for intensity VHF wavelength-resolution SAR images. In Proceedings of the Submitted to SPIE Remote Sensing Symposium: Image and Signal Processing for Remote Sensing XXVII, Online, 13–17 September 2021. [Google Scholar]
- Lundberg, M.; Ulander, L.M.; Pierson, W.E.; Gustavsson, A. A challenge problem for detection of targets in foliage. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XIII, Orlando, FL, USA, 17–21 April 2006; Volume 6237, pp. 160–171. [Google Scholar]
- Frolind, P.O.; Ulander, L. Motion compensation effects for repeat-pass processing in wavelength-resolution SAR. In Proceedings of the IGARSS’98—Sensing and Managing the Environment: 1998 IEEE International Geoscience and Remote Sensing. Symposium Proceedings (Cat. No. 98CH36174), Seattle, WA, USA, 6–10 July 1998; IEEE: New York, NY, USA, 1998; Volume 5, pp. 2637–2639. [Google Scholar]
- Machado, R.; Vu, V.T.; Pettersson, M.I.; Dammert, P.; Hellsten, H. The Stability of UWB Low-Frequency SAR Images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1114–1118. [Google Scholar] [CrossRef]
- Voigt, G.H.; Alves, D.I.; Müller, C.; Machado, R.; Vu, V.T.; Pettersson, M.I. Target Detection Method for Intensity VHF Wavelength-Resolution SAR Images. In Proceedings of the XXXIX Simpósio Brasileiro de Telecomunicações e Processamento de Sinais, Online, 26–29 September 2021. [Google Scholar]
- Alves, D.I.; Palm, B.G.; Pettersson, M.I.; Vu, V.T.; Machado, R.; Uchôa-Filho, B.F.; Dammert, P.; Hellsten, H. A Statistical Analysis for Wavelength-Resolution SAR Image Stacks. IEEE Geosci. Remote Sens. Lett. 2020, 17, 227–231. [Google Scholar] [CrossRef]
- Vu, V.T.; Pettersson, M.I.; Machado, R.; Dammert, P.; Hellsten, H. False Alarm Reduction in Wavelength-Resolution SAR Change Detection Using Adaptive Noise Canceler. IEEE Trans. Geosci. Remote Sens. 2017, 55, 591–599. [Google Scholar] [CrossRef]
- Campos, A.B.; Pettersson, M.I.; Vu, V.T.; Machado, R. False Alarm Reduction in Wavelength–Resolution SAR Change Detection Schemes by Using a Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Vinholi, J.G.; Palm, B.G.; Silva, D.; Machado, R.; Pettersson, M.I. Change Detection Based on Convolutional Neural Networks Using Stacks of Wavelength-Resolution Synthetic Aperture Radar Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Alves, D.I.; Müller, C.; Palm, B.G.; Pettersson, M.I.; Vu, V.T.; Machado, R.; Uchôa-Filho, B.F.; Dammert, P.; Hellsten, H. Neyman–Pearson Criterion-Based Change Detection Methods for Wavelength–Resolution SAR Image Stacks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Harris, B.W.; Milo, M.W.; Roan, M.J. Symbolic target detection in SAR imagery via rotationally invariant-weighted feature extraction. Int. J. Remote Sens. 2013, 34, 8724–8740. [Google Scholar] [CrossRef]
- Gao, G. Statistical modeling of SAR images: A survey. Sensors 2010, 10, 775–795. [Google Scholar] [CrossRef]
- Matsuoka, M.; Yamazaki, F. Use of satellite SAR intensity imagery for detecting building areas damaged due to earthquakes. Earthq. Spectra 2004, 20, 975–994. [Google Scholar] [CrossRef]
- Gong, M.; Li, Y.; Jiao, L.; Jia, M.; Su, L. SAR change detection based on intensity and texture changes. ISPRS J. Photogramm. Remote Sens. 2014, 93, 123–135. [Google Scholar] [CrossRef]
- Wang, C.; Bi, F.; Zhang, W.; Chen, L. An intensity-space domain CFAR method for ship detection in HR SAR images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 529–533. [Google Scholar] [CrossRef]
- Ulander, L.M.H.; Lundberg, M.; Pierson, W.; Gustavsson, A. Change detection for low-frequency SAR ground surveillance. IEE Proc. Radar Sonar Navig. 2005, 152, 413–420. [Google Scholar] [CrossRef]
- Vu, V.T.; Gomes, N.R.; Pettersson, M.I.; Dammert, P.; Hellsten, H. Bivariate Gamma Distribution for Wavelength-Resolution SAR Change Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 473–481. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- DeVore, M.D.; O’Sullivan, J.A. Statistical assessment of model fit for synthetic aperture radar data. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery VIII, Orlando, FL, USA, 16–19 April 2001; SPIE: Paris, France, 2001; Volume 4382, pp. 379–388. [Google Scholar]
- Dodge, Y. The Concise Encyclopedia of Statistics; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Makarov, A.; Simonova, G. Studying the Power of the Two-Sample Anderson–Darling Test in the Case of Contamination of One Sample. J. Math. Sci. 2017, 221, 580–587. [Google Scholar] [CrossRef]
- U.S. Air Force. The Sensor Data Management System; U.S. Air Force: Columbus, OH, USA, 2021. [Google Scholar]
- Hellsten, H.; Ulander, L.M.; Gustavsson, A.; Larsson, B. Development of VHF CARABAS II SAR. In Radar Sensor Technology; SPIE: Paris, France, 1996; Volume 2747, pp. 48–60. [Google Scholar]
- Wang, H.; Yang, E.h.; Zhao, Z.; Zhang, W. Spectrum sensing in cognitive radio using goodness of fit testing. IEEE Trans. Wirel. Commun. 2009, 8, 5427–5430. [Google Scholar] [CrossRef]
- D’Agostino, R. Goodness-of-Fit-Techniques; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Marsaglia, G.; Marsaglia, J. Evaluating the anderson-darling distribution. J. Stat. Softw. 2004, 9, 1–5. [Google Scholar] [CrossRef]
- Thomas, M.; Joy, A.T. Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Fisher, R.A. Statistical methods for research workers. In Breakthroughs in Statistics; Springer: Cham, Switzerland, 1992; pp. 66–70. [Google Scholar]
- Leone, F.C.; Nelson, L.S.; Nottingham, R. The folded normal distribution. Technometrics 1961, 3, 543–550. [Google Scholar] [CrossRef]
- Byers, R. Half-Normal Distribution. In Wiley StatsRef: Statistics Reference Online; Wiley: New York, NY, USA, 2014. [Google Scholar]
- Brockwell, P.J.; Brockwell, P.J.; Davis, R.A.; Davis, R.A. Introduction to Time Series and Forecasting; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Lundberg, M.; Ulander, L.M.H.; Pierson, W.E.; Gustavsson, A. A challenge problem for detection of targets in foliage. In Algorithms for Synthetic Aperture Radar Imagery XIII; SPIE: Paris, France, 2006; Volume 6237. [Google Scholar]
- Vu, V.T.; Alves, D.I.; Palm, B.G.; Pettersson, M.I.; Dammert, P.; Hellsten, H. A Detector for Wavelength Resolution SAR Incoherent Change Detection. In Proceedings of the IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).