Abstract
The use of geostationary meteorological satellites for land remote sensing has attracted much attention after the launch of the Himawari-8 satellite equipped with a sensor with enhanced land observation capabilities. In the context of land remote sensing, geolocation errors are often a critical issue, especially in mountainous regions, where a precise orthorectification process is required to maintain high geometric accuracy. The present work addresses the issues related to orthorectification of the new-generation geostationary Earth orbit (GEO) satellites by applying an algorithm known as the ray-tracing indirect method to the data acquired by the Advanced Himawari Imager (AHI) aboard the Himawari-8 satellite. The orthorectified images of the AHI were compared with data from the Sentinel-2 Multispectral Instrument (MSI). The comparison shows a clear improvement of the geometric accuracy, especially in high-elevation regions located far from the subsatellite point. The results indicate that approximately 7.3% of the land pixels are shifted more than 3 pixels during the orthorectification process. Furthermore, the maximum displacement after the orthorectification is up to 7.2 pixels relative to the location in the original image, which is of the Tibetan Plateau. Moreover, serious problems caused by occlusions in the images of GEO sensors are clearly indicated. It is concluded that special caution is needed when using data from GEO satellites for land remote sensing in cases where the target is in a mountainous region and the pixels are located far from the subsatellite point.
1. Introduction
Geometric accuracy is one of the key characteristics of remotely sensed satellite images. It directly affects accuracy in data analysis and therefore influences the validity of any conclusion drawn based on such analyses. Various factors govern geometric accuracy, including those associated with acquisition systems, such as aviation information and sensor mechanisms, and those associated with observed targets, such as atmospheric conditions, topographic effects, and assumed ellipsoidal models []. The influences of the former factors on geometric accuracy can be mostly eliminated through a commonly used systematic algorithm known as the Earth location algorithm [], in conjunction with information such as sensor-target geometry. Further corrections are often performed to precisely correct image distortion to minimize the influence of factors associated with the observed target. Among these factors, terrain relief can cause quite complex image distortion when a target is viewed from the off-nadir direction. Because land remote sensing has been conducted mainly by low Earth orbit (LEO) satellites, geometric correction of data collected by these satellites has been intensively studied. By contrast, for geostationary Earth orbit (GEO) satellites, whose primary purpose is meteorological observations, room remains for discussion, and hence investigation of the geometric accuracy in the context of land remote sensing [,,]. In particular, investigations should be conducted by noting the differences in observation geometries between the LEO and GEO satellites [,].
In the case of land remote sensing of mountainous regions, where geometric accuracy tends to be lower, high geometric accuracy should be achieved through an orthorectification process that corrects the image distortion caused by terrain relief. The distortion increases with increasing view zenith angle and the increasing elevation of a target. Correction schemes can be categorized into two approaches depending on the resolution of the target images. One approach involves a group of algorithms known as the rational polynomial coefficients (RPC) algorithm for images with a relatively high spatial resolution [,,,,]. The RPC algorithm employs rational functions to model the image distortion caused by terrain relief. This algorithm has been used to orthorectify data from SPOT satellite sensors [,] and has been intensively used to orthorectify data from high-resolution satellite sensors such as IKONOS [,]. The other group of algorithms is referred to as the ray-tracing method [,,], which has mainly been used for relatively low-resolution data such as those from the moderate-resolution imaging spectroradiometer (MODIS) instruments aboard the Terra and Aqua satellites []. The ray-tracing method is further subdivided into two categories: the direct method [,,] and the indirect method [,,,,]. The direct and indirect methods differ in the projection direction represented by a starting image frame. The direct method starts from the input image frame, where a pixel of the original image (in two dimensions) is projected onto a three-dimensional surface (digital elevation model; DEM) in the frame of an output image. In general, the direct method requires an iterative algorithm with a precise digital elevation model. Therefore, it is suitable for geometric correction of relatively high-spatial-resolution data. By contrast, the indirect method starts from the three-dimensional surface of an output image frame []. In this approach, a pixel of the output image is related to a pixel of the input image. Because our interest lies in correcting the data from GEO satellites with low spatial resolution and a large coverage area, we employ the latter approach in the present work.
The ray-tracing algorithm, also known as the terrain interaction algorithm [], has been frequently applied to data from LEO satellites. The orthorectification process has received relatively little attention as a method for processing GEO satellite data. One reason for this lack of attention is that the primary purpose of GEO satellites is meteorological observations; thus, the primary objectives are not influenced by the geometric accuracy of inland surfaces (with varying elevation). This trend, however, has gradually changed since the introduction of new-generation GEO satellites with advanced sensors for land monitoring (i.e., the Spinning Enhanced Visible and Infrared Imager (SEVIRI) on the Meteosat Second Generation (MSG) satellite, the Advanced Himawari Imager (AHI) on the Himawari-8 and -9 satellites, the Advanced Baseline Imager (ABI) on Geostationary Environmental Satellites (GOES)-16 and -17, the Advanced Geosynchronous Radiation Imager (AGRI) on satellites Fengyun (FY)-4A and -4B, and the Advanced Meteorological Imager (AMI) on the Geostationary Korea Multi-Purpose SATellite (Geo-KOMPSAT)) []. Because these satellites can monitor land surfaces, their geometric accuracy should also be investigated in the context of land remote sensing. For example, Takeuchi and Yasuoka [] have shown that in the context of land remote sensing without precise geometric correction, the geometric accuracy in the average of the root mean square error of Multi-purpose Transmission SATellite (MTSAT) imagery reaches nearly 5.71 pixels.
The present study attempts to shed light on the orthorectification process, which is considered an established task widely applied to remotely sensed imagery from various satellite platforms. For instance, the legendary data from the Landsat sensor series [] and the Terra and Aqua MODIS sensors [] have been subjected to an orthorectification process, which enhances the geometric accuracy; this enhancement is especially important in the case of mountainous terrain. Toutin comprehensively reviewed these techniques in 2004 []. In the case of GEO satellites, orthorectification tasks have also been reported several times since the early development of meteorological satellites [,,,,,,]. In recent years, several groups have reported notable works related to the new-generation GEO satellites [,,,,,,]. Among them, Takeuchi et al. [,], Wang et al. [], and Pestana and Lundquist [,] applied orthorectification processes to data from new-generation GEO satellites. Takeuchi et al. [,] investigated the geometric accuracy of Himwari-8 and its predecessor satellite. Their report showed that geometric accuracy was improved by an orthorectification process based on the indirect ray-tracing technique. However, a precise description of the orthorectification algorithm they employed was not given. Wang et al. [] attempted the operational implementation of an orthorectification process that employed an RPC-based algorithm of the type used for data from the LANDSAT series [,]. This method differs from the ray-tracing technique used in the present study. Pestana and Ludquist [,] mainly examined the influence of terrain on the thermal bands of GOES-16 ABI. Given this background in the context of land remote sensing, the objective of the present study is to focus the attention of researchers who use data from new-generation GEO satellites on the issues related to orthorectification. The intention of this work is to discuss existing techniques rather than to develop new methods. In the case of land observation by GEO satellites, pixel displacement caused by target elevation varies dramatically depending on the relative distance of the target pixel from the subsatellite point. Most notably, because observations are carried out at a certain view zenith angle fixed for each pixel, this displacement is also fixed to each pixel. This fact makes the process of orthorectification of GEO satellite data somewhat easier than that of LEO satellite data. In addition, the displacement pattern is unique to each GEO sensor, which is basically fixed throughout the sensor’s lifetime. An important drawback of the fixed-view angle is that occlusion will also continue to be a problem throughout the sensor’s lifetime. Thus, the pixels at which occlusion occurs have never been observed by the GEO sensor. Data from other sensors, including those on LEO satellites, should be used to compensate for this problem. The fact that the displacement is fixed to each pixel also implies that even for data from GEO satellites, the influence of the parallax effect caused by the elevation of a pixel and its surroundings should be understood thoroughly prior to any observation activities. This information becomes especially important to achieving high geometric accuracy for mountainous regions, which are often included as regions of interest in land remote sensing.
The aims of the present study are to provide information regarding the influence of parallax effects in the context of land surface monitoring by third-generation GEO satellites. This study focuses on data acquired by the AHI aboard the Himawari-8 satellite operated by the Japan Meteorological Agency (JMA) and distributed by the Japanese National Institute of Information and Communications Technology (NICT). The objectives are (1) to summarize the analytical formula and data processing scheme used to compute pixel displacement caused by the parallax effect over land, (2) to apply the formula to actual observation data from the Himawari-8 AHI, and (3) to evaluate its performance by comparison with higher-resolution satellite data. For the third objective, we have chosen Sentinel-2 MSI Level 1C data, which have already been operationally orthorectified []. Finally, we discuss our results to draw special attention to the benefits of improving geometric accuracy, which should be a topic of interest to researchers who use GEO satellites for land monitoring.
2. Materials
2.1. The Himawari-8 AHI
The Himawari-8 AHI has 16 spectral bands with 0.5, 1, and 2 km spatial resolution [,]. There are five observation areas: Full Disk, Japan Area, Target Area, and two Landmark Areas. We used the Full Disk data acquired at 4:00 UTC on 8 April 2022, which were provided by JMA via the Himawari project in the NICT ScienceCloud (https://sc-web.nict.go.jp/himawari/ accessed on 20 February 2023). The Full Disk observation frequency was every 10 min, and the image size was 11,000 × 11,000 pixels for the 1 km resolution band.
Our orthorectification process involves two map projections. One is the projection of the given input image of the standard data, and the other is the projection for the frame of an output image. The given map projection of the standard Himawari data as an input is the normalized geostationary projection [], which has been widely used for geostationary meteorological satellites [,,]. By contrast, as the output image frame, we chose the equirectangular projection (which is also referred to as the plate carrée projection or latitude longitude projection) for the sake of usability. The spatial range of the output frame is from 60°N to 60°S in latitude and from 80°E to 160°W in longitude. Note that this range includes the international date line. The sampling distance (spatial resolution) of the output image frame is 0.01° in both directions, which is approximately 1100 m at the equator.
2.2. Height Data
For the height from Earth ellipsoid, we used the elevation of Global Multi-resolution Terrain Elevation Data 2010 (GMTED 2010) [] and the geoid height of Earth Gravitational Model 2008 (EGM2008) []. The 7.5 arc-second spatial resolution GMTED 2010 was downloaded via EarthExplorer (https://earthexplorer.usgs.gov/ accessed on 20 February 2023) and reprojected to our projection using GDAL commands (https://gdal.org/ accessed on 20 February 2023). Similarly, the EGM2008 geoid model (2.5 min interpolation grid data) [] was downloaded from the Office of Geomatics, National Geospatial-Intelligence Agency (https://earth-info.nga.mil/index.php accessed on 20 February 2023) and reprojected using the attached interpolation code. Finally, we summed these two heights for the ellipsoidal height.
3. Methods
This section describes the orthorectification method we used for the geostationary sensor, along with a comparison between the methods with and without orthorectification. The theoretical basis of the orthorectification method is similar to those reported by Yasukawa and Takagi [] and by Pestana [,].
3.1. Orthorectification
Orthorectification is a process that relates a pixel position in an output image to a pixel position in an input image by considering the influence of the pixel height. Notably, the output image is usually projected onto a map by a certain projection method. Because we used an indirect method, we implemented an orthorectification process as a series of coordinate transformations from the two-dimensional “output image” to the “input image”. During this transformation process, three-dimensional geospatial coordinates were used as intermediate coordinates. Figure 1 shows the computational steps of the orthorectification algorithm implemented in the present study. All the steps will be explained individually in the following subsections, along with the actual implementation.
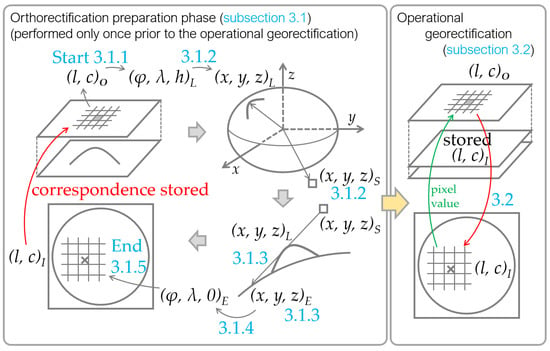
Figure 1.
Orthorectification process of a geostationary sensor. In the orthorectification process, a pixel position in an output image is related to a pixel position in an input image by a series of coordinate transformations via intermediate three-dimensional geospatial coordinates. This process was performed only once prior to the operational phase because the resultant relationship can be used repeatedly. Thus, in the operational georectification phase, the value for an output pixel can simply be interpolated from the values of an input image on the basis of the pixel position derived by the orthorectification process.
3.1.1. Output Image Frame to Latitude, Longitude, and Height
The vertical and horizontal positions of a pixel in the output image (line and column) can be converted to geodetic latitude and longitude on the basis of the known information of a map projection type used for the output image frame. For this conversion process, the map projection type should be known. Because we use the equirectangular projection in the present study, this conversion process is a linear transformation:
where is the target pixel position (line and column) in the output image, is the geodetic latitude and longitude at the top-left corner of the output image (northwest corner in the map projection), is the geodetic coordinates of the center of the target pixel, and r is the spatial resolution of the output frame (pixel size), which is 0.01° in the present study. Note that for the equirectangular projection, the pixel width (east–west) and pixel depth (north–south) are equal (0.01° in the present case). Moreover, after the latitude and longitude are computed, the ellipsoidal height (h) of each pixel can also be obtained as a sum of the elevation (derived from GMTED) and the geoid height (EGM) introduced in Section 2.2.
3.1.2. Latitude, Longitude, and Height to the Earth-Centered, Earth-Fixed Coordinates
The land surface position can be converted to position in the Earth-centered, Earth-fixed (ECEF) coordinate system to relate it to the satellite position. In the ECEF coordinate system, the center of the Earth’s ellipsoid is the origin, the x axis is directed toward the intersection of the Greenwich meridian and the equator, the z axis is directed toward the North Pole, and the y axis corresponds to the direction of the outer product of the z and x axes (or E on the Equator). The transformation is expressed as
with N and are defined as
where a and b are the equatorial and polar radii of the Earth, respectively [].
To proceed further in the framework of the ray-tracing algorithm, the satellite position should also be known in the ECEF coordinate system. This information is obtained from the header of the Himawari Standard Data. In the header information, the satellite position is provided as parameter “sub_lon”, which represents subsatellite longitude and “distance from Earth’s center to virtual satellite”. We assumed that the subsatellite latitude is zero degrees. Note that we use only these nominal values throughout the present study even though the Himawari Standard Data also contains the observed values.
3.1.3. Intersection of Line-of-Sight Vector and the Earth’s Ellipsoid
To find the projected target position on the Earth’s ellipsoid, the intersection of the “line-of-sight vector” (LOS vector: the vector from the satellite position to the target land surface) and the Earth’s ellipsoid was obtained from the linear relationship represented by
where and are the positions (position vectors) of the satellite and target land surface in the ECEF coordinate system, respectively. In the above representation, is the LOS vector, is the intersection of the LOS vector and the Earth’s ellipsoid, and q is the scale factor for adjusting the length of the LOS vector to the distance from the satellite to the intersection. This scale factor q is the one we need to find. Under the procedure explained in Section 3.1 of [], q becomes
where the center dot “·” denotes the inner product of two vectors, (and ) represents the length of vector (and ), and the vectors and are the satellite position vector and LOS vector, respectively. The last two vectors are defined as the rescaled form by the equatorial radius (a) and polar radius (b) of Earth, respectively:
3.1.4. Latitude and Longitude of Intersection
The next step is coordinate conversion from the ECEF system to the geodetic latitude and longitude. Using Equation (4) and given that the height is zero at the surface of the Earth’s ellipsoid, the coordinate of the intersection in ECEF can be converted to the geodetic latitude and longitude by the following:
3.1.5. Latitude and Longitude to Pixel Position in Input Image
The basic products (i.e., Himawari Standard Data, radiance product of GOES-R ABI, and level 1 data of FY-4 AGRI) have their own fixed image frames [,,]. This advantage arises from the fact that a geostationary satellite maintains a fixed position relative to the Earth. It also makes the forward and backward conversion methods between the geographic position (latitude, longitude) and image position (line, column) easier. In the case of the Himawari Standard Data, the original image frame is the normalized geostationary projection defined by the “Low Rate Image Transmission/High Rate Image Transmission (LRIT/HRIT) Global Specification”, which provides specific parameters for this projection [,]. These specific parameters are also stored in the header record of the standard data. In addition, the JMA provided the sample source code for coordinate transformation []. We used the functions included in this code to transform the latitude and longitude coordinate to the pixel position in the AHI full disk image. Note that there is a difference in the definition of pixel coordinates (line and column number) between the LRIT/HRIT Global Specification and the image frame used in the present study. Specifically, the former defines the coordinate at the center of the top-left pixel as (1.0, 1.0), whereas the latter defines the pixel center coordinate as (0.5, 0.5). During the transformation process, we adjusted these differences of the definitions systematically.
3.2. Operational Georectification
Once the correspondence of pixel positions between an orthorectified output image and an input satellite image has been computed, the georectification operation becomes rather simple because of the fixed image coordinates of geostationary satellite products. In the present study, the pixel positions (line and column) in an input Himawari-8 AHI image were stored in files that had the same image frame as the output image. For the operational georectification process, the digital number of an output pixel was simply retrieved via interpolation of the corresponding pixel position, as illustrated in the right side of Figure 1. In addition, because we stored the corresponding pixel position for the highest resolution band (500 m in band 3 for the Himawari AHI), the stored data could be applied to the other bands by scaling to a lower resolution (1 km or 2 km). In fact, this operation can be simply carried out by dividing the position by the ratio of the spatial resolutions of two bands. This simplicity makes the orthorectification process easier to be operational (which would eventually lead to the orthorectified product of a geostationary sensor to the level of data fusion in the framework of the GEO to other GEO and also the GEO to LEO sensors).
3.3. Orthorectification of the Himawari-8 AHI and Its Generalization
We conducted two simple analyses to examine the effect of orthorectification: comparisons with Sentinel-2 MSI and visualization of the pixel shift. Orthorectified Sentinel-2 MSI (level-1C) products were downloaded via the Copernicus Open Access Hub (https://scihub.copernicus.eu/ accessed on 1 September 2022) for three areas: the Tibet Autonomous Region in China, the Akaishi Mountains in Japan, and the Otago Region in New Zealand, as shown in Figure 2b. These images were overlaid with orthorectified and nonorthorectified AHI images using the QGIS software (Open Source Geospatial Foundation Project https://qgis.org/ accessed on 1 September 2022).
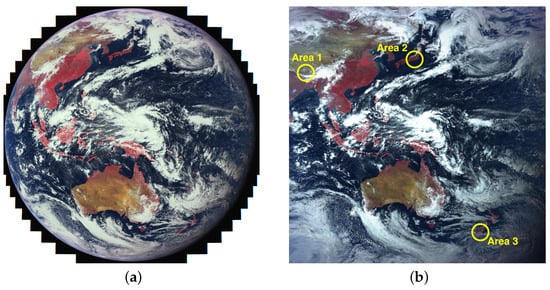
Figure 2.
Himawari-8 AHI Full Disk Data observed at 4:00 UTC on 8 April 2022: (a) false-color composite of the original image and (b) the orthorectified image. Three areas were used for comparison with the Sentinel-2 MSI image (Figure 3).
Interpretation of the results requires awareness of two analogical facts. First, if the ellipsoidal height is set to zero in our orthorectification process (despite most of the land pixels having a height greater than zero), the resultant pixel position would be identical to that without the orthorectification (where no shifting occurred). Second, although the difference in pixel positions between the data with and without orthorectification was computed with respect to the 1 km resolution band, this pixel displacement increases with increasing altitude and increasing distance from the subsatellite point. Even for the same height of target, the displacement distance becomes larger with increasing distance between the target location and the subsatellite point. However, because the footprint of the original Himawari pixel on the ground also becomes larger with increasing distance from the subsatellite point, these two factors compensate for each other to some extent. As a result, the displacement distance would be somewhat smaller than expected if these displacements were measured on the basis of the pixel size of the image frame. Deep awareness of these two analogies is necessary to interpret the results presented in the next section.
We also attempted to extend our approach to the cases of other satellite missions. In the present study, we chose GOES-16 and FY-4 as examples to discuss the applicability of our implementation strategy. In addition, we attempted to generalize our results within a framework of geostationary satellites by adapting several hypotheses during the discussion. The details of these approaches will be explained further in Section 4.3.
4. Results
Figure 2 shows the original Full Disk image and orthorectified image used in the present study. Three areas of the orthorectified image were used for the comparison with the image from the Sentinel-2 MSI. We processed a series of AHI scenes to visually inspect the time dependence (consistency) of the relative geolocation errors in the orthorectified AHI images. We carried out these inspections by making animations from the series of images. Although this qualitative approach is simple, we confirmed that time fluctuations are barely noticeable (observed as vibrations, if any exist) in the animation. These visual inspections indicated that temporal variation of the geolocation inconsistency (among the scenes) is almost negligible. The results imply that the orthorectified images are geolocationally consistent, meaning that geolocation errors in these images are almost identical in the data.
4.1. Comparison with Sentinel-2 MSI
Figure 3 shows the overlaid Himawari-8 AHI and Sentinel-2 MSI images for the three testing areas (Areas 1, 2, and 3). A false-color MSI image is also shown to identify the landscapes of the testing areas. We selected MSI data whose acquisition dates are closest to the selected AHI date: April 8, April 12, and April 6 for Areas 1, 2, and 3, respectively. The near-infrared bands of the AHI (band 4) and MSI (band 8) were overlaid with transparency. The left and center panels show the images with and without orthorectification, respectively. The yellow pixels show the occlusions where the land surface is not visible from the AHI sensor because of terrain shadow (calculated and shown in 0.005° resolution). We assigned a red color to the bright pixels in the MSI image for purposes of comparison.
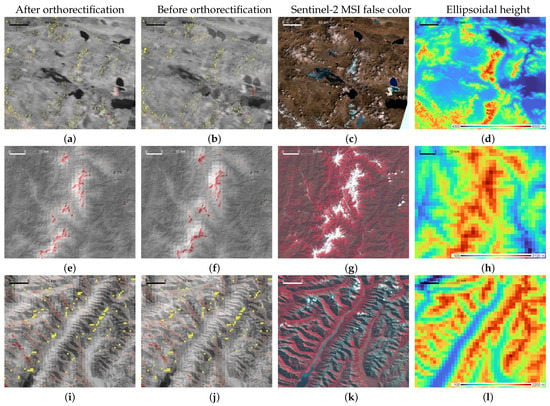
Figure 3.
Comparison of orthorectified and nonorthorectified Himawari-8 AHI images overlaid with the corresponding Sentinel-2 MSI image. Left panels (a,e,i) are orthorectified AHI band 4. Panels (b,f,j) are the same but without orthorectification. Panels (c,g,k) are false-color MSI images. Left panels (d,h,l) are ellipsoidal height. Red in the left two panels indicates bright pixels in the MSI image. Yellow pixels show the pixel locations where occlusions were detected on the basis of the ellipsoidal height data with a resolution of 0.005°. (a–d) are the results for the Tibet Autonomous Region in China. Likewise, (e–h) are the results for the Akaishi Mountains in Japan, and (i–l) are the results for the Otago Region in New Zealand.
The geometrical characteristics of Area 1, the Tibetan Plateau, include an ellipsoidal height greater than 5000 m. Moreover, this area is located at the northwestern edge in the AHI Full Disk image, which is far from the subsatellite point of the AHI (140.7°E). Therefore, a larger relief displacement resulted in greater geolocational disagreement between the AHI and MSI, as evident in Figure 3b. By contrast, the orthorectified image (Figure 3a) corrects them by selecting the pixels from appropriate positions based on the information of these pixel displacements. In addition, because of the high geometric accuracy of the Himawari-8 AHI, the geometric correction was performed well without any additional compensation with ground control points.
For Area 2, a mountainous region in Japan, Figure 3f shows a relatively smaller displacement than that for Area 1 (Figure 3b) because Area 2 has a relatively lower height and is closer to the subsatellite point than Area 1. The shifting direction in the image before the orthorectification (Figure 3f) is almost northward because of the relative location from the subsatellite point; the site is located nearly true north of the subsatellite point. Even though the pixel displacement is smaller, it can strongly influence the research results for mountainous regions because the target surface tends to show high contrast due to snow, dense vegetation, and shadow. Thus, even a small displacement can cause an unexpectedly large difference in reflectance and temperature [].
A major characteristic of the image of Area 3 (Figure 3i,j), the Otago region in New Zealand, is a high brightness contrast along the mountains. Because the local time of the Himawari observation was 16:00, the brightness contrast between the northwestern and southeastern slopes is relatively greater. Note that the acquisition time of the MSI data (Figure 3k) differs from that of the AHI data (Figure 3i,j), and the MSI false-color image does not show this contrast. The orthorectified image shows higher contrast, along with the slope (the direction from southwest to northeast). Because the contrast is greater in Figure 3i than in Figure 3j, we confirmed that our orthorectification process generates the terrain-affected reflectance correctly.
4.2. Change in Pixel Positions from Orthorectification
Figure 4a,b show the pixel displacement of the AHI Full Disk image by the orthorectification process in terms of the pixel size at 1 km spatial resolution. In general, as a target pixel is located farther from the subsatellite position and its ellipsoidal height is greater, the displacement by the orthorectification increases. The histogram in Figure 4b shows the frequency distribution of the pixel displacement only for the land pixels including inland water. Approximately 61% of the pixels are shifted less than 0.5 pixels; these pixels mostly correspond to locations in Southeast Asia, Australia, the North China Plain, and lower-altitude areas in Siberia. By contrast, approximately 7.3% of the land-area pixels are shifted more than 3 pixels; the majority of these pixels correspond to locations in the Tibetan Plateau and the Mongolian Plateau. We note that the largest displacement of approximately 7.2 pixels also occurs for pixels in these regions. For the area of Japan, the shift values range from 0.01 to 2.28 pixels, with the maximum corresponding to the top of Mt. Fuji.
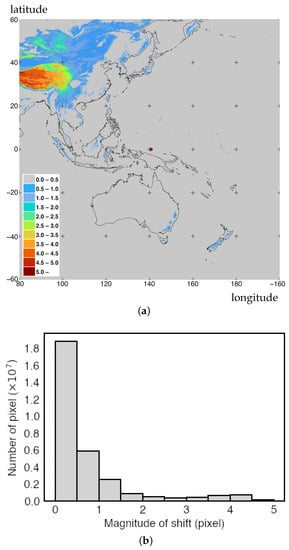
Figure 4.
Pixel displacement by orthorectification of 1 km-resolution Himawari-8 AHI Full Disk data: (a) geographic view, where the red circle at the center is the subsatellite point; and (b) a histogram for land and inland water pixels. The shoreline in the map is from “A Global Self-consistent, Hierarchical, High-resolution Geography Database” (GSHHG) [].
4.3. Generalization
We attempted to extend the above results to cases of other GEO sensors and then attempted to draw universal conclusions in the context of land remote sensing with the new-generation GEO satellites. We first repeated the same computation of pixel displacement using the orthorectification shown in Figure 4a to the cases of the GOES-16 ABI and FY-4A AGRI. The results are plotted in Figure 5, where the latitude range is limited from 60°N to 60°S for both sensors. The longitude range is defined independently for these sensors, ranging from 135°W to 15°W for the GOES-16 ABI and from 45°E to 165°E for the FY-4 AGRI.
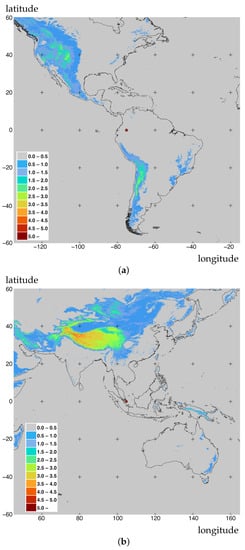
Figure 5.
Pixel displacement by orthorectification for the 1 km-resolution products of the (a) GOES-16 ABI and (b) FY-4A AGRI sensor data. The red circle at the center is the subsatellite point.
These figures show a large displacement in the high-altitude regions as we expected from the results of the Himawari-8 AHI in Figure 4a. The displacement is especially larger in mountainous areas, including the Rocky Mountains in North America and the Andes Mountains in South America in Figure 5a. In the case of the FY-4 AGRI data (Figure 5b), the results show similar trends as those in the case of the Himawari-8 AHI data (Figure 4a). However, some differences can be observed in the degree of displacement, especially in the Tibetan Plateau region, between the Himawari-8 (Figure 4a) and FY-4 (Figure 5b) cases. In this area, the displacement becomes smaller in the case of FY-4 (mostly less than 4 pixels) than in the case of Himawari-8 (4 to 5 pixels). This smaller displacement is attributed to the subsatellite point of FY-4 (105°E) being much closer to the Tibetan Plateau (88°E) than that of Himawari-8 (140.7°E). Therefore, the difference in the subsatellite point between the two (by approximately 35° in longitude) causes the difference in parallax effects, especially in this high-altitude region. These results indicate that the introduced approach is applicable to other cases of GEO satellites and thus imply a possible generalization of our approach for better understanding the influence of orthorectification in a framework of land remote sensing with GEO satellites. We further explore this possibility in the following discussion.
To this point, we have represented the displacement distance in terms of pixels (the number of pixels displaced from a target location in the original image frame) for the sake of operational orthorectification. Using this approach, one can easily find a “true” pixel location within an original image frame. This approach can also avoid the complexity associated with variations in the sampling distance within an original image frame. The reader is reminded that because the map projection of the Himawari standard data is the normalized geostationary projection [], the sampling distance depends on the relative location of the target pixel from the subsatellite point. In the following discussion, to make our discussion somewhat more universal and intuitively perceivable, we represent the displacement distance in a unit of length (meters) instead of pixels.
We focus on two parameters in our generalization process. Because the pixel displacement depends on (1) the height of the pixel and (2) the distance from the subsatellite point of each GEO sensor, we used these two parameters for the generalization. When both the height of the pixel above the ellipsoidal surface and the distance of the pixel from the subsatellite points becomes larger, the displacement in meters as a measure of the parallax effects increases. Given these parameters, we computed the displacement distance (in meters) as a function of (1) the height of the assumed target pixel (indicated as “target height” in the figures) and (2) the location of the pixel, which is measured in “relative latitude” and “relative longitude” from the subsatellite point in absolute degrees, meaning that we did not discriminate between northward and southward or between eastward and westward. To compute the influence, we first assumed hypothetical pixels (surfaces) of a certain height for the entire regions. We assumed three cases of different heights: 500 m, 1000 m, and 1500 m. The pixel displacement (distance) caused by the parallax effect was then computed for all the pixels of the assumed height located at all the gridded geolocations. Notably, during the computation of this displacement, we defined the location of each pixel in terms of relative latitude and longitude from a subsatellite point. For example, given the subsatellite point of 140.7°E for the Himawari-8 AHI, the pixels located at the coordinates (30°N (or 30°S), 150.7°E (or 130.7°E)) are represented simply as (30° in relative latitude, 10° in relative longitude) in this generalization process because the displacement distance is the same for these pixels.
Figure 6 shows the results of displacement distance with contours for assumed pixel heights of (a) 500 m, (b) 1000 m, and (c) 1500 m. As evident in the figures, the displacement distance increases as both the assumed height of the pixel and the relative distance from the subsatellite point increase. Most notably, for any surface whose height from the reference ellipsoidal surface is greater than 500 m (Figure 6a), the displacement also becomes equal to or greater than 500 m in the locations whose relative latitude or longitude is greater than 40°. The displacement becomes even worse in the cases of 1000 m (Figure 6b) and 1500 m (Figure 6c). Because the elevation of mountainous regions is often greater than 500 m in the middle-to-high latitudes of the Northern Hemisphere, we expected to see a larger influence. Lastly, we note that the displacement direction for each pixel is identical to the direction of the position vector of a target pixel.
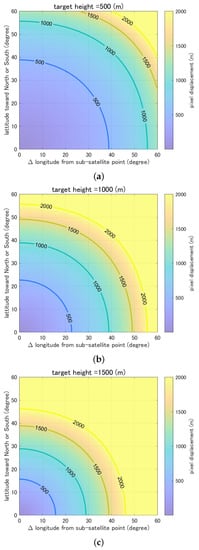
Figure 6.
Color plot of the displacement distance for the assumed pixel height of (a) 500 m, (b) 1000 m, and (c) 1500 m. The x and y axes are both the relative geolocation from the subsatellite points; the X and Y axes are the absolute relative longitude and the absolute relative latitude, respectively. Three contour lines corresponding to displacements of 500 m, 1000 m, and 1500 m are also shown.
The results shown in Figure 6a–c can be applied to the cases of other GEO sensors by simply shifting the plot area based on the subsatellite points of each GEO satellite. To demonstrate the generality of Figure 6, we considered six GEO satellites plotted row-wise in Figure 7 for the satellites Himawari-8 (a–c), FY-4A (d–f), Geo-KOMPSAT-2A (g–i), GOES-16 (j–l), GOES-17 (m–o), and MSG (p–r). The figures in the left column show the cases for a 500 m target height. Similarly, the results for the 1000 m and 1500 m cases are shown as the figures arranged in the center and left columns, respectively. In all the figures, the coastlines are overlayed on the displacement results.
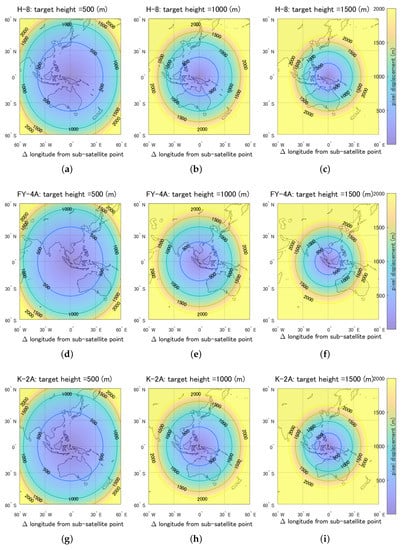
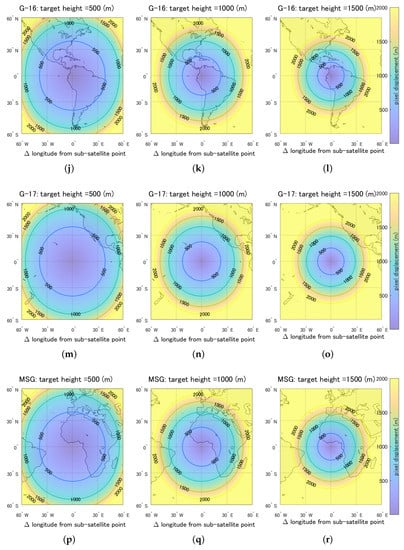
Figure 7.
Applications of the results shown in Figure 6 derived by considering the subsatellite points of six GEO satellites. The results of the displacement distance are plotted row-wise for each case of satellites: (a–c) Himawari-8, (d–f) FY-4A, (g–i) Geo-KOMPSAT-2A, (j–l) GOES-16, (m–o) GOES-17, and (p–r) MSG. The figures in the left column show the results for a 500 m target height. Similarly, the results for the 1000 m and 1500 m cases are shown in the center and left columns, respectively.
These figures will be useful for quickly estimating the influence of the parallax effect with the GEO sensors. For instance, given the height of the regions of interest, it is possible to find the approximate displacement distance from the figure of closest height (either 500 m, 1000 m, or 1500 m) of the corresponding satellites intended to be used. If the displacement of the regions is less than 500 m, then the displacement will be smaller than one-half of the nominal spatial resolution of band 1 (blue), band 2 (green), and band 4 (NIR). This information therefore can be used as a rapid prior estimation of possible difficulties related to geometric accuracy without the orthorectification. Note that considering locations at the same distance from subsatellite points, the displacement distance changes almost linearly as a function of ellipsoidal height. Combining this linearly with the constraint that the displacement distance is zero when the ellipsoidal height is zero, the topographic effect can be estimated even more easily from the results shown in Figure 6 by interpolation or extrapolation.
5. Discussion
For low-altitude targets, Himawari-8 AHI images have high geometric accuracy without orthorectification and show good agreement with Sentinel-2 MSI images, as demonstrated in Figure 3. Monitoring of the navigation status [] derived from landmark area observations has shown that an accurate and stable geometric conditions of the AHI can be achieved with a geometric accuracy much less than 0.5 pixels for the bands whose nominal resolution is 2 km. Our results support the high geometric accuracy of the Himawari-8 AHI for targets at altitudes lower than 500 m (see, for example, Figure 6a), where most of the regions whose relative latitude and relative longitude are less than 55°, the displacement is less than 1000 m, which is approximately one-half of the nominal resolution (2 km) of the thermal bands. However, our findings also show that for targets with heights greater than 1000 m, attention should be devoted to geometric accuracy. In particular, when the target height is greater than 1500 m, the displacement distance exceeds 1000 m for a target whose relative latitude or relative longitude is greater than 30°.
High temporal-resolution data provided by recent geostationary sensors, in combination with ground observations, lower-altitude airborne observations, and higher-altitude GEO/LEO satellite observations, has greatly advanced the understanding of Earth’s changing environmental system. Accurate matching in geolocation improves the monitoring and modeling of the dynamics of climate, vegetation, land cover, and terrestrial carbon budget. Because of its fixed image frame, a geostationary sensor can be orthorectified quite simply by interpolation based on a fixed pixel coordinate in the input image after it has been calculated for a unique output image frame. However, considerable computer resources would be necessary for the larger data volume of a geostationary sensor because of its high temporal resolution. (For instance, the size of the 7-year-long (2016–2022) Himawari-8 AHI data reaches approximately 890 TB.)
Given the displacement distance caused by the parallax effect for the sensors of geostationary satellites, geometric accuracy should also be evaluated for the targets located in mountainous region. However, in general, a set of ground control points (GCPs) is often selected on the basis of coastline data [,]. In particular, for wide-swath sensors, coastlines are reasonable choices because they are most likely included in acquired scenes. In such a case, because the elevations of the selected GCPs are nearly sea level, the displacement caused by the viewing geometry becomes less important. (The elevation tends to be relatively lower compared with that in an instantaneous field of view). Moreover, when an observation is performed in a near-nadir direction, which is often the case for narrow-swath sensors, elevation differences will not be problematic in the nadir-looking acquisition mode. On the contrary, in the cases of geostationary satellites, because the viewing geometry is fixed for each pixel and will remain the same during the sensor’s lifetime, the influence of the parallax effect also continues to affect the geometric accuracy at the same level of magnitude. This scenario implies that evaluating the geometric accuracy on the basis of inland targets, preferably mountainous regions, is important for ensuring a high performance of the orthorectification process.
The influences of the parallax effect fundamentally differ between LEO and GEO satellites. One notable characteristic of the pixel displacement caused by the parallax effect in the case of LEO satellites is that because their operations are conducted in polar orbits, the displacement occurs in an across-track direction (approximately eastward or westward). Because the viewing direction changes substantially for the wide-swath sensors, one target pixel can be observed from different directions within a revisit cycle. Unlike GEO satellites, LEO satellites, due the variations in the view zenith angle, can avoid possible occlusions if observation data acquired (at various viewing angles) during a revisit cycle are selected. Moreover, because this direction (eastward or westward) differs substantially from the displacement direction of the GEO satellites (the same direction of the pixel position from the subsatellite point), data from the LEO satellites can compensate for the occlusion pixels of the GEO satellite images, which would be a great advantage of combining the data from both satellites. To facilitate such a compensation algorithm, techniques for comparing the data between GEO and LEO sensors need to be established, especially for targets located in middle-latitude mountainous regions, which is considered a challenging task [,,]. Comparisons between GEO and LEO sensors are a far more complicated issue than are comparisons between orthorectified data and original (before rectification) data. They thus should be addressed thoroughly in the future.
6. Conclusions
Orthorectification of geostationary sensors was demonstrated in this study using Himawari-8 AHI full disk data. Because of the fixed satellite position and fixed image frame of geostationary sensors, the methodology of orthorectification is less complicated than that of LEO sensors; hence, applying the algorithm to operational processes is straightforward. The orthorectification introduced in the present study has only modest methodological novelty. Nevertheless, our results indicate that the pixel displacement caused by the parallax effects cannot be ignored, especially for mountainous regions located far from the subsatellite point.
The results of two experiments (a comparison with Sentinel-2 MSI images and a calculation of the pixel displacement) revealed the advantages of orthorectified data, especially in the case of mountainous areas or regions at the edge of the full disk image, where the influence of the parallax effect becomes especially significant. These results imply an important fact: Because the high temporal resolution of a geostationary satellite gives reliable observations in mountainous areas where the climate and land surface change drastically and the chance of a clear sky condition is low, the orthorectified images combined with higher-spatial-resolution sensors would enable the even more accurate monitoring of these vulnerable environments.
The results computed as the displacement distance for the Himawari-8 AHI and its generalized results could be used to estimate the influence of orthorectification for targets of interest.
The displacement distance could be used as a quick reference and a source of information for evaluating the influence (prior to analysis) of a given set of data regarding (1) target geodetic location, (2) target ellipsoidal height, and (3) the choice of GEO satellite (which determines the subsatellite point). Finally, from these results, we should be cognizant of the influence of orthorectification when GEO and LEO data are compared. This point should be investigated in detail in a future study.
Author Contributions
Conceptualization, M.M. and H.Y.; methodology, M.M.; software, M.M.; validation, M.M. and H.Y.; formal analysis, M.M. and H.Y.; investigation, M.M. and H.Y.; resources, M.M. and H.Y.; data curation, M.M. and H.Y.; writing—original draft preparation, M.M. and H.Y.; writing—review and editing, M.M. and H.Y.; visualization, M.M. and H.Y.; project administration, M.M. and H.Y.; funding acquisition, M.M. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the JSPS KAKENHI under grant numbers 21K05669, 20K20487, 20KK0237, 20K12259 and 22H05004.
Data Availability Statement
The Himawari-8 AHI data were provided by JMA and can be downloaded via the NICT Science Cloud (https://sc-web.nict.go.jp/himawari/). GMTED2010 elevation data were provided by the USGS and can be downloaded via EarthExplorer (https://earthexplorer.usgs.gov/). EGM2008 geoid height data were provided by and can be downloaded from the Office of Geomatics, National Geospatial-intelligence Agency (https://earth-info.nga.mil/index.php). Sentinel-2 MSI data were provided by the ESA and can be downloaded via the Sentinel Open Access Hub (https://scihub.copernicus.eu/). GSHHG shoreline data were provided by and can be downloaded from the University of Hawai’i (https://www.soest.hawaii.edu/pwessel/gshhg/).
Acknowledgments
The authors would like to thank the NICT Science Cloud for providing Himawari AHI Standard Data and the Center for Environmental Remote Sensing (CEReS), Chiba University, for supporting the joint research program “Multi-Institutional Working Group on the Development, Application, and Promotion of Himawari-8/9 Land Products”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Toutin, T. Review article: Geometric processing of remote sensing images: Models, algorithms and methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Nishihama, M.; Wolfe, R.; Solomon, D.; Patt, F.; Blanchette, J.; Fleig, A.; Masuoka, E. MODIS Level 1A Earth Location: Algorithm Theoretical Basis Document Version 3.0. 1997. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod28_v3.pdf (accessed on 30 August 2022).
- Matsuoka, M.; Honda, R.; Nonomura, A.; Moriya, H.; Akatsuka, S.; Yoshioka, H.; Takagi, M. A method to improve geometric accuracy of Himawari-8/AHI “Japan area” data. Jpn. Soc. Photogramm. Remote Sens. 2016, 54, 280–289, (In Japanese with English Summary). [Google Scholar] [CrossRef]
- Takenaka, H.; Sakashita, T.; Higuchi, A.; Nakajima, T. Geolocation correction for geostationary satellite observations by a phase-only correlation method using a visible channel. Remote Sens. 2020, 12, 2472. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Ichii, K.; Higuchi, A.; Takenaka, H. Geolocation accuracy assessment of Himawari-8/AHI imagery for application to terrestrial monitoring. Remote Sens. 2020, 12, 1372. [Google Scholar] [CrossRef]
- Kocaman, S.; Debaecker, V.; Bas, S.; Saunier, S.; Garcia, K.; Just, D. A comprehensive geometric quality assessment approach for MSG SEVIRI imagery. Adv. Space Res. 2022, 69, 1462–1480. [Google Scholar] [CrossRef]
- Pestana, S.; Lundquist, J.D. Evaluating GOES-16 ABI surface brightness temperature observation biases over the central Sierra Nevada of California. Remote Sens. Environ. 2022, 281, 113221. [Google Scholar] [CrossRef]
- Greve, C.W.; Molander, C.W.; Gordon, D.K. Image processing on open systems. Photogramm. Eng. Remote Sens. 1992, 58, 85–89. [Google Scholar]
- Dowman, I.; Dolloff, J.T. An evaluation of rational functions for photogrammetric restitution. Int. Arch. Photogramm. Remote Sens. 2000, 33, 254–266. [Google Scholar]
- Tao, C.V.; Hu, Y. A comprehensive study of the rational function model for photogrammetric processing. Photogramm. Eng. Remote Sens. 2001, 67, 1347–1358. [Google Scholar]
- Dowman, I.; Tao, V. An update on the use of rational functions for photogrammetric restitution. ISPRS Highlights 2002, 7, 22–29. [Google Scholar]
- Hu, Y.; Tao, V.; Croitoru, A. Understanding the rational function model: Methods and applications. Int. Arch. Photogramm. Remote Sens. 2004, 20, 119–124. [Google Scholar]
- Sadeghian, S.; Zoej, M.J.V.; Delavar, M.R.; Abootalebi, A. Precision rectification of high resolution satellite imagery without ephemeris data. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 366–371. [Google Scholar] [CrossRef]
- Gerlach, F. Characteristics of Space Imaging’s one-meter resolution satellite imagery products. Int. Arch. Photogramm. Remote Sens. 2000, 33, 128–135. [Google Scholar]
- Baltsavias, E.P.; Pateraki, M.N.; Zhang, L. Radiometric and geometric evaluation of Ikonos GEO images and their use for 3D building modelling. In Proceedings of the Joint Workshop of ISPRS Working Groups I/2, I/5 and IV/7 High Resolution Mapping from Space 2001. ETH Hönggerberg, Institute of Geodesy and Photogrammetry, Hanover, Germany, 19–21 September 2001. [Google Scholar]
- Wiesel, J. Digital image processing for orthophoto generation. Photogrammetria 1985, 40, 69–76. [Google Scholar] [CrossRef]
- O’Neill, M.; Dowman, I. The generation of epipolar synthetic stereo mates for SPOT images using a DEM. Int. Arcives Photogramm. Remote Sens. 1988, 27, 587–598. [Google Scholar]
- Mayr, W.; Heipke, C. A contribution to digital orthophoto generation. Int. Arch. Photogramm. Remote Sens. 1988, 27, 430–439. [Google Scholar]
- Sheng, Y. Comparative evaluation of iterative and non-iterative methods to ground coordinate determination from single aerial images. Comput. Geosci. 2004, 30, 267–279. [Google Scholar] [CrossRef]
- Sheng, Y. Theoretical analysis of the iterative photogrammetric method to determining ground coordinates from photo coordinates and a DEM. Photogramm. Eng. Remote Sens. 2005, 71, 863–871. [Google Scholar] [CrossRef]
- Chen, L.C.; Lee, L.H. Rigorous generation of digital orthophotos from SPOT images. Photogramm. Eng. Remote Sens. 1993, 59, 655–661. [Google Scholar]
- Kim, T.; Shin, D.; Lee, Y.R. Development of a robust algorithm for transformation of a 3D object point onto a 2D image point for linear pushbroom imagery. Photogramm. Eng. Remote Sens. 2001, 67, 449–452. [Google Scholar]
- Marsetič, A.; Oštir, K.; Fras, M.K. Automatic Orthorectification of High-Resolution Optical Satellite Images Using Vector Roads. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6035–6047. [Google Scholar] [CrossRef]
- Miura, T.; Nagai, S. Monitoring terrestrial vegetation and the environment with new-generation geostationary satellites. J. Remote Sens. Soc. Jpn. 2019, 39, 377–383. [Google Scholar] [CrossRef]
- Takeuchi, W.; Yasuoka, Y. Precise geometric correction of MTSAT imagery. In Proceedings of the Asian Conference on Remote Sensing (ACRS), Kuala Lumpur, Malaysia, 12–16 November 2007. [Google Scholar]
- Tucker, C.J.; Grant, D.M.; Dykstra, J.D. NASA’s global orthorectified Landsat data set. Photogramm. Eng. Remote Sens. 2004, 70, 313–322. [Google Scholar] [CrossRef]
- Aksakal, S.K.; Baltsavias, E.; Schindler, K. Analysis of the geometric accuracy of MSG-SEVIRI imagery with focus on estimation of climate variables. In Proceedings of the 34th Asian Conference on Remote Sensing 2013, Bali, Indonesia, 20–24 October 2013. [Google Scholar]
- Aksakal, S.K. Geometric accuracy investigations of SEVIRI High Resolution Visible (HRV) Level 1.5 imagery. Remote Sens. 2013, 5, 2475–2491. [Google Scholar] [CrossRef]
- Kocaman, S.; Debaecker, V.; Bas, S.; Saunier, S.; Garcia, K.; Just, D. Investigations on the global image datasets for the absolute geometric quality assemement of MSG SEVIRI imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 1339–1346. [Google Scholar] [CrossRef]
- Debaecker, V.; Kocaman, S.; Saunier, S.; Garcia, K.; Bas, S.; Just, D. On the geometric accuracy and stability of MSG SEVIRI images. Atmos. Environ. 2021, 262, 118645. [Google Scholar] [CrossRef]
- Yasukawa, M.; Takagi, M. Geometric Correction Considering the Elevation for GMS S-VISSR Data. J. Jpn. Soc. Photogramm. Remote Sens. 2004, 42, 33–41, (In Japanese with English Summary). [Google Scholar] [CrossRef]
- Takeuchi, W.; Oyoshi, K.; Akatsuka, S. Precise geometric correction of Himawari-8 (AHI). In Proceedings of the International Stereotactic Radiosurgery Society (ISRS2015), Tainan, Taiwan, 22–24 April 2015; pp. 45–46. [Google Scholar]
- Takeuchi, W. Assessment of geometric errors of Advanced Himawari-8 Imager (AHI) over one year operation. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Kuala Lumpur, Malaysia, 13–14 April 2016; Volume 37, p. 012004. [Google Scholar] [CrossRef]
- Wang, W.; Li, S.; Hashimoto, H.; Takenaka, H.; Higuchi, A.; Kalluri, S.; Nemani, R. An introduction to the Geostationary-NASA Earth Exchange (GeoNEX) products: 1. Top-of-atmosphere reflectance and brightness temperature. Remote Sens. 2020, 12, 1267. [Google Scholar] [CrossRef]
- Pestana, S.; Lundquist, J. Orthorectifying GOES ABI imagery for mountain surface temperature observations. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 13–17 December 2021; Volume 2021, p. A22B–03. Available online: https://www.youtube.com/watch?v=MNX-abbf6TE (accessed on 30 August 2022).
- ESA. Sentinel-2 User Handbook. 2015. Available online: https://sentinel.esa.int/documents/247904/685211/sentinel-2_user_handbook (accessed on 31 October 2022).
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9-Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Japan Meteorological Agency. Himawari–8/9 Himawari Standard Data User’s Guide (Version 1.3). 2017. Available online: https://www.data.jma.go.jp/mscweb/en/support/support.html (accessed on 30 August 2022).
- Coordination Group for Meteorological Satellites. LRIT/HRIT Global Specification (Issue 2.8). 2013. Available online: https:118//www.cgms-info.org/wp-content/uploads/2021/10/cgms-lrit-hrit-global-specification-(v2-8-of-30-oct-2013).pdf (accessed on 30 August 2022).
- National Satellite Meteorological Center. FENGYUN Satellite Data Center Home Page. Available online: http://satellite.nsmc.org.cn/PortalSite/Data/Satellite.aspx (accessed on 30 August 2022).
- NOAA; NASA. GOES R Series Product Definition and Users’ Guide (Revision 2.2). 2019. Available online: https://www.goes-r.gov/users/docs/PUG-L1b-vol3.pdf (accessed on 30 August 2022).
- Danielson, J.J.; Gesch, D.B. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010). 2011. Available online: https://www.usgs.gov/publications/global-multi-resolution-terrain-elevation-data-2010-gmted2010 (accessed on 30 August 2022).
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Soild Earth 2012, 117, B04406. [Google Scholar] [CrossRef]
- Meteorological Satellite Center of Japan Meteorological Agency. Sample Source Code (C Programming Language). Available online: https://www.data.jma.go.jp/mscweb/en/himawari89/space_segment/spsg_sample.html (accessed on 30 August 2022).
- Wessel, P.; Smith, W.H. A global, self-consistent, hierarchical, high-resolution shoreline database. J. Geophys. Res. Soild Earth 1996, 101, 8741–8743. [Google Scholar] [CrossRef]
- Meteorological Satellite Center of Japan Meteorological Agency. Himawari Series Satellite Image Navigation and Registration (INR). Available online: https://www.data.jma.go.jp/mscweb/data/monitoring/navigation.html (accessed on 1 September 2022).
- Kim, H.G.; Son, J.H.; Kim, T. Geometric correction for the geostationary ocean color imager from a combination of shoreline matching and frequency matching. Sensors 2018, 18, 3599. [Google Scholar] [CrossRef]
- Adachi, Y.; Kikuchi, R.; Obata, K.; Yoshioka, H. Relative azimuthal-angle matching (RAM): A screening method for GEO-LEO reflectance comparison in middle latitude forests. Remote Sens. 2019, 11, 1095. [Google Scholar] [CrossRef]
- Obata, K.; Yoshioka, H. A Simple Algorithm for Deriving an NDVI-Based Index Compatible between GEO and LEO Sensors: Capabilities and Limitations in Japan. Remote Sens. 2020, 12, 2417. [Google Scholar] [CrossRef]
- Obata, K.; Taniguchi, K.; Matsuoka, M.; Yoshioka, H. Development and Demonstration of a Method for GEO-to-LEO NDVI Transformation. Remote Sens. 2021, 13, 4085. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).