Abstract
Target recognition is the core application of radar image interpretation. In recent years, deep learning has become the mainstream solution. However, this family of methods is highly dependent on a great deal of training samples. Limited samples may lead to problems such as underfitting and poor robustness. To solve the problem, numerous generative models have been presented. The generated samples played an important role in target recognition. It is therefore needed to assess the quality of simulated images. However, few studies were performed in the preceding works. To fill the gap, a new evaluation strategy is proposed in this paper. The proposed method is composed of two schemes: the sample-wise assessment and the class-wise one. The simulated images can then be evaluated from two different perspectives. The sample-wise assessment combines the Fisher separability criterion, fuzzy comprehensive evaluation, analytic hierarchy process, and image feature extraction into a unified framework. It is used to evaluate whether the relative intensity of the speckle noise of the SAR image and the target backscattering coefficients are well simulated. Contrarily, the class-wise assessment is designed to compare the application capability of the simulated images holistically. Multiple comparative experiments are performed to verify the proposed method.
1. Introduction
Synthetic Aperture Radar (SAR) has the unique advantage of monitoring the target all-weather and all-day. With the advancement of microelectronics technology, SAR is capable of high-resolution imaging. Therefore, SAR has been widely applied in recent years.
SAR target recognition is a research hot spot. The early studies on target recognition usually rely on the physical model-based algorithms. They are usually used for specific tasks. They have poor expansion capabilities. So currently, a variety of Machine Learning methods especially Deep Learning strategies have been applied. However, some issues should be considered.
The family of deep learning methods is typically data-driven. Typically, Convolutional Neural Networks (CNNs) can quickly and efficiently learn corresponding features. They only require a small amount of human involvement in the whole process. However, acquiring parameters and weights of an excellent network structure requires a large number of samples for training. With limited training samples, it can easily lead to problems such as poor performance, overfitting, and poor model robustness. However, there are insufficient SAR images. It is very time-consuming and labor-intensive to acquire a great many labeled SAR samples due to the limitations of acquisition conditions, especially for non-cooperative targets. So it is difficult to obtain sufficient SAR images under various conditions.
It is crucial to solve the problem of insufficient SAR images. It is the key to breaking through the bottleneck for the application of deep learning in this field. There are three typical solutions to solve the limited-sample circumstance at present. Their schematics are displayed in Figure 1.
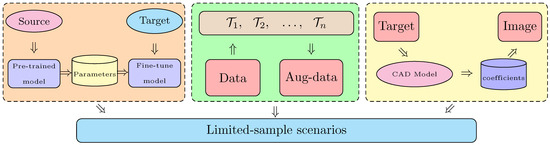
Figure 1.
Three typical solutions for limited-sample scenarios. Transfer learning, data augmentation and image simulation.
The first is transfer learning. A large amount of data is used as the training samples in the source domain. The pre-trained model and corresponding network parameters are obtained by supervised training on the source tasks in the source domain. The network parameters are transferred to the target model as the initialization parameters of the target model. The SAR image dataset is used as the training samples in the target domain to fine-tune the network. Finally, the transfer of feature information from the source domain to the target domain is realized. Transfer learning uses the knowledge of source domain to assist in improving the performance of the target domain. Ke Wang et al. [1] pre-trained the model with sufficient simulated data and a few real data. However, the differences between different domains are huge for radar images. The reliability of transferred knowledge cannot be guaranteed. So they proposed a model that combined meta-learning and adversarial domain adaptation.
The second is data augmentation. This method augments the SAR image dataset by cropping, adding noise, or segmenting and reconstructing existing images. This is without considering the imaging mechanism of SAR images. And usually, we perform modulo processing on the original SAR data. Therefore, it is unable to exploit phase information and radar imaging principles. This method is not a truly effective method.
The third method is SAR image simulation. The traditional SAR image simulation is based on the calculation of electromagnetic theory and an accurate Computer Aided Design (CAD) target model. The quality of the simulated image is related to the surface accuracy of the CAD model. However, it is not feasible to accurately measure the target. Accurate measurement of each target is expensive due to the large scene in SAR images. Many monitored targets are non-cooperative. So some electromagnetic coefficients of these targets cannot be directly measured. Affected by the real environment, the electromagnetic coefficients of the target surface will be changed in practical applications. It results in the inability to obtain the real electromagnetic coefficients. The quality of the simulated image could be significantly deteriorated by these factors.
With the development of deep learning in the field of image processing, deep generative models provide more possibilities for SAR image simulation. Generative models use data with a certain probability density distribution to fit the data distribution of samples, and no feature extraction occurs during this process. The so-called generative model is that generating new data with the same distribution as the given training data. Deep generative models have been gradually applied to SAR image simulation due to their strong generation ability, stable training, fast convergence speed, diverse generated samples, and superior performance in optical image simulation.
Image quality assessment analyzes the relevant characteristics of images in order to measure the similarity of the data. How to evaluate generated data has been a hot spot since the birth of generative models. It has developed some quantitative evaluation methods. At present, the major idea of most of the methods is as follows: first, extract the features of generated images and real images, and then measure the differences or distances of the extracted features according to measurement criteria. For generation tasks, popular evaluation indexes include Inception Score (IS) [2] and Fréchet Inception Distance (FID) [3]. For image super-resolution reconstruction, objective quantification quality evaluation indexes mainly include the peak signal to noise ratio (PSNR) and the structural similarity index method (SSIM) [4]. And these methods above are mostly designed for optical images. Due to the inherent imaging modes of SAR and speckle noise, the traditional assessments of optical images can not apply well to SAR images. And current quality evaluation methods [5,6] in the SAR image simulation field are mostly proposed for traditional simulation.
All of the above result in the lack of effective quantitative quality evaluation methods for simulated SAR images generated by deep generative models. It is necessary to design a scheme that can evaluate the similarity between real and simulated SAR images. This paper is an extension of our previous work [7]. Our initial paper only evaluated a single generative model from a single perspective. It only compares the application capability of the simulated images. This paper adds a new assessment and more generative models for comparison to prove the effectiveness of our methods. The added assessment is designed to evaluate whether the relative intensity of the speckle noise of the SAR image and the target backscattering coefficients are well simulated. And we provide additional experiments and analysis, including the effect of dataset size, analysis of statistics, t-SNE visualization of generated data, and comparison with traditional simulation. Finally, we get a more comprehensive assessment conclusion. Figure 2 shows our work in this paper. The proposed method is composed of two schemes, the sample-wise assessment and the class-wise one. The simulated images can be then evaluated from two different perspectives.
- (a)
- The sample-wise assessment is used to evaluate whether the relative intensity of the speckle noise of the SAR image and the target backscattering coefficients are well simulated.
- (b)
- The class-wise assessment is designed to compare the application capability of the simulated images in holistic.
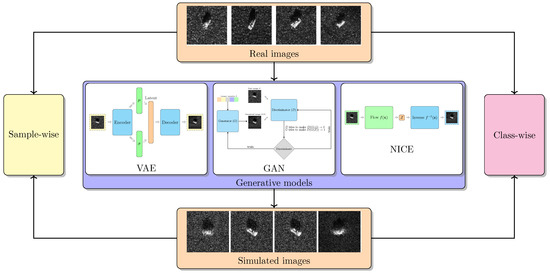
Figure 2.
Summary of work in this article.
2. The Related Works
The traditional simulation of a SAR image is based on the calculation of electromagnetic theory and an accurate CAD target model. With the popularity of deep learning, deep generative models have also received wide attention in recent years. At present, there are three main families of mainstream generative models. This section introduces electromagnetic simulation and the three families of generative models.
2.1. Simulation via Electromagnetic Computational Tools
As an important way to acquire SAR images, electromagnetic computational tools has been a fairly mature technology. It utilizes the powerful data processing capabilities of computers to generate images. Currently, there are two typical methods: SAR image simulation based on an echo signal and feature-based SAR image simulation.
2.1.1. SAR Image Simulation Based on Echo Signal
SAR image simulation based on an echo signal pays attention to the process of electromagnetic scattering. It completely simulates the process of SAR imaging and reproduces the working process of the SAR system. This method is combined with the electromagnetic computational method. It simulates the original echo signal and obtains the simulated SAR image through modeling the complex ground object and the motion of the SAR platform.
In the simulation, the geometric parameters and electromagnetic parameters of the SAR systems are pre-set. And then the electromagnetic scattering coefficients of each small surface element are calculated with the three-dimensional model of the target as input. Different methods of echo simulation are used to generate echo signals. An appropriate imaging algorithm is used to obtain the simulated SAR target image. This method has a large amount of calculation and a slow simulation speed. The process is shown in Figure 3.
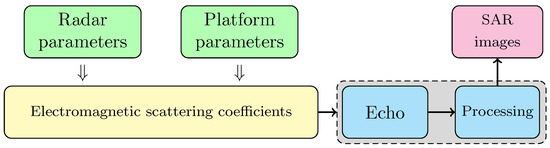
Figure 3.
Process of SAR image simulation based on echo signal.
2.1.2. Feature-Based SAR Image Simulation
Feature-based SAR image simulation focuses on simulating the geometric and radiation characteristics of sar images. It pursues the similarity between the simulated image and the real image, such as the similarities of shape and the distribution of scattering points [8]. The working process of the SAR system, the electromagnetic scattering process of targets, and the environment in the scene are not considered in this method. The scattering information of the target is directly mapped to the image domain to obtain a SAR gray image. It realizes a mapping from a three-dimensional scene to a two-dimensional image. This method is simple in principle but fast in simulation. Figure 4 shows the process of simulation.
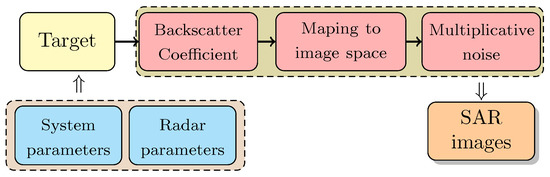
Figure 4.
Process of feature-based SAR image simulation.
Both methods have their pros and cons. According to the working principle of the SAR system, SAR image simulation based on echo signals obtains the SAR’s original echo signal by the parameters of radar and the scene (including the target). The feature-based SAR image simulation directly simulates the target without generating the SAR original echo signal. It can only simulate the intensity (or amplitude), while the former method can simulate not only the intensity (or amplitude) but also the phase. Compared with feature-based method, the method based on echo signals more realistically simulates the interaction mechanism between electromagnetic waves and the target. It can more comprehensively and truly reflect the electromagnetic scattering coefficients.
2.2. Simulation via Deep Generative Models
This part introduces three families of mainstream generative models.
2.2.1. The Family of Adversarial Model
Generative Adversarial Nets (GAN) are a framework for estimating generative models via an adversarial process. The core architectures of GAN are two models: a generative model G that captures the data distribution, and a discriminative model D that judges whether a sample comes from the training data and estimates the probability. The training goal for G is to minimize the probability of D correctly distinguishing. ‘This framework corresponds to a minimax two-player game’ [9]. The schematic diagram is shown in Figure 5.
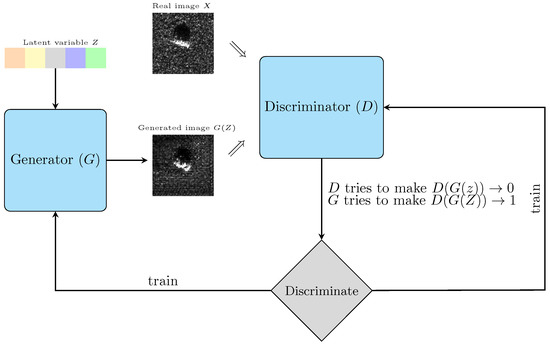
Figure 5.
The schematic diagram of GAN.
Since its birth in 2014, GAN has always attracted wide attention. Hundreds of variants have emerged to solve the lack diversity and the instability of the training process. Here are several typical variants [10,11,12]. Deep convolutional generative adversarial networks (DCGAN) combine generative adversarial networks and convolutional neural networks. DCGAN adopts the following improvements to GAN: the generator uses fractional-strided convolutions to implement upsampling, and the discriminator uses strided convolutions to realize downsampling. Wasserstein GAN (WGAN) pointed out that Jensen–Shannon divergence is not suitable for measuring the distance between two distributions, and that’s the reason the instability of training. Earth-Mover distance is introduced to replace Jensen–Shannon divergence. It improves the stability of learning and gets rid of problems such as mode collapse. Based on WGAN, WGAN-GP proposes gradient penalty to substitute weight clipping. GAN and its variants have been widely used in sar image simulation [13,14,15].
2.2.2. The Family of Variational Model
Variational Auto-Encoder (VAE) [16] uses the existing image to generate a latent vector in the encoder. This vector, obeying the Gaussian distribution, well retains the characteristics of the original image. An autoencoder consists of two parts—an encoder and a decoder. The aim of the encoder is to compress the vector of the input feature space into the latent feature space to obtain the latent variable. The decoder restores the representation of the latent feature space to the original input space. VAE is proposed on the basis of the conventional autoencoder, it adds ‘Gaussian noise’ to the result of the encoder to make it robust to noise. VAE assumes that latent variable Z obeys some common distribution (such as a normal or uniform distribution) and aims to train a model to map the original probability distribution to the probability distribution of the training set. The schematic diagram of VAE is shown in Figure 6.
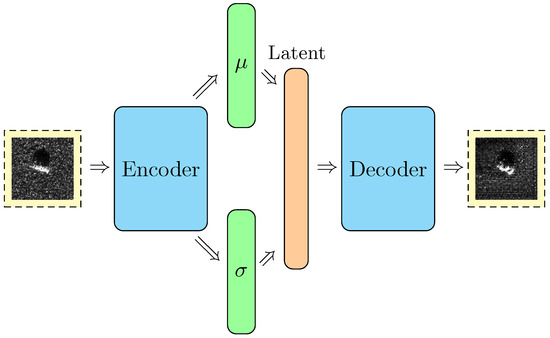
Figure 6.
The schematic diagram of VAE.
The images generated by VAE do not retain the clarity of the original image. They are usually blurry due to the fact that the loss can only be measured by error, such as the mean square error (MSE).
2.2.3. The Family of Flow-Based Model
Flow-based models have become popular in recent years. Different from the above models, they calculate the probability integral directly. There are currently three articles on flow-based generative models [17,18,19]. Different from GAN and VAE, flow-based models allow the likelihood function to be accurately calculated by techniques such as reversible non-linear transformation. This section only introduces non-linear independent components estimation (NICE). NICE learns a non-linear deterministic transformation of the data. It performs nonlinear transformations on complex, high-dimensional data and maps high-dimensional data to latent space in order to generate independent latent variables. This process is reversible, that is, it can be mapped from high-dimensional data to latent space and vice versa. It introduces additive coupling to make the Jacobian determinant easy to calculate. When the training is completed, a generating model and an encoding model can be obtained. The idea of NICE is shown in Figure 7.
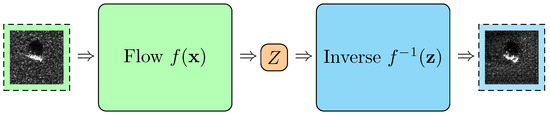
Figure 7.
The schematic diagram of NICE.
3. The Proposed Strategy
This section presents the proposed assessment strategy for SAR target simulated images. The strategy consists of two parts, including a statistical method based on Fuzzy Comprehension Evaluation Method (FCE) and The Analytic Hierarchy Process (AHP) according to a sample perspective, and the Hybrid Recognition Rate Curve (HRR) according to a class perspective.
3.1. Sample-Wise Assessment
The sample-wise assessment is proposed on the theory of FCE. FCE is a comprehensive evaluation method based on fuzzy mathematics. It makes qualitative evaluation transform into quantitative evaluation based on the degree of membership in fuzzy mathematics. It makes a general evaluation of objects restricted by many factors by fuzzy mathematics [20].
In sample-wise part, some objective parameters of SAR images are selected as evaluation indicators to establish an evaluation model. The basic process of sample-wise assessment is as follows:
- The feature extraction of simulated and real SAR images.
- Calculation of similarity and construction of fuzzy relationship matrix.
- Establishment of a FCE SAR simulated images evaluation model and obtaining evaluation result.
3.1.1. Construction of Evaluation Indicators
The texture feature is important in SAR’s automatic target recognition. In order to compare the similarity between simulated images and real images, we pick out four representative objective parameters. They are mean, variance, radiation resolution, and entropy. The calculation formulas are as follows:
- MeanThe average pixel value of the entire image is defined as mean. Its calculation formula of a image with a size is:
- VarianceThe variance represents the unevenness of the image and reflects the fluctuation of gray value. For image of size, it can be defined as:
- Radiation resolutionRadiation resolution is a measure of image gray resolution and reflects the ability of target backscatter coefficient.The higher the radiation resolution, the higher the image quality.
- EntropyEntropy is a statistics based on information theory. For an image with a size , Its entropy is defined as:Smaller entropy means more information and better quality of the image.
For the above formulas, represents the pixel value of the image , is the probability of .
These four parameters are selected to initially reflect whether there are commonalities between the simulated and real images in terms of the relative intensity of speckle noise and the ability to reconstruct the target backscatter coefficient [13]. The means and variances are descriptions of the whole image. The value of radiation resolution is affected by the intensity of speckle noise in the SAR image.
3.1.2. Evaluation Model
Evaluation Set
We formulate the evaluation set as level 5: excellent, good, medium, poor, and very poor. They are respectively used to describe the quality of the image at different levels.
The Weight
The Fisher separability criterion is an outstanding criterion in the area of SAR target recognition. It selects the factor with good separability by maximizing the inter-class distribution and minimizing the intra-class distribution. AHP is an analysis method that combines qualitative and quantitative research. It is applicable to situation with evaluation factors that are difficult to quantify and complicated in structure. To this end, AHP and the Fisher value are applied to our evaluation system in order to determine the weight more reasonable. The value of Fisher is calculated by:
where, and are the mean and variance of the i class and C is the total number of categories.
Fuzzy Membership Function
According to the characteristics of SAR image quality assessment, fuzzy membership is indicated by the reduced half trapezium function. Figure 8 shows the fuzzy membership function. is the ratio of a characteristic of the simulated and real SAR image. It is used to measure the similarity of simulated images and real images in certain characteristics. can be expressed as follows [21].
and express values of a certain characteristic of the generated and real SAR image, respectively.
In this step, for any parameter i, we can calculate by calculating. Enter the to the fuzzy membership function to get the single-factor fuzzy membership matrix , where m is the length of the evaluation set. Get fuzzy membership matrix R in combination with n evaluation matrices .
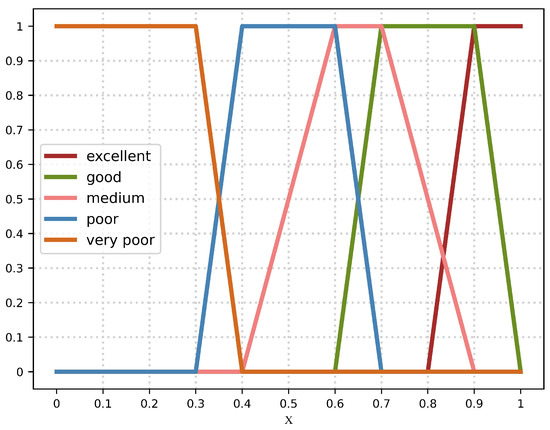
Figure 8.
Fuzzy membership function. X reflects the relationship of a certain characteristic between simulated and real images.
3.1.3. Evaluation Results
We synthesize the weight vector and fuzzy relationship matrix to carry out the result vector.The final results are obtained in accordance with the maximum membership principle. That is, the final evaluation result belongs to the one with the maximum membership.
3.2. Class-Wise Assessment
Simulated images are commonly applied as an augment to the training dataset to evaluate the performance of simulated images in the recognition task. In previous studies, scholars added simulated images generated by generative models to real images for training. The changes in the number of training samples make it difficult to accurately determine whether the simulated images have a positive impact on the accuracy.
Therefore, we propose an objective assessment method for combining classification and hybrid for the utility evaluation of simulated training data. The core of the method is to keep the total number constant. We keep this fixed total number by reducing the real images for each category in the training dataset by a gradually increasing proportion and adding the corresponding number of simulated images. Hybrid training sets with different hybrid ratios are obtained. We train neural networks using hybrid training sets with different hybrid ratios to get the curve we call Hybrid Recognition Rate Curve (HRR). As shown in Figure 9, the blue part indicates real images and the red part indicates simulated images. Hybrid training sets consist of real and simulated images. The ratio of simulated images in hybrid training sets gradually increases by ten percentages.

Figure 9.
Hybrid training sets with the same total number. The blue part indicates real images and the red part indicates simulated images.
3.3. Discussion
The experiments in this article are realized in the real number domain; our method can be promoted to the complex field. There are two solutions for complex data, as shown in Figure 10. One is to have two independent channels for real and imaginary and get two outputs in the simulation stage. The only difference in the other method is the modulo operation in the training process to get one output. The two-dimensional complex data obtained from the first idea can be sent into the sample-wise assessment after modulo operation. The related studies can be found in [22,23].
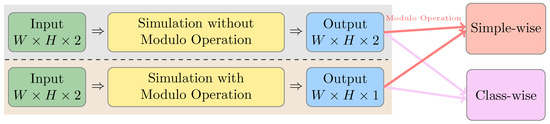
Figure 10.
Sketch map of assessment in the complex field.
4. Experiments and Discussion
The Moving and Stationary Target Acquisition and Recognition (MSTAR) database is widely used in the field of SAR target recognition. The dataset includes multiple SAR target images, including tanks, armored vehicles, weapons systems, and military engineer vehicles. We select four similar military vehicles, the BMP2, BTR60, T72, and T62, to form the training dataset. Optical images and SAR images of the four military vehicles are shown in Figure 11.

Figure 11.
The top row shows the optical pictures and the bottom row exhibits the corresponding SAR image. (a) The optical image and the SAR image of BMP2. (b) The optical image and the SAR image of BTR60. (c) The optical image and the SAR image of T72. (d) The optical image and the SAR image of T62.
BMP2 and T72 have three variants with structural modifications. The standards, SN _9563 and SN_132, taken at a 17 depression angle are used for training. SN_9566, SN_c21, SN_812, and SN_s7, collected at a 15 depression angle, are used for testing. All images in the following experiments are cropped by 128 × 128 pixels. The details can be found in Table 1.

Table 1.
Details of our MSTAR dataset.
The simulated images obtained via electromagnetic computational tools are taken from the Synthetic and Measured Paired Labeled Experiment (SAMPLE) dataset [24]. We select four categories, incuding 2S1, BMP2, BTR70, and T72, as electromagnetic dataset. The details are shown in Table 2.

Table 2.
Detail of SAMPLE data for each class.
4.1. Settings and Simulation
This part introduces settings for generative models and the simulation of SAR images. The original data of MSTAR is complex data. The targets used in our experiment are stationary targets. In order to facilitate statistical calculation, we take the modulo value of the original data as the input of the deep generative models. In addition to this, no preprocessing is performed on the training data.
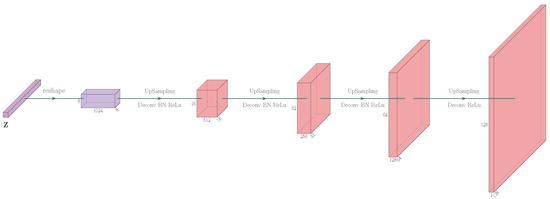
Figure 12.
The network structure of generator in DCGAN. Deconv is the abbreviation of deconvolutions. BN is the abbreviation of batch normalization. Relu is activation function.
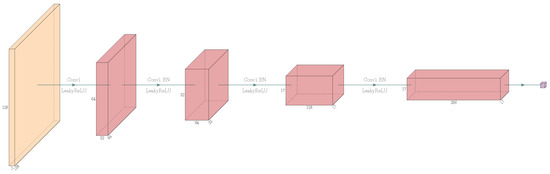
Figure 13.
The network structure of discriminator in DCGAN. Conv is the abbreviation of convolutional. BN is the abbreviation of batch normalization. LeakyReLu is activation function.
The structure of the generator and the discriminator in WGAN-GP is shown in Figure 14 and Figure 15.

Figure 14.
The network structure of generator in WGAN-GP. Deconv is the abbreviation of deconvolutions. BN is the abbreviation of batch normalization. Relu is activation function.
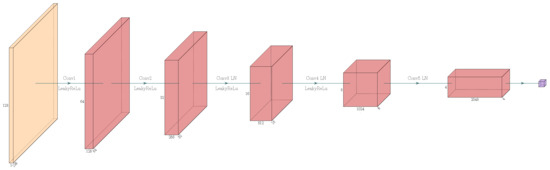
Figure 15.
The network structure of discriminator in WGAN-GP. Conv is the abbreviation of convolutional. LN is the abbreviation of layer normalization. LeakyReLu is activation function.
The structure of the VAE is shown in Figure 16.
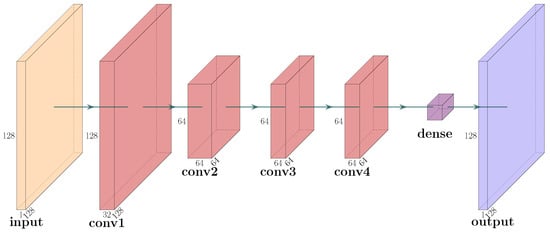
Figure 16.
The network structure of VAE. Conv is the abbreviation of convolutional.
Both generators have a tanh function in the last layer. And there is a sigmoid function in the DCGAN discriminator’s last layer. In all figures, Conv is the abbreviation of convolutions and Deconv is the abbreviation of deconvolutions, BN is the abbreviation of batch normalization, and LN is the abbreviation of layer normalization, Relu and LeakyReLu are activation functions. In the LeakyReLU, the slope of the leak was set to 0.2 in all models. We used the Adam optimizer with a learning rate of 0.0001 in WGAN-GP and a learning rate of 0.0002 in DCGAN.
With the MSTAR dataset as input, visualization of simulated images is shown in Figure 17. Some studies have shown that deconvolution of generators can cause checkerboard artifacts [25], that is, there are some textures similar to checkerboard artifacts after magnification of the generated images. We can find the checkerboard artifacts in DCGAN and WGAN-GP simulated images. VAE-simulated images are more blurred. All simulated images are identical to real images in shadow and the locations of scattering centers. They have satisfying visual similarity and are difficult to evaluate visually.
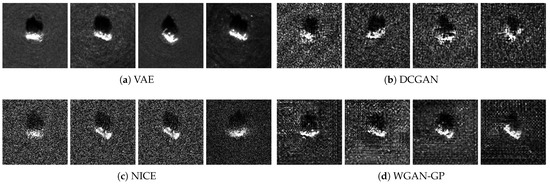
Figure 17.
Visualization of simulated images. The four images of each models represent BMP2, BTR60, T72 and T62 respectively. (a) Simulated images generated by VAE. (b) Simulated images generated by DCGAN. (c) Simulated images generated by WGAN-GP. (d) Simulated images generated by NICE.
4.2. Simple-Wise
We calculate the fisher values mentioned in Section “The Weight” of our MSRAR dataset to construct judgment matrix according to AHP. Fisher values of the four representative objective parameters in Section 3.1.1 are carried out.
As the method shown in Table 3, we get matrix through pairwise comparisons of the Fisher values. represents Fisher value of a certain parameter.

Table 3.
Judgment matrix.
Maximum eigen value and its eigenvector are got by performing eigenvalue decomposition on judgment matrix [20].
After normalization,
We get Consistency Ratio , which indicates each element of the eigenvector can be used as the weight of the four parameters.
Since the images have different angles, it is difficult to meet one-to-one correspondence between the simulated images and real images. We apply random sampling to solve the problem, 10 samples are selected randomly in the same category of each dataset [20]. We average the values of 10 samples to obtain the final value and carry out fuzzy membership matrix . The final evaluation vector is defined as
A hundred groups of experiments have been done for each model. The results are shown in the Table 4.

Table 4.
Statistics of valuetion results.
From Table 4, we can draw some conclusions.
- (a)
- For each category and each model, there are no evaluations with poor and very poor, and a few medium evaluations. It shows that the effect of simulation is good.
- (b)
- NICE, WGAN-GP, and DCGAN have relatively similar results.
- (c)
- For the four models, the evaluations of BMP2 have relatively poor results, and the evaluations of T62 are the best.
- (d)
- VAE has the lowest number of excellent.This is probably because VAE does not well retain the clarity of the original images.
- (e)
- The rate of excellence in NICE is highest. This shows that the simulated images preserve the backscattering coefficient.
NICE directly calculates the probability distribution, and VAE is approximately fitting. So NICE can better retain the relative intensity of the speckle noise and the target backscattering coefficient.
4.3. Class-Wise
4.3.1. Electromagnetic Computational Tools
The seleted SAMPLE dataset referred to in Table 2 is used in this part to get hybrid Recognition Rate Curve as shown in Figure 18. The x-axis represents the ratio of substitution, and the y-axis indicates the accuracy. We replace the real training images with simulated images at different scales to get Hybrid training sets and select MobileNet [26] to detect and recognize. In all experiments in this part, the training set and the testing set are divided by 7 to 3.
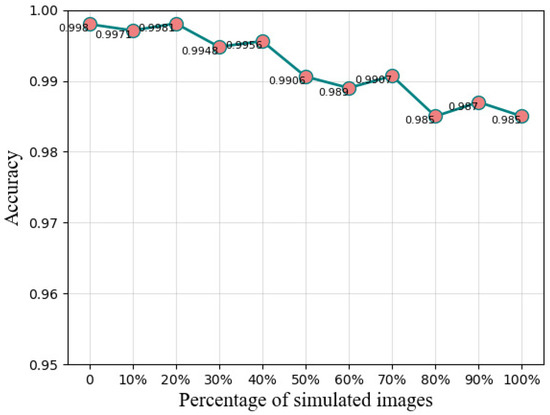
Figure 18.
Hybrid Recognition Rate curve of electromagnetic simulation. The x-axis represents the ratio of substitution, and the y-axis indicates the accuracy.
From Figure 18, we can draw some conclusions. With the increase in the ratio of substitution, the accuracy remains stable and all above 98%. Stable accuracy displays that the simulated images can be used as a supplement to real SAR images. The variance of the 11 accuracies is 0.000023. The small variance further validates the small fluctuations in accuracy.
T-distributed stochastic neighbor embedding (t-SNE) [27] is a nonlinear dimensionality reduction algorithm. It is suitable for dimensionality reduction and visualization of high-dimensional data. We use t-SNE to perform dimensionality reduction on the final feature layer of the convolutional neural network. Figure 19 displays the t-SNE two-dimensional representation of the features of real and simulated images. Both datasets are well clustered. The distribution of real data is more scattered, while the distribution of simulated data is compact but overlapping. Because of the repetitiveness of simulated data is too high.
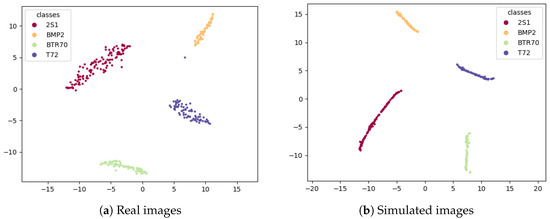
Figure 19.
(a) The two-dimensional t-SNE representation of features in real images. (b) The two-dimensional t-SNE representation of features in simulated images.
4.3.2. Deep Generative Models
In this part, the seleted MSTAR dataset refered in Table 1 is used as the real dataset. Its training set is used as input to the four generative models to obtain the corresponding number of simulated images respectively. We replace the real training images with simulated images at different scales to get hybrid training sets of four generative models. And the testing set remains the same as the original testing set. In order to obtain the Hybrid Recognition Rate curve, MobileNet is selected in this experiment to detect and recognize. Then four four-class Hybrid Recognition Rate curves can be obtained, as shown in Figure 20.
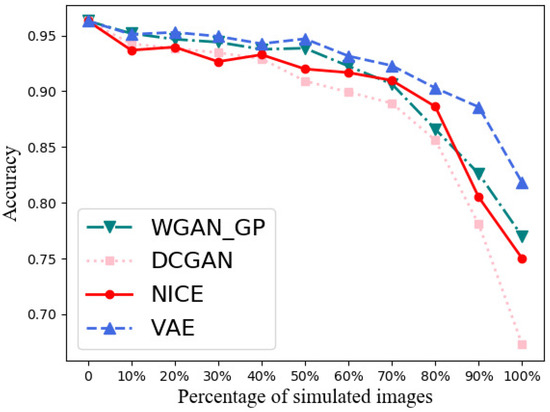
Figure 20.
Hybrid Recognition Rate curves of deep generative models. The x-axis represents the ratio of substitution and the y-axis indicates the accuracy.
The x-axis represents the ratio of substitution, and the y-axis indicates the accuracy. From Figure 20, we can get the followings.
- (a)
- Without simulated images, the recognition accuracy achieves 96.30%.
- (b)
- The recognition rates of simulated datasets are 76.99%, 67.28%, 75.00%, and 81.80%.
- (c)
- The accuracy of VAE is the highest. It means that the images simulated by VAE have better application capabilities.
- (d)
- When the percetage of simulated images is lower than 50%, the fluctuation of the accuracy is small and the values are all higher than 90%. These prove the simulated images can be used to augment the dataset in classification tasks.
The variances of the 11 accuracies obtained by four models are shown in Table 5.

Table 5.
The values of variance.
The variance can reflect the fluctuation of the data. All four models achieved small variance. That means the stability of the simulated data. The VAE model with the smallest variance gets the best performance, while the DCGAN model with the largest variance gets the worst performance.
In order to analyze the distribution of features, we reduce the final feature layer output of the convolutional neural network to two-dimensional by t-SNE. The t-SNE two-dimensional representation of the features is shown in Figure 21. All datasets are well clustered. This means good intra-class cohesion and large inter-class variance.
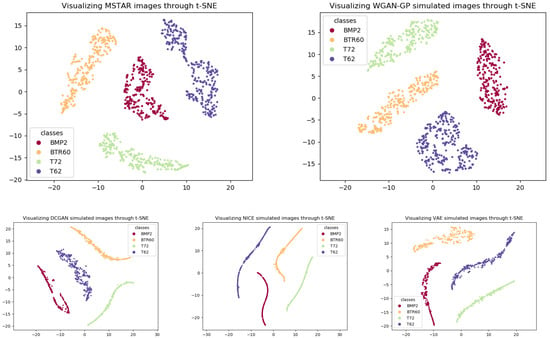
Figure 21.
The two-dimensional t-SNE representation of features. From top to bottom, from left to right, the representation of real detaset, WGAN-GP, DCGAN, NICE, VAE respectively.
The distribution of WGAN-GP is more similar to the distribution of real data, and they are all more scattered. While the distribution of NICE, VAE, and DCGAN is compact and overlapping, especially with NICE. This indicates that the data is not diverse enough. That is, the generated images lack of diversity.
4.3.3. The Effect of Dataset Size
To demonstrate the stability of the method, randomly sample from the original training sets according to initial class ratio to form new datasets with different numbers. Take DCGAN for example; we respectively sample 1000, 900, 800, 700, and 600 samples from the original MSTAR dataset. A series of HRR curves are obtained, as shown in Figure 22. The five curves have similar curvatures and shapes. From the figures, we can summarize that the accuracy of the five curves remains stable under different ratios of hybrid. The accuracy of real datasets is all about 95%, and the accuracy of simulated datasets are all about 70%. This means that our method can be applied to datasets of various sizes, and the results are independent of the size of the data.

Figure 22.
A series of HRR curves with different amount of training data.
4.4. Comparison with Other Criteria
In order to further demonstrate the effectiveness of the proposed method and validate the authenticity of the generated images from the perspective of their statistical characteristics of images, gray histograms is used in this part. The distribution of the gray histogram can reflect the statistical characteristics of SAR images. The comparison between the simulated images of the four generative methods and the real image is shown in Figure 23. The gray histogram requires a one-to-one correspondence between the simulated image and the real image. It cannot be implemented in the experiment. Therefore, the images under the same or closest azimuth angle in the same category are picked.

Figure 23.
Gray histogram results of four simulated images, and the real image. From left to right: BMP2,BTR60,T72,T62.
In terms of the shape of the gray histogram, the DCGAN and WGAN-GP simulated images are closer to the real image than the others. We can also find that the simulated images generated by the WGAN-GP method appear similar to the simulated images generated by DCGAN, except T62. Compared with the real image, the gray values of the image generated by the NICE model increase overall and have a wider coverage, while the gray values of the image generated by the VAE model have a narrower coverage. For this reason, the overall image of NICE looks brighter. However, the gray histogram can only reflect the gray distribution of the image without knowing the position of each image pixel.
4.5. Comprehensive Analysis
Theis et al. [28] believe that different measurement methods can lead to contradictory conclusions. Choosing which evaluation indicator to use depends on the purposes of simulating images. Judging from our experiment results, NICE can better retain the relative intensity of the speckle noise and the target backscattering coefficient but generates data with high repetitiveness. VAE cannot retain the speckle noise and the target backscattering coefficient well, but it is better for classification tasks. WGAN-GP has the best comprehensive performance.
5. Conclusions
This paper proposes a new assessment strategy including two parts: sample-wise assessment and class-wise assessment. They evaluate the simulated images from different perspectives. Sample-wise assessment is used to compare similarity considering some SAR coefficients, and Class-wise assessment is designed to compare the application capability of the simulated images. We use four generative models to simulate MSTAR images and apply our method to simulated images. We can choose appropriate evaluation indicators for different purpose of simulating images.
In the future, the authors will try to concentrate on comparing the results with other similarity distances often used in the SAR domain and combining the structural similarity, geometric similarity, and outline similarity with our method. The authors are trying to propose a comprehensive method. An interesting direction for our future work is to design an evaluation method for SLC(Single Look Complex)-SAR images. And it will be the focus of our next research. The complex-valued CNNs are under our consideration. We believe that the full potential of complex-valued CNNs is yet to be uncovered.
Author Contributions
Conceptualization, Z.Y., G.D. and H.L.; methodology, Z.Y., G.D. and H.L.; software, Z.Y.; validation, Z.Y. and G.D.; formal analysis, Z.Y. and G.D.; resources, Z.Y. and G.D.; data curation, Z.Y.; writing and original draft preparation, Z.Y.; writing—review and editing, Z.Y. and G.D.; visualization, Z.Y.; supervision, G.D. and H.L.; project administration, G.D. and H.L.; funding acquisition, G.D. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant Number 61971324 and 61525105.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, K.; Zhang, G.; Leung, H. SAR Target Recognition Based on Cross-Domain and Cross-Task Transfer Learning. IEEE Access 2019, 7, 153391–153399. [Google Scholar] [CrossRef]
- Xu, Q.; Huang, G.; Yuan, Y.; Guo, C.; Sun, Y.; Wu, F.; Weinberger, K. An empirical study on evaluation metrics of generative adversarial networks. arXiv 2018, arXiv:1806.07755. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30, 6629–6640. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Yoo, J.; Kim, J. SAR Image Generation of Ground Targets for Automatic Target Recognition Using Indirect Information. IEEE Access 2021, 9, 27003–27014. [Google Scholar] [CrossRef]
- Nie, C.; Kong, Y.; Leung, H.; Yan, S. Evaluation methods of similarity between simulated SAR images and real SAR images. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar]
- Yu, Z.; Dong, G. A New Quantitative Evaluation Strategy for Deep Generated Sar Images. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 2626–2629. [Google Scholar]
- Niu, S.; Qiu, X.; Lei, B.; Ding, C.; Fu, K. Parameter Extraction Based on Deep Neural Network for SAR Target Simulation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1–14. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Tolstikhin, I.; Bousquet, O.; Gelly, S.; Schoelkopf, B. Wasserstein auto-encoders. arXiv 2017, arXiv:1711.01558. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved training of wasserstein gans. arXiv 2017, arXiv:1704.00028. [Google Scholar]
- Cui, Z.; Zhang, M.; Cao, Z.; Cao, C. Image Data Augmentation for SAR Sensor via Generative Adversarial Nets. IEEE Access 2019, 7, 42255–42268. [Google Scholar] [CrossRef]
- Cao, C.; Cao, Z.; Cui, Z. LDGAN: A Synthetic Aperture Radar Image Generation Method for Automatic Target Recognition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3495–3508. [Google Scholar] [CrossRef]
- Xie, D.; Ma, J.; Li, Y.; Liu, X. Data Augmentation of Sar Sensor Image via Information Maximizing Generative Adversarial Net. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 454–458. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. Nice: Non-linear independent components estimation. arXiv 2014, arXiv:1410.8516. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using Real NVP. arXiv 2016, arXiv:1605.08803. [Google Scholar]
- Kingma, D.P.; Dhariwal, P. Glow: Generative flow with invertible 1 × 1 convolutions. Adv. Neural Inf. Process. Syst. 2018, 31, 10215–10224. [Google Scholar]
- Yu, Z.; Dong, G. Similarity Analysis of Simulated SAR Target Images. In Proceedings of the 2022 30th European Signal Processing Conference (EU-SIPCO), Belgrade, Serbia, 29 August–2 September 2022; pp. 588–592. [Google Scholar]
- Huo, W.; Huang, Y.; Pei, J.; Liu, X.; Yang, J. Virtual SAR target image generation and similarity. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 914–917. [Google Scholar]
- Mu, H.; Zhang, Y.; Ding, C.; Jiang, Y.; Er, M.H.; Kot, A.C. DeepImaging: A Ground Moving Target Imaging Based on CNN for SAR-GMTI System. IEEE Geosci. Remote Sens. Lett. 2021, 18, 117–121. [Google Scholar] [CrossRef]
- Oveis, A.H.; Giusti, E.; Ghio, S.; Martorella, M. CNN for Radial Velocity and Range Components Estimation of Ground Moving Targets in SAR. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 8–14 May 2021; pp. 1–6. [Google Scholar]
- Lewis, B.; Scarnati, T.; Sudkamp, E.; Nehrbass, J.; Rosencrantz, S.; Zelnio, E. A SAR dataset for a TR development: The Synthetic and Measured Paired Labeled Experiment (SAMPLE). In Algorithms for Synthetic Aperture Radar Imagery XXVI; SPIE: Bellingham, WA, USA, 2019; Volume 10987, pp. 39–54. [Google Scholar]
- Sugawara, Y.; Shiota, S.; Kiya, H. Super-Resolution Using Convolutional Neural Networks without Any Checkerboard Artifacts. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 66–70. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Theis, L.; van den Oord, A.; Bethge, M. A note on the evaluation of generative models. arXiv 2015, arXiv:1511.01844. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).