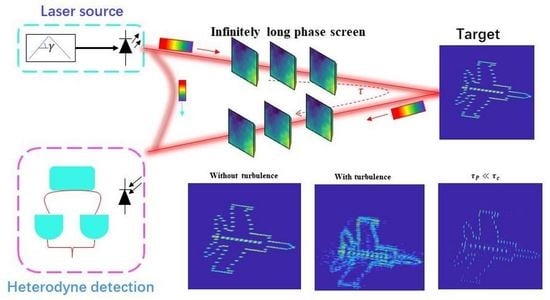
Effects of Atmospheric Coherent Time on Inverse Synthetic Aperture Ladar Imaging through Atmospheric Turbulence
Abstract
1. Introduction
2. Numerical Methods
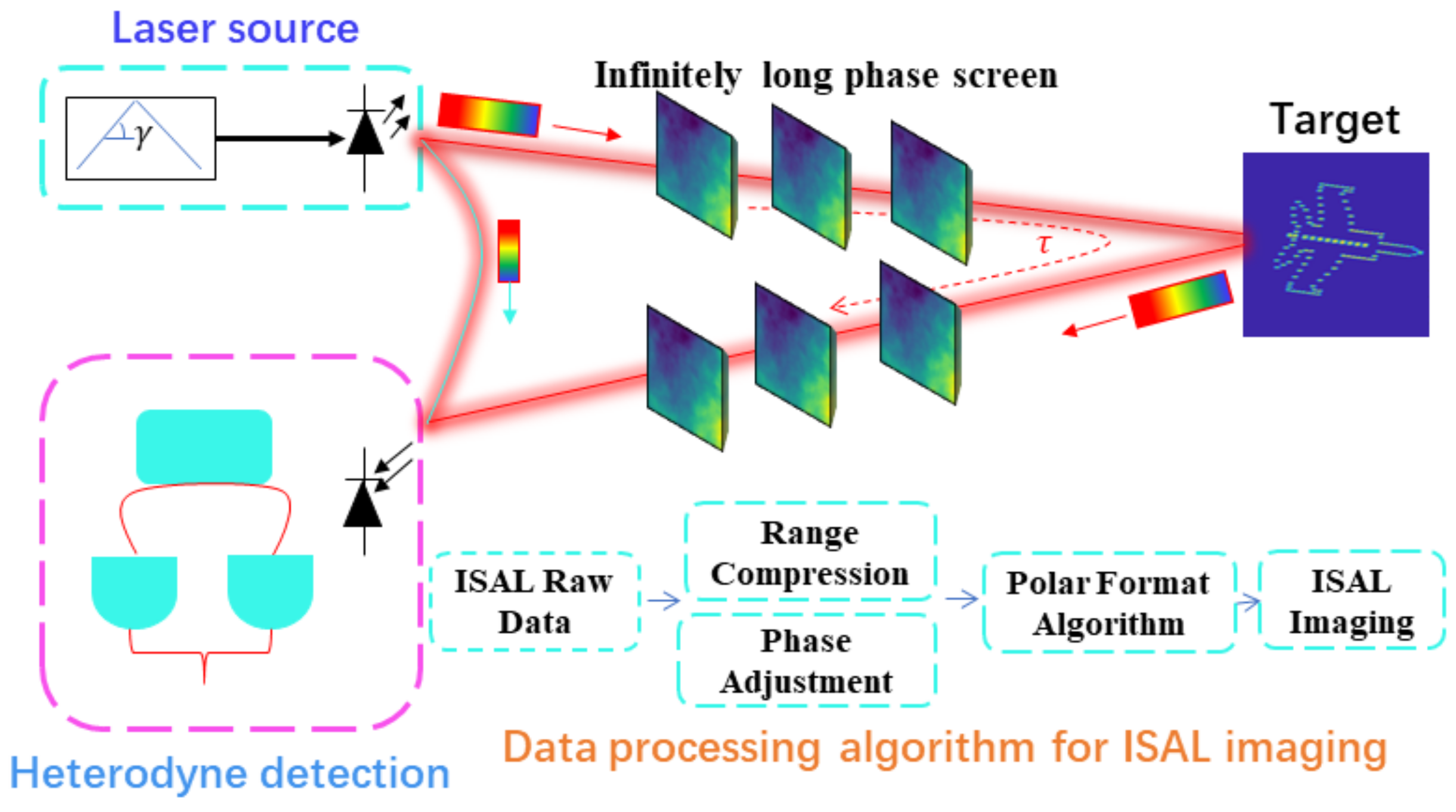
2.1. ISAL Image Processing Model
2.2. Infinitely Long Phase Screen
2.3. Heterodyne Detection Processes with ISAL
2.4. Range-Doppler Algorithm
3. Simulation Results
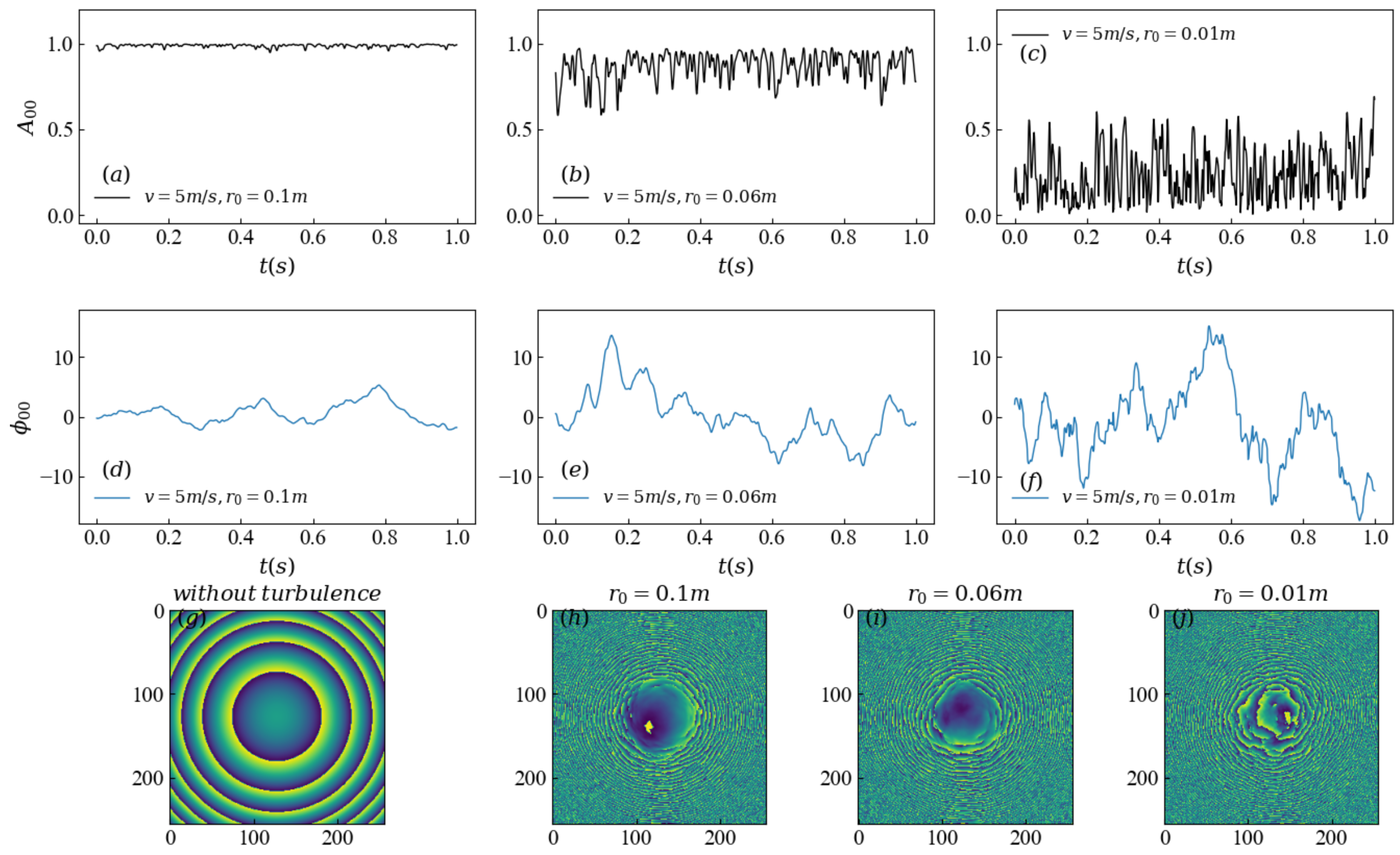
3.1. Laser Beam Propagation in Atmospheric Turbulence
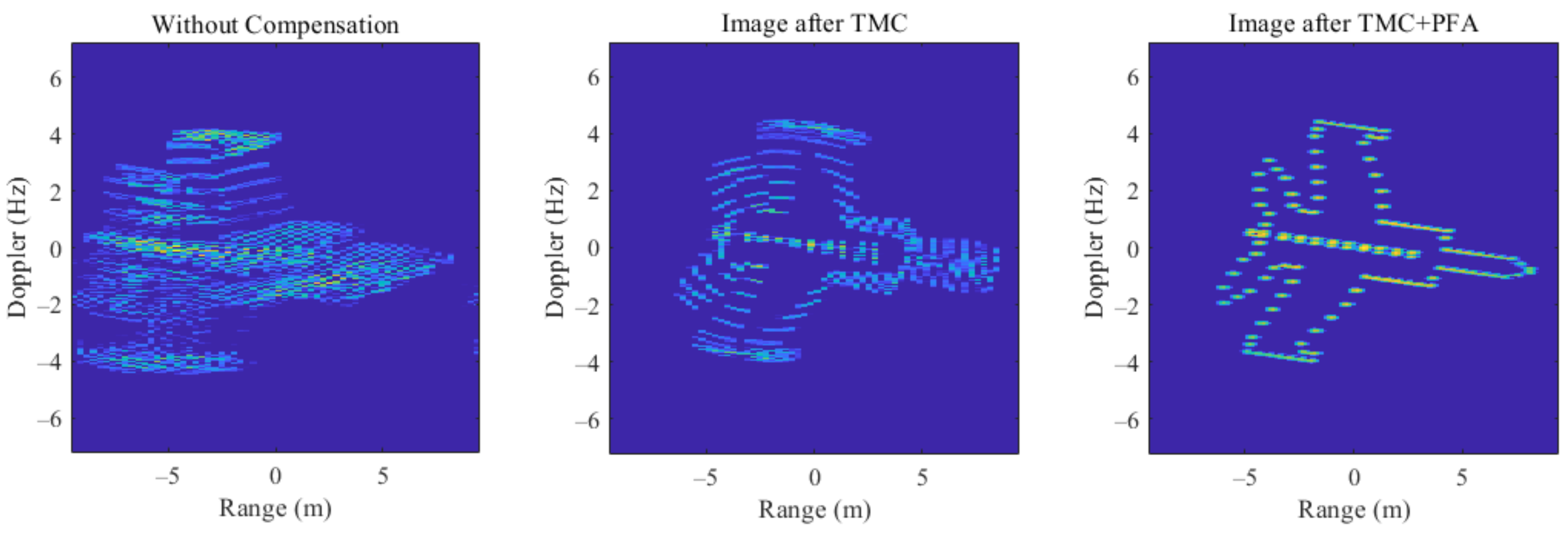
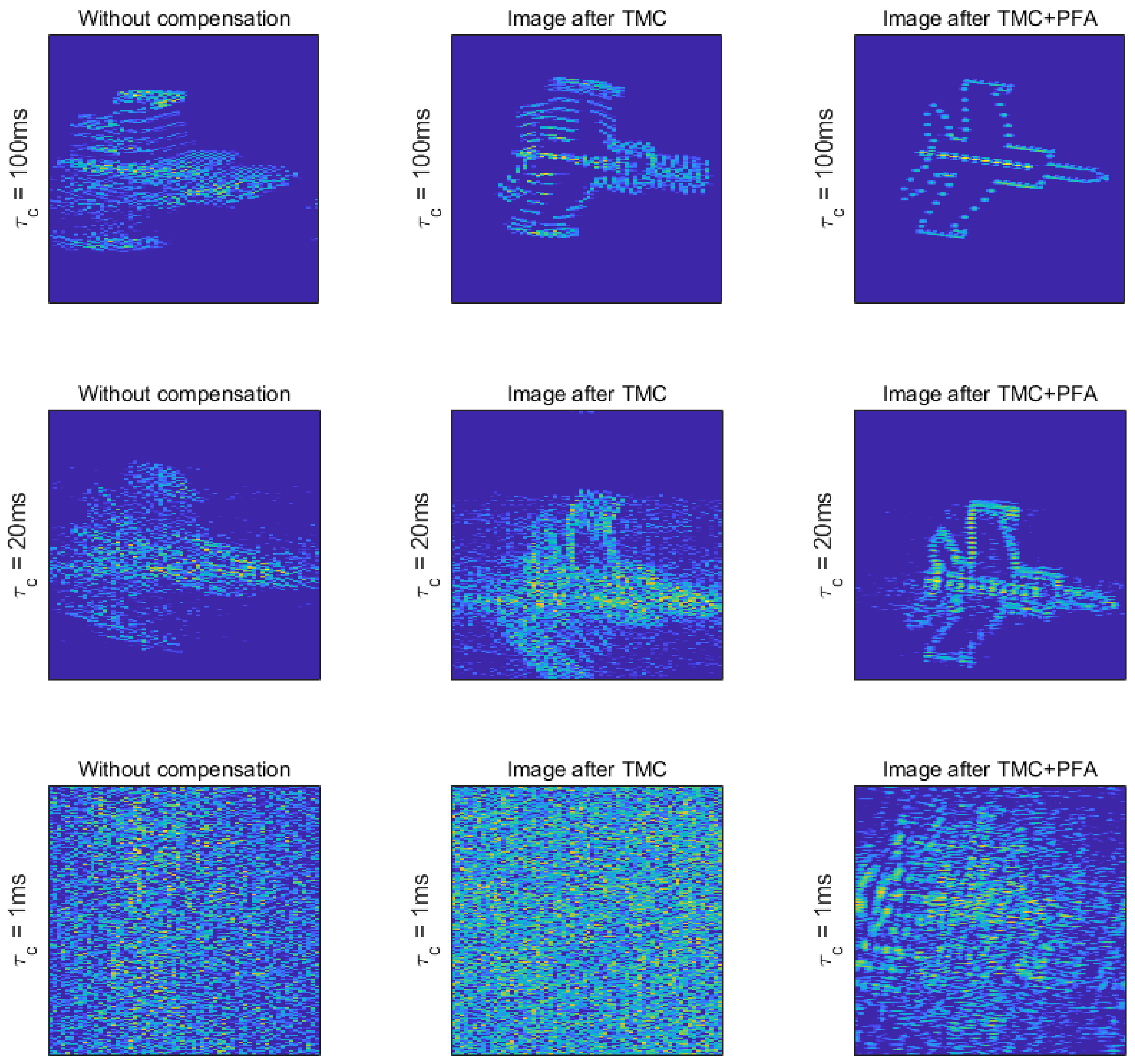
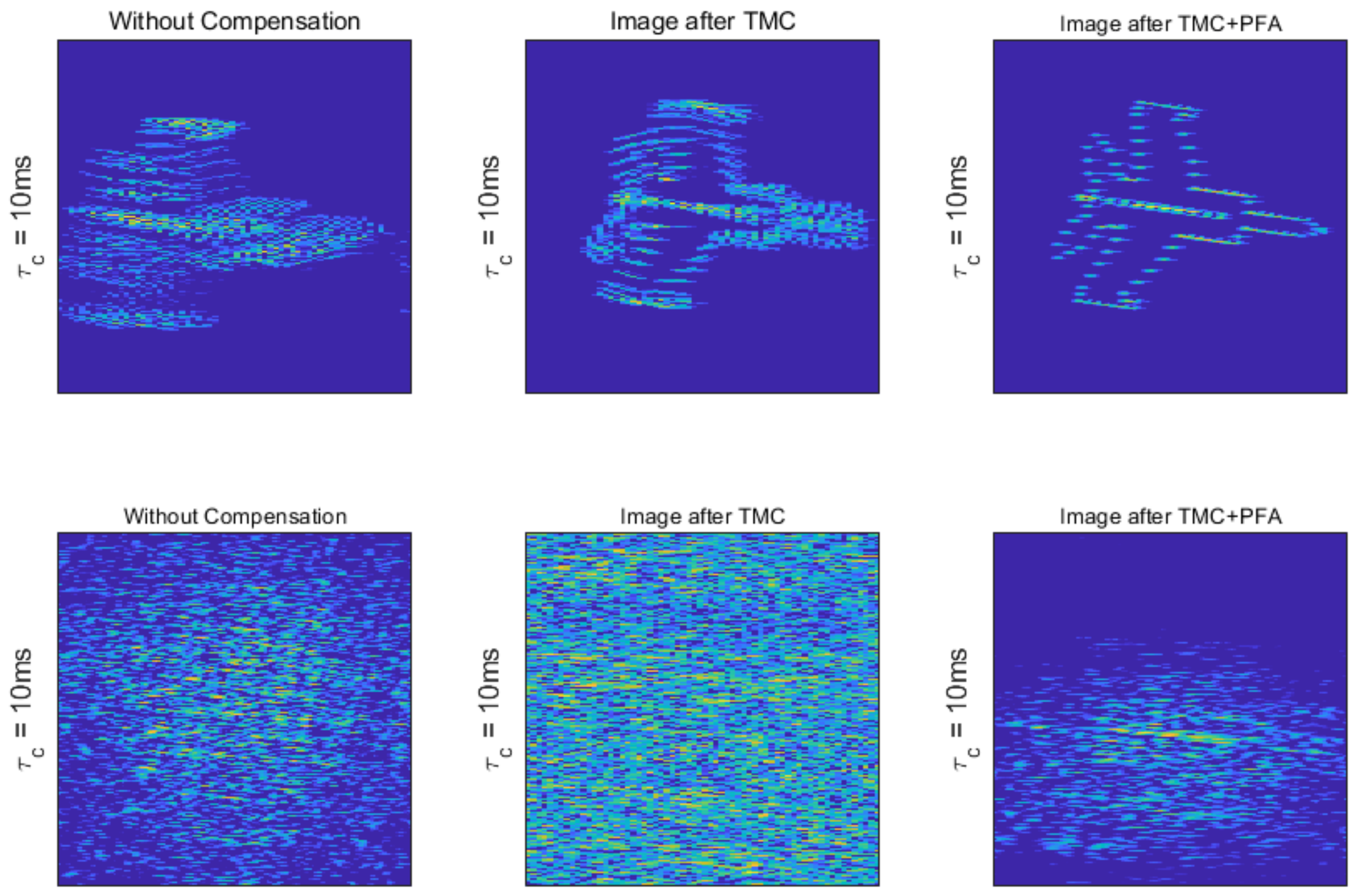
3.2. RDA Compensation Simulation
3.3. Quantitative Evaluation of Image Quality
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Crouch, S.; Barber, Z.W. Laboratory demonstrations of interferometric and spotlight synthetic aperture ladar techniques. Opt. Express 2012, 20, 24237–24246. [Google Scholar] [CrossRef] [PubMed]
- Green, T.J.; Marcus, S.; Colella, B.D. Synthetic-aperture-radar imaging with a solid-state laser. Appl. Opt. 1995, 34, 6941–6949. [Google Scholar] [CrossRef]
- Trahan, R.; Nemati, B.; Zhou, H.; Shao, M.; Hahn, I.; Schulze, W. Low-CNR inverse synthetic aperture LADAR imaging demonstration with atmospheric turbulence. In Proceedings of the Long-Range Imaging, Baltimore, MD, USA, 17–21 April 2016; Volume 9846, pp. 87–99. [Google Scholar]
- Hua, Z.; Li, H.; Gu, Y. Atmosphere turbulence phase compensation in synthetic aperture ladar data processing. In Proceedings of the MIPPR 2007: Multispectral Image Processing, Wuhan, China, 15 November 2007; Volume 6787, pp. 560–566. [Google Scholar]
- Guo, L.; Xing, M.; Tang, Y.; Dan, J. A novel modified Omega-k algorithm for synthetic aperture imaging lidar through the atmosphere. Sensors 2008, 8, 3056–3066. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lu, T.A.; Li, H.P. Atmospheric turbulence induced synthetic aperture lidar phase error compensation. Opt. Commun. 2016, 381, 214–221. [Google Scholar] [CrossRef]
- Wang, C. Study of synthetic aperture ladar imaging through atmospheric turbulence. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2011: Laser Sensing and Imaging; and Biological and Medical Applications of Photonics Sensing and Imaging, Beijing, China, 24–26 May 2011; Volume 8192, pp. 408–418. [Google Scholar]
- Karr, T.J. Synthetic aperture ladar resolution through turbulence. In Proceedings of the Atmospheric Propagation, San Jose, CA, USA, 28–29 January 2003; Volume 4976, pp. 22–33. [Google Scholar]
- Pellizzari, C.; Spencer, M.; Steinhoff, N.; Belsher, J.; Tyler, G.; Williams, S.; Williams, S. Inverse synthetic aperture ladar: A high-fidelity modeling and simulation tool. In Proceedings of the Unconventional Imaging and Wavefront Sensing 2013, San Diego, CA, USA, 25–29 August 2013; Volume 8877, p. 88770B. [Google Scholar]
- Schumm, B.E.; Dierking, M.P. Wave optics simulations of synthetic aperture ladar performance through turbulence. J. Opt. Soc. Am. A 2017, 34, 1888–1895. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Cao, Y.; Wu, Z.; Li, Y.; Zhang, G.; Yang, K.; Gao, R. Inverse synthetic aperture lidar imaging and compensation in slant atmospheric turbulence with phase gradient algorithm compensation. Opt. Laser Technol. 2022, 154, 108329. [Google Scholar] [CrossRef]
- Pellizzari, C.J.; Bos, J.; Spencer, M.F.; Williams, S.; Williams, S.E.; Calef, B.; Senft, D.C. Performance characterization of Phase Gradient Autofocus for inverse synthetic aperture LADAR. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014; pp. 1–11. [Google Scholar]
- Wang, N.; Wang, R.; Li, G.; Zhang, K.; Wu, Y. Experiment of inverse synthetic aperture ladar at 1.1 km. In Proceedings of the Optical Measurement Technology and Instrumentation, Beijing, China, 9–11 May 2016; Volume 10155, p. 101551G. [Google Scholar]
- Depoy, R.S.; Shaw, A.K. Mitigating atmospheric phase-errors in SAL data using model-based reconstruction. In Proceedings of the 2019 IEEE National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 15–19 July 2019; pp. 384–390. [Google Scholar]
- Depoy, R.S.; Shaw, A.K. Algorithm to overcome atmospheric phase errors in SAL data. Appl. Opt. 2020, 59, 140–150. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Li, Y.; Du, Y.; Lei, T.; Qiu, J.; Hong, X.; Guo, H.; Wu, J. Performance Analysis of Synthetic Aperture Ladar System with Photonic Lantern Coupling under Atmospheric Turbulence. In Proceedings of the 2022 IEEE 10th International Conference on Information, Communication and Networks (ICICN), Zhangye, China, 23–24 August 2022; pp. 479–484. [Google Scholar]
- Assémat, F.; Wilson, R.W.; Gendron, E. Method for simulating infinitely long and non stationary phase screens with optimized memory storage. Opt. Express 2006, 14, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Azizigul, A.; Zhi-Wei, T.; Shi-Wei, L.; Yan-Ling, L.; Rui-Zhong, R.; Yi-Chong, R. Influence of atmospheric turbulence on temporal coherence characteristics of received optical field. Acta Phys. Sin. 2022, 71. [Google Scholar] [CrossRef]
- Rao, R. Light Propagation in Turbulent Atmosphere; Anhui Science and Technology Publishing House: Hefei, China, 2005; Volume 5. [Google Scholar]
- McGlamery, B.L. Computer simulation studies of compensation of turbulence degraded images. In Proceedings of the Image Processing, Pacific Grove, CA, USA, 24–26 February 1976; Volume 74, pp. 225–233. [Google Scholar]
- Wu, H.; Yan, H.; Li, X.; Li, S. Generation of rectangular turbulence phase screens based on fractal characteristics of distorted wavefront. Acta Opt. Sin. 2009, 129, 114–119. [Google Scholar]
- Roddier, N.A. Atmospheric wavefront simulation using Zernike polynomials. Opt. Eng. 1990, 29, 1174–1180. [Google Scholar] [CrossRef]
- Sedmak, G. Implementation of fast-Fourier-transform-based simulations of extra-large atmospheric phase and scintillation screens. Appl. Opt. 2004, 43, 4527–4538. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G.I. Statistical theory of turbulenc. Proc. R. Soc. Lond. A 1935, 151, 421–444. [Google Scholar] [CrossRef][Green Version]
- Roddier, F. V the effects of atmospheric turbulence in optical astronomy. In Progress in Optics; Elsevier: Amsterdam, The Netherlands, 1981; Volume 19, pp. 281–376. [Google Scholar]
- Ziad, A.; Borgnino, J.; Martin, F.; Maire, J.; Mourard, D. Towards the monitoring of atmospheric turbulence model. Astron. Astrophys. 2004, 414, L33–L36. [Google Scholar] [CrossRef][Green Version]
- Fried, D.L. Optical resolution through a randomly inhomogeneous medium for very long and very short exposures. JOSA 1966, 56, 1372–1379. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Optical Engineering Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Liu, Y. Research on Synthetic Aperture Ladar Imaging System. Ph.D. Thesis, Graduate School of National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 108–110. [Google Scholar]
- Zhao, J.; Zhou, Y.; Braverman, B.; Liu, C.; Pang, K.; Steinhoff, N.K.; Tyler, G.A.; Willner, A.E.; Boyd, R.W. Performance of real-time adaptive optics compensation in a turbulent channel with high-dimensional spatial-mode encoding. Opt. Express 2020, 28, 15376–15391. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Jin, K.; Jiang, C.; Li, J.; Song, A.; Wei, K.; Zhang, Y. Amplitude compensation using homodyne detection for inverse synthetic aperture LADAR. Appl. Opt. 2021, 60, 10594–10599. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Wang, Y.; Jin, S. A Quantitative Evaluation Approach for ISAR Image Performance. Radar Sci. Technol. Pap. 2017, 15, 43–49. [Google Scholar]



| Radar and Target Parameter | Value |
|---|---|
| Laser wavelength (nm) | 1024 |
| Pulse repetition frequency (Hz) | 17,987 |
| Range sampling number | 64 |
| Pulse number | 512 |
| Distance of the target (m) | 1000 |
| Range resolution (m) | 0.2927 |
| Cross-range resolution (m) | 0.0556 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdukirim, A.; Ren, Y.; Tao, Z.; Liu, S.; Li, Y.; Deng, H.; Rao, R. Effects of Atmospheric Coherent Time on Inverse Synthetic Aperture Ladar Imaging through Atmospheric Turbulence. Remote Sens. 2023, 15, 2883. https://doi.org/10.3390/rs15112883
Abdukirim A, Ren Y, Tao Z, Liu S, Li Y, Deng H, Rao R. Effects of Atmospheric Coherent Time on Inverse Synthetic Aperture Ladar Imaging through Atmospheric Turbulence. Remote Sensing. 2023; 15(11):2883. https://doi.org/10.3390/rs15112883
Chicago/Turabian StyleAbdukirim, Azezigul, Yichong Ren, Zhiwei Tao, Shiwei Liu, Yanling Li, Hanling Deng, and Ruizhong Rao. 2023. "Effects of Atmospheric Coherent Time on Inverse Synthetic Aperture Ladar Imaging through Atmospheric Turbulence" Remote Sensing 15, no. 11: 2883. https://doi.org/10.3390/rs15112883
APA StyleAbdukirim, A., Ren, Y., Tao, Z., Liu, S., Li, Y., Deng, H., & Rao, R. (2023). Effects of Atmospheric Coherent Time on Inverse Synthetic Aperture Ladar Imaging through Atmospheric Turbulence. Remote Sensing, 15(11), 2883. https://doi.org/10.3390/rs15112883