Quantitative Assessment of Apple Mosaic Disease Severity Based on Hyperspectral Images and Chlorophyll Content
Abstract
1. Introduction
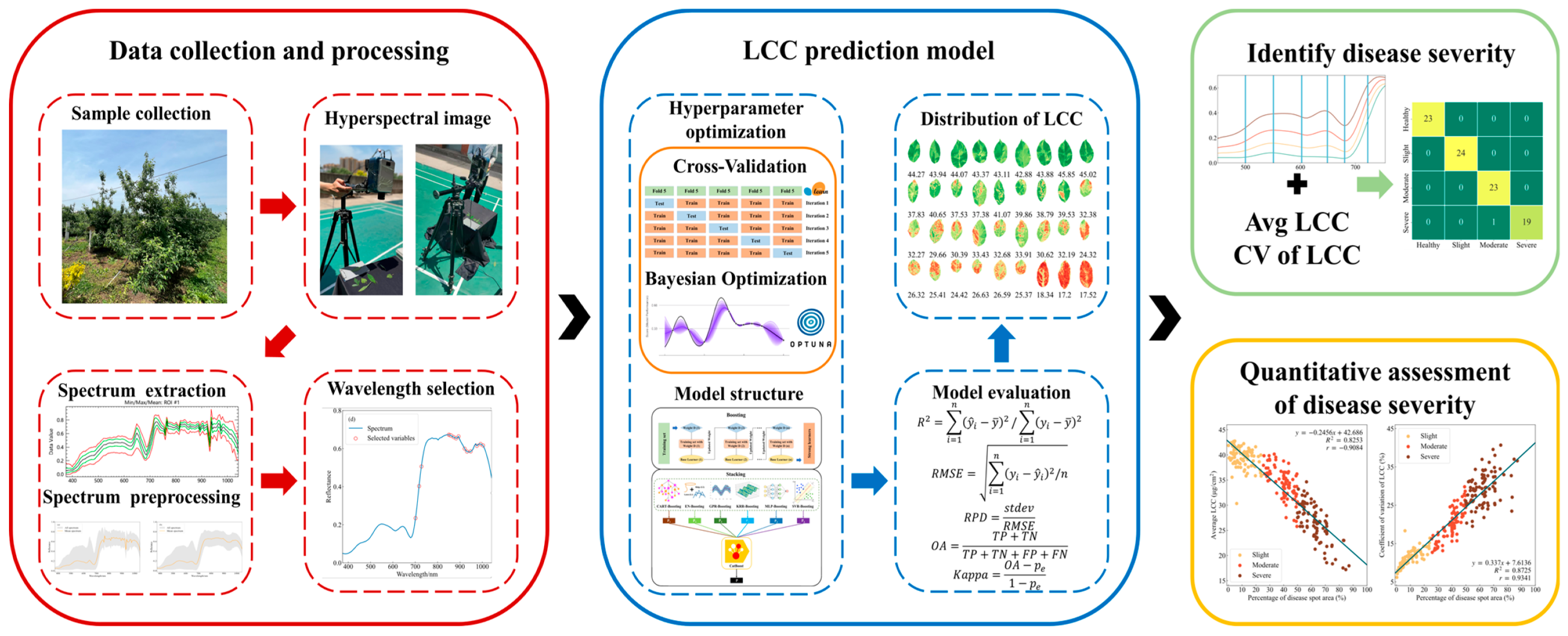
2. Materials and Methods
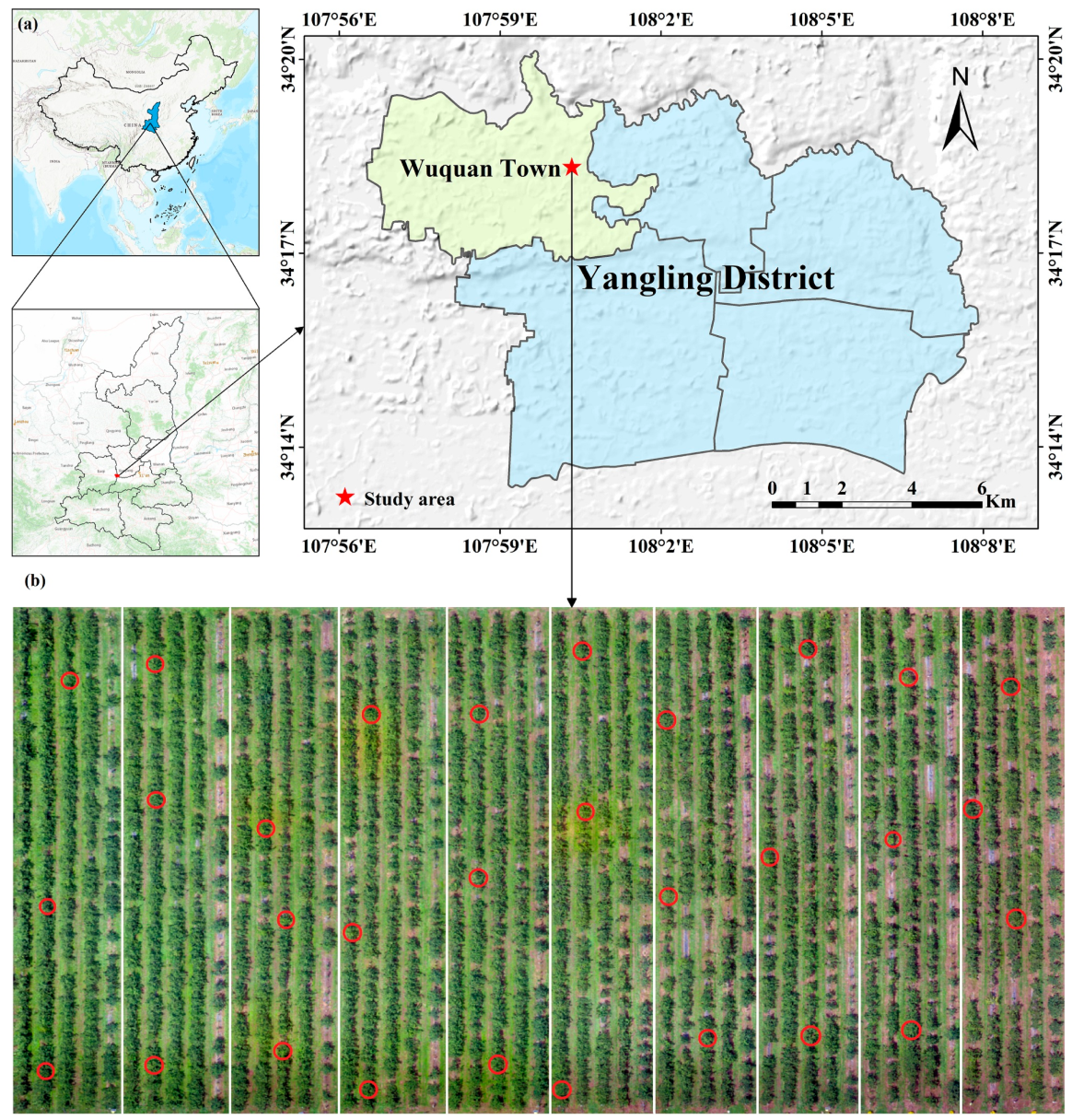
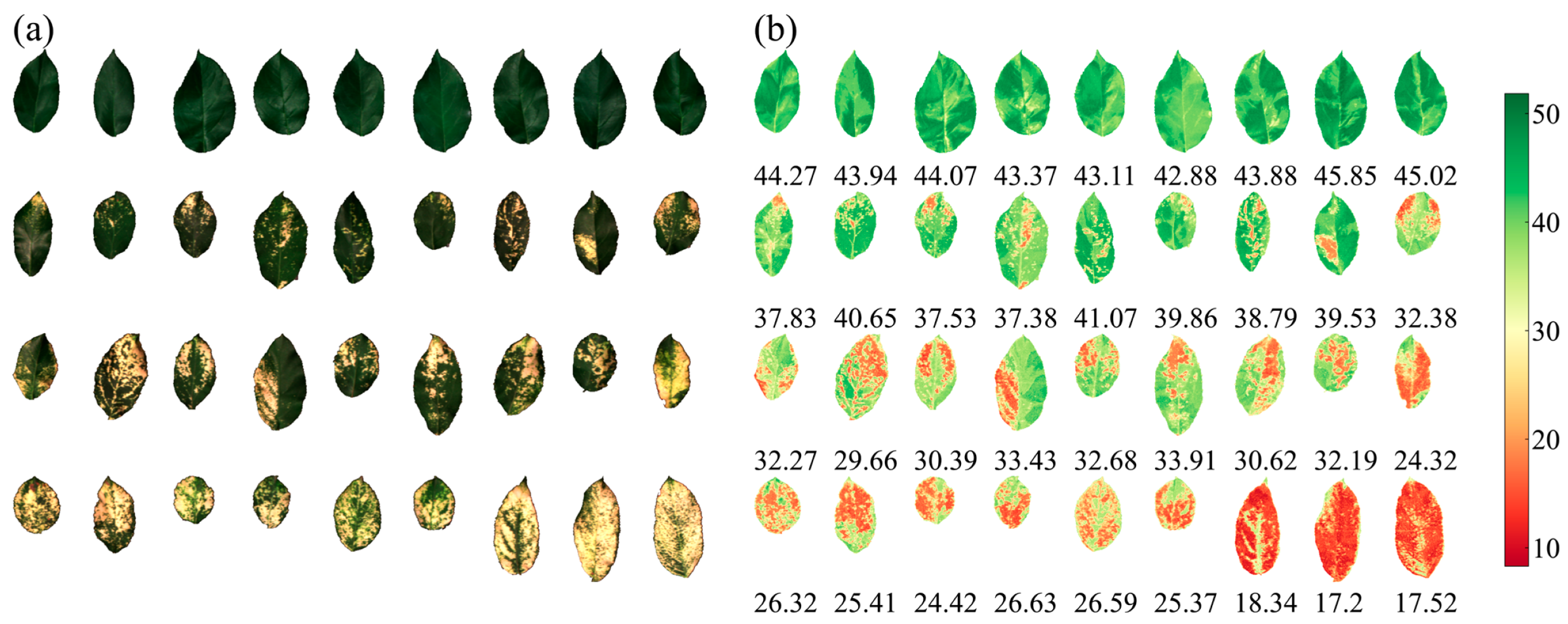
2.1. Leaf Sample Collection
2.2. Data Acquisition
2.2.1. LCC Determination
2.2.2. Hyperspectral Image Acquisition
2.3. Data Processing
2.3.1. Spectral Data Pre-Processing
2.3.2. Sample Split
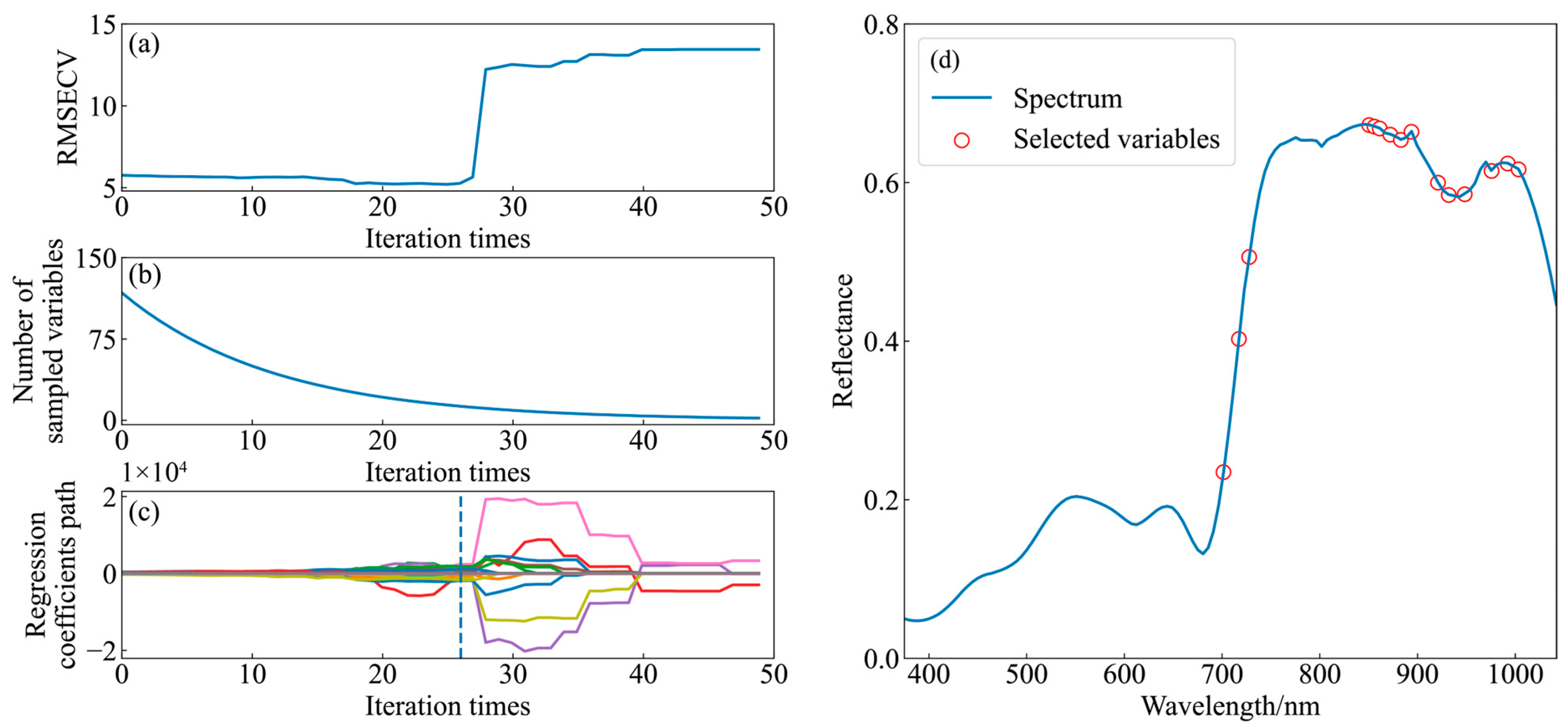
2.3.3. Feature Selection Method
2.3.4. Spectral Sensitivity Index
2.3.5. Coefficient of Variation
2.4. Modeling Method
2.4.1. Basic Models
2.4.2. Stacked–Boosting for Predictive Models
2.4.3. Model Evaluation Methodology
3. Results
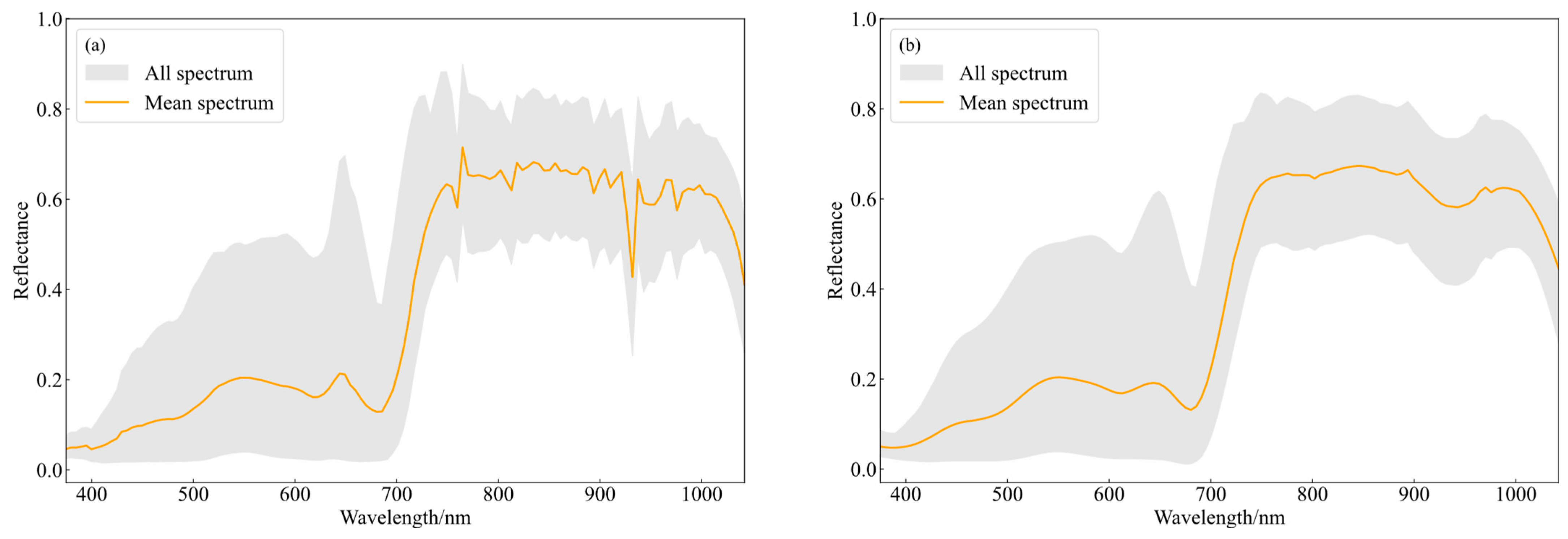
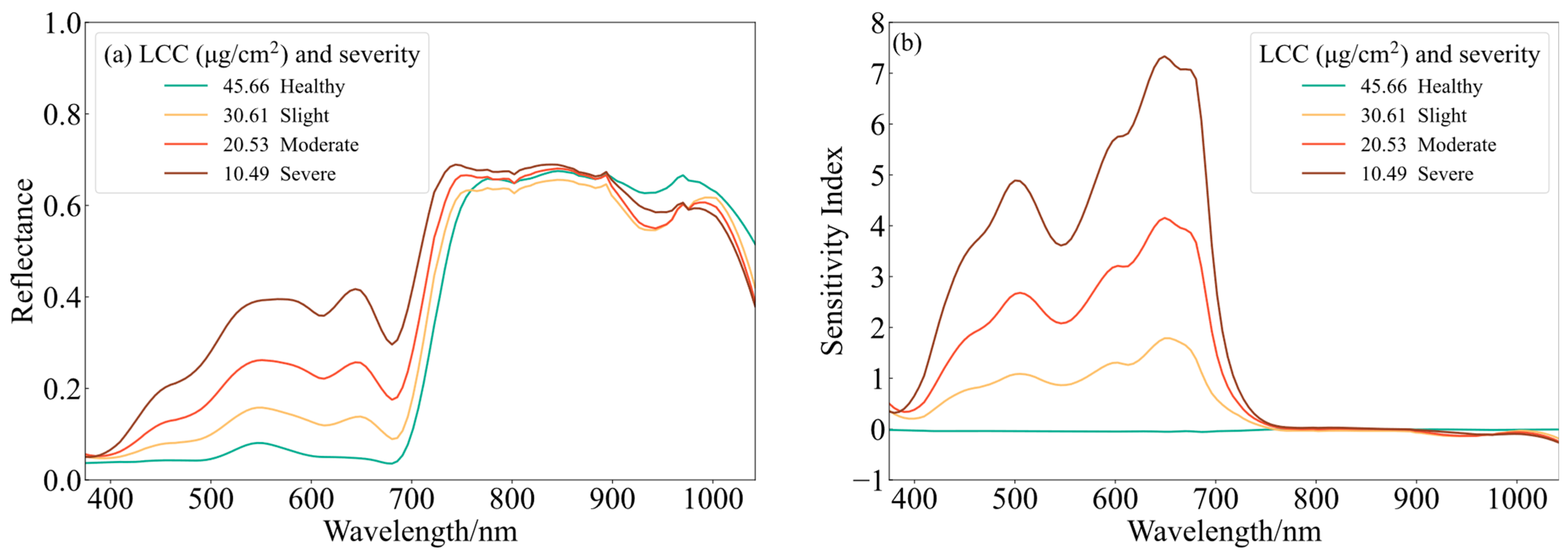
3.1. Spectral Characteristics of Leaves
3.2. Characteristic Wavelength Extraction
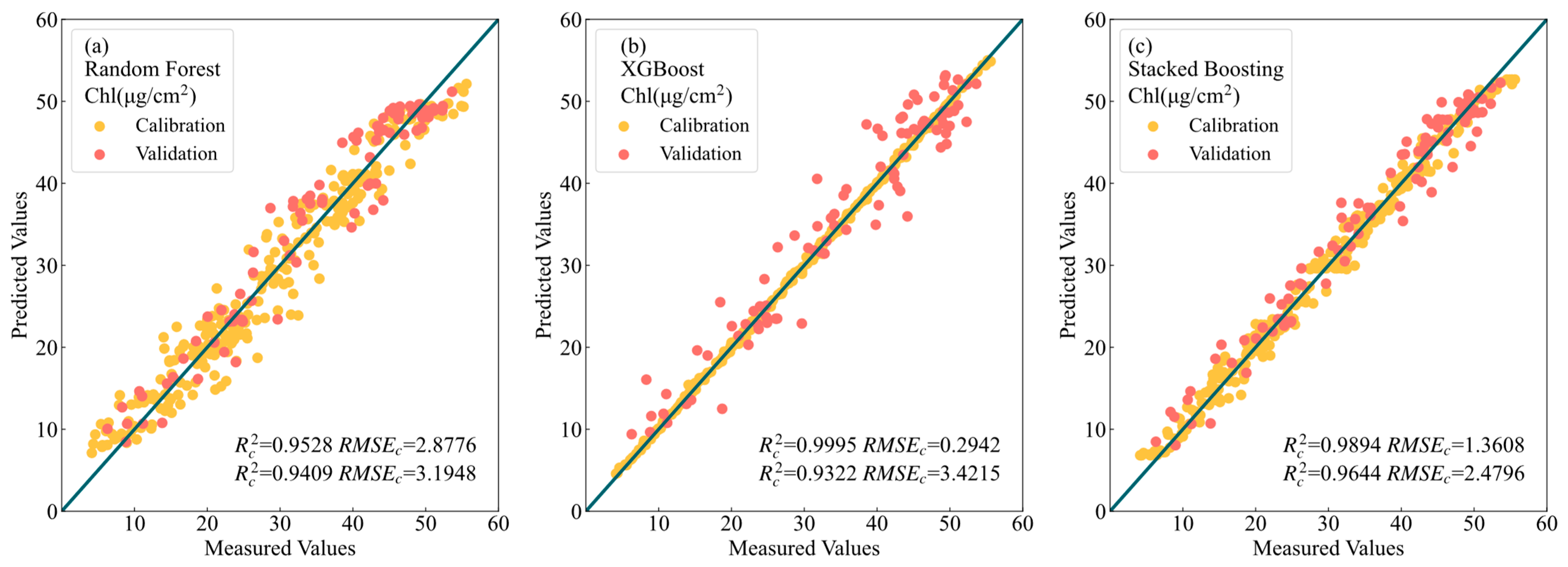
3.3. Modeling Evaluation of LCC Prediction
3.4. Inversion of LCC by HSI
3.5. Relationship between LCC Statistics and Percentage of Disease Spot Area
3.6. Identify Disease Severity Based on Average LCC and Sensitive Wavelengths
4. Discussion
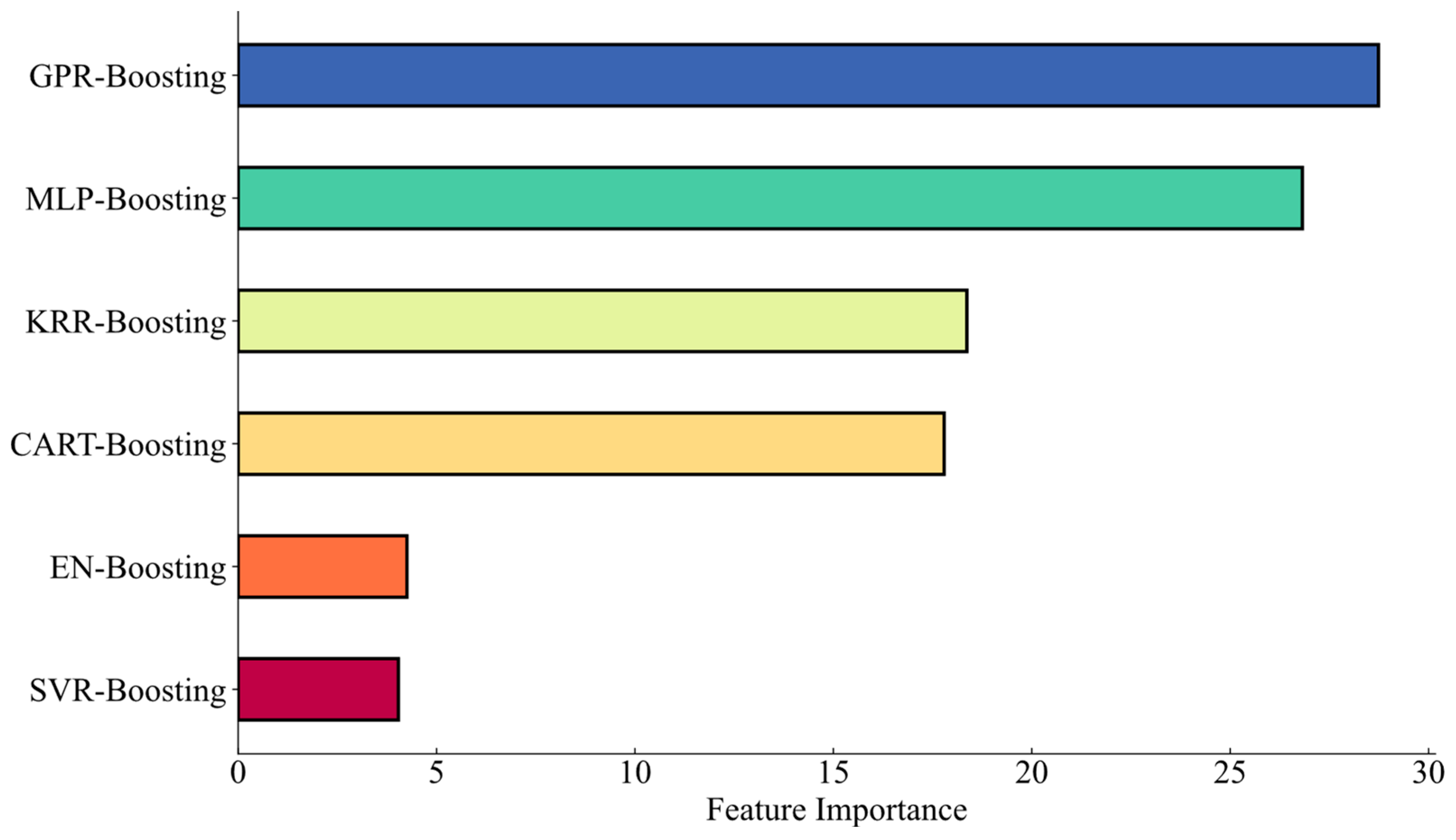
4.1. Stacked–Boosting Modeling Summary
4.2. Quantitative Description of Disease Severity Using Chlorophyll Content
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grimova, L.; Winkowska, L.; Konrady, M.; Rysanek, P. Apple mosaic virus. Phytopathol. Mediterr. 2016, 55, 1–19. [Google Scholar]
- Dursunoglu, S.; Ertunc, F. Distribution of Apple Mosaic Ilarvirus (ApMV) in Turkey. Acta Hortic. 2008, 781, 131–134. [Google Scholar]
- Chen, T.; Zeng, R.; Guo, W.; Hou, X.; Lan, Y.; Zhang, L. Detection of Stress in Cotton (Gossypium hirsutum L.) Caused by Aphids Using Leaf Level Hyperspectral Measurements. Sensors 2018, 18, 2798. [Google Scholar] [CrossRef] [PubMed]
- Un Nabi, S.; Yadav, M.; Yousuf, N.; Raja, W.; Sidharthan, K.; Dubey, S.; Kumar, M.; Jaiswal, D. Apple Mosaic Disease: Potential Threat to Apple Productivity. EC Agric. 2019, 5, 614–618. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Moustakas, M.; Calatayud, Á.; Guidi, L. Chlorophyll fluorescence imaging analysis in biotic and abiotic stress. Front. Plant Sci. 2021, 12, 658500. [Google Scholar] [CrossRef]
- Jiang, X.; Zhen, J.; Miao, J.; Zhao, D.; Shen, Z.; Jiang, J.; Gao, C.; Wu, G.; Wang, J. Newly-developed three-band hyperspectral vegetation index for estimating leaf relative chlorophyll content of mangrove under different severities of pest and disease. Ecol. Indic. 2022, 140, 108978. [Google Scholar] [CrossRef]
- Peng, Y.; Nguy-Robertson, A.; Arkebauer, T.; Gitelson, A.A. Assessment of Canopy Chlorophyll Content Retrieval in Maize and Soybean: Implications of Hysteresis on the Development of Generic Algorithms. Remote Sens. 2017, 9, 226. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Tian, M.L.; Ban, S.T.; Chang, Q.R.; Zhang, Z.R.; Xu-Mei, W.U.; Wang, Q. Quantified Estimation of Anthocyanin Content in Mosaic Virus Infected Apple Leaves Based on Hyperspectral Imaging. Spectrosc. Spectr. Anal. 2017, 37, 3187–3192. [Google Scholar]
- Ban, S.; Tian, M.; Chang, Q. Estimating the severity of apple mosaic disease with hyperspectral images. Int. J. Agric. Biol. Eng. 2019, 12, 148–153. [Google Scholar] [CrossRef]
- Medina-Puche, L.; Lozano-Duran, R. Tailoring the cell: A glimpse of how plant viruses manipulate their hosts. Curr. Opin. Plant Biol. 2019, 52, 164–173. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, S.; Wu, H.; Han, W.; Li, C.; Chen, H. Joint optimization of autoencoder and Self-Supervised Classifier: Anomaly detection of strawberries using hyperspectral imaging. Comput. Electron. Agric. 2022, 198, 107007. [Google Scholar] [CrossRef]
- Lowe, A.; Harrison, N.; French, A.P. Hyperspectral image analysis techniques for the detection and classification of the early onset of plant disease and stress. Plant Methods 2017, 13, 80. [Google Scholar] [CrossRef]
- Cui, B.; Ye, H.; Liu, L.; Wu, M.; Huang, W.; Dong, Y.; Shi, Y. Progress and prospects of crop diseases and pests monitoring by remote sensing. Smart Agric. 2019, 1, 1. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, G.; Zhao, C.; Zhang, J.; Yang, X.; Pan, Y.; Huang, W.; Xu, B.; Li, M.; Zhu, X. Progress and prospects of hyperspectral remote sensing technology for crop diseases and pests. Natl. Remote Sens. Bull. 2021, 25, 403–422. [Google Scholar]
- Liu, F.; Xiao, Z. Disease spots identification of potato leaves in hyperspectral based on locally adaptive 1D-CNN. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 27–29 June 2020; pp. 355–358. [Google Scholar]
- Wei, X.; Johnson, M.A.; Langston, D.B.; Mehl, H.L.; Li, S. Identifying Optimal Wavelengths as Disease Signatures Using Hyperspectral Sensor and Machine Learning. Remote Sens. 2021, 13, 2833. [Google Scholar] [CrossRef]
- Abdulridha, J.; Batuman, O.; Ampatzidis, Y. UAV-Based Remote Sensing Technique to Detect Citrus Canker Disease Utilizing Hyperspectral Imaging and Machine Learning. Remote Sens. 2019, 11, 1373. [Google Scholar] [CrossRef]
- Khan, I.H.; Liu, H.; Li, W.; Cao, A.; Wang, X.; Liu, H.; Cheng, T.; Tian, Y.; Zhu, Y.; Cao, W.; et al. Early Detection of Powdery Mildew Disease and Accurate Quantification of Its Severity Using Hyperspectral Images in Wheat. Remote Sens. 2021, 13, 3612. [Google Scholar]
- Guo, A.; Huang, W.; Dong, Y.; Ye, H.; Ma, H.; Liu, B.; Wu, W.; Ren, Y.; Ruan, C.; Geng, Y. Wheat Yellow Rust Detection Using UAV-Based Hyperspectral Technology. Remote Sens. 2021, 13, 123. [Google Scholar] [CrossRef]
- Gao, Z.; Khot, L.R.; Naidu, R.A.; Zhang, Q. Early detection of grapevine leafroll disease in a red-berried wine grape cultivar using hyperspectral imaging. Comput. Electron. Agric. 2020, 179, 105807. [Google Scholar] [CrossRef]
- Bock, C.; Poole, G.; Parker, P.; Gottwald, T. Plant disease severity estimated visually, by digital photography and image analysis, and by hyperspectral imaging. Crit. Rev. Plant Sci. 2010, 29, 59–107. [Google Scholar]
- Singhal, G.; Bansod, B.; Mathew, L.; Goswami, J.; Choudhury, B.; Raju, P. Chlorophyll estimation using multi-spectral unmanned aerial system based on machine learning techniques. Remote Sens. Appl. Soc. Environ. 2019, 15, 100235. [Google Scholar]
- Sudu, B.; Rong, G.; Guga, S.; Li, K.; Zhi, F.; Guo, Y.; Zhang, J.; Bao, Y. Retrieving SPAD Values of Summer Maize Using UAV Hyperspectral Data Based on Multiple Machine Learning Algorithm. Remote Sens. 2022, 14, 5407. [Google Scholar] [CrossRef]
- Gutierrez, S.; Diago, M.; Fernandez-Novales, J.; Tardaguila, J. Hyperspectral imaging application under field conditions: Assessment of the spatio-temporal variability of grape composition within a vineyard. In Precision Agriculture’19; Wageningen Academic Publishers: Wageningen, The Netherlands, 2019; pp. 811–817. [Google Scholar]
- Luo, L.; Chang, Q.; Gao, Y.; Jiang, D.; Li, F. Combining Different Transformations of Ground Hyperspectral Data with Unmanned Aerial Vehicle (UAV) Images for Anthocyanin Estimation in Tree Peony Leaves. Remote Sens. 2022, 14, 2271. [Google Scholar]
- Liu, N.; Wu, L.; Chen, L.; Sun, H.; Dong, Q.; Wu, J. Spectral characteristics analysis and water content detection of potato plants leaves. IFAC-PapersOnLine 2018, 51, 541–546. [Google Scholar] [CrossRef]
- Zou, Z.; Wu, Q.; Chen, J.; Long, T.; Wang, J.; Zhou, M.; Zhao, Y.; Yu, T.; Wang, Y.; Xu, L. Rapid determination of water content in potato tubers based on hyperspectral images and machine learning algorithms. Food Sci. Technol. 2022, 42, e46522. [Google Scholar] [CrossRef]
- Zhao, Y.-R.; Li, X.; Yu, K.-Q.; Cheng, F.; He, Y. Hyperspectral Imaging for Determining Pigment Contents in Cucumber Leaves in Response to Angular Leaf Spot Disease. Sci. Rep. 2016, 6, 27790. [Google Scholar] [CrossRef]
- Luo, L.; Chang, Q.; Wang, Q.; Huang, Y. Identification and Severity Monitoring of Maize Dwarf Mosaic Virus Infection Based on Hyperspectral Measurements. Remote Sens. 2021, 13, 4560. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Peng, F.; Liu, J.; Han, G. Estimating the distribution of chlorophyll content in CYVCV infected lemon leaf using hyperspectral imaging. Comput. Electron. Agric. 2022, 198, 107036. [Google Scholar] [CrossRef]
- Fang, X.; Zhu, X.; Wang, Z.; Zhao, G.; Jiang, Y.; Wang, Y.a. Hyperspectral characteristics of apple leaves based on different disease stress. Remote Sens. Sci. 2014, 2, 14–21. [Google Scholar]
- Cerovic, Z.G.; Masdoumier, G.; Ghozlen, N.B.; Latouche, G. A new optical leaf-clip meter for simultaneous non-destructive assessment of leaf chlorophyll and epidermal flavonoids. Physiol. Plant. 2012, 146, 251–260. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Galvao, R.K.H.; Araujo, M.C.U.; José, G.E.; Pontes, M.J.C.; Silva, E.C.; Saldanha, T.C.B. A method for calibration and validation subset partitioning. Talanta 2005, 67, 736–740. [Google Scholar] [CrossRef]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef]
- Yu, L.; Hong, Y.; Zhou, Y.; Zhu, Q.; Xu, L.; Li, J.; Nie, Y. Wavelength variable selection methods for estimation of soil organic matter content using hyperspectral technique. Trans. Chin. Soc. Agric. Eng. 2016, 32, 95–102. [Google Scholar]
- Li, H.-D.; Xu, Q.-S.; Liang, Y.-Z. libPLS: An integrated library for partial least squares regression and linear discriminant analysis. Chemom. Intell. Lab. Syst. 2018, 176, 34–43. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kanda, E.; Kitada, K.; Ishiguro, K.; Torigoe, Y. Detection of rice panicle blast with multispectral radiometer and the potential of using airborne multispectral scanners. Phytopathology 2001, 91, 316–323. [Google Scholar] [CrossRef]
- Zhang, J.; Jing, X.; Song, X.; Zhang, T.; Duan, W.; Su, J. Hyperspectral estimation of wheat stripe rust using fractional order differential equations and Gaussian process methods. Comput. Electron. Agric. 2023, 206, 107671. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: Abingdon-on-Thames, UK, 2017. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Applications to nonorthogonal problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Nickisch, H. Gaussian processes for machine learning (GPML) toolbox. J. Mach. Learn. Res. 2010, 11, 3011–3015. [Google Scholar]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 2007; Volume 1. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Soui, M.; Mansouri, N.; Alhamad, R.; Kessentini, M.; Ghedira, K. NSGA-II as feature selection technique and AdaBoost classifier for COVID-19 prediction using patient’s symptoms. Nonlinear Dyn. 2021, 106, 1453–1475. [Google Scholar] [CrossRef]
- Quan, D.; Feng, W.; Dauphin, G.; Wang, X.; Huang, W.; Xing, M. A Novel Double Ensemble Algorithm for the Classification of Multi-Class Imbalanced Hyperspectral Data. Remote Sens. 2022, 14, 3765. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Ross Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In Proceedings of the International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; pp. 1–15. [Google Scholar]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Ge, Y.; Bai, G.; Stoerger, V.; Schnable, J.C. Temporal dynamics of maize plant growth, water use, and leaf water content using automated high throughput RGB and hyperspectral imaging. Comput. Electron. Agric. 2016, 127, 625–632. [Google Scholar] [CrossRef]
- He, R.; Li, H.; Qiao, X.; Jiang, J. Using wavelet analysis of hyperspectral remote-sensing data to estimate canopy chlorophyll content of winter wheat under stripe rust stress. Int. J. Remote Sens. 2018, 39, 4059–4076. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, D.; Chang, Q.; Zheng, Z.; Fu, X.; Li, K.; Mo, H. Estimation of Anthocyanins in Leaves of Trees with Apple Mosaic Disease Based on Hyperspectral Data. Remote Sens. 2023, 15, 1732. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Wang, G.; Sun, Y.; Wang, J. Automatic image-based plant disease severity estimation using deep learning. Comput. Intell. Neurosci. 2017, 2017, 2917536. [Google Scholar] [CrossRef]
- Alachew, E.; Muhammad, H.; Azamal, H.; Samuel, S.; Kasim, M. Differential sensitivity of Pisum sativum L. cultivars to water-deficit stress: Changes in growth, water status, chlorophyll fluorescence and gas exchange attributes. J. Agron. 2016, 15, 45–57. [Google Scholar]
- Fu, W.; Li, P.; Wu, Y. Effects of different light intensities on chlorophyll fluorescence characteristics and yield in lettuce. Sci. Hortic. 2012, 135, 45–51. [Google Scholar] [CrossRef]
- Bhusal, N.; Sharma, P.; Sareen, S.; Sarial, A. Mapping QTLs for chlorophyll content and chlorophyll fluorescence in wheat under heat stress. Biol. Plant. 2018, 62, 721–731. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Ju, W.; Chen, B.; Chen, J.; Croft, H.; Mickler, R.A.; Yang, F. Estimation of leaf photosynthetic capacity from leaf chlorophyll content and leaf age in a subtropical evergreen coniferous plantation. J. Geophys. Res. Biogeosci. 2020, 125, e2019JG005020. [Google Scholar] [CrossRef]



| Disease Severity | Percentage of Disease Spot Area | Number of Measurements | Measurement Area |
|---|---|---|---|
| health | 0% | 2 | Two random uninfected areas |
| slight | 0~25% | 3 | Two random uninfected areas and one infected area |
| moderate | 25~50% | 3 | One random uninfected area and two infected areas |
| severe | >50% | 2 | Two random infected areas |
| Sample | Number of Samples | Minimum (μg/cm2) | Maximum (μg/cm2) | Mean (μg/cm2) | Standard Deviation |
|---|---|---|---|---|---|
| Calibration set | 270 | 4.14 | 55.60 | 28.93 | 13.27 |
| Validation set | 90 | 6.30 | 53.62 | 35.42 | 13.21 |
| Total | 360 | 4.14 | 55.60 | 30.55 | 13.53 |
| Models | Hyperparameters and the Search Range |
|---|---|
| CART | max_depth: (2~20) |
| EN | alpha: (0.01~10), L1_ratio: (0~1) |
| GPR | alpha: (1 × 10−10), n_restarts_optimizer: (1~50) |
| KNN | weight: distance, n_neighbors: (1~10), p: (1~10) |
| KRR | kernel: laplacian, alpha: (0.01~1) |
| MLP | solver: lbfgs, hidden_layer_sizes: (0~100,0~100), learning_rate: (0.01~1) |
| SVR | kernel: rbf, C: (1~10), gamma: (0.5~5) |
| AdaBoost | base_estimator: (CART, EN, GPR, KRR, MLP, SVR), n_estimators: (1~100), learning_rate: (0.01~1) |
| CatBoost | task_type: GPU, iterations: (10~500), depth: (2~10), learning_rate: (0.01~1), L2_leaf_reg: (1~50) |
| Model | |||||
|---|---|---|---|---|---|
| CART | 3.8288 | 0.9164 | 4.6980 | 0.8722 | 2.6818 |
| EN | 3.0413 | 0.9473 | 3.4346 | 0.9317 | 3.3022 |
| GPR | 2.1294 | 0.9741 | 3.8393 | 0.9146 | 3.3059 |
| KNN | 0.0000 | 1.0000 | 3.3096 | 0.9367 | 3.9322 |
| KRR | 2.1399 | 0.9739 | 3.0436 | 0.9463 | 4.0729 |
| MLP | 3.0368 | 0.9474 | 3.2271 | 0.9397 | 4.1084 |
| SVR | 2.7234 | 0.9577 | 3.4373 | 0.9316 | 3.4026 |
| CART-Boosting | 2.4479 | 0.9658 | 2.7598 | 0.9559 | 4.7031 |
| EN-Boosting | 3.0095 | 0.9484 | 3.3658 | 0.9344 | 3.3512 |
| GPR-Boosting | 1.4083 | 0.9887 | 3.1167 | 0.9437 | 4.1014 |
| KNN-Boosting | 0.0493 | 1.0000 | 3.0414 | 0.9404 | 4.3078 |
| KRR-Boosting | 2.0279 | 0.9765 | 2.9451 | 0.9498 | 4.2451 |
| MLP-Boosting | 2.5351 | 0.9634 | 2.7623 | 0.9558 | 4.7044 |
| SVR-Boosting | 2.6465 | 0.9601 | 3.3853 | 0.9336 | 3.4364 |
| Stacked-Boosting | 1.3608 | 0.9894 | 2.4796 | 0.9644 | 5.1054 |
| Feature | ||||
|---|---|---|---|---|
| 500.02 nm | 97.04 | 0.9604 | 74.44 | 0.6573 |
| 550.95 nm | 93.70 | 0.9161 | 86.67 | 0.8188 |
| 602.36 nm | 96.67 | 0.9556 | 85.56 | 0.8045 |
| 649.05 nm | 97.04 | 0.9604 | 78.89 | 0.7150 |
| 680.39 nm | 93.70 | 0.9159 | 66.67 | 0.5550 |
| 722.44 nm | 90.37 | 0.8713 | 57.78 | 0.4441 |
| Average LCC | 91.85 | 0.8913 | 91.11 | 0.8811 |
| CV of LCC | 93.33 | 0.9111 | 81.11 | 0.7468 |
| all sensitive wavelengths | 97.41 | 0.9654 | 92.22 | 0.8960 |
| all LCC statistics | 97.78 | 0.9704 | 95.56 | 0.9406 |
| sensitive wavelengths + LCC statistics | 99.26 | 0.9901 | 98.89 | 0.9852 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, Y.; Jiang, D.; Zhang, Z.; Chang, Q. Quantitative Assessment of Apple Mosaic Disease Severity Based on Hyperspectral Images and Chlorophyll Content. Remote Sens. 2023, 15, 2202. https://doi.org/10.3390/rs15082202
Liu Y, Zhang Y, Jiang D, Zhang Z, Chang Q. Quantitative Assessment of Apple Mosaic Disease Severity Based on Hyperspectral Images and Chlorophyll Content. Remote Sensing. 2023; 15(8):2202. https://doi.org/10.3390/rs15082202
Chicago/Turabian StyleLiu, Yanfu, Yu Zhang, Danyao Jiang, Zijuan Zhang, and Qingrui Chang. 2023. "Quantitative Assessment of Apple Mosaic Disease Severity Based on Hyperspectral Images and Chlorophyll Content" Remote Sensing 15, no. 8: 2202. https://doi.org/10.3390/rs15082202
APA StyleLiu, Y., Zhang, Y., Jiang, D., Zhang, Z., & Chang, Q. (2023). Quantitative Assessment of Apple Mosaic Disease Severity Based on Hyperspectral Images and Chlorophyll Content. Remote Sensing, 15(8), 2202. https://doi.org/10.3390/rs15082202








