Next Article in Journal
Mapping Agricultural Land in Afghanistan’s Opium Provinces Using a Generalised Deep Learning Model and Medium Resolution Satellite Imagery
Previous Article in Journal
Estimating Agricultural Cropping Intensity Using a New Temporal Mixture Analysis Method from Time Series MODIS
Previous Article in Special Issue
Quantitative Assessment of Apple Mosaic Disease Severity Based on Hyperspectral Images and Chlorophyll Content
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 19
10.3390/rs15194713
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimation and Mapping of Soil Organic Matter Content Using a Stacking Ensemble Learning Model Based on Hyperspectral Images

by
Menghong Wu
1,2,
Sen Dou
1,*,
Nan Lin
2,
Ranzhe Jiang
2 and
Bingxue Zhu
3
1
College of Resource and Environmental Science, Jilin Agricultural University, Changchun 130118, China
2
College of Surveying and Exploration Engineering, Jilin Jianzhu University, Changchun 130118, China
3
State Key Laboratory of Black Soils Conservation and Utilization, Northeast Institute of Geography and Agroecology, Chinese Academy of Sciences, Changchun 130012, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(19), 4713; https://doi.org/10.3390/rs15194713
Submission received: 17 July 2023 / Revised: 29 August 2023 / Accepted: 19 September 2023 / Published: 26 September 2023
(This article belongs to the Special Issue Application of Hyperspectral Imagery in Precision Agriculture)
Browse Figures
Versions Notes

Abstract

:
Fast and accurate SOM estimation and spatial mapping are significant for cultivated land planning and management, crop growth monitoring, and soil carbon pool estimation. It is a key problem to construct a fast and efficient estimation model based on hyperspectral remote sensing image data to realize the inversion mapping of SOM in large areas. In order to solve the problem that the estimation accuracy is not high due to the influence of hyperspectral image quality and soil sample quantity during the estimation model construction, this study explored a method for constructing an estimation model of SOM contents based on a new stacking ensemble learning algorithm and hyperspectral images. Surface soil samples in Huangzhong County of Qinghai Province were collected, and their ZY1-02D hyperspectral remote sensing images were investigated. As input data, a feature band dataset was constructed using the Pearson correlation coefficient and successive projections algorithm. Based on the dataset, a new SOM estimation model under the stacking ensemble learning framework combined with heterogeneous models was developed by optimizing the combination of base and meta-learners. Finally, the spatial distribution map of SOM was plotted based on the result of the model over the study area. The result suggested that the input data quality of the estimation model is improved by constructing a feature band dataset. The multi-class ensemble learning estimation model with the combination strategy of the base and meta-learners has better predictive effects and stability than the single-algorithm and single-level ensemble models with homogeneous learners. The coefficient of determination is 0.829, the residual prediction deviation is 2.85, and the predictive set root mean square error is 1.953. The results can provide new ideas for estimating SOM content using hyperspectral images and ensemble learning algorithms, and serve as a reference for mapping large-scale SOM spatial distribution using space-borne hyperspectral images.

1. Introduction

Soil is recognized as a primary component in the human living environment and a basic structural unit of the biosphere [1]. It converts solar energy into biochemical energy and provides fundamental natural resources for plants, animals, and humans from a production perspective [2]. Soil organic matter (SOM) is the collective term for various carbon-containing organic compounds in soil. It is an important indicator of soil fertility and farmland quality [3,4,5]. The accumulation and decomposition of SOM provide nutritional support for crop growth [6]. Rapid and accurate estimation and spatial mapping of regional SOM content are crucial for cultivated land quality evaluation, crop growth monitoring, soil carbon pool estimation, and smart agriculture application.
Hyperspectral data usually contain spectral information in multiple bands [7]. Minor changes in the physical and chemical properties of the soil can be effectively identified through closely aligned and continuous hyperspectral bands [8]. Numerous studies have shown that the absorption characteristics of soil hyperspectral data in the visible (350–700 nm) [9], near-infrared (700–1100 nm) [10], and short-wave infrared radiation (SWIR, 1100–2500 nm) [11] ranges are closely related to the content of soil components [12]. In this sense, SOM content can be quantitatively estimated using hyperspectral remote sensing technology by analyzing its reflective spectral characteristics [13]. Due to the short detection range and minor interference from the external environments, a model with ground-based soil hyperspectral data has high accuracy in estimating the SOM content [14]. Despite the advantage, this method cannot realize rapid estimation over large spatial scales periodically [15].
Space-borne hyperspectral imaging enables quick acquisition of soil spectral information over large areas, owing to its extensive coverage, high temporal resolution, and easy access to image data [16]. Existing studies have shown that the estimation model of SOM based on space-borne hyperspectral images has some problems, such as low computational efficiency, unstable accuracy, and weak reliability [14,15,16]. The reasons may include two aspects. On the one hand, the estimation model based on image pixel spectra and soil sample content is a data-driven framework with high requirements on the quality and quantity of the input data. Conversely, the input pixel reflectance values of space-borne hyperspectral images are easily affected by external factors in the acquisition, such as electromagnetic interference, cross-mixing issues among band channels, natural illumination, and topographic conditions [17,18,19], leading to biased pixel reflectance values and weakened response relationships between spectral reflectance and the SOM content. Additionally, the large number of spectral channels in hyperspectral images induces high collinearity and information redundancy among spectral data, reducing the quality of input data to a certain extent.
On the other hand, progress has been made in establishing regression models for SOM estimation based on hyperspectral remote sensing data using traditional machine learning algorithms [20,21,22], such as extreme learning machine (ELM) [23], backpropagation neural network (BPNN) [24], support vector machine (SVM) [25], and multilayer perceptron (MLP) [23], exhibiting strong nonlinearity and excellent data mining ability. Chang et al. demonstrated that the integrated model of discrete particle swarm optimization and BPNN had a more stable and accurate predictive ability than the multiple linear regression one, providing support for applying hyperspectral remote sensing data to SOM estimation [26]. To improve efficiency and reduce cost, it is common practice to have a limited number of known soil samples for training learning models, and yet the insufficient sample size often leads to challenges in accurately acquiring the desired hypothesis [27]. In addition, most the actual target assumptions often reside outside the hypothesis space in applications of machine learning models, which complicates the model learning structure, increasing the computational complexity, and the performance in improving the accuracy and efficiency of the estimation model is moderate [28]. Numerous studies have shown that machine learning models usually suffer from high computational complexity and model overfitting problems [29,30].
Ensemble learning has been a research hotspot in machine learning [31]. It integrates multiple learning results with a specific combination strategy using a series of learners to achieve better learning effects than individual learners. Relatively mature ensemble learning frameworks include bagging, boosting, and stacking [32]. Compared with the former two, the stacking ensemble learning framework with a multilayer classification structure supports parallel stacking of heterogeneous learners. By constructing and combining base learners of the same or different kinds for learning, the target assumption absent in the hypothesis space may be represented by the integration of assumptions of these leaners, enabling the final predictive result to be closer to the actual objective function value. The integrated idea of stacking supports data mining from different spatial and structural perspectives to obtain optimization results with improved promotion effects and generalization ability. In response to the small sample sizes, the stacking ensemble learning model can effectively address the high computational complexity and overfitting phenomena of previous machine learning models, with a higher predictive accuracy than a single model [33]. Ruhollah et al. found that the estimation accuracy of the stacking ensemble learning model in SOC estimation was superior to that of any single machine learning model, such as random forest (RF), ELM, and artificial neural network [34]. Tan et al. constructed a soil content inversion model based on the stacking framework using 95 soil samples. This model avoided overfitting problems caused by uneven samples and small sample sizes, with superior accuracy to other machine learning models [35]. However, there are few studies on constructing a high-precision stacking ensemble learning model based on hyperspectral images for the estimation of SOM content, especially around the input data quality and framework combination. Enhancing the quality of the input data by various spectral pre-processing methods is expected to improve the accuracy of data-driven estimation models. The main advantage of the stacking ensemble learning framework is the diverse and flexible combinations in the selection and design of base and meta-learners. By combining different models and feature indicators, computational complexity and deep feature mining ability can be complemented, effectively improving the adaptability of the model prediction. In summary, the optimization of input data and combination of learning tools under the ensemble learning framework with improved performance for estimating SOM content need further exploration.
This study aims to explore a novel method for estimating the SOM content of farmland through space-borne hyperspectral images. A stacking ensemble learning strategy was constructed to improve the estimation accuracy of the model with limited samples. The ZY1-02D hyperspectral images in the study area were pre-processed, and the spectral characteristics and SOM feature bands of 67 soil samples were analyzed. The Pearson correlation coefficient and successive projections algorithm (SPA) were selected to extract the feature band dataset as the input variables for modeling. The combination of base and meta-learners was optimized using evaluation indicators such as the correlation coefficient and predictive differential degree. Then, a multi-class heterogeneous stacking ensemble learning framework was established for a high-precision and robust SOM content estimation model. The main contributions of this study are as follows: (1) The spectral feature band dataset was constructed by combining spectral pre-processing with SPA feature selection methods to improve the quality of training samples of the model effectively. (2) An optimal combination strategy of base and meta-learners was proposed based on the construction principle of the ensemble learning framework to solve the limited number of known training samples from the characteristics and construction principles of different learners, significantly enhancing the estimation capability and reliability of the model. This study provides a reference for a rapid estimation of soil component content, further broadens the application performance of space-borne hyperspectral remote sensing images, and serves as a basis and technical support for modern agriculture applications.

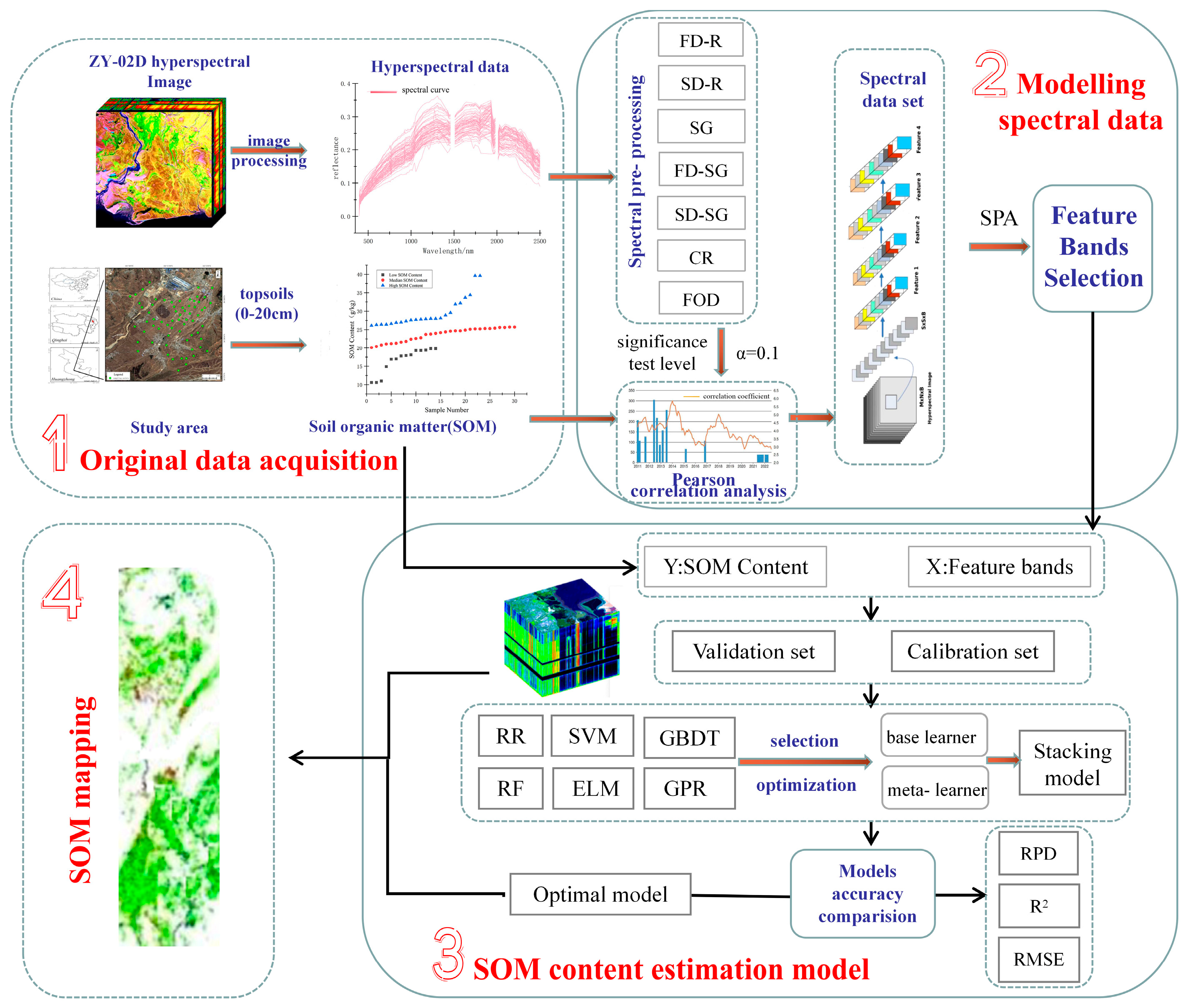
2. Materials and Methods

ZY1-02D hyperspectral images and soil samples are prepared to estimate SOM content in the study area. The hyperspectral image is pre-processed, and spectral curves are extracted from the image position by ground point coordinates. After the spectral feature pre-processing step, Pearson correlation analysis and SPA are conducted between the spectral curve and SOM content to acquire the feature band dataset, and the modeling spectral data are extracted. Then, the SOM content is estimated based on a new stacking ensemble learning model. The stability and accuracy of the model are evaluated by precision evaluation indexes. Finally, the spatial distribution map of SOM in the study area is plotted.
The workflow of this study is presented below (Figure 1).

2.1. Study Area

The study area is in Huangzhong County, Xining City, Qinghai Province, China, in the middle reaches of the Huangshui River Basin. The geographical coordinates range from 101°09′32″ to 101°54′50″ east longitude and 36°13′32″ to 37°03′19″ north latitude (Figure 2). Huangzhong County is one of the major agricultural regions in Qinghai Province, serving as an important base for grains, oils, vegetables, meat, and eggs. The main vegetation is warm-temperate grassland. It is a typical farming-pastoral ecotone with a fragile ecological environment. The major soil types comprise chestnut and sierozem. The predominant crops cultivated in the area include wheat, potato, corn, and rapeseed, with specialty crops (e.g., Chinese medicinal herbs) accounting for more than 75% of the total crop production. The study area has been underdeveloped for a long time. Given the limitation of geographical conditions, agriculture is the pillar industry. In this sense, quickly grasping and mapping the soil nutrient situation play a guiding role in improving crop quality and yield, and are of practical significance for the social and economic development in this area.

2.2. Data Processing

2.2.1. Soil Sample Selection and Chemical Analysis

In May 2021, a typical farmland plot was selected in the experimental area and sampled using a five-point mixed method. The sampling distance from the road was at least 150 m. Five surface soil samples with a 0–15 cm depth were collected in a 5 × 5 m area around the sampling points and fully mixed in a sealed bag. A total of 67 soil samples were obtained. The geographical coordinates of samples were recorded using a handheld GPS. Soil samples were brought back to the laboratory in sealed bags. After removing debris such as roots and gravel, these samples were air-dried, ground, and sieved to a particle smaller than 0.25 mm. Each soil sample was divided into two parts for the soil element content and ground hyperspectral measurement. The SOM content of the soil was determined using the potassium dichromate method following the technical specifications, such as the quality requirements for the analysis of multi-target samples and the “Soil Agricultural Chemical Analysis Method”. The SOM content of the 67 soil samples was statistically analyzed (Table 1). Each sample was measured in the range of 10.6–39.6 g/kg, with a mean value of 24.16 g/kg. The overall value was relatively low, and the variation coefficient was 22.94%, indicating moderate variability. All samples were divided into 17 groups according to the SOM content from high to low, and 1 sample was randomly selected from each group to form a validation set of 17 samples. The remaining 50 samples were used as the calibration set.

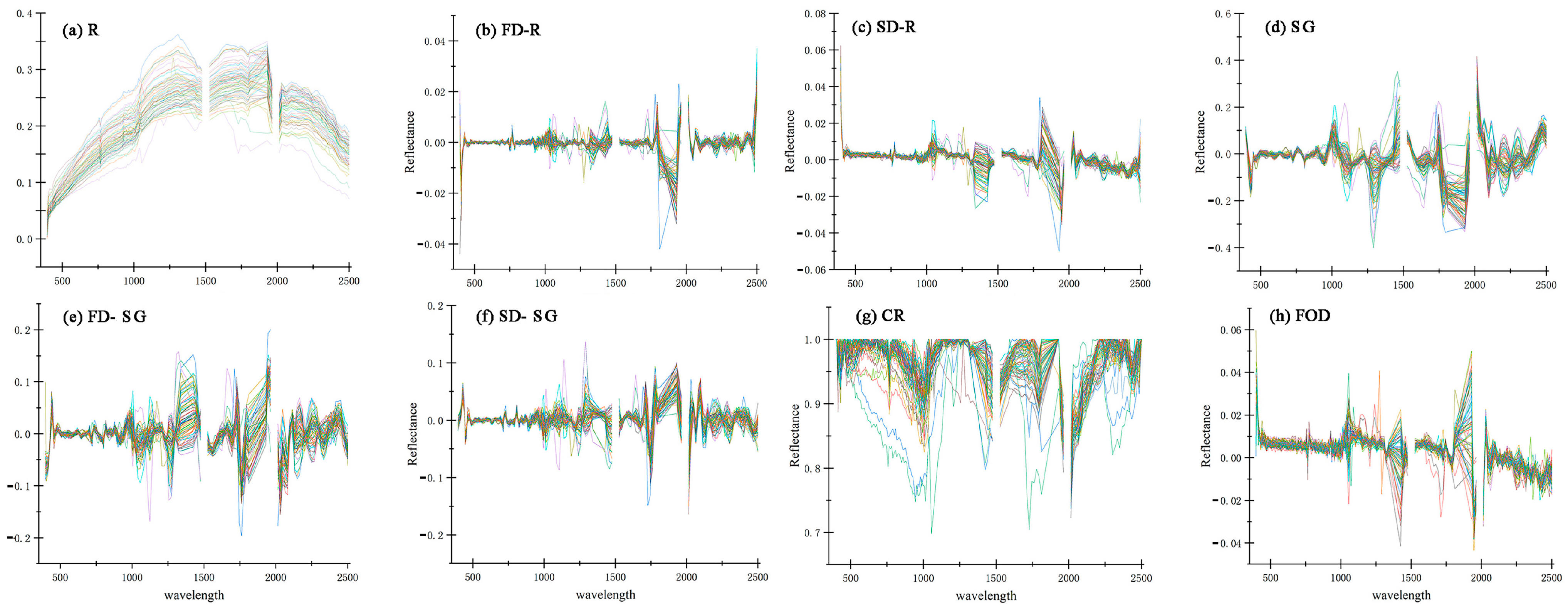
2.2.2. Image Data Pre-Processing

The ZY1-02D has visible near-infrared radiation (VNIR) and hyperspectral sensors with two payloads: an 8-band VNIR sensor and an advanced hyperspectral imager (AHSI) with 166 bands. The spectral coverage range is 400–2500 nm, and the AHSI has a width of 60 km and a spatial resolution of 30 m. The AHSI sensor includes 76 VNIR bands with a spectral resolution of 10 nm and 90 SWIR bands with a spectral resolution of 20 nm.
In this study, the ZY1-02D hyperspectral satellite images were acquired on 8 May 2021, with a cloud cover of less than 5% over the transit test area, and pre-processed. Due to the significant stripe phenomena in SWIR band data obtained by the ZY1-02D hyperspectral camera, stripe repair was performed by a “global stripe removal” method to exclude the severely affected and overlapping bands. The VNIR-SWIR parts, comprising 151 spectral bands, were merged and stored. The image was geometrically corrected, radiometrically calibrated, and atmospherically corrected using the ENVI5.3 software to obtain the true reflectance of ground objects. To verify the accuracy of the ZY1-02D hyperspectral imagery processing, the images were spatially overlaid with field-sampled soil. The spectral curves of the image pixels were compared with the ground hyperspectral data and analyzed according to the collection locations of the soil samples [27]. The Pearson correlation coefficients of different spectral bands were calculated (Figure 3). It was shown that although differences between the image pixel spectrum and the ground measurement spectrum were observed due to various factors such as sensor attitude, atmospheric transmission, soil surface roughness, and soil moisture content, the reflectance curve of soil image pixels after the spectral correction is similar to the spectral curve of the ground in morphological characteristics, and the absorption position of the feature is basically the same. The spectral shape is highly consistent. The correlation coefficients of the spectral bands (about 72%) between the image and the ground were mostly above 0.65, indicating that the accuracy of the ZY1-02D hyperspectral image correction meets the requirements of SOM content estimation [36].
Mathematical transformation methods, such as spatial and frequency domains for image denoising and spectral pre-processing effects, are regarded as an effective approach to eliminate pixel spectral noise, amplify the peak and valley variations in the spectral curves, and enhance the spectral characteristics of the soil [37,38,39]. The first-order differential (FD-R) transformation can improve the signal-to-noise ratio of the response spectral bands by eliminating baseline drift and improving spectral resolution [40]; the fractional-order differential (FOD) transformation is considered an efficient method for the peak and valley amplification of the spectra by capturing increasing subtle spectral information [41]; the Savitzky–Golay (SG) filter can remove spectral noise of hyperspectral remote sensing images in the spectral domain by smoothing spectral curves and dividing the original reflectance spectra and the envelope [42]; the continuum removal (CR) method is characterized by the highlights of the absorption and reflection features of the spectral curves, significantly diminishing the influence of terrain and illumination conditions on the spectral intensity and the absorption depth [43]. The spectral reflectance curves of hyperspectral images after pre-processing are shown in Figure 4.

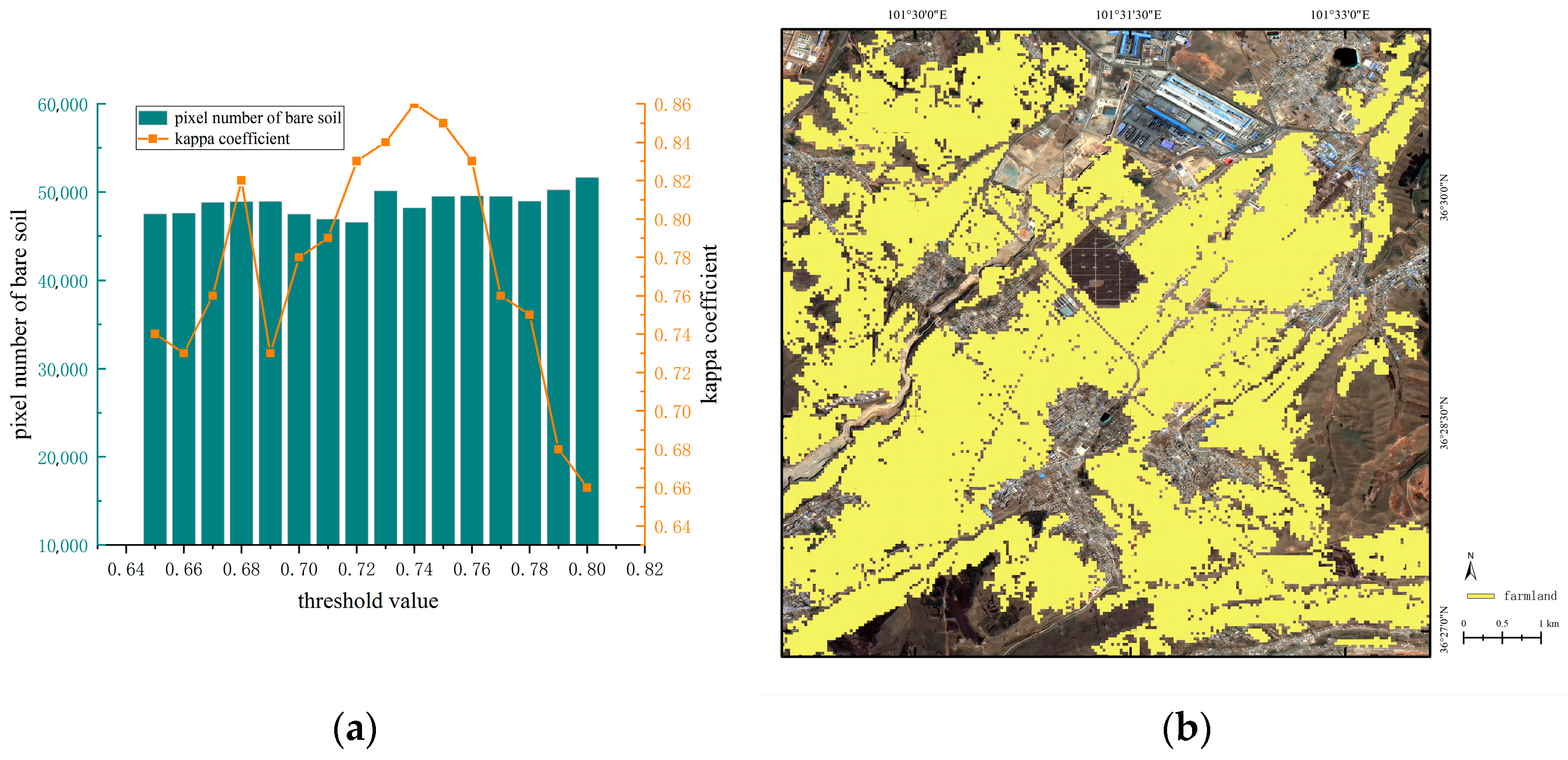
2.2.3. Boundary Extraction of Farmland

To improve the accuracy of estimating and mapping SOM content in the study area, it is necessary to extract the farmland boundary and remove non-soil information (e.g., roads and buildings) before using hyperspectral images for estimation. The soil index is an efficient method for extracting farmland (bare soil period) pixels from images [44,45,46]. In this experiment, the normalized difference soil index (NDSI) and Landsat OLI multispectral remote sensing images instead of ZY1-02D hyperspectral images were selected to extract farmland pixels, as the ZY1-02D image lacks the mid-infrared band. The Landsat OLI image has a similar period as the ZY1-02D image. The NDSI mainly uses the characteristics of the highest reflectance of bare soil in the mid-infrared bands and combines the mid-infrared and near-infrared bands to construct a normalized index that enhances the bare soil information. The formula is as follows:
N D S I = M I R − N I R M I R + N I R
where MIR and NIR denote the reflectance values of mid- and near-infrared spectra, respectively.
Figure 5a shows the optimal threshold selection process for extracting bare soil pixels when using the NDSI method. The statistical results by visual interpretation and manual debugging of various threshold values indicated that when the value was 0.74, the kappa coefficient was the highest, proving that the accuracy of bare soil patches extracted in the study area is the highest. At this time, the extraction accuracy of farmland (bare soil period) pixels can meet the needs of subsequent research. Figure 5b shows the extraction results of the farmland boundary. The boundaries between the extracted samples and non-farmland pixels, such as rivers, roads, and construction land, were clear, and the patch was relatively complete.

2.3. Methods

2.3.1. Feature Selection

The sensitive bands and the band characteristics of the hyperspectral image and SOM content vary in different spectral ranges. The Pearson correlation coefficient threshold method was adopted to obtain sensitive bands after various pre-processing methods. Combining the sensitive bands and constructing the spectral feature band dataset can enrich the characteristic information of image band spectra and comprehensively reflect the correlation and singularity rule between soil spectra and SOM contents.
This spectral feature band dataset has a certain degree of information redundancy, and applying it to the construction of a soil content estimation model requires a large amount of computation, which affects the training speed. Therefore, reducing the dimensionality of the image spectral feature set is necessary to achieve coordination among accuracy, computational efficiency, and applicability.
The successive projections algorithm (SPA) was proposed by Bregmant in 1965 [47]. It is a forward–backward vector selection algorithm that selects the maximum vector through vector projection analysis and ultimately extracts several characteristic wavelengths through model calibration. The advantage of SPA is that it can select the variable combinations with the minimum collinearity from the spectral matrix. Thus, the redundancy of the model can be reduced, and its stability and accuracy are improved. The specific steps are as follows:
(1) Randomly select the K-th column in the spectral matrix, assign it to x k , and record it as x p ( 0 ) .
(2) The remaining columns form the set M:
M = { k , 1 ≤ k ≤ K ,         k ∉ { p ( 0 ) , ⋯ , p ( n − 1 ) } }
(3) Calculate the projection of x k onto each of the remaining column vectors:
P x k = x k − ( x k T x p ( n − 1 ) ) x p ( m − 1 ) ( x p ( m − 1 ) T x p ( m − 1 ) ) − 1 , p ∈ m
(4) Extract the wavelength of the maximum projection vector:
k ( m ) = arg ( max ( ∥ P ( x k ) ∥ ) , k ∈ m
x k = P x , k ∈ m
(5) m = m + 1 , if m   <   M , calculate iteratively according to Formula (2).
where x p ( 0 ) is the initial iteration vector, M is the number of variables to be extracted, and K is the number of columns in the spectral matrix.
At last, the variable set { x p ( n ) = 0 , ⋯ , M − 1 } was constructed, a multiple linear regression model for p ( 0 ) and M in each iteration of the loop was established, a root mean square error (RMSE) value was obtained through cross-validation, and the p ( 0 ) and M that correspond to the smallest RMSE value were selected from the candidate subset. The final optimal values for p ( 0 ) and M were determined.

2.3.2. Estimation Model

In this paper, a SOM content estimation model was proposed based on the stacking framework. Stacking is a parallel ensemble learning strategy with multiple layers of learning structures. By selecting several individual machine learning algorithms and combining them with the optimization method, an ensemble learning model with better performance can be obtained [48]. Stacking allows the combination of outputs from multiple classifiers, and the model has two layers, one called base learners (first layer) and the other one called meta-learners (second layer). The base learner of the stacking ensemble learning model includes heterogeneous and homogeneous learners. The input variable of the base learner is the original feature variable, the input variable of the meta-learner is the learning result of the base learner, and the output of the meta-learner is the final prediction result of the model. The training set of the stacking model learner is not directly composed of the base learner training data to avoid repeated training of data. Instead, a cross-validation mechanism is used. Each base learner retains a portion of the data as the validation set during training, and the results of the K validation sets are combined to form a new output, thus effectively preventing overfitting.
According to the characteristics of sample data, a new SOM estimation model based on the stacking ensemble learning framework was constructed in this paper. The promotion effect of stacking algorithms depends mainly on the input data and the design of the base learner and the meta-learner. The image hyperspectral data were pre-processed, and feature band data were obtained using SPA. The selected results are the input data for modeling. A reasonable division of the data can prevent the overfitting caused by the repeated learning of the two-layer learner. According to the selected six base learners, the original training dataset was first divided into six sub-datasets, ensuring that each data subset does not overlap. One data subset was selected for each base learner as the prediction set during operation, and the rest of the data subsets were the training sets. Through the combination of multiple base learners, the stacking framework can achieve deeper learning effects on training data. The learning performance and structural differences between base learners are important issues to focus on when designing and constructing the stacking framework. Considering accuracy and difference, the gradient boosting decision tree (GBDT), RF, ELM, SVM, Gaussian process regression (GPR), and ridge regression (RR) were selected as alternative models for base learners in this study. The original input data were used for training and learning alternative models after k-fold cross-validation. The optimal base learner combination (four base learners) was selected to obtain the prediction result of the first layer through precision verification index analysis. A new dataset was constructed from the prediction results of the base learners and used as the training set of the meta-learner in the second layer. The RR was selected as a meta-learner for the stacking framework model, and L2 regular term was added to the loss function to buffer and prevent overfitting caused by the small sample size. Finally, the prediction results of the model were obtained by the meta-learner (Figure 6).
The models with strong learning abilities and large differences were selected as the base learners of the layer to ensure prediction accuracy. During data processing, data can be observed from different data dimensions and structural perspectives, and the advantages of each base learner can be complemented. GBDT combines decision trees with the boosting method, which belongs to the ensemble learning model [49]. It is a method of combining multiple weak learners to form a strong learner [50,51,52]. RF is a combined classification model that includes multiple unpruned classification regression trees proposed by Breiman in 2001 based on the bagging parallel ensemble learning idea [53,54,55]. ELM is a new model for learning and training single-hidden-layer feedforward neural networks [56]. ELM learning aims to construct a neural network model with L hidden-layer neurons and their activation function g ( x ) [57]. SVM adopts the structural risk minimization principle and obtains the optimal value by the quadratic optimization method, which belongs to the classical machine learning model and is currently widely used [58,59]. GPR belongs to the nonparametric model [60]. The basic idea is to assume that the multivariable characteristics conform to the joint Gaussian distribution, and the model uses the edge probability density to achieve the target condition [61]. RR is a biased-estimation linear regression algorithm used for analyzing multicollinearity data [62]. The algorithm principle is to add a penalty term k I ( k > 0 ) based on the correlation matrix X ′ X when there is multicollinearity among independent variables, which solves the overfitting of the model caused by the small sample size, and improves the estimation performance of the model.

2.3.3. Estimation Accuracy Indexes

In this study, RMSE, coefficient of determination (R2), and residual prediction deviation (RPD) were selected as indicators to evaluate the performance of the prediction model. RMSE represents the accuracy of the model prediction, and the smaller the value, the better the estimation effect of the model. R2 represents the fitting ability of the prediction model, with a range of 0–1. The closer the value is to 1, the higher the fitting effect of the model and the more stable the model is. The larger the RPD, the stronger the prediction ability of the model. RPD > 2.5 indicates that the model has excellent prediction ability; 2.0 < RPD < 2.5 indicates the model has a good prediction ability; 1.0 < RPD < 2.0 indicates that the model has prediction ability; RPD < 1 means that the model does not have prediction ability. Overall, the larger the R2 and RPD, the smaller the RMSE, and the better the prediction model.

3. Results

3.1. Spectral Pre-Processing and Acquisition of Modeling Data

Based on the location information of the soil sample collection points, the spectral information of 67 sample points corresponding to the pixels was extracted from the pre-processed hyperspectral images. The Pearson correlation coefficient between SOM content and reflectance was calculated. A significance test was conducted on the correlation coefficient results to quantitatively determine the degree of correlation between SOM content and soil reflectance. A two-tailed significance test level was set to alpha = 0.01, and the correlation coefficient threshold was determined with a sample size of ±0.31. The correlation coefficient statistical table (Table 2) shows that some correlation values after different feature transformations exceed the threshold range. Among them, the FOD transformation has the highest maximum value of the correlation coefficient and the most sensitive bands. The results demonstrate that the FOD transformation is an effective spectral pre-processing method, which is consistent with the study by Hong [63]. After FD-SG and SD-SG transformations, the highest correlation coefficient values are 0.715 and 0.682, respectively. After the SG transformation, the number of sensitive bands significantly increases, but the correlation coefficient values fluctuate slightly.
Spectral features can be obtained with different methods of spectral pre-processing on the original hyperspectral data. The sensitive band range and the form of band characteristics vary in different spectral intervals. A total of 110 sensitive bands obtained by spectral pre-processing methods were combined. Among them, 25 sensitive bands were obtained after FOD, 18 were obtained from SG, 17 were obtained from FD-SG, 16 were obtained from both FD-R and SD-SG, 10 were obtained from SD-R, and 8 were obtained from CR. The results are shown in Figure 7. It can be seen that the feature bands are mostly distributed in the short-wave infrared range, with 67 bands accounting for 61%, while the visible radiation bands are the least distributed, with only 20 bands accounting for 18%. Although the bands have been processed by different spectral pre-processing, the combined sensitive band dataset still has a certain degree of spectral information redundancy. The SPA algorithm was used for feature extraction calculation, and the RMSE was used as the evaluation index to maximize the retention of spectral feature information and reduce data redundancy. As shown in Figure 8, when the number of features N is 18, the corresponding RMSE reaches the minimum value, and these 18 feature bands were selected as input variables for estimating the SOM content. The distribution interval of the feature bands has similar characteristics to the published research results [42,64]. The SPA feature selection results showed that the spectral feature bands mostly selected were those treated with FOD transformation (8 bands), followed by those treated with CR and FD-R (both have 3 bands).

3.2. SOM Content Estimation Based on the Stacking Model

There are six machine learning models as the alternate base learner in this paper. Among them, GBDT and RF adopt boosting and bagging ensemble learning algorithms, respectively, demonstrating excellent learning ability and rigorous mathematical theories. ELM is a new model for learning and training single-hidden-layer feedforward neural networks. SVM is dedicated to solving the problems of data nonlinearity, high dimension, and small samples in model construction. GPR is a probability model with favorable versatility, analyzability, smoothness, and fitting ability of non-linear data, exhibiting excellent practical application performance. Compared with the base learning model in the first layer, which needs to complement the advantages and disadvantages of different algorithms from spatial perspectives, the second layer meta-learning model tends to select a simple model with strong generalization ability and fast operation speed, which is used to correct the biases of multiple learning algorithms to the calibration set and prevent overfitting. The RR was selected as a meta-learner for the stacking framework model. With simple parameters and fast training speed, it can prevent overfitting of the model and preserve the characteristics of the base learners to the maximum extent.
The accurate and effective determination of the hyperparameters in different machine learning models is significant for the application of the models to regression prediction (Table 3). In this paper, random search and grid search were combined to calculate the hyperparameter optimization of different models. First, the random search was applied to obtain the best point in a large range by coarse search with stride length. Afterward, the grid was divided into small steps near the best point to search and select the optimal global solution. The optimal hyperparameter combination of each model was measured by the RMSE of each model on the test set. The results are shown in Table 3. It can be seen that the prediction accuracy of the RF model is relatively high (R2 = 0.785), followed by the GBDT, ELM, SVM, GPR, and RR models.
It is important to analyze the individual prediction ability of each base learner and compare their combined performance to achieve the best prediction effect of the stacking model. Different from traditional ensemble learning, stacking can combine heterogeneous algorithm models. The greater differences among the base learner models indicate the stronger final generalization ability. To obtain the optimal combination of base learner models, the distribution of prediction errors for different base learning models was compared and analyzed, and the Pearson correlation coefficients of the errors for each model were calculated (Figure 9).
From the calculation result of the correlation coefficient, it can be seen that a strong correlation was found between two sets of models, i.e., the RF and GBDT models and the ELM and SVM models. Although the RF and GBDT models have slightly different construction principles, both belong to ensemble algorithms based on decision trees, and their data observation methods are similar. Despite the quite different principles of the ELM and SVM models, the similarity of the error distribution intervals between them is high, and the precision evaluation indicators are close. Introducing highly correlated base learners increases the risk of model overfitting. GPR and RR are a non-linear probability and a linear regression model, respectively, with significant differences in the learning and training mechanisms compared to other machine learning models and lower error correlation. Considering factors such as strong learning ability, low correlation, and large differences, RF, ELM, GPR, and RR were selected as the base learner combination for this study.

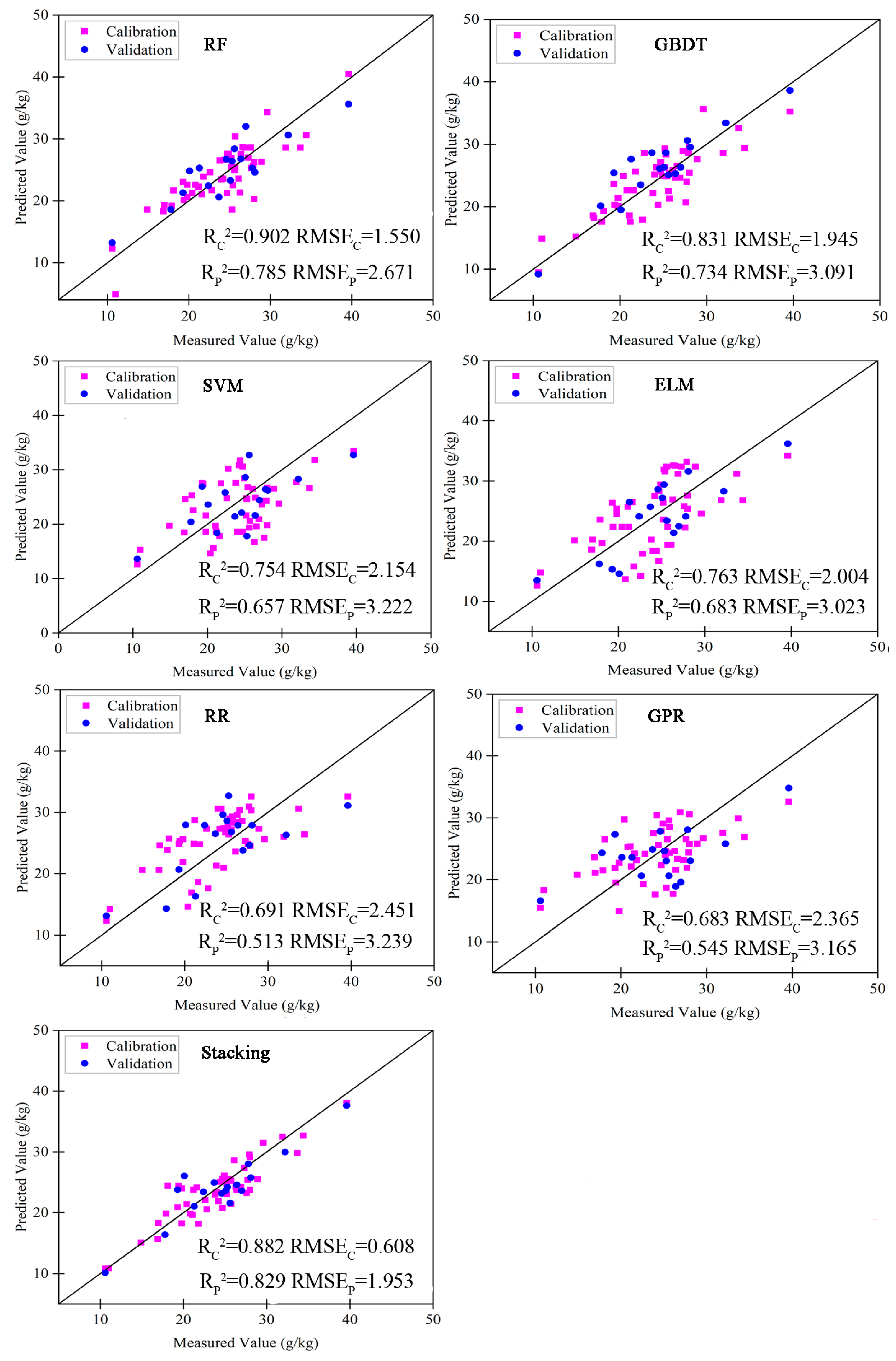
3.3. SOM Estimation Result and Analyze

The stacking ensemble learning framework consists of two layers. The base learners of the model constructed in this study were the RF, ELM, GPR, and RR models, and the meta-learner was the RR model. The pixel spectra of soil samples, which were transformed by spectral pre-processing and SPA feature extraction, were used as the input of the model. The SOM content of the soil samples was adopted as the output. The hyperparameters of each learner were set by optimizing with random search and grid search. To compare and analyze the estimation performance of the constructed multi-algorithm fusion stacking ensemble learning model, evaluation indicators (Table 4) were calculated for the stacking ensemble model and each algorithm model on the calibration and validation datasets.
The calculation results indicate that a single estimation model has advantages and disadvantages regarding different evaluation indicators. Overall, the prediction accuracy of RF and GBDT is high, while that of GPR and RR is relatively low. The R2 of the RF calibration set reaches 0.902, suggesting that the model has the risk of overfitting. Each precision evaluation index of the constructed stacking model is superior to the corresponding one of the single models, with an R2 of 0.829 and a PRD of 2.85 on the validation set. Compared to RF, the Rp2 of the stacking model increased 5.6%. The results suggest that it is necessary to choose and design the framework of the stacking ensemble model reasonably. Different algorithms were used to observe data spaces and structures from diverse angles, enabling the complementarity of these algorithms and better performance in forecasting and stability. More importantly, the result avoids the defect of overfitting that emerges in a single model; thus, a more accurate and reliable prediction result is obtained. To further compare and analyze the prediction performance of different models, the fitting effect diagram was plotted using the predicted and measured values of the models (Figure 10).
It can be seen that the calibration and validation set samples of the model constructed in the stacking framework are closer to the 1:1 line compared with the single model, indicating that the data fitting ability and stability of the constructed learning model are better than those of a single learning model. It can be seen from the soil sample content (Table 1) that the sample data are small, with a large standard deviation and a high degree of data dispersion, indicating that the sample content data may be affected by noise information, which puts forward higher requirements for the fault tolerance and robustness of the model. This might be the reason for the lower prediction fitting effect of a single learner than that of the stacking ensemble learning model. When processing small sample datasets, the ensemble learning model can overcome the problems of any single machine learning model in forecasting and training, such as low fault tolerance and poor robustness in the face of sample noise information. Moreover, the overall fitting ability can also be improved by reducing errors caused by the poor performance of the single learner and small samples.

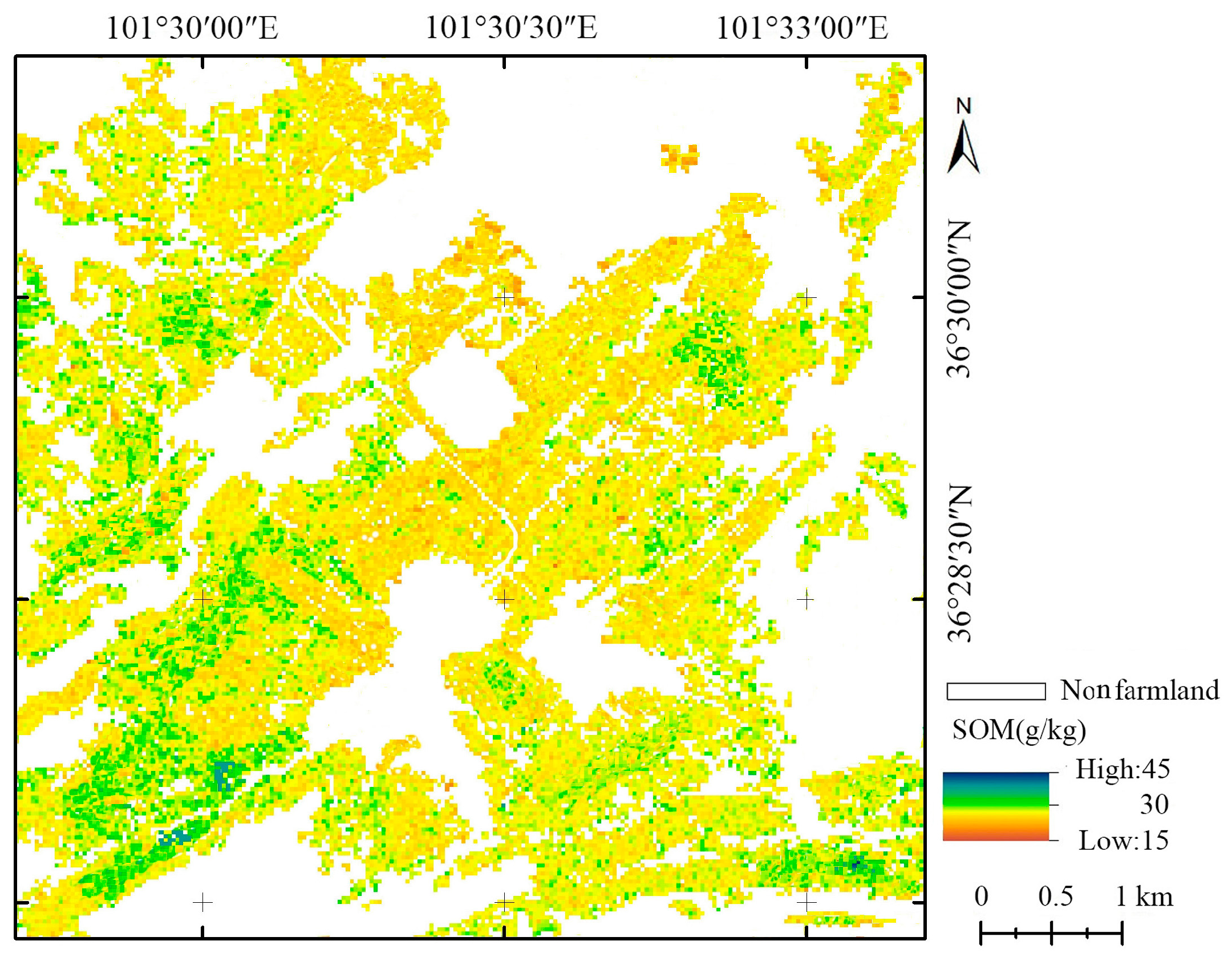
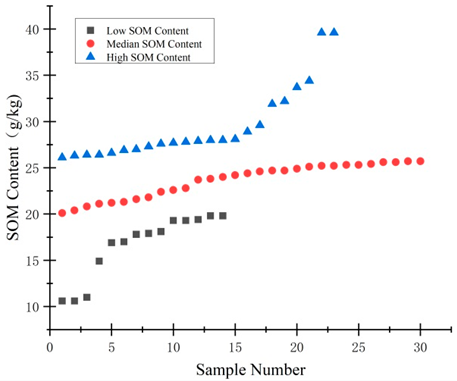
3.4. SOM Estimation from the Hyperspectral Images

Combining the feature spectral band selection with the extraction results of farmland pixels using ZY1-02D hyperspectral image data as inputs, a multi-algorithm fusion stacking ensemble learning model was developed to estimate the SOM content in the farmland of the study area. A spatial distribution map of SOM content was plotted using the GIS software (Figure 11). By comparing the land use status map in the study area, the spatial distribution trend of SOM in the inversion map was qualitatively evaluated, and the results proved the reliability of the SOM map. According to the inversion results, the SOM content in the cultivated land of the study area is moderate. For spatial distribution, the SOM content is slightly lower in the central and north part of the study area than in other parts, and the highest content is observed in the southwest part of the study area. Compared with the high-resolution image map of the study area, it can be seen that the SOM estimation result has a high coincidence degree with the land use status. As it is affected by human activities, the content of SOM far from the construction land is higher than that in the area near the construction land.

4. Discussion

4.1. Comparison of Different Spectral Pre-Processing Treatments

Space-borne hyperspectral imaging belongs to passive imaging. Remote sensing platforms observe the Earth from a distance. When acquiring images with sensors, the spectral quality of the image pixels is affected by multiple factors, such as sensor orientation, hardware loss, light intensity, and atmospheric transmission. These factors cause different degrees of complex noise interference, resulting in abrupt changes and outliers in the spectral curves. Compared with vegetation, roads, and built-up areas, bare soil has a lower reflectance and is more susceptible to noise interference, which results in the low quality of training samples for modeling. Therefore, calibration and noise filtering of hyperspectral satellite data is a prerequisite for obtaining accurate soil spectral reflectance. Spectral pre-processing can effectively enhance the quality of training samples in the model and improve the accuracy of subsequent model estimation [65,66]. Based on the principles of remote sensing physical radiation and transmission models, multiple methods, including differential transformation, SG, and CR, were used to process the spectral characteristics of image pixels in this study. However, different spectral pre-processing methods improve the sample quality to different degrees. To compare the performance and effects of the single and multi-method combined models on pixel spectral pre-processing, the stacking ensemble learning model was constructed to calculate the model accuracy indicators for SOM estimation using spectral band variables after spectral transformations. The sensitive bands were obtained using the Pearson correlation coefficient method as modelling data (Table 2). The calculation results are shown in Table 5. In mathematical transformations, the integer-order differential transformation belongs to the spatial domain image pre-processing method, which can highlight the sharp transition parts of the images. The spectral peak and valley features of the images can be effectively amplified through convolution filtering. The SG is used for image smoothing and noise suppression. Table 5 shows that more spectral band data pass the correlation threshold after SG than the integer-order differential transformation. Furthermore, the number of spectral bands increases with the application of the integer-order transformation after SG. Combining SG with integer-order differential transformation can improve the model inversion performance. CR can reduce the redundancy of hyperspectral data, highlight characteristic bands, and improve the stability of subsequent modeling. However, the modeling effect in this experiment is moderate, which may be limited by the small sample size. Considering the low SOM content in the study area, FOD was introduced to capture the close relationship between the sample spectra and SOM content. The result shows that the FOD outperforms all other pre-processing methods, with more spectral bands and superior modeling effects. Therefore, FOD can be applied to hyperspectral inversion research of SOM content in regions with low SOM content.

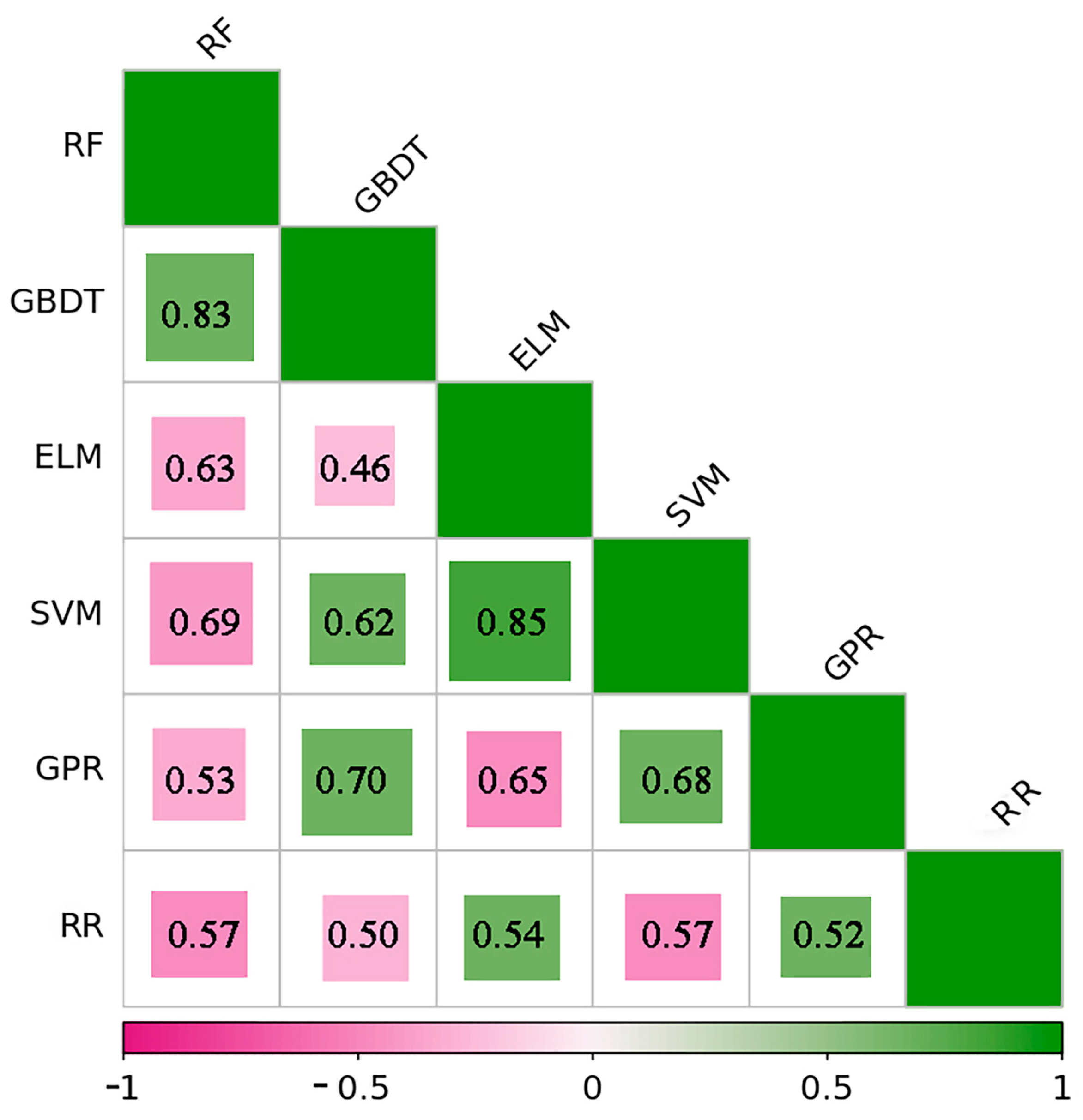
4.2. Analysis of the Effect of Combining Multiple Learning Models

The estimation accuracy considering two combination schemes was measured to further validate the rationality of the single model combination method and the impact of base learner and meta-learner selection on the prediction results. The results are shown in Table 6. The two schemes involve the same meta-learner corresponding to different base learner combinations and the same base learner combination with different meta-learner selections. When the meta-learner is the same, the estimation accuracy of the ensemble framework model in the stacking is upgraded with the increase in the number of different model classifiers (combination 01–06). When the number of classifiers in the base model is constant, the performance of the stacking ensemble structure is improved significantly after adding the base learning models from significantly different machine learning algorithms. For both validation and calibration sets (combination 03 with Rc2 = 0.859, Rp2 = 0.755, and combination 06 with Rc2 = 0.852, Rp2 = 0.749), the learning performance of the stacking ensemble structure decreases when the base learning tools with few differences or strong learning ability in model algorithms are employed. The result indicates that the number and learning ability of the base learner are not factors improving the prediction accuracy of the stacking model. The prediction accuracy of the ensemble model is the best when the base learning model of the minimum correlation (combination 07) is used. The reason for the result is that the essence of machine learning algorithms is to observe data in different data spaces and then build corresponding models according to their own algorithm rules [67]. Highly correlated model algorithms can lead to repeated data training, thus reducing the generalization of the model. Choosing algorithms with large differences can reflect the advantages of different algorithms to the greatest extent. The data have been analyzed using the diversity and difference of the base learners from a multi-dimensional perspective, making the prediction results more robust and accurate, thus, greatly improving the prediction effect.
Performance analysis of meta-learner construction methods 07–10 was conducted using a comparative framework. The evaluation results indicate that RF and ELM, as meta-learners, exhibit excellent performance on the calibration dataset for the ensemble framework model. However, their evaluation metrics on the validation dataset are lower than those for GPR and RR. The reason may be that the RF and ELM models have more hyperparameters and complex model structures, resulting in the overfitting of the ensemble framework model in the face of an insufficient number of training samples and unbalanced sample quality. In this sense, the RR model with an L2 regularization mechanism has been adopted in this paper, which has a simple model structure, strong generalization ability, short running time, and good performance on both the calibration and validation datasets.
It is shown that the reasonable selection and optimal combination of multi-class base learners and meta-learners can improve the performance of an ensemble learning framework model. Multiple heterogeneous learners can dig deeper into potential data information from multiple perspectives, thus improving the accuracy and reliability of the estimation model constructed with small samples and unbalanced data [68]. Furthermore, this extends the universality of the model in the stacking ensemble learning framework.

4.3. Estimation Model Accuracy Improvement and the Uncertainty Analysis

Establishing a robust and efficient inversion model based on hyperspectral remote sensing images is key to improve the accuracy of SOM estimation and mapping in large areas. Hyperspectral image data are huge and the signal-to-noise ratio is low. However, the availability of known soil samples eligible for learner training is limited. Traditional machine learning models achieve undesirable results caused by insufficient instances to learn accurately the target hypothesis in modeling and predicting, leading to poor performance in improving the accuracy and efficiency of SOM content estimation. The construction method of the model based on the stacking framework proposed in the paper performs well. Based on the stacking framework, this study improves the overall estimation accuracy by enhancing the quality of input data and constructing a two-layer heterogeneous integrated learning model. The main advantage of stacking is the introduction of the concept of meta-learner [46]. If the base models learn incorrectly in the feature space, resulting in incorrect prediction information, the meta-learner can identify this problem in the subsequent learning process and compensate for the model learning in this feature space. The construction theory of the stacking model enables the meta-learner to give full play to the advantages of the base learner in the learning process, further resolving the learning errors of the base learner and thus improving the operational accuracy of the entire model. By constructing and combining multiple base learners, the stacking ensemble learning framework with a multi-level classification structure integrates the assumptions of learners, thus making it possible to represent a target hypothesis beyond the hypothesis space. In so doing, the final predictive results are close to the actual objective function values, effectively improving the accuracy and efficiency of the estimation model.
The design structure of the stacking ensemble framework is complex, and each base model needs to be trained. Although the base learner is reduced based on optimization mechanism, a distributed computing environment is important for reducing training and computational time. In addition, in the process of hyperspectral image acquisition, radiation intensity, weather conditions and sample point quality all affect the spectral reflectance of the end element of the image spectrum, which leads to uncertainty in the estimation of SOM. Therefore, during the experiment, the reliability of SOM estimation mapping can be improved to some extent by ensuring that the sampling point is located in the pure bare soil pixel, that the sampling time is the window period of surface soil exposure and is consistent with the satellite transit detection time, and that strict image pre-processing is carried out during the experiment. In this study, the SOM content was estimated based on single remote sensing spectral observation data, resulting in problems such as incomplete observations, low inversion accuracy, and weak transferability. By introducing relevant environmental variables to the traditional remote sensing spectral inversion of SOM research, combining multi-source remote sensing big data with the big environmental data, and establishing a multi-source soil information spatial dataset, the collaborative inversion of SOM content can be achieved. This can effectively strengthen the accuracy, transferability, and interpretability of remote sensing technology for land estimation. These influencing factors will be further emphasized in future studies.

5. Conclusions

The accuracy of a SOM content estimation model is easily affected by image quality and soil sample quantity when using hyperspectral remote sensing images. In this study, a method of constructing an estimation model based on hyperspectral images was proposed, which effectively improved the prediction accuracy and stability of the model. After various kinds of pre-processing of hyperspectral data, the feature band dataset is constructed, and the modeling factors are extracted by SPA as the input data for the SOM estimation model. This method can effectively enhance the quality of modeling data and improve the estimation accuracy of data-driven models. A multi-class fusion model was proposed for estimating the SOM content under the stacking ensemble framework. The model is expansible and can flexibly select different statistical learning algorithms as the base learners. Based on the construction principles of these learners, the model fully considered the differences in the learning styles of heterogeneous learners for sample data during the training process, the correlation and prediction performance of a single learner, and the simplicity and generalization ability of the meta-learner structure. This model effectively addresses problems faced by traditional ensemble learning models such as the poor generalization ability of a single machine learning model and small samples, low tolerance to sample noise information, and poor robustness. By accessing the accuracy indicators of each model, the constructed stacking ensemble learning model had better prediction performance than single algorithm models and single-layer ensemble models with homogeneous learners, with a validation set RMSE of 1.953 and R2 of 0.829. Based on the model estimation results, the distribution map of SOM content in the study area was successfully drawn. The results showed that the mapping of SOM content by hyperspectral image was a reliable method to obtain large-scale soil nutrient information.

Author Contributions

Conceptualization, M.W. and S.D.; methodology, N.L.; software, M.W.; validation, M.W., S.D. and N.L.; formal analysis, M.W.; investigation, M.W.; resources, S.D.; data curation, R.J.; writing—original draft preparation, M.W.; writing—review and editing, M.W. and R.J.; visualization, M.W. and B.Z.; supervision, N.L.; project administration, M.W. and N.L.; funding acquisition, N.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Science and Technology Development Project of Jilin Province (20210203016SF), the Education Department Research Project of Jilin Province (JJKH20230342KJ), the Natural Science Foundation of Jilin Province (20230101373JC), and the Major Project of High Resolution Earth Observation System (71-Y50G10-9001-22/23).

Data Availability Statement

Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Li, T.; Mu, T.; Liu, G.; Yang, X.; Zhu, G.; Shang, C. A Method of Soil Moisture Content Estimation at Various Soil Organic Matter Conditions Based on Soil Reflectance. Remote Sens. 2022, 14, 2411. [Google Scholar] [CrossRef]
  2. Yuan, Y.; Li, B.; Yu, W.; Gao, X. Estimation and Mapping of Soil Organic Matter Content at a National Scale Based on Grid Soil Samples, a Soil Map and DEM Data. Ecol. Inform. 2021, 66, 101487. [Google Scholar] [CrossRef]
  3. Hu, W.; Shen, Q.; Zhai, X.; Du, S.; Zhang, X. Impact of Environmental Factors on the Spatiotemporal Variability of Soil Organic Matter: A Case Study in a Typical Small Mollisol Watershed of Northeast China. J. Soils Sediments 2021, 21, 736–747. [Google Scholar] [CrossRef]
  4. Liu, X.; Dou, S.; Zheng, S. Effects of Corn Straw and Biochar Returning to Fields Every Other Year on the Structure of Soil Humic Acid. Sustainability 2022, 14, 15946. [Google Scholar] [CrossRef]
  5. Gao, L.; Zhu, X.; Han, Z.; Wang, L.; Zhao, G.; Jiang, Y. Spectroscopy-Based Soil Organic Matter Estimation in Brown Forest Soil Areas of the Shandong Peninsula, China. Pedosphere 2019, 29, 810–818. [Google Scholar] [CrossRef]
  6. Chen, Y.; Wang, J.; Liu, G.; Yang, Y.; Liu, Z.; Deng, H. Hyperspectral Estimation Model of Forest Soil Organic Matter in Northwest Yunnan Province, China. Forests 2019, 10, 217. [Google Scholar] [CrossRef]
  7. Mulla, D.J. Twenty Five Years of Remote Sensing in Precision Agriculture: Key Advances and Remaining Knowledge Gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
  8. Wang, F.; Gao, J.; Zha, Y. Hyperspectral Sensing of Heavy Metals in Soil and Vegetation: Feasibility and Challenges. ISPRS J. Photogramm. 2018, 136, 73–84. [Google Scholar] [CrossRef]
  9. Mehl, P.M.; Chen, Y.-R.; Kim, M.S.; Chan, D.E. Development of Hyperspectral Imaging Technique for the Detection of Apple Surface Defects and Contaminations. J. Food Eng. 2004, 61, 67–81. [Google Scholar] [CrossRef]
  10. Galvão, L.S.; Vitorello, Í. Variability of Laboratory Measured Soil Lines of Soils from Southeastern Brazil. Remote Sens. Environ. 1998, 63, 166–181. [Google Scholar] [CrossRef]
  11. Serbin, G.; Daughtry, C.S.T.; Hunt, E.R.; Reeves, J.B.; Brown, D.J. Effects of Soil Composition and Mineralogy on Remote Sensing of Crop Residue Cover. Remote Sens. Environ. 2009, 113, 224–238. [Google Scholar] [CrossRef]
  12. Choe, E.; van der Meer, F.; van Ruitenbeek, F.; van der Werff, H.; de Smeth, B.; Kim, K.-W. Mapping of Heavy Metal Pollution in Stream Sediments Using Combined Geochemistry, Field Spectroscopy, and Hyperspectral Remote Sensing: A Case Study of the Rodalquilar Mining Area, SE Spain. Remote Sens. Environ. 2008, 112, 3222–3233. [Google Scholar] [CrossRef]
  13. Sun, W.; Liu, S.; Zhang, X.; Li, Y. Estimation of Soil Organic Matter Content Using Selected Spectral Subset of Hyperspectral Data. Geoderma 2022, 409, 115653. [Google Scholar] [CrossRef]
  14. Angelopoulou, T.; Chabrillat, S.; Pignatti, S.; Milewski, R.; Karyotis, K.; Brell, M.; Ruhtz, T.; Bochtis, D.; Zalidis, G. Evaluation of Airborne HySpex and Spaceborne PRISMA Hyperspectral Remote Sensing Data for Soil Organic Matter and Carbonates Estimation. Remote Sens. 2023, 15, 1106. [Google Scholar] [CrossRef]
  15. Guo, L.; Zhang, H.; Shi, T.; Chen, Y.; Jiang, Q.; Linderman, M. Prediction of Soil Organic Carbon Stock by Laboratory Spectral Data and Airborne Hyperspectral Images. Geoderma 2019, 337, 32–41. [Google Scholar] [CrossRef]
  16. Nanni, M.R.; Demattê, J.M.; Rodrigues, M.; Santos, G.L.; Reis, A.S.; de Oliveira, K.M.; Cezar, E.; Furlanetto, R.H.; Crusiol, L.G.T.; Sun, L. Mapping Particle Size and Soil Organic Matter in Tropical Soil Based on Hyperspectral Imaging and Non-Imaging Sensors. Remote Sens. 2021, 13, 1782. [Google Scholar] [CrossRef]
  17. Zhao, L.; Tan, K.; Wang, X.; Ding, J.; Liu, Z.; Ma, H.; Han, B. Hyperspectral Feature Selection for SOM Prediction Using Deep Reinforcement Learning and Multiple Subset Evaluation Strategies. Remote Sens. 2022, 15, 127. [Google Scholar] [CrossRef]
  18. Reis, A.S.; Rodrigues, M.; Alemparte Abrantes Dos Santos, G.; Mayara De Oliveira, K.; Furlanetto, R.; Teixeira Crusiol, L.G.; Cezar, E.; Nanni, M.R. Detection of Soil Organic Matter Using Hyperspectral Imaging Sensor Combined with Multivariate Regression Modeling Procedures. Remote Sens. Appl. 2021, 22, 100492. [Google Scholar] [CrossRef]
  19. Meng, X.; Bao, Y.; Ye, Q.; Liu, H.; Zhang, X.; Tang, H.; Zhang, X. Soil Organic Matter Prediction Model with Satellite Hyperspectral Image Based on Optimized Denoising Method. Remote Sens. 2021, 13, 2273. [Google Scholar] [CrossRef]
  20. Yanli, L.; Youlu, B.; Liping, Y.; Hongjuan, W. Hyperspectral Extraction of Soil Organic Matter Content Based on Principal Component Regression. N. Z. J. Agric. Res. 2007, 50, 1169–1175. [Google Scholar] [CrossRef]
  21. Gomez, C.; Lagacherie, P.; Coulouma, G. Regional Predictions of Eight Common Soil Properties and Their Spatial Structures from Hyperspectral Vis–NIR Data. Geoderma 2012, 189–190, 176–185. [Google Scholar] [CrossRef]
  22. Tan, K.; Wang, H.; Chen, L.; Du, Q.; Du, P.; Pan, C. Estimation of the Spatial Distribution of Heavy Metal in Agricultural Soils Using Airborne Hyperspectral Imaging and Random Forest. J. Hazard. Mater. 2020, 382, 120987. [Google Scholar] [CrossRef]
  23. Rocha Neto, O.; Teixeira, A.; Leão, R.; Moreira, L.; Galvão, L. Hyperspectral Remote Sensing for Detecting Soil Salinization Using ProSpecTIR-VS Aerial Imagery and Sensor Simulation. Remote Sens. 2017, 9, 42. [Google Scholar] [CrossRef]
  24. Arif, M.; Qi, Y.; Dong, Z.; Wei, H. Rapid Retrieval of Cadmium and Lead Content from Urban Greenbelt Zones Using Hyperspectral Characteristic Bands. J. Clean. Prod. 2022, 374, 133922. [Google Scholar] [CrossRef]
  25. Fassnacht, F.E.; Latifi, H.; Ghosh, A.; Joshi, P.K.; Koch, B. Assessing the Potential of Hyperspectral Imagery to Map Bark Beetle-Induced Tree Mortality. Remote Sens. Environ. 2014, 140, 533–548. [Google Scholar] [CrossRef]
  26. Chang, R.; Chen, Z.; Wang, D.; Guo, K. Hyperspectral Remote Sensing Inversion and Monitoring of Organic Matter in Black Soil Based on Dynamic Fitness Inertia Weight Particle Swarm Optimization Neural Network. Remote Sens. 2022, 14, 4316. [Google Scholar] [CrossRef]
  27. Lin, N.; Jiang, R.; Li, G.; Yang, Q.; Li, D.; Yang, X. Estimating the Heavy Metal Contents in Farmland Soil from Hyperspectral Images Based on Stacked AdaBoost Ensemble Learning. Ecol. Indic. 2022, 143, 109330. [Google Scholar] [CrossRef]
  28. Wu, M.; Lin, N.; Li, G.; Liu, H.; Li, D. Hyperspectral Estimation of Petroleum Hydrocarbon Content in Soil Using Ensemble Learning Method and LASSO Feature Extraction. Environ. Pollut. Bioavail. 2022, 34, 308–320. [Google Scholar] [CrossRef]
  29. Vicente, L.E.; de Souza Filho, C.R. Identification of Mineral Components in Tropical Soils Using Reflectance Spectroscopy and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Data. Remote Sens. Environ. 2011, 115, 1824–1836. [Google Scholar] [CrossRef]
  30. Sun, X.; Qu, Y.; Gao, L.; Sun, X.; Qi, H.; Zhang, B.; Shen, T. Ensemble-Based Information Retrieval with Mass Estimation for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5508123. [Google Scholar] [CrossRef]
  31. Krawczyk, B.; Minku, L.L.; Cheng, J.; Stefanowski, J.; Woźniak, M. Ensemble Learning for Data Stream Analysis: A Survey. Inform. Fusion 2017, 37, 132–156. [Google Scholar] [CrossRef]
  32. Wang, G.; Hao, J.; Ma, J.; Jiang, H. A Comparative Assessment of Ensemble Learning for Credit Scoring. Expert Syst. Appl. 2011, 38, 223–230. [Google Scholar] [CrossRef]
  33. Shu, C.; Burn, D.H. Artificial Neural Network Ensembles and Their Application in Pooled Flood Frequency Analysis: Artificial Neural Network Ensembles. Water Resour. Res. 2004, 40, W09301. [Google Scholar] [CrossRef]
  34. Taghizadeh-Mehrjardi, R.; Schmidt, K.; Amirian-Chakan, A.; Rentschler, T.; Zeraatpisheh, M.; Sarmadian, F.; Valavi, R.; Davatgar, N.; Behrens, T.; Scholten, T. Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space. Remote Sens. 2020, 12, 1095. [Google Scholar] [CrossRef]
  35. Tan, K.; Ma, W.; Chen, L.; Wang, H.; Du, Q.; Du, P.; Yan, B.; Liu, R.; Li, H. Estimating the Distribution Trend of Soil Heavy Metals in Mining Area from HyMap Airborne Hyperspectral Imagery Based on Ensemble Learning. J. Hazard. Mater. 2021, 401, 123288. [Google Scholar] [CrossRef]
  36. Wang, Y.; Zhang, X.; Sun, W.; Wang, J.; Ding, S.; Liu, S. Effects of Hyperspectral Data with Different Spectral Resolutions on the Estimation of Soil Heavy Metal Content: From Ground-Based and Airborne Data to Satellite-Simulated Data. Sci. Total Environ. 2022, 838, 156129. [Google Scholar] [CrossRef]
  37. Han, T. Design and Application of Multicolor Image Identification in Soil Pollution Component Detection. Arab. J. Geosci. 2020, 13, 905. [Google Scholar] [CrossRef]
  38. Zhang, S.; Shen, Q.; Nie, C.; Huang, Y.; Wang, J.; Hu, Q.; Ding, X.; Zhou, Y.; Chen, Y. Hyperspectral Inversion of Heavy Metal Content in Reclaimed Soil from a Mining Wasteland Based on Different Spectral Transformation and Modeling Methods. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 211, 393–400. [Google Scholar] [CrossRef]
  39. Chen, T.; Chang, Q.; Clevers, J.G.P.W.; Kooistra, L. Rapid Identification of Soil Cadmium Pollution Risk at Regional Scale Based on Visible and Near-Infrared Spectroscopy. Environ. Pollut. 2015, 206, 217–226. [Google Scholar] [CrossRef]
  40. Cui, Y.; Meng, F.; Fu, P.; Yang, X.; Zhang, Y.; Liu, P. Application of Hyperspectral Analysis of Chlorophyll a Concentration Inversion in Nansi Lake. Ecol. Inform. 2021, 64, 101360. [Google Scholar] [CrossRef]
  41. Hasan, U.; Jia, K.; Wang, L.; Wang, C.; Shen, Z.; Yu, W.; Sun, Y.; Jiang, H.; Zhang, Z.; Guo, J.; et al. Retrieval of Leaf Chlorophyll Contents (LCCs) in Litchi Based on Fractional Order Derivatives and VCPA-GA-ML Algorithms. Plants 2023, 12, 501. [Google Scholar] [CrossRef]
  42. Shen, L.; Gao, M.; Yan, J.; Li, Z.; Leng, P.; Yang, Q.; Duan, S. Hyperspectral Estimation of Soil Organic Matter Content Using Different Spectral Preprocessing Techniques and PLSR Method. Remote Sens. 2020, 12, 1206. [Google Scholar] [CrossRef]
  43. Yan, B.; Wang, R.; Gan, F.; Wang, Z. Minerals Mapping of the Lunar Surface with Clementine UVVIS/NIR Data Based on Spectra Unmixing Method and Hapke Model. Icarus 2010, 208, 11–19. [Google Scholar] [CrossRef]
  44. Qiu, B.; Zhang, K.; Tang, Z.; Chen, C.; Wang, Z. Developing Soil Indices Based on Brightness, Darkness, and Greenness to Improve Land Surface Mapping Accuracy. GISci. Remote Sens. 2017, 54, 759–777. [Google Scholar] [CrossRef]
  45. Vaudour, E.; Gomez, C.; Lagacherie, P.; Loiseau, T.; Baghdadi, N.; Urbina-Salazar, D.; Loubet, B.; Arrouays, D. Temporal Mosaicking Approaches of Sentinel-2 Images for Extending Topsoil Organic Carbon Content Mapping in Croplands. Int. J. Appl. Earth Obs. 2021, 96, 102277. [Google Scholar] [CrossRef]
  46. Zhao, H.; Chen, X.; Zhang, Z.; Zhou, Y. Exploring an Efficient Sandy Barren Index for Rapid Mapping of Sandy Barren Land from Landsat TM/OLI Images. Int. J. Appl. Earth Obs. 2019, 80, 38–46. [Google Scholar] [CrossRef]
  47. Zou, X.; Zhao, J.; Povey, M.J.W.; Mel, H.; Mao, H. Variables Selection Methods in Near-Infrared Spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar] [CrossRef]
  48. Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved Landslide Assessment Using Support Vector Machine with Bagging, Boosting, and Stacking Ensemble Machine Learning Framework in a Mountainous Watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
  49. Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Soft. 2010, 33, 1–22. [Google Scholar] [CrossRef]
  50. Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
  51. Tang, J.; Liang, J.; Han, C.; Li, Z.; Huang, H. Crash Injury Severity Analysis Using a Two-Layer Stacking Framework. Accident Anal. Prev. 2019, 122, 226–238. [Google Scholar] [CrossRef] [PubMed]
  52. Sun, X.; Liu, M.; Sima, Z. A Novel Cryptocurrency Price Trend Forecasting Model Based on LightGBM. Financ. Res. Lett. 2020, 32, 101084. [Google Scholar] [CrossRef]
  53. Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
  54. Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef] [PubMed]
  55. Breiman, L. Random Forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  56. Huang, G.; Huang, G.; Song, S.; You, K. Trends in Extreme Learning Machines: A Review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
  57. Zhu, Q.; Qin, A.K.; Suganthan, P.N.; Huang, G. Evolutionary Extreme Learning Machine. Pattern Recogn. 2005, 38, 1759–1763. [Google Scholar] [CrossRef]
  58. Huang, G.; Zhu, Q.; Siew, C.-K. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
  59. Rossel, R.A.V.; Behrens, T. Using Data Mining to Model and Interpret Soil Diffuse Reflectance Spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
  60. Marquand, A.; Howard, M.; Brammer, M.; Chu, C.; Coen, S.; Mourão-Miranda, J. Quantitative Prediction of Subjective Pain Intensity from Whole-Brain FMRI Data Using Gaussian Processes. NeuroImage 2010, 49, 2178–2189. [Google Scholar] [CrossRef]
  61. Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.P.W.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI Estimation Using Parametric, Non-Parametric and Physical Retrieval Methods—A Comparison. ISPRS J. Photogramm. 2015, 108, 260–272. [Google Scholar] [CrossRef]
  62. Frank, I.E.; Friedman, J.H. A Statistical View of Some Chemometrics Regression Tools. Technometrics 1993, 35, 109–135. [Google Scholar] [CrossRef]
  63. Hong, Y.; Liu, Y.; Chen, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Application of Fractional-Order Derivative in the Quantitative Estimation of Soil Organic Matter Content through Visible and near-Infrared Spectroscopy. Geoderma 2019, 337, 758–769. [Google Scholar] [CrossRef]
  64. Gu, X.; Wang, Y.; Sun, Q.; Yang, G.; Zhang, C. Hyperspectral Inversion of Soil Organic Matter Content in Cultivated Land Based on Wavelet Transform. Comput. Electron. Agric. 2019, 167, 105053. [Google Scholar] [CrossRef]
  65. Zhang, Z.; Ding, J.; Zhu, C.; Wang, J. Combination of Efficient Signal Pre-Processing and Optimal Band Combination Algorithm to Predict Soil Organic Matter through Visible and near-Infrared Spectra. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 240, 118553. [Google Scholar] [CrossRef]
  66. Davari, M.; Karimi, S.; Bahrami, H.; Taher Hossaini, S.M.; Fahmideh, S. Simultaneous Prediction of Several Soil Properties Related to Engineering Uses Based on Laboratory Vis-NIR Reflectance Spectroscopy. CATENA 2021, 197, 104987. [Google Scholar] [CrossRef]
  67. Cui, S.; Yin, Y.; Wang, D.; Li, Z.; Wang, Y. A Stacking-Based Ensemble Learning Method for Earthquake Casualty Prediction. Appl. Soft. Comput. 2021, 101, 107038. [Google Scholar] [CrossRef]
  68. He, Y.; Xiao, J.; An, X.; Cao, C.; Xiao, J. Short-Term Power Load Probability Density Forecasting Based on GLRQ-Stacking Ensemble Learning Method. Int. J. Electr. Power. 2022, 142, 108243. [Google Scholar] [CrossRef]
Remotesensing 15 04713 g001
Figure 1. Flowchart of this study.
Figure 1. Flowchart of this study.
Remotesensing 15 04713 g001
Remotesensing 15 04713 g002
Figure 2. (left) Location of the study area and (right) the spatial distribution of soil samples.
Figure 2. (left) Location of the study area and (right) the spatial distribution of soil samples.
Remotesensing 15 04713 g002
Remotesensing 15 04713 g003
Figure 3. Image spectrum, measured spectrum, and correlation coefficients.
Figure 3. Image spectrum, measured spectrum, and correlation coefficients.
Remotesensing 15 04713 g003
Remotesensing 15 04713 g004
Figure 4. Original and transformation spectral reflectance curves : (a) original spectral curves (R); (b) spectral first-order differential transformation curves (FD-R); (c) spectral second-order differential transformation curves (SD−R); (d) spectral Savitzky-Golay filter transformation curves (SG); (e) spectral continuum removal first-order differential transformation curves (FD-SG); (f) spectral continuum removal second-order differential transformation curves (SD-SG); (g) spectral continuum removal transformation curves (CR); (h) spectral fractional-order transformation curves (FOD).
Figure 4. Original and transformation spectral reflectance curves : (a) original spectral curves (R); (b) spectral first-order differential transformation curves (FD-R); (c) spectral second-order differential transformation curves (SD−R); (d) spectral Savitzky-Golay filter transformation curves (SG); (e) spectral continuum removal first-order differential transformation curves (FD-SG); (f) spectral continuum removal second-order differential transformation curves (SD-SG); (g) spectral continuum removal transformation curves (CR); (h) spectral fractional-order transformation curves (FOD).
Remotesensing 15 04713 g004
Remotesensing 15 04713 g005
Figure 5. (a) The threshold value for extracting bare soil pixel; (b) bare soil pixel extraction results. The yellow part is bare soil and the rest is non-bare soil.
Figure 5. (a) The threshold value for extracting bare soil pixel; (b) bare soil pixel extraction results. The yellow part is bare soil and the rest is non-bare soil.
Remotesensing 15 04713 g005
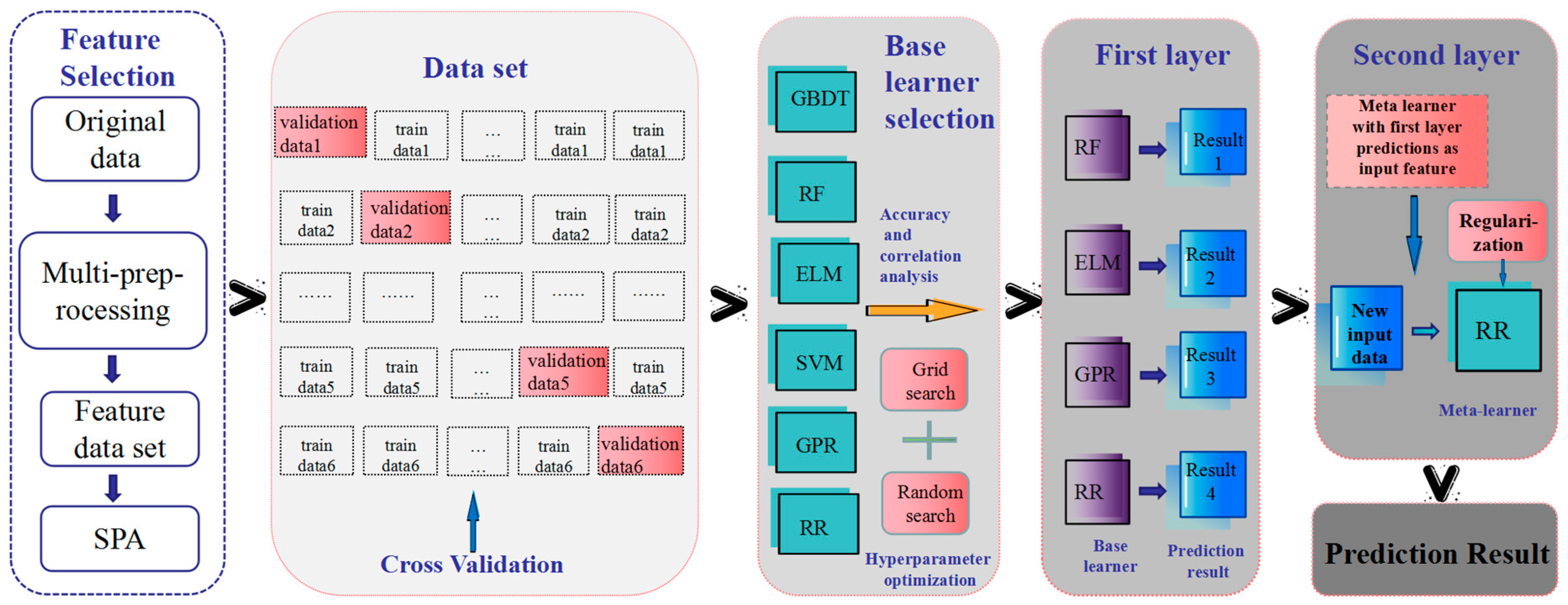
Remotesensing 15 04713 g006
Figure 6. Flowchart of the stacking ensemble learning model.
Figure 6. Flowchart of the stacking ensemble learning model.
Remotesensing 15 04713 g006
Remotesensing 15 04713 g007
Figure 7. Sensitive band distribution after different spectral pre-processing methods.
Figure 7. Sensitive band distribution after different spectral pre-processing methods.
Remotesensing 15 04713 g007
Remotesensing 15 04713 g008
Figure 8. Feature band distribution based on SPA selection result: (a) the calculation results of RMSE with the different variables; (b) feature band distribution map.
Figure 8. Feature band distribution based on SPA selection result: (a) the calculation results of RMSE with the different variables; (b) feature band distribution map.
Remotesensing 15 04713 g008
Remotesensing 15 04713 g009
Figure 9. The correlation between the prediction results of each individual model.
Figure 9. The correlation between the prediction results of each individual model.
Remotesensing 15 04713 g009
Remotesensing 15 04713 g010
Figure 10. Scatter plots of the estimated values against the measured values of different inversion models (RF, GBDT, SVM, ELM, RR, GPR, and stacking).
Figure 10. Scatter plots of the estimated values against the measured values of different inversion models (RF, GBDT, SVM, ELM, RR, GPR, and stacking).
Remotesensing 15 04713 g010
Remotesensing 15 04713 g011
Figure 11. Spatial distribution results of SOM based on the stacking model.
Figure 11. Spatial distribution results of SOM based on the stacking model.
Remotesensing 15 04713 g011
Table 1. SOM information of samples (g/kg).
Table 1. SOM information of samples (g/kg).
Remotesensing 15 04713 i001Number
Minimum
Maximum
Mean value
Standard Deviation
Variation Coefficient		67
10.6 (g/kg)
39.6 (g/kg)
24.16 (g/kg)
5.57
22.94%
Table 2. Maximum correlation coefficients and sensitive bands.
Table 2. Maximum correlation coefficients and sensitive bands.
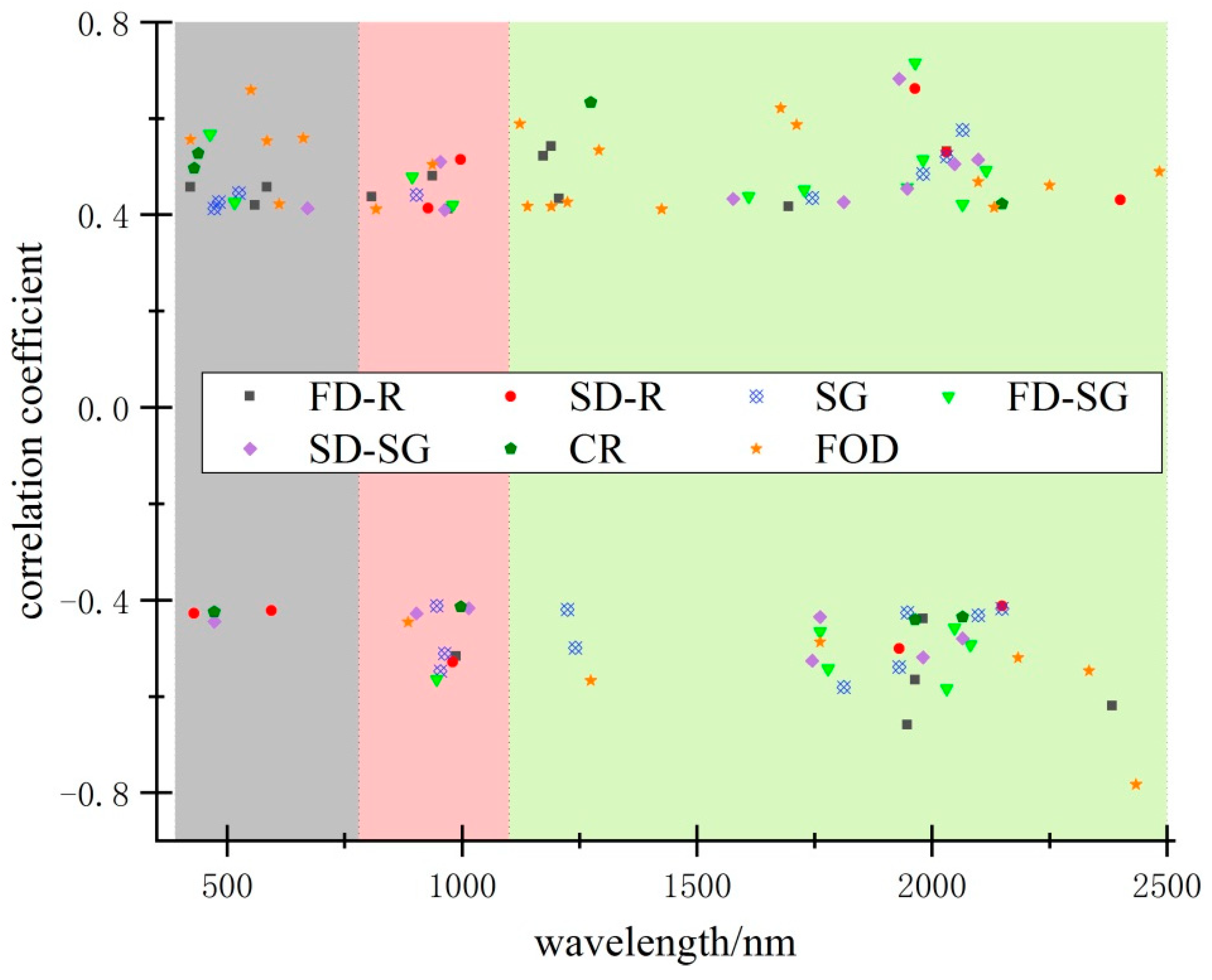
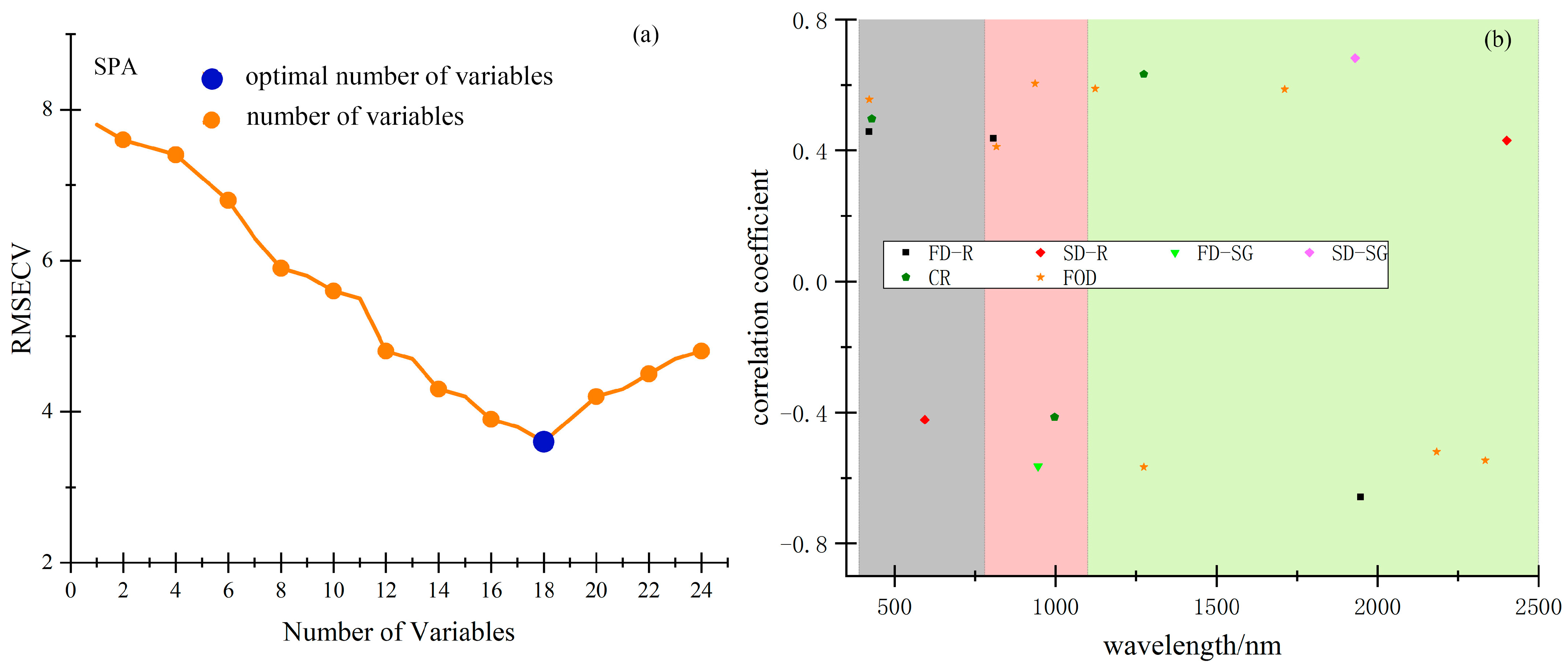
Transformation--FD-RSD-RSGFD-SGSD-SG CRFOD
Pearson calculation resultMaximum−0.6590.662−0.5810.7150.6820.633−0.783
Corresponding
band		1947196418121964193012742434
Number of sensitive bands1610181716825
Table 3. Hyperparameters selection for different machine learning models.
Table 3. Hyperparameters selection for different machine learning models.
ModelHyperparametersRMSE
RFn_estimators = 100, max_depth = 52.671
GBDTlearning_rate = 0.01, subsample = 0.9, n_estimators = 200,
max_depth = 3		3.091
ELMnumber of neuron nodes = 10, wi = 33.023
SVMkernel = ‘rbf’, gamma = auto, C = 103.222
GPRkernel = ‘rbf’, alpha = fioat, random_satate = int3.165
RRalpha = 1.03.239
Table 4. Estimation index results for different machine learning models.
Table 4. Estimation index results for different machine learning models.
ModelRC2RMSECRP2RMSEPRPD
SOM estimation
result		RF0.9021.550.7852.6712.09
GBDT0.8311.9450.7343.0911.85
ELM0.7632.0040.6833.0231.84
SVM0.7542.1540.6573.2221.73
GPR0.6833.3650.5453.1651.76
RR0.6911.0320.5133.2391.72
Stacking0.8820.6080.8291.9532.85
Table 5. Evaluation indexes of different spectral pre-processing methods.
Table 5. Evaluation indexes of different spectral pre-processing methods.
Spectral TransformationAlgorithmBandsRC2RMSECRP2RMSEPRPD
FD-RStacking160.8611.3650.7412.6112.13
SD-RStacking100.8041.4420.7252.8621.95
SGStacking180.7542.1580.5533.8551.44
FD-SGStacking170.8541.1560.7532.6522.10
SD-SGStacking160.8571.9520.7362.4932.23
CRStacking80.8351.7890.7134.1121.35
FODStacking250.8780.8960.8022.3232.40
Table 6. Evaluation result of combining multiple learning models.
Table 6. Evaluation result of combining multiple learning models.
CombinationBase LearnerMeta-LearnerRc2RMSEcRP2RMSEP
01RF, GBDT, ELMRR0.8651.4550.7632.837
02RF, GPR, ELMRR0.8741.3480.7742.565
03RF, GBDT, ELM, SVMRR0.8591.5250.7552.944
04RF, ELM, SVM, GPRRR0.8621.4380.7652.749
05RF, GBDT, ELM, SVM, GPRRR0.8611.4840.7612.832
06RF, GBDT, ELM, SVM, GPR, RRRR0.8521.6540.7492.986
07RF, ELM, GPR, RRRR0.8820.6080.8291.953
08RF, ELM, GPR, RRRF0.9030.5840.7542.063
09RF, ELM, GPR, RRELM0.8920.7110.7472.611
10RF, ELM, GPR, RRGPR0.8670.7190.8042.105
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wu, M.; Dou, S.; Lin, N.; Jiang, R.; Zhu, B. Estimation and Mapping of Soil Organic Matter Content Using a Stacking Ensemble Learning Model Based on Hyperspectral Images. Remote Sens. 2023, 15, 4713. https://doi.org/10.3390/rs15194713

AMA Style

Wu M, Dou S, Lin N, Jiang R, Zhu B. Estimation and Mapping of Soil Organic Matter Content Using a Stacking Ensemble Learning Model Based on Hyperspectral Images. Remote Sensing. 2023; 15(19):4713. https://doi.org/10.3390/rs15194713

Chicago/Turabian Style

Wu, Menghong, Sen Dou, Nan Lin, Ranzhe Jiang, and Bingxue Zhu. 2023. "Estimation and Mapping of Soil Organic Matter Content Using a Stacking Ensemble Learning Model Based on Hyperspectral Images" Remote Sensing 15, no. 19: 4713. https://doi.org/10.3390/rs15194713

APA Style

Wu, M., Dou, S., Lin, N., Jiang, R., & Zhu, B. (2023). Estimation and Mapping of Soil Organic Matter Content Using a Stacking Ensemble Learning Model Based on Hyperspectral Images. Remote Sensing, 15(19), 4713. https://doi.org/10.3390/rs15194713

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop