Creation of a Walloon Pasture Monitoring Platform Based on Machine Learning Models and Remote Sensing

Abstract

The use of remote sensing data and the implementation of machine learning (ML) algorithms is growing in pasture management. In this study, ML models predicting the available compressed sward height (CSH) in Walloon pastures based on Sentinel-1, Sentinel-2, and meteorological data were developed to be integrated into a decision support system (DSS). Given the area covered (>4000 km² of pastures of 100 m² pixels), the consequent challenge of computation time and power requirements was overcome by the development of a platform predicting CSH throughout Wallonia. Four grazing seasons were covered in the current study (between April and October from 2018 to 2021, the mean predicted CSH per parcel per date ranged from 48.6 to 67.2 mm, and the coefficient of variation from 0 to 312%, suggesting a strong heterogeneity of variability of CSH between parcels. Further exploration included the number of predictions expected per grazing season and the search for temporal and spatial patterns and consistency. The second challenge tackled is the poor data availability for concurrent acquisition, which was overcome through the inclusion of up to 4-day-old data to fill data gaps up to the present time point. For this gap filling methodology, relevancy decreased as the time window width increased, although data with 4-day time lag values represented less than 4% of the total data. Overall, two models stood out, and further studies should either be based on the random forest model if they need prediction quality or on the cubist model if they need continuity. Further studies should focus on developing the DSS and on the conversion of CSH to actual forage allowance.

1. Introduction

The first working group of experts of the Intergovernmental Panel on Climate Change recently highlighted the importance of a greater understanding of greenhouse gas emissions in pastures [1]. Some experts have claimed that pastures are an unmissable opportunity to mitigate carbon dioxide ($C{O}_2$), methane ($C{H}_4$), and nitrous oxide ($N_{2}O$) emissions [2]. Others have underlined the importance of grasslands in the assessment of biomass stocks and subsequent carbon storage [3] and asserted that carbon sequestration could be improved through better grazing management [4]. Besides these climatic considerations, [5] underlined a political interest as the European Union has deployed greening policies, including significant usage of pastures ([6,7,8,9]). These authors have also pointed out other key motivations, such as farmers’ awareness of the preservation of landscapes and consumer perceptions ([5,10]). Moreover, grasslands represent a significant part of the global landmass (assessed as representing between 26% [11] and 40% [12]). In southern Belgium, 42.1% of the total cultivated area is dedicated to grassland, and more than 85% of these pastures are grazed [13]. All these reasons lead us to conclude that there is a strong positive economic advantage in grazing in appropriate climates (e.g., [14,15]), although some studies tend to be less affirmative, especially concerning grazing in the Netherlands [16] or Greece [17].

Unfortunately, as mentioned by [18,19], grass-based livestock ruminant production has not completely leveraged the advances in precision technologies to better understand and manage pasture, probably due to the constraints inherent in outdoor applications. [20] included remote sensing, global positioning systems (GPS), geographic information systems (GIS), and the Internet of Things (IoT), among the underlying technologies. A short, up-to-date review of the literature on the most relevant models to help the understanding and management of pastures highlighted some trends (Annex/SM 1). There is an increased use of remote sensing, as established in [21]. A progressive transition from mechanistic models to statistical/machine learning models is also observed with a diversification of their structure. Most papers using remotely sensed datasets stress the advantage of detecting the spatial heterogeneity of pastures, which, as underlined by [22], is a key component of grazing dynamics.

Given the multiple scientific, political, and economic interests of pastures and the technological opportunities available, there is an interest in developing a decision support system (DSS) from a prediction model. However, this has rarely been attempted. Only 11% of models mentioned in Annex/SM 1 are implemented into a DSS. This shortfall might either be located at the production level due to the poor performances of the prediction models, as suggested in [23], or at the user level. Sometimes the DSS design and the choice of information delivered by this application did not seem to match the needs of farmers fully [24]. Furthermore, there is a time lag induced by the information overload inherent in the integration of new data sources and data treatments, and that hinders the actual decision making [25]. Therefore, proper attention should be paid to data integration and transfer, as underlined in [24]. For the models that reach the DSS step, the underlying structure and resulting user application should be cheap, rapid, and provide relevant information to increase the interest and adoption rate by farmers.

Recently, to address the underexploitation of the recent advances in sensor and machine learning algorithms, we have developed machine learning models to predict the compressed sward height (CSH) using cheap data available at a large scale, including Sentinel-1 (S1) and Sentinel-2 (S2) satellite images and meteorological data. Models with a prediction quality around 20 mm [26] present the advantage of producing pixel-based predictions, which enables the consideration of spatial heterogeneity as proposed by [22]. We intend to build a DSS based on these models. The use of CSH in the context of decision making was already included in decision making as an input feature in DSS, such as GrassQ and PastureBase Ireland. To meet the speed criterion and to decrease the computational power requirement, in this study, we focused on implementing and analyzing the usefulness of a platform that handles the prediction of CSH at the scale of Wallonia. Furthermore, the platform was designed to handle data acquired at different times. We assumed that predicting the available CSH at such a large scale with a fine temporal and spatial resolution would require greater time and computational power than would be acceptable for the application’s end users. Therefore, this platform is intended to be the data provider for a future DSS that would handle the translation of the transmitted information into relevant metrics. Another major innovation is that, to our knowledge, other DSS primarily rely on mechanistic and empirical models and then try to integrate the remote sensed data, while our goal is to implement integration at the core of the DSS. Moreover, we did not find any DSS or DSS data provider that could be easily and rapidly adapted to changes either in the model structure or needs of the user, whereas this platform can offer this modularity as recommended by [27].

A last prospect highlighted by the process of implementing the prediction platform was the ability to study the behavior of the models that are trained and validated with relatively limited datasets once they are applied to huge databases. This led to a refinement of the selection process for the most relevant model to be used as the data provider for future DSS and other applications, depending on the most critical aspect: accuracy or temporal continuity.

2. Materials and Methods

2.1. Study Area

The models predicting CSH were primarily developed with datasets covering areas located in the southern part of Belgium [26]. So, the same geographical region was used to test the prediction platform. To tackle different meteorological scenarios, the considered grazing periods (from April to October) ranged from 2018 to 2021.

2.2. Global Design

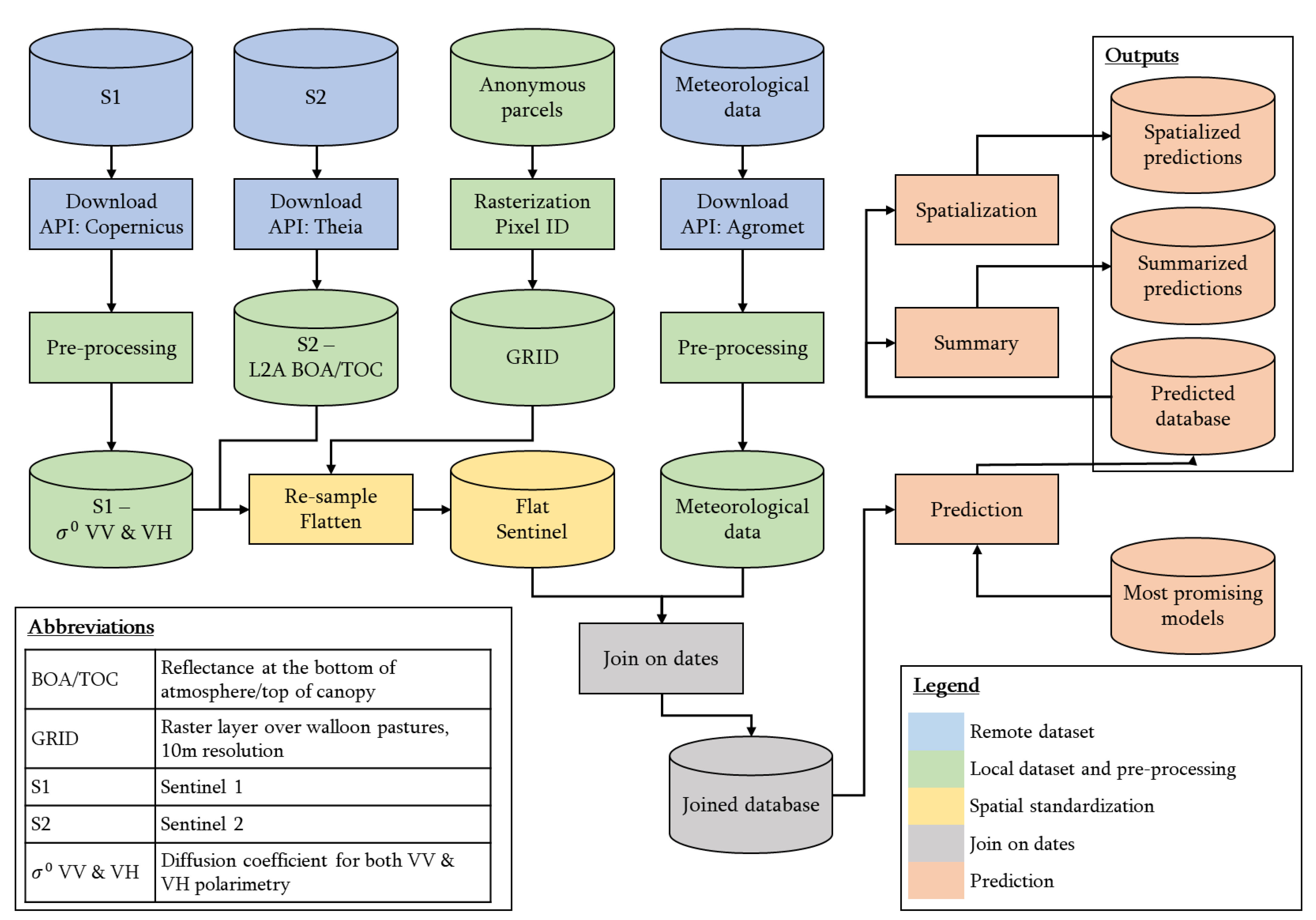
The global architecture of the prediction platform, developed with both R v4.1 [28] and Python 3.6 [29], is summarized in Figure 1. For the sake of completeness, it should be noted that this platform was designed with a batch processing approach. This choice is in opposition to a streaming approach that is not suited for the combination of data with different acquisition frequencies. The R and python packages, as well as the other programs used, are referenced in

Table 1. List of software and package used.

Software/Package	Version	Reference
R
R	4.1	[28]
sf	1.0–2	[29]
data.table	1.14.0	[30]
raster	3.4–13	[31]
future	1.21.0	[32]
future.apply	1.7.0	[33]
caret	6.0–88	[34]
dplyr	1.0.7	[35]
e1071	1.7–8	[36]
Python
Python v3.6		[37]
subprocess		[38]
os		[39]
time		[40]
glob		[41]
datetime		[42]
re		[43]
sentinelsat		[44]
pandas		[45]
Other
SNAP geoprocessing toolbox	8.0.0	[46]
7zip		[47]

. The Python scripts were used to configure and launch the R scripts in independent environments to avoid memory leaks that had happened when developing only in R.

2.3. Data Acquisition

The acquisition of remote data is illustrated in blue in Figure 1.

The S1 constellation is a set of two satellites, S1A and S1B, collecting space-borne synthetic-aperture radar data in the C-Band. Data was accessed from the European Space Agency’s (ESA) API [48] for S1 with the help of the Sentinelsat Python package; the S1 data were retrieved in the form of GRD products. Both VV and VH polarization were used. The 37, 88, 110, and 161 relative orbits were used as they offer good coverage of the studied Walloon area. There are discussions in the scientific and remote sensing community about the speckle effect and the need to include the coherence product to get better and more consistent outputs. The drawback of this type of data handling is the need to consider the whole parcel, and the changing nature of these parcels makes this task challenging. In order to include improvements, the platform presented in this study was made to be modular regarding the models and the data treatment workflow. Regarding the consideration of the neighboring pixel values, [49] suggested that stacking convolution could help algorithms detect multi-scale effects. This would translate into a future evolution of the pretreatments, for the model training process and the platform, into a spatial convolution and the addition of features in the models.

The S2 constellation is a set of 2 satellites, S2A and S2B, collecting reflectance/optical data over 12 spectral bands. Theia’s API [50] was accessed with the help of the theia_download.py script [51] and provided bottom-of-atmosphere/top-of-canopy reflectance products, also known as level-2A (L2A) products. The tiles covering the extent of Wallonia were: T31UDS, T31UER, T31UES, T31UFQ, T31UFR, T31UFS, T31UGR, and T31UGS. The main reason for the change in data provider was that the MAJA algorithm implemented behind Theia’s API allows L2A products based on the exact computation of correction formulae, instead of using the lookup-table methodology underlying the L2A products acquired from the ESA API. Moreover, downloading past data was much easier using Theia’s API compared to the difficulty generated by the long-term archiving policy of the ESA.

In our previous article, we used meteorological data from a meteorological station located on an experimental farm [26]. To be able to predict grass growth over the entirety of the Walloon Region, it was more relevant to consider meteorological data covering all of this geographical area. So, the Agromet platform [52] was used and provided data, on a minute basis, related to the air, soil, and under leaf temperatures (°C), the wind speed at 2 meters above soil level (m/s), and its direction, solar radiation (J/cm²), precipitation (mm), relative air humidity (%), and the potential evapotranspiration (mm/day), computed according to the FAO/Penmann-Monteith formula [53]. The data with the corresponding station identifier geographically localized were retrieved under .csv files from the day before the launch of the acquisition to ensure a complete recording of data within a day. The change in the data provider compared to the one used in [26] was motivated by a finer representation of Wallonia than was possible with one meteorological station, the standardization of the acquisition conditions, the near real-time availability of the information, and the convenience of retrieving the data through an API. Compared to [26], another change was made concerning the meteorological data. The choice between the previous computation of the degree-days, also used by [54], and the method currently proposed, also used by [55,56], was based on questioning the meaning of this variable. The 0 °C base temperature referred to the ability to grow in winter, and the 35 °C peak approximated the temperature of the diminishing activity of RuBisCO activase [57,58]. The lower threshold could be queried because some plants do not tolerate 0 °C, but this temperature was kept as it represents the water freezing point and, therefore, the limit of water availability.

2.4. Data Preprocessing

The data preprocessing is illustrated in green in Figure 1. Before being usable by the models, the S1 GRD images need to be geocoded (i.e., properly projected from SAR geometry to “classical”/GiS usable geometry). The framework presented by [59] and based on the use of the Sentinel-1 Toolbox as a part of the SNAP software v8.0 [46] was applied to each tile. The S1 data was then converted using the backscatter coefficient (${\sigma }^0$) and stored in .img raster files.

To ensure the quality of S2 data, some filters were applied: S2 tiles having more than 95% “NoData” values in the pixels, 95% saturated pixels, or 95% cloud-covered pixels were discarded to avoid biased information entering the data treatment chain. Furthermore, these “NoData”, “Saturation”, and “Cloud mask” filters were applied to the remaining tiles. Another filtering step was to remove the values inferior or equal to zero and superior to 1, given that the reflectance is supposed to be within the [0;1] range. The S2 data were then transformed into .tif raster files.

The meteorological data initially recorded on a minute basis were aggregated at the day level and recomputed to obtain the minimum, mean, and maximal temperature, the cumulative sum of the solar radiation, the cumulative sum of rain, wind speed, relative air humidity, and evapotranspiration. The degree days were computed on a 0 °C basis with an upper limit of 35 °C. This is translated in the following pseudo-code:

If(((Tmax+Tmin)/2)>Tbase):

 If (((Tmax+Tmin)/2)<Tup):

  DJ_00=((Tmax+Tmin)/2)-Tbase

 Else:

  DJ_00=Tup

Else:

 DJ_00=Tbase

where Tbase is the base temperature (here 0 °C), Tmax corresponds to the maximum temperature of the day, Tmin is the minimum temperature of the day, and Tup is the upper limit temperature (here 35 °C). Moreover, the rolling sum of precipitation and degree days over the previous 3, 7, and 15 days was also computed for each acquisition date. The meteorological data were incrementally added to a .csv file that acts as a database.

2.5. Spatial Standardization

The manipulation of spatial data requires that special attention be paid to the format and referencing of data. To ease reference processing, the S1 and S2 datasets were spatially standardized according to the same reference, as illustrated in yellow in Figure 1. The spatial reference was obtained as follows. First, Walloon farmers have an obligation to report the parcels they use to the authority and their allocations. These data are then anonymized and available on the WalOnMap platform [60]. For this study, the parcel assignment declared for 2018 was used and was composed of 194,657 pasture parcels stored in a shapefile polygon file. A raster extending over the whole Walloon area with a resolution of 10 m was created using QGis v3.20.2 [61]. Parcels were identified and a unique identification number was attributed to each pixel, and both were encoded as integers. Finally, this gridded version of the parcels was projected into EPSG:32631 and saved in a .tif file using integer encoding to avoid uncertainties on the high pixel values. For this study, the spatial standardization was based on the Walloon parcel assignment realized in 2018. In theory, it would be optimal to use the parcels reported for the year of prediction. However, some constraints prevented this: parcel repartition is uploaded one year after the actual report, and some parcel IDs change. Thus, it might be relevant to discuss the use of the last repartition available. The substantial amount of permanently grazed swards, i.e., 89% of all the Walloon pastures were permanent [62] (for more details, see Annex/SM 3), reinforced the choice of ignoring this source of complexity. This implied that some land patches might either be predicted, although they are not supposed to be, or the opposite. The future DSS should therefore include a step to determine the parcels that farmers want to monitor. The inclusion of the pixel ID should ease this process.

The standardization step consisted in projecting and resampling each S1 and S2 tile independently into a copy of the reference spatial dataset. The resulting raster datasets were forced into a tabular dataset where each row represented a pixel, and the columns corresponded to the pixel ID, the parcel ID, and the S1 or S2 data. Each converted tile was saved in a .csv file

To cover the area of Wallonia, it was necessary to define how the meteorological stations impact each pixel. A simple assumption was chosen: the meteorological data for a pixel corresponds to the data acquired at the nearest station. Therefore, Voronoï polygons were drawn between the meteorological stations. To cover the entirety of the Walloon Region with these polygons, artificial stations were placed far away from the Walloon borders. After making sure that these stations did not appear inside the area of Wallonia, the polygon layer was cropped according to the actual limits of Wallonia with a 2 km buffer to include the pasture parcels that were shared between the 2 countries. The resulting spatial file was a polygon shapefile with the station ID. Then, an intersection with the parcel shapefile was performed to generate a correspondence table that links the parcel IDs to the meteorological stations. In cases of multiple correspondences, only the first appearance was kept.

2.6. Merging Datasets

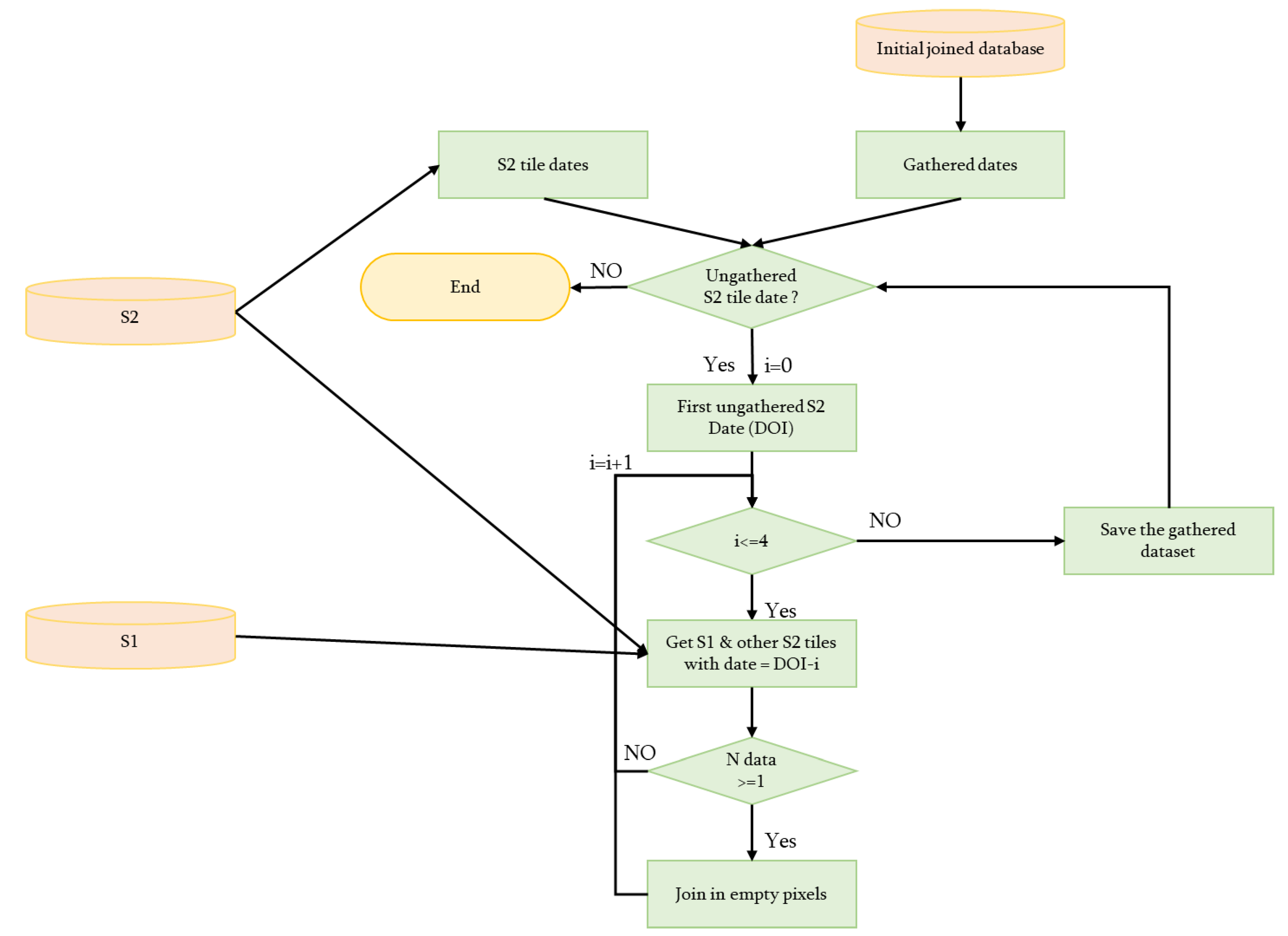
The merging of datasets is illustrated in grey in Figure 1, and the precise workflow is shown in Figure 2. The first steps concern the joining of S1 and S2 data from the pixel identifier. First, the dates when the S2 tiles were acquired were identified. These dates were compared to those present in the joined database. Each date not yet treated was then processed one at a time. For the first date, all the S1 and S2 tiles acquired on the same day were fetched and joined based on the pixel identifier. The joining did not require an identifier match between the two datasets; therefore, parts of the joined dataset were filled with only S1 or S2 data. Then, the data acquired one day before were also retrieved and used to fill the remaining empty pixels. To mark the time lag between the datasets, a flag containing this time lag (dt) was included in the file. This filling continued until four days before the date of interest had been obtained. This methodology implies that there could be different dts for S1 and S2 records for one pixel. The joined dataset was then saved in the joined database, and the process was repeated for each date not yet gathered.

Once S1 and S2 datasets were joined, the addition of the meteorological data was realized from the original S2 date.

2.7. Model

Although we have already developed models predicting CSH [26] at the pixel level, new models were retrained due to the availability of more reference CSH values and some changes in the data treatment like the computation of degree days on a 0–35 °C basis, and the removal of the feature transformation related to band 01 of the S2 dataset due to the absence of this band in the dataset coming from Theia. Moreover, a new type of model was tested: an extreme gradient boosting variant (xgbTree). The feature selection process did not change from [26]. The hyperparameters used for every tested model are summarized in

Table 2. Hyperparameters tested and final values for the models used.

Model	Parameter	Final Hyper-Parameter Value
xgbTree	Nrounds; max_depth; eta; gamma; colsample_bytree; min_child_weight; subsample	200; 6; 0.1; 1; 0.5; 1; 1
Cubist	committees; neighbors	10; 0
Random Forest (RF)	mtry	88
glmnet	Alpha Lambda	1; 0.1
nnet	Size; decay	3; 0.01

; the detail of the hyperparameters explored is presented with other prospects related to the model creation in Annex/SM 2. They were selected from the range of values published in [26] through the application of k-fold cross-validation based on the k dates of acquisition to avoid operator and meteorological data leakage. An alternative could be to perform a 10-fold stratified validation based on the dates to increase the range of data on which the model was trained, but with the drawback of data leakage and the induced risk of over fitting. The accuracy of the models was assessed through computation of the root mean squared error (RMSE) for the hyperparameter tuning cross-validation, for the actual calibration with the best set of hyperparameters, and for the validation applied on an independent dataset, here consisting of data collected on a different farm. The validation ratio to performance deviation (RPD) was also computed. Moreover, the mean, standard deviation of the prediction, and percentage of underestimated values from the validation set were also used to assess the quality of the models. This percentage corresponds to the ratio of the number of underestimated values to the total amount of values. The calibration dataset was composed of 9376 records collected on 2 farms between 2018 and 2020. The validation dataset contained 871 records collected on another farm in 2019.

2.8. Prediction

Once the whole dataset was gathered in the form of a table whose rows are the records representing one pixel and the columns are the features needed by the built model, the dataset was split into subsections of 100,000 rows to bypass the internal memory limitations of R. The following process was applied in parallel to these chunks: (1) check that all values are actual numbers (i.e., not logic); (2) apply all the required feature transformations; (3) perform the prediction. Due to the different handling of the missing values between the models, special attention had to be paid to the way those values were transferred or not. The resulting predictions were then gathered in a .csv file containing the parcel identification, pixel identifier, S1 and S2 data, as well as the meteorological data and the predictions. Each .csv file corresponds to one date.

2.9. Analysis of the Predictions

The analysis of the prediction consisted of a visual check and statistical analysis.

The visual check required that the tabular data be transformed into raster data. This was achieved through a five-step process: (1) create a vector of “not a number” (NA) values with the number of cells in the Walloon pastures raster; (2) fill the places where there were predictions using the pixel ID; (3) convert the vector into a matrix respecting the fill order used in the raster; (4) stack this matrix with the original Walloon pastures raster; and (5) write the raster. The visual checks were performed with QGis and aimed to observe the global predicted CSH evolution and the occurrence of abrupt predicted CSH changes in parcels.

The quantitative approach consisted of (1) the study of the performances of the model in calibration, cross-validation, and validation; (2) the number of predictions at the parcel or pixel scale depending on the year and the restriction(s) applied in the joining process; (3) the variability of the CSH predictions performed at a large scale; and (4) a temporal analysis.

The analysis revealed criteria not used in [26] that could be relevant to assess the quality of the models and their appropriateness to the platform’s ends. All the criteria were: the RMSE of validation, RPD of validation, the trend to over-/under-estimate, sensitivity to the time-lag inclusion, production of out-of-range values, temporal stability (changes in the values of the mean/standard deviation over the time and appearance of transient spikes), and the spatial heterogeneity of the predictions. Each model was given a ranking for each criterion, and the sum of the ranking gave the total ranking of the model. The exact relationship between the criterion and the ranking is that lower validation RMSE implies a lower ranking; idem for validation RPD; an over- or underestimation ratio closer to 50% implies a lower ranking; the less sensitivity to the time lag inclusion, the lower the ranking; the less production of out of plausible range values, the lower the ranking; the better the temporal stability, the lower the ranking; and the lower the spatial heterogeneity on known homogeneous parcels, the lower the ranking.

3. Results and Discussion

First, we will present the constraints related to the prediction process and the interest in the proposed solution to increase the frequency of data acquisition. Then, we will discuss the data choices and changes, the practical implications of the data fusion, the newly trained models’ accuracy, and their prediction relevancy.

3.1. Practical Constraints

3.1.1. Data Availability

The interest in the developed prediction platform is strongly related to its ability to provide the farmer with reliable information on a routine basis. The prediction models proposed in this paper used three kinds of raw information: S1 and S2 satellite images and meteorological data. The data availability was critical as it directly impacts the potential prediction frequency. As the prediction model used daily aggregated meteorological data, the prediction of CSH can only be made after the test day. As the Agromet API provides meteorological records in real-time, if the day is not yet over, the aggregated value cannot reflect the entirety of the day. For this reason, we had to restrict the data download to the day before the launch. So, the platform should be launched after midnight to provide close to real-time CSH predictions. However, this is the easiest constraint to solve in terms of data availability.

3.1.2. Frequency of Acquisition

The biggest problem is the acquisition of S1 and S2 data. The first part of this problem is the S2 revisit frequency. Theoretically, at the equator, each satellite has a revisit frequency of 10 days, leading to a total revisit frequency of 5 days when accounting for both satellites. Given the latitude of the Walloon Region, the satellite orbits partly cover each other. This leads to a part of Wallonia (the center in this case) witnessing acquisitions more often than the rest. This asynchronous acquisition of S2 produced a requirement to account for spatially partial and asynchronous acquisitions. Furthermore, another complex factor was the acquisition frequency of S1 and the coverage of those tiles that were not synchronized with the S2 tiles. The last main constraint on the acquisition frequency was the presence of clouds that decreased the availability of S2 data. This led to an unbalanced dataset representation of S1 and S2 datasets, although the difference in the number of dates of acquisition is not in favor of one or the other dataset. The huge increase in the number of S1 tiles used in 2021 is, in fact, a lack of tiles for the previous years; the long-term archiving policy of the ESA made the acquisition of old tiles difficult.

3.1.3. Hardware and Time

Besides data availability, another constraint is the time needed for the prediction computation. Despite using up to 16 CPU cores and 250 Gb of RAM, the platform requires up to 5 h to deliver predictions at the Walloon scale for one day if the data acquisition is particularly complex. This reinforces the need for launching the platform in the middle of the night. Moreover, consequent storage is needed: if no cleaning of the temporary files is performed, the storage required rapidly adds up. In the case of this study, for monitoring four years with missing dates, we used around 8 TB of disk space without accounting for the temporary files.

3.2. Model Accuracy

The feature selection process led to a different number of features selected in this study compared to [26], where the nnet model was based on 47 variables, and the other most promising model on 160, while the newly trained model included either 143 or 158 most promising features (

Table 3. Performances of the newly trained models with the new data and feature definition. (RMSEcv = cross-validation root mean squared error (RMSE); RMSEcal = calibration RMSE; RMSEval = validation RMSE; RPD = validation standard deviation (SD)/validation RMSE).

Model.	N Features	RMSEcv (Mean ± SD) [mm CSH]	RMSE cal [mm CSH]	RMSE val [mm CSH]	RPD val	Mean ± SD Prediction (Validation Set) [mm CSH]	Percentage of under-Estimated Values (Validation Set)
Cubist	158	23.77 ± 16.20	17.61	17.91	0.85	53.69 ± 9.95	57.52%
Glmnet (Gaussian)	158	22.48 ± 7.00	21.59	15.15	1.01	53.24 ± 6.85	63.15%
Nnet	158	24.08 ± 7.26	23.11	18.67	0.82	46.71 ± 6.36	78.07%
RF	143	22.39 ± 5.55	7.08	17.68	0.86	50.56 ± 8.67	66.70%
xgbTree	143	21.90 ± 6.10	10.68	17.93	0.85	50.16 ± 9.38	66.70%

). The order of importance of the features slightly changed and more details are provided in Annex/SM 4. The main takeaway is that this variable importance ranking indicates a majority of meteorological and S2 variables in the most informative features, therefore, the choice of the S2 acquisition date as the key point for the gap filling seems relevant as a small shift in these variables might induce a greater change in the final values.

The RMSE performances observed during the hyperparameter tuning cross-validation, calibration, and validation processes (Table 3) were similar to the values reported in [26]. Furthermore, the smaller calibration RMSE values observed for RF and xgbTree were due to their high capability to fit the dataset, and the difference in the validation RMSE for these models indicates a potential overfit. Although the RMSE of calibration and validation seems high in this configuration, the high value of the RMSE of cross-validation and the inherent variability (standard deviation) shows that we should expect a higher error than the error of validation when confronting the models to different conditions and that a fine tuning of the hyperparameters was required, especially for the Cubist model.

The validation RPD was similar between the models, although it seems to imply that the glmnet model could better reflect the variability of the validation dataset. The mean and standard deviation of the predicted values calculated on the validation set suggest a global underestimation of the actual CSH compared to the original mean and standard deviation validation CSH values that were 57.1 ± 5.23 mm. This trend is also highlighted by the percentage of underestimated values that ranged from 57.52 to 78.07 %. It seems that the cubist model shows better respect for the original distribution of the data, whilst nnet underpredicts a lot. This trend to underestimate is compared to the impact of the rising plate meter used. As shown in [63], the ratchet-counter RPM used to calibrate our models tends to underestimate the actual height on hard supports. Therefore, it should be expected that the actual height will be higher than the predicted one.

3.3. Data Fusion

3.3.1. Dt Tolerance

To improve the prediction frequency and the area covered, a time tolerance was applied when merging S1 and S2 data, consisting of considering data acquired within the previous four days. The reference data for this merging was the S2 acquisition date, hence the similarity between the number of dates covered and the number of dates of S2 acquisition in

Table 4. Descriptive statistics of the available dataset. (*) the number of available dates = number of dates for S2 data acquisition.

	2018	2019	2020	2021
N dates without time delay	29	30	19	26
N dates *	86	71	70	49
N records/pixel	40.43	26.27	37.17	19.16
N records	1,611,879,463	1,047,054,399	1,481,945,618	764,039,165
Total amount of S1 tiles used	87	95	94	219
N dates acquisition S1	75	79	57	68
Total amount of S2 tiles used	352	276	298	164
N dates acquisition S2	86	71	70	49

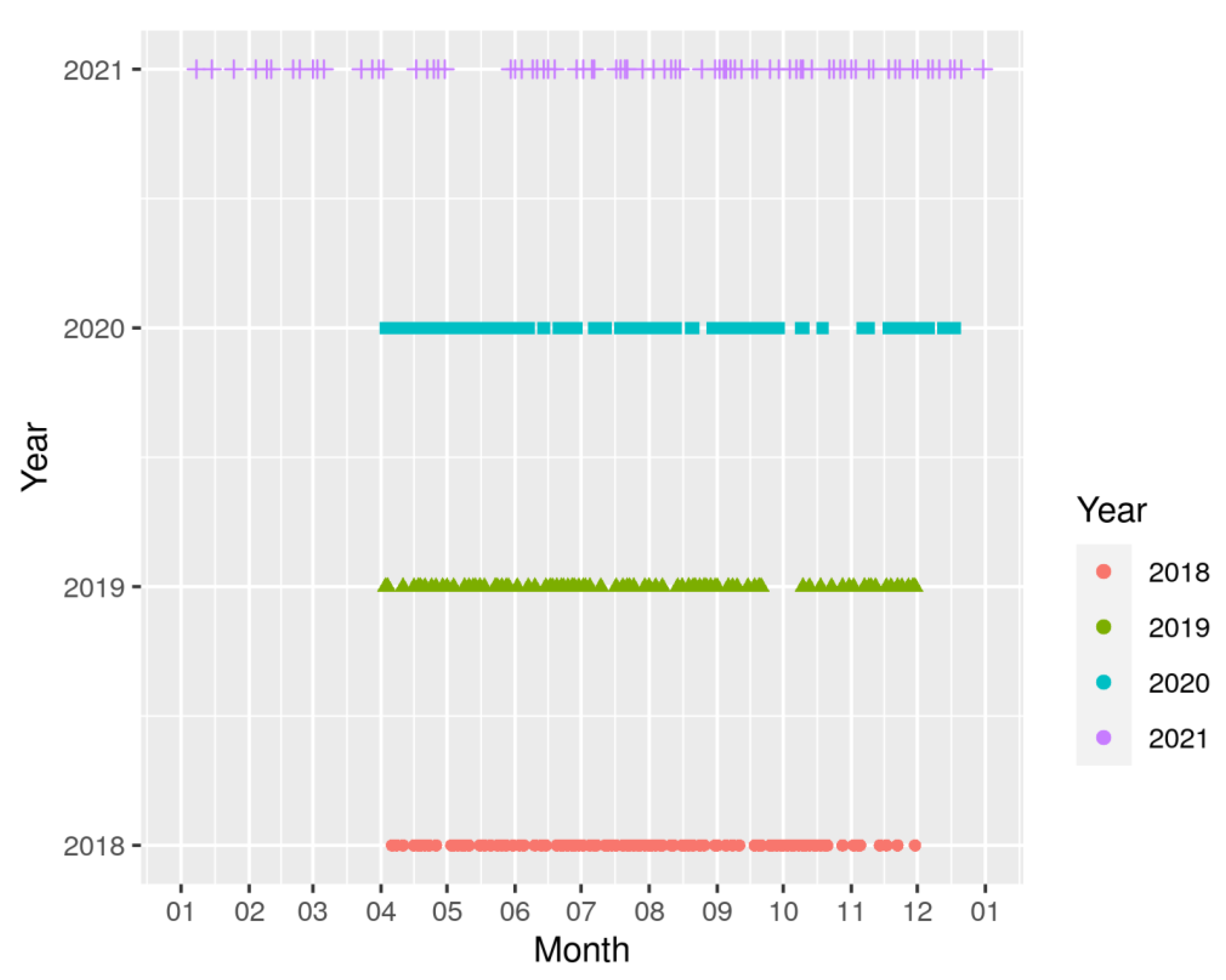
. To assess the improvement in terms of data acquisition (i.e., an increase in the quantity of data and dates covered), we compared the number of available dates with a delay of 0 days (dt0) and up to 4 days (all dts) (Table 4). This tolerance allowed the number of available dates to increase more than 2.5 times (from 104 without data augmentation to 276 with the gap filling) during the grazing period (214 days) if we consider the whole 4 years studied. The global frequency acquisition reached a mean value of 4 days. This improved temporal coverage can be explained not only by the merging tolerance used but also by the considered constraint for cloud presence. If we strengthened the condition of the cloud presence, described in the metadata description, to 25% to exclude a tile, 138 dates could be available for the whole studied period instead of 276 obtained when permitting up to 95% of cloudy/shadow area before excluding the tiles. This was possible because the prediction was made on a pixel basis and a strict application of the cloud mask to remove any biased (flagged as cloudy/shadowed) pixel. However, assuming a constant acquisition of 4 days is not true, as marked differences were observed between years (Table 4). 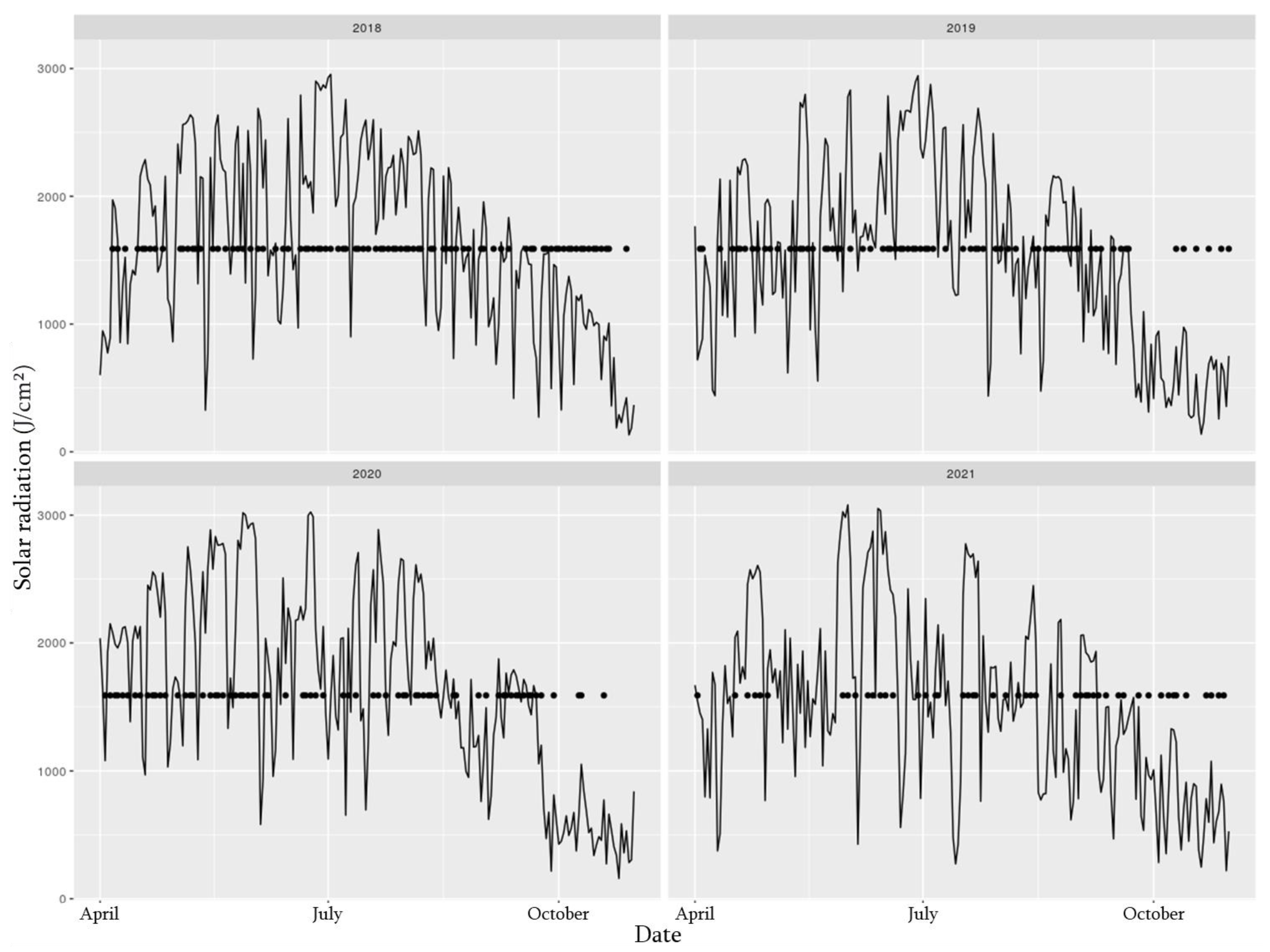Thanks to the merging tolerance, the number of available dates per year ranged from 49 to 86, and this acquisition was also not constant within a year (Figure 3). This is mainly explained by the meteorological conditions. Gaps in the prediction frequency correspond to drops in the mean daily solar radiation received on all the Agromet meteorological stations (Figure 4). The difference between the years matches reports from the Royal Meteorological Institute of Belgium [64], where some seasons were more humid than the average of the last 30 years, while others were significantly drier than the 4 years observed. The same is true for global temperatures.

In the raw prediction files, there was NA in the columns related to the time lag and the predictions. The number of records affected by at least one NA was significantly higher than the number of not affected records (e.g., in 2018, there were 3,118,009,467 records in total, compared to 1,611,879,463 full records). This mismatch was due to a non-exhaustive combination of the edgy pixel position (relative to the satellite orbits), poor weather, out-of-range/missing input values, or even absence of data acquisition, and part of the pixels filled with data from one dataset and not from the other. This led to partly incomplete databases. The amount of NA was smaller in the S1-related data, mainly due to the lower sensitivity to weather perturbations. Given the models currently implemented, the incomplete pixels could not be considered as inputs of the models to produce reliable predictions; hence they were excluded.

3.3.2. N Parcels and N Pixels

Even if the number of dates changed between the years studied, the numbers of parcels and pixels represented were equal (N = 194,364 and 39,866,540, respectively). This is expected as the covered area is the same, although the small number of not predicted parcels might indicate minor flaws in the coverage of the area of interest. However, the changes in the number of records per year implied different coverage within the year. The number of records per pixel ranged from 19.16 to 40.43. Although the number of tiles used for the last year was greater than for the other years, the number of records did not increase proportionally. This is due to the filling methodology applied that implied the discarding of past records if there was a temporally close record available.

3.3.3. Impact of the Merging Tolerance

The goal of the gap filling is to produce maps that are as complete as possible. We decided to only work with past data to ensure that the platform could be deployed on a real-time basis. The main idea was that the most reliable information about a parcel should be the last time data were acquired and with a revisit frequency between 3 and 5 days. A time window of 4 days was found to be the best option. The impact of the merging tolerance on the predicted CSH was dependent on the satellite platform and the year considered (as illustrated in Annex/SM 5), especially for higher time lag windows; the increase or decrease (depending on the model) of the range of predictions was more pronounced. This underlines the need for caution about the application of this gap filling methodology.

However, this does not mean that the predictions were completely biased. Using this gap filling method increased the available data between 2 and 3 times for the S1 data and between 2 and 1.5 times for S2. The breakdown of the percentage of data added by the increment of the time lag tolerance is shown in

Table 5. Percentage of data acquired within a given time lag (dt) from the computed date.

Time Delay (Days)	S1				S2
	2018	2019	2020	2021	2018	2019	2020	2021
0	31.61%	38.35%	33.06%	43.72%	47.44%	50.17%	52.46%	59.84%
−1	36.17%	40.05%	26.17%	32.01%	23.31%	19.39%	20.86%	12.92%
−2	20.66%	14.83%	18.74%	20.87%	7.12%	6.48%	9.56%	5.26%
−3	7.71%	3.84%	18.01%	0.06%	21.98%	23.87%	17.05%	21.82%
−4	3.85%	2.93%	4.02%	3.34%	0.15%	0.09%	0.07%	0.16%

. It appears that most of the filled data were acquired between 0 and 2 days before the date of the merging (which corresponds to the most stable predictions), and the fourth-day consideration brings only a limited amount of information (maximum 4%) which corresponds to the most unreliable data. Therefore, there are two possible interpretations of the changed scope of prediction values observed at the four-day time lag repartition of prediction: either there are so few values that the entire scope of the values possible could not be represented, or the inclusion of the fourth day diminishes the reliability of the predictions—although this second hypothesis should be mitigated by the difference in impact between the models. The increase in the use of older information seen in 2020 and 2021 might be due to the poorer meteorological conditions of these 2 years.

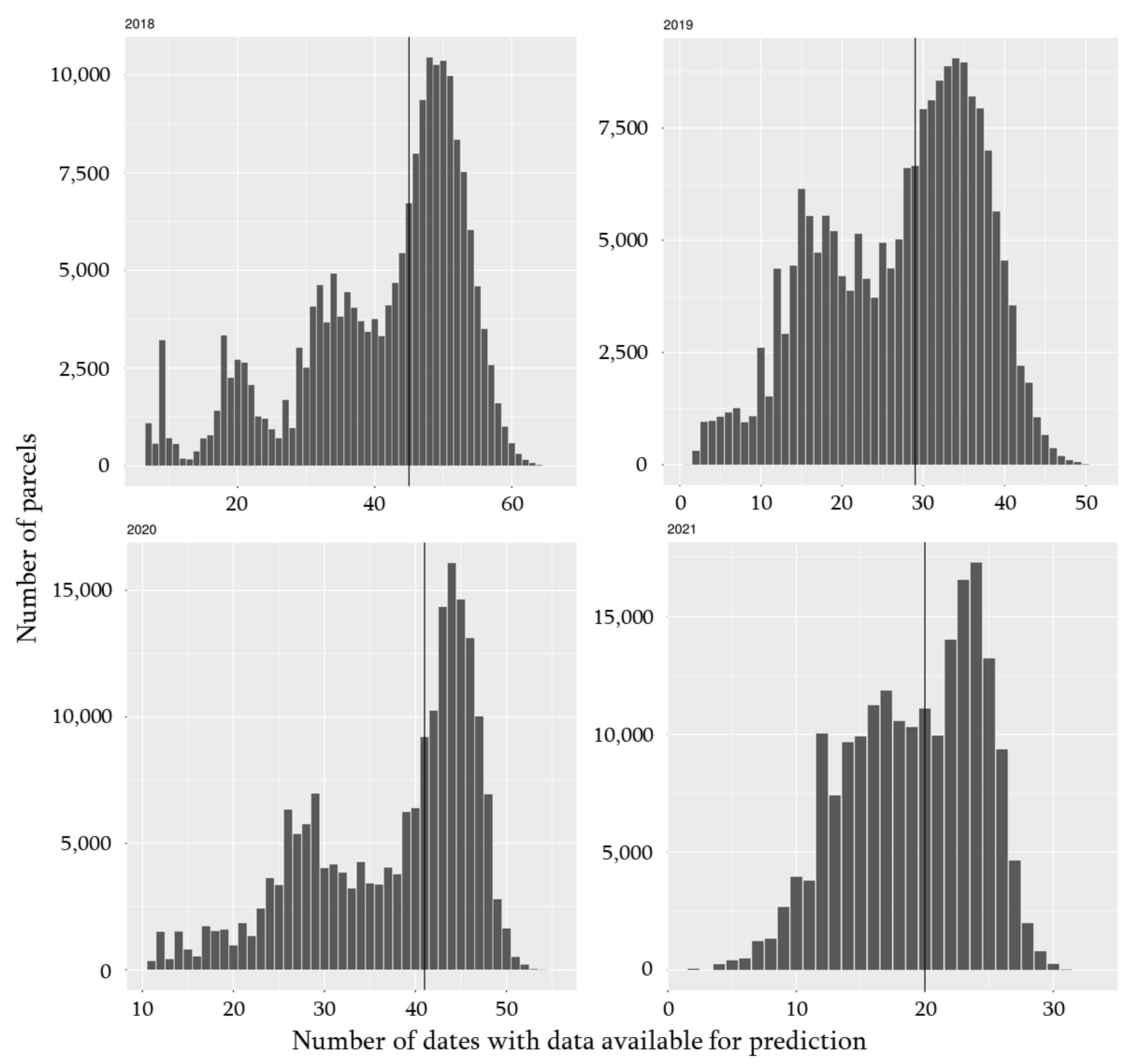
The number of predictions that can be made over each grazing season was increased by better temporal and spatial coverage. Indeed, using data in the past for S1 and S2 completion led to the retrieval of data on areas that were not covered at the specific date of acquisition. This type of partial recompletion is partly due to the satellite coverage of the Walloon extent. Indeed, in the case of S2, there are two acquisition orbits. Therefore, if the acquisition through these orbits were close enough temporally speaking, the past data re-usage implies an increase in the level of spatial completion. However, it does not always happen, and another related phenomenon induces data augmentation; these two acquisition orbits partly overlap, leading to better coverage of these areas and, thus, of some parcels. The effect of this data augmentation can be seen in Figure 5, which illustrates the distribution of the number of times a parcel is represented based on the actual number of occurrences of each parcel per year. Multiple modes can be guessed. As the distribution is quite spread out, summarizing the information is complex. Nevertheless, the median seems to reflect well the majority of the information. The median number of occurrences per parcel was: 45, 29, 41, and 20 for the years 2018, 2019, 2020, and 2021, respectively. This means a median parcel coverage rate, with the proposed gap filling methodology, between 41% (=20 days of the potentially 49 covered for the year 2021) and 59% (=45 days of the potentially 86 covered for the year 2018). As these percentage of odds to have a parcel covered during irregularly spaced time periods with varying numbers of recording dates across the said periods might seem hard to use for future users, a simpler yet more valuable approach could be the assessment of the probability of getting X prediction a year that is illustrated in Annex/SM 6.

3.4. Prediction Relevancy

By studying the predictions made in the Walloon Region of Belgium during four annual grazing periods, the aim of this paper was mainly to check if the outputs of the prediction platform were believable and consistent. The amount of different topological and geopedological conditions studied was limited in our training and validation datasets compared to the variety of possibilities present in Wallonia (two agricultural areas were represented out of eleven). To increase the representativeness of the calibration and validation sets, the best method would be to increase the dataset size. This requires a consequent greater sampling effort. Even if this complex approach is needed, it might also be relevant to study the behavior of the prediction at a large scale to see whether parts of the predictions were inconsistent.

Although CSH predicted values were mainly positive using all tested models, less than 1% of the CSH values predicted from the glmnet model were negative. This model also had a tendency for less than 1% of the obtained predictions to give values much greater than 250 mm, which is the maximum CSH measured by the rising plate meter [26]. For the other models, we observed positive values lower than 250 mm, even if the cubist model can sometimes present a maximum value greater than this threshold. It also appeared, following a model-by-model removal of the extreme values and iterative check of all the model predictions, that the records with an out-of-range prediction from the glmnet model did not correspond to the extreme values predicted with other models.

Table 6. Descriptive statistics of the cleaned dataset using the five studied models predicting the compressed sward height (mm). CV = coefficient of variation, the ratio of the standard deviation (SD) by the mean multiplied by 100, N stands for the number of cases.

	2018 (N = 1,137,991,583)	2019 (N = 1,046,797,529)	2020 (N = 1,481,945,618)	2021 (N = 763,510,335)	Between Year CV (%)
Model	Mean ± SD	Mean ± SD	Mean ± SD	Mean ± SD
Cubist	56.01 ± 19.94	63.77 ± 20.11	60.07 ± 20.10	59.16 ± 18.48	5.34
Glmnet	48.62 ± 20.35	58.22 ± 21.24	54.97 ± 21.23	54.22 ± 17.95	7.39
Nnet	61.09 ± 21.85	66.48 ± 25.46	67.21 ± 25.44	61.26 ± 19.45	5.14
Rf	54.99 ± 20.63	65.51 ± 20.11	62.14 ± 20.11	61.27 ± 17.33	7.20
xgbTree	53.58 ± 21.16	64.11 ± 20.92	60.51 ± 20.92	60.61 ± 17.85	7.39
CV (%)	8.19	5.04	7.21	5.01

presents the annual descriptive statistics of the values predicted per pixel using the five studied models after removing the records with extreme values out of the 0–250 mm of CSH range (less than 2%), i.e., 346,465; 256,870; 447,156; and 528,830 records were removed in 2018, 2019, 2020, and 2021, respectively. The five models predicted 75% of the values below 75 mm. A direct interpretation of these values would be that all farmers are using their swards efficiently by maintaining the grass in a constant state of maximum growth. This interpretation should be counter-balanced with the accuracy of the models (most had an RMSE of independent validation around 20 mm of CSH) and the trend to over-/underestimate the actual CSH, assessed through the percentage of over- or under-predicted values. In [26], the models developed tended to overestimate; whilst, in this new study, they tend to underestimate. More statistics are gathered in Annex/SM 7.

Concerning the variability of the prediction, the first approach compares the mean and standard deviation values shown in Table 6. The small variability reflected by the coefficient of variation, computed as the ratio of the standard deviation by the mean multiplied by 100 (CV), values (below 10%) computed on the means indicate global consistency in the predictions—one year did not seem to be completely offset, nor groups appear to form, and no significant difference can be found for the model relevancy.

The CSH values observed during the model calibration and validation and for the predicted values on a larger scale were lower than the corresponding values observed in Norway [65], Germany [66], or England [67]. This difference is mainly seen because the goals of the pastures were not the same: those parcels were used to grow forage for harvest, while the parcels on which we trained our models and most pasture parcels in Wallonia are grazed. Therefore, the fact of obtaining a mean grass height per parcel ranging from ±30 cm to ±60 cm (Norway) or with more than 50% of values above 10.5 cm (England) would be considered a loss in our study, whereas it would be relevant for good forage yields. This difference is less pronounced when compared to the data from Germany (CSH ranged from 5.82 cm to 19.1 cm with a mean ranging from 7.27 to 14.87 cm).

The shape of the distribution of the prediction matches the “commonly used” descriptive distribution of pasture herbage mass as defined in [68], which is a log-normal/gamma distribution. [67] also reported a similar distribution of the sward height. Furthermore, a similar distribution pattern can be deduced from the comparison between the unmanned aerial vehicle (UAV)-derived sward height and CSH in [69] or in the comparison between the light detection and ranging (LiDAR) sward height and the UAV-based sward height in [70]. The distribution of the predictions in this study included 75% of the predicted values in the [30–70 mm] range and a tail extended to the higher values.

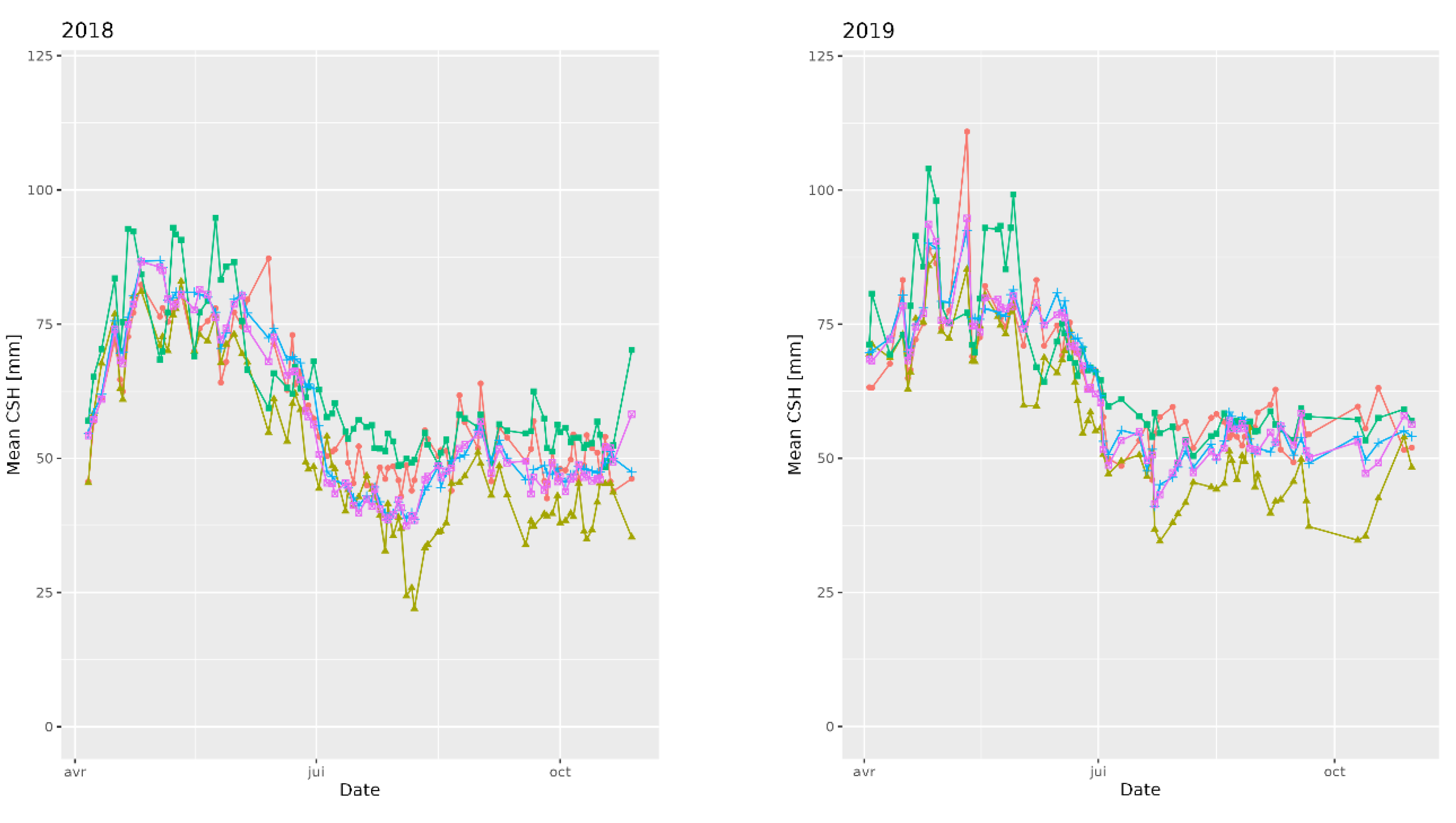
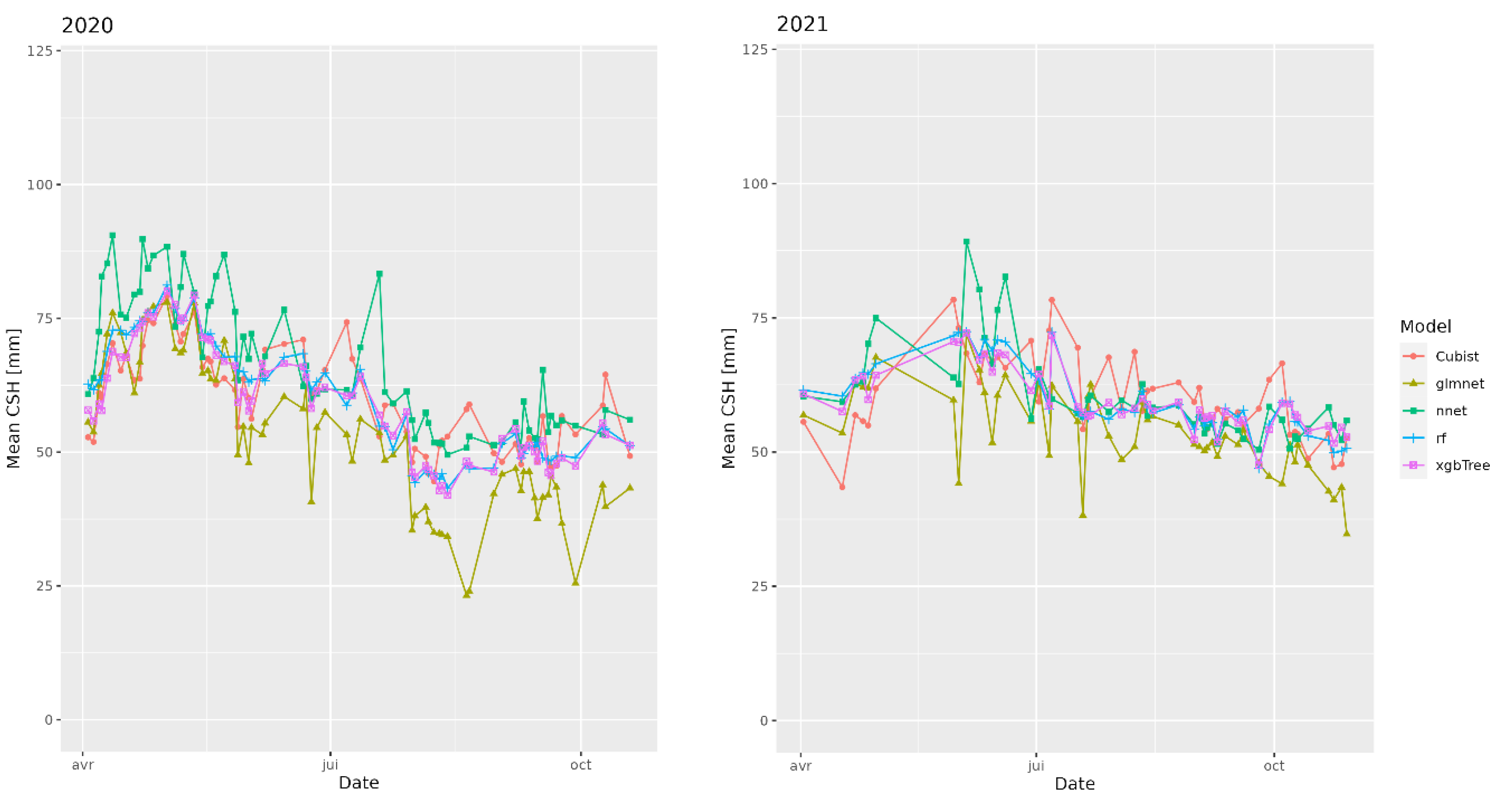
To go further into the temporal analysis of the predictions, it might be relevant to study the within-year temporal variability of the predictions. In theory, there should be an increase during spring until the moment the cows return to pasture, and then, depending on the cattle load, the CSH should remain stable or even decrease. This kind of pattern is observed in Figure 6, where the mean CSH per date of each parcel is represented for each model. The glmnet model seems to react in the same way as modeled in [26]: the values seem to be globally lower for this model than for the others. The annual behavior of grass growth matches the results of [71]: an increase of the CSH (which is directly linked to the actual biomass) during the first part of the year and then a decrease throughout the grazing season. The variability during the year 2021 was more important than within the other years, and the relative decrease of the summer period trend was less pronounced than in the other years. Both those trends could be explained by the high amount of precipitation that occurred during that summer: fewer acquisitions were valid due to cloud cover, which decreased the acquisition frequency and the reliability quality, and the drought of the previous years was considered as a feed loss for breeders using pasture. The relative decrease of the summer compared to spring in 2018 and 2019 was more pronounced than during the 2 following years, and it correlates well with the drought periods.

3.5. Spatial Heterogeneity Analysis

Besides the study of temporal behavior, it is necessary to consider spatial heterogeneity as proposed by [22]. Thus, the variability of the predictions inside a parcel was studied. For each parcel and date, the coefficient of variation was computed. These statistics are shown in

Table 7. Descriptive statistics of the coefficient of variation of the CSH computed for each date for each parcel.

	Cubist	Glmnet	Nnet	RF	xgbTree
Minimum	0.00	0.00	0.00	0.00	0.00
1%	2.34	3.46	0.00	2.27	5.14
1st quartile	6.87	8.02	3.81	6.32	9.82
Median	10.18	10.69	11.24	9.18	12.59
Mean	11.55	11.85	13.43	10.30	13.56
Standard deviation	6.60	6.18	11.41	5.49	5.29
3rd quartile	14.72	14.19	21.06	13.12	16.26
99%	32.97	33.01	40.78	28.13	30.45
Maximum	128.85	330.39	68.65	73.39	79.85

. Globally, the median values were always lower than 15%, which means there was high stability in the predicted values. The few extreme values are either due to extremely low standard deviation or extremely low means together with high standard deviation coefficients. The presence of trees, bushes, or hedges inside or at the border of the parcels could induce a higher prediction variability. One way to discard this part of the problem is to erode the parcel file with a negative buffer that should decrease the impact of trees and bushes near the parcel edge. However, there are parcels with edge and solitary trees inside their boundaries. Thus, to further decrease the impact of woody vegetation, an additional step to detect and remove the woody vegetation area from the parcels could be considered in future developments of the platform. The globally lower CV values observed for the prediction compared to the observations of [72] are probably due to climatic differences (both climates are temperate, yet Uruguay has a drier period in winter that Wallonia does not). Moreover, the methodology of [72] to assess the grass height was based on a visual discrete-scale analysis that was then transformed into actual height measurements. This meant that close to extreme heights could have been poorly identified, meaning a higher dispersion of the results and, thus, a higher CV. Lastly, concerning the study by [72], a factor linked to the grass species might also explain the difference, although the composition of the pastures was not disclosed. The observed CV values in the present study fit more of the values than observed in [73]: with uncompressed sward height deduced from image analysis, they got coefficients of variation from 4.5% to 39.0%, which corresponds to 99% of the values observed in the current study.

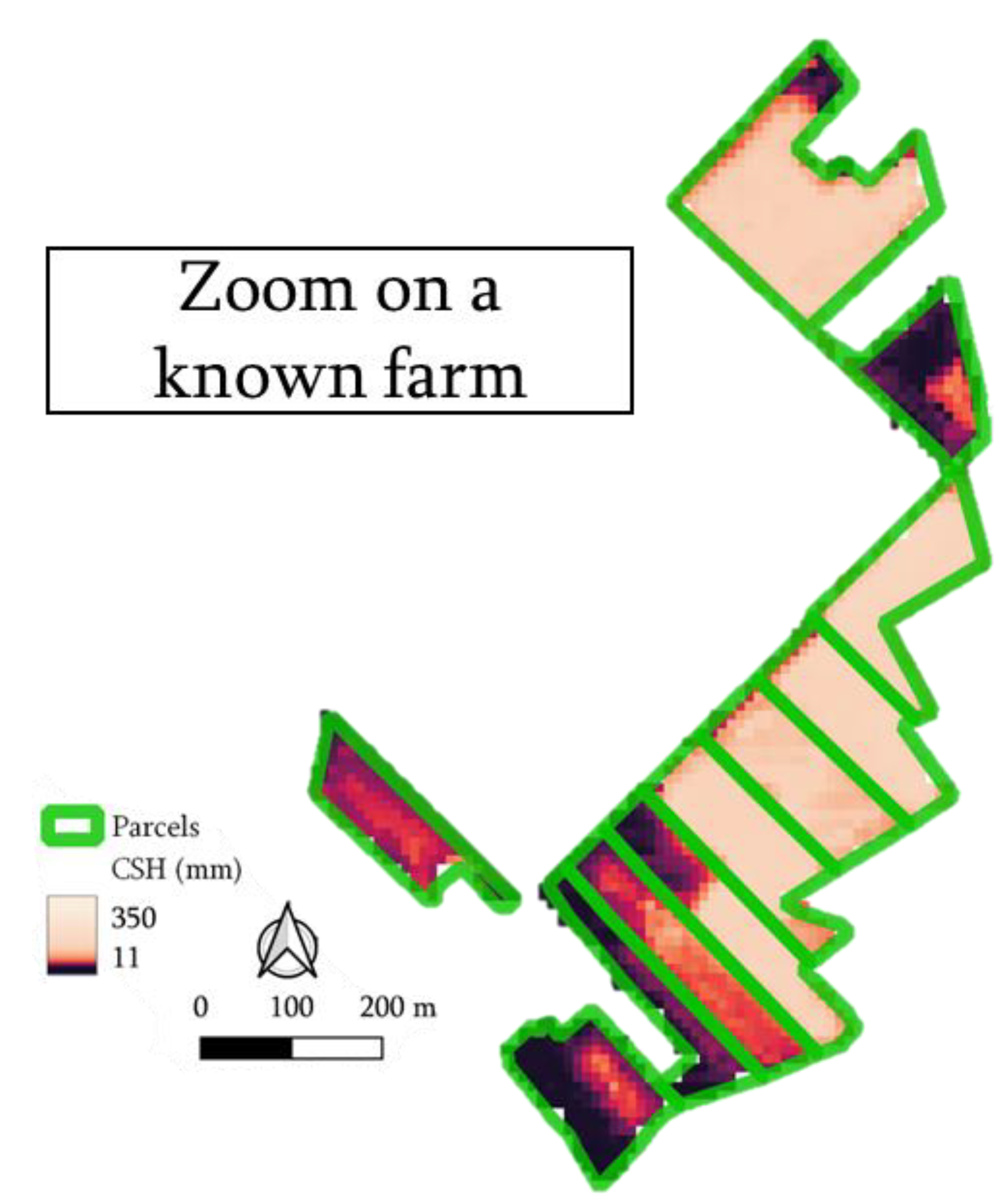
The variability within a parcel can be easily visualized. Figure 7 represents predictions at the scale of the parcels of a known farm for 21 April 2019 for a specific parcel. This date was chosen for the exact co-occurrence of S1 and S2 and for the absence of cloud cover. Checking for the presence of clusters of high/low values revealed a good repartition of the prediction, meaning that spatial over-fitting seemed to have been avoided. The specific zoom on this known farm revealed the ability to see patterns due to the topography and management.

Although a 10-m resolution might seem too fine given the area of the Walloon Region (16,901 km²), it is quite coarse when considering precision grazing, as underlined in [72] concerning the ability to reflect the internal variability of pastures. There could be improvement using the already available datasets: S1 tiles have a 5-m resolution. However, the gain in resolution would not be enormous for a huge increase in computation power needed, given that the current raster already had 15,413 rows, 26,006 columns, and 400,830,478 cells. If both datasets were to have a finer resolution, the increased computation cost could be more relevant. There are ways to create super-sampled datasets using algorithms, like the one created by [74], which generate space-borne optical data using the spectral resolution of the S2 satellites and the spatial resolution of the Planet satellites (around 2.5 m). This was not included in the first development of the platform, mainly to reduce complexity. It might be an improvement for future development.

Another spatial data improvement could be the inclusion of meteorological data spatialized at a finer level than the station. Although the Agromet platform [51] provides higher resolution data for air temperature and relative air humidity, a standard spatialization was chosen to avoid adding more complexity, but the modularity of the platform offers this possibility as an evolution. Furthermore, using kriging techniques might lead to a better representation of the link between the meteorological data and the parcel. However, the inherent complexity and the need to account for local and geopedological/topographical variations made this choice irrelevant in this study. The modular conception of the platform allows for later integration of this type of spatial standardization.

3.6. Model Selection

The use of this platform as a DSS data provider is currently hindered by the study of five models simultaneously, although the final user needs clear indications and thus should not have to choose between the models without knowing what lies behind them. Therefore, we suggest a complement to the analysis made in [26] to get the “best” model. Until now, the RMSE, RPD, and percentage of over-/underestimation were the major drivers to determine the models as “most promising” [26]. Here, criteria based on the application of the models at a large scale were added: sensitivity to the time lag inclusion, the trend to produce completely out-of-range possible values, temporal stability of the predictions (mean and standard deviation values of the prediction per year and the trend to witness abrupt changes during one year), and finally spatial heterogeneity. Furthermore, the capability to ignore missing data and substitute them could also be added as a criterion, although it might also be a problem given that the substitution is not controlled. The resulting ranking for the currently developed models is shown in

Table 8. Ranking of the most promising models according to multiple criteria.

Criterion	Cubist	Glmnet	Nnet	RF	xgbTree
RMSE (val)	3	1	5	2	4
RPD (val)	3	1	5	2	3
Over-/underestimation (1)	1	2	5	3	3
Sensitivity to the time lag inclusion	1	4	5	1	1
Production of out-of-range values	4	5	1	1	1
Temporal stability (mean & SD)	2	5	1	3	4
Temporal stability (spikes)	3	5	4	1	1
Spatial heterogeneity	2	5	1	2	4
Cumulated ranking	19	28	27	15	21

and suggests that the RF model is the best model for raw prediction performance, and Cubist is best for applications that require better temporal continuity.

3.7. On the Choice of Working with Compressed Sward Height

In this study, we worked with compressed sward height. It might be argued that it is more relevant to model actual biomass. The first point to highlight is that the spatial resolution of the pixels (10 m) is larger than traditional sampling quadrats: [71] used bands of 1 × 3.5 m for assessing biomass, [66] used bands of 1.5 × 3 m, and [75] used bands of 7 × 1.5 m. All those dimensions are below the actual resolution, which means that using the S1 and S2 data for the assessment of biomass is likely to introduce a lot of “not-exactly related” information and, thus, imprecision. Although we had datasets of biomass, the bands mown to get the biomass information were also smaller than the pixel resolution and were laid next to each other, which meant that the previous cut would influence the pixel value and therefore give inaccurate results. Besides this issue of coherence in the sampling, another problem was the small size of the dataset and the temporal variability of the relationship between the compressed sward height and the actual biomass, as illustrated in [76]. Furthermore, this variability was emphasized by the variability of the composition of pastures.

However, this platform was made to be modular. This means that if models were created using the same input variables names as we did, they could be implemented and used to perform predictions at a large scale. Therefore, this platform could be used to predict the biomass or the quality of the grass (e.g., protein/fiber content) from remote sensing data. Another approach that is currently being developed adds a conversion layer over the predicted CSH that would translate this value into the other aforementioned features, such as, in our case, the available dry biomass.

4. Conclusions

We assumed that predicting the CSH at the whole Walloon scale would require an intermediary platform to perform the prediction in order to decrease the computing load on the backend server of our future DSS. Given the time and resources required for the computation, this proved to be relevant. Despite issues underlined in the study, the platform is now up and running and is ready to serve as the data source for the future DSS. The main advantage of the models and data sources considered is their low cost. They are free to obtain, but a non-null cost is still considered as some processing is needed, and this requires hardware that has a certain cost. Another key advantage of the platform for the future DSS is that most of the computation will be performed beforehand, which means that the end-user application would not be computationally heavy and instead could be as reactive as the end-user hardware allows.

Although the platform is now operational, improvements are still underway. Concerning the prediction models, more CSH data are currently being sampled in order to increase the calibration and validation sets, and therefore, the robustness of the models that currently have a 20 mm of CSH RMSE at a pixel scale. Regarding the translation of CSH into available biomass, models are being tested to be used as a post-prediction layer. Some further developments might also be needed to implement the possibility of the user more precisely specifying their parcels with minimal additional computational cost on the user side, allowed by the use of a standardized sub-parcel/pixel reference spatialization. Furthermore, another important change will be the restriction of access to the data; if not enough restrictions are set in the DSS, there might be problems related to the European General Data Protection Regulation. Concerning the availability of the prediction, the current gap filling methodology restricts the prediction frequency to the acquisition of S2 information as this was the most informative data source (deduced from the relative variable importance in the models). Further research into the gap filling methodology and some paradigm changes would enable us to predict the CSH for every day of the year. Concerning the features considered, until now, we have focused on traditional feature resampling regarding the S1 and S2 datasets. Encompassing more pretreatments is considered for the future.

Concerning the analysis of the models and the determination of the best model to use, the application of the models at a large scale revealed strengths and weaknesses for all models, resulting in the designation of the random forest model as the best model to predict CSH at our scale with our data. To expand the analysis of the spatial quality of CSH predictions, it might be relevant to account for the relationship between the spatial and temporal behavior and the topographical/geopedological properties.