Next Article in Journal
Study of the Cn2 Model through the New Dimensionless Temperature Structure Function near the Sea Surface in the South China Sea
Next Article in Special Issue
Creation of a Walloon Pasture Monitoring Platform Based on Machine Learning Models and Remote Sensing
Previous Article in Journal
Monitoring of 35-Year Mangrove Wetland Change Dynamics and Agents in the Sundarbans Using Temporal Consistency Checking
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 3
10.3390/rs15030630
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Novel Framework for Correcting Satellite-Based Precipitation Products for Watersheds with Discontinuous Observed Data, Case Study in Mekong River Basin

by
Giha Lee
1,
Duc Hai Nguyen
2 and
Xuan-Hien Le
2,3,*
1
Department of Advanced Science and Technology Convergence, Kyungpook National University, 2559 Gyeongsang-daero, Sangju 37224, Republic of Korea
2
Faculty of Water Resources Engineering, Thuyloi University, 175 Tay Son, Dong Da, Hanoi 10000, Vietnam
3
Disaster Prevention Emergency Management Institute, Kyungpook National University, 2559 Gyeongsang-daero, Sangju 37224, Republic of Korea
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(3), 630; https://doi.org/10.3390/rs15030630
Submission received: 20 December 2022 / Revised: 18 January 2023 / Accepted: 19 January 2023 / Published: 20 January 2023
(This article belongs to the Special Issue AI-Driven Satellite Data for Global Environment Monitoring)
Browse Figures
Versions Notes

Abstract

Satellite-based precipitation (SP) data are gaining scientific interest due to their advantage in producing high-resolution products with quasi-global coverage. However, since the major reliance of precipitation data is on the distinctive geographical features of each location, they remain at a considerable distance from station-based data. This paper examines the effectiveness of a convolutional autoencoder (CAE) architecture in pixel-by-pixel bias correction of SP products for the Mekong River Basin (MRB). Two satellite-based products (TRMM and PERSIANN-CDR) and a gauge-based product (APHRODITE) are gridded rainfall products mined in this experiment. According to the estimated statistical criteria, the CAE model was effective in reducing the gap between SP products and benchmark data both in terms of spatial and temporal correlations. The two corrected SP products (CAE_TRMM and CAE_CDR) performed competitively, with CAE TRMM appearing to have a slight advantage over CAE CDR, however, the difference was minor. This study’s findings proved the effectiveness of deep learning-based models (here CAE) for bias correction of SP products. We believe that this technique will be a feasible alternative for delivering an up-to-current and reliable dataset for MRB studies, given that the sole available gauge-based dataset for this area has been out of date for a long time.

1. Introduction

Precipitation, a fundamental element of the hydrological processes, aids us in comprehending the relationships between hydrological and climatic systems. Rainfall data monitoring is critical for managing water resources and projecting extreme hydro-climate occurrences, such as droughts and floods [1]. The ground-based precipitation stations are one of the most commonly utilized data sources due to the reliability and historical number of observations they can provide. The fact that these data sources only cover the region immediately surrounding the measuring device’s position, however, is a fundamental restriction of these data sources [2,3]. Additionally, the uneven distribution of rain gauges throughout regions, particularly in mountainous areas, can lead to bias in the mapping of the regional distributions of precipitation [4]. In contrast, SP estimates and subsequent reanalysis are promising as trustworthy data sources for describing the geographical distribution of precipitation since they can provide high-resolution and wide coverage outputs.
Several gridded SP products with a quasi-global coverage include Global Satellite Mapping of Precipitation (GSMaP) [5], Climate Prediction Center morphing technique (CMORPH) [6], Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks-Climate Data Record (PERSIANN-CDR) [7], or Tropical Rainfall Measuring Mission (TRMM) [8]. The fundamental distinction between SP products is the employment of different data extraction techniques as well as the variety of satellite sensor measurement equipment [9]. This causes uncertainty in the gridded precipitation (GP) products because they may contain faults due to random and systematic errors [10]. As a result, re-analysis of SP data by area is essential before these data may be exploited for further studies, such as drought or hydrological models.
Numerous solutions have been developed to minimize the bias of SP products in order to improve their quality. Several prominent approaches include regression analysis [11], quantile mapping [12,13], power transformation [14,15], and linear scaling [16]. In essence, these approaches rely mostly on the distribution network of rain gauge stations, which may be unequal in some places, such as mountainous areas. In certain cases where it is difficult to access the ground-based gauges database or to synchronize updated data, these methods can be error-prone in correcting SP products. In addition, most bias correction methods depend on the update of gauge-based data [17]. This means that in some cases when the gauge-based data series is not continuous for certain reasons such as equipment failure or the project running out of funding, the traditional methods fail to generate a corrected dataset. Moreover, traditional bias correction methods rely on empirical relationships or mathematical models to adjust the biases present in SP data. These methods have limitations in terms of the accuracy of the correction, especially when dealing with large variations in precipitation across different geographical regions.
Deep neural network models have recently proved their advantage in capturing non-linear relationships of data [18]. There have been a few studies demonstrating the capacity of deep learning-based techniques to correct the bias of SP products. For example, Yang et al. [19] applied an LSTM model (long short-term memory) to rectify the IMERG product, Tao et al. [20] established a stacked denoising autoencoder model to adjust the PERSIANN-CCS product, and Le et al. [3] introduced a CNN model (convolutional neural network) to minimize the SP data bias. However, these methods have yet to see broad acceptance in the domain of bias reduction of SP products, particularly ones using CNNs.
In this work, we examined the efficiency of the convolutional autoencoder (CAE) architecture, an upgraded variant of the CNN model, in bias correction of SP products for the MRB. It is one of the world’s biggest watersheds, located in Asia, and spans the territory of six developing nations. Despite being one of the most important watersheds in the world (with an impact on more than 60 million people) [21], little has been studied to date to reduce the bias of SP products for MRB. This might be because access to ground-based rainfall data sources, as well as the capacity to create an up-to-date dataset for the whole basin, remains a substantial barrier [3]. The most widely utilized reference data source for MRB studies these days is APHRODITE (Asian Precipitation-Integrating High-Resolution Observational Data towards Water Resources Assessment) [22,23,24]. This is the result of an international collaboration between Japan and Asian countries to produce a gridded observation rainfall dataset for the whole Asia area [25]. This project, however, was completed in 2015, hence the APHRODITE rainfall product has not been updated since 2016.
The CAE model is introduced as a novel approach to this challenge, with the objective of producing a modified product that is more up-to-date than APHRODITE. We picked two SP products, PERSIANN-CDR and TRMM, with the same spatial resolution of 0.25° to assess the efficacy of the CAE model in adjustment. The model can capture the complex patterns and relationships between the SP data and the benchmark data, making it more effective in reducing the gap between the two datasets. Additionally, unlike traditional methods, the CAE model is able to learn from the data and make adjustments accordingly. This approach makes the CAE model more adaptable to different regions and different types of SP data, hence making it a powerful and flexible tool for bias correction in the MRB and other regions.
The remaining article is organized as: Section 2 describes the theoretical background of the methodology as well as the availability of various forms of GP data, such as satellite-based and gauge-based data. Section 3 presents the process of modeling, specifying hyperparameters in particular. The efficiency of GP products before and after bias adjustment is presented and analyzed in Section 4. Section 5 summarizes the research, highlighting the key findings.

2. Materials and Method

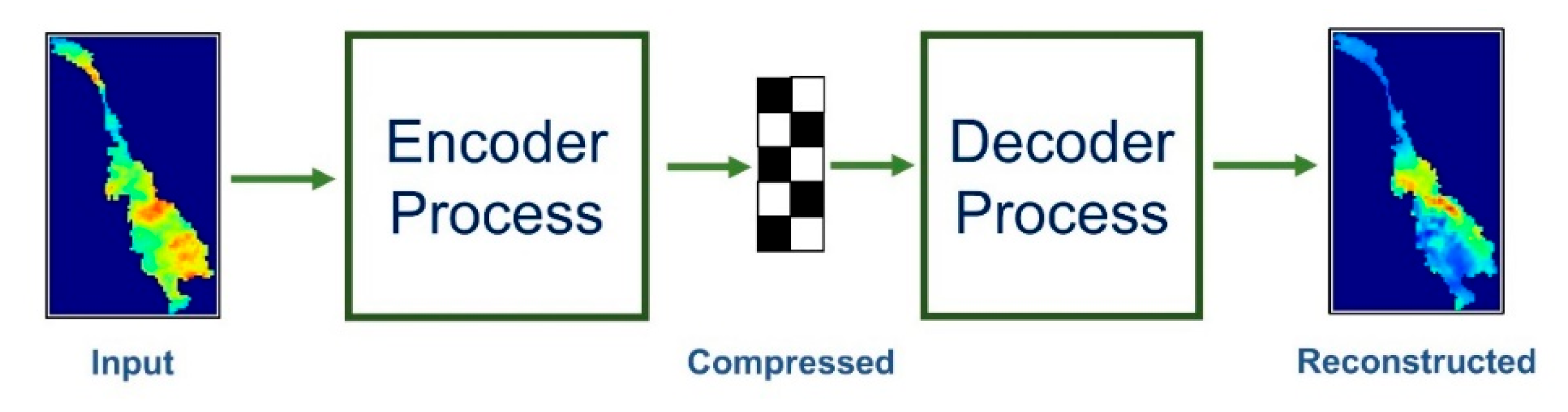
2.1. CAE Model

The proposed CAE model is a combination of two architectural paradigms, including CNN and Encoder-Decoder (ED) architecture, which belongs to the category of supervised learning under the classification of deep learning. CNNs are a particular sort of neural network and are designed toward working and processing efficiently with two-dimensional data such as image data [26,27]. Theoretically, the information encoding and processing in CNN is implemented through mathematical transformations of the convolutional, pooling, and fully connected layers (in certain cases). For complex tasks that require a substantial computational operation, the architecture of CNN can be a flexible stacking of various layers [28] or can also be flexibly combined with other types of architecture such as encoder-decoder [29] or LSTM [30,31].
In this study, we have exploited the advantage of ED architecture in combination with CNN to perform a correction problem of SP products where both input and output are in the same format as two-dimensional data. The proposed CAE architecture is inspired by the study of Le et al. [3]. In which, the input information from the GP data is compressed and encoded through the weight layers by the mathematical operations of convolutions and poolings. The decoding process is performed in the opposite direction of the encoding stage, where the previous compressed information is then decoded and reconstructed till the desired size is obtained. Figure 1 depicts a simplified representation of the CAE’s basic structure. At any given time step, both input and output data are daily GP data information with a resolution of 0.25°, corresponding to images of size 100 × 60 pixels.

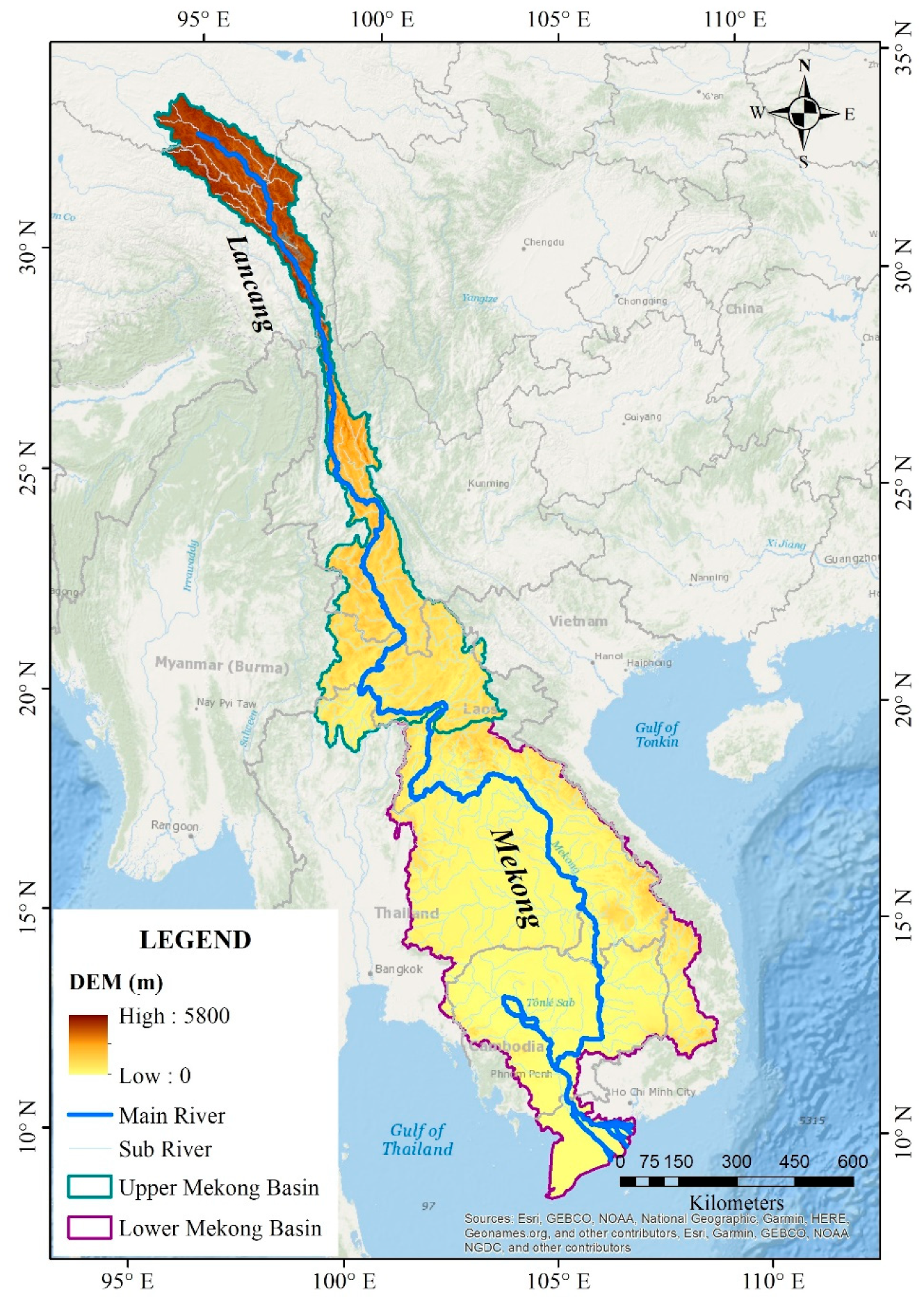
2.2. Study Area

The MRB is a large and complex region that spans six countries in Southeast Asia, including Laos, Thailand, Vietnam, Cambodia, Myanmar, and China. The area is characterized by a tropical monsoon climate, with a distinct wet and dry season. The rainy season is typically from May to November and is characterized by heavy rainfall and high humidity, with an average of about 2000 mm/year [32]. The rainfall is mainly caused by the monsoon winds, which blow from the southwest and bring with them moisture from the Indian Ocean [21]. During this time of the year, the basin experiences frequent heavy rainfall, flooding, and landslides. The dry season runs from November to April, and during this time the monsoon wind shifts to blow from the north-east and the basin receives less rainfall, usually lower than 100 mm/year. The dry season is characterized by low humidity and little to no precipitation, which leads to water scarcity and drought in some areas. The annual mean temperature in this area is around 27 °C, with little variation throughout the year. Temperature extremes are rare, with temperatures reaching the upper 30 s only in exceptional cases [33]. The temperature variations in the MRB are not as significant as the precipitation variations.
Moreover, MRB is known for its high levels of precipitation variability, with large differences between the wet and dry seasons and within the wet season as well. The variation in precipitation is caused by the region’s complicated geography, the basin is located in a transition zone between the Himalayas and the sea and the specific location of the monsoon wind system [34]. This basin is rich in biodiversity, and many habitats including forests, wetlands, and wetlands are influenced by the seasonal floods and droughts that are caused by the monsoon winds. Climate variations in the MRB have a direct effect on the livelihoods of the people living in the region, and an understanding of the climate characteristics of this region is essential for planning and managing the basin’s water resources. The location of the MRB is presented in Figure 2.

2.3. Gridded Precipitation (GP) Products

2.3.1. Satellite-Based Precipitation (SP) Data

Two SP products used for bias correction in this work are PERSIANN-CDR (short name CDR) and TRMM. Both of these data sources have the same grid of 0.25° × 0.25° and global coverage of 60°S-N for CDR [7] and 50°S-N for TRMM [8], respectively. CDR is one of the SP products of the PERSIANN family. It was generated with the aim of serving research on assessing trends in daily precipitation changes as well as extreme rainfall events due to climate change [35]. CDR product is computed using the rate of precipitation at each grid cell of 0.25° × 0.25° given by geostationary satellites and the infrared brightness temperature picture. The dataset is then adjusted by the monthly precipitation data that is available from GPCP (Global Precipitation Climatology Project). CDR delivers data from January 1983 to the date with a three to six-month delay [36] and can be accessible at ftp://persiann.eng.uci.edu/.
The TRMM product is generated for the quantitative measurement of rainfall in tropical and subtropical regions of the world. Data are produced by integrating rainfall estimations from multiple sources, including microwave data of low earth orbit satellites, infrared image data, and rainfall-gauge analysis from GPCP [8]. Precipitation information with a 3 h or daily temporal scale can be provided from the project for temporal coverage from 1998 to 2020. The effectiveness and importance of the two SP products mentioned above have been demonstrated in a myriad of meteorological, climatological, and hydrological studies [37,38,39,40], as well as in studies on the Mekong River basin [41].

2.3.2. Gauge-Based Precipitation Data

With respect to reference precipitation data, the APHRODITE rainfall product was used as observed data to correct for biases of SP products. This is an international collaborative initiative led by the Meteorological Agency of Japan with the aim of generating a daily GP product for the whole of Asia based on rainfall data gathered and analyzed from large numbers of ground-based stations across Asia. The APHRODITE project, according to Yatagai et al. [42], provides the output of a gridded rainfall dataset with a resolution of 0.25° for the whole of Asia during the period from 1951 to 2015 with three main regions: Russia, the Middle East, and Monsoon Asia. When it comes to Japan, this project can provide GP data with a high resolution of 0.05°, corresponding to a grid cell with a size of approximately 5 km × 5 km [43]. Therefore, this data has been utilized as the observation data in a variety of studies implemented for river basins in Asia as a whole [17,44], as well as, for the MRB [45,46]. For this study, we exploited the latest version of the APHRODITE (version V1901) for the domain of Monsoon Asia, which provided the available gridded daily precipitation product with a resolution of 0.25° between 1998 and 2015.

3. Model Processes

Because of the properties of GP products, the input data (those known as CDR and TRMM) and the referenced data (APHRODITE) of the CAE model are treated as single-band images. In terms of the data structure, the data volume has sizes of 100 × 60 × 1, corresponding to the 3D of width, height, and depth, respectively. The model is a flexible hybrid of two architectures, CNN and encoder-decoder. Figure 3 depicts the architectural information of the CAE.
Basically, two types of block processing units have been identified and developed corresponding to the two operating processes of the CAE model, the encoding and the decoding processes [47]. Each of these processing unit blocks is defined as a group of convolution and pooling operations, where these layers can be arranged in a certain sequence. During the encoder phase, important information from the input data will be extracted and stored in the weight layers of the model through the operation of processing blocks [48]. Where, the processing unit block is an arranged stack of two convolution layers, which is then followed by a pooling layer (here, the MaxPooling) [49]. In contrast to the information encoder process, the processing unit block in the decoder phase is the sequential arrangement of an UpSampling layer and two subsequent convolution layers. With such a configuration, the paradigm architecture becomes larger and deeper [50], however, this allows for the CAE model to accurately represent the complex spatial properties of the data.
With respect to the convolution layer, the filter parameters perform convolutional operations on the original image to generate feature maps. The depth of the feature map (number of channels) is determined by the number of filters used [51]. In this research, the number of filters in convolution layers is recommended as a power of 2, which is started with 32, 64, and increases to 256 in the deepest layer. In addition, the spatial dimension of each filter is 3 × 3 uniformly applied in the convolutional layer of this research. For pooling layers, a pooling operation is performed in the computational unit blocks of the encoder stage with a pool size of 2 × 2 aiming to halve the dimensions of the feature map (height and width) [52]. In the decoder phase, the stored information will be decompressed and scaled up until the desired spatial dimension is obtained via the mathematical operations of the UpSampling layers in computational blocks.
Selecting the optimal set of hyperparameters for deep learning models can be a challenging task, as there is no standard approach for determining the best values [53,54]. In this study, the selection of hyperparameters was based on a combination of theoretical knowledge and experimental evaluation. Regarding the loss function, the mean squared error is selected as is commonly utilized in autoencoder models and it proved to be superior when compared with other loss functions such as MAE or MAPE. For the optimizer, the Adam [55] is selected as it is a robust optimizer that adjusts the learning rate adaptively during training [56], and is known to have higher performance and stability in problems related to hydrology when compared to other algorithms such as SGD, RMSprop [28]. The learning rate was set to the recommended value of 0.001, which goes with the Adam algorithm. In order to determine the appropriate batch size for our model, we first carried out a number of tests using a range of various values. After doing so, we discovered that using a batch size of 32 produced the best results. The CAE model was configured with a maximum number of epochs of 10,000; however, we used machine learning techniques such as model checkpoint or early stopping to terminate the training if the validation dataset’s loss function did not reduce after 500 consecutive calculations. This allowed us to find the global extreme early and avoid unnecessary computation, enhancing the learning efficiency of the deep learning model and avoiding over-fitting problems [57].
In this study, the GP products available over an 18-year period, from 1998 to 2015, were utilized for different purposes. During the training and validation processes, the CAE model mines 16-year time series data for the period 1998–2013. Where, 14-year data are fed for the training process, and the remaining two years (2012 and 2013) are for the purpose of tuning parameters and validating model performance. Finally, an independent dataset of 2 years (period of 2014–2015) that has been unseen before is applied to quantify how well the chosen model performs.

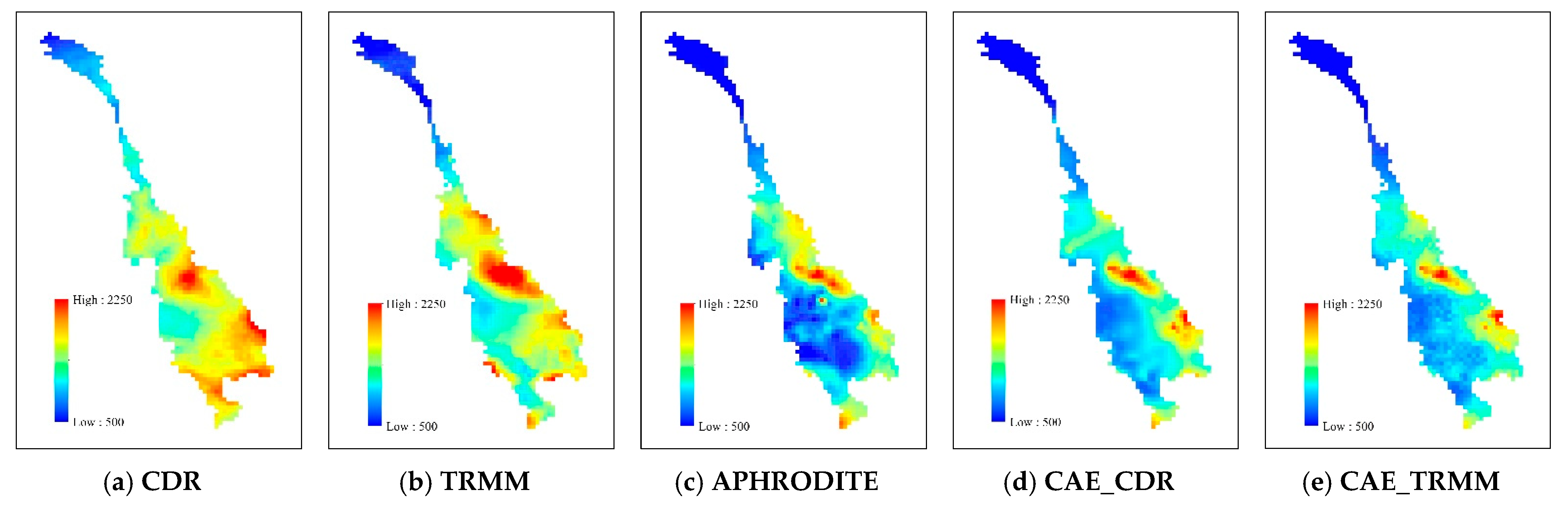
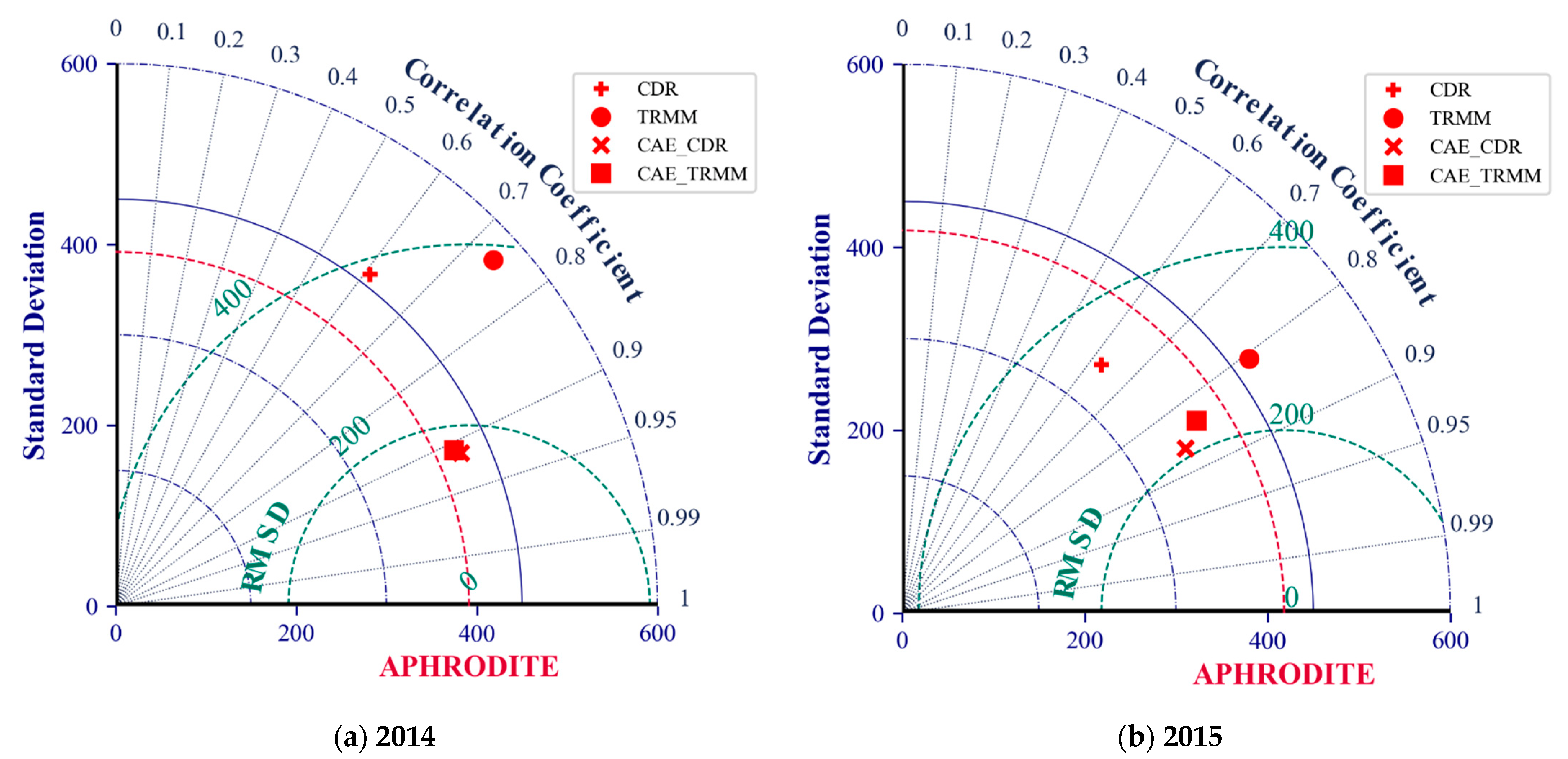
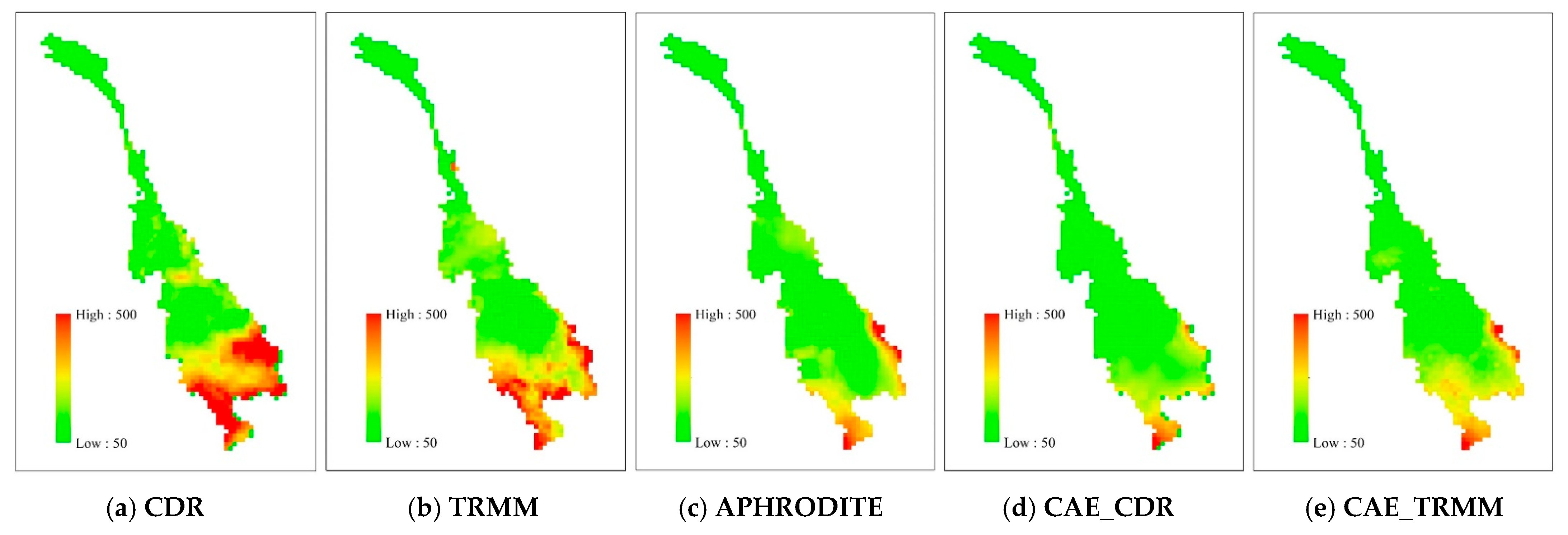
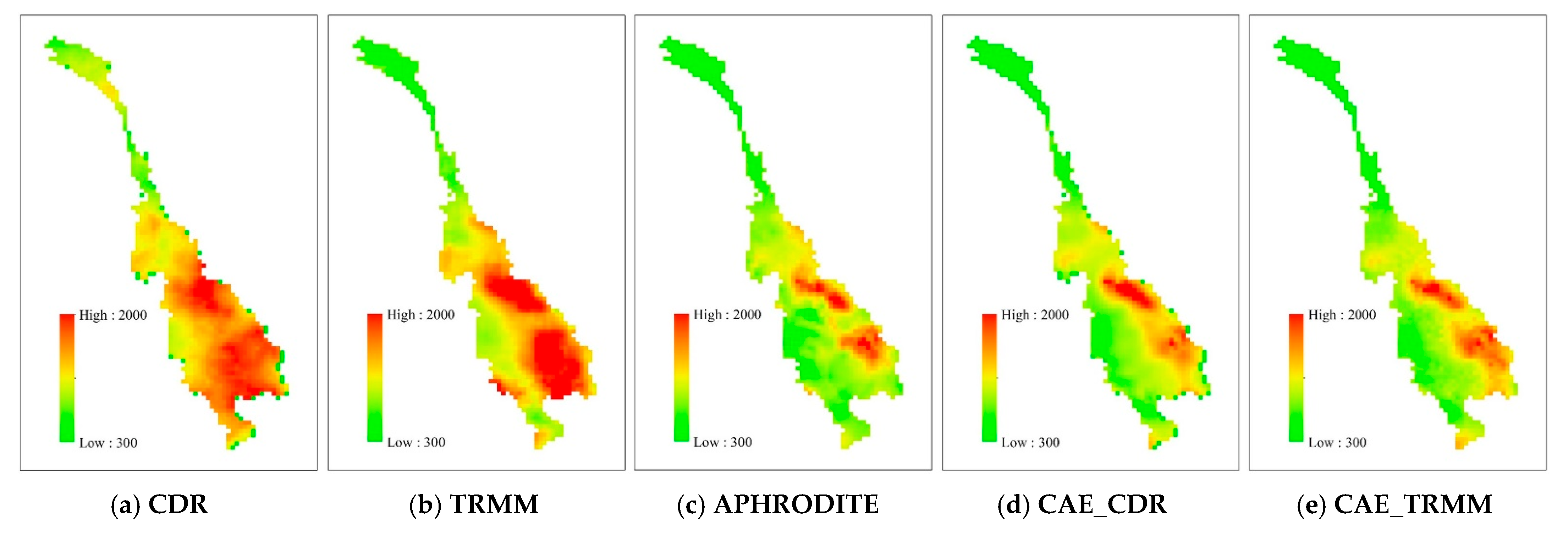
4. Results and Discussion

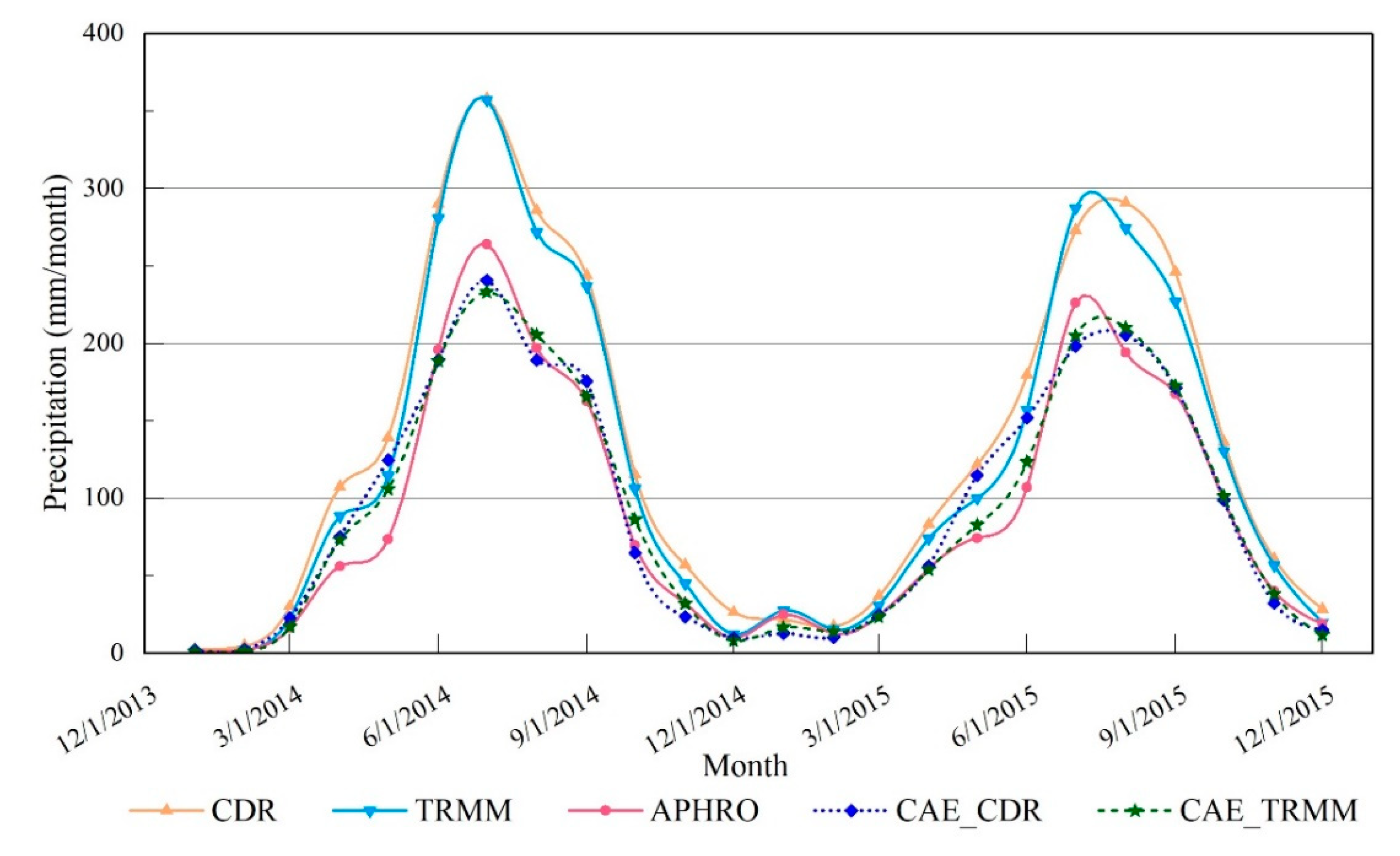
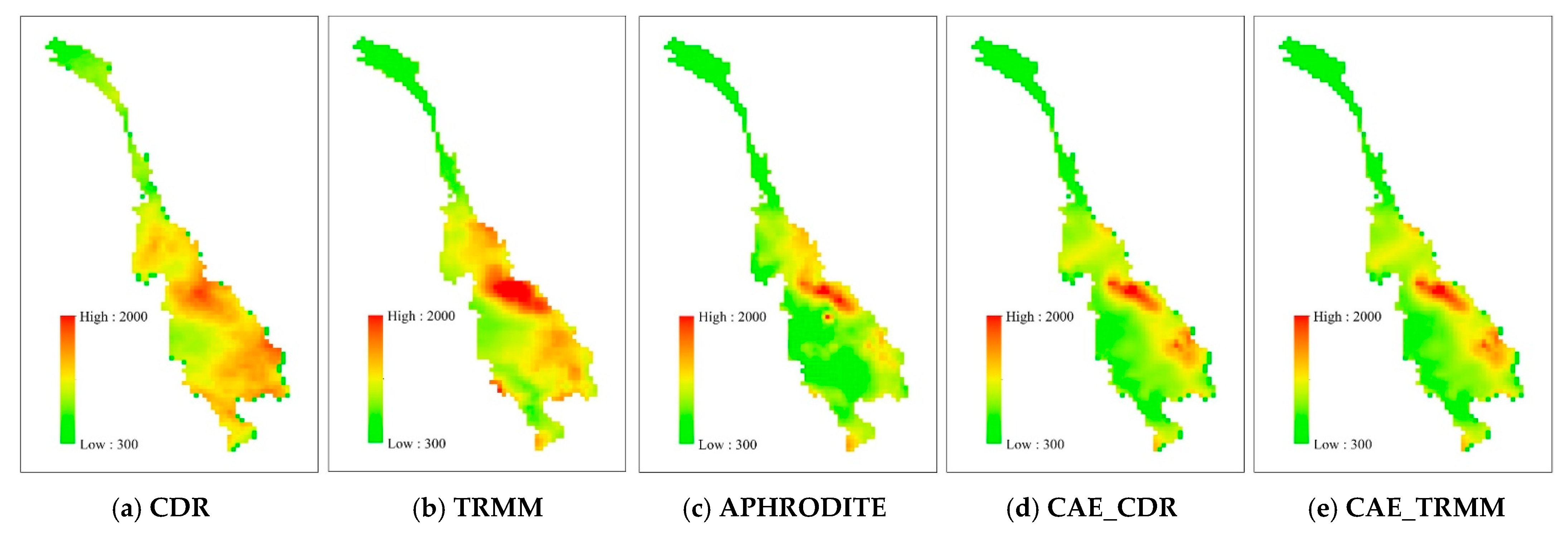
4.1. Evaluation of Temporal Correlation

To assess the CAE model’s effectiveness in terms of temporal correlation, an overview comparison between corrected and observed rainfall products was investigated. Here, we are interested in evaluating these rainfall products on a monthly scale and annual scale across the MRB. For bias-corrected datasets, the monthly and annual precipitation data of each pixel were grouped based on the corrected daily data from the proposed model. Then, an average value that represents the total precipitation throughout the whole basin for each scale was estimated. The comparison results are visualized in Figure 4, and the quantitative correlation information is depicted in Table 1 and Table 2.
In general, the information presented in Table 1 reveals a well-recognized tendency that both SP products are overestimated relative to the APHRODITE dataset (or reference data). The mean annual precipitation for these two products during the testing period was 157 mm and 1471 mm for CDR and TRMM, respectively, while the corresponding figure for the observed data was only 1068 mm. Although CDR and TRMM provide relatively good monthly precipitation correlations with NSE values in the range of 0.6–0.74, the bias of these products is undeniable by the RMSD values (root-mean-square deviation) and are recorded in Table 2 up to 55 mm and 45.6 mm, respectively. These biases are more clearly witnessed during the rainy season in Figure 4, especially in July and August, when these disparities can be up to approximately 100 mm.
On the other hand, the two GP datasets adjusted by the CAE exhibit substantial agreement with the reference data because the difference in mean yearly rainfall of these two datasets is only about 20–40 mm. The superiority of two bias-adjusted GP products (here, CAE_CDR and CAE_TRMM) is more obviously expressed in Figure 4 and Table 2, where monthly scale precipitation is of interest. Compared with SP data, two corrected product exhibits a higher temporal correlation as well as significantly lower errors. The NSE correlation coefficient is up to 0.97 with CAE_CDR and 0.99 with CAE_TRMM, while the values of mean absolute deviation (MAD) of these two datasets are 12.4 mm and 8.7 mm, respectively.

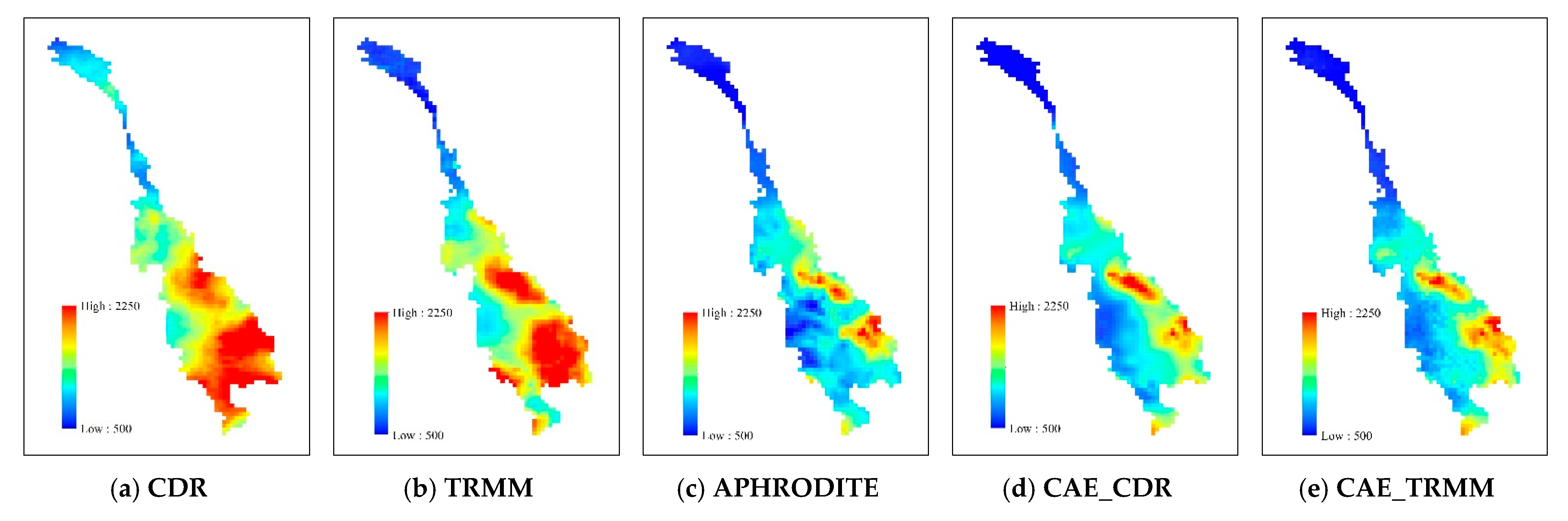
4.2. Evaluation of Spatial Correlation

In addition to the quantitative comparison of rainfall products over various time scales, their spatial variation under different scales was also taken into account. The measurement criteria used to estimate the pixel-by-pixel difference between rainfall data sources (both satellite-based and corrected precipitation) and observed data include RMSD, MAD, Bias index, and spatial correlation index. The pixel-by-pixel annual precipitation distribution is illustrated in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, and the spatial pattern variation between the GP products is quantified in Table 3 and Table 4.
As can be clearly seen in Figure 5 and Figure 6, the spatial trend of annual rainfall distribution over the MRB is different among the GP products. Both SP products (CDR and TRMM) exhibited a trend that is overestimated relative to the reference data (see Figures a,b). The respective bias values (which are positive values) for these two datasets in 2014 are 574 mm and 453 mm, and those figures for 2015 are 448 mm and 352 mm, respectively.
For APHRODITE data, annual precipitation in the MRB has a large range of 500–2250 mm and is unevenly distributed among regions. While the upper Mekong (most of its territory is in China) receives an average annual rainfall of 500–1000 mm, the observed precipitation for the lower Mekong River broadly ranges from just under 1500 to well above 2250 mm. Several typical areas where dramatic higher rainfall (>2250 mm) was recorded are the north-central region of Laos, the eastern hilly area of Laos (the part contiguous to Vietnam), or the Ca Mau cape of Vietnam.
Regarding the two GP products that were bias-corrected from the CAE model, the two-year annual rainfall spatial distribution patterns in the test period indicated significant similarity with the observed data. With the same color scale selected, both CAE_CDR and CAE_TRMM excellently represent the spatial variation in the precipitation distribution of the Mekong basin compared with observed data—APHRODITE, including the changing trend of annual rainfall for the upper and lower Mekong basin. As we can see in Figure 5 and Figure 6, the estimated precipitation per pixel with these products ranges between 500 and 1000 mm for the upper Mekong basin. By contrast, the recorded rainfall corresponding to the lower Mekong basin varies from roughly 1500 to more than 2500 mm. Quantitative assessments of the spatial variations of the total annual precipitation by pixel are described in more detail in Table 3 and these statistics are visualized in Figure 7.
From these numbers, it is generally understood that the two bias-corrected products provided a significantly higher benchmark than the SP products for spatial correlation, bias index, and error metrics. In 2014, the spatial correlation index of CAE_CDR and CAE_TRMM compared to the reference data is up to 0.91, and the corresponding error value is about 175 mm for RMSD and 135 mm for MAD. Meanwhile, for two SP products, the respective measurement criteria exhibit much lower performance where the spatial correlation is only 0.61 and the RMSD value of 690 mm for CDR data. Moreover, the bias value that measures the mean deviation of the pixels across the basin has also described the remarkable effectiveness of the CAE model since this value is decreased sharply compared to the bias of the products before being adjusted, the reduction from 453 mm to only 35 mm for the product of CDR_TRMM. The statistics of yearly precipitation in pixels over the MRB denoted that the standard deviation of the two corrected rainfall products is approximately 410 mm, close to the standard deviation of the referenced product with about 390 mm (see Figure 7).
A similar development was witnessed in the year 2015, two bias-corrected precipitation datasets outperformed the SP products in all of the criteria mentioned in Table 3. In regard to the CDR data, the spatial correlation coefficient of this rainfall product has improved from 0.63 to 0.84 for the CAE_CDR product, and the error quantification criteria have been dropped, respectively, from 561 to 236 mm for RMSD and 480 to 186 mm for MAD. Along with the CAE_CDR, the CAE_TRMM precipitation data, which is corrected from the TRMM by the CAE model also exhibits outstanding advantages. Despite the spatial correlation of this corrected product being just slightly enhanced by that of the TRMM product (0.86 vs. 0.81), the improvement in performance can be obviously identified in the error evaluation criteria remaining as RMSD, MAD, and especially in Bias value. Here, the bias value or mean deviation of grid cells in the entire MRB is reported as 8 mm, a speedy decline from the mean bias of 352 mm for the TRMM.
Looking at Table 4 and Figure 8, Figure 9, Figure 10 and Figure 11, we can see that for the dry season in 2014, the highest spatial correlation is achieved by the CAE_TRMM product, with a value of 0.89. This means that there is a significant degree of agreement between the CAE_TRMM product and the reference data (APHRODITE). In contrast, the lowest spatial correlation is achieved by the CDR product, with a value of 0.70. This indicates that there is a lower degree of similarity between the CDR product and APHRODITE. Similarly, for the wet season in 2015, the highest spatial correlation is achieved by the CAE_TRMM product, with a value of 0.87, while the lowest spatial correlation is achieved by the CDR product, with a value of 0.62.
In general, the CAE_TRMM and CAE_CDR products tend to have higher spatial correlation values than the CDR and TRMM products. Additionally, the RMSD and MAD values are generally lower in CAE_TRMM and CAE_CDR products compared to others; this means that these products have a lower deviation from the observed data. The bias values are also often lower in CAE_TRMM and CAE_CDR products compared to others; this means that these products have a better accuracy compared to others. Assessing the RMSD, MAD, and bias data reveal that the CAE TRMM and CAE CDR products have the lowest values, indicating that these products have the best results in terms of deviation, accuracy, and bias. In addition, the CAE TRMM and CAE CDR products have the highest spatial correlation values, indicating that these products have the strongest performance in terms of resemblance to the APHRODITE.
From the qualitative and quantitative comparisons of rainfall datasets, we can confirm that the bias-adjusted precipitation products present a higher quality than the original SP products in all of these metrics. Moreover, these results proved the effectiveness of the proposed CAE model. Despite employing various input data sources (CDR and TRMM), the bias-corrected rainfall products (CAE_CDR and CAE_TRMM) still exhibit competitively excellent performance. With regard to the two adjusted products, it seems that CAE_TRMM is a little higher than CAE_CDR, and this difference was specifically mentioned in 2015. Even so, both of these products have demonstrated their prominence in capturing the trend of precipitation distribution and rainfall intensity in terms of spatial and temporal.

5. Conclusions

Although SP products can offer a dataset with global (or near-global) coverage, there is still a significant disparity in comparison to gauge-based data. To tackle this question, we have developed a CAE model that may minimize bias and boost the dependability of SP products. Statistical criteria were utilized to measure the effectiveness of datasets before and after minimizing the error. The following are several findings of this study.
  • For the SP products studied in this study, TRMM exhibited a more favorable connection with observational data compared to CDR in most of the evaluation criteria.
  • CAE succeeded in narrowing the spatiotemporal gap between the SP and APHRODITE products. The difference in MAD, in particular, has dropped dramatically to just 12.4 mm/month with CDR and 8.7 mm/month with TRMM, equating to a decrease of 30.8 mm/month and 25.3 mm/month for these two products, respectively. Meanwhile, the temporal correlation of the basin-wide average monthly rainfall of the corrected products is up to [0.97–0.99].
  • The quantified statistical criteria indicate that both bias-adjusted SP products perform equally well when compared with observed data. In this regard, CAE_TRMM appears to have a minor advantage over CAE_CDR, although the difference is insignificant.
  • Because the APHRODITE product has not been upgraded since 2016, the CAE model is intended to be the solution for providing a more up-to-date and trustworthy data set for experiments in the MRB.
The CAE model was effective in addressing the SP bias correction problem; however, certain limitations must be acknowledged. The outcomes of this study are closely tied to the source of GP products utilized. In particular, this research used TRMM and PERSIANN-CDR as SP datasets and APHRODITE as the observed dataset. It is crucial that all of these gridded daily rainfall datasets have a consistent spatial resolution of 0.25°. Additionally, it is worth noting that APHRODITE is a product of an international cooperation program and may have a closer relationship to sources of data offered by governments in the area of relevance.
This study’s findings proved the potential of deep learning-based models (here CAE) to correct for bias of GP products. We expect that this approach will be a viable option for large study basins with restricted data availability such as the MRB.

Author Contributions

G.L.: supervision, data curation. D.H.N.: formal analysis, investigation. X.-H.L.: writing—original draft, formal analysis. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1A2C1102758).

Data Availability Statement

Data will be made available on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
  2. Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
  3. Le, X.H.; Lee, G.; Jung, K.; An, H.-U.; Lee, S.; Jung, Y. Application of Convolutional Neural Network for Spatiotemporal Bias Correction of Daily Satellite-Based Precipitation. Remote Sens. 2020, 12, 2731. [Google Scholar] [CrossRef]
  4. López, P.L.; Immerzeel, W.W.; Rodríguez Sandoval, E.A.; Sterk, G.; Schellekens, J. Spatial Downscaling of Satellite-Based Precipitation and Its Impact on Discharge Simulations in the Magdalena River Basin in Colombia. Front. Earth Sci. 2018, 6, 68. [Google Scholar] [CrossRef]
  5. Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
  6. Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
  7. Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
  8. Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
  9. Hsu, K.-L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks. J. Appl. Meteorol. Climatol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
  10. Habib, E.; Haile, A.T.; Sazib, N.; Zhang, Y.; Rientjes, T. Effect of Bias Correction of Satellite-Rainfall Estimates on Runoff Simulations at the Source of the Upper Blue Nile. Remote Sens. 2014, 6, 6688–6708. [Google Scholar] [CrossRef]
  11. Chen, S.; Xiong, L.; Ma, Q.; Kim, J.-S.; Chen, J.; Xu, C.-Y. Improving daily spatial precipitation estimates by merging gauge observation with multiple satellite-based precipitation products based on the geographically weighted ridge regression method. J. Hydrol. 2020, 589, 125156. [Google Scholar] [CrossRef]
  12. Katiraie-Boroujerdy, P.-S.; Rahnamay Naeini, M.; Akbari Asanjan, A.; Chavoshian, A.; Hsu, K.-L.; Sorooshian, S. Bias Correction of Satellite-Based Precipitation Estimations Using Quantile Mapping Approach in Different Climate Regions of Iran. Remote Sens. 2020, 12, 2102. [Google Scholar] [CrossRef]
  13. Ajaaj, A.A.; Mishra, A.K.; Khan, A.A. Comparison of BIAS correction techniques for GPCC rainfall data in semi-arid climate. Stoch. Environ. Res. Risk Assess. 2016, 30, 1659–1675. [Google Scholar] [CrossRef]
  14. Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
  15. Gumindoga, W.; Rientjes, T.H.M.; Haile, A.T.; Makurira, H.; Reggiani, P. Performance of bias-correction schemes for CMORPH rainfall estimates in the Zambezi River basin. Hydrol. Earth Syst. Sci. 2019, 23, 2915–2938. [Google Scholar] [CrossRef]
  16. Mendez, M.; Maathuis, B.; Hein-Griggs, D.; Alvarado-Gamboa, L.-F. Performance Evaluation of Bias Correction Methods for Climate Change Monthly Precipitation Projections over Costa Rica. Water 2020, 12, 482. [Google Scholar] [CrossRef]
  17. Ji, X.; Li, Y.; Luo, X.; He, D.; Guo, R.; Wang, J.; Bai, Y.; Yue, C.; Liu, C. Evaluation of bias correction methods for APHRODITE data to improve hydrologic simulation in a large Himalayan basin. Atmos. Res. 2020, 242, 104964. [Google Scholar] [CrossRef]
  18. Ho, H.V.; Nguyen, D.H.; Le, X.-H.; Lee, G. Multi-step-ahead water level forecasting for operating sluice gates in Hai Duong, Vietnam. Environ. Monit. Assess. 2022, 194, 442. [Google Scholar] [CrossRef]
  19. Yang, X.; Yang, S.; Tan, M.L.; Pan, H.; Zhang, H.; Wang, G.; He, R.; Wang, Z. Correcting the bias of daily satellite precipitation estimates in tropical regions using deep neural network. J. Hydrol. 2022, 608, 127656. [Google Scholar] [CrossRef]
  20. Tao, Y.; Gao, X.; Hsu, K.; Sorooshian, S.; Ihler, A. A Deep Neural Network Modeling Framework to Reduce Bias in Satellite Precipitation Products. J. Hydrometeorol. 2016, 17, 931–945. [Google Scholar] [CrossRef]
  21. MRC. Summary State of the Basin Report 2018; Mekong River Commission: Vientiane, Laos, 2020. [Google Scholar]
  22. Irannezhad, M.; Liu, J. Evaluation of six gauge-based gridded climate products for analyzing long-term historical precipitation patterns across the Lancang-Mekong River Basin. Geogr. Sustain. 2022, 3, 85–103. [Google Scholar] [CrossRef]
  23. Tian, W.; Liu, X.; Wang, K.; Bai, P.; Liang, K.; Liu, C. Evaluation of six precipitation products in the Mekong River Basin. Atmos. Res. 2021, 255, 105539. [Google Scholar] [CrossRef]
  24. Chen, A.; Chen, D.; Azorin-Molina, C. Assessing reliability of precipitation data over the Mekong River Basin: A comparison of ground-based, satellite, and reanalysis datasets. Int. J. Climatol. 2018, 38, 4314–4334. [Google Scholar] [CrossRef]
  25. Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a Long-Term Daily Gridded Precipitation Dataset for Asia Based on a Dense Network of Rain Gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
  26. Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
  27. Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning. arXiv 2021, arXiv:2106.11342. [Google Scholar]
  28. Le, X.H.; Nguyen, D.H.; Jung, S.; Yeon, M.; Lee, G. Comparison of Deep Learning Techniques for River Streamflow Forecasting. IEEE Access 2021, 9, 71805–71820. [Google Scholar] [CrossRef]
  29. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
  30. Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. arXiv 2015, arXiv:1506.04214. [Google Scholar]
  31. Tuyen, D.N.; Tuan, T.M.; Le, X.H.; Tung, N.T.; Chau, T.K.; Van Hai, P.; Gerogiannis, V.C.; Son, L.H. RainPredRNN: A New Approach for Precipitation Nowcasting with Weather Radar Echo Images Based on Deep Learning. Axioms 2022, 11, 107. [Google Scholar] [CrossRef]
  32. MRC. Annual Mekong Flood Report 2014; Mekong River Commission: Vientiane, Laos, 2015; p. 70. Available online: http://www.mrcmekong.org/publications/reports/basin-reports/ (accessed on 20 January 2021).
  33. MRC. Overview of the Hydrology of the Mekong Basin; Mekong River Commission: Vientiane, Laos, 2005; p. 73. [Google Scholar]
  34. Adamson, P.T.; Rutherfurd, I.D.; Peel, M.C.; Conlan, I.A. Chapter 4—The Hydrology of the Mekong River. In The Mekong; Campbell, I.C., Ed.; Academic Press: San Diego, CA, USA, 2009; pp. 53–76. [Google Scholar] [CrossRef]
  35. Ashouri, H.; Nguyen, P.; Thorstensen, A.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D. Assessing the Efficacy of High-Resolution Satellite-Based PERSIANN-CDR Precipitation Product in Simulating Streamflow. J. Hydrometeorol. 2016, 17, 2061–2076. [Google Scholar] [CrossRef]
  36. Nguyen, P.; Shearer, E.J.; Tran, H.; Ombadi, M.; Hayatbini, N.; Palacios, T.; Huynh, P.; Braithwaite, D.; Updegraff, G.; Hsu, K.; et al. The CHRS Data Portal, an easily accessible public repository for PERSIANN global satellite precipitation data. Sci. Data 2019, 6, 180296. [Google Scholar] [CrossRef] [PubMed]
  37. Islam, M.A.; Yu, B.; Cartwright, N. Assessment and comparison of five satellite precipitation products in Australia. J. Hydrol. 2020, 590, 125474. [Google Scholar] [CrossRef]
  38. Araujo Palharini, R.S.; Vila, D.A.; Rodrigues, D.T.; Palharini, R.C.; Mattos, E.V.; Pedra, G.U. Assessment of extreme rainfall estimates from satellite-based: Regional analysis. Remote Sens. Appl. Soc. Environ. 2021, 23, 100603. [Google Scholar] [CrossRef]
  39. Brasil Neto, R.M.; Santos, C.A.G.; da Costa Silva, J.F.C.B.; da Silva, R.M.; dos Santos, C.A.C.; Mishra, M. Evaluation of the TRMM product for monitoring drought over Paraíba State, northeastern Brazil: A trend analysis. Sci. Rep. 2021, 11, 1097. [Google Scholar] [CrossRef] [PubMed]
  40. Vu, T.T.; Li, L.; Jun, K.S. Evaluation of Multi-Satellite Precipitation Products for Streamflow Simulations: A Case Study for the Han River Basin in the Korean Peninsula, East Asia. Water 2018, 10, 642. [Google Scholar] [CrossRef]
  41. Try, S.; Tanaka, S.; Tanaka, K.; Sayama, T.; Oeurng, C.; Uk, S.; Takara, K.; Hu, M.; Han, D. Comparison of gridded precipitation datasets for rainfall-runoff and inundation modeling in the Mekong River Basin. PLoS ONE 2020, 15, e0226814. [Google Scholar] [CrossRef]
  42. Yatagai, A.; Arakawa, O.; Kamiguchi, K.; Kawamoto, H.; Nodzu, M.I.; Hamada, A. A 44-Year Daily Gridded Precipitation Dataset for Asia Based on a Dense Network of Rain Gauges. SOLA 2009, 5, 137–140. [Google Scholar] [CrossRef]
  43. Kamiguchi, K.; Arakawa, O.; Kitoh, A.; Yatagai, A.; Hamada, A.; Yasutomi, N. Development of APHRO_JP, the first Japanese high-resolution daily precipitation product for more than 100 years. Hydrol. Res. Lett. 2010, 4, 60–64. [Google Scholar] [CrossRef]
  44. Dangol, S.; Talchabhadel, R.; Pandey, V.P. Performance evaluation and bias correction of gridded precipitation products over Arun River Basin in Nepal for hydrological applications. Theor. Appl. Climatol. 2022, 148, 1353–1372. [Google Scholar] [CrossRef]
  45. Try, S.; Lee, G.; Yu, W.; Oeurng, C.; Jang, C. Large-Scale Flood-Inundation Modeling in the Mekong River Basin. J. Hydrol. Eng. 2018, 23, 05018011. [Google Scholar] [CrossRef]
  46. Dandridge, C.; Lakshmi, V.; Bolten, J.; Srinivasan, R. Evaluation of Satellite-Based Rainfall Estimates in the Lower Mekong River Basin (Southeast Asia). Remote Sens. 2019, 11, 2709. [Google Scholar] [CrossRef]
  47. Hubens, N. Deep Inside: Autoencoders. Available online: https://towardsdatascience.com/deep-inside-autoencoders-7e41f319999f (accessed on 20 January 2021).
  48. Chollet, F. Building Autoencoders in Keras. Available online: https://blog.keras.io/building-autoencoders-in-keras.html (accessed on 6 June 2022).
  49. Karpathy, A. CS231n: Convolutional Neural Networks for Visual Recognition. Available online: http://cs231n.github.io/convolutional-networks/ (accessed on 10 September 2021).
  50. Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar] [CrossRef]
  51. Rosebrock, A. Keras Conv2D and Convolutional Layers. Available online: https://www.pyimagesearch.com/2018/12/31/keras-conv2d-and-convolutional-layers/ (accessed on 1 March 2022).
  52. Brownlee, J. A Gentle Introduction to Pooling Layers for Convolutional Neural Networks. Available online: https://machinelearningmastery.com/pooling-layers-for-convolutional-neural-networks/ (accessed on 15 January 2020).
  53. Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
  54. Le, X.-H.; Nguyen Van, L.; Duc Hai, N.; Nguyen, G.V.; Jung, S.; Lee, G. Comparison of bias-corrected multisatellite precipitation products by deep learning framework. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103177. [Google Scholar] [CrossRef]
  55. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
  56. Ruder, S. An Overview of Gradient Descent Optimization Algorithms. Available online: https://ruder.io/optimizing-gradient-descent/ (accessed on 6 June 2020).
  57. Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar] [CrossRef]
Remotesensing 15 00630 g001
Figure 1. Illustrated diagram of CAE network architecture.
Figure 1. Illustrated diagram of CAE network architecture.
Remotesensing 15 00630 g001
Remotesensing 15 00630 g002
Figure 2. Location of MRB.
Figure 2. Location of MRB.
Remotesensing 15 00630 g002
Remotesensing 15 00630 g003
Figure 3. The architectural paradigm of the CAE model.
Figure 3. The architectural paradigm of the CAE model.
Remotesensing 15 00630 g003
Remotesensing 15 00630 g004
Figure 4. Correlation of average monthly rainfall of data sources for the whole MRB.
Figure 4. Correlation of average monthly rainfall of data sources for the whole MRB.
Remotesensing 15 00630 g004
Remotesensing 15 00630 g005
Figure 5. Spatial rainfall distribution of products over the MRB in 2014.
Figure 5. Spatial rainfall distribution of products over the MRB in 2014.
Remotesensing 15 00630 g005
Remotesensing 15 00630 g006
Figure 6. Spatial rainfall distribution of products over the MRB in 2015.
Figure 6. Spatial rainfall distribution of products over the MRB in 2015.
Remotesensing 15 00630 g006
Remotesensing 15 00630 g007
Figure 7. Taylor diagram presents quantitative information of three statistical indicators of rainfall products compared with reference data—APHRODITE product.
Figure 7. Taylor diagram presents quantitative information of three statistical indicators of rainfall products compared with reference data—APHRODITE product.
Remotesensing 15 00630 g007
Remotesensing 15 00630 g008
Figure 8. Spatial rainfall distribution of products over the MRB in the dry season of 2014.
Figure 8. Spatial rainfall distribution of products over the MRB in the dry season of 2014.
Remotesensing 15 00630 g008
Remotesensing 15 00630 g009
Figure 9. Spatial rainfall distribution of products over the MRB in the wet season of 2014.
Figure 9. Spatial rainfall distribution of products over the MRB in the wet season of 2014.
Remotesensing 15 00630 g009
Remotesensing 15 00630 g010
Figure 10. Spatial rainfall distribution of products over the MRB in the dry season of 2015.
Figure 10. Spatial rainfall distribution of products over the MRB in the dry season of 2015.
Remotesensing 15 00630 g010
Remotesensing 15 00630 g011
Figure 11. Spatial rainfall distribution of products over the MRB in the wet season of 2015.
Figure 11. Spatial rainfall distribution of products over the MRB in the wet season of 2015.
Remotesensing 15 00630 g011
Table 1. Annual rainfall of data sources for the whole MRB.
Table 1. Annual rainfall of data sources for the whole MRB.
PurposeYearCDR
(mm/Year)		TRMM
(mm/Year)		APHRODITE
(mm/Year)		CAE_CDR
(mm/Year)		CAE_TRMM
(mm/Year)
Testing201416611540108611251121
201514981402105010951058
Average precipitation15791471106811101090
Table 2. Comparative correlation of average monthly rainfall between the precipitation products and APHRODITE data.
Table 2. Comparative correlation of average monthly rainfall between the precipitation products and APHRODITE data.
Compared with APHRODITEPeriodMAD (mm/Month)RMSD (mm/Month)NSE
CDRJan 2014–Dec 201543.254.10.61
TRMMJan 2014–Dec 201534.045.60.74
CAE_CDRJan 2014–Dec 201512.419.00.97
CAE_TRMMJan 2014–Dec 20158.712.70.99
Table 3. Quantitative assessment of annual precipitation spatial correlation of products.
Table 3. Quantitative assessment of annual precipitation spatial correlation of products.
YearCompared with APHRODITERMSD
(mm/Year)		MAD
(mm/Year)		Bias
(mm/Year)		Spatial
Correlation
2014CDR6905825740.61
TRMM5944614530.74
CAE_CDR174134390.91
CAE_TRMM177137350.91
2015CDR5614804480.63
TRMM4503663520.81
CAE_CDR236186460.84
CAE_TRMM21016680.86
Table 4. Quantitative assessment of seasonal precipitation spatial correlation of products.
Table 4. Quantitative assessment of seasonal precipitation spatial correlation of products.
YearSeasonCompared with
APHRODITE		RMSD
(mm/Year)		MAD
(mm/Year)		Bias
(mm/Year)		Spatial
Correlation
2014DryCDR1151561040.70
TRMM65100580.78
CAE_CDR4052−70.86
CAE_TRMM3948140.89
WetCDR4885744740.60
TRMM4065204000.78
CAE_CDR122154450.93
CAE_TRMM113151220.92
2015DryCDR108128810.67
TRMM7597610.82
CAE_CDR6080−270.79
CAE_TRMM4962−150.88
WetCDR3964583700.62
TRMM3043782960.82
CAE_CDR149193740.85
CAE_TRMM129170230.87
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Lee, G.; Nguyen, D.H.; Le, X.-H. A Novel Framework for Correcting Satellite-Based Precipitation Products for Watersheds with Discontinuous Observed Data, Case Study in Mekong River Basin. Remote Sens. 2023, 15, 630. https://doi.org/10.3390/rs15030630

AMA Style

Lee G, Nguyen DH, Le X-H. A Novel Framework for Correcting Satellite-Based Precipitation Products for Watersheds with Discontinuous Observed Data, Case Study in Mekong River Basin. Remote Sensing. 2023; 15(3):630. https://doi.org/10.3390/rs15030630

Chicago/Turabian Style

Lee, Giha, Duc Hai Nguyen, and Xuan-Hien Le. 2023. "A Novel Framework for Correcting Satellite-Based Precipitation Products for Watersheds with Discontinuous Observed Data, Case Study in Mekong River Basin" Remote Sensing 15, no. 3: 630. https://doi.org/10.3390/rs15030630

APA Style

Lee, G., Nguyen, D. H., & Le, X.-H. (2023). A Novel Framework for Correcting Satellite-Based Precipitation Products for Watersheds with Discontinuous Observed Data, Case Study in Mekong River Basin. Remote Sensing, 15(3), 630. https://doi.org/10.3390/rs15030630

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop