Up-Scaling Fuel Hazard Metrics Derived from Terrestrial Laser Scanning Using a Machine Learning Model
Abstract
1. Introduction
- To estimate cover and height of near-surface, elevated, and canopy fuel layers derived from TLS point clouds;
- To evaluate the performance of a random forest model trained with TLS observation and compared to random forest models trained with visual assessment, where appropriate;
- To map fuel metrics derived from TLS point clouds across an area relevant to operational fire management decisions and compared to a map of fuel metrics obtained from visual assessments, where appropriate.
2. Study Area and Fuel Data
2.1. Study Area
2.2. Fuel Data
2.2.1. Terrestrial Laser Scanning
2.2.2. Visual Assessments
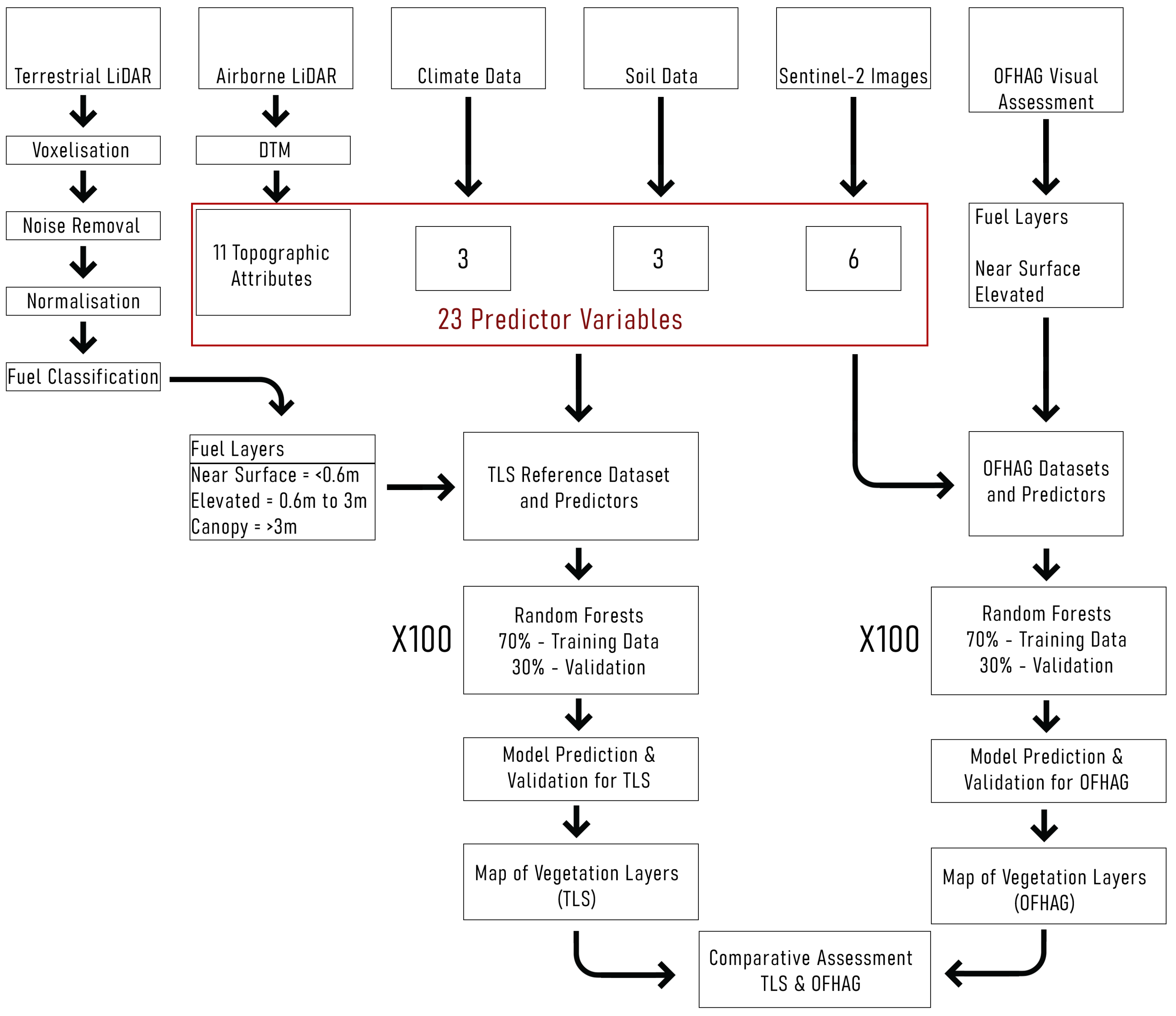
3. Method
3.1. TLS Point Cloud to Fuel Metrics
3.1.1. Voxelisation
3.1.2. Noise Detection and Removal
3.1.3. Normalisation
3.1.4. Fuel Strata Classification
3.1.5. Fuel Metric Derivation
3.2. Landscape Fuel Hazard
3.2.1. Random Forest Model Configuration
3.2.2. Topographic Variables from ALS
3.2.3. Soil Variables from Soil Data
3.2.4. Climate Variables from Climate Data
3.2.5. Vegetative Indices from Sentinel MSI-2
3.3. Model Evaluation
4. Results
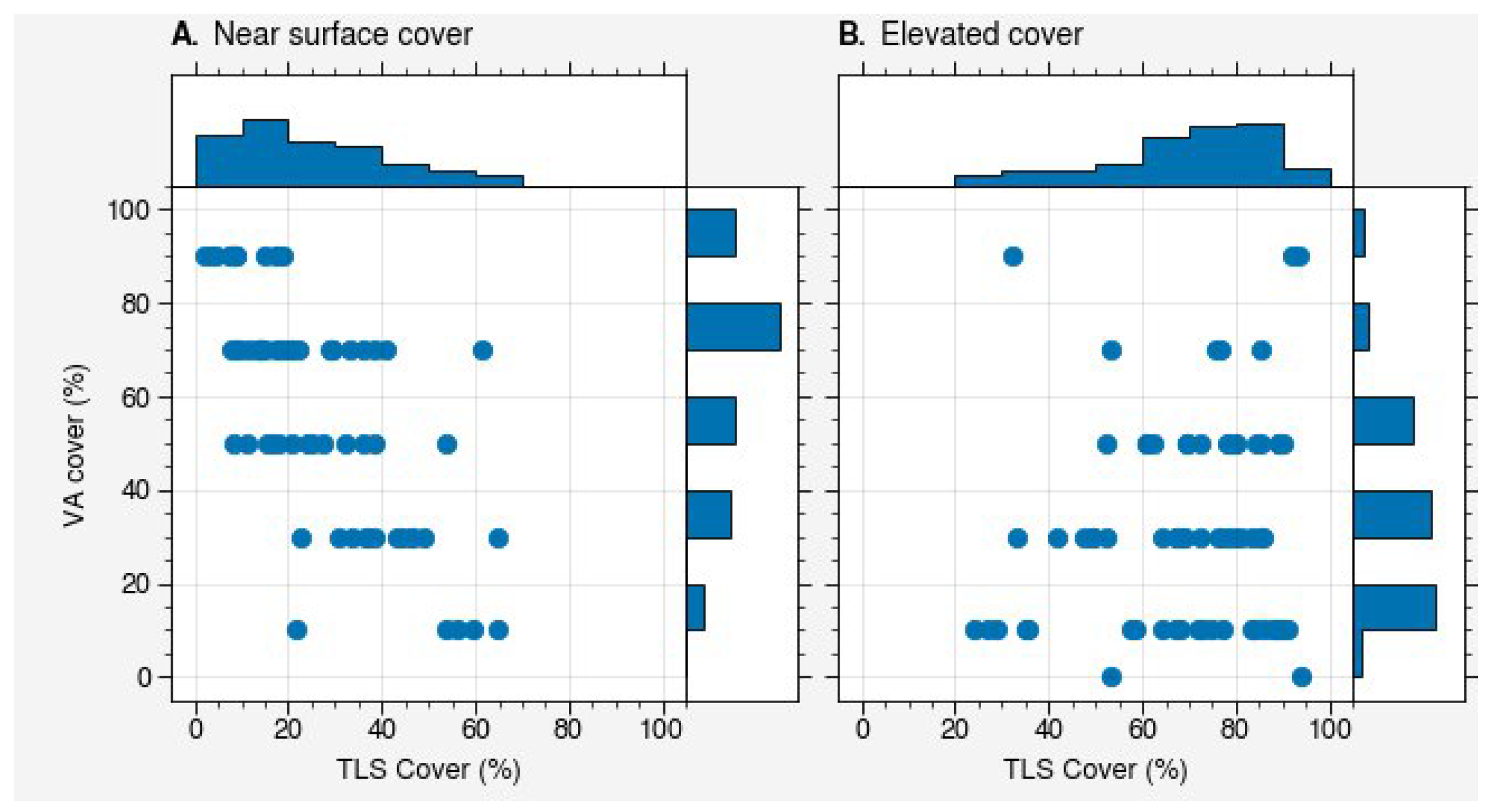
4.1. Plot-Level Fuel Estimates
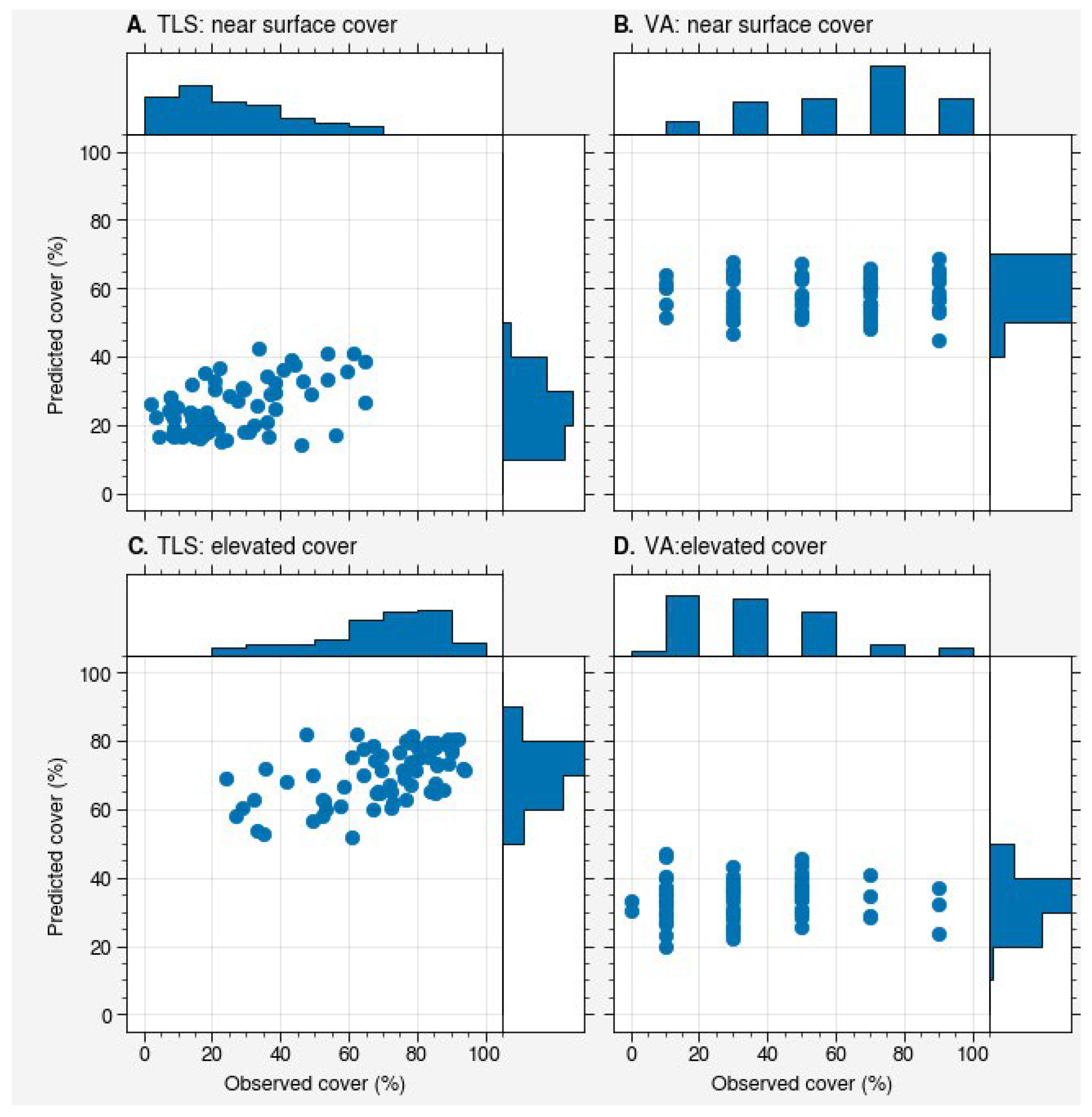
4.2. Random Forest Model Predictions for Near-Surface and Elevated Fuel Cover
4.3. Fuel Metrics Predicted Using TLS Measurements Only
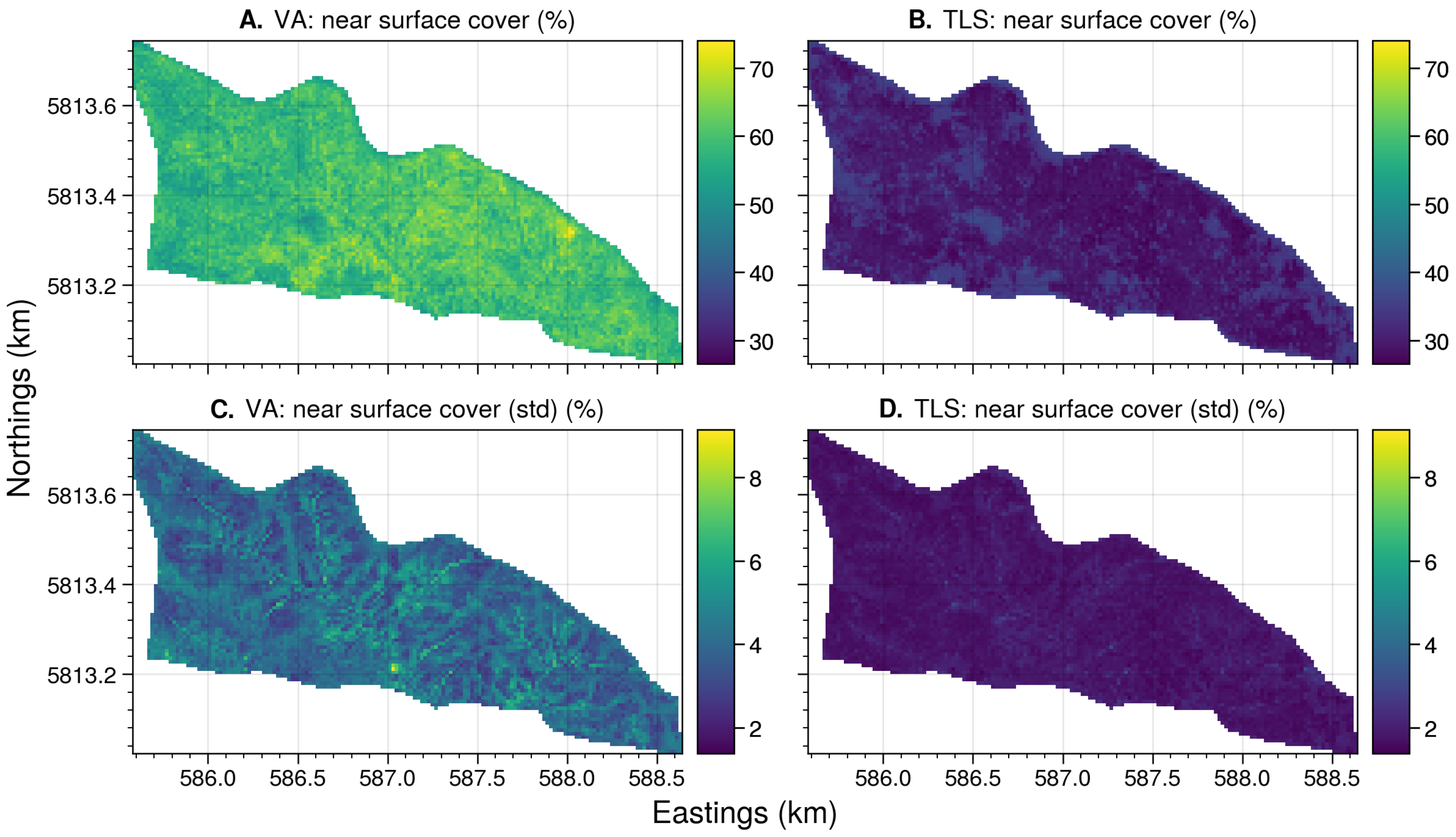
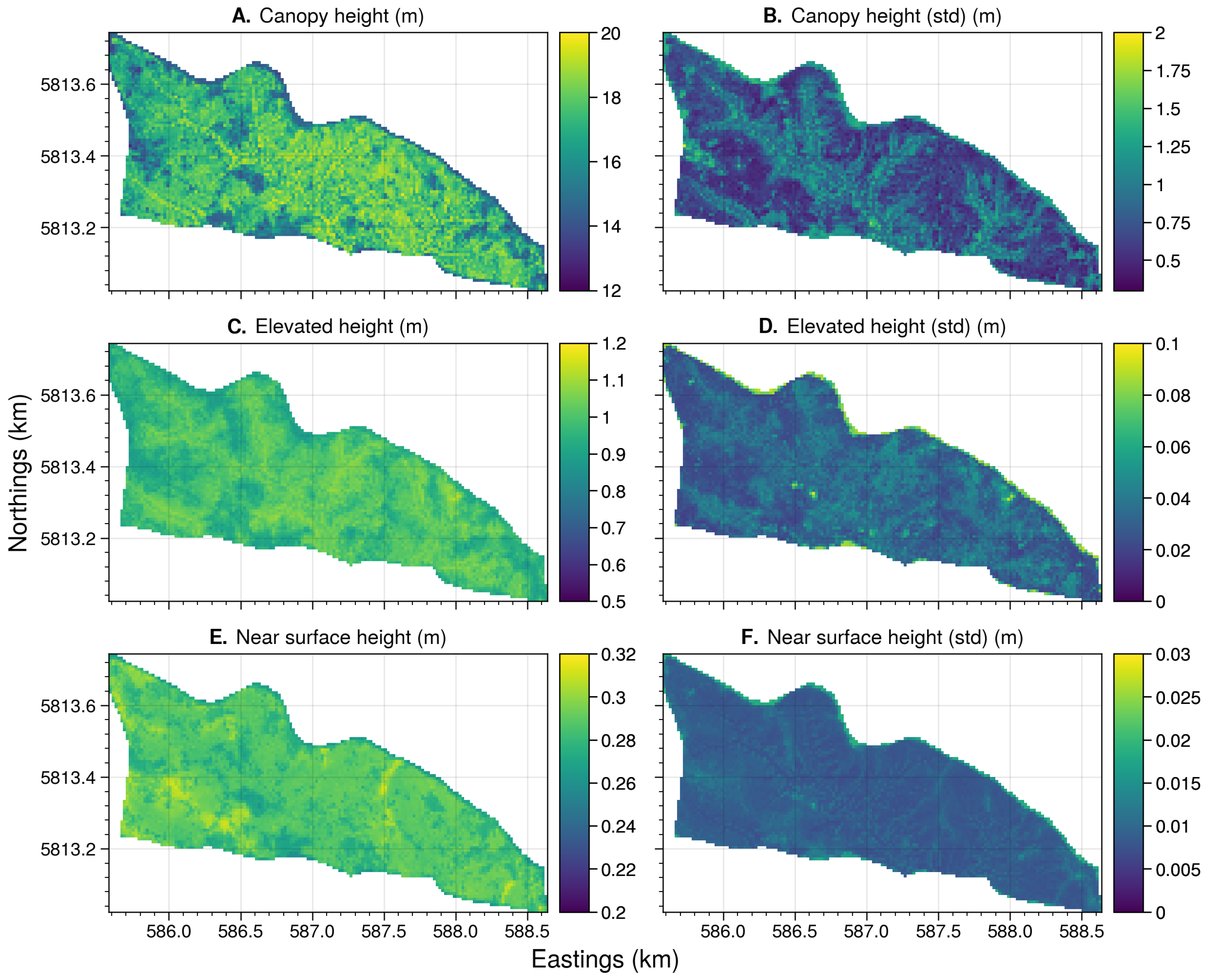
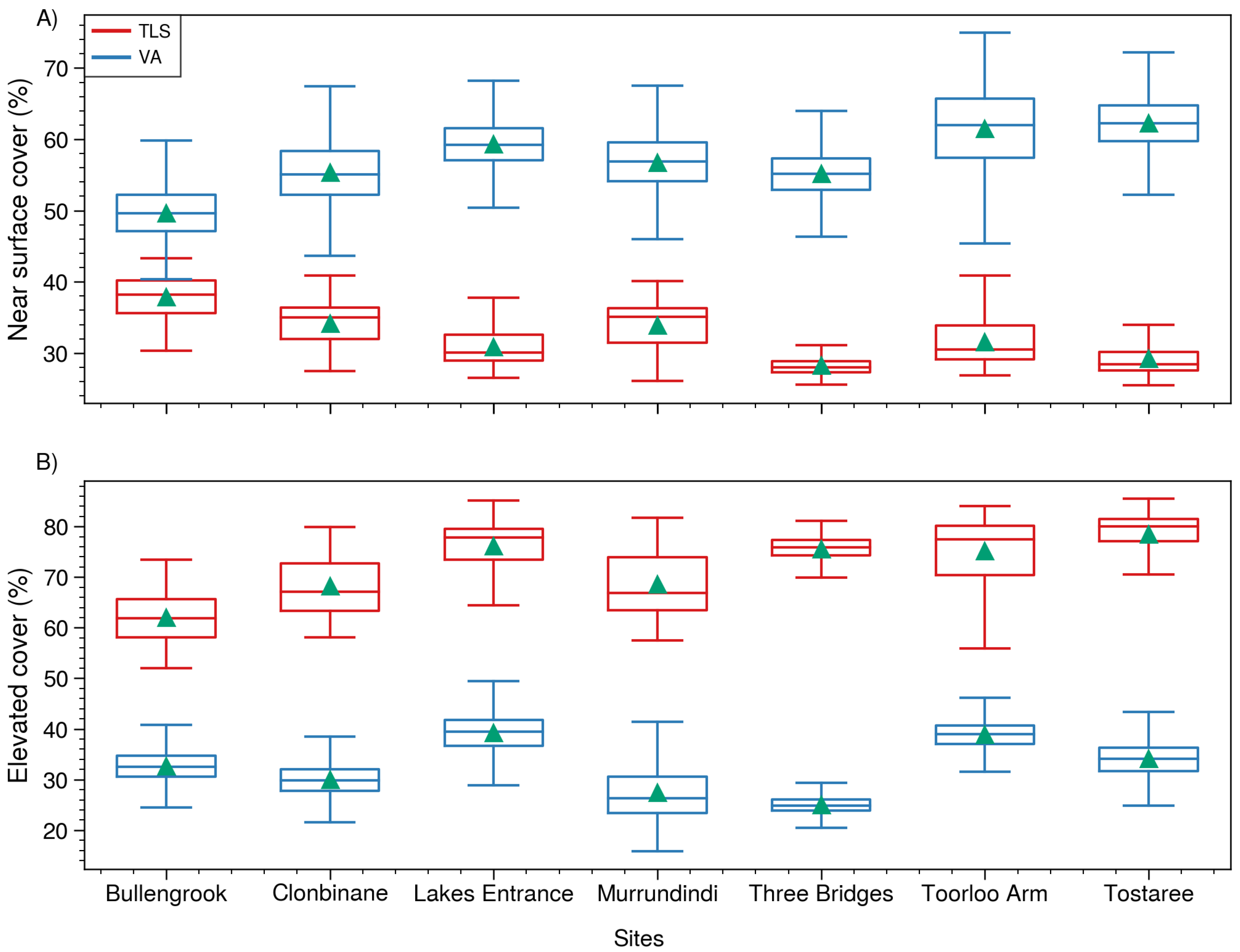
4.4. Landscape Level Fuel Properties
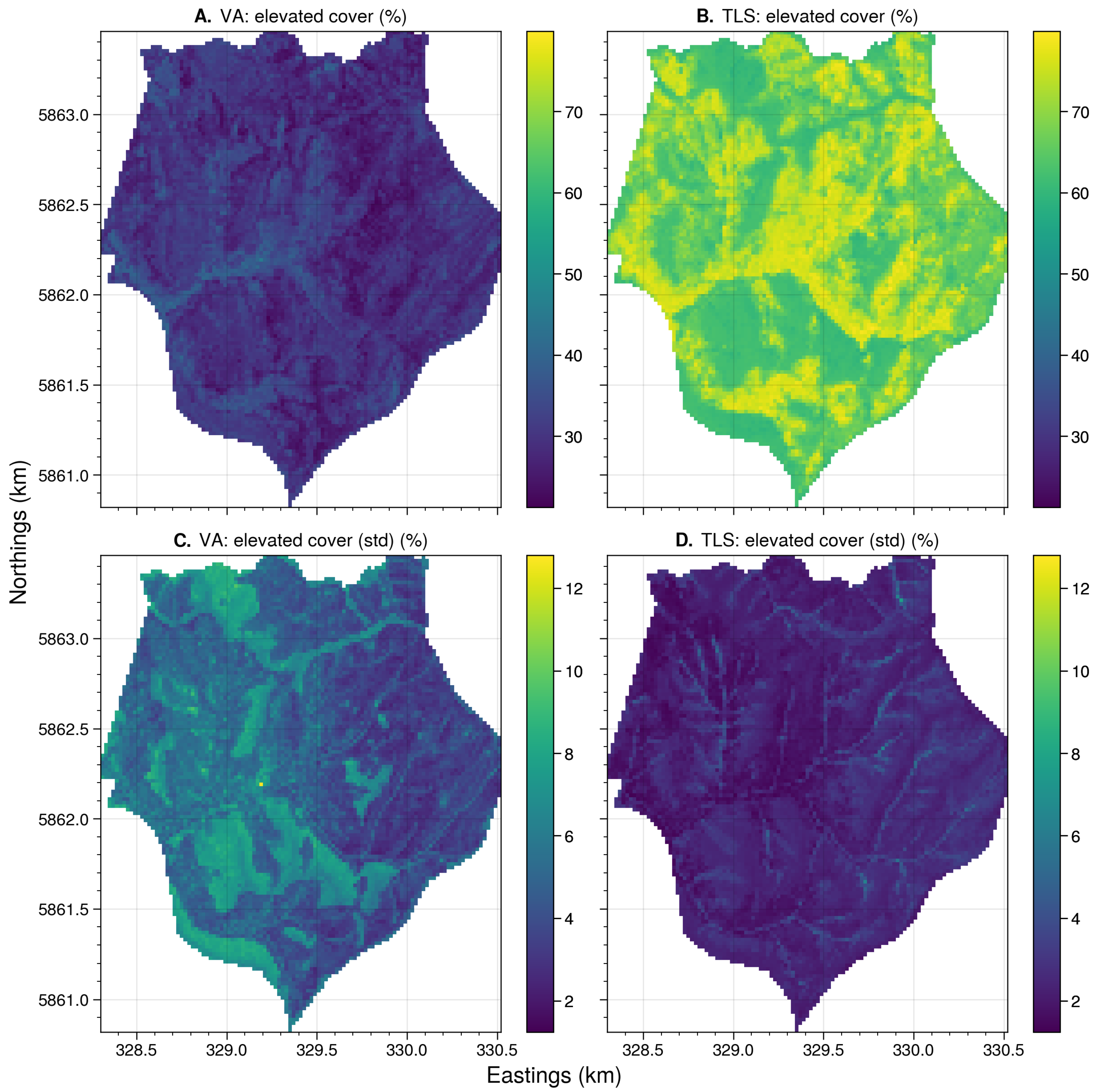
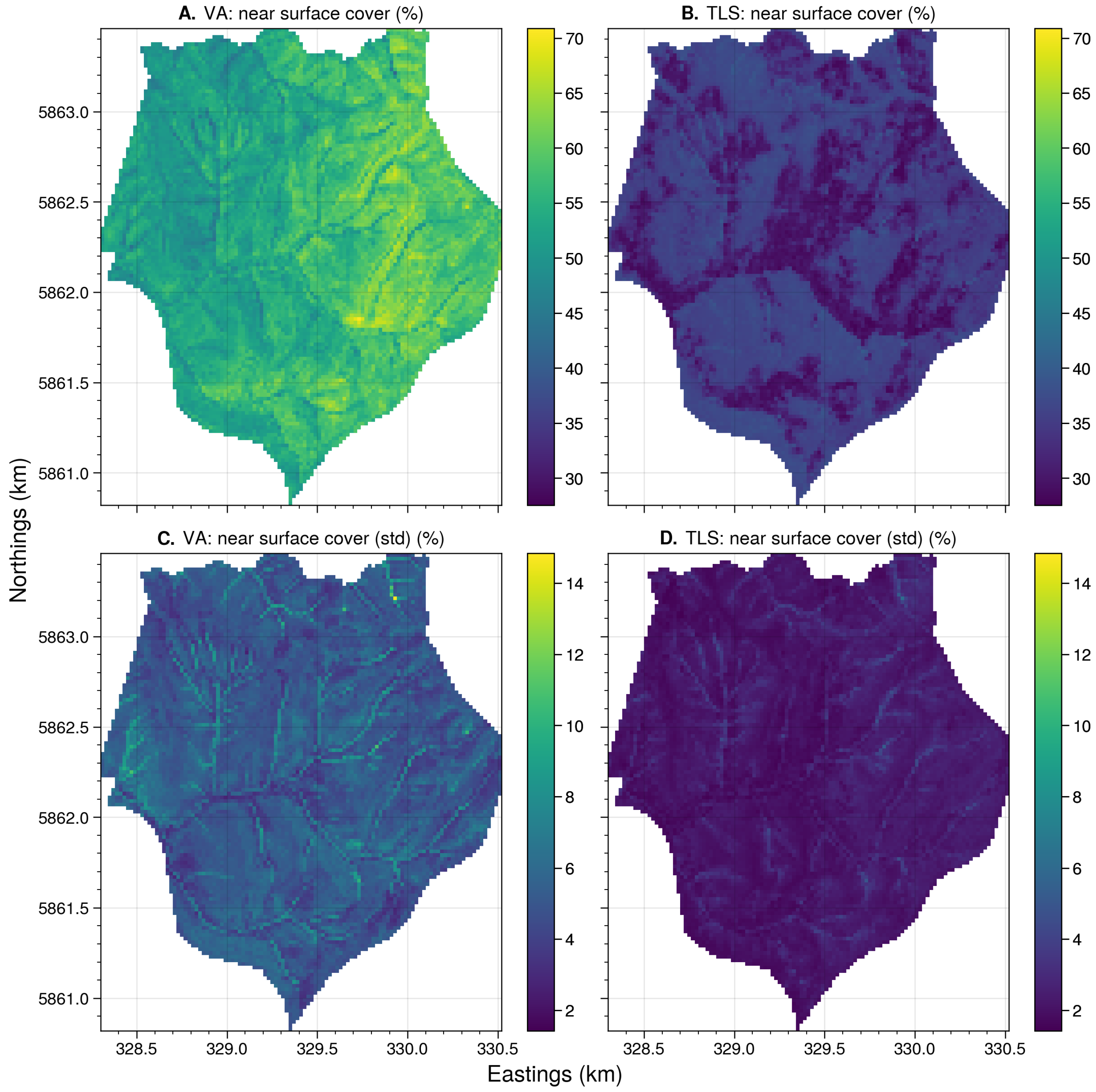
4.4.1. Near-Surface and Elevated Cover
4.4.2. Fuel Height
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALS | Airborne Laser Scanning |
| CFDs | Computational Fluid Dynamics |
| CSF | Cloth Simulation Filter |
| DELWP | Department of Environment, Land, Water, and Planning |
| DTM | Digital Terrain Model |
| FCCS | Fuel Characteristic Classification System |
| OFHAG | Overall Fuel Hazard Assessment Guide |
| TLS | Terrestrial Laser Scanning |
| VA | Visual Assessment |
Appendix A
| Topographic Variables | Description |
|---|---|
| Slope | Calculated by fitting a plane to the eight neighbouring cells [87]. |
| Aspect | The orientation of the cell relative to the north [87]. |
| Catchment area | The upstream area of each cell [88]. |
| Profile curvature | The rate of change of slope in a down-slope direction: a proxy for acceleration and deceleration of water over the terrain [89]. |
| Plan curvature | The curvature of a contour at the central pixel. It can be used as a proxy for convergence and divergence of water [89]. |
| Potential solar radiation ratio | The ratio of the potential solar radiation on a sloping surface to that on a horizontal surface [90]. |
| Topographic Position Index | Classifying terrain such that the altitude of each data point is evaluated against its neighbourhood to verify whether any particular data point forms part of a positive (e.g., crest) or negative (e.g., trough) feature of the surrounding terrain [91]. |
| Terrain Ruggedness Index | The sum change in elevation between a grid cell and its eight neighbouring grid cells [92]. |
| Stream Power Index | A measure of the erosive power of flowing water [93]. |
| Topographic Wetness Index | A measure of soil moisture potential that combines contextual and site information and is used to identify potential locations of ephemeral gullies [94]. |
| Convergence Index | The average bias of the slope directions of the adjacent cell from the direction of the central cell minus 90 degrees [88]. |
| Climate Variables | Description |
|---|---|
| Annual mean temperature (bio1) | The annual mean temperature approximates the total energy inputs for an ecosystem. Calculated by taking the average over twelve months of average temperature for each month [95]. |
| Max temperature of warmest month (bio5) | Calculated by selecting the maximum temperature value across all months within a given year [95]. |
| Precipitation of warmest quarter (bio18) | Calculated by first identifying the warmest quarter of the year and then summing up the precipitation values for that quarter [95]. |
| Soil Variables | Description |
|---|---|
| Soil bulk density (BDW) | Bulk Density of the whole soil (including coarse fragments) in mass per unit volume by a method equivalent to the core method [67]. |
| Soil clay content (CLY) | <2 mass fraction of the <2 soil material determined using the pipette method [67]. |
| Soil pH CaCl2 (pH) | pH of 1:5 soil/0.01 M calcium chloride extract [67]. |
| Vegetative Indices Derived from Sentinel-2 | Description |
|---|---|
| Normalized Difference Vegetation Index (NDVI) | Describes the difference between visible and near-infrared reflectance of vegetation cover and can be used to estimate the density of green on an area of land [96]. |
| Normalized Burn Ratio (NBR) | Identify burned areas and provide a measure of burn severity. |
| Tasseled cap transformation | Technique generally used in land cover mapping or other classification projects [97]. It takes the linear combination of satellite imagery bands and a specialised coefficient matrix to create an n-band image with the first three bands containing the majority of the useful information. The first three bands created represents brightness, greenness, and wetness, which are used as predictors here [98]. |
| Chlorophyll red-edge index | Estimate the chlorophyll content of leaves, using the ratio of reflectivity in the near-infrared (NIR) and red-edge bands [98,99]. |
| Shortwave infrared to near infrared ratio | Provides an indication of leaf chlorophyll content [99]. |
Appendix B
Appendix B.1. Site: Lakes Entrance

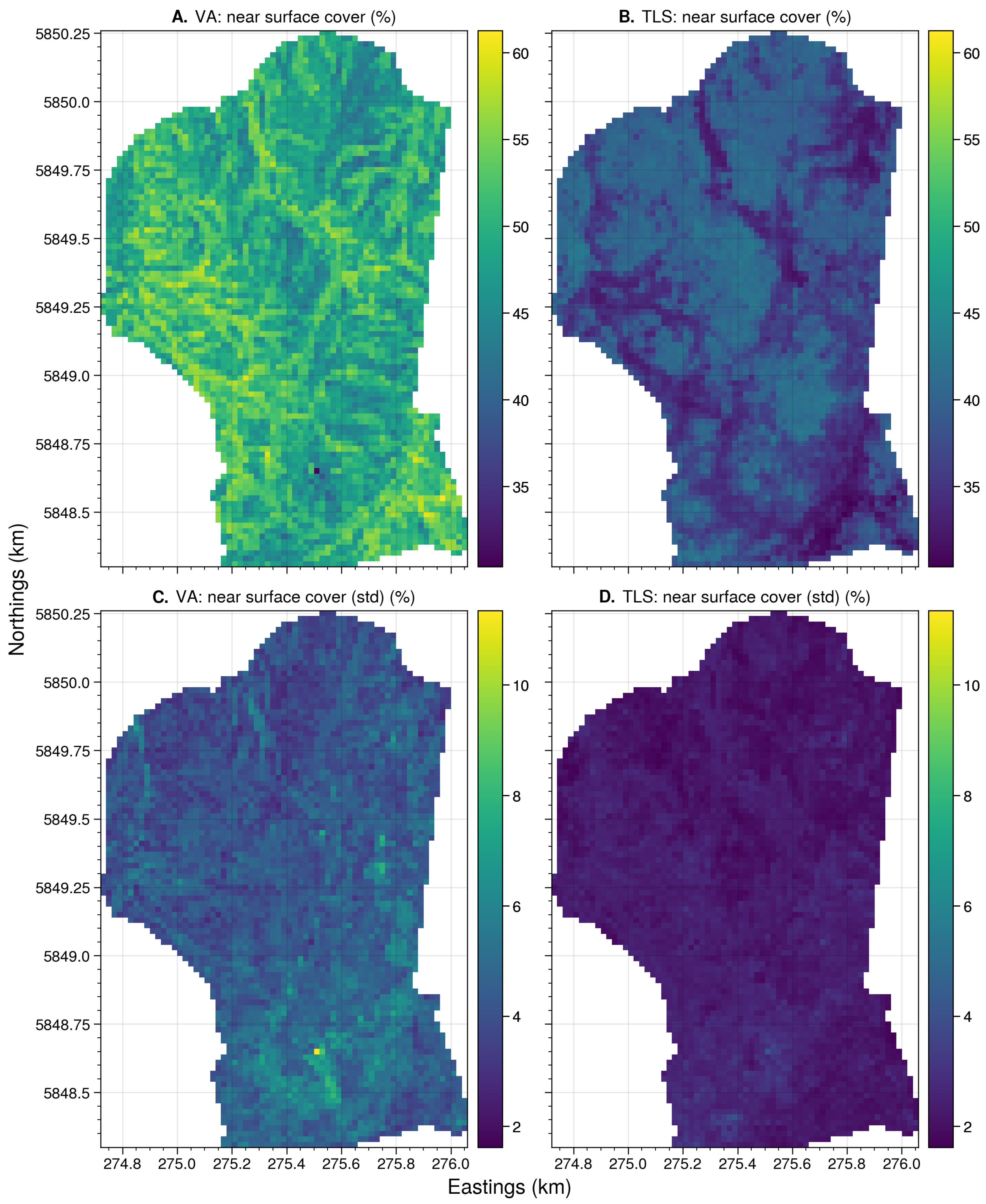
Appendix B.2. Site: Bullengrook
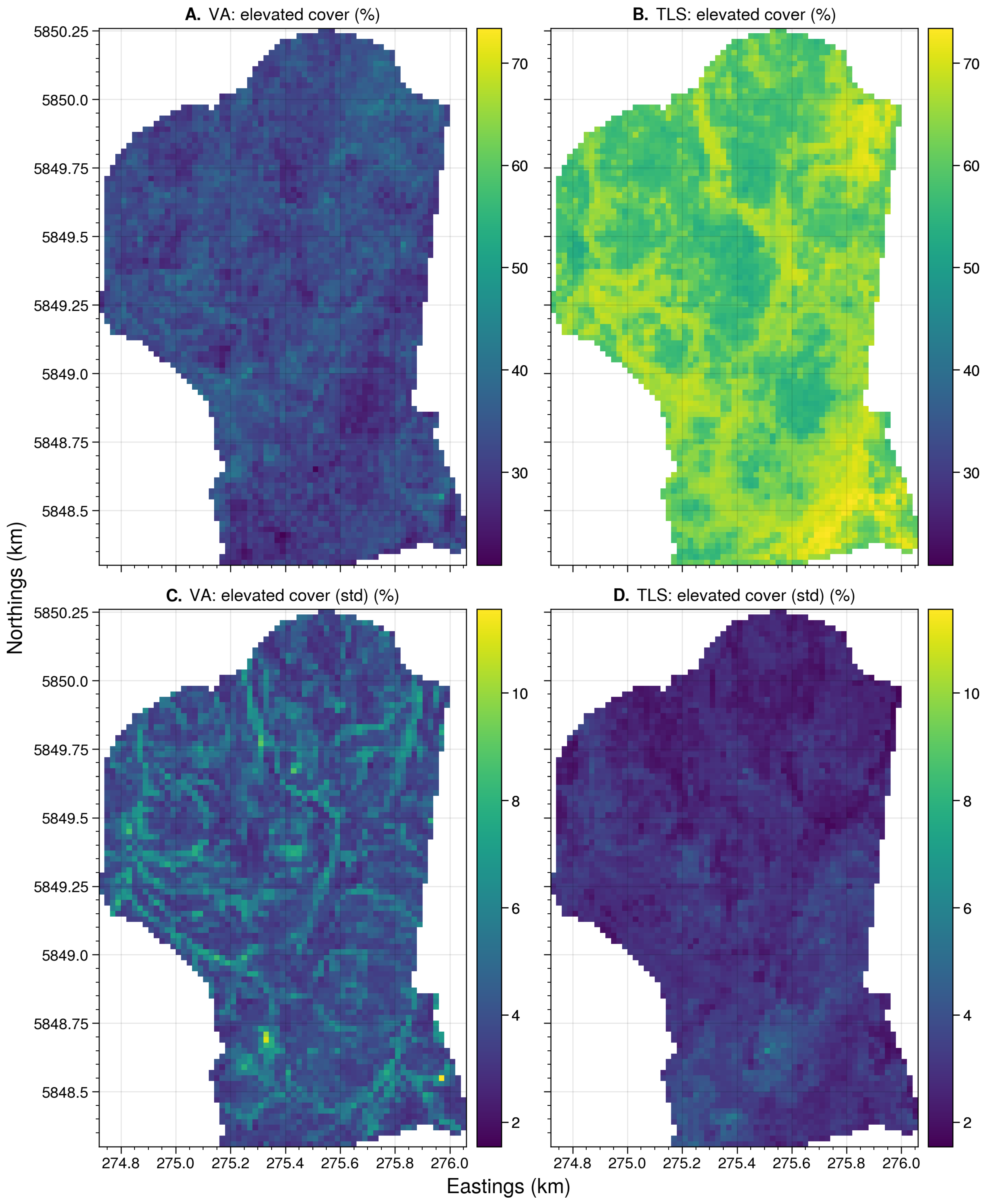

Appendix B.3. Site: Toorloo Arm
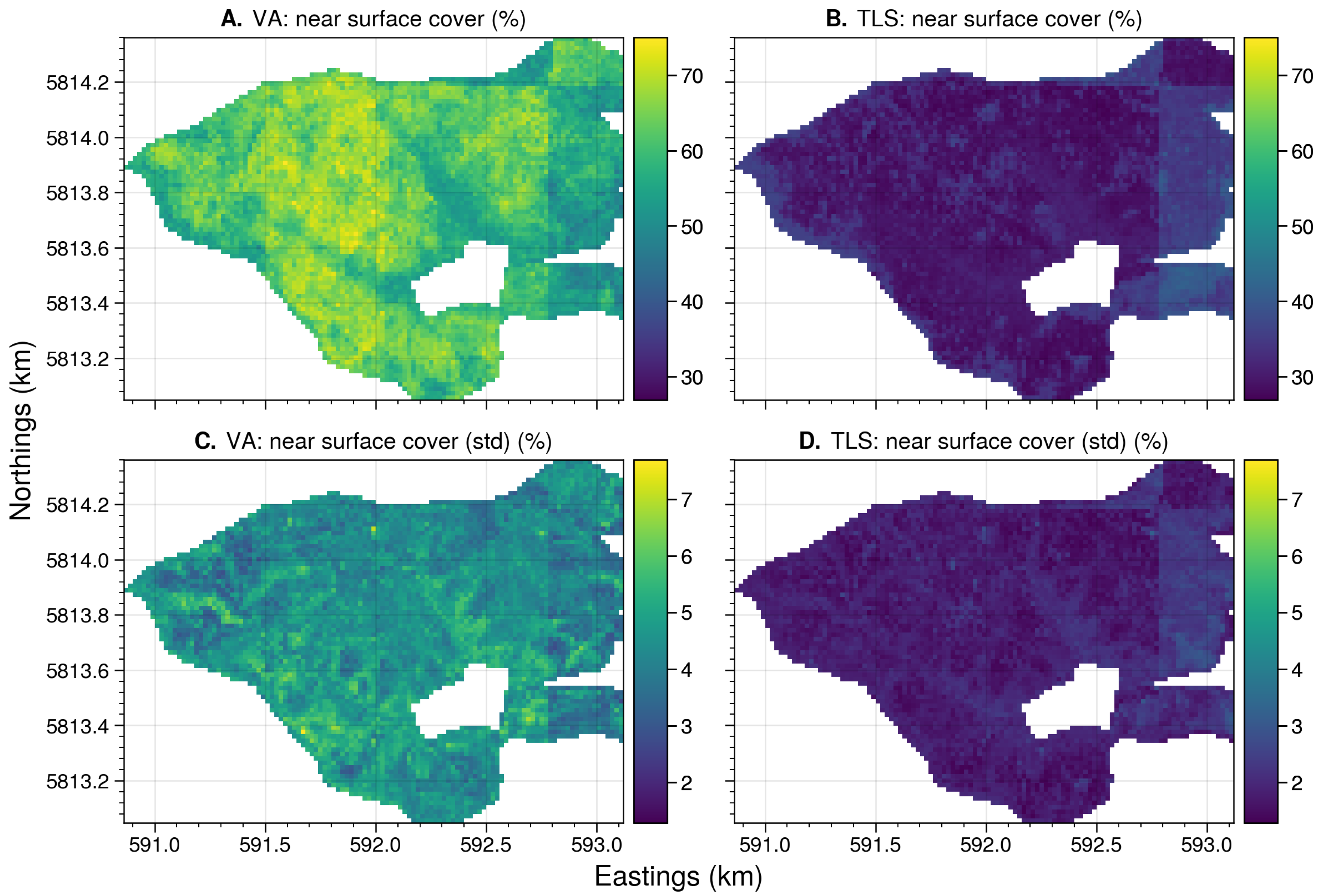

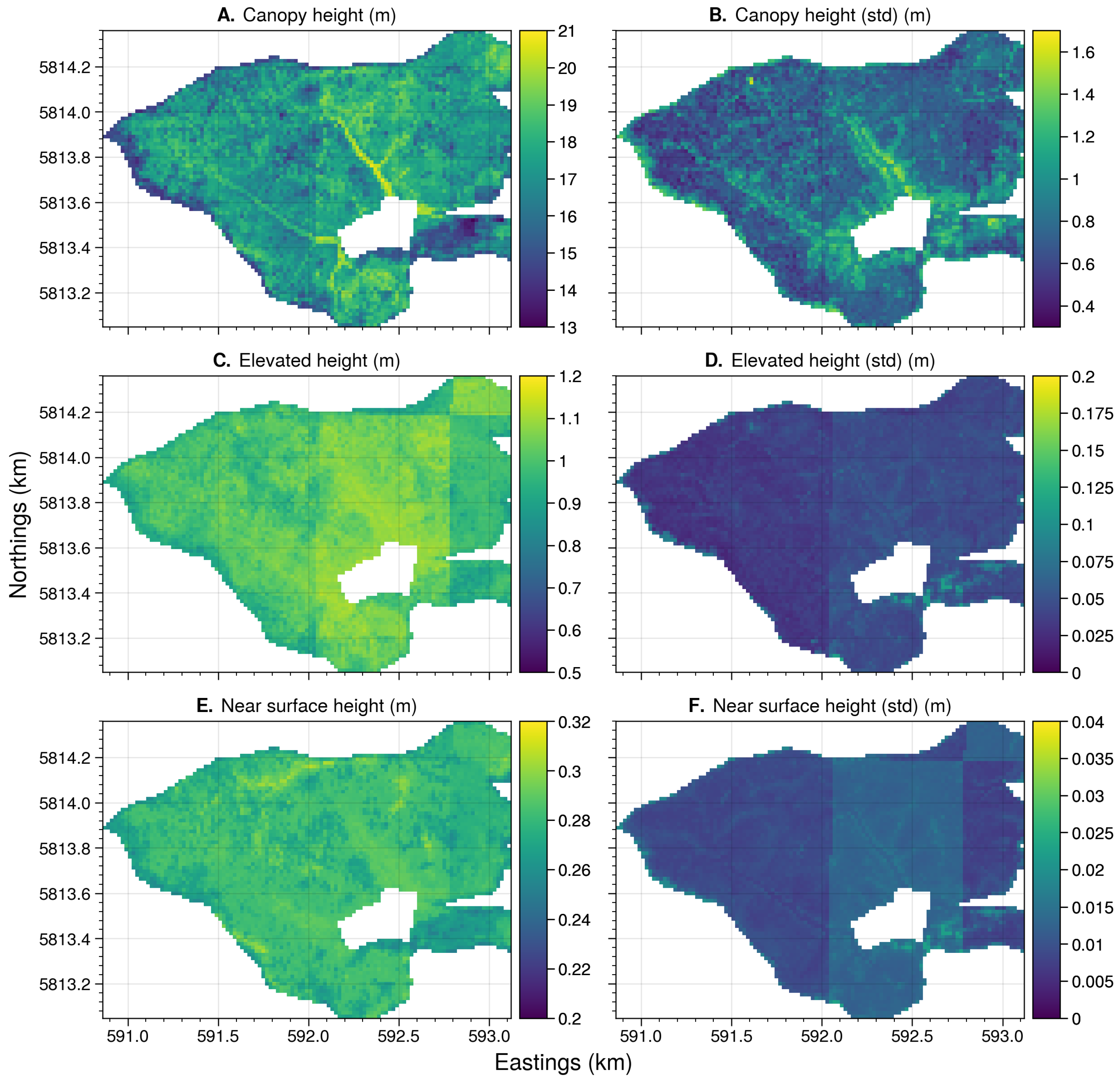
Appendix B.4. Site: Murrindindi


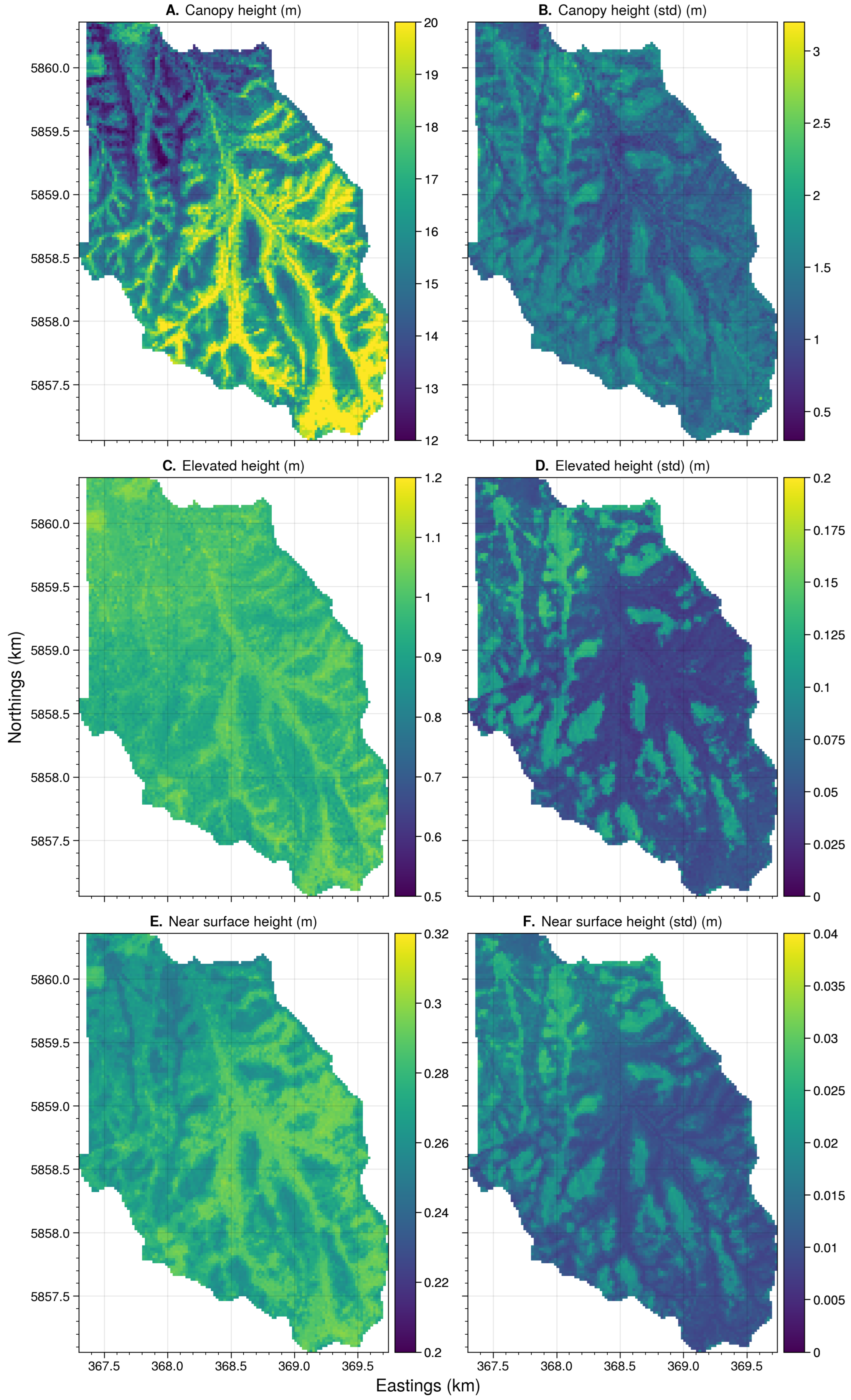
Appendix B.5. Site: Three Bridges

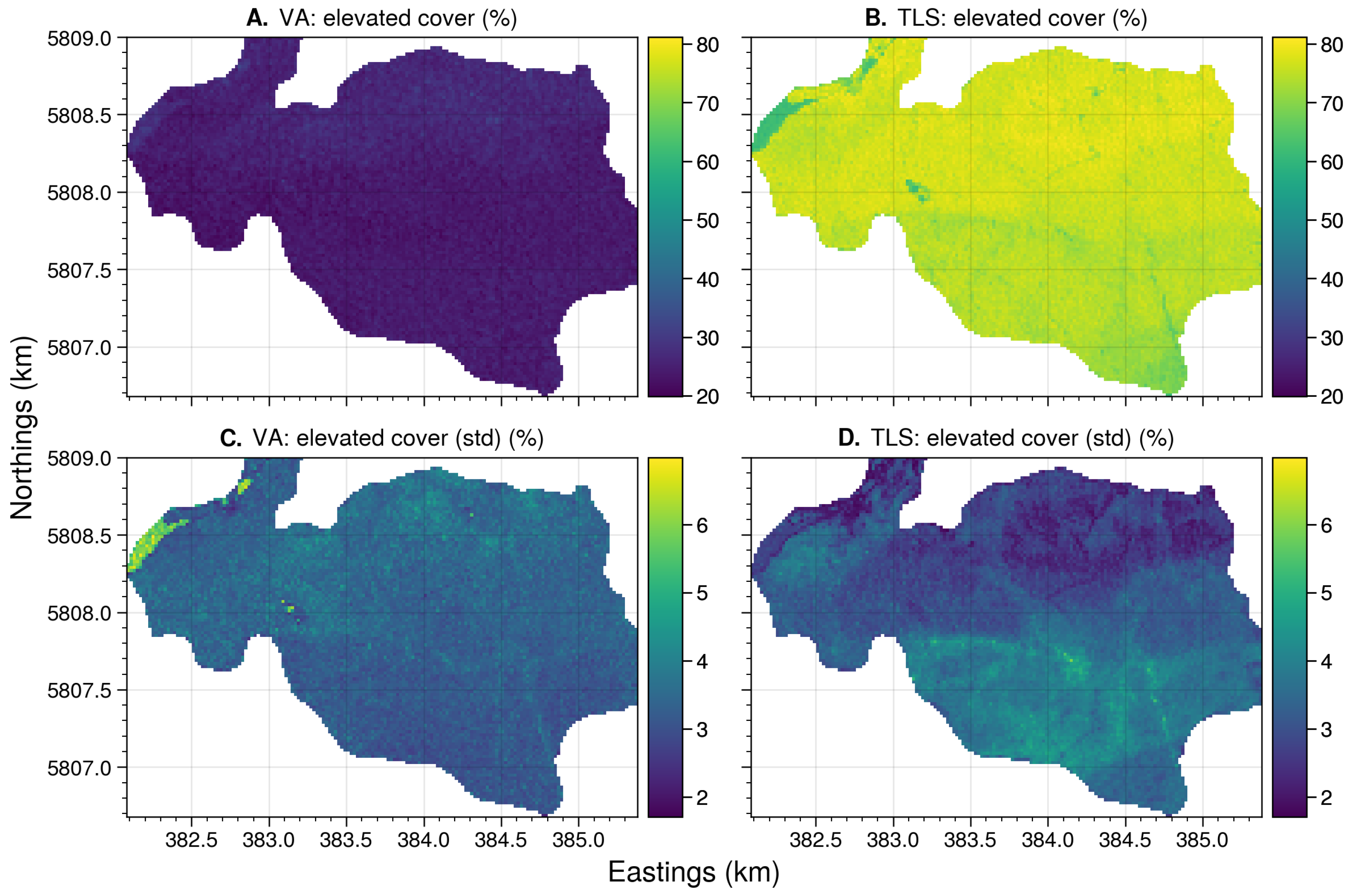
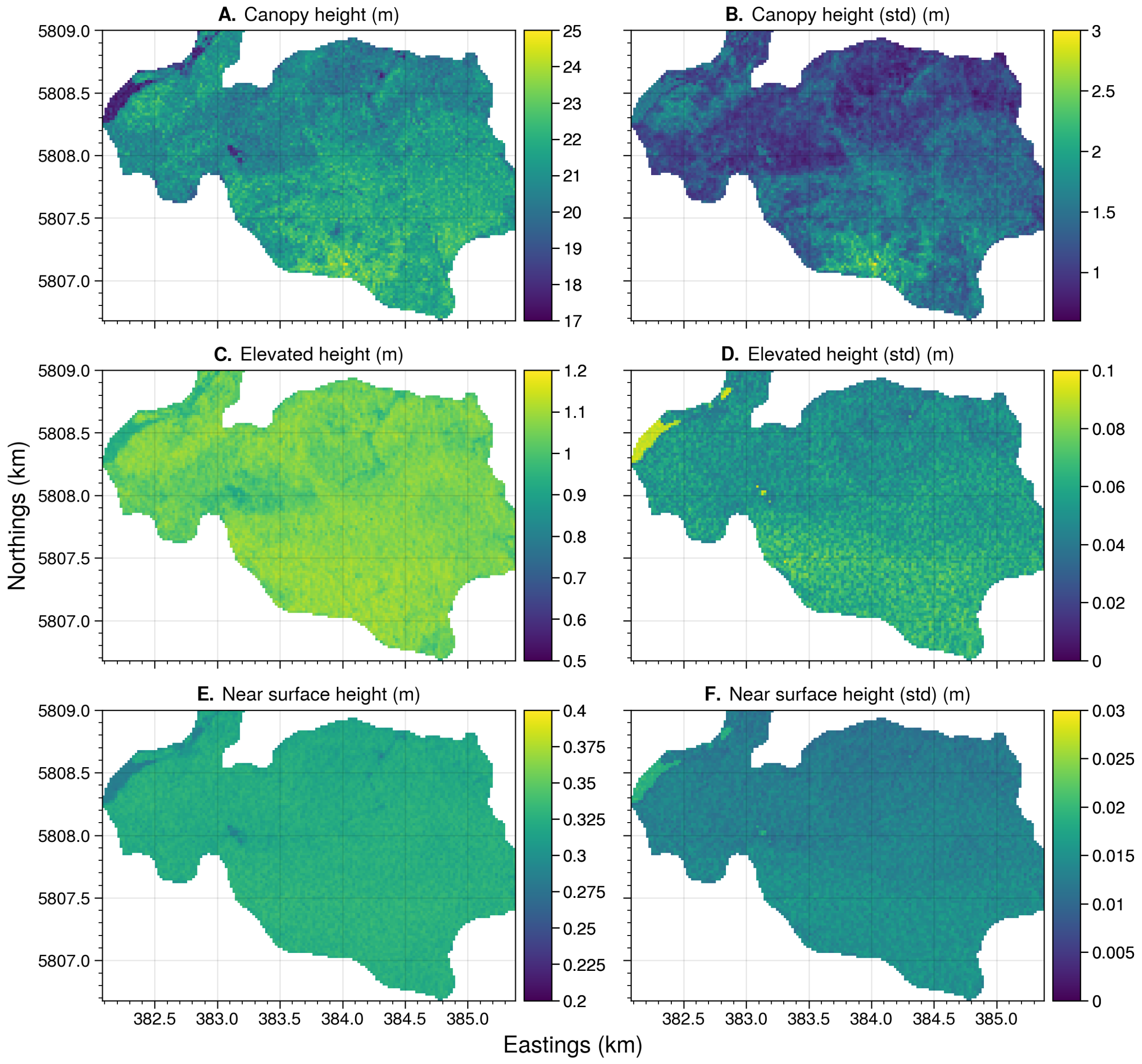
Appendix B.6. Site: Tostaree

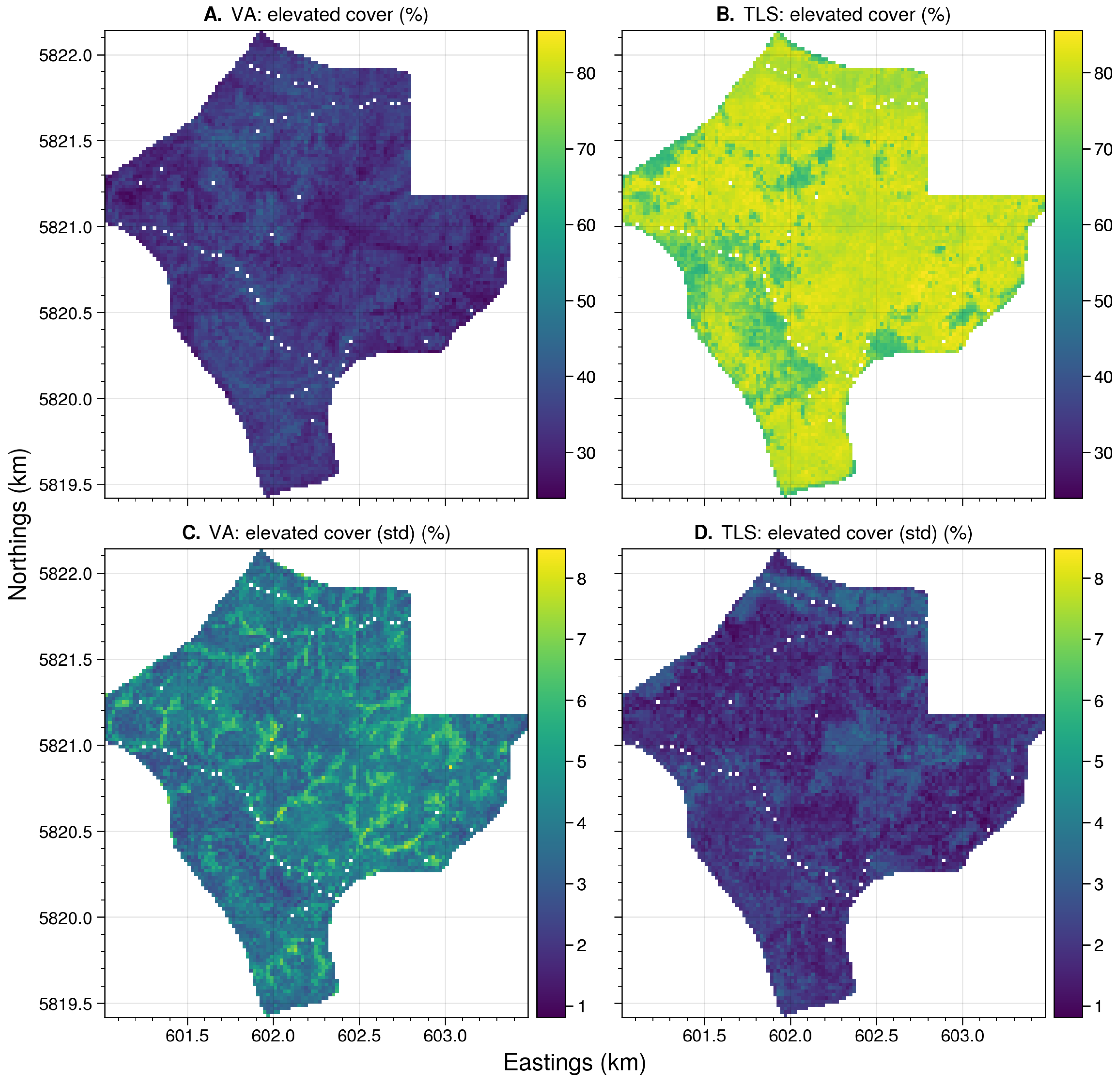
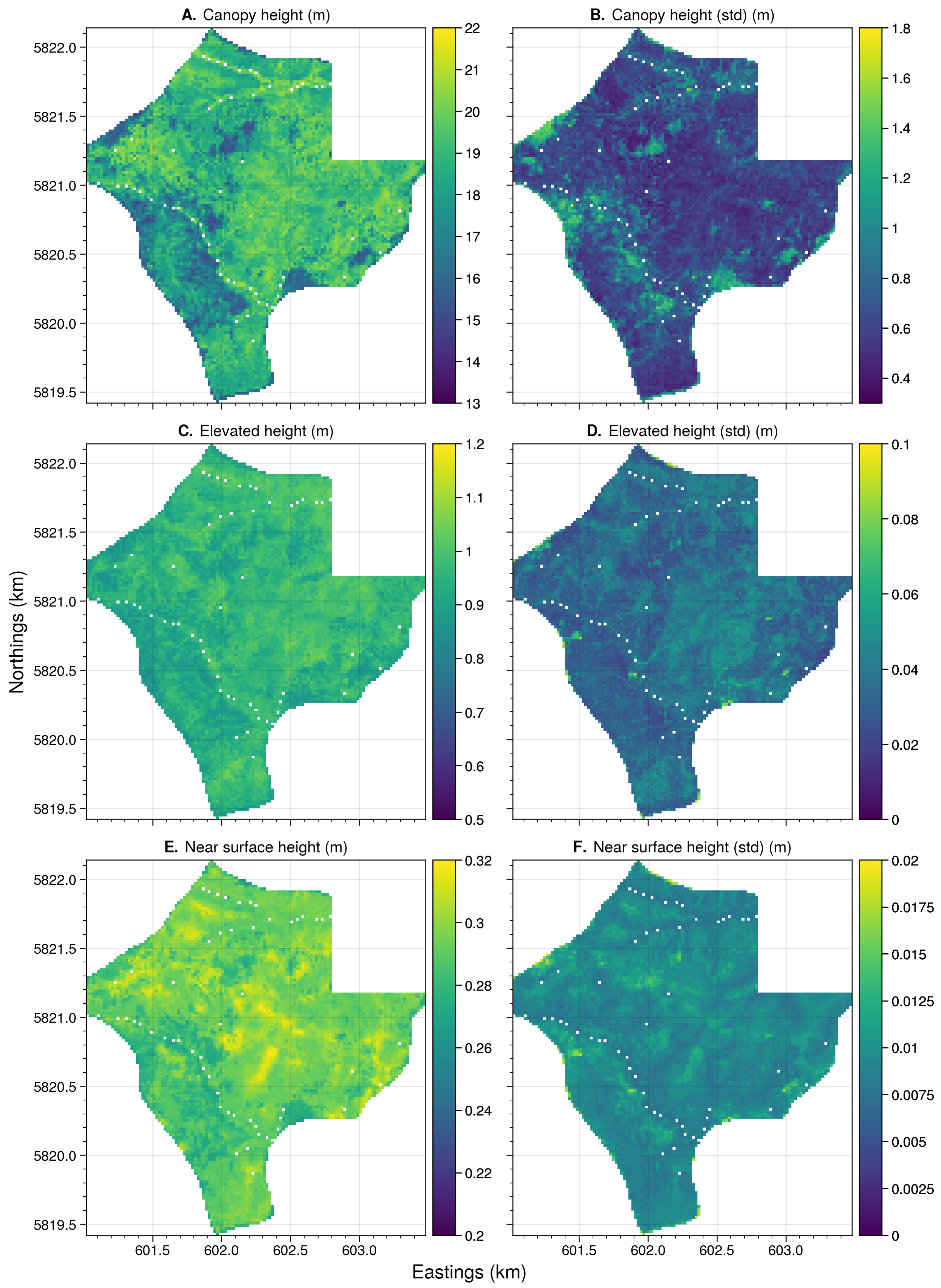
References
- Balch, J.; Bradley, B.; Abatzogloue, J.; Nagy, R.; Fuscod, E.; Mahood, A. Human-started wildfires expand the fire niche acrossthe United States. Environ. Sci. Sustain. Sci. 2017, 114, 2946–2951. [Google Scholar]
- Cattau, M.; Wessman, C.; Mahood, A.; Balch, J. Anthropogenic and lightning-started fires are becoming larger and more frequent over a longer season length in the U.S.A. Glob. Ecol. Biogeogr. 2020, 29, 668–681. [Google Scholar] [CrossRef]
- Liu, M.; Yang, L. Human-caused fires release more carbon than lightning-caused fires in the conterminous United States. Environ. Res. Lett. 2020, 16, 014013. [Google Scholar] [CrossRef]
- Duane, A.; Castellnou, M.; Brotons, L. Towards a comprehensive look at global drivers of novel extreme wildfire events. Clim. Chang. 2021, 165, 43. [Google Scholar] [CrossRef]
- Nauslar, N.; Abatzoglou, J.; Marsh, P. The 2017 North Bay and Southern California Fires: A case study. Fire 2018, 1, 18. [Google Scholar] [CrossRef]
- Porter, T.W.; Crowfoot, W.; Newsom, G. Wildfire Activity Statistics; California Department of Forestry and Fire Protection: Sacramento, CA, USA, 2019. Available online: https://www.fire.ca.gov/incidents/2019 (accessed on 17 November 2022).
- Coogan, S.; Robinne, F.; Jain, P.; Flannigan, M. Scientists’ warning on wildfire—A Canadian perspective. Can. J. For. Res. 2019, 49, 1015–1023. [Google Scholar] [CrossRef]
- Munawar, H.; Ullah, F.; Khan, S.; Qadir, Z.; Qayyum, S. UAV assisted spatiotemporal analysis and management of bushfires: A case study of the 2020 Victorian Bushfires. Fire 2021, 4, 40. [Google Scholar] [CrossRef]
- Cruz, M.; Cheney, N.; Gould, J.; McCaw, W.; Kilinc, M.; Sullivan, A. An empirical-based model for predicting the forward spread rate of wildfires in eucalypt forests. Int. J. Wildland Fire 2022, 31, 81–95. [Google Scholar] [CrossRef]
- Linn, R.; Goodrick, S.; Brown, M.; Middleton, R.; OBrien, J.; Hiers, J. QUIC-fire: A fast-running simulation tool for prescribed fire planning. Environ. Model. Softw. 2020, 125, 104616. [Google Scholar] [CrossRef]
- Miller, C.; Hilton, J.; Sullivan, A.; Prakash, M. SPARK—A bushfire spread prediction tool. IFIP Adv. Inf. Commun. Technol. 2015, 448, 262–271. [Google Scholar]
- Taneja, R.; Hilton, J.; Wallace, L.; Reinke, K.; Jones, S. Effect of fuel spatial resolution on predictive wildfire models. Int. J. Wildland Fire 2021, 30, 776–789. [Google Scholar] [CrossRef]
- Cruz, M.; McCaw, W.; Anderson, W.; Gould, J. Fire behavior modelling in semi-arid Mallee-heath shrublands of southern Australia. Environ. Model. Softw. 2013, 40, 21–34. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Botelho, H.S. A review of prescribed burning effectiveness in fire hazard reduction. Int. J. Wildland Fire 2003, 12, 117–128. [Google Scholar] [CrossRef]
- Jenkins, M.E.; Bedward, M.; Price, O.; Bradstock, R.A. Modelling bushfire fuel hazard using biophysical parameters. Forests 2020, 11, 925. [Google Scholar] [CrossRef]
- Thompson, M.; Vaillant, N.; Hass, J.; Gebert, K. Modelling surface fine fuel dynamics across climate gradients in eucalypt forests of south-eastern Australia. J. For. 2013, 111, 49–58. [Google Scholar]
- Catchpole, W.; Wheeler, C. Estimating plant biomass: A review of techniques. Aust. J. Ecol. 1992, 17, 121–131. [Google Scholar] [CrossRef]
- Price, O.; Gordon, C. The potential for LiDAR technology to map fire fuel hazard over large areas of australian forest. J. Environ. Manag. 2016, 181, 663–673. [Google Scholar] [CrossRef] [PubMed]
- Van Wagner, C. The line intersect method in forest fuel sampling. For. Sci. 1968, 14, 20–26. [Google Scholar]
- Elshikha, D. Using RGB-based vegetation indices for monitoring guayule biomass, moisture content and rubber. In Proceedings of the ASABE Annual International Meeting, Orlando, FL, USA, 17–20 July 2016. [Google Scholar]
- Rowell, E.; Loudermilk, E.L.; Hawley, C.; Pokswinski, S.; Seielstad, C.; Queen, L.; O’Brien, J.J.; Hudak, A.T.; Goodrick, S.; Hiers, J.K. Coupling terrestrial laser scanning with 3D fuel biomass sampling for advancing wildland fuels characterization. For. Ecol. Manag. 2020, 462, 117945. [Google Scholar] [CrossRef]
- Loudermilk, E.; Hiers, J.; O’Brien, J.; Mitchell, R.; Singhania, A.; Fernandez, J.; Cropper, W.; Slatton, K. Ground-based LiDAR: A novel approach to quantify fine-scale fuelbed characteristics. Int. J. Wildland Fire 2009, 18, 676–685. [Google Scholar] [CrossRef]
- Hines, F.; Tolhurst, K.G.; Wilson, A.A.G.; McCarthy, G.J. Overall Fuel Hazard Assessment Guide, 4th ed.; Victorian Government, Department of Sustainability and Environment: East Melbourne, Australia, 2010; Volume 82, pp. 1–41.
- 24.Prichard, S.J.; Sandberg, D.V.; Ottmar, R.D.; Eberhardt, E.; Andreu, A.; Eagle, P.; Swedin, K. Fuel Characteristic Classification System Version 3.0: Technical Documentation; Gen. Tech. Rep. PNW-GTR-887; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2013; Volume 887, 79p.
- Prichard, S.J.; Andreu, A.G.; Ottmar, R.D.; Eberhardt, E. Fuel Characteristic Classification System (FCCS) Field Sampling and Fuelbed Development Guide; Gen. Tech. Rep. PNW-GTR-972; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2019; p. 77.
- Duff, T.J.; Bell, T.L.; York, A. Predicting continuous variation in forest fuel load using biophysical models: A case study in south-eastern Australia. Int. J. Wildland Fire 2012, 22, 318–332. [Google Scholar] [CrossRef]
- McColl-Gausden, S.; Bennett, L.; Duff, T.; Cawson, J.; Penman, T. Climatic and edaphic gradients predict variation in wildland fuel hazard in south-eastern Australia. Ecography 2020, 43, 443–455. [Google Scholar] [CrossRef]
- Penman, T.; McColl-Gausden, S.; Cirulis, B.; Kultaev, D.; Bennett, L. Improved accuracy of wildfire simulations using fuel hazard estimates based on environmental data. J. Environ. Manag. 2022, 301, 113789. [Google Scholar] [CrossRef]
- Gosper, C.R.; Yates, C.J.; Prober, S.M.; Wiehl, G. Application and validation of visual fuel hazard assessments in dry Mediterranean-climate woodlands. Int. J. Wildland Fire 2014, 23, 385. [Google Scholar] [CrossRef]
- Spits, C.; Wallace, L.; Reinke, K. Investigating Surface and Near-Surface Bushfire Fuel Attributes: A Comparison between Visual Assessments and Image-Based Point Clouds. Sensors 2017, 17, 910. [Google Scholar] [CrossRef]
- Watson, P.J.; Penman, S.H.; Bradstock, R.A. A comparison of bushfire fuel hazard assessors and assessment methods in dry sclerophyll forest near Sydney, Australia. Int. J. Wildland Fire 2012, 21, 755–763. [Google Scholar] [CrossRef]
- Gajardo, J.; García, M.; Riaño, D. Applications of airborne laser scanning in forest fuel assessment and fire prevention. In Forestry Applications of Airborne Laser Scanning; Springer: Berlin/Heidelberg, Germany, 2014; pp. 439–462. [Google Scholar] [CrossRef]
- Lovell, J.L.; Jupp, D.L.; Culvenor, D.S.; Coops, N.C. Using airborne and ground-based ranging LiDAR to measure canopy structure in Australian forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Newnham, G.J.; van Leeuwen, M.; Wulder, M.A.; Stewart, J.; Culvenor, D.S. Comparison of Terrestrial and Airborne LiDAR in Describing Stand Structure of a Thinned Lodgepole Pine Forest. J. For. 2012, 110, 97–104. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Gupta, V.; Reinke, K.; Jones, S.; Wallace, L.; Holden, L. Assessing Metrics for Estimating Fire Induced Change in the Forest Understorey Structure Using Terrestrial Laser Scanning. Remote Sens. 2015, 7, 8180–8201. [Google Scholar] [CrossRef]
- Hillman, S.; Wallace, L.; Reinke, K.; Jones, S. A comparison between TLS and UAS LiDAR to represent eucalypt crown fuel characteristics. ISPRS J. Photogramm. Remote Sens. 2021, 181, 295–307. [Google Scholar] [CrossRef]
- Hudak, A.; Bright, B.; Rowell, E.; Robertson, K.; Pokswinski, S.; Hiers, K.; Prichard, S.; Nowell, H.; Holmes, C.; Gargulinski, E.; et al. Estimating Surface Fuel Density from TLS and ALS: A Two-Tiered Approach that Accounts for Sampling Scale. In Proceedings of the SilviLaser Conference, Vienna, Austria, 28–30 September 2021; pp. 123–125. [Google Scholar]
- Levick, S.R.; Whiteside, T.; Loewensteiner, D.A.; Rudge, M.; Bartolo, R. Leveraging TLS as a Calibration and Validation Tool for MLS and ULS Mapping of Savanna Structure and Biomass at Landscape-Scales. Remote Sens. 2021, 13, 257. [Google Scholar] [CrossRef]
- Pokswinski, S.; Gallagher, M.R.; Skowronski, N.S.; Loudermilk, E.L.; Hawley, C.; Wallace, D.; Everland, A.; Wallace, J.; Hiers, J.K. A simplified and affordable approach to forest monitoring using single terrestrial laser scans and transect sampling. MethodsX 2021, 8, 101484. [Google Scholar] [CrossRef] [PubMed]
- Wallace, L.; Hillman, S.; Hally, B.; Taneja, R.; McGlade, J. Terrestrial Laser Scanning: An Operational Tool for Fuel Hazard Mapping? Fire 2022, 5, 85. [Google Scholar] [CrossRef]
- Muir, J.; Phinn, S.; Eyre, T.; Scarth, P. Measuring plot scale woodland structure using terrestrial laser scanning. Remote Sens. Ecol. Conserv. 2018, 4, 320–338. [Google Scholar] [CrossRef]
- Newnham, G.J.; Armston, J.D.; Calders, K.; Disney, M.I.; Lovell, J.L.; Schaaf, C.B.; Strahler, A.H.; Danson, F.M. Terrestrial laser scanning for plot-scale forest measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef]
- State Government of Victoria. Fuel Management Report 2020–21: Statewide Outcomes and Delivery-Victorian Bushfire Monitoring Program; State Government of Victoria: Melbourne, Australia, 2021.
- Cartus, O.; Kellndorfer, J.; Rombach, M.; Walker, W. Mapping canopy height and growing stock volume using airborne LiDAR, ALOS PALSAR and Landsat ETM+. Remote Sens. 2012, 4, 3320–3345. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Haywood, A.; Skidmore, A.K. Mapping Forest Canopy Height Across Large Areas by Upscaling ALS Estimates with Freely Available Satellite Data. Remote Sens. 2015, 7, 12563–12587. [Google Scholar] [CrossRef]
- Armston, J.; Denham, R.; Danaher, T.; Scarth, P.; Moffiet, T. Prediction and validation of foliage projective cover from Landsat-5 TM and Landsat-7 ETM+. J. Appl. Remote Sens. 2009, 3, 033540. [Google Scholar] [CrossRef]
- Leite, R.; Silva, C.; Broadbent, E.; Amaral, C.; Liesenberg, V.; Almeida, D.; Mohan, M.; Godinho, S.; Cardil, A.; Hamamura, C.; et al. Large scale multi-layer fuel load characterization in tropical savanna using GEDI spaceborne LiDAR data. Remote Sens. Environ. 2022, 268, 112764. [Google Scholar] [CrossRef]
- D’Este, M.; Elia, M.; Vincenzo, G.; Giuseppina, S.; Raffaele, L.; Giovanni, S. Machine Learning Techniques for Fine Dead Fuel Load Estimation Using Multi-Source Remote Sensing Data. Remote Sens. 2021, 13, 1658. [Google Scholar] [CrossRef]
- Lau, A.; Bentley, L.; Martius, C. Quantifying branch architecture of tropical trees using terrestrial LiDAR and 3D modelling. Int. J. Wildland Fire 2018, 32, 1219–1231. [Google Scholar] [CrossRef]
- Ashcroft, M.; Gollan, J.; Ramp, D. Creating vegetation density profiles for a diverse range of ecological habitats using terrestrial laser scanning methods. Ecol. Evol. 2014, 5, 263–272. [Google Scholar]
- Palace, M.; Sullivan, F.; Ducey, M.; Herrick, C. Estimating tropical forest structure using a terrestrial LiDAR. PLoS ONE 2016, 11, e0154115. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhu, X.; Yebra, M.; Harris, S.; Tapper, N. Strata-based forest fuel classification for wild fire hazard assessment using terrestrial LiDAR. J. Appl. Remote Sens. 2016, 10, 046025. [Google Scholar] [CrossRef]
- Hudak, A.; Evans, J.; Stuart Smith, A. LiDAR utility for natural resource managers. Remote Sens. 2009, 1, 934–951. [Google Scholar] [CrossRef]
- Vosselman, G.; Gorte, B.; Sithole, G. Recognising strucutre in laser scanner point clouds. Remote Sens. Spat. Inf. Sci. 2004, 32, 33–38. [Google Scholar]
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Dolha, M.; Beetz, M. Towards 3D Point cloud based object maps for household environments. Robot. Auton. Syst. 2008, 56, 927–941. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Gould, J.S.; Lachlan McCaw, W.; Phillip Cheney, N. Quantifying fine fuel dynamics and structure in dry eucalypt forest (Eucalyptus marginata) in Western Australia for fire management. For. Ecol. Manag. 2011, 262, 531–546. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Linusson, H. Multi-Output Random Forests. Master’s Thesis, University of Borås, Borås, Sweden, 2013. [Google Scholar]
- Yadav, B.K.V.; Lucieer, A.; Jordan, G.J.; Baker, S.C. Using topographic attributes to predict the density of vegetation layers in a wet eucalypt forest. Aust. For. 2022, 85, 25–37. [Google Scholar] [CrossRef]
- Hageer, Y.; Esperón-Rodríguez, M.; Baumgartner, J.B.; Beaumont, L.J. Climate, soil or both? Which variables are better predictors of the distributions of Australian shrub species? PeerJ 2017, 5, e3446. [Google Scholar] [CrossRef] [PubMed]
- DeCastro, A.; Juliano, T.; Kosović, B.; Ebrahimian, H.; Balch, J. A computationally efficient Method for Updating Fuel Inputs for Wildfire Behavior Models Using Sentinel Imagery and Random Forest Classification. Remote Sens. 2022, 14, 1447. [Google Scholar] [CrossRef]
- Hudak, A.T.; Kato, A.; Bright, B.C.; Loudermilk, E.L.; Hawley, C.; Restaino, J.C.; Ottmar, R.D.; Prata, G.A.; Cabo, C.; Prichard, S.J.; et al. Towards Spatially Explicit Quantification of Pre- and Postfire Fuels and Fuel Consumption from Traditional and Point Cloud Measurements. For. Sci. 2020, 66, 428–442. [Google Scholar] [CrossRef]
- Meddens, A.; Hicke, J.; Vierling, L.; Hudak, A. Evaluating methods to detect bark beetle-caused tree mortality using single-date and multi-date Landsat imagery. Remote Sens. Environ. 2013, 132, 49–58. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, G.; Duan, J. Relationship between topography and the distribution of understory vegetation in a Pinus massoniana forest in Southern China. Int. Soil Water Conserv. Res. 2015, 3, 291–304. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Chen, C.; Grundy, M.; Searle, B.; Clifford, D.; Campbell, P. The Australian three-dimensional soil grid: Australia’s contribution to the GlobalSoilMap project. Soil Res. 2015, 53, 845–864. [Google Scholar] [CrossRef]
- Fick, S.; Hijmans, R. WorldClim 2: New 1km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Machine Learning. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Qian, W.; Yang, Y.; Zou, H. Tweedie’s compound poisson model with grouped elastic net. J. Comput. Graph. Stat. 2016, 25, 606–625. [Google Scholar] [CrossRef]
- Yang, Y.; Qian, W.; Zou, H. Insurance premium prediction via gradient tree-boosted tweedie compound poisson models. J. Bus. Econ. Stat. 2018, 36, 456–470. [Google Scholar] [CrossRef]
- Freeman, E.; Moisen, G.; Coulston, J.; Wilson, B. Random forests and stochastic gradient boosting for predicting tree canopy cover: Comparing tuning processes and model performance. Can. J. For. Res. 2015, 46, 323–339. [Google Scholar] [CrossRef]
- Fletcher, R.S. Using Vegetation Indices as Input into Random Forest for Soybean and Weed Classification. Am. J. Plant Sci. 2016, 7, 2186–2198. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Rocha, A.; Groen, T.; Skidmore, A.; Darvishzadeh, R.; Willemen, L. Machine learning using hyperspectral data inaccurately predicts plant traits under spatial dependency. Remote Sens. 2018, 10, 1263. [Google Scholar] [CrossRef]
- State Government of Victoria. Monitoring, Evaluation and Reporting Framework for Bushfire Management on Public Land; State Government of Victoria: Melbourne, Australia, 2015.
- Goodbody, T.R.H.; Coops, N.C.; Queinnec, M.; White, J.C.; Tompalski, P.; Hudak, A.T.; Auty, D.; Valbuena, R.; LeBoeuf, A.; Sinclair, I.; et al. sgsR: A structurally guided sampling toolbox for LiDAR-based forest inventories. For. Int. J. Forest Res. 2023, cpac055. [Google Scholar] [CrossRef]
- Massetti, A.; Rüdiger, C.; Yebra, M.; Hilton, J. The Vegetation Structure Perpendicular Index (VSPI): A forest condition index for wildfire predictions. Remote Sens. Environ. 2019, 224, 167–181. [Google Scholar] [CrossRef]
- Chhabra, A.; Rüdiger, C.; Yebra, M.; Jagdhuber, T.; Hilton, J. RADAR-Vegetation Structural Perpendicular Index (R-VSPI) for the Quantification of Wildfire Impact and Post-Fire Vegetation Recovery. Remote Sens. 2022, 14, 3132. [Google Scholar] [CrossRef]
- Collins, L.; Griffioen, P.; Newell, G.; Mellor, A. The utility of Random Forests for wildfire severity mapping. Remote Sens. Environ. 2018, 216, 374–384. [Google Scholar] [CrossRef]
- Gibson, R.K.; White, L.A.; Hislop, S.; Nolan, R.H.; Dorrough, J. The post-fire stability index; a new approach to monitoring post-fire recovery by satellite imagery. Remote Sens. Environ. 2022, 280, 113151. [Google Scholar] [CrossRef]
- Gould, J.S.; McCaw, W.; Cheney, N.; Ellis, P.; Knight, I.; Sullivan, A. Project Vesta: Fire in Dry Eucalypt Forest: Fuel Structure, Fuel Dynamics and Fire Behaviour; CSIRO Publishing: Clayton, Australia, 2008. [Google Scholar]
- Krisanski, S.; Taskhiri, M.S.; Aracil, G.; Muneri, A.; Gurung, M.B.; Montgomery, J.; Turner, P. Forest Structural Complexity Tool—An Open Source, Fully-Automated Tool for Measuring Forest Point Clouds. Remote Sens. 2021, 13, 4677. [Google Scholar] [CrossRef]
- Bienert, A.; Georgi, L.; Kunz, M.; Maas, H.; Oheimb, G. Comparison and Combination of Mobile and Terrestrial Laser Scanning for Natural Forest Inventories. Forests 2018, 9, 395. [Google Scholar] [CrossRef]
- William, W.; Mariela, S.B.; Lola, S.; Simon D., J.; Michael, H.; Phil, W.; Christoffer, A.; Andrew, H.; Andrew, M. Searching for the Optimal Sampling Design for Measuring LAI in an Upland Rainforest. In Proceedings of the Geospatial Science Research Symposium GSR2, Melbourne, Australia, 10–12 December 2012. [Google Scholar]
- EPA Technical Guidance—Flora and Vegetation Surveys for Environmental Impact Assessment; Technical Report; EPA: Joondalup, Australia, 2016.
- Travis, M.; Elsner, G.; Iverson, W.; Jonnson, C. VIEWIT: Computation of Seen Areas, Slope, and Aspect for Landuse Planning; Department of Agriculture, Forest Service, Pacific Southwest Forest and Range Experiment Station: Berkeley, CA, USA, 1975.
- Kiss, R. Determination of drainage network in digital elevation models, utilities and limitations. J. Hung. Geomath. 2004, 2, 16–29. [Google Scholar]
- Wilson, M.; O’Connell, B.; Brown, C.; Guinan, J.; Grehan, A. Multiscale terrain analysis of multibeam bathymetry data for habitat mapping on the continental slope. Mar. Geodesy. 2007, 30, 3–35. [Google Scholar] [CrossRef]
- Lukovic, J.; Bajat, B.; Kilibarda, M.; Filipovic, D. High resolution grid of potential incoming solar radiation for Serbia. Therm. Sci. 2015, 19, s427–s435. [Google Scholar] [CrossRef]
- De Reu, J.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; De Smedt, P.; Chu, W.; Antrop, M.; De Maeyer, P.; Finke, P. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Riley, S.; Stephen, D.; Elliot, R. A terrain ruggedness index that quantifies topographic heterogeneity. Int. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Jacoby, B.; Peterson, E.; Dogwiler, T. Identifying the stream erosion potential of cave levels in Carter Cave State Resort Park, Kentucky, USA. J. Geogr. Inf. Syst. 2011, 3, 323–333. [Google Scholar] [CrossRef]
- Sørensen, R.; Zinko, U.; Seibert, J. On the calculation of the topographic wetness index: Evaluation of different methods based on field observations. Hydrol. Earth Syst. Sci. 2006, 10, 101–112. [Google Scholar] [CrossRef]
- O’Donnell, M.; Ignizio, D. Bioclimatic Predictors for Supporting Ecological Applications in the Conterminous United States; U.S. Geological Survey: Reston, VA, USA, 2012; p. 10.
- Weier, J.; Herring, D. Measuring Vegetation (NDVI & EVI); NASA Earth Observatory: Washington, DC, USA, 2000.
- Nedkov, R. Orthogonal transformation of segmented images from the satellite Sentinel-2. Comptes Rendus L’acad. Bulg. Sci. 2017, 70, 687–692. [Google Scholar]
- Gitelson, A.; Gritz, Y.; Merzlyak, M. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.; Gritz, Y.; Merzlyak, M. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Lett. 2006, 33, L11402. [Google Scholar] [CrossRef]



| Site | Burn Unit Area (ha) | Vegetation Type | Year of Last Burn | Number of Plots |
|---|---|---|---|---|
| Bullengarook | 182.9 | Dry forests | 2012 | 11 |
| Clonbinane | 384.5 | Dry and lowland forests | 2009 | 12 |
| Lakes Entrance | 268 | Lowland forests | 2011 | 11 |
| Murrindindi | 540 | Dry forests, lowland forests with gullies of wet forest | 2008 | 8 |
| Three Bridges | 482.7 | Wet forests, spurs of dry forest | 2000 | 4 |
| Toorloo Arm | 242 | Lowland forests—significant bracken | 1981 | 8 |
| Tostaree | 341.3 | Lowland forests | 2001 | 14 |
| Site Name | Date of Capture | ALS Sensor | Pulse Density (pts/m) |
|---|---|---|---|
| Bullengarook | 2017–2018 | Trimble AX-60 | 8 |
| Clonbinane | 2019 | Trimble AX-60 | 9.45 |
| Lakes Entrance | 2019 | Riegl VQ780 | 8 |
| Murrindindi | 2016 | Trimble AX-60 | 4 |
| Three Bridges | 2016 | Trimble AX-60 | 4 |
| Toorloo Arm | 2019 | Riegl VQ780 | 8 |
| Tostaree | 2019 | Riegl VQ780 | 8 |
| Fuel Metrics | Approach | (OOB) | r | RMSE | |||
|---|---|---|---|---|---|---|---|
| Near-surface cover (%) | TLS | 0.51 | 0.07 | 0.5 | 0.16 | 15 | 2.1 |
| VA | −0.1 | 0.09 | 0.04 | 0.18 | 25 | 2.6 | |
| Elevated cover (%) | TLS | 0.31 | 0.09 | 0.55 | 0.14 | 16 | 2.4 |
| VA | −0.1 | 0.09 | 0.12 | 0.17 | 23 | 3.3 | |
| Canopy cover (%) | TLS | 0.10 | 0.08 | 0.38 | 0.15 | 12 | 1.70 |
| Near-surface height (m) | TLS | 0.23 | 0.08 | 0.47 | 0.11 | 0.04 | 0.01 |
| Elevated height (m) | TLS | −0.09 | 0.11 | 0.12 | 0.22 | 0.22 | 0.04 |
| Canopy height (m) | TLS | 0.25 | 0.07 | 0.6 | 0.15 | 4.41 | 0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taneja, R.; Wallace, L.; Hillman, S.; Reinke, K.; Hilton, J.; Jones, S.; Hally, B. Up-Scaling Fuel Hazard Metrics Derived from Terrestrial Laser Scanning Using a Machine Learning Model. Remote Sens. 2023, 15, 1273. https://doi.org/10.3390/rs15051273
Taneja R, Wallace L, Hillman S, Reinke K, Hilton J, Jones S, Hally B. Up-Scaling Fuel Hazard Metrics Derived from Terrestrial Laser Scanning Using a Machine Learning Model. Remote Sensing. 2023; 15(5):1273. https://doi.org/10.3390/rs15051273
Chicago/Turabian StyleTaneja, Ritu, Luke Wallace, Samuel Hillman, Karin Reinke, James Hilton, Simon Jones, and Bryan Hally. 2023. "Up-Scaling Fuel Hazard Metrics Derived from Terrestrial Laser Scanning Using a Machine Learning Model" Remote Sensing 15, no. 5: 1273. https://doi.org/10.3390/rs15051273
APA StyleTaneja, R., Wallace, L., Hillman, S., Reinke, K., Hilton, J., Jones, S., & Hally, B. (2023). Up-Scaling Fuel Hazard Metrics Derived from Terrestrial Laser Scanning Using a Machine Learning Model. Remote Sensing, 15(5), 1273. https://doi.org/10.3390/rs15051273









