ET Partitioning Assessment Using the TSEB Model and sUAS Information across California Central Valley Vineyards

Abstract

Evapotranspiration (ET) is a crucial part of commercial grapevine production in California, and the partitioning of this quantity allows the separate assessment of soil and vine water and energy fluxes. This partitioning has an important role in agriculture since it is related to grapevine stress, yield quality, irrigation efficiency, and growth. Satellite remote sensing-based methods provide an opportunity for ET partitioning at a subfield scale. However, medium-resolution satellite imagery from platforms such as Landsat is often insufficient for precision agricultural management at the plant scale. Small, unmanned aerial systems (sUAS) such as the AggieAir platform from Utah State University enable ET estimation and its partitioning over vineyards via the two-source energy balance (TSEB) model. This study explores the assessment of ET and ET partitioning (i.e., soil water evaporation and plant transpiration), considering three different resistance models using ground-based information and aerial high-resolution imagery from the Grape Remote sensing Atmospheric Profile and Evapotranspiration eXperiment (GRAPEX). We developed a new method for temperature partitioning that incorporated a quantile technique separation (QTS) and high-resolution sUAS information. This new method, coupled with the TSEB model (called TSEB-2T_Q), improved sensible heat flux (H) estimation, regarding the bias, with around 61% and 35% compared with the H from the TSEB-PT and TSEB-2T, respectively. Comparisons among ET partitioning estimates from three different methods (Modified Relaxed Eddy Accumulation—MREA; Flux Variance Similarity—FVS; and Conditional Eddy Covariance—CEC) based on EC flux tower data show that the transpiration estimates obtained from the FVS method are statistically different from the estimates from the MREA and the CEC methods, but the transpiration from the MREA and CEC methods are statistically the same. By using the transpiration from the CEC method to compare with the transpiration modeled by different TSEB models, the TSEB-2T_Q shows better agreement with the transpiration obtained via the CEC method. Additionally, the transpiration estimation from TSEB-2T_Q coupled with different resistance models resulted in insignificant differences. This comparison is one of the first for evaluating ET partitioning estimation from sUAS imagery based on eddy covariance-based partitioning methods.

1. Introduction

Climate change and water scarcity are elevating the importance of sustainable irrigation management, as agriculture accounts for approximately 70% of the worldwide freshwater demands [1]. Precision irrigation management can improve crop growing status and yield production [2] and prevent soil erosion, while also balancing the relationship between urban and agricultural water distribution. The accurate estimation of evapotranspiration (ET) and its component fluxes transpiration (T) and soil evaporation (E), along with detailed corresponding spatial information at the sub-field (plant) scale, is of particular interest for supporting site-specific, precision irrigation management [3,4]. Quantification of the percentage of ET arising from T aids the understanding of changes in carbon assimilation and water cycling in a changing environment [5]; however, obtaining estimates of ET partitioning at spatiotemporal scales pertinent to management activities remains challenging.

Remote sensing techniques provide a path for ET mapping and monitoring at the field scale using satellite and airborne imagery [6,7,8,9,10]. Although satellites can generate useful timeseries imagery for research and field-scale management over broad areas, the relatively coarse spatial resolution of these images, especially the satellite thermal infrared (TIR) resolution used in surface energy balance models, limits its application to field and sub-field scales with their utility for precision applications [11,12]. Conversely, sUAS, a type of platform equipped with high-resolution sensors, can potentially provide high-resolution data to meet precision agricultural requirements [9]. UAVs are not only a cost-effective tool for obtaining high-resolution data, but also a flexible platform that users can equip with sensors and schedule flight times based on their requirements [13,14,15].

High-resolution aerial images and ground measurements collected by the Grape Remote sensing Atmospheric Profiling and Evapotranspiration eXperiment (GRAPEX) program [16] provide a unique opportunity for ET monitoring and mapping over California vineyards at the plant scale. A two-source energy balance (TSEB) model [17,18] has been used to connect those two types of data, upscaling the spatial scale from a single vine scale to the vineyard scale. With the corresponding eddy-covariance flux tower monitoring ET on the ground, these sites provide an excellent comparison for ET modeling [19,20,21,22,23,24,25,26] and transpiration partitioning via TSEB models at the plant scale.

Two versions of the TSEB model have been designed to accommodate the resolution of input surface temperature data. For coarser resolution imagery that does not allow for the direct separation of soil and canopy temperatures, Norman et al., 1995 [17] developed a method to retrieve soil and canopy temperatures by using a single observation of the bulk directional radiometric temperature. This method iteratively adjusts a Priestley–Taylor coefficient controlling the transpiration flux to find the realistic solution, and is referred to here as the TSEB-PT model. A second method has been developed to use higher resolution (sub-meter) land-surface temperature (LST) imagery supporting the separation of soil and canopy temperatures, known as TSEB-2T [27].

Leaf area index (LAI) and LST are two key inputs used by both TSEB versions to partition evaporative fluxes between the soil and the canopy—or, in vineyards, between the grape vine and interrow soil or cover crop [28,29]. Although Gao et al., 2022 [30] used machine learning techniques to generate a robust approach to estimate LAI at the plant scale for vineyards across California, challenges related to modeling and evaluating TSEB partitioning remain.

One such challenge arises because separated canopy and soil temperatures significantly affect available energy partitioning and the sensible heat fluxes from the soil and canopy components and, thus, ultimately the soil evaporation and plant transpiration [31]. Errors in the soil and canopy temperatures can result in overestimation or underestimation of soil evaporation and plant transpiration [9]. Previous research has used the relationship between the normalized difference vegetation index (NDVI) and the corresponding temperature value to obtain separated temperatures [21,26,32]. However, errors resulting from shadows [33,34], image quality, etc., can affect the relationship between NDVI and temperature, which in turn can affect TSEB modeling results.

Another challenge is determining the optimal TSEB model framework for ET partitioning. Several previous studies have shown that TSEB-2T can estimate ET more accurately than TSEB-PT [27]. However, another study for a vineyard in Israel using ground-based LST observations with ground-based measurements of soil E, and eddy covariance (EC) based ET to derive T (T = ET − E), suggested TSEB-2T does poorly in partitioning ET compared to TSEB-PT [3]. In that study, they found improvements were needed in soil heat flux estimation, a better algorithm for radiation partitioning, and accounting for vine canopy structure to improve the partitioning using TSEB-PT.

The final challenge is how to verify the TSEB estimated E and T. While high-frequency EC flux monitoring data are useful for the model validation of total ET [35,36], E and T are not directly measured by the EC flux tower. Fortunately, several techniques have been developed to partition EC water and carbon dioxide fluxes into ground and plant components [37], including Modified Relaxed Eddy Accumulation, MREA; Flux-Variance Similarity, FVS; and Conditional Eddy-Covariance, CEC. This potentially provides a method for comparison with remote sensing-based estimates aggregated over the EC tower footprint [38], and Nassar et al., 2020 [22] and Gao et al., 2021 [39,40] discussed the footprint calculation for the EC tower in California vineyards.

The objectives of this research are (1) to improve the method for temperature separation based on high-resolution LST imagery; (2) to evaluate the performance of different TSEB models coupled with different aerodynamic resistance models in comparison with energy components measured by the EC flux tower; and (3) to quantify the performance of ET partitioning via TSEB models. The modeling and measurement approaches are first described in the Materials and Methods section, and then they are intercompared toward identifying an optimal configuration in assessing ET and ET partitioning in vineyard systems.

2. Materials and Methods

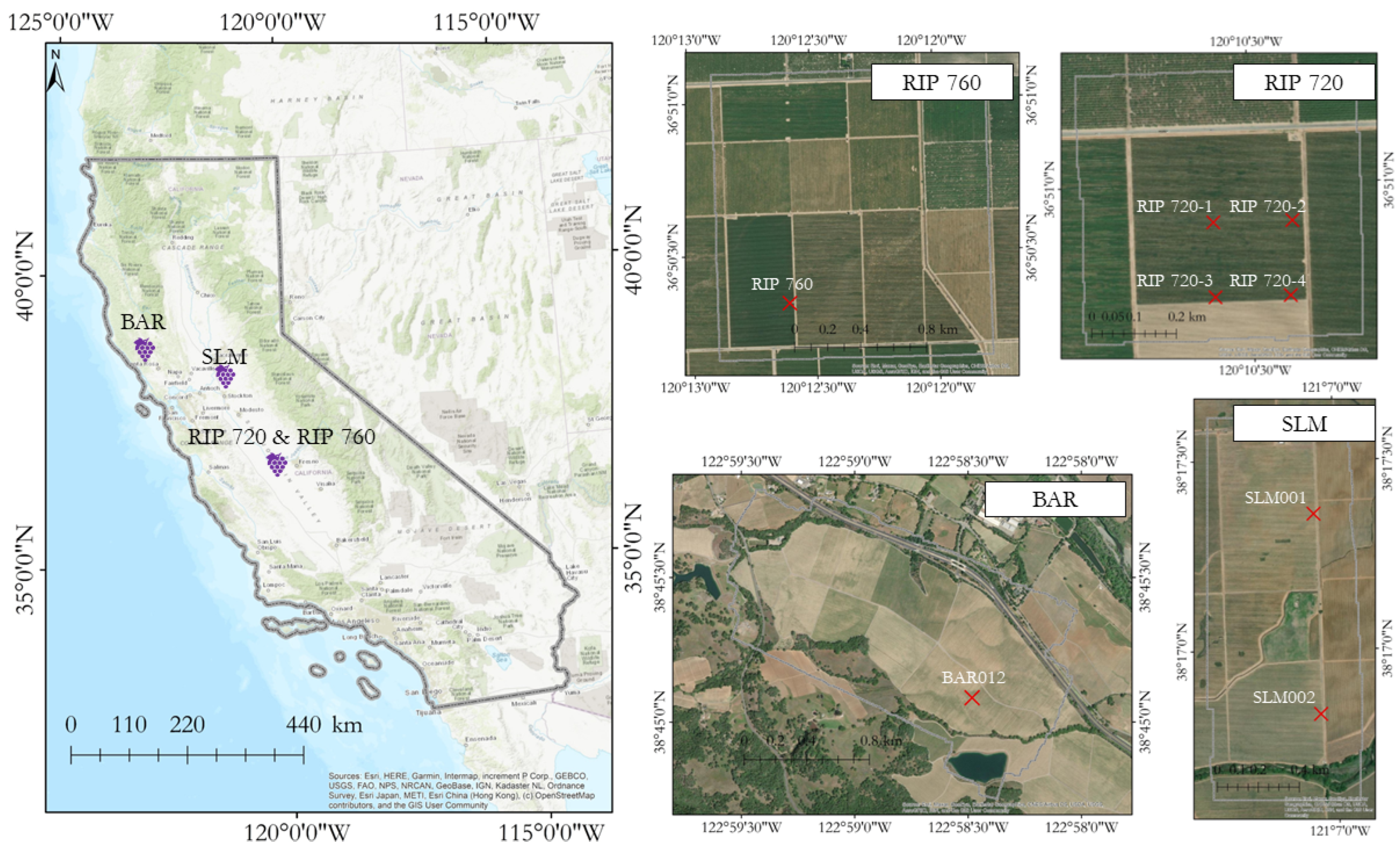
2.1. Study Area

This study is part of the ongoing GRAPEX project started in 2013, which seeks to improve water-use efficiency through the modeling of ET and plant stress in vineyards [41,42]. Vineyard blocks included in this study were located in three different climatic regions in California. Vineyard blocks equipped with EC flux towers BAR012 and BAR007 were furthest north, in Sonoma County, approximately 6 km south of Cloverdale, CA; EC flux towers SLM001 and SLM002 were located in Sacramento County, approximately 20 km northeast of Lodi, CA; and block RIP 720 equipped with four different EC flux towers (RIP 720-1, RIP 720-2, RIP 720-3, and RIP 720-4) in the same vineyard block and EC flux tower RIP 760 were located in Madera County, about 30 km west of Fresno, CA. The four EC flux towers in block RIP 720 were intended to monitor the flux from the corresponding sub-blocks with different amounts of irrigation applied to cause variations in vine stress, as it was a variable rate deficit irrigation (VRDI) study site. Figure 1 shows the geographical location of each set of vineyard blocks. The position and name of the EC flux towers are labeled with a red cross symbol and white font, respectively, in Figure 1, and the study-site geographic information is presented in

Table A1. Study-site geographic information.

Study Sites	Latitude	Longitude	Elevation above the Sea Level (m)
SLM	38°16′49.76″	−121°7′3.35″	40
BAR	38°45′4.91″	−122°58′28.77″	120
RIP760	36°50′20.52″	−120°12′36.60″	62
RIP720	36°50′57.27″	−120°10′26.50″	62

.

2.2. Data

2.2.1. sUAS Platform Collection

Remote sensing data gathered via the AggieAir sUAS platform (https://uwrl.usu.edu/aggieair/, accessed on 10 January 2020) between 2014 and 2019 were used in this study. Details of the data are presented in Nassar et al., 2021 [23] and in

Table A2. The flight date and time of the sUAS platform over vineyards. Azimuth and elevation of the sun corresponding to the time are also shown.

Sites	Year	Month	Day	Time Flight	Azimuth	Elevation
RIP 720-1 RIP 720-2 RIP 720-3 RIP 720-4	2018	6	19	11:20	144.1	74.0
	2018	6	19	13:17	236.1	68.8
	2018	6	19	15:38	269.8	41.8
	2018	7	12	12:29	201.0	74.2
	2018	7	12	15:32	266.5	43.1
	2018	7	13	10:40	123.3	66.3
	2018	7	13	15:22	264.6	45.1
	2018	8	5	10:44	132.4	63.3
	2018	8	5	12:33	198.9	69.2
	2018	8	6	10:41	131.2	62.8
	2019	5	4	10:25	130.1	60.9
RIP 760	2018	6	19	11:20	144.1	74.0
	2018	6	19	13:17	236.1	68.8
	2018	6	19	15:38	269.8	41.8
	2018	7	12	12:29	201.0	74.2
	2018	7	12	15:32	266.5	43.1
	2018	7	13	10:40	123.3	66.3
	2018	8	5	10:44	132.4	63.3
	2018	8	5	12:33	198.9	69.2
	2018	8	6	10:41	131.2	62.8
BAR012	2017	8	8	10:52	144.9	63.6
	2017	8	9	10:43	141.1	62.3
	2019	6	27	10:41	131.9	68.9
	2019	6	27	12:07	193.6	74.2
	2019	6	27	14:21	255.2	54.7
	2019	7	29	10:51	140.8	65.8
	2019	7	29	13:09	224.2	64.4
	2019	7	30	10:28	130.9	62.5
	2019	7	30	13:09	223.9	64.2
	2019	7	30	15:40	264.2	37.5
SLM001	2014	8	9	10:41	136.3	61.5
	2015	6	2	10:43	131.9	67.9
	2015	6	2	14:07	250.2	57.2
	2015	7	11	10:35	125.1	65.5
	2015	7	11	14:14	250.1	57.3
	2019	5	3	10:38	139.1	62.0
SLM002	2014	8	9	10:41	136.3	61.5
	2015	6	2	10:43	131.9	67.9
	2015	6	2	14:07	250.2	57.2
	2015	7	11	10:35	125.1	65.5
	2015	7	11	14:14	250.1	57.3

. These data include 4-band spectral images (B, G, R, and NIR) at 10 × 10 cm² resolution, digital surface model (DSM) data at 10 × 10 cm² resolution, and thermal imagery (Tr) at 60 × 60 cm² resolution [43]. Images of 6 bands collected via the AggieAir sUAS platform are included as an example, and can be seen in Gao et al. 2022 [30].

2.2.2. Eddy-Covariance Flux Tower Data

High-frequency eddy covariance (EC) flux data were also collected in conjunction with intensive observation periods (IOPs) at the tower sites identified in Figure 1. Tower measurements of net radiation (Rn, Wm⁻²), latent heat flux (or evapotranspiration rate, LE, Wm⁻²), sensible heat flux (H, Wm⁻²), and soil surface heat flux (G, Wm⁻²) are used in this study to assess the TSEB-PT and TSEB-2T output. More information about the EC flux tower can be found in Kustas et al., 2018 [16] and Bambach et al., 2022 [44], while details about energy closure and ET partitioning for the EC tower data are provided in Section 2.3.3.

2.3. Methodology

Figure 2 shows a flowchart of the process for comparing ET rate (LE converted to mass units of mm d⁻¹) and ET partitioning between the EC flux tower monitored data and the TSEB modeling results within the corresponding footprint area. The top 5 boxes, along with surface temperature in the second row, are the inputs for the TSEB models. Canopy height, the ratio of canopy width and height, and fractional cover are obtained with a python program [45]; LAI is obtained from the products of recent studies [30,46], using sUAS information and ground-based LAI measurements via machine learning approach. In this study, the weather data are obtained from the flux tower instrumentation. The TSEB-2T model requires partitioned temperature input (canopy and soil temperature), but other inputs to the two model formulations are the same.

A python-program tool developed by Gao et al., 2021 [35] was used to extract TSEB modeling results on LE and ET partitioning within the footprint area around each tower for comparison with EC flux tower measurements using the approach by Kljun et al., 2015 [38].

2.3.1. Temperature Separation

This study uses the normalized difference vegetation index (NDVI) as an indicator to separate the total surface radiometric temperature, gridded at 3.6 m resolution, into representative canopy and soil temperature grids at 3.6 m resolution. This method is based on work from prior studies [21,22,26,27,30,34]. In this study, we also included a framework to remove shadow effects in the temperature partitioning process (Figure 3). The removal process is divided into 4 steps. (1) Shadow pixels are identified geometrically at the time of satellite overpass based on DSM data at 0.15 m pixel level. (2) Shadow pixels are aggregated from 0.15 m to 0.60 m pixel scale, with any 0.60 m pixel containing at least one 0.15 m shadow pixel recognized as a shadow pixel. The reason for choosing 0.60 m is because the coarse resolution for the thermal images is 0.6 m. (3) NDVI is generated based on the 0.15 m optical image and then aggregated to the 0.60 m pixel level. (4) Within each 3.6 m pixel in the final modeling domain, the 0.6 m temperature, NDVI, and shadow data are aligned. Any 0.6 m temperature and NDVI pixels that are collocated with a shadow pixel are ignored in building the temperature-NDVI relationship used in the temperature partitioning, as described below.

In previous research, NDVI thresholds were created to identify the category of each pixel in the model domain. For example, in the 1:1 plot shown in Figure 3, NDVI = 0.3 is recognized as the threshold to identify whether or not the pixel (point) is senescent cover crop stubble (interrow); the pixel is identified as an interrow pixel when the NDVI value is lower than 0.30. Likewise, the pixel is identified as a vegetation pixel when the NDVI value is higher than 0.65. The corresponding soil and vegetation temperature are normally averaged based on the temperature values within the corresponding zone, with NDVI < 0.3 for soil zone and NDVI > 0.65 for vegetation zone, respectively.

In some cases, the plot of temperature vs. NDVI shows low correlation, with significant scatter. Figure 4 is one such example, showing the temperature separation process for one 3.6 m modeling pixel at SLM (9 August 2014, 10:41 am, the air temperature is around 27.7 °C). Figure 4a–c displays an 0.15 m resolution spectral image of the modeling pixel, the corresponding 0.6 m resolution temperature image, and the 0.6 m resolution NDVI image, respectively. The three pixels highlighted by black dashed boxes in Figure 4b,c contain shadows, and the 0.15 m resolution shadows are represented by the red squares in Figure 4c. The solid trend line in Figure 4d is generated based on all (36) points, and the corresponding slope and intercept are shown on the figure. According to previous research experience, the separated soil temperature is calculated based on the trend line at the soil NDVI threshold (e.g., NDVI = 0.4), and the separated vegetation temperature is averaged based on the pixel temperature within the pure vegetation zone. In this case, the separated soil temperature is potentially underestimated, and the separated vegetation temperature is overestimated due to the large spread in values in the pure vegetation zone. The maximum spread vegetation temperatures is around 5 °C; however, relatively small changes in the assumed canopy temperature will impact TSEB-2T [3], so it is important to better constrain temperature samples considered in determining the endpoint pure soil and vegetation temperatures.

The reason for the high variation of vegetation and soil temperature within a TSEB modeling pixel is potentially coming from the data collection and data processing. The imagery collection process is finished based on multiple spectral sensors, and the pixels of each sensor do not perfectly align with each other. During the imagery processing, the image–pixel alignment issue is still difficult to address. Therefore, it potentially results in a high variation of temperature in a TSEB modeling pixel. However, this issue can be addressed by upgrading the sensor in the future work, or flying the sensor at a lower elevation. Another reason for the high variation of vegetation temperature is because of the vegetation type within the TSEB modeling pixel. The interrow pixel is a mixture of bare soil and senescent cover crop stubble, and the senescent cover crop stubble is short and not well irrigated. When upscaling NDVI from 0.15 m to 0.6 m pixels, most interrow pixels are recognized as healthy vegetation pixels. Therefore, the temperature of the interrow vegetation pixel is higher than the temperature of the vine vegetation, which is well irrigated compared with the senescent cover crop stubble.

Quartile tests were performed to optimize the removal of contaminated pure vegetation pixel temperatures. For example, the averaged vegetation temperature, considering all vegetation pixels, is around 32.4 °C. If the pixel with a corresponding temperature higher than the 50th (75th) percentile of all vegetation–pixel temperatures is eliminated, the corresponding vegetation temperature is around 31.3 °C (32.9 °C) (Figure 4e–g). Based on extensive testing, the 75th percentile of the vegetation temperature was identified as the threshold to eliminate the high-vegetation temperature effect on the vegetation temperature estimation, based on further data analysis. This temperature-separation method is named quantile temperature separation (QTS).

Another modification in this QTS method relates to the linear relationship between the NDVI and temperature. Typically, pixel temperature decreases with increasing NDVI within a TSEB modeling pixel (e.g., 3.6 m resolution pixel). After the elimination of high vegetation temperatures in the pure vegetation zone, some high points in the middle region (NDVI $\in$ [0.40, 0.70]) still remain (Figure 4h). These anomalous pixels can affect the linear relationship between the temperature and NDVI [27].

Therefore, a tool called RANSACRegressor (Scikit-learn developers) from the “sklearn.linear_model” is used in this study. This tool is an iterative method for the robust estimation of parameters from a subset of inliers from the complete dataset. The three points highlighted by the red dash-line box (Figure 4h), for example, were eliminated by the tool and then the linear relationship was obtained based on the remaining red points.

At the end, a soil temperature was estimated based on the linear relationship at 0.40 (NDVI value). If there was at least one soil pixel within the TSEB modeling pixel, the soil temperature was calculated as an average value based on the temperature value on the soil pixels. The canopy temperature was calculated as the average temperature of pixels above 0.70 NDVI and within the lower 75th percentile of temperature in that vegetation zone. If there were no vegetation pixels found in that TSEB modeling pixel, an “NAN” value was used to represent the canopy temperature.

2.3.2. TSEB Model

The two-source energy balance (TSEB) model has been widely used for ET estimation over agricultural lands (e.g., corn, soybeans, cotton, grapevines, almonds, pastures and grazing lands) based on ground, aerial and satellite remote sensing data. A schematic diagram from Kustas et al., 2018 [16] shows the TSEB model resistance network for the sensible heat flux, and lists the set of equations used to obtain the iterative solution. The soil and canopy temperatures constrain the sensible heat fluxes, net radiation, and soil heat flux with the added initial estimate of canopy latent heat flux based on the Priestley–Taylor (PT). This version of the TSEB model is called TSEB-PT [17]. For applications using higher resolution (e.g., sUAS), thermal imagery of the soil and canopy temperatures are derived using the methods described in Section 2.3.1. This version of the model is referred to as TSEB-2T [27]. It is also noted that an earlier study by Kustas and Norman., 1997 [47], using radiometric temperatures at significantly different viewing angles, could estimate soil and canopy temperatures.

In the TSEB, net radiation, including soil and canopy net radiation, is estimated based on a set of land surface parameters (e.g., longwave emissions from soil, canopy, and sky, solar transmittance through the canopy; canopy and soil albedo). The ground heat flux, G, is estimated as a fraction of the soil net radiation (R_nS). Nieto et al., 2019 [27] show the empirical G/R_nS curve fit as a function of time of the day. Considering that all sUAS images were collected between 10 am to 4 pm, a constant G-ratio value (0.33) is used in this research.

Equation (1) shows the sensible heat flux calculation—the difference between TSEB-PT and TSEB-2T lies in the approach to obtaining T_C and T_S. In addition to these component temperatures, the aerodynamic resistance of the canopy ($R_x$) and soil ($R_s$) also affect the H, but a systematic assessment of different methods for defining these resistances within the TSEB context has not been conducted to date. Three different resistance models for canopy and soil were tested in this study for both TSEB-PT and TSEB-2T: Norman and Kustas (called NK resistance model in this paper, expressed by Equations (2) and (3)), McNaughton and Van (MV model, by Equations (4) and (5)), and Choudhury and Monteith (CM model, by Equations (6) and (7)), respectively. Because the separated temperature images illustrated in Section 2.3.1 are used as input for the TSEB-2T model, the TSEB-2T model coupled with QTS in this study is named as TSEB-2T_Q.

$$H=H_C+H_S={\rho }_{air}{C}_p\frac{T_C-T_{AC}}{R_x}+{\rho }_{air}{C}_p\frac{T_S-T_{AC}}{R_s}$$

(1)

$$R_s=\frac{1}{c\sqrt[3]{T_s-T_A}+b{u}_s}$$

(2)

$$R_x=\frac{C^{\prime }}{LAI}\sqrt{\frac{l_w}{U_{d_0+z_{0M}}}}$$

(3)

$$R_s=\frac{10}{u^{*}}$$

(4)

$$R_x=\frac{C^{\prime }}{F}\sqrt{l_w\times u^{*}}+\frac{0.36}{u^{*}}$$

(5)

$$R_s=\frac{h_c\times e^{{\alpha }_k}}{{\alpha }_k\times k_h}\left(e^{-{\alpha }_k\times \frac{z_{0\_soil}}{h_c}}-e^{-{\alpha }_k\frac{d_0-z_{0M}}{h_c}}\right)$$

(6)

$$R_x=\frac{1}{F\times 2\frac{C{M}_a}{{\alpha }^{\prime }}\sqrt{\frac{u_c}{l_w}}\times \left(1-e^{\frac{-{\alpha }^{\prime }}{2}}\right)}$$

(7)

$$k_h=k\times u^{*}\times \left(h_c-d_0\right)$$

(8)

In the above equations, $R_s$ is the aerodynamic resistance of the soil; $R_x$ is the aerodynamic resistance of the canopy; $c$ and $b$ are the coefficients depending on the turbulent length scale in the canopy, soil-surface roughness, and turbulence intensity in the canopy; $T_S$ is the soil-surface temperature (K); $T_A$ is the air temperature (K); $u_s$ is the wind speed near the soil surface (ms⁻¹); $u^{*}$ is the friction velocity (ms⁻¹); $C^{\prime }$ is derived from weighting a coefficient in the equation for leaf boundary layer resistance over the height of the canopy [48] and it is assumed to be 90 s^1/2 m⁻¹; LAI is the leaf area index (m² m⁻²); $l_w$ is the average leaf width (m); $U_{d_0+z_{0M}}$ is the wind speed at the heat source-sink (ms⁻¹); $F$ is the local leaf area index; $h_c$ is the canopy height; ${\alpha }_k$ is the heat diffusion coefficient; $k$ is the von Karman’s constant (0.41); $z_{0\_soil}$ is the roughness length of the soil layer; $d_0$ is the zero-plane displacement height (m); $z_{0M}$ is the aerodynamic roughness length for momentum transport (m); $C{M}_a$ is the leaf drag coefficient [49]; ${\alpha }^{\prime }$ is the wind extinction coefficient; and $u_c$ is the wind speed at the canopy interface (ms⁻¹).

2.3.3. Validation Data from the Eddy Covariance Tower

Energy Components

Energy closure of the EC flux monitored data is a concern [19,24] for validating the TSEB modeling results. Nieto et al., 2022 [24], for example, used the arithmetic-mean value for the sensible heat flux and the latent heat flux based on three calculated possible closure corrections to evaluate TSEB modeling results: (1) assigning all the residual error to H; (2) assigning all the residual to LE; and (3) assigning the residual proportionally to H and LE by preserving the Bowen Ratio. In this research, the geometric-mean value (Equation (9)) of the sensible heat flux and the geometric-mean value of the latent heat flux are calculated to validate the corresponding TSEB modeling results [50], considering that the geometric-mean value is less influenced by skewed distributions compared with the arithmetic-mean value.

$${\left({\displaystyle \prod }_{i=1}^n{x}_i\right)}^{\frac{1}{n}}=\sqrt[n]{x_1{x}_2\cdots x_n}$$

(9)

where $n$ is the number of values, and $x_i$ are the values included in the average.

Transpiration

Zahn et al., 2022 [37] proposed the Conditional Eddy Covariance (CEC) method using the high frequency water vapor and CO₂ measurements from eddy covariance measurements to estimate soil evaporation from plant transpiration, and compared results with the modified Relaxed Eddy Accumulation (MREA) method and the Flux Variance Similarity (FVS) method. They found that the CEC and MREA framework can be used as a qualitative measure to identify stomatal and non-stomatal components. Methods to evaluate the transpiration modeled by the TSEB models using these measurements are explained in Section 3.2.1.

3. Results and Discussion

3.1. TSEB Modeling Results

3.1.1. TSEB Component Comparison Considering Different Resistance Models

Figure 5 shows the comparison of modeled versus measured energy components (Rn, G, H, and LE), considering different TSEB models (TSEB-PT, TSEB-2T, and TSEB-2T_Q) coupled with different resistance models (NK, CM, and MV). In Figure 5, observed H and LE have been adjusted for closure using the technique discussed in Section 2.3.3.

Statistical metrics of evaluation for each flux, model, and resistance formulation are provided in

Table 1. Statistics of the goodness of fit showing the performance of each TSEB modeling result within the footprint area. N is the number of cases used for validation, RMSE is the root mean square error (Wm⁻²), Bias is the mean bias computed as the measured minus the modeled (Wm⁻²), r is the Pearson correlation coefficient between the measured and modeled, and d is the Willmott’s index of agreement [51]. When N is different in different groups, d is still calculated but not a representative metric to compare the model performance.

		TSEB-PT (NK)	TSEB-PT (CM)	TSEB-PT (MV)	TSEB-2T (NK)	TSEB-2T (CM)	TSEB-2T (MV)	TSEB-2TQ (NK)	TSEB-2TQ (CM)	TSEB-2TQ (MV)
Net radiation	N	60	60	60	60	60	60	60	60	60
	RMSE	22	22	22	21	21	21	23	23	23
	Bias	−4	−5	−4	−5	−5	−5	−10	−10	−10
	r	0.96	0.97	0.97	0.97	0.97	0.97	0.97	0.97	0.97
	d	0.98	0.98	0.98	0.98	0.98	0.98	0.98	0.98	0.98
Ground heat flux	N	60	60	60	60	60	60	60	60	60
	RMSE	41	40	41	41	41	41	39	39	39
	Bias	−27	−26	−27	−26	−26	−26	−24	−24	−24
	r	0.25	0.24	0.25	0.26	0.26	0.26	0.27	0.27	0.27
	d	0.52	0.52	0.52	0.54	0.54	0.54	0.55	0.55	0.55
Sensible heat flux	N	60	60	60	60	60	60	60	60	60
	RMSE	78	85	84	71	71	69	65	71	65
	Bias	21	45	17	−16	14	−19	−3	26	−3
	r	0.63	0.62	0.61	0.62	0.60	0.64	0.63	0.61	0.63
	d	0.78	0.74	0.76	0.78	0.77	0.79	0.77	0.75	0.77
Latent heat flux	N	60	60	60	60	60	60	60	60	60
	RMSE	82	84	90	80	73	81	69	71	70
	Bias	−7	−32	−3	34	3	36	16	−13	16
	r	0.53	0.55	0.51	0.55	0.57	0.58	0.58	0.59	0.58
	d	0.73	0.73	0.71	0.71	0.76	0.72	0.75	0.78	0.75

. Statistics show that the modeled Rn from different TSEB models, in general, has a good agreement with the Rn from the EC flux tower. However, the modeled G calculated via the ratio of the modeled soil net radiation has a lower agreement with the G from the EC flux tower, which may result from the constant value (0.33) adopted for the time period from 10 am to 4 pm. This suggests that a time-varying ratio needs to be used for the G estimation, based on sUAS information for different times during the day, as suggested by Nieto et al., 2019 [27]. Sensible heat estimates from TSEB models coupled with the NK and/or the MV resistance models have better agreement with tower measurements as quantified by the index of agreement, d (Table 1). Based on the RMSE and d values, the H and LE estimated from the TSEB-2T_Q shows better agreement with measurement fluxes. This shows that the QTS method considering shadow and extreme pixel-value effects, characteristics of the high-resolution pixel within the smallest TSEB modeling domain, in general improved the flux estimation.

Considering that previous research adopted the NK model and that the difference between H and LE based on the NK and the MV model coupled with the TSEB-2T_Q is small, the TSEB-2T_Q coupled with the NK model was adopted in this research for energy component estimation.

3.1.2. Time-Based Performance of the TSEB-2T_Q NK Model

The sUAS flight times were between 10 am and 4 pm local time (Table A2), which is a fairly wide time frame. Considering the change in the solar altitude and azimuth for the different overpass times, the sUAS overpasses were grouped into three different time periods. The first time period, between 10:00 am and 11:59 am, was called the “Landsat” (LS) time period since the Landsat passes over between 10:30 am and 11:00 am (Pacific Standard Time—PST). The second time period, between 12:00 pm and 1:59 pm, is called the “solar noon” (SN) time period since the sun reaches its highest point for the day at around 1:00 pm (PST). The third time period, after 2:00 pm (between 2:00 pm and 5:00 pm, PST), is called the “afternoon” (AF) time period.

Figure 6 shows the performance of TSEB-2T_Q coupled with the NK model in estimating energy components at each time period.

Table A3. The performance of the TSEB-2T model coupled with the Norman and Kustas (NK) resistance model at different research sites with different times shown by different evaluation metrics. “LS” stands for the results that occurred in Landsat time; “SN” near solar noon; and “AF” afternoon. The unit of RMSE and Bias is Wm⁻².

Time Periods	Net Radiation				Ground Heat Flux				Sensible Heat Flux				Latent Heat Flux
	N	RMSE	Bias	r	N	RMSE	Bias	r	N	RMSE	Bias	r	N	RMSE	Bias	r
LS	29	21	−9	0.91	29	45	−28	−0.43	29	66	2	0.33	29	68	16	0.62
SN	17	21	−3	0.79	17	40	−28	−0.38	17	69	−23	0.63	17	81	49	0.64
AF	14	29	−23	0.96	14	20	−12	0.64	14	58	8	0.63	14	56	−22	0.46

contains the corresponding metrics associated with the comparisons displayed in Figure 6.

Net radiation shows highest correlation with observations during the AF period, although the relationship has higher bias and yields higher RMSE than the LS and SN periods. This may result from using spatially and temporally constant values of emissivity ($\epsilon$) and the solar transmittance through the canopy (${\tau }_s$) in the TSEB. Torres-Rua et al., 2020 [26] illustrated the challenge for spatial emissivity estimation, and they proved that spatial emissivity (not a constant value) can improve TSEB model performance. Gao et al., 2021 [52] pointed out that the solar spectrum reflectance and transmittance changes along with the leaf water content. From these aspects, the spatial and temporal variability in these parameters (e.g., $\epsilon$ and ${\tau }_s$) need to be further studied if the Rn estimation is to be improved, particularly in the afternoon period.

Metrics for the performance of G estimation suggest that the G ratio value (0.33) used in the TSEB-2T_Q model is more appropriate at the AF time period than for the LS and SN time periods. For example, the labeled points in Figure 6a,b, “RIP760 20180806 10:41” and “RIP760 20180805 12:33”, indicate that G was overestimated, indicating that the G ratio should be smaller than 0.33. This behavior was also noted by Nieto et al., 2019 [27], who found that a double asymmetric sigmoid function gave better results than using a constant value, and better fits the observations than the sinusoidal function proposed by Santanello and Friedl., 2003 [53].

RMSE in sensible and latent heat flux from the TSEB-2T_Q is minimized in the AF period. Examining scenes where outliers in H and LE are observed in Figure 6c showed no significant issues from the QTS model based on the separated average soil and canopy temperatures within the corresponding footprint area, in comparison with the remaining image dates (

Table A4. Separated average soil and canopy temperatures within the corresponding footprint area via the QTS model (the temperature unit is °C).

Site	Date	Time	Sonic Air Temperature	Soil Temperature	Canopy Temperature	Soil–Canopy Temperature Difference
SLM001	20150711	14:14	28.1	32.9	28.7	4.2
SLM002	20150711	14:14	30.7	32.9	28.7	4.2
BAR012	20190627	14:21	25.7	31.0	26.6	4.4
BAR012	20190730	15:40	30.9	34.2	29.4	4.8
RIP760	20180619	15:38	32.1	36.2	31.6	4.6
RIP720-1	20180619	15:38	34.0	35.5	32.1	3.4
RIP720-1	20180712	15:32	38.3	36.8	33.1	3.7
RIP720-1	20180713	15:22	38.1	36.7	33.3	3.4
RIP720-2	20180619	15:38	34.5	37.3	32.5	4.8
RIP720-2	20180712	15:32	38.8	37.8	33.0	4.8
RIP720-2	20180713	15:22	38.5	38.6	34.4	4.2
RIP720-3	20180713	15:22	38.5	35.1	31.1	4.0
RIP720-4	20180619	15:38	35.9	35.6	31.8	3.8
RIP720-4	20180713	15:22	40.5	37.1	32.9	4.2

), so the cause of poor performance is unknown.

3.2. Transpiration

3.2.1. Transpiration Estimation via CEC, MREA, and FVS

Based on the sUAS flight time, both CEC and MREA methods provided 50 transpiration estimations, while the FVS method provided 19. The CEC and MREA methods provided consistent estimates over the daytime period, while the FVS method often produced no solution. Figure 7 shows that the transpiration estimated via the FVS method has a significant difference from the transpiration estimated via the CEC and MREA method.

An analysis of variance (ANOVA) and a Tukey test (

Table 2. ANOVA and Tukey test results showing the difference between the transpiration estimated based on different methods (CEC, MREA, and FVS). The null hypothesis is that the mean transpiration between different groups is the same (shown in the last column). “Mean difference” is the mean difference between “Group 1” and “Group 2.” “Lower boundary” and “Upper boundary” are the lower and upper 95% confidence interval boundaries, respectively. The unit for “Mean difference,” “Lower boundary,” and “Upper boundary” is Wm⁻².

Group 1	Group 2	Mean Difference	p-Adj	Lower Boundary	Upper Boundary	The Mean Transpiration Is the Same
CEC	FVS	−84	0.004	−152	−15	NO
CEC	MREA	0	0.900	−69	68	YES
MREA	FVS	−84	0.004	−152	−15	NO

) was then processed to not only show the transpiration difference between different groups, but also to show if the null hypothesis (i.e., the mean transpiration between different groups is the same) was acceptable [54]. Table 2 suggests that the mean transpiration estimated via the FVS method yielded a significant difference from estimates from the CEC and MREA methods, and the mean transpiration via CEC is statistically the same as the mean transpiration via the MREA method. This is consistent with the findings of Zahn et al., 2022 [37]. Since the CEC and MREA methods yielded essentially the same values, CEC values were used in subsequent analyses.

3.2.2. Transpiration Comparison

Figure 8 contains three scatter plots showing all comparisons between the transpiration based on CEC method and the transpiration modeled by different TSEB models and the sUAS information.

Table A5. ANOVA and Tukey test results showing the difference between the transpiration calculated via the CEC method and the transpiration modeled via the TSEB models. The null hypothesis is that the mean transpiration between different groups is the same. “Mean difference” is the mean difference between “Group 1” and “Group 2.” “Lower boundary” and “Upper boundary” are the lower and upper 95% confidence interval boundaries, respectively. “CEC” represents the transpiration calculated via the CEC method. The unit for “Mean difference,” “Lower boundary,” and “Upper boundary” is Wm⁻².

Group 1	Group 2	Mean Difference	p-Adj	Lower Boundary	Upper Boundary	The Mean Transpiration Is the Same
CEC	TSEB-PT (NK)	−25	0.674	−69	18	YES
CEC	TSEB-PT (CM)	−16	0.900	−60	27	YES
CEC	TSEB-PT (MV)	−32	0.372	−75	12	YES
CEC	TSEB-2T (NK)	−36	0.194	−80	7	YES
CEC	TSEB-2T (CM)	−30	0.456	−74	13	YES
CEC	TSEB-2T (MV)	−39	0.132	−82	5	YES
CEC	TSEB-2TQ (NK)	−10	0.900	−53	34	YES
CEC	TSEB-2TQ (CM)	−7	0.900	−51	36	YES
CEC	TSEB-2TQ (MV)	−9	0.900	−53	34	YES

contains the results from the ANOVA and Tukey test, showing the statistical differences of the mean values. The null hypothesis for the ANOVA test is that the mean value from two different groups is statistically the same, and the last column suggests that all mean values from “Group 1” and “Group 2” are statistically the same. Importantly, two factors shown in Table A5 explain that transpiration estimated via the CEC and MREA methods has a stronger relationship with transpiration modeled via TSEB-2T_Q. The first factor is the corresponding “p-adj” values, which are 0.900 (higher than most other “p-adj” values, and higher than α = 0.05). The second is that the corresponding “Mean difference” is smaller than 10 Wm⁻², which is generally smaller than other experiments.

Table A6. Metrics for model evaluation shown in Figure 8. N is the number of scatters in Figure 8; RMSE is the root mean square error; Bias is the mean bias computed as the observed minus the predicted; r is the Pearson correlation coefficient between the observed and the predicted; and d is Willmott’s index of agreement.

	TSEB-PT			TSEB-2T			TSEB-2TQ
	NK	CM	MV	NK	CM	MV	NK	CM	MV
N	50	50	50	50	50	50	50	50	50
RMSE	71	68	77	84	77	83	72	70	71
Bias	25	16	32	36	30	39	10	7	9
r	0.58	0.58	0.56	0.54	0.55	0.56	0.54	0.54	0.54
d	0.73	0.73	0.72	0.71	0.72	0.72	0.73	0.72	0.73

is another supplement, showing the model performance displayed and illustrated by Figure 8 and Table A5, respectively. The “Bias” (Table A6) explains the same information as shown by “Mean difference” in Table A5 regarding the transpiration from the CEC method. Except for r and d, since the value in each column performs at a similar level, RMSE shows that the transpiration modeled via TSEB-2T_Q, in general, is closer to the transpiration estimated via the CEC method.

However, one must consider the fact that most of the vineyard sites used in this study contain a cover crop used to remove excess moisture in the early spring for controlling vine growth and the timing of initiating irrigation (Figure 9a). This complicates both the modeling of vineyard ET and EC-based partitioning, since there is a period of time when T sources come from both vine and cover crop.

An EC flux tower measuring water and carbon fluxes for the site with a bare soil interrow as shown in Figure 9b will have T coming only from the grapevine. For the site shown in Figure 9a, the EC flux tower cannot separate T from the grapevine and cover crop. For this situation, measurements below the vine canopy in the interrow are necessary for estimating the ET contribution from the cover crop using, for example, micro-Bowen ratio systems which were deployed in the SLM vineyard site for several IOPs [16]. High-resolution imagery separating interrow from the vine canopy, especially for the situation shown in Figure 9a, is necessary because ET from the interrow needs to be considered. Data that have been collected in the GRAPEX program will eventually shed light on this. From a modeling perspective, for example, this is being addressed using a three-source model (3SEB), which is a modification of TSEB and has been initially tested in the RIP720 vineyard using tower-based land surface temperature and found to provide a more reliable ET partitioning account for the interrow cover crop [55].

4. Conclusions

In this study, we assessed the performance of the TSEB model in energy component estimation and evapotranspiration partitioning. Three different versions of TSEB coupled with three different resistance models were used to model the energy components (Rn, G, H, and LE). Modeled estimates were compared with monitored data from the EC flux tower within the corresponding footprint area. Results show that the QTS method adopted in this research can improve the estimation of H, and TSEB-2T_Q (TSEB-2T model coupled with the QTS method for temperature separation) coupled with the NK (Norman and Kustas) resistance model can appropriately provide energy-component estimations. The ET partitioning comparison regarding transpiration illustrated that all TSEB models are statistically acceptable for ET partitioning, but the TSEB-2T_Q showed better agreement with the CEC method. Further work, focused on augmenting the EC flux tower system with measurements of ET for the interrow, upgrading the sUAS image processing system for creating near-real time products, and implementing a 3SEB formulation to explicitly account for the interrow cover crop, is necessary to accurately estimate vine transpiration [55]. These advancements will improve management practices that promote great water use efficiency in vineyards and will improve growers’ and researchers’ understanding of the role of cover crop and vine water use at the canopy and sub-block scale.