G-Rep: Gaussian Representation for Arbitrary-Oriented Object Detection
Abstract
1. Introduction
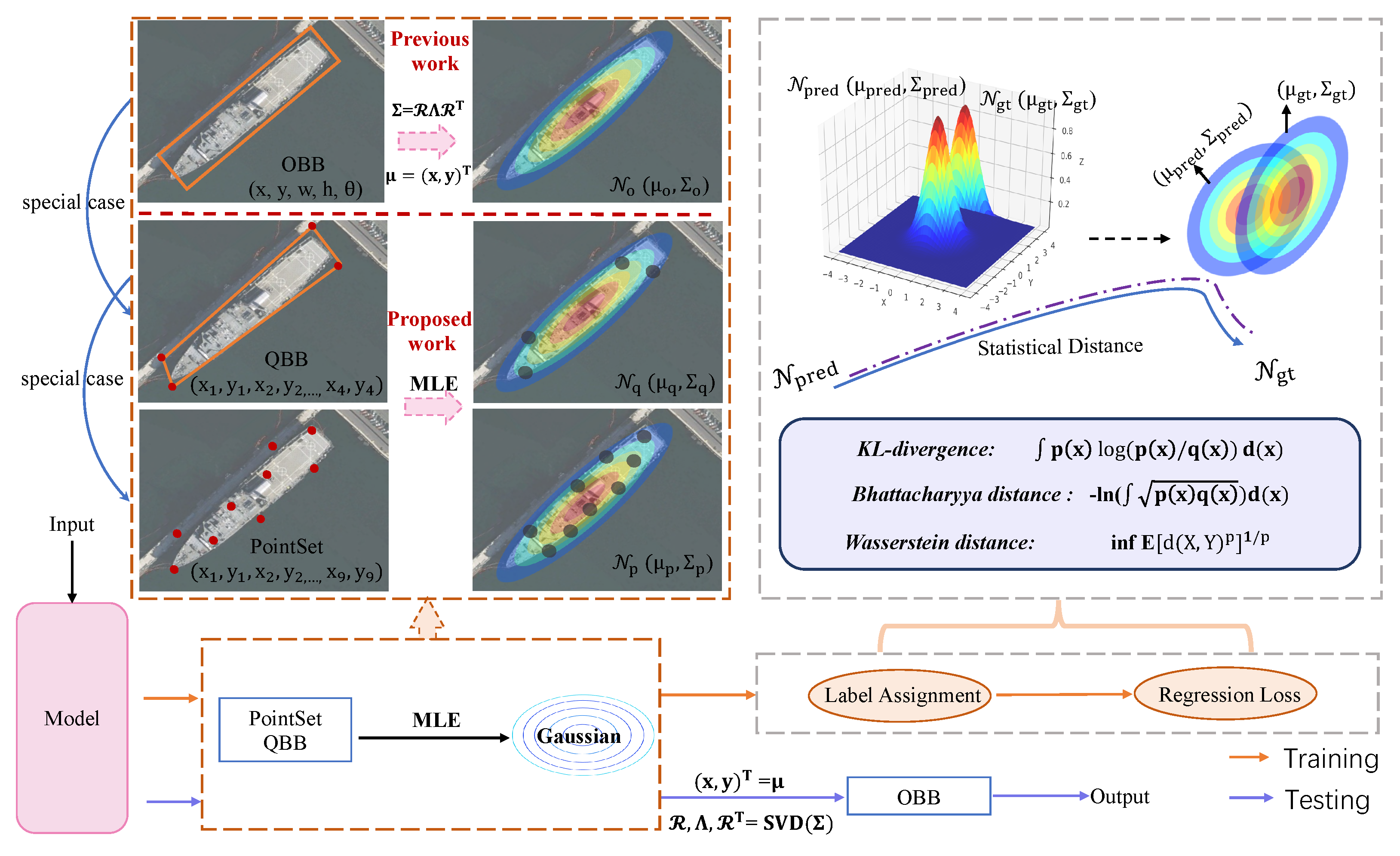
- PointSet uses several individual points to represent the overall arbitrary-oriented object. The independent optimization between the points makes the trained detector very sensitive to isolated points, particularly for objects with large aspect ratios, because a slight deviation causes a sharp drop in the intersection-over-union (IoU) value. As shown in Figure 1a, although most of the points are predicted correctly, an outlier makes the final prediction fail. Therefore, the joint optimization loss (e.g., IoU loss [17,18,19]) based on the point set is more popular than the independent optimization loss (e.g., loss).
- As a special case of PointSet, QBB is defined as the four corners of a quadrilateral bounding box. In addition to the inherent problems of PointSet described above, QBB also suffers from the representation ambiguity problem [15]. Quadrilateral detection often sorts the points first (as shown in Figure 1b, represented by the green box) to facilitate point matching between the ground-truth and prediction bounding boxes to calculate the final loss. Although the red prediction box in Figure 1b does not satisfy the sorting rule and obtains a large loss value accordingly using the loss, this prediction is correct according to the IoU-based evaluation metric.
- OBB is the most popular choice for oriented object representation because of its simplicity and intuitiveness. However, the boundary discontinuity and square-like problem are obstacles to high-precision locating, as detailed in [5,20,21,22]. Figure 1c illustrates the boundary problem of OBB representation, considering the OpenCV acute angle definition () as an example [14]. The height (h) and width (w) of the box swap at the angle boundary, resulting in a sudden change in the loss value, which is coupled with the periodicity of the angle and makes regression difficult.
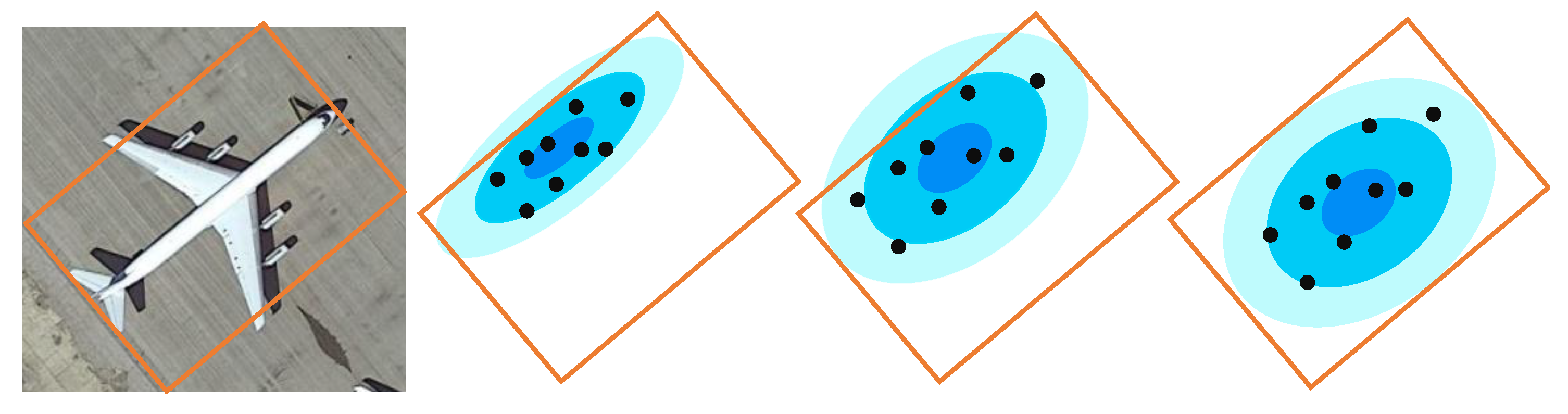
- To uniformly solve the different problems introduced by different representations (OBB, QBB, and PointSet), Gaussian representation (G-Rep) is proposed to construct the Gaussian distribution using the MLE algorithm.
- To achieve an effective and robust measurement for the Gaussian distribution, three statistical distances, the Kullback–Leibler divergence (KLD) [25], the Bhattacharyya distance (BD) [26], and the Wasserstein distance (WD) [27], are explored and corresponding regression loss functions are designed and analyzed.
- To realize the consistency in measurement between sample selection and loss regression, fixed and dynamic label assignment strategies are constructed based on a Gaussian metric to further boost performance.
- Extensive experiments were conducted on several publicly available datasets, e.g., DOTA, HRSC2016, UCAS-AOD, and ICDAR2015, and the results demonstrated the excellent performance of the proposed techniques for arbitrary-oriented object detection.
2. Related Work
2.1. Oriented Object Representations
2.2. Regression Loss in Arbitrary-Oriented Object Detection
2.3. Label Assignment Strategies
3. Proposed Method
3.1. Object Representation Based on Gaussian Distribution
3.2. Gaussian Distance Metrics
3.3. Regression Loss Based on Gaussian Metric
3.4. Label Assignment Based on Gaussian Metric
4. Experiments
4.1. Datasets and Implementation Details
4.2. Normalized Function Design
4.3. Ablation Study
| Rep. | mAP (%) | ||
|---|---|---|---|
| PointSet | IoU (ATSS) | GIoU | 78.07 |
| G-Rep | (Max) | 73.44 | |
| (Max) | 46.71 | ||
| (Max) | 84.39 | ||
| (ATSS) | 88.06 | ||
| (ATSS) | 85.32 | ||
| (ATSS) | 88.56 | ||
| (ATSS) | 88.90 | ||
| (ATSS) | 88.80 | ||
| (ATSS) | 85.32 | ||
| (ATSS) | 85.28 |
- Elongated objects. On the datasets containing a large number of elongated objects (e.g., HRSC2016, ICDAR2015), the improvement in G-Rep applied to PointSet was more pronounced than that applied to QBB, as shown in Table 3, mainly because the greater the number of points, the more accurate the Gaussian distribution obtained, and, thus, the more accurate the representation of the elongated object.
- Size of dataset. The performance on the small datasets (e.g., UCAS-AOD) tended to be saturated, so the improvement was relatively small.
- High baseline. Models with a high-performance baseline were hard to improve significantly (e.g., HRSC2016-QBB, DOTA-PointSet).
4.4. Time Cost Analysis
4.5. Comparison with Other Methods
4.6. Visualization Analysis
4.7. More Discussion
5. Conclusions
- G-Rep uses Gaussian representation to alleviate the challenges posed by other common representations. The experimental results in Table 5 show that G-Rep resulted in a substantial increase of up to 9.99% of mAP on the HRSC2016 dataset when applied to PointSet.
- G-Rep uses the normalized Gaussian distance for the regression loss function and a label assignment strategy instead of the IoU-based metric, which resulted in significant increases in mAP, up to 3.20% on the DOTA dataset and 11.07% on the HRSC2016 dataset, as shown in Table 2.
- G-Rep utilizes a Gaussian distribution to guide the regression of points in PointSet and QBB, which makes the detection results less sensitive to outliers and more accurate for elongated objects. As shown in Table 3, G-Rep resulted in a 6.18% improvement in mAP for elongated objects on the DOTA dataset.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Azimi, S.M.; Vig, E.; Bahmanyar, R.; Körner, M.; Reinartz, P. Towards multi-class object detection in unconstrained remote sensing imagery. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 4–6 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 150–165. [Google Scholar]
- Ding, J.; Xue, N.; Long, Y.; Xia, G.S.; Lu, Q. Learning RoI Transformer for Oriented Object Detection in Aerial Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 2849–2858. [Google Scholar]
- Yang, X.; Yang, J.; Yan, J.; Zhang, Y.; Zhang, T.; Guo, Z.; Sun, X.; Fu, K. Scrdet: Towards more robust detection for small, cluttered and rotated objects. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8232–8241. [Google Scholar]
- Yang, X.; Yan, J.; Feng, Z.; He, T. R3Det: Refined Single-Stage Detector with Feature Refinement for Rotating Object. AAAI Conf. Artif. Intell. 2021, 35, 3163–3171. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Qi, M.; Wang, W.; Xiaopeng, Z.; Qi, T. Rethinking Rotated Object Detection with Gaussian Wasserstein Distance Loss. In Proceedings of the International Conference on Machine Learning, Virtual Event, 18–24 July 2021. [Google Scholar]
- Han, J.; Ding, J.; Li, J.; Xia, G.S. Align deep features for oriented object detection. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]
- Paolo, F.; Lin, T.T.T.; Gupta, R.; Goodman, B.; Patel, N.; Kuster, D.; Kroodsma, D.; Dunnmon, J. xView3-SAR: Detecting Dark Fishing Activity Using Synthetic Aperture Imagery. arXiv 2022, arXiv:2206.00897. [Google Scholar]
- Ye, J.; Chen, Z.; Liu, J.; Du, B. TextFuseNet: Scene Text Detection with Richer Fused Features. IJCAI 2020, 20, 516–522. [Google Scholar]
- Zhou, C.; Li, D.; Wang, P.; Sun, J.; Huang, Y.; Li, W. ACR-Net: Attention Integrated and Cross-Spatial Feature Fused Rotation Network for Tubular Solder Joint Detection. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Zolfi, A.; Amit, G.; Baras, A.; Koda, S.; Morikawa, I.; Elovici, Y.; Shabtai, A. YolOOD: Utilizing Object Detection Concepts for Out-of-Distribution Detection. arXiv 2022, arXiv:2212.02081. [Google Scholar]
- Liu, H.; Jiao, L.; Wang, R.; Xie, C.; Du, J.; Chen, H.; Li, R. WSRD-Net: A Convolutional Neural Network-Based Arbitrary-Oriented Wheat Stripe Rust Detection Method. Front. Plant Sci. 2022, 13, 876069. [Google Scholar] [CrossRef]
- Shi, X.; Shan, S.; Kan, M.; Wu, S.; Chen, X. Real-time rotation-invariant face detection with progressive calibration networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2295–2303. [Google Scholar]
- Chen, Z.; Chen, K.; Lin, W.; See, J.; Yu, H.; Ke, Y.; Yang, C. Piou loss: Towards accurate oriented object detection in complex environments. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 195–211. [Google Scholar]
- Yang, X.; Sun, H.; Fu, K.; Yang, J.; Sun, X.; Yan, M.; Guo, Z. Automatic ship detection in remote sensing images from google earth of complex scenes based on multiscale rotation dense feature pyramid networks. Remote Sens. 2018, 10, 132. [Google Scholar] [CrossRef]
- Ming, Q.; Miao, L.; Zhou, Z.; Yang, X.; Dong, Y. Optimization for Arbitrary-Oriented Object Detection via Representation Invariance Loss. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, C.; Zhang, X.; Jiao, J.; Ji, X.; Ye, Q. Beyond Bounding-Box: Convex-Hull Feature Adaptation for Oriented and Densely Packed Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8792–8801. [Google Scholar]
- Yu, J.; Jiang, Y.; Wang, Z.; Cao, Z.; Huang, T. Unitbox: An advanced object detection network. In Proceedings of the 24th ACM International Conference on Multimedia, Amsterdam, The Netherlands, 15–19 October 2016; pp. 516–520. [Google Scholar]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized intersection over union: A metric and a loss for bounding box regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 658–666. [Google Scholar]
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression. AAAI Conf. Artif. Intell. 2020, 35, 12993–13000. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J. Arbitrary-Oriented Object Detection with Circular Smooth Label. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 677–694. [Google Scholar]
- Yang, X.; Hou, L.; Zhou, Y.; Wang, W.; Yan, J. Dense label encoding for boundary discontinuity free rotation detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15819–15829. [Google Scholar]
- Yang, X.; Yang, X.; Yang, J.; Ming, Q.; Wang, W.; Tian, Q.; Yan, J. Learning high-precision bounding box for rotated object detection via kullback-leibler divergence. Adv. Neural Inf. Process. Syst. 2021, 34, 18381–18394. [Google Scholar]
- Qian, W.; Yang, X.; Peng, S.; Yan, J.; Guo, Y. Learning Modulated Loss for Rotated Object Detection. AAAI Conf. Artif. Intell. 2021, 35, 2458–2466. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. Proc. R. Stat. Soc. 1977, 39, 1–22. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 1943, 35, 99–109. [Google Scholar]
- Villani, C. Optimal Transport: Old and New; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 338. [Google Scholar]
- Xu, Y.; Fu, M.; Wang, Q.; Wang, Y.; Chen, K.; Xia, G.S.; Bai, X. Gliding vertex on the horizontal bounding box for multi-oriented object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 1452–1459. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, S.; Hu, H.; Wang, L.; Lin, S. Reppoints: Point set representation for object detection. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9657–9666. [Google Scholar]
- Zhou, L.; Wei, H.; Li, H.; Zhang, Y.; Sun, X.; Zhao, W. Arbitrary-oriented object detection in remote sensing images based on polar coordinates. IEEE Access 2020, 8, 223373–223384. [Google Scholar] [CrossRef]
- Zhao, P.; Qu, Z.; Bu, Y.; Tan, W.; Guan, Q. Polardet: A fast, more precise detector for rotated target in aerial images. Int. J. Remote Sens. 2021, 42, 5821–5851. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Y.; Chang, Z.; Li, H.; Wang, H.; Sun, X. Oriented objects as pairs of middle lines. ISPRS J. Photogramm. Remote Sens. 2020, 169, 268–279. [Google Scholar] [CrossRef]
- Llerena, J.M.; Zeni, L.F.; Kristen, L.N.; Jung, C. Gaussian Bounding Boxes and Probabilistic Intersection-over-Union for Object Detection. arXiv 2021, arXiv:2106.06072. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Zhang, S.; Chi, C.; Yao, Y.; Lei, Z.; Li, S.Z. Bridging the Gap Between Anchor-Based and Anchor-Free Detection via Adaptive Training Sample Selection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9756–9765. [Google Scholar] [CrossRef]
- Kim, K.; Lee, H.S. Probabilistic Anchor Assignment with IoU Prediction for Object Detection. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 355–371. [Google Scholar]
- Ming, Q.; Zhou, Z.; Miao, L.; Zhang, H.; Li, L. Dynamic Anchor Learning for Arbitrary-Oriented Object Detection. AAAI Conf. Artif. Intell. 2021, 35, 2355–2363. [Google Scholar] [CrossRef]
- Zhang, X.; Wan, F.; Liu, C.; Ji, X.; Ye, Q. Learning to Match Anchors for Visual Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3096–3109. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gong, Z.; Liu, X.; Guo, H.; Yu, D.; Ding, L. Object Detection Based on Adaptive Feature-Aware Method in Optical Remote Sensing Images. Remote Sens. 2022, 14, 3616. [Google Scholar] [CrossRef]
- Wang, J.; Cui, Z.; Zang, Z.; Meng, X.; Cao, Z. Absorption Pruning of Deep Neural Network for Object Detection in Remote Sensing Imagery. Remote Sens. 2022, 14, 6245. [Google Scholar] [CrossRef]
- Zhang, T.; Zhuang, Y.; Wang, G.; Dong, S.; Chen, H.; Li, L. Multiscale Semantic Fusion-Guided Fractal Convolutional Object Detection Network for Optical Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–20. [Google Scholar] [CrossRef]
- Ma, W.; Li, N.; Zhu, H.; Jiao, L.; Tang, X.; Guo, Y.; Hou, B. Feature Split–Merge–Enhancement Network for Remote Sensing Object Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Yu, D.; Ji, S. A New Spatial-Oriented Object Detection Framework for Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Li, X.; Deng, J.; Fang, Y. Few-Shot Object Detection on Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Richards, F.S. A method of maximum-likelihood estimation. J. R. Stat. Soc. Ser. B Methodol. 1961, 23, 469–475. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Xia, G.S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A large-scale dataset for object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3974–3983. [Google Scholar]
- Liu, Z.; Yuan, L.; Weng, L.; Yang, Y. A high resolution optical satellite image dataset for ship recognition and some new baselines. In Proceedings of the International Conference on Pattern Recognition Applications and Methods, Porto, Portugal, 24–26 February 2017; Volume 2, pp. 324–331. [Google Scholar]
- Zhu, H.; Chen, X.; Dai, W.; Fu, K.; Ye, Q.; Jiao, J. Orientation robust object detection in aerial images using deep convolutional neural network. In Proceedings of the 2015 IEEE International Conference on Image Processing, Quebec City, QC, Canada, 27–30 September 2015; pp. 3735–3739. [Google Scholar]
- Karatzas, D.; Gomez-Bigorda, L.; Nicolaou, A.; Ghosh, S.; Bagdanov, A.; Iwamura, M.; Matas, J.; Neumann, L.; Chandrasekhar, V.R.; Lu, S.; et al. ICDAR 2015 competition on robust reading. In Proceedings of the 2015 13th International Conference on Document Analysis and Recognition, Tunis, Tunisia, 23–26 August 2015; pp. 1156–1160. [Google Scholar]
- Chen, K.; Wang, J.; Pang, J.; Cao, Y.; Xiong, Y.; Li, X.; Sun, S.; Feng, W.; Liu, Z.; Xu, J.; et al. MMDetection: Open MMLab Detection Toolbox and Benchmark. arXiv 2019, arXiv:1906.07155. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Newell, A.; Yang, K.; Deng, J. Stacked hourglass networks for human pose estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 483–499. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Li, W.; Wei, W.; Zhang, L. GSDet: Object Detection in Aerial Images Based on Scale Reasoning. IEEE Trans. Image Process. 2021, 30, 4599–4609. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Huang, Q.; Pei, X.; Jiao, L.; Shang, R. Radet: Refine feature pyramid network and multi-layer attention network for arbitrary-oriented object detection of remote sensing images. Remote Sens. 2020, 12, 389. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, S.; Zhang, W. Cad-net: A context-aware detection network for objects in remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10015–10024. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Zhang, Y.; Zhao, L.; Sun, X.; Guo, Z. SARD: Towards scale-aware rotated object detection in aerial imagery. IEEE Access 2019, 7, 173855–173865. [Google Scholar] [CrossRef]
- Li, C.; Xu, C.; Cui, Z.; Wang, D.; Zhang, T.; Yang, J. Feature-attentioned object detection in remote sensing imagery. In Proceedings of the 2019 IEEE International Conference on Image Processing, Taipei, Taiwan, 22–25 September 2019; pp. 3886–3890. [Google Scholar]
- Yang, F.; Li, W.; Hu, H.; Li, W.; Wang, P. Multi-Scale Feature Integrated Attention-Based Rotation Network for Object Detection in VHR Aerial Images. Sensors 2020, 20, 1686. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, W.; Li, H.C.; Zhang, H.; Xia, G.S. Learning center probability map for detecting objects in aerial images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4307–4323. [Google Scholar] [CrossRef]
- Song, Q.; Yang, F.; Yang, L.; Liu, C.; Hu, M.; Xia, L. Learning point-guided localization for detection in remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1084–1094. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Yang, X.; Tang, J.; Liao, W.; He, T. SCRDet++: Detecting Small, Cluttered and Rotated Objects via Instance-Level Feature Denoising and Rotation Loss Smoothing. arXiv 2020, arXiv:2004.13316. [Google Scholar] [CrossRef]
- Dai, P.; Yao, S.; Li, Z.; Zhang, S.; Cao, X. ACE: Anchor-Free Corner Evolution for Real-Time Arbitrarily-Oriented Object Detection. IEEE Trans. Image Process. 2022, 31, 4076–4089. [Google Scholar] [CrossRef]
- Yu, F.; Wang, D.; Shelhamer, E.; Darrell, T. Deep layer aggregation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2403–2412. [Google Scholar]
- Yi, J.; Wu, P.; Liu, B.; Huang, Q.; Qu, H.; Metaxas, D. Oriented object detection in aerial images with box boundary-aware vectors. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 2150–2159. [Google Scholar]
- Pan, X.; Ren, Y.; Sheng, K.; Dong, W.; Yuan, H.; Guo, X.; Ma, C.; Xu, C. Dynamic refinement network for oriented and densely packed object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11207–11216. [Google Scholar]
- Hou, L.; Lu, K.; Xue, J. Refined One-Stage Oriented Object Detection Method for Remote Sensing Images. IEEE Trans. Image Process. 2022, 31, 1545–1558. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Li, W.; Xia, X.G.; Tao, R. A General Gaussian Heatmap Label Assignment for Arbitrary-Oriented Object Detection. IEEE Trans. Image Process. 2022, 31, 1895–1910. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Shao, W.; Ye, H.; Wang, L.; Wang, H.; Zheng, Y.; Xue, X. Arbitrary-oriented scene text detection via rotation proposals. IEEE Trans. Multimed. 2018, 20, 3111–3122. [Google Scholar] [CrossRef]




| Metric | Func. of | Range of | Func. of | Range of | mAP (%) |
|---|---|---|---|---|---|
| KLD | 87.32 | ||||
| 50.73 | |||||
| 88.06 | |||||
| 87.96 | |||||
| BD | 81.02 | ||||
| 69.32 | |||||
| 85.32 | |||||
| 85.12 | |||||
| WD | 87.04 | ||||
| 88.24 | |||||
| 88.56 | |||||
| 87.54 |
| Dataset | Rep. | mAP (%) | ||
|---|---|---|---|---|
| DOTA | PointSet | IoU (Max) | GIoU | 63.97 |
| G-Rep | IoU (Max) | 64.63 (+0.66) | ||
| (Max) | 65.07 (+1.10) | |||
| PointSet | IoU (ATSS) | GIoU | 68.88 | |
| G-Rep | (ATSS) | 70.45 (+1.57) | ||
| (PATSS) | 72.08 (+3.20) | |||
| HRSC2016 | PointSet | IoU (ATSS) | GIoU | 78.07 |
| G-Rep | (ATSS) | 88.06 (+9.99) | ||
| (PATSS) | 89.15 (+11.07) |
| Rep. | BR (2.93) | SV (1.72) | LV (3.45) | SH (2.40) | HC (2.34) | mAP (%) |
|---|---|---|---|---|---|---|
| PointSet | 46.87 | 77.10 | 71.65 | 83.71 | 32.93 | 62.45 |
| G-Rep | 50.82 | 79.33 | 75.07 | 87.32 | 50.63 | 68.63 |
| (+3.95) | (+2.23) | (+3.51) | (+3.61) | (+17.70) | (+6.18) |
| Dataset | Rep. | Eval. | Gain ↑ |
|---|---|---|---|
| DOTA | PointSet * | 68.88 | – |
| G-Rep * (PointSet) | 70.45 | +1.57 | |
| QBB | 63.05 | – | |
| G-Rep (QBB) | 67.92 | +4.87 | |
| HRSC2016 | PointSet * | 78.07 | – |
| G-Rep * (PointSet) | 88.06 | +9.99 | |
| QBB | 87.70 | – | |
| G-Rep (QBB) | 88.01 | +0.31 | |
| UCAS-AOD | PointSet * | 90.15 | – |
| G-Rep * (PointSet) | 90.20 | +0.05 | |
| QBB | 88.50 | – | |
| G-Rep (QBB) | 88.82 | +0.32 | |
| ICDAR2015 | PointSet * | 76.20 | – |
| G-Rep * (PointSet) | 81.30 | +5.10 | |
| QBB | 75.10 | – | |
| G-Rep (QBB) | 75.83 | +0.73 |
| Method | mAP (%) | Params | Speed |
|---|---|---|---|
| RepPoints | 70.39 | 36.1M | 24.0fps |
| SANet | 74.12 | 37.3M | 19.9fps |
| G-Rep (ours) | 75.56 | 36.1M | 19.3fps |
| Method | Backbone | MS | PL | BD | BR | GTF | SV | LV | SH | TC | BC | ST | SBF | RA | HA | SP | HC | mAP (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| two-stage: | ||||||||||||||||||
| ICN [1] | R-101 | ✓ | 81.40 | 74.30 | 47.70 | 70.30 | 64.90 | 67.80 | 70.00 | 90.80 | 79.10 | 78.20 | 53.60 | 62.90 | 67.00 | 64.20 | 50.20 | 68.20 |
| GSDet [59] | R-101 | 81.12 | 76.78 | 40.78 | 75.89 | 64.50 | 58.37 | 74.21 | 89.92 | 79.40 | 78.83 | 64.54 | 63.67 | 66.04 | 58.01 | 52.13 | 68.28 | |
| RADet [60] | RX-101 | ✓ | 79.45 | 76.99 | 48.05 | 65.83 | 65.45 | 74.40 | 68.86 | 89.70 | 78.14 | 74.97 | 49.92 | 64.63 | 66.14 | 71.58 | 62.16 | 69.06 |
| RoI-Transformer [2] | R-101 | ✓ | 88.64 | 78.52 | 43.44 | 75.92 | 68.81 | 73.68 | 83.59 | 90.74 | 77.27 | 81.46 | 58.39 | 53.54 | 62.83 | 58.93 | 47.67 | 69.56 |
| CAD-Net [61] | R-101 | 87.80 | 82.40 | 49.40 | 73.50 | 71.10 | 63.50 | 76.70 | 90.90 | 79.20 | 73.30 | 48.40 | 60.90 | 62.00 | 67.00 | 62.20 | 69.90 | |
| SCRDet [3] | R-101 | ✓ | 89.98 | 80.65 | 52.09 | 68.36 | 68.36 | 60.32 | 72.41 | 90.85 | 87.94 | 86.86 | 65.02 | 66.68 | 66.25 | 68.24 | 65.21 | 72.61 |
| SARD [62] | R-101 | 89.93 | 84.11 | 54.19 | 72.04 | 68.41 | 61.18 | 66.00 | 90.82 | 87.79 | 86.59 | 65.65 | 64.04 | 66.68 | 68.84 | 68.03 | 72.95 | |
| FADet [63] | R-101 | ✓ | 90.21 | 79.58 | 45.49 | 76.41 | 73.18 | 68.27 | 79.56 | 90.83 | 83.40 | 84.64 | 53.40 | 65.42 | 74.17 | 69.69 | 64.86 | 73.28 |
| MFIAR-Net[64] | R-152 | ✓ | 89.62 | 84.03 | 52.41 | 70.30 | 70.13 | 67.64 | 77.81 | 90.85 | 85.40 | 86.22 | 63.21 | 64.14 | 68.31 | 70.21 | 62.11 | 73.49 |
| Gliding Vertex [28] | R-101 | 89.64 | 85.00 | 52.26 | 77.34 | 73.01 | 73.14 | 86.82 | 90.74 | 79.02 | 86.81 | 59.55 | 70.91 | 72.94 | 70.86 | 57.32 | 75.02 | |
| CenterMap [65] | R-101 | ✓ | 89.83 | 84.41 | 54.60 | 70.25 | 77.66 | 78.32 | 87.19 | 90.66 | 84.89 | 85.27 | 56.46 | 69.23 | 74.13 | 71.56 | 66.06 | 76.03 |
| CSL (FPN-based) [20] | R-152 | ✓ | 90.25 | 85.53 | 54.64 | 75.31 | 70.44 | 73.51 | 77.62 | 90.84 | 86.15 | 86.69 | 69.60 | 68.04 | 73.83 | 71.10 | 68.93 | 76.17 |
| RSDet [23] | R-152 | ✓ | 89.93 | 84.45 | 53.77 | 74.35 | 71.52 | 78.31 | 78.12 | 91.14 | 87.35 | 86.93 | 65.64 | 65.17 | 75.35 | 79.74 | 63.31 | 76.34 |
| OPLD [66] | R-101 | ✓ | 89.37 | 85.82 | 54.10 | 79.58 | 75.00 | 75.13 | 86.92 | 90.88 | 86.42 | 86.62 | 62.46 | 68.41 | 73.98 | 68.11 | 63.69 | 76.43 |
| SCRDet++ [67] | R-101 | ✓ | 90.05 | 84.39 | 55.44 | 73.99 | 77.54 | 71.11 | 86.05 | 90.67 | 87.32 | 87.08 | 69.62 | 68.90 | 73.74 | 71.29 | 65.08 | 76.81 |
| one-stage: | ||||||||||||||||||
| P−RSDet [30] | R-101 | 89.02 | 73.65 | 47.33 | 72.03 | 70.58 | 73.71 | 72.76 | 90.82 | 80.12 | 81.32 | 59.45 | 57.87 | 60.79 | 65.21 | 52.59 | 69.82 | |
| [32] | H-104 | 89.31 | 82.14 | 47.33 | 61.21 | 71.32 | 74.03 | 78.62 | 90.76 | 82.23 | 81.36 | 60.93 | 60.17 | 58.21 | 66.98 | 61.03 | 71.04 | |
| ACE [68] | DAL34[69] | 89.50 | 76.30 | 45.10 | 60.00 | 77.80 | 77.10 | 86.50 | 90.80 | 79.50 | 85.70 | 47.00 | 59.40 | 65.70 | 71.70 | 63.90 | 71.70 | |
| [4] | R-152 | ✓ | 89.24 | 80.81 | 51.11 | 65.62 | 70.67 | 76.03 | 78.32 | 90.83 | 84.89 | 84.42 | 65.10 | 57.18 | 68.10 | 68.98 | 60.88 | 72.81 |
| BBAVectors [70] | R-101 | ✓ | 88.35 | 79.96 | 50.69 | 62.18 | 78.43 | 78.98 | 87.94 | 90.85 | 83.58 | 84.35 | 54.13 | 60.24 | 65.22 | 64.28 | 55.70 | 73.32 |
| DRN [71] | H-104 | ✓ | 89.71 | 82.34 | 47.22 | 64.10 | 76.22 | 74.43 | 85.84 | 90.57 | 86.18 | 84.89 | 57.65 | 61.93 | 69.30 | 69.63 | 58.48 | 73.23 |
| GWD [5] | R-152 | 88.88 | 80.47 | 52.94 | 63.85 | 76.95 | 70.28 | 83.56 | 88.54 | 83.51 | 84.94 | 61.24 | 65.13 | 65.45 | 71.69 | 73.90 | 74.09 | |
| ROD [72] | R-101 | ✓ | 88.69 | 79.41 | 52.26 | 65.51 | 74.72 | 80.83 | 87.42 | 90.77 | 84.31 | 83.36 | 62.64 | 58.14 | 66.95 | 72.32 | 69.34 | 74.44 |
| CFA [16] | R-101 | 89.26 | 81.72 | 51.81 | 67.17 | 79.99 | 78.25 | 84.46 | 90.77 | 83.40 | 85.54 | 54.86 | 67.75 | 73.04 | 70.24 | 64.96 | 75.05 | |
| KLD [22] | R-50 | 88.91 | 83.71 | 50.10 | 68.75 | 78.20 | 76.05 | 84.58 | 89.41 | 86.15 | 85.28 | 63.15 | 60.90 | 75.06 | 71.51 | 67.45 | 75.28 | |
| [6] | R-101 | 88.70 | 81.41 | 54.28 | 59.75 | 78.04 | 80.54 | 88.04 | 90.69 | 84.75 | 86.22 | 65.03 | 65.81 | 76.16 | 73.37 | 58.86 | 76.11 | |
| PolarDet [31] | R-101 | ✓ | 89.65 | 87.07 | 48.14 | 70.97 | 78.53 | 80.34 | 87.45 | 90.76 | 85.63 | 86.87 | 61.64 | 70.32 | 71.92 | 73.09 | 67.15 | 76.64 |
| DAL () [38] | R-50 | ✓ | 89.69 | 83.11 | 55.03 | 71.00 | 78.30 | 81.90 | 88.46 | 90.89 | 84.97 | 87.46 | 64.41 | 65.65 | 76.86 | 72.09 | 64.35 | 76.95 |
| GGHL [73] | D-53 | 89.74 | 85.63 | 44.50 | 77.48 | 76.72 | 80.45 | 86.16 | 90.83 | 88.18 | 86.25 | 67.07 | 69.40 | 73.38 | 68.45 | 70.14 | 76.95 | |
| DCL () [21] | R-152 | ✓ | 89.26 | 83.60 | 53.54 | 72.76 | 79.04 | 82.56 | 87.31 | 90.67 | 86.59 | 86.98 | 67.49 | 66.88 | 73.29 | 70.56 | 69.99 | 77.37 |
| RIDet [15] | R-50 | 89.31 | 80.77 | 54.07 | 76.38 | 79.81 | 81.99 | 89.13 | 90.72 | 83.58 | 87.22 | 64.42 | 67.56 | 78.08 | 79.17 | 62.07 | 77.62 | |
| QBB (baseline) | R-50 | 77.52 | 57.38 | 37.20 | 65.97 | 56.29 | 69.99 | 70.04 | 90.31 | 81.14 | 55.34 | 57.98 | 49.88 | 56.01 | 62.32 | 58.37 | 63.05 | |
| PointSet (baseline) | R-50 | 87.48 | 82.53 | 45.07 | 65.16 | 78.12 | 58.72 | 75.44 | 90.78 | 82.54 | 85.98 | 60.77 | 67.68 | 60.93 | 70.36 | 44.41 | 70.39 | |
| G-Rep (QBB) | R-101 | 88.89 | 74.62 | 43.92 | 70.24 | 67.26 | 67.26 | 79.80 | 90.87 | 84.46 | 78.47 | 54.59 | 62.60 | 66.67 | 67.98 | 52.16 | 70.59 | |
| G-Rep (PointSet) | R-50 | 87.76 | 81.29 | 52.64 | 70.53 | 80.34 | 80.56 | 87.47 | 90.74 | 82.91 | 85.01 | 61.48 | 68.51 | 67.53 | 73.02 | 63.54 | 75.56 | |
| G-Rep (PointSet) | RX-101 | ✓ | 88.98 | 79.21 | 57.57 | 74.35 | 81.30 | 85.23 | 88.30 | 90.69 | 85.38 | 85.25 | 63.65 | 68.82 | 77.87 | 78.76 | 71.74 | 78.47 |
| G-Rep (PointSet) | Swin-T | ✓ | 88.15 | 81.64 | 61.30 | 79.50 | 80.94 | 85.68 | 88.37 | 90.90 | 85.47 | 87.77 | 71.01 | 67.42 | 77.19 | 81.23 | 75.83 | 80.16 |
| Method | mAP (%) |
|---|---|
| RoI-Transformer [2] | 86.20 |
| RSDet [23] | 86.50 |
| Gliding Vertex [28] | 88.20 |
| BBAVectors [70] | 88.60 |
| [4] | 89.26 |
| DCL [21] | 89.46 |
| G-Rep (QBB) | 88.02 |
| G-Rep (PointSet) | 89.46 |
| Method | Car | Airplane | mAP (%) |
|---|---|---|---|
| RetinaNet [35] | 84.64 | 90.51 | 87.57 |
| Faster RCNN [34] | 86.87 | 89.86 | 88.36 |
| RoI-Transformer [2] | 88.02 | 90.02 | 89.02 |
| RIDet-Q [15] | 88.50 | 89.96 | 89.23 |
| RIDet-O [15] | 88.88 | 90.35 | 89.62 |
| DAL [38] | 89.25 | 90.49 | 89.87 |
| G-Rep (QBB) | 87.35 | 90.30 | 88.82 |
| G-Rep (PointSet) | 89.64 | 90.67 | 90.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, L.; Lu, K.; Yang, X.; Li, Y.; Xue, J. G-Rep: Gaussian Representation for Arbitrary-Oriented Object Detection. Remote Sens. 2023, 15, 757. https://doi.org/10.3390/rs15030757
Hou L, Lu K, Yang X, Li Y, Xue J. G-Rep: Gaussian Representation for Arbitrary-Oriented Object Detection. Remote Sensing. 2023; 15(3):757. https://doi.org/10.3390/rs15030757
Chicago/Turabian StyleHou, Liping, Ke Lu, Xue Yang, Yuqiu Li, and Jian Xue. 2023. "G-Rep: Gaussian Representation for Arbitrary-Oriented Object Detection" Remote Sensing 15, no. 3: 757. https://doi.org/10.3390/rs15030757
APA StyleHou, L., Lu, K., Yang, X., Li, Y., & Xue, J. (2023). G-Rep: Gaussian Representation for Arbitrary-Oriented Object Detection. Remote Sensing, 15(3), 757. https://doi.org/10.3390/rs15030757






