Study of the
Abstract
1. Introduction
2. Methods and Data
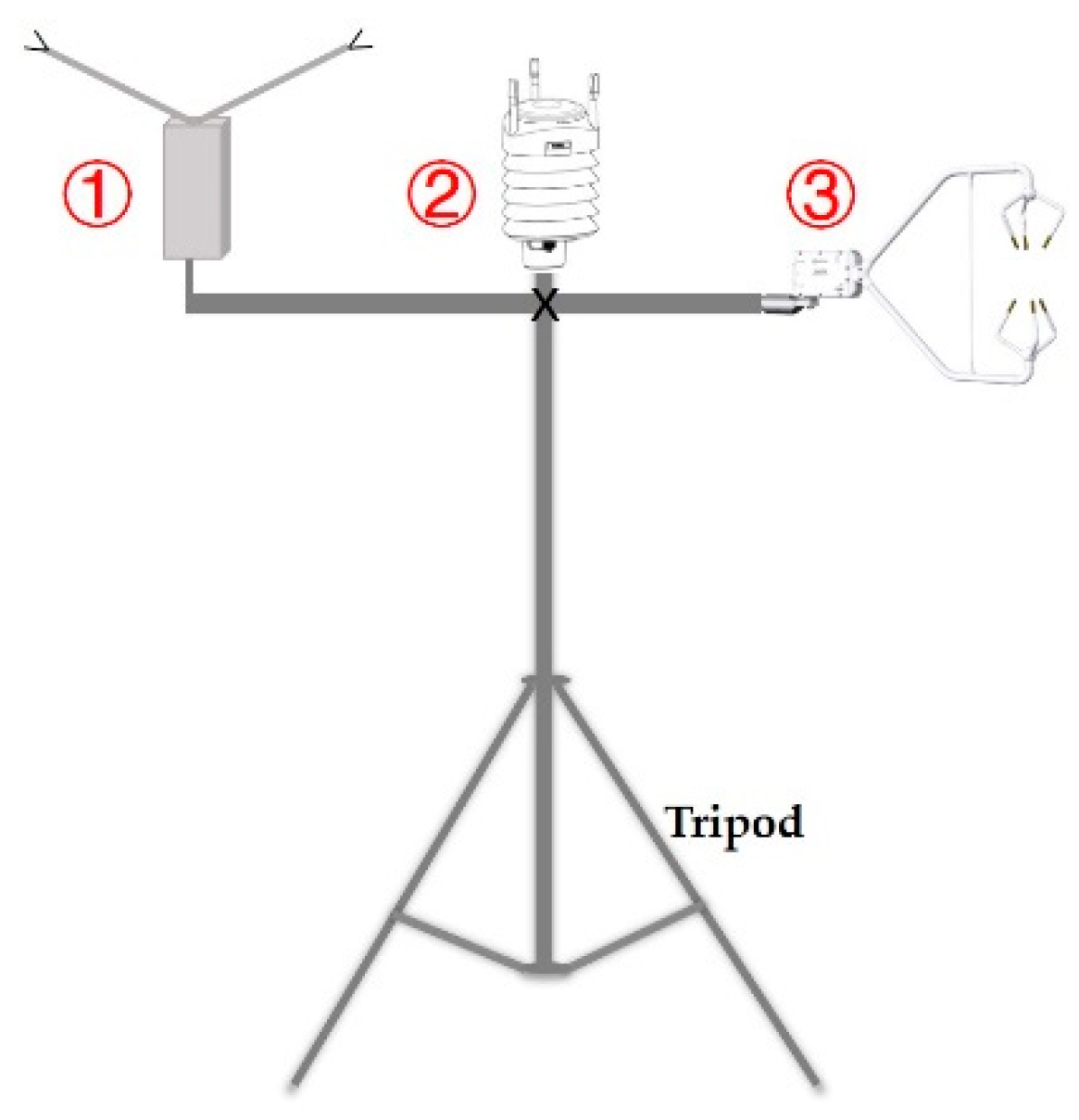
2.1. Observation Site and Instruments
2.2. Model of Parametric near the Surface
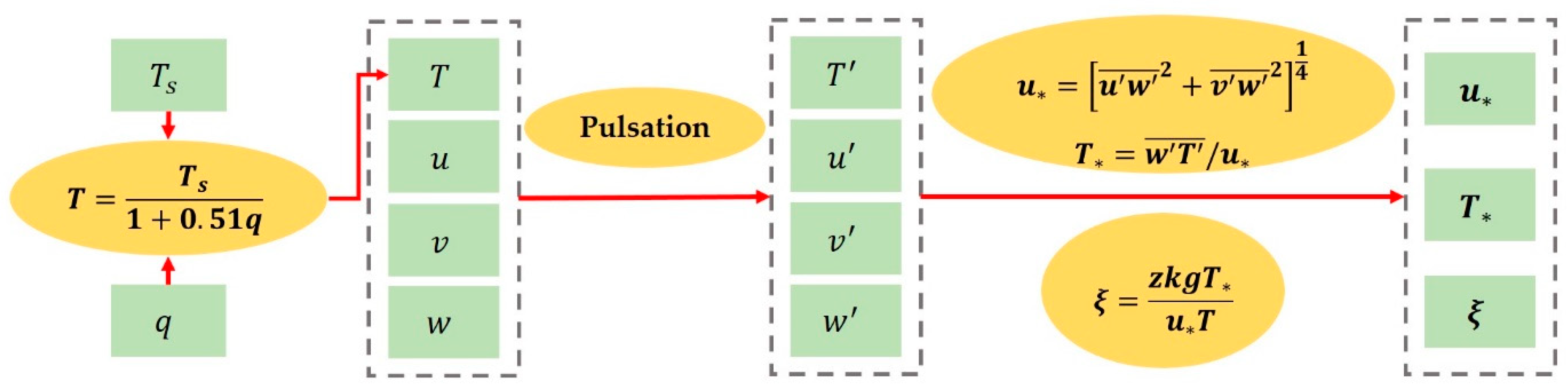
2.3. Calculation Method of Turbulence-Scaling Parameters
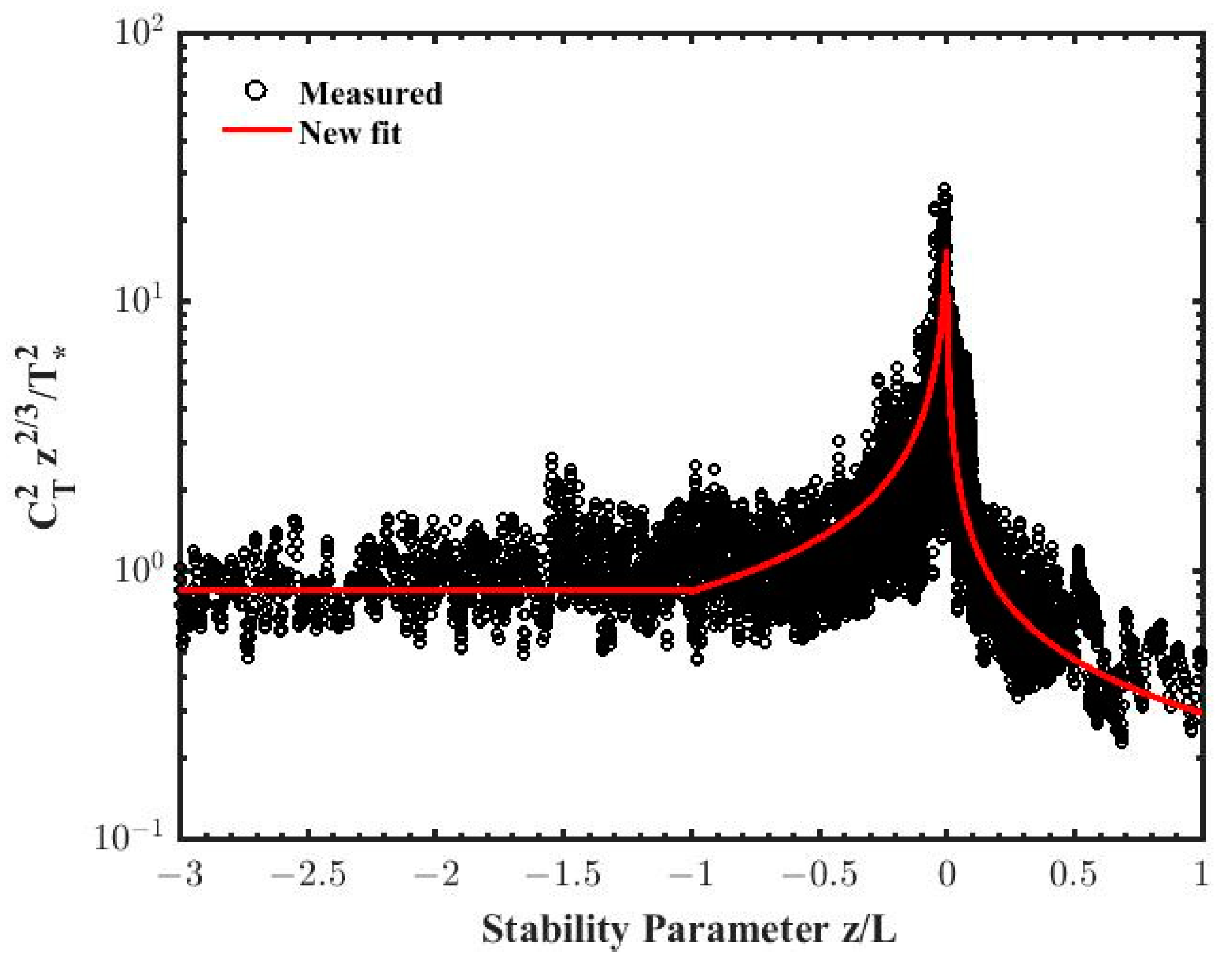
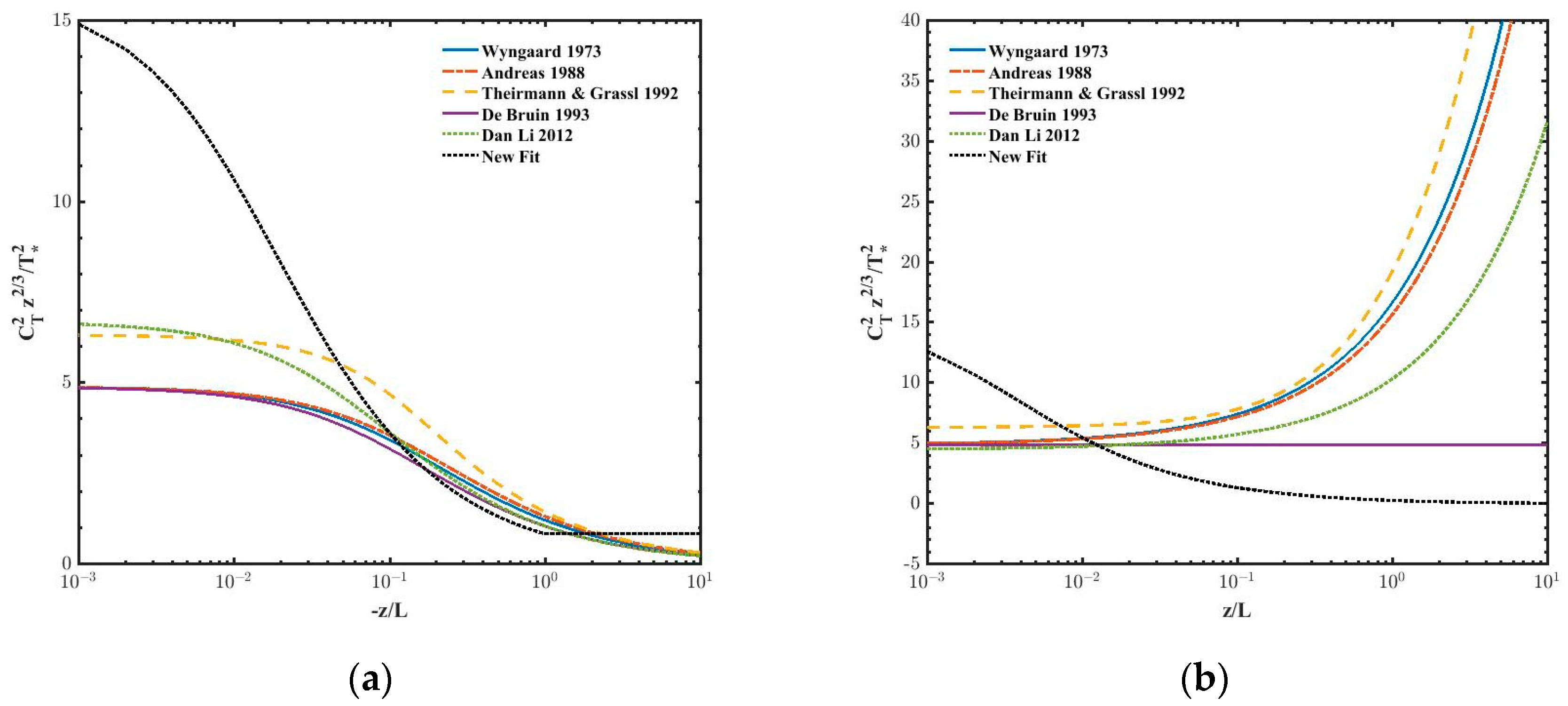
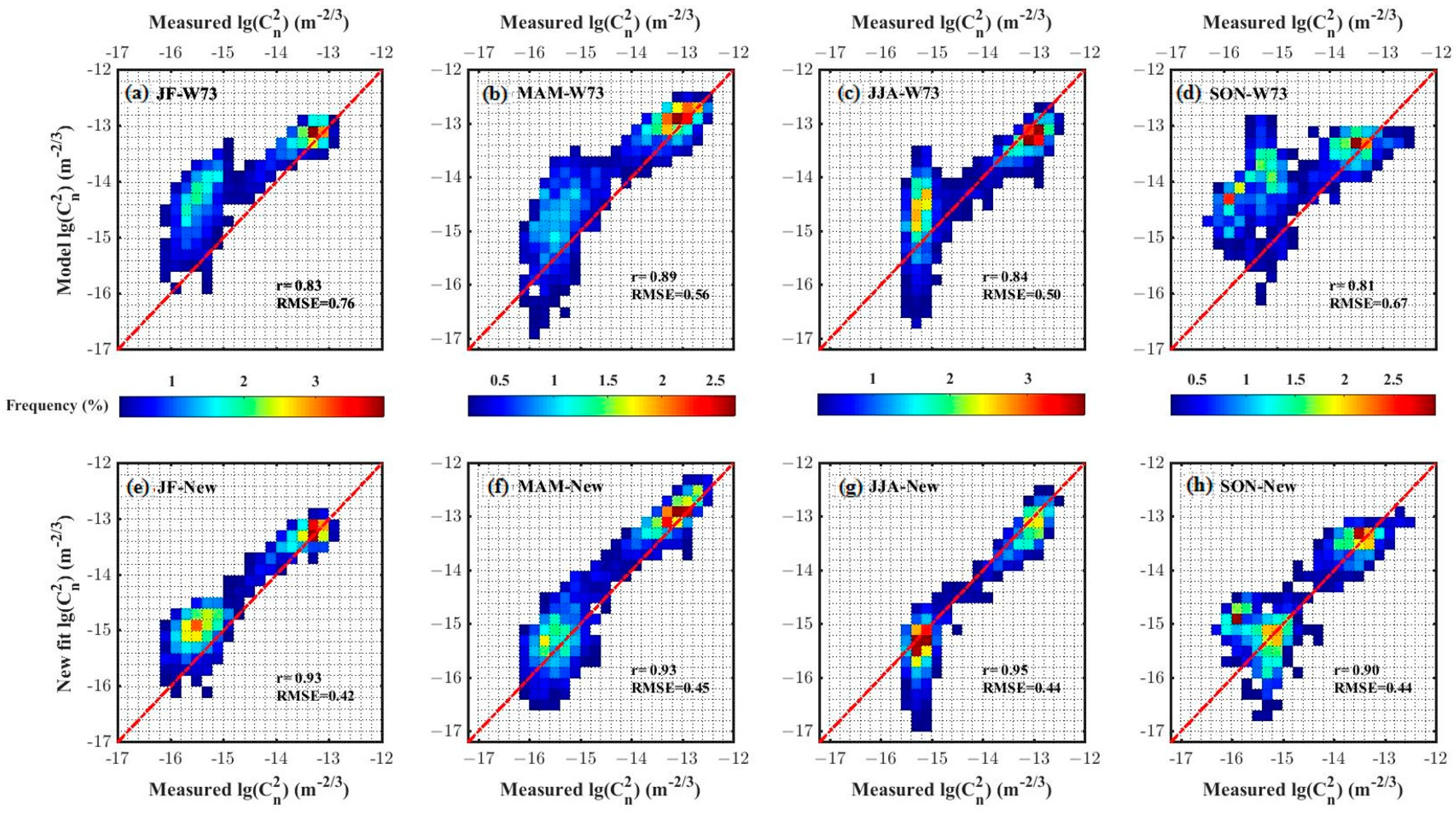
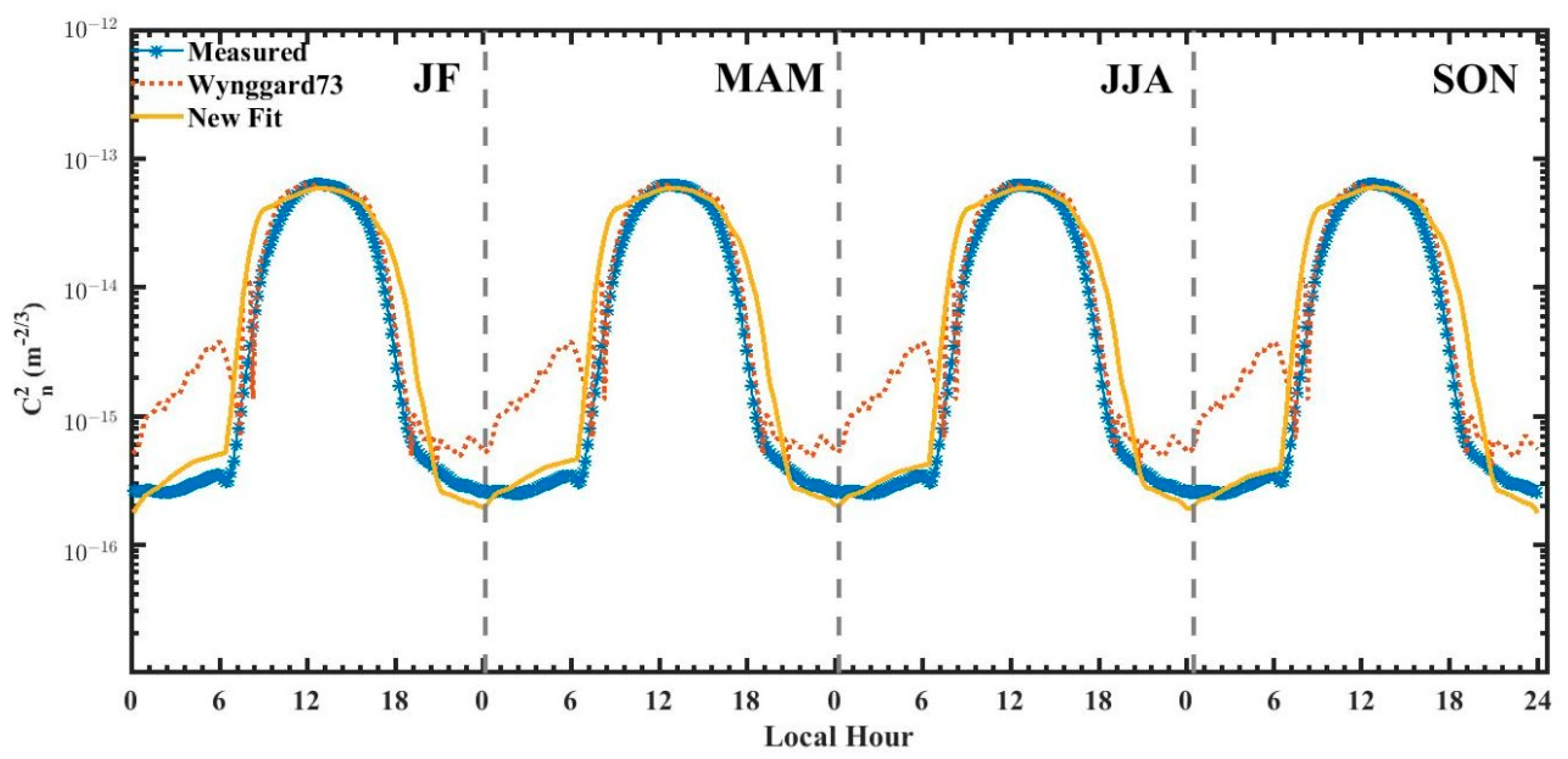
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sheng, P.; Mao, J. Atmospheric Physics; Peking University Press: Beijing, China, 2013; p. 222. [Google Scholar]
- Andrews, L.C.; Philips, R.L.; Hopen, C.Y. Laser Beam Scintillation with Applications; SPIE: Bellingham, WA, USA, 2001; pp. 201–204. [Google Scholar]
- Yang, Q.K.; Wu, X.Q.; Luo, T.; Qing, C.; Yuan, R.M.; Su, C.D.; Xu, C.S.; Wu, Y.; Ma, X.B.; Wang, Z.Y. Forecasting surface-layer optical turbulence above the Tibetan Plateau using the WRF model. Opt. Laser Technol. 2022, 153, 6. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, J.; Lu, S. From the Clasic Theory of Turbulence to the Nonequilibrium Thermodynamic Theory of Atmospheric Turbulence. Plateau Meteorol. 2012, 31, 1–27. [Google Scholar]
- Toselli, I.; Gladysz, S. Adaptive optics correction of scintillation for oceanic turbulence-affected laser beams. In Proceedings of the Conference on Environmental Effects on Light Propagation and Adaptive Systems, Berlin, Germany, 12–13 September 2018. [Google Scholar]
- Baykal, Y.; Gercekcioglu, H. Multimode laser beam scintillations in strong atmospheric turbulence. Appl. Phys. B-Lasers Opt. 2019, 125, 6. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the ground layer of the atmosphere (osnovne zakonomernosti turbulentnogo peremeshivaniya v prizemnom sloe atmosfery). Doki Akad Nauk Sssr 1954, 24, 163–187. [Google Scholar]
- Foken, T. 50 years of the Monin-Obukhov similarity theory. Bound.-Layer Meteor. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Hill, R.J.; Ochs, G.R.; Wilson, J.J. Measuring surface-layer fluxes of heat and momentum using optical scintillation. Bound.-Layer Meteor. 1992, 58, 391–408. [Google Scholar] [CrossRef]
- Chehbouni, A.; Watts, C.; Lagouarde, J.P.; Kerr, Y.H.; Rodriguez, J.C.; Bonnefond, J.M.; Santiago, F.; Dedieu, G.; Goodrich, D.C.; Unkrich, C. Estimation of heat and momentum fluxes over complex terrain using a large aperture scintillometer. Agric. For. Meteorol. 2000, 105, 215–226. [Google Scholar] [CrossRef]
- Moene, A.F.; Meijninger, W.; Hartogensis, O.K.; Kohsiek, W.; Debruin, H. A Review of the Relationships Describing the Signal of a Large Aperture Scintillometer; Wageningen Universiteit: Wageningen, The Netherlands, 2004; Available online: https://www.researchgate.net/publication/40123688_A_review_of_the_relationships_describing_the_signal_of_a_Large_Aperture_Scintillometer (accessed on 29 November 2022).
- Bai, J.; Liu, S.; Ding, X. Temporal-spatial characteristics analysis of area-averaged sensible heat fluxes by large aperture scintillometer over Hai River Basin. Adv. Earth Sci. 2010, 25, 1187–1198. [Google Scholar]
- Niu, S.; Zhao, L.; Lu, C.; Yang, J.; Wang, J.; Wang, W. Observational evidence for the Monin-Obukhov similarity under all stability conditions. Adv. Atmos. Sci. 2012, 29, 285–294. [Google Scholar] [CrossRef]
- Andreas, E.L. Estimating Cn2 over snow and sea ice from meteorological data. J. Opt. Soc. Am. A 1988, 5, 481–495. [Google Scholar] [CrossRef]
- Cai, J.; Wu, X.; Li, X.; Huang, H.; Qing, C. Estimation model of atmospheric optical turbulence and its similarity functions. High Power Laser Part. Beams (China) 2016, 28, 1–5. [Google Scholar]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Wyngaard, J.C.; Izumi, Y.; Collins, J.; Stuart, A. Behavior of the refractive-index-structure parameter near the ground*. J. Opt. Soc. Am. 1971, 61, 1646–1650. [Google Scholar] [CrossRef]
- Wyngaard, J.C. On Surface Layer Turbulence.Workshop on Micrometeorology; American Meteorological Society: Boston, MA, USA, 1973; pp. 101–149. [Google Scholar]
- Yuan, R.; Zeng, Z.; Ma, C. Estimation Optical Turbulence by Meteorology Factors. Chin. J. Quantum Electron. 2001, 18, 87–91. [Google Scholar]
- Andreas, E.L. Atmospheric stability from scintillation measurements. Appl. Optics 1988, 27, 2241–2246. [Google Scholar] [CrossRef] [PubMed]
- Bruin, H.A.R.; Kohsiek, W.; Hurk, B.J.J.M. A verification of some methods to determine the fluxes of momentum, sensible heat, and water vapour using standard deviation and structure parameter of scalar meteorological quantities. Bound.-Layer Meteor. 1993, 63, 231–257. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E.; Henk, A.R.; Bruin, D. Monin-Obukhov similarity functions for the structure parameters of temperature and humidity. Bound.-Layer Meteorol. 2012, 145, 45–67. [Google Scholar] [CrossRef]
- Thiermann, V.; Grassl, H. The measurement of turbulent surface-layer fluxes by use of bichromatic scintillation. Bound.-Layer Meteor. 1992, 58, 367–389. [Google Scholar] [CrossRef]
- Braam, M.; Bosveld, F.C.; Moene, A.F. On Monin–Obukhov scaling in and above the atmospheric surface layer: The complexities of elevated scintillometer measurements. Bound.-Layer Meteorol. 2012, 144, 157–177. [Google Scholar] [CrossRef]
- Wang, L.; Hu, N.; Wang, Y.; Wang, L.; Zhao, X.; Liu, S. Comparative analysis of sensible heat flux observed by large aperture scintillometer and eddy-covariance system in Nanjing. Chin. J. Ecol. 2020, 39, 315–325. [Google Scholar]
- Ding, X.B.; Zou, Y.F.; Li, C.Y.; Jian, W. Study of the Ultrasonic Three-Dimensional Wind Speed Measurement Methods Based on the Phase Difference. In Proceedings of the 2016 Sixth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 21–23 July 2016. [Google Scholar]
- Zhou, X.; Yang, Q.; Zhen, X.; Li, Y.; Hao, G.; Shen, H.; Gao, T.; Sun, Y.; Ning, Z. Recovery of the three-dimensional wind and sonic temperature data from a physically deformed sonic anemometer. Atmos. Meas. Tech. 2018, 11, 5981–6002. [Google Scholar] [CrossRef]
- Ma, Y.M.; Hu, Z.Y.; Xie, Z.P.; Ma, W.Q.; Wang, B.B.; Chen, X.L.; Li, M.S.; Zhong, L.; Sun, F.L.; Gu, L.L.; et al. A long-term (2005-2016) dataset of hourly integrated land-atmosphere interaction observations on the Tibetan Plateau. Earth Syst. Sci. Data 2020, 12, 2937–2957. [Google Scholar] [CrossRef]
- Xiao, L.; Weng, N.; Ma, C. Embedded micro-thermal meter. 2004. [Google Scholar]
- Weng, N.; Xiao, L.; Gong, Z. Refractive index structure constant profile and the average model. J. Atmos. Environ. Opt. 2007, 2, 16–22. [Google Scholar]
- Qing, C.; Wu, X.Q.; Huang, H.H.; Tian, Q.G.; Zhu, W.Y.; Rao, R.Z.; Li, X.B. Estimating the surface layer refractive index structure constant over snow and sea ice using Monin-Obukhov similarity theory with a mesoscale atmospheric model. Opt. Express 2016, 24, 20424–20436. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, Y.; Wang, F.F.; Li, X.B.; Cui, S.C.; Zhang, Z.H.; Wu, X.Q.; Weng, N.Q.; Luo, T.; Huang, Y.B. Characteristics of the vertical structure of the atmospheric turbulence in the Tibetan Plateau. Sci. China-Earth Sci. 2022, 65, 1368–1378. [Google Scholar] [CrossRef]
- Nosov, V.; Lukin, V.; Nosov, E.; Torgaev, A.; Bogushevich, A. Measurement of Atmospheric Turbulence Characteristics by the Ultrasonic Anemometers and the Calibration Processes. Atmosphere 2019, 10, 460. [Google Scholar] [CrossRef]
- Shikhovtsev, A.; Kovadlo, P.; Lukin, V.; Nosov, V.; Kiselev, A.; Kolobov, D.; Kopylov, E.; Shikhovtsev, M.; Avdeev, F. Statistics of the Optical Turbulence from the Micrometeorological Measurements at the Baykal Astrophysical Observatory Site. Atmosphere 2019, 10, 661. [Google Scholar] [CrossRef]
- Tatarski, V.I. Wave Propagation in a Turbulent Medium; Courier Dover: Mineola, NY, USA, 1961. [Google Scholar]
- Frehlich, R.; Sharman, R.; Vandenberghe, F.; Yu, W.; Jumper, G. Estimates of Cn2 from numerical weather prediction model output and comparison with thermosonde data. J. Appl. Meteorol. Climatol. 2009, 49, 1742–1755. [Google Scholar] [CrossRef]
- Friehe, C.A. Estimation of the refractive-index temperature structure parameter over the ocean. Appl. Optics 1977, 16, 334–340. [Google Scholar] [CrossRef]
- Li, Y.; Xu, D. A method for calculating U* from data measured by a ship-borne supersonic anemometer. Period. Ocean. Univ. China 2006, 13–19. Available online: https://www.cnki.com.cn/Article/CJFDTotal-QDHY2006S2002.htm (accessed on 29 November 2022).
- Wang, J.; Duan, Z.; Yao, X.; Gao, H. Correction of ship-based turbulent wind velocity and characterization of turbulence in the Northwest Pacific. J. Trop. Oceanogr. 2013, 32, 9–15. [Google Scholar]
- Duan, Z.; Gao, H.; Gao, Z. The moving ship-based eddy covariance measurement of atmospheric turbulence in the North Yellow Sea. Period. Ocean. Univ. China 2014, 44, 81–88. [Google Scholar] [CrossRef]
- Meng, X.; Liu, H.; Du, Q.; Liu, Y.; Xu, L. Factors controlling the latent and sensible heat fluxes over Erhai Lake under different atmospheric surface layer stability conditions. Atmos. Ocean. Sci. Lett. 2020, 13, 400–406. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, R.; Shi, R.; He, Y.; Chen, J.; Wang, D.; Xie, Q. A study of data processing and quality assessment of the eddy convariance system off Yongxing Island. J. Trop. Oceanogr. 2017, 36, 48–59. [Google Scholar]
- Zhang, H. Basis of Atmospheric Turbulence; Peking University Press: Beijing, China, 2014. [Google Scholar]
- Liu, Y.; Li, S.; Lu, S.; Ao, Y.; Gao, Y. Comparison of flux correction methods for eddy-covariance measurement. Plateau Meteorol. 2013, 32, 1704–1711. [Google Scholar]
- Wang, J.; Wang, W.; Ao, Y.; Sun, F.; Wang, S. Turbulence flux measurements under complicated conditions. Adv. Earth Sci. 2007, 22, 791–797. [Google Scholar]
- Vickers, D.; Mahrt, L. Quality Control and Flux Sampling Problems for Tower and Aircraft Data. J. Atmos. Ocean. Technol. 1997, 14, 514–526. [Google Scholar] [CrossRef]
- Tunick, A. Statistical analysis of optical turbulence intensity over a 2.33 km propagation path. Opt. Express 2007, 15, 3619–3628. [Google Scholar] [CrossRef]
- Liu, H.; Hong, Z. Turbulent characteristics in the surface layer over gerze area in the Tibetan Plateau. Chin. J. Atmos. Sci. 2000, 24, 289–300. [Google Scholar]
- Guo, W.; Liu, S.; Liu, S.; Xu, Z. Analysis on the Applicability of similarity theory in large aperure scintillometer obeservation. Plateau Meteorol. 2013, 32, 944–955. [Google Scholar]
- Frederickson, P.A.; Hammel, S.; Tsintikidis, D. Improving bulk Cn2 models for over-ocean applications through new determinations of the dimensionless temperature structure parameter. In Proceedings of SPIE–The International Society for Optical Engineering; SPIE: Bellingham, WA, USA, 2007; p. 6708. [Google Scholar]
- Li, Y.; Huang, X.; Yu, J.; Zhao, Y. Comparison and improvement of the atmospheric optical turbulence model in near sea surface. Acta Opt. Sin. 2012, 32, 6. [Google Scholar]
- Liang, J.; Zhang, L.; Bao, J.; Zhao, S.; Huagn, J.; Zhang, W. Turbulence Influenced by Mesoscale Motions in the Stable Boundary Layer over Complex Terrain of the Loess Plateau. Chin. J. Atmos. Sci. 2013, 37, 113–123. [Google Scholar]
- Mahrt, L.; Thomas, C.K.; Prueger, J.H. Space-time structure of mesoscale motions in the stable boundary layer. Q. J. R. Meteorol. Soc. 2009, 135, 67–75. [Google Scholar] [CrossRef]
- Qing, C.; Wu, X.; Li, X.; Zhu, W.; Qiao, C.; Rao, R.; Mei, H. Use of weather research and forecasting model outputs to obtain near-surface refractive index structure constant over the ocean. Opt. Express 2016, 24, 13303–13315. [Google Scholar] [CrossRef]
- Curley, M.J.; Peterson, B.H.; Wang, J.C.; Sarkisov, S.S.; Sarkisov, S.S.; Edlin, G.R.; Snow, R.A.; Rushing, J.F. Statistical analysis of cloud-cover mitigation of optical turbulence in the boundary layer. Opt. Express 2006, 14, 8929–8946. [Google Scholar] [CrossRef]
- van Meijgaard, E.; van Ulden, A.P. A first order mixing-condensation scheme for nocturnal stratocumulus. Atmos. Res. 1998, 45, 253–273. [Google Scholar] [CrossRef]
- Siebert, H.; Szodry, K.E.; Egerer, U.; Wehner, B.; Henning, S.; Chevalier, K.; Lückerath, J.; Welz, O.; Weinhold, K.; Lauermann, F. Observations of Aerosol, Cloud, Turbulence, and Radiation Properties at the Top of the Marine Boundary Layer over the Eastern North Atlantic Ocean: The ACORES Campaign. Am. Meteorol. Soc. 2021, 102, E123–E147. [Google Scholar] [CrossRef]
- Sun, W.Q.; Li, J.; Wang, B. Reducing the biases in shortwave cloud radiative forcing in tropical and subtropical regions from the perspective of boundary layer processes. Sci. China-Earth Sci. 2016, 59, 1427–1439. [Google Scholar] [CrossRef]
| Formula | a | b | Model |
|---|---|---|---|
| 4.9 | 7 | Wyngaard (1973) | |
| 4.9 | 6.1 | Andreas (1988) | |
| 4.9 | 9 | De Bruin (1993) | |
| 6.7 | 14.9 | Dan Li (2012) | |
| 7 | 75 | T and G (1992) |
| Formula | a | b | Model |
|---|---|---|---|
| 4.9 | 2.4 | Wyngaard (1973) | |
| 4.9 | 2.2 | Andreas (1988) | |
| 4.9 | 0 | De Bruin (1993) | |
| 6.7 | 1.3 | Dan Li (2012) | |
| 7 | 20 | T and G (1992) |
| JF (Winter) | MAM (Spring) | JJA (Summer) | SON (Autumn) | |||||
|---|---|---|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | RMSE | |||||
| Wyngaard 73 | 0.83 | 0.76 | 0.89 | 0.56 | 0.84 | 0.50 | 0.62 | 0.96 |
| Andreas 88 | 0.84 | 0.76 | 0.90 | 0.56 | 0.85 | 0.49 | 0.64 | 0.94 |
| Theirmann 92 | 0.85 | 0.82 | 0.89 | 0.60 | 0.85 | 0.49 | 0.63 | 1.00 |
| De Bruin 93 | 0.87 | 0.65 | 0.90 | 0.50 | 0.89 | 0.45 | 0.78 | 0.73 |
| Dan Li 12 | 0.85 | 0.70 | 0.90 | 0.53 | 0.86 | 0.47 | 0.68 | 0.86 |
| New fit | 0.94 | 0.32 | 0.94 | 0.41 | 0.95 | 0.46 | 0.89 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Zhang, K.; Sun, G.; Liu, Q.; Li, X.; Luo, T.
Study of the
Wang F, Zhang K, Sun G, Liu Q, Li X, Luo T.
Study of the
Wang, Feifei, Kun Zhang, Gang Sun, Qing Liu, Xuebin Li, and Tao Luo.
2023. "Study of the
Wang, F., Zhang, K., Sun, G., Liu, Q., Li, X., & Luo, T.
(2023). Study of the







