Deformation Monitoring and Trend Analysis of Reservoir Bank Landslides by Combining Time-Series InSAR and Hurst Index
Abstract
1. Introduction
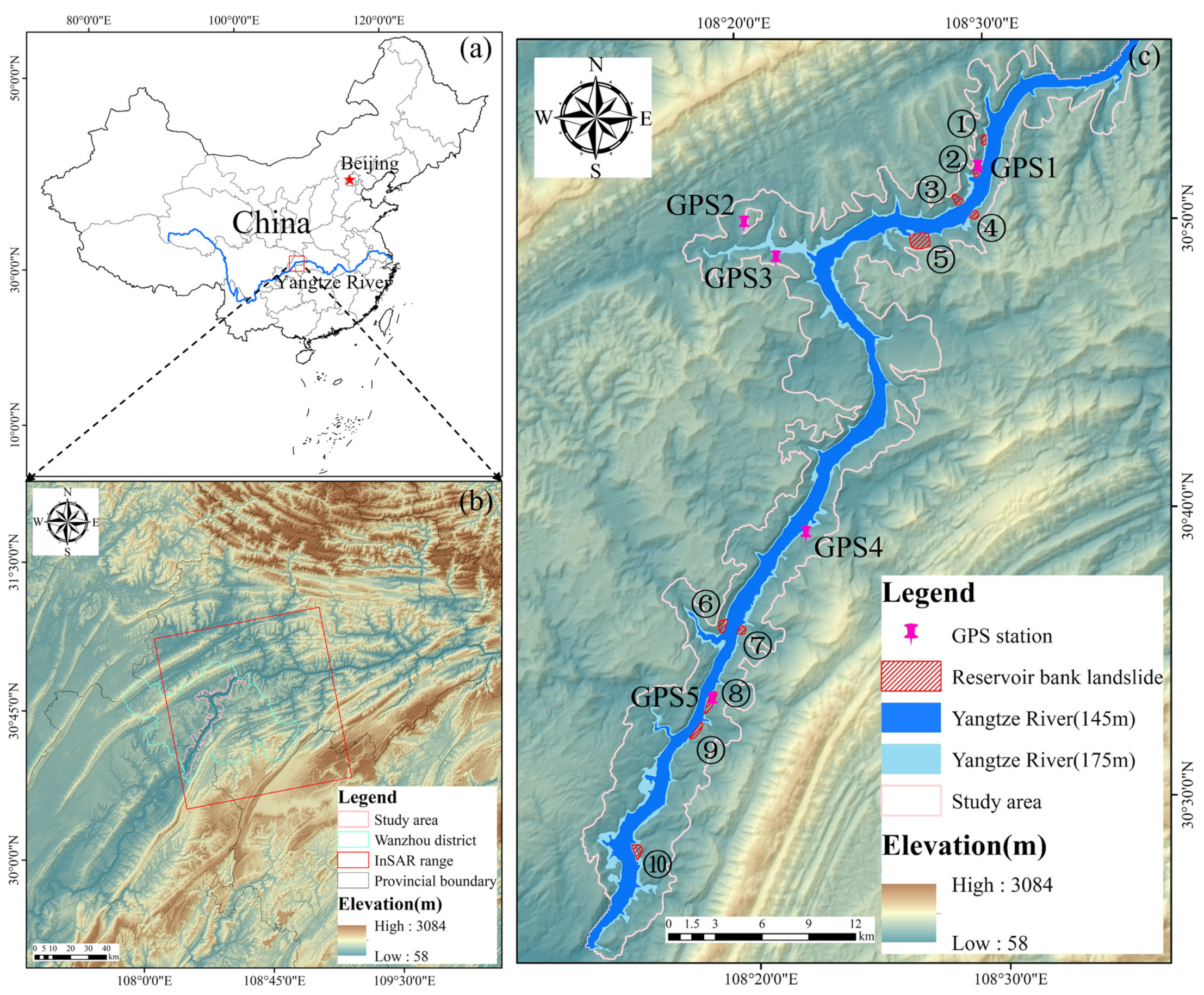
2. Study Area and Datasets
2.1. Study Area
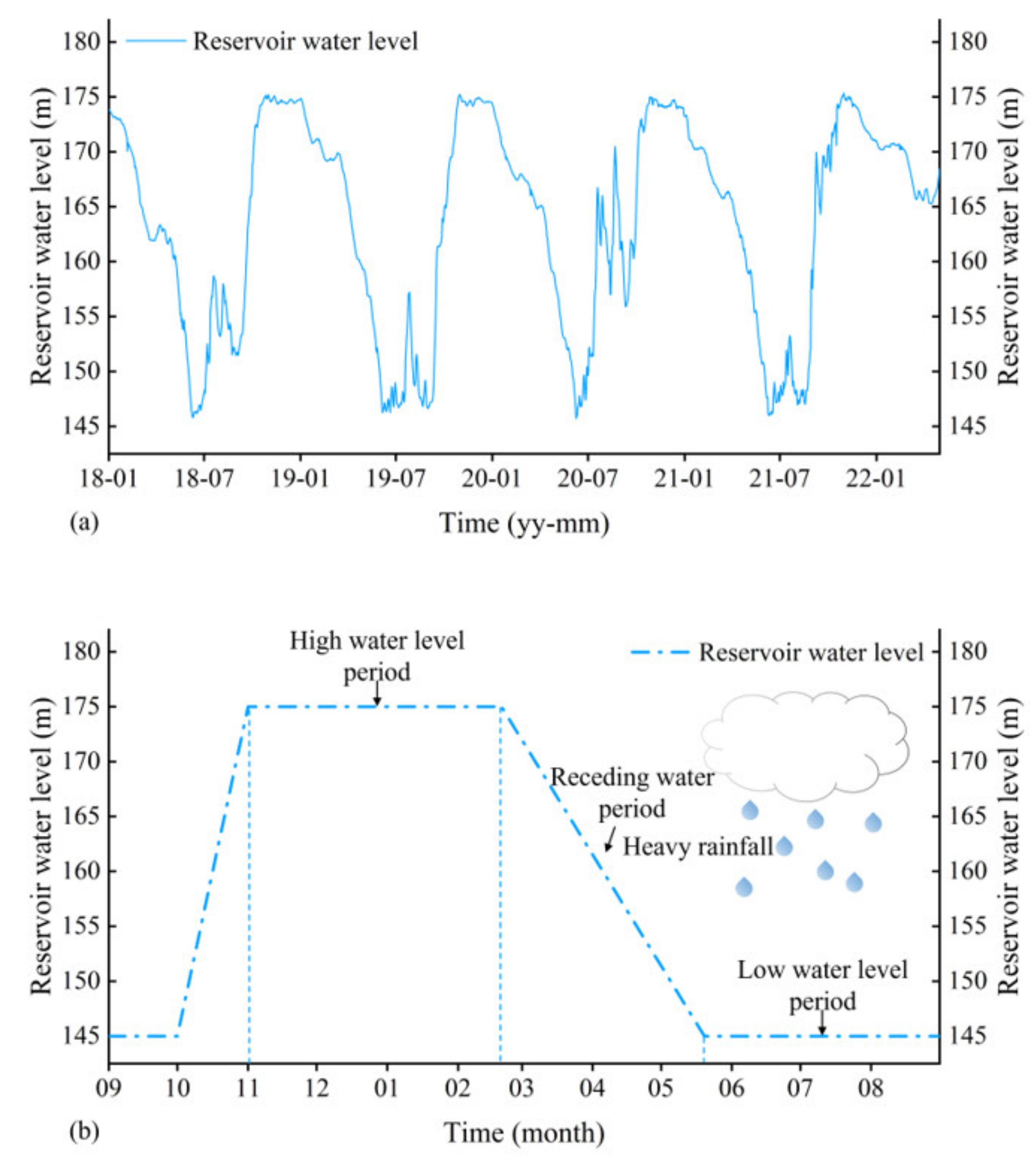
2.2. Datasets
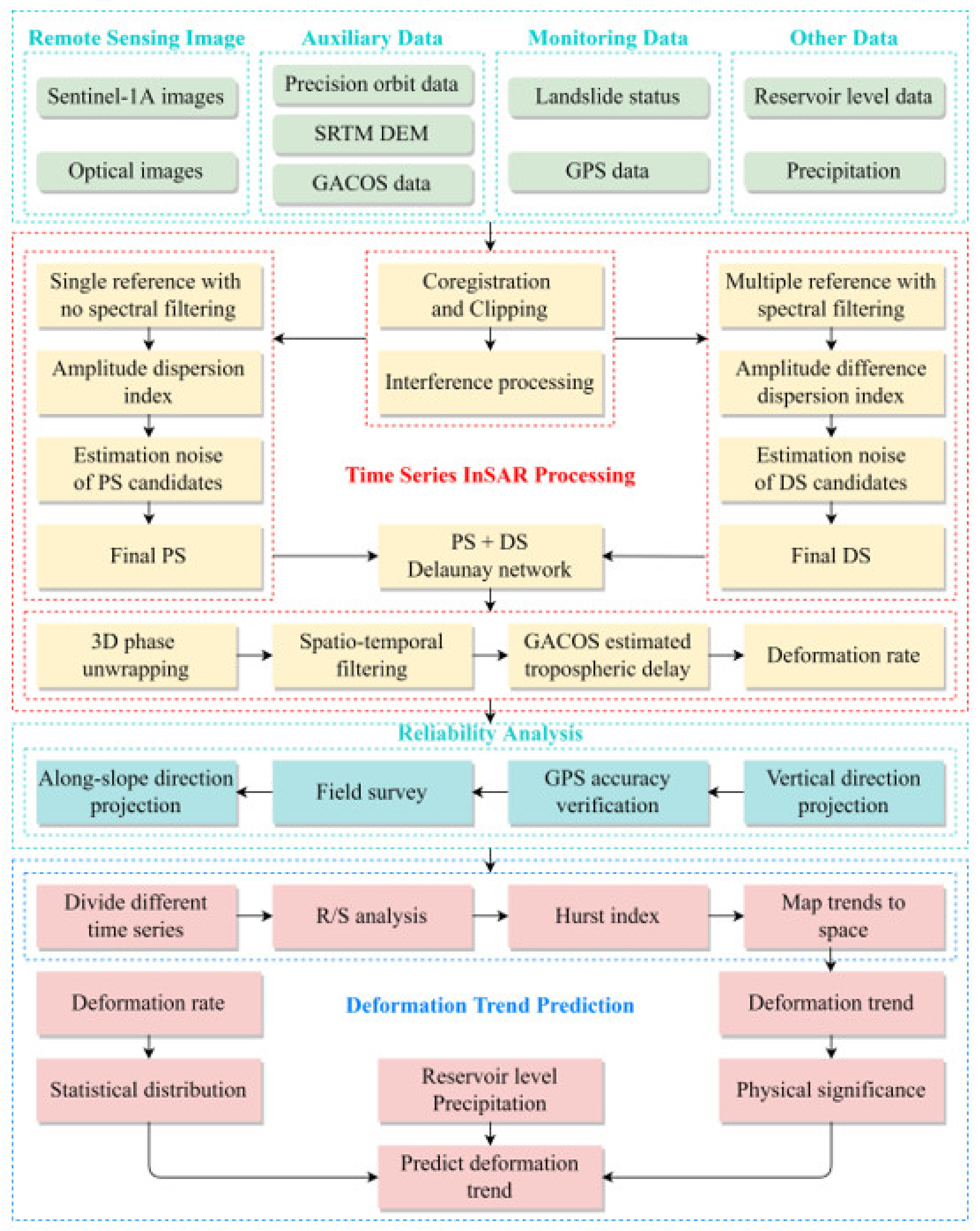
3. Methods
3.1. PS and DS Selection
3.2. Time-Series InSAR Processing
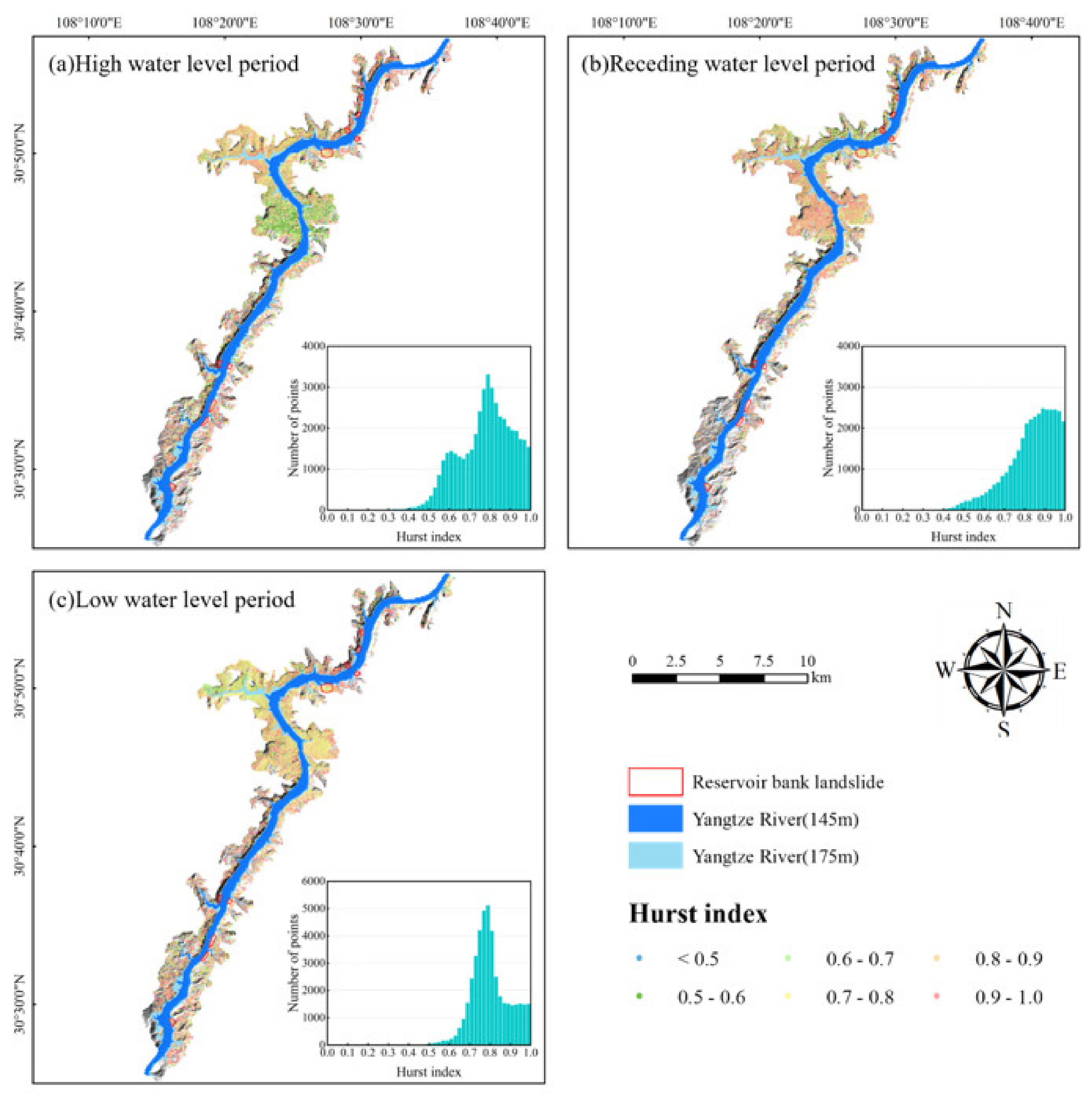
3.3. Hurst Index
3.4. Deformation Trend Prediction
4. Results and Analysis
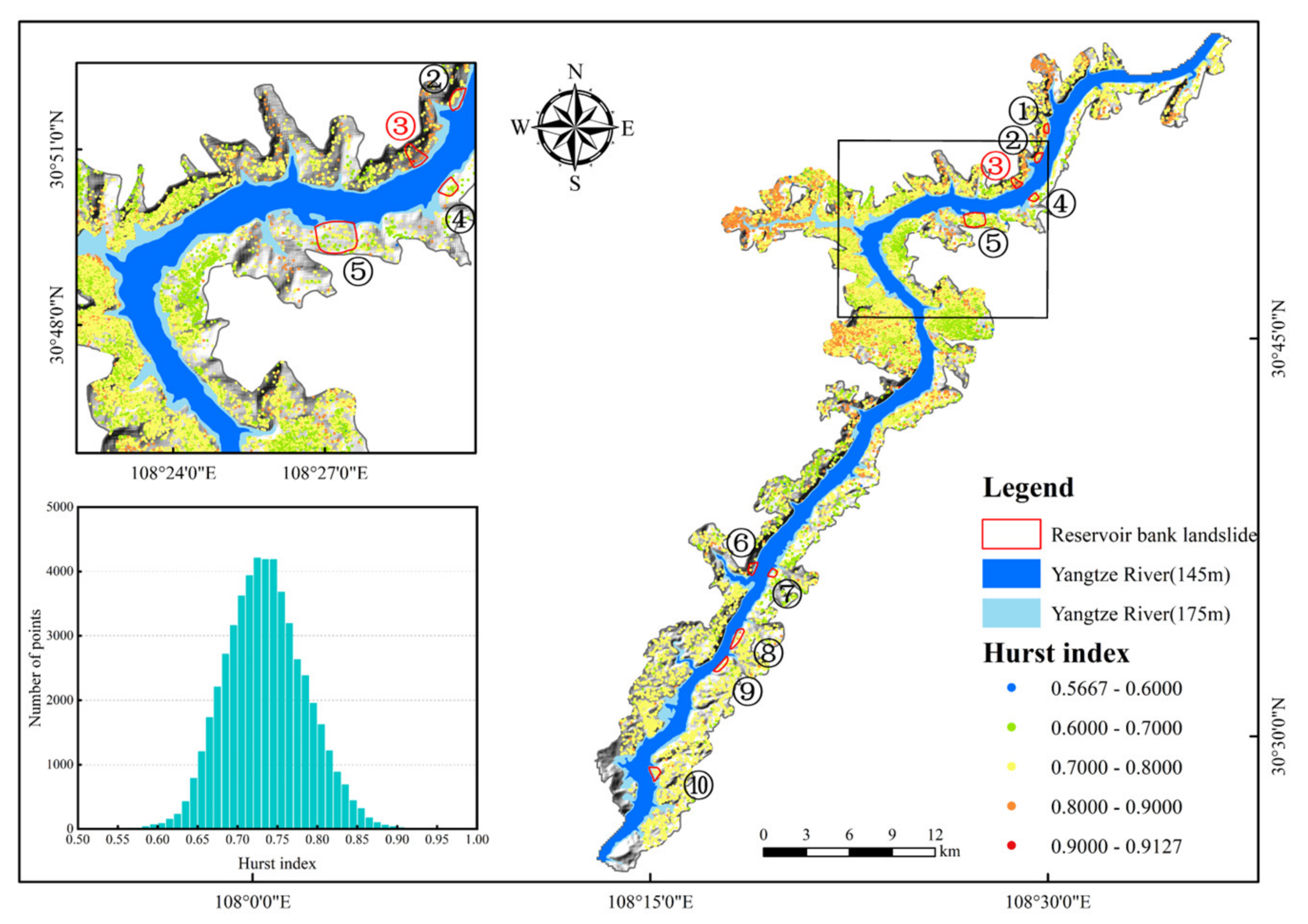
4.1. Slope Deformation Rate
4.2. Slope Deformation Trend Analysis
4.3. Deformation Trend Analysis of Sifangbei Landslide
5. Discussion
5.1. Reliability Analysis of Slope Deformation Trend
- (a)
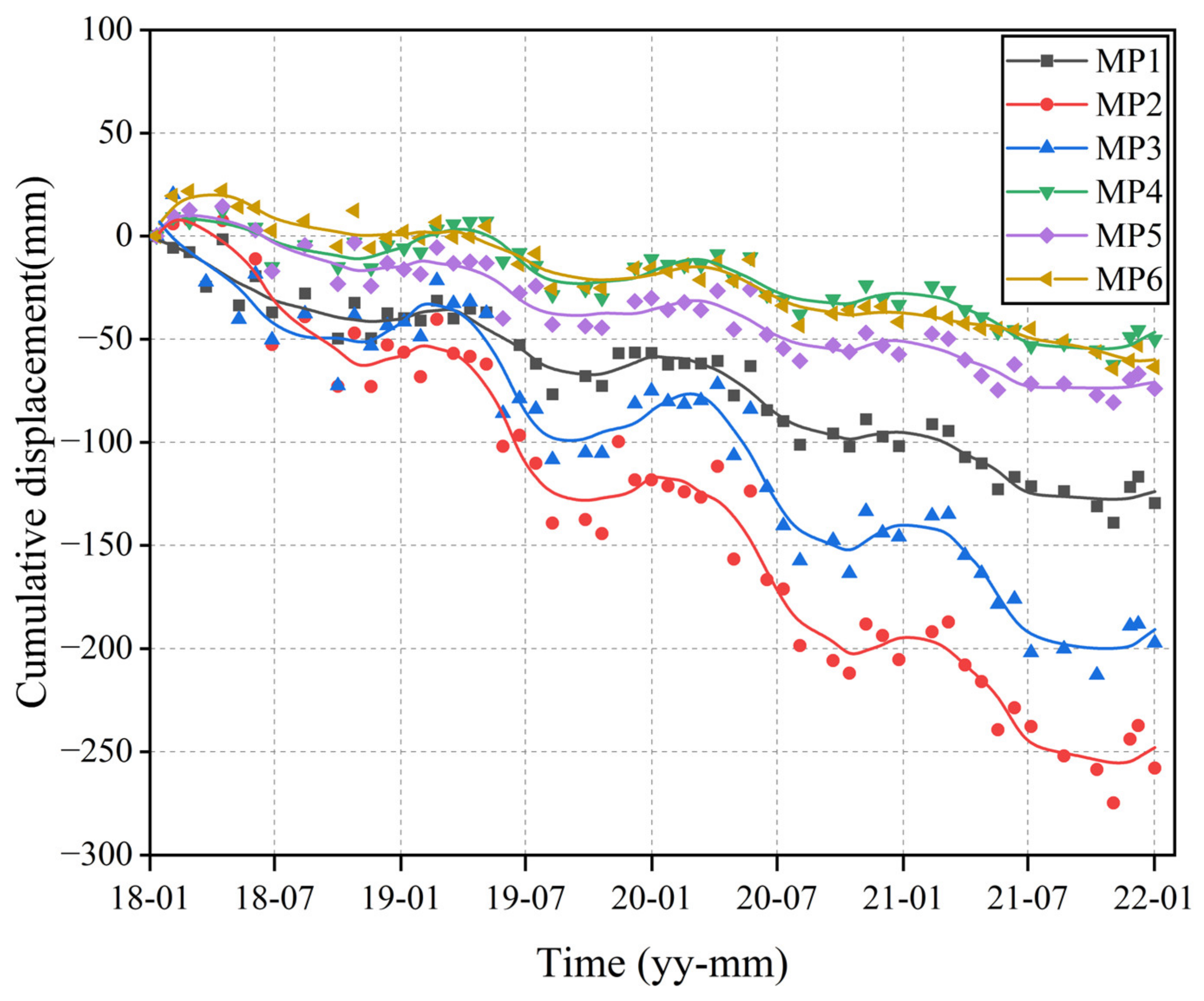
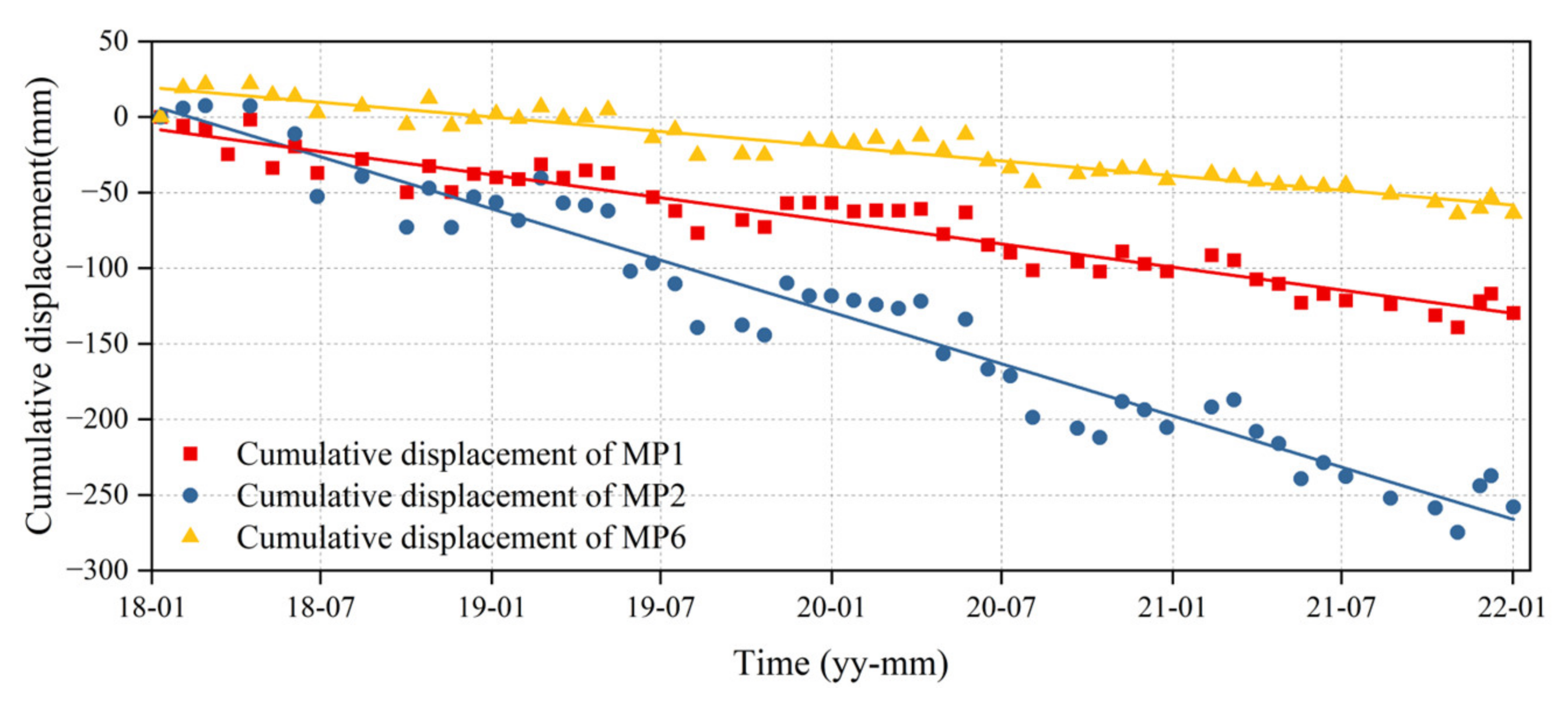
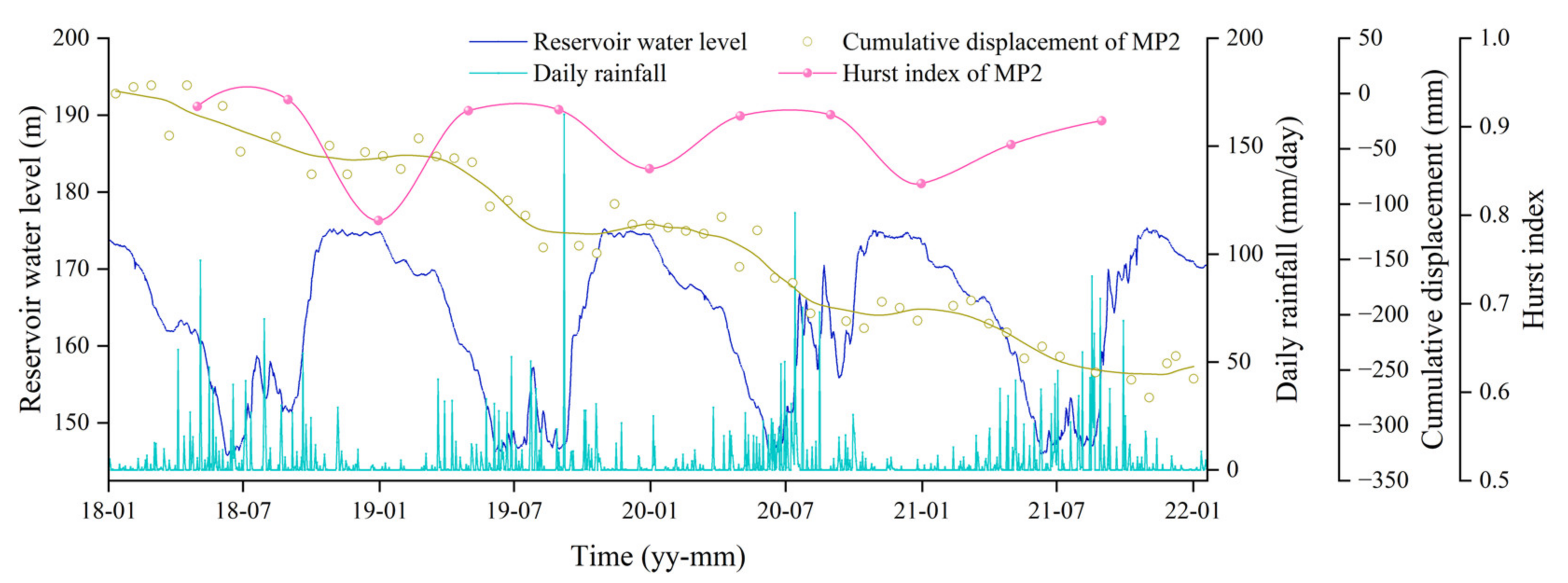
- Consistency between the strength of the deformation trend and the magnitude of the Hurst index at the Sifangbei landslide measurement points. The cumulative displacement curves and the corresponding Hurst index value at MP1, MP2, and MP6 are shown in Figure 10. We found that Hurst index values calculated using measurement points in different positions were different but presented a certain regularity. MP2 is at the leading edge of the Sifangbei landslide and had the largest cumulative deformation, with a corresponding Hurst index value of 0.8833. The cumulative deformation of MP1 and MP6 decreased in turn, and the trend line gradually slowed down, with corresponding Hurst index values of 0.8698 and 0.8082, respectively. Through comparison, it was found that the deformation trend of the measurement points was consistent with the Hurst index, which can, therefore, effectively represent the deformation trend of the landslide.
- (b)
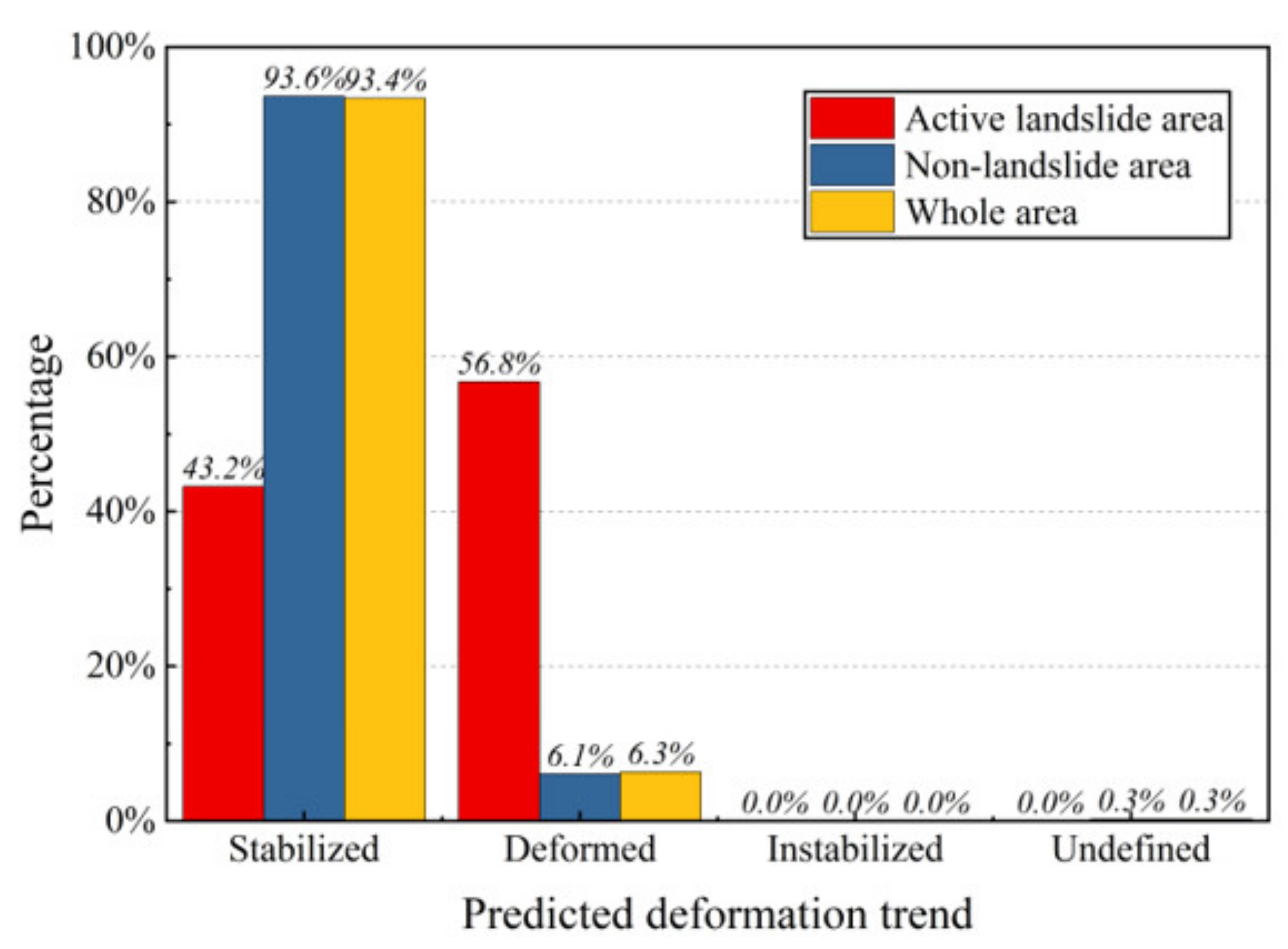
- Consistency between the predicted deformation trend percentage and the actual situation in the active landslide area and the non-landslide area. The percentages of the four deformation states predicted for the active landslide area and the non-landslide area were counted (Figure 11), and it was found that 93.7% of the non-landslide areas were stabilized, while the deformation areas only accounted for 6.1%. In the known active landslide areas, the stabilized and deformed areas accounted for 43.2% and 56.8%, respectively. From the collected data (Table 1), it can be seen that the deformation rates of the Datangbang landslide and the Wuzhuba landslide were low in 2021. The predicted results also indicated that they would gradually stabilize. The deformation ratio of the active landslide area to the non-landslide area was in line with the reality detailed in Table 1.
5.2. Spatial and Temporal Differences of Slope Deformation Trend
5.3. Relationship between Landslide Deformation Trend and Influencing Factors
5.4. Limitations and Prospects
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schuster, R.L. Reservoir-induced landslides. Bull. Int. Assoc. Eng. Geol. 1979, 20, 8–15. [Google Scholar] [CrossRef]
- Reyes-Carmona, C.; Barra, A.; Galve, J.; Monserrat, O.; Pérez-Peña, J.; Mateos, R.; Notti, D.; Ruano, P.; Millares, A.; López-Vinielles, J.; et al. Sentinel-1 DInSAR for monitoring active landslides in critical infrastructures: The case of the rules reservoir (Southern Spain). Remote Sens. 2020, 12, 809. [Google Scholar] [CrossRef]
- Li, Y.; Chen, L.; Yin, K.; Zhang, Y.; Gui, L. Quantitative risk analysis of the hazard chain triggered by a landslide and the generated tsunami in the three gorges reservoir area. Landslides 2021, 18, 667–680. [Google Scholar] [CrossRef]
- Ouyang, C.; An, H.; Zhou, S.; Wang, Z.; Su, P.; Wang, D.; Cheng, D.; She, J. Insights from the failure and dynamic characteristics of two sequential landslides at Baige Village along the Jinsha River, China. Landslides 2019, 16, 1397–1414. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, C.; Zhang, Q.; Lu, Z.; Li, Z.; Yang, C.; Zhu, W.; Liu-Zeng, J.; Chen, L.; Liu, C. Integration of Sentinel-1 and ALOS/PALSAR-2 SAR datasets for mapping active landslides along the Jinsha River Corridor, China. Eng. Geol. 2021, 284, 106033. [Google Scholar] [CrossRef]
- Panizzo, A.; De Girolamo, P.; Di Risio, M.; Maistri, A.; Petaccia, A. Great landslide events in italian artificial reservoirs. Nat. Hazards Earth Syst. Sci. 2005, 5, 733–740. [Google Scholar] [CrossRef]
- Paronuzzi, P.; Rigo, E.; Bolla, A. Influence of filling–drawdown cycles of the vajont reservoir on mt. toc slope stability. Geomorphology 2013, 191, 75–93. [Google Scholar] [CrossRef]
- Wang, F.-W.; Zhang, Y.-M.; Huo, Z.-T.; Matsumoto, T.; Huang, B.-L. The July 14, 2003 Qianjiangping Landslide, Three Gorges Reservoir, China. Landslides 2004, 1, 157–162. [Google Scholar] [CrossRef]
- Gutiérrez, F.; Lucha, P.; Galve, J.P. Reconstructing the Geochronological Evolution of Large Landslides by Means of the Trenching Technique in the Yesa Reservoir (Spanish Pyrenees). Geomorphology 2010, 124, 124–136. [Google Scholar] [CrossRef]
- Liang, X.; Gui, L.; Wang, W.; Du, J.; Ma, F.; Yin, K. Characterizing the Development Pattern of a Colluvial Landslide Based on Long-Term Monitoring in the Three Gorges Reservoir. Remote Sens. 2021, 13, 224. [Google Scholar] [CrossRef]
- Li, D.; Yin, K.; Leo, C. Analysis of Baishuihe landslide influenced by the effects of reservoir water and rainfall. Environ. Earth Sci. 2010, 60, 677–687. [Google Scholar] [CrossRef]
- Huang, F.; Chen, L.; Yin, K.; Huang, J.; Gui, L. Object-oriented change detection and damage assessment using high-resolution remote sensing images, Tangjiao Landslide, Three Gorges Reservoir, China. Environ. Earth Sci. 2018, 77, 183. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Huo, Z.; Peng, X.; Araiba, K.; Wang, G. Movement of the Shuping Landslide in the First Four Years after the Initial Impoundment of the Three Gorges Dam Reservoir, China. Landslides 2008, 5, 321–329. [Google Scholar] [CrossRef]
- Du, J.; Yin, K.; Lacasse, S. Displacement Prediction in Colluvial Landslides, Three Gorges Reservoir, China. Landslides 2013, 10, 203–218. [Google Scholar] [CrossRef]
- Intrieri, E.; Raspini, F.; Fumagalli, A.; Lu, P.; Del Conte, S.; Farina, P.; Allievi, J.; Ferretti, A.; Casagli, N. The Maoxian Landslide as Seen from Space: Detecting Precursors of Failure with Sentinel-1 Data. Landslides 2018, 15, 123–133. [Google Scholar] [CrossRef]
- Solari, L.; Del Soldato, M.; Raspini, F.; Barra, A.; Bianchini, S.; Confuorto, P.; Casagli, N.; Crosetto, M. Review of Satellite Interferometry for Landslide Detection in Italy. Remote Sens. 2020, 12, 1351. [Google Scholar] [CrossRef]
- Mondini, A.C.; Guzzetti, F.; Chang, K.-T.; Monserrat, O.; Martha, T.R.; Manconi, A. Landslide Failures Detection and Mapping Using Synthetic Aperture Radar: Past, Present and Future. Earth-Sci. Rev. 2021, 216, 103574. [Google Scholar] [CrossRef]
- Zhou, C.; Cao, Y.; Yin, K.; Wang, Y.; Shi, X.; Catani, F.; Ahmed, B. Landslide Characterization Applying Sentinel-1 Images and InSAR Technique: The Muyubao Landslide in the Three Gorges Reservoir Area, China. Remote Sens. 2020, 12, 3385. [Google Scholar] [CrossRef]
- Mishra, V.; Jain, K. Satellite Based Assessment of Artificial Reservoir Induced Landslides in Data Scarce Environment: A Case Study of Baglihar Reservoir in India. J. Appl. Geophys. 2022, 205, 104754. [Google Scholar] [CrossRef]
- Fruneau, B.; Achache, J.; Delacourt, C. Observation and Modelling of the Saint-Tienne-de-Tinée Landslide Using SAR Interferometry. Tectonophysics 1996, 265, 181–190. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, S.; Tao, Q.; Liu, G.; Wang, L.; Wang, F. Accuracy Verification and Correction of D-InSAR and SBAS-InSAR in Monitoring Mining Surface Subsidence. Remote Sens. 2021, 13, 4365. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 13. [Google Scholar] [CrossRef]
- Del Soldato, M.; Riquelme, A.; Bianchini, S.; Tomàs, R.; Di Martire, D.; De Vita, P.; Moretti, S.; Calcaterra, D. Multisource Data Integration to Investigate One Century of Evolution for the Agnone Landslide (Molise, Southern Italy). Landslides 2018, 15, 2113–2128. [Google Scholar] [CrossRef]
- Solari, L.; Barra, A.; Herrera, G.; Bianchini, S.; Monserrat, O.; Béjar-Pizarro, M.; Crosetto, M.; Sarro, R.; Moretti, S. Fast Detection of Ground Motions on Vulnerable Elements Using Sentinel-1 InSAR Data. Geomat. Nat. Hazards Risk 2018, 9, 152–174. [Google Scholar] [CrossRef]
- Wasowski, J.; Pisano, L. Long-Term InSAR, Borehole Inclinometer, and Rainfall Records Provide Insight into the Mechanism and Activity Patterns of an Extremely Slow Urbanized Landslide. Landslides 2020, 17, 445–457. [Google Scholar] [CrossRef]
- Fobert, M.-A.; Singhroy, V.; Spray, J.G. InSAR Monitoring of Landslide Activity in Dominica. Remote Sens. 2021, 13, 815. [Google Scholar] [CrossRef]
- Lu, P.; Catani, F.; Tofani, V.; Casagli, N. Quantitative Hazard and Risk Assessment for Slow-Moving Landslides from Persistent Scatterer Interferometry. Landslides 2014, 11, 685–696. [Google Scholar] [CrossRef]
- Hurst, H.E. Methods of using long-term storage in reservoirs. Proc. Inst. Civ. Eng. 1956, 5, 519–543. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Albulescu, C.T.; Yoon, S.-M. A Multifractal Detrended Fluctuation Analysis of Financial Market Efficiency: Comparison Using Dow Jones Sector ETF Indices. Phys. A Stat. Mech. Its Appl. 2017, 483, 182–192. [Google Scholar] [CrossRef]
- Qu, S.; Wang, L.; Lin, A.; Yu, D.; Yuan, M.; Li, C. Distinguishing the Impacts of Climate Change and Anthropogenic Factors on Vegetation Dynamics in the Yangtze River Basin, China. Ecol. Indic. 2020, 108, 105724. [Google Scholar] [CrossRef]
- He, K.; Sun, L.; Wang, S. Displacement Fractal Parameter Hurst Index and Its Application to Prediction of Debris Landslides. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2009, 28, 1107–1115. [Google Scholar]
- Cao, Y.; Yin, K.; Zhou, C. Comprehensive Assessment on Sanzhouxi Landslide Stability Considering Displacement Monitoring. Electron. J. Geotech. Eng. 2013, 18, 5507–5524. [Google Scholar]
- Roccati, A.; Paliaga, G.; Luino, F.; Faccini, F.; Turconi, L. Rainfall Threshold for Shallow Landslides Initiation and Analysis of Long-Term Rainfall Trends in a Mediterranean Area. Atmosphere 2020, 11, 1367. [Google Scholar] [CrossRef]
- Li, H.; Xu, Q.; He, Y.; Fan, X.; Yang, H.; Li, S. Temporal Detection of Sharp Landslide Deformation with Ensemble-Based LSTM-RNNs and Hurst Exponent. Geomat. Nat. Hazards Risk 2021, 12, 3089–3113. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, H.; Wang, S.; Xu, L.; Peng, J. Monitoring and Stability Analysis of the Deformation in the Woda Landslide Area in Tibet, China by the DS-InSAR Method. Remote Sens. 2022, 14, 532. [Google Scholar] [CrossRef]
- Cascini, L.; Fornaro, G.; Peduto, D. Advanced Low- and Full-Resolution DInSAR Map Generation for Slow-Moving Landslide Analysis at Different Scales. Eng. Geol. 2010, 112, 29–42. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, L.; Zhou, C.; Li, M.; Liao, M. Retrieval of Time Series Three-Dimensional Landslide Surface Displacements from Multi-Angular SAR Observations. Landslides 2018, 15, 1015–1027. [Google Scholar] [CrossRef]
- Domino, K. The Use of the Hurst Exponent to Predict Changes in Trends on the Warsaw Stock Exchange. Phys. A Stat. Mech. Its Appl. 2011, 390, 98–109. [Google Scholar] [CrossRef]
- Jiang, L.; Jiapaer, G.; Bao, A.; Guo, H.; Ndayisaba, F. Vegetation Dynamics and Responses to Climate Change and Human Activities in Central Asia. Sci. Total Environ. 2017, 599, 967–980. [Google Scholar] [CrossRef]
- Hooper, A. A Multi-Temporal InSAR Method Incorporating Both Persistent Scatterer and Small Baseline Approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.A. Phase Unwrapping in Three Dimensions with Application to InSAR Time Series. J. Opt. Soc. Am. A 2007, 24, 2737. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z. Generation of Real-time Mode High-resolution Water Vapor Fields from GPS Observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric Synthetic Aperture Radar Atmospheric Correction Using a GPS-Based Iterative Tropospheric Decomposition Model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Herrera, G.; Gutiérrez, F.; García-Davalillo, J.C.; Guerrero, J.; Notti, D.; Galve, J.P.; Fernández-Merodo, J.A.; Cooksley, G. Multi-Sensor Advanced DInSAR Monitoring of Very Slow Landslides: The Tena Valley Case Study (Central Spanish Pyrenees). Remote Sens. Environ. 2013, 128, 31–43. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage of Reservoirs: An Experimental Study. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Mandelbrot, B. Statistical methodology for nonperiodic cycles: From the covariance to R/S analysis. Ann. Econ. Soc. Meas. 1972, 1, 259–290. [Google Scholar]
- Mandelbrot, B.B.; Wallis, J.R. Robustness of the rescaled range r/s in the measurement of noncyclic long run statistical dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar] [CrossRef]
- Necsoiu, M.; McGinnis, R.N.; Hooper, D.M. New insights on the salmon falls creek canyon landslide complex based on geomorphological analysis and multitemporal satellite InSAR techniques. Landslides 2014, 11, 1141–1153. [Google Scholar] [CrossRef]
- López-Vinielles, J.; Fernández-Merodo, J.A.; Ezquerro, P.; García-Davalillo, J.C.; Sarro, R.; Reyes-Carmona, C.; Barra, A.; Navarro, J.A.; Krishnakumar, V.; Alvioli, M.; et al. Combining satellite InSAR, slope units and finite element modeling for stability analysis in mining waste disposal areas. Remote Sens. 2021, 13, 2008. [Google Scholar] [CrossRef]
- Ma, Y.; Li, F.; Wang, Z.; Zou, X.; An, J.; Li, B. Landslide Assessment and Monitoring along the Jinsha River, Southwest China, by Combining InSAR and GPS Techniques. J. Sens. 2022, 2022, 9572937. [Google Scholar] [CrossRef]


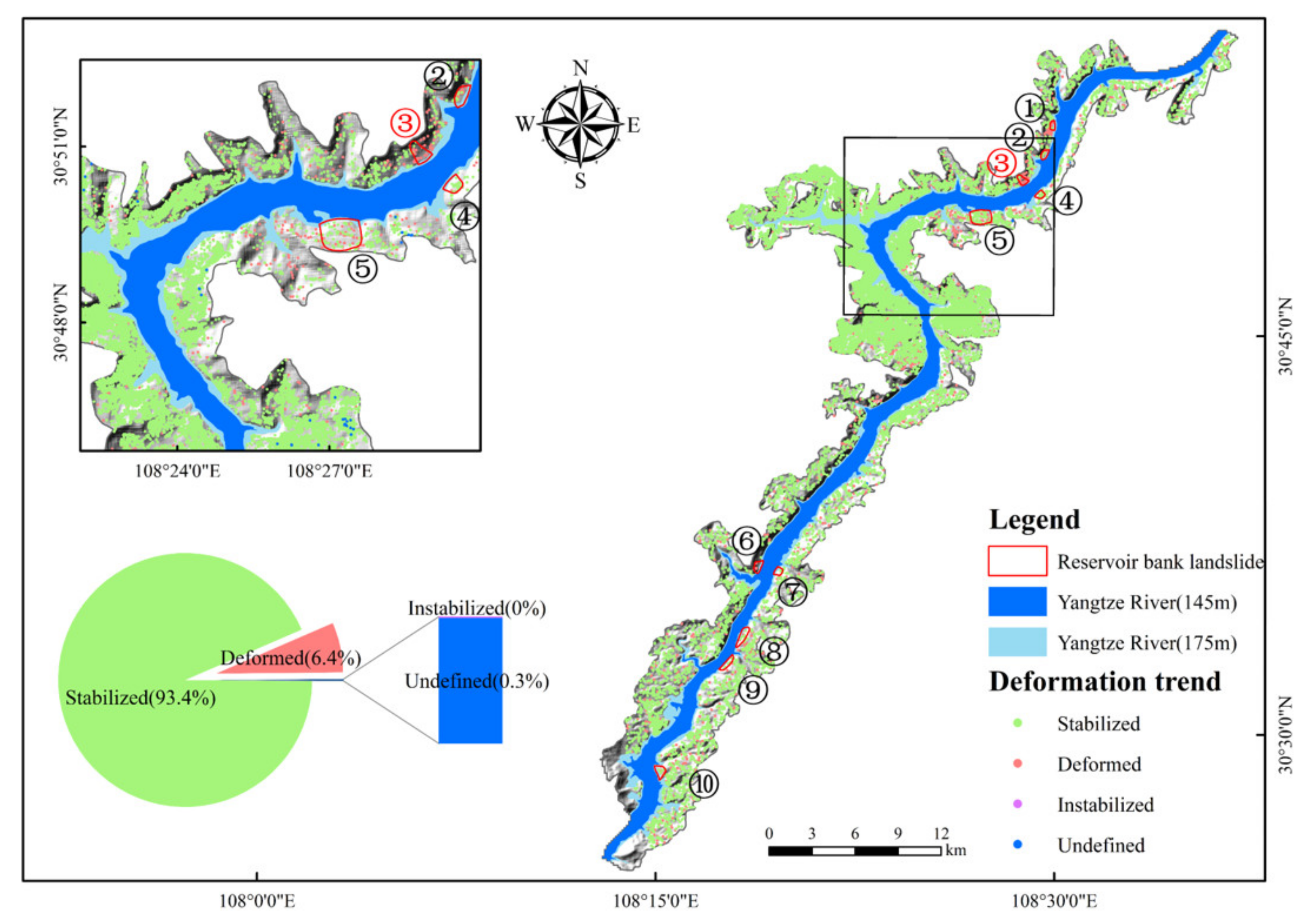

| Number | Landslides | Elevation Range (m) | Average Thickness (m) | Volume (m3) | Deformation Rate in 2021 (mm/yr) | Activity State |
|---|---|---|---|---|---|---|
| ① | Laotangfang landslide | 125–190 | 35.6 | 925 × 104 | −22.6–13 | Active |
| ② | Sharentian landslide | 160–210 | 28 | 750 × 104 | −14.5–6.2 | Active |
| ③ | Sifangbei landslide | 110–335 | 22 | 643.28 × 104 | −86.4–−1.2 | Active |
| ④ | Xiangjiaping landslide | 113–260 | 20 | 660 × 104 | −34.2–−7.5 | Active |
| ⑤ | Tangjiao landslide | 140–320 | 20 | 2672.4 × 104 | −39.6–1.2 | Reactive |
| ⑥ | Rangduchangbei landslide | 165–270 | 25 | 528 × 104 | −408.6–−0.2 | Active |
| ⑦ | Datangbang landslide | 130–270 | 15 | 218 × 104 | −13.4–2.4 | Stabilized |
| ⑧ | Jinjinzi landslide | 110–225 | 30 | 1600 × 104 | −68.9–−9.8 | Active |
| ⑨ | Wuchiba landslide | 160–245 | 10 | 260 × 104 | −12.2–7.2 | Stabilized |
| ⑩ | Zhangjiaci tang landslide | 121–250 | 17 | 952 × 104 | −40.3–−1.6 | Active |
| v | / | ||||
| H | |||||
| Location | GPS | InSAR Deformation Rate | GPS Deformation Rate | Deviation | RMSE |
|---|---|---|---|---|---|
| Active landslide area | GPS1 | −2.15 | 1.21 | 3.36 | 2.55 |
| GPS5 | 0.85 | −3.00 | 3.85 | ||
| Non-landslide area | GPS2 | −11.08 | −12.08 | 1.00 | |
| GPS3 | −0.58 | 1.70 | 2.28 | ||
| GPS4 | −7.28 | −6.82 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, L.; Zhou, C. Deformation Monitoring and Trend Analysis of Reservoir Bank Landslides by Combining Time-Series InSAR and Hurst Index. Remote Sens. 2023, 15, 619. https://doi.org/10.3390/rs15030619
Zhang X, Chen L, Zhou C. Deformation Monitoring and Trend Analysis of Reservoir Bank Landslides by Combining Time-Series InSAR and Hurst Index. Remote Sensing. 2023; 15(3):619. https://doi.org/10.3390/rs15030619
Chicago/Turabian StyleZhang, Xingchen, Lixia Chen, and Chao Zhou. 2023. "Deformation Monitoring and Trend Analysis of Reservoir Bank Landslides by Combining Time-Series InSAR and Hurst Index" Remote Sensing 15, no. 3: 619. https://doi.org/10.3390/rs15030619
APA StyleZhang, X., Chen, L., & Zhou, C. (2023). Deformation Monitoring and Trend Analysis of Reservoir Bank Landslides by Combining Time-Series InSAR and Hurst Index. Remote Sensing, 15(3), 619. https://doi.org/10.3390/rs15030619







