Propagation of Meteorological Drought to Agricultural and Hydrological Droughts in the Tropical Lancang–Mekong River Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Description
2.2.1. Meteorological Reanalysis Data
2.2.2. Land Cover Data
2.2.3. Vegetation and Terrain Data
2.3. Methods
2.3.1. Standardized Drought Indices
2.3.2. Determination of DRT
- The linear method—Pearson correlation coefficient
- 2.
- The nonlinear method—mutual information
2.3.3. Determination of the Relationship between Different Types of Droughts
2.3.4. Variable Importance Based on Random Forest
3. Results
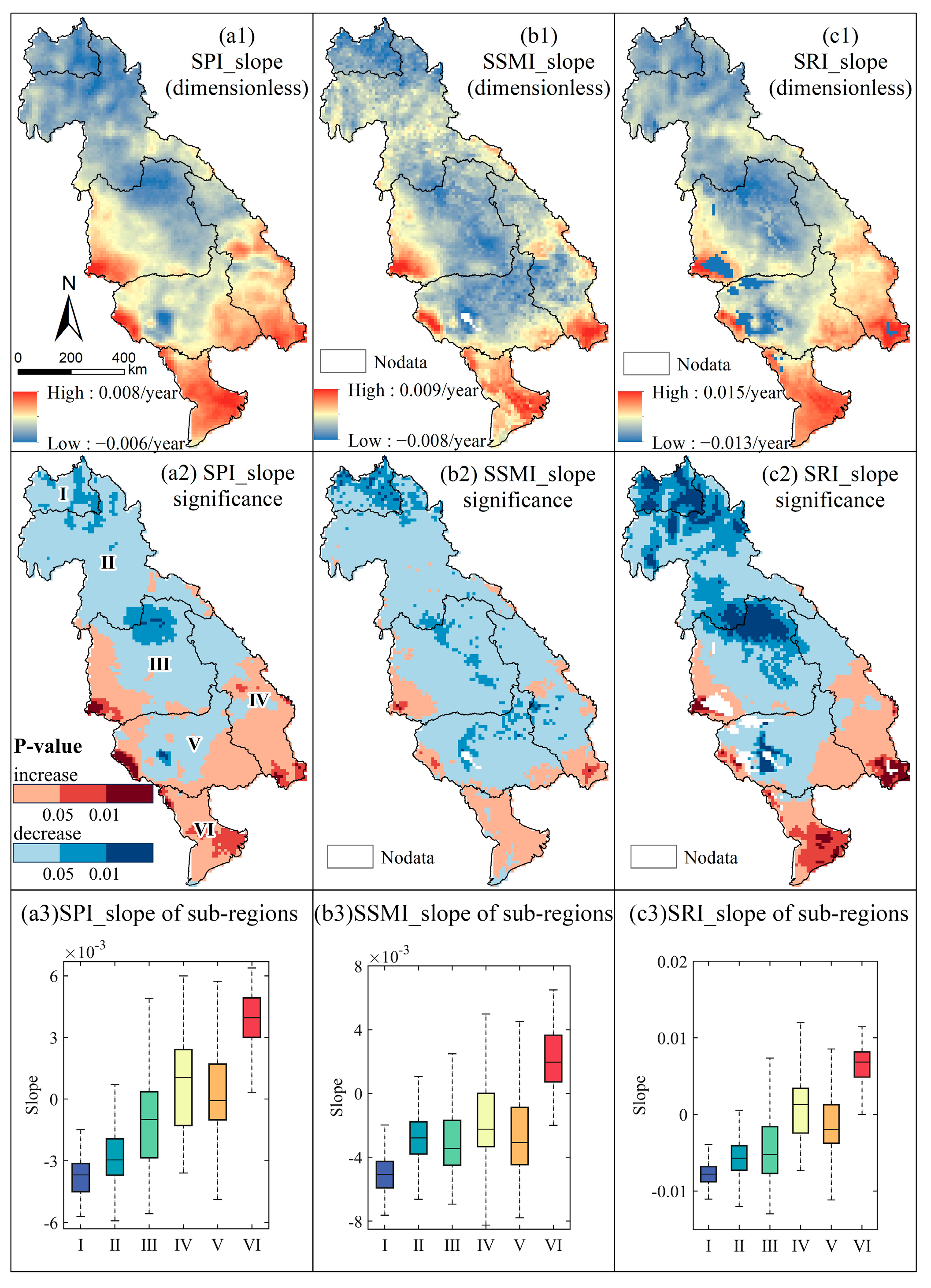
3.1. Spatial and Temporal Characteristics of the Three Drought Types
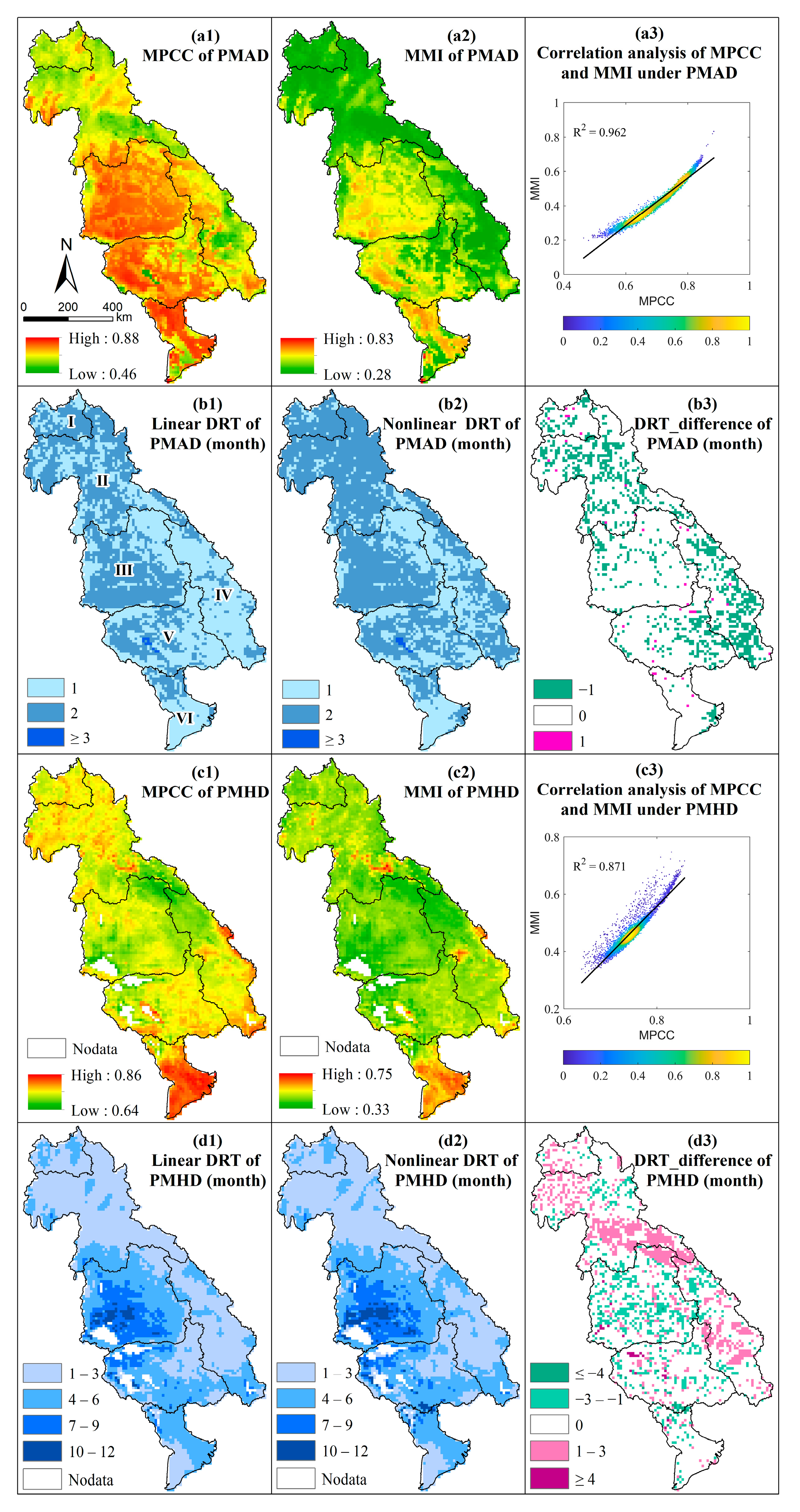
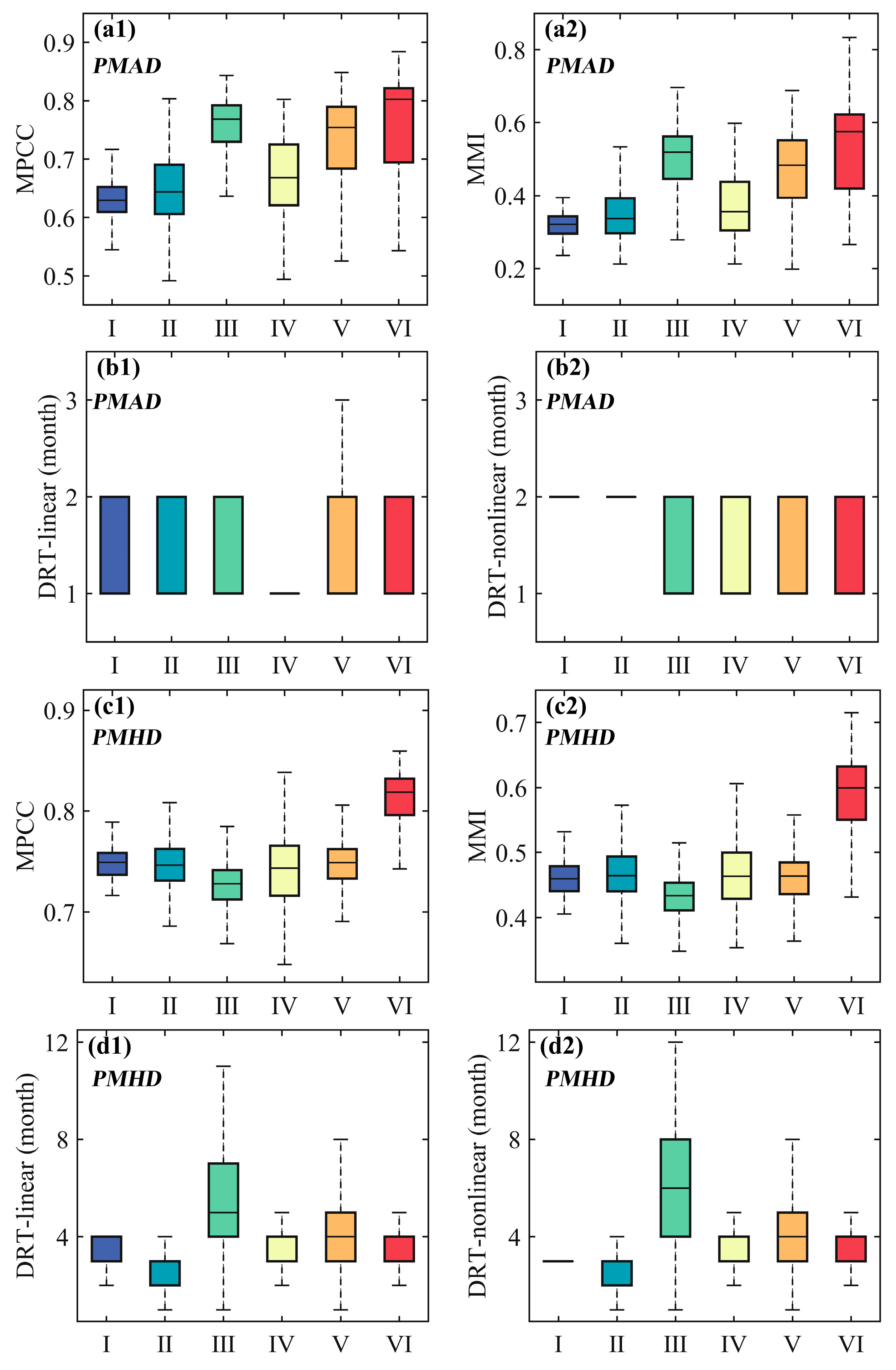
3.2. The Process of PMAD and PMHD
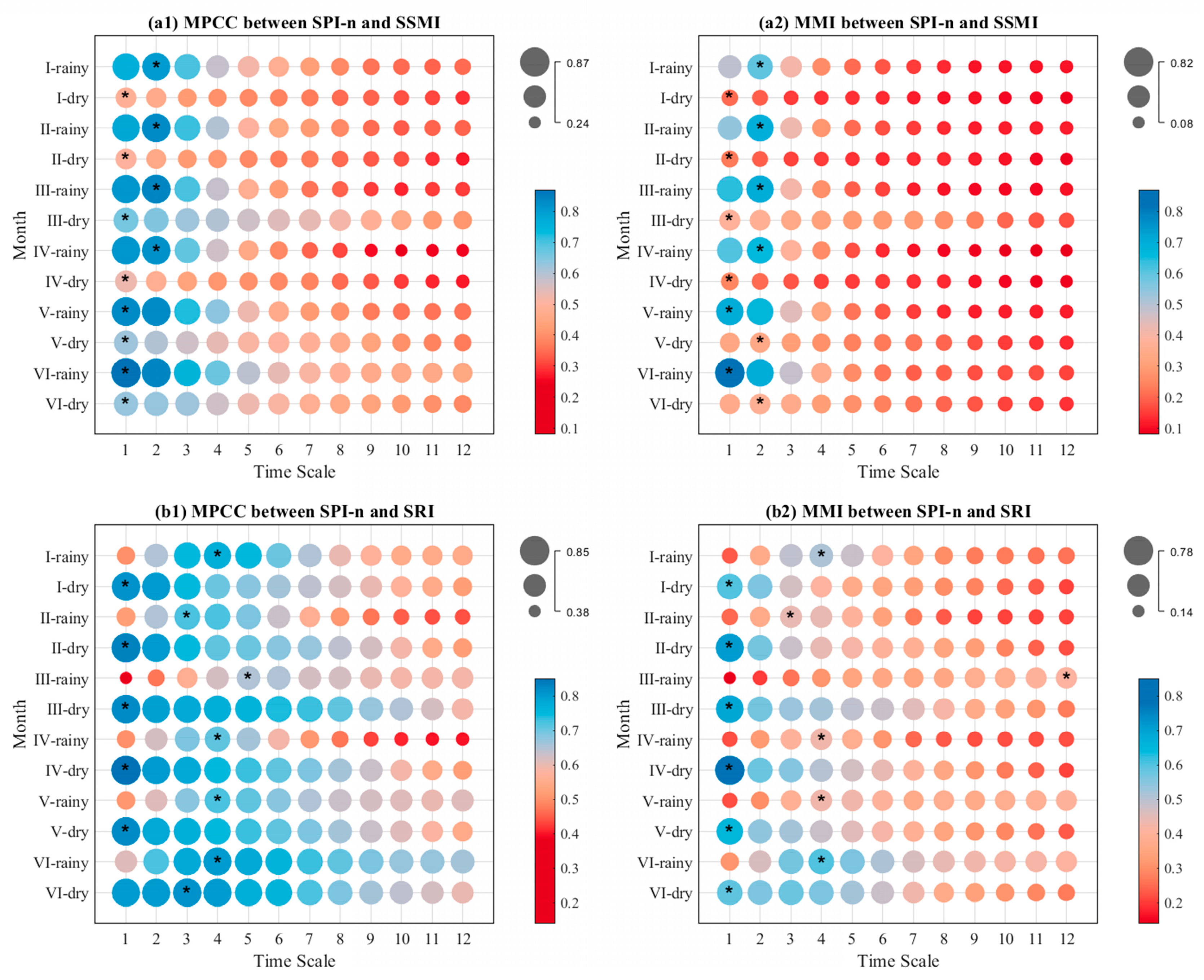
3.3. The Relationship between Meteorological Drought and Other Two Drought Types
3.3.1. The Relationship between Meteorological Drought and Agricultural Drought
3.3.2. The Relationship between Meteorological Drought and Hydrological Drought
4. Discussion
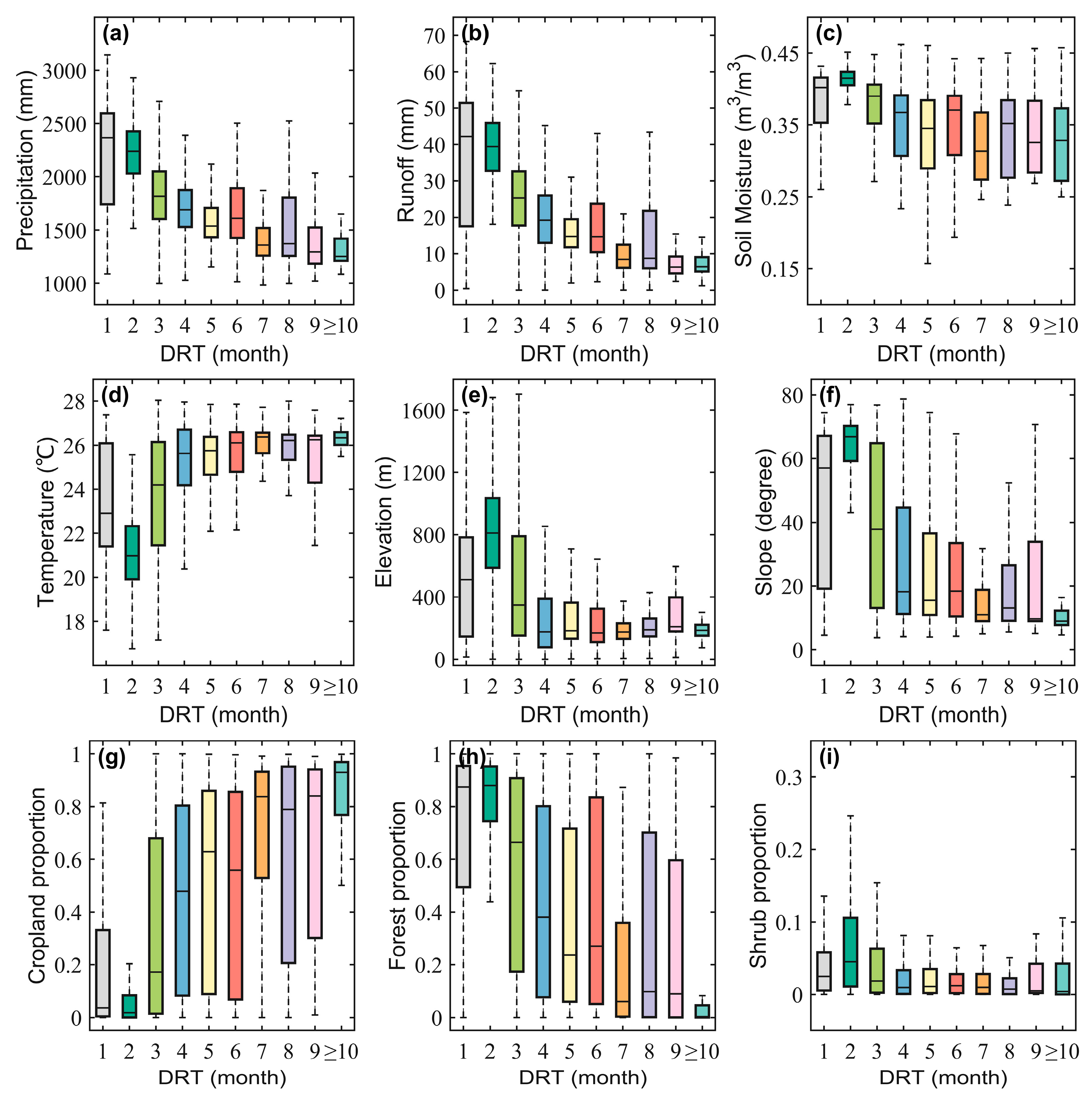
4.1. Reasons for the DRT Variations in Each Sub-Region
4.2. Comparison with Previous Research
4.3. Uncertainties, Limitations, and Future Direction
5. Conclusions
- (1)
- The SPI, SSMI, and SRI exhibited a high degree of spatial and temporal consistency in their trends with an insignificant decreasing trend dominating in most parts of the upper region and an insignificant upward trend dominating in most parts of the lower region. Moreover, the SRI displayed the most significant variation, with most regions showing a significant increasing/decreasing trend.
- (2)
- Both linear and nonlinear methods exhibited strong temporal and spatial consistency under PMAD and PMHD, with linear relationships being stronger than nonlinear ones. More than 80% and 70% of the study area showed identical DRTs for the two methods for PMAD and PMHD, respectively.
- (3)
- The DRTs of PMAD and PMHD were around 1–2 months and 3–5 months, respectively. Significant differences existed in the DRT between the dry season and the rainy season. For agricultural drought, the DRT was 1 month in the dry season and 1–2 months in the rainy season. Regarding hydrological drought, the DRT was 1–3 months in the dry season and 3–5 months in the rainy season.
- (4)
- Divergent spatial patterns of the proportion of DRT were observed between PMAD and PMHD. The upper sub-regions with a larger proportion of areas showed a longer DRT of PMAD but a shorter DRT of PMHD, while the lower sub-regions with a larger proportion of areas showed a shorter DRT of PMAD but a longer DRT of PMHD.
- (5)
- Significant statistical correlations between meteorological drought and agricultural drought and between meteorological drought and hydrological drought were observed in specific periods for each sub-region. Significant coherence was exhibited between SPI-m (m represents the DRT under PMAD in each sub-region) and SSMI and between SPI-n (n represents the DRT under PMHD in each sub-region) and SRI in most parts of each sub-region. This suggests that meteorological drought is the key driver of agricultural and hydrological drought.
- (6)
- Hydrometeorological factors and environmental characteristics collectively influenced the DRT. The hydrometeorological factors contributed the most to DRT, followed by terrain factors, and the land cover types contributed the least. Specifically, the areas with increased precipitation, soil moisture, or runoff had a shorter DRT, and the regions with higher elevations and slopes tended to exhibit a longer DRT of PMAD and a shorter DRT of PMHD, while the areas with a low proportion of cropland and high proportion of forest tended to display shorter DRTs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X. Global drought trends under 1.5 and 2 °C warming. Int. J. Climatol. 2019, 39, 2375–2385. [Google Scholar] [CrossRef]
- Chimwamurombe, P.M.; Mataranyika, P.N. Factors influencing dryland agricultural productivity. J. Arid Environ. 2021, 189, 104489. [Google Scholar] [CrossRef]
- Haile, G.G.; Tang, Q.; Sun, S.; Huang, Z.; Zhang, X.; Liu, X. Droughts in East Africa: Causes, impacts and resilience. Earth-Sci. Rev. 2019, 193, 146–161. [Google Scholar] [CrossRef]
- Katiyatiya, C.L.F.; Majaha, J.; Chikwanha, O.C.; Dzama, K.; Kgasago, N.; Mapiye, C. Drought’s implications on agricultural skills in South Africa. Outlook Agric. 2022, 51, 293–302. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Lai, C.; Wang, R.Y.; Chen, X.; Lian, Y. Drying tendency dominating the global grain production area. Glob. Food Secur. 2018, 16, 138–149. [Google Scholar] [CrossRef]
- Bhaga, T.D.; Dube, T.; Shekede, M.D.; Shoko, C. Impacts of Climate Variability and Drought on Surface Water Resources in Sub-Saharan Africa Using Remote Sensing: A Review. Remote Sens. 2020, 12, 4184. [Google Scholar] [CrossRef]
- Murphy, K.W.; Ellis, A.W. An analysis of past and present megadrought impacts on a modern water resource system. Hydrol. Sci. J. 2019, 64, 45–65. [Google Scholar] [CrossRef]
- Veijalainen, N.; Ahopelto, L.; Marttunen, M.; Jääskeläinen, J.; Britschgi, R.; Orvomaa, M.; Belinskij, A.; Keskinen, M. Severe Drought in Finland: Modeling Effects on Water Resources and Assessing Climate Change Impacts. Sustainability 2019, 11, 2450. [Google Scholar] [CrossRef]
- Jiao, W.; Wang, L.; Wang, H.; Lanning, M.; Chang, Q.; Novick, K.A. Comprehensive Quantification of the Responses of Ecosystem Production and Respiration to Drought Time Scale, Intensity and Timing in Humid Environments: A FLUXNET Synthesis. J. Geophys. Res. Biogeosciences 2022, 127, e2021JG006431. [Google Scholar] [CrossRef]
- Lei, T.; Feng, J.; Zheng, C.; Li, S.; Wang, Y.; Wu, Z.; Lu, J.; Kan, G.; Shao, C.; Jia, J.; et al. Review of drought impacts on carbon cycling in grassland ecosystems. Front. Earth Sci. 2020, 14, 462–478. [Google Scholar] [CrossRef]
- Müller, L.M.; Bahn, M. Drought legacies and ecosystem responses to subsequent drought. Glob. Change Biol. 2022, 28, 5086–5103. [Google Scholar] [CrossRef] [PubMed]
- Edwards, B.; Gray, M.; Hunter, B. The social and economic impacts of drought. Aust. J. Soc. Issues 2019, 54, 22–31. [Google Scholar] [CrossRef]
- Shahpari, G.; Sadeghi, H.; Ashena, M.; García-León, D. Drought effects on the Iranian economy: A computable general equilibrium approach. Environ. Dev. Sustain. 2022, 24, 4110–4127. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, Z.; Singh, V.P.; Zhang, Y.; Feng, S.; Xu, Y.; Hao, F. Drought propagation under global warming: Characteristics, approaches, processes, and controlling factors. Sci. Total Environ. 2022, 838, 156021. [Google Scholar] [CrossRef]
- Ding, Y.; Gong, X.; Xing, Z.; Cai, H.; Zhou, Z.; Zhang, D.; Sun, P.; Shi, H. Attribution of meteorological, hydrological and agricultural drought propagation in different climatic regions of China. Agric. Water Manag. 2021, 255, 106996. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Chang, J.; Leng, G.; Xing, L. The response of agricultural drought to meteorological drought and the influencing factors: A case study in the Wei River Basin, China. Agric. Water Manag. 2015, 159, 45–54. [Google Scholar] [CrossRef]
- Huang, S.; Li, P.; Huang, Q.; Leng, G.; Hou, B.; Ma, L. The propagation from meteorological to hydrological drought and its potential influence factors. J. Hydrol. 2017, 547, 184–195. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Gao, L.; Yao, H.; Chen, Y.; Liu, M. Response of Hydrological Drought to Meteorological Drought under the Influence of Large Reservoir. Adv. Meteorol. 2016, 2016, 2197142. [Google Scholar] [CrossRef]
- Cao, S.; Zhang, L.; He, Y.; Zhang, Y.; Chen, Y.; Yao, S.; Yang, W.; Sun, Q. Effects and contributions of meteorological drought on agricultural drought under different climatic zones and vegetation types in Northwest China. Sci. Total Environ. 2022, 821, 153270. [Google Scholar] [CrossRef]
- Fuentes, I.; Padarian, J.; Vervoort, R.W. Spatial and Temporal Global Patterns of Drought Propagation. Front. Environ. Sci. 2022, 10, 788248. [Google Scholar] [CrossRef]
- Wang, F.; Lai, H.; Li, Y.; Feng, K.; Tian, Q.; Guo, W.; Zhang, W.; Di, D.; Yang, H. Dynamic variations of terrestrial ecological drought and propagation analysis with meteorological drought across the mainland China. Sci. Total Environ. 2023, 896, 165314. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Lai, H.; Wang, F.; Feng, K.; Qi, Q.; Li, Y. Spatial-Temporal Patterns and Propagation Dynamics of Ecological Drought in the North China Plain. Water 2022, 14, 1542. [Google Scholar] [CrossRef]
- Zhou, K.; Li, J.; Zhang, T.; Kang, A. The use of combined soil moisture data to characterize agricultural drought conditions and the relationship among different drought types in China. Agric. Water Manag. 2021, 243, 106479. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological drought explained. WIREs Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Li, Q.; Ye, A.; Zhang, Y.; Zhou, J. The Peer-To-Peer Type Propagation From Meteorological Drought to Soil Moisture Drought Occurs in Areas With Strong Land-Atmosphere Interaction. Water Resour. Res. 2022, 58, e2022WR032846. [Google Scholar] [CrossRef]
- Bai, M.; Li, Z.; Huo, P.; Wang, J.; Li, Z. Propagation characteristics from meteorological drought to agricultural drought over the Heihe River Basin, Northwest China. J. Arid Land 2023, 15, 523–544. [Google Scholar] [CrossRef]
- Li, C.; Zhang, X.; Yin, G.; Xu, Y.; Hao, F. Evaluation of Drought Propagation Characteristics and Influencing Factors in an Arid Region of Northeast Asia (ARNA). Remote Sens. 2022, 14, 3307. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, S.; Huang, Q.; Duan, W.; Leng, G.; Guo, Y.; Zheng, X.; Nie, M.; Han, Z.; Dong, H.; et al. Seasonal Propagation Characteristics from Meteorological to Hydrological Drought and Their Dynamics in the Headstreams of the Tarim River Basin. J. Hydrometeorol. 2022, 23, 1487–1506. [Google Scholar] [CrossRef]
- Bhardwaj, K.; Shah, D.; Aadhar, S.; Mishra, V. Propagation of Meteorological to Hydrological Droughts in India. J. Geophys. Res. Atmos. 2020, 125, e2020JD033455. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, F.; Yue, H.; Wang, X.; Fan, Y. Global analysis of the correlation and propagation among meteorological, agricultural, surface water, and groundwater droughts. J. Environ. Manag. 2023, 333, 117460. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Duan, X.; Guo, Q.; Lu, S.; Hsu, K. The spatiotemporal variations and propagation of droughts in Plateau Mountains of China. Sci. Total Environ. 2022, 805, 150257. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Zhang, X.; Chen, N.; Li, B.; Ma, H.; Xu, L.; Li, R.; Niyogi, D. Drought propagation modification after the construction of the Three Gorges Dam in the Yangtze River Basin. J. Hydrol. 2021, 603, 127138. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Hao, Z.; Singh, V.P.; Hao, F. Characterization of agricultural drought propagation over China based on bivariate probabilistic quantification. J. Hydrol. 2021, 598, 126194. [Google Scholar] [CrossRef]
- Lin, Q.; Wu, Z.; Zhang, Y.; Peng, T.; Chang, W.; Guo, J. Propagation from meteorological to hydrological drought and its application to drought prediction in the Xijiang River basin, South China. J. Hydrol. 2023, 617, 128889. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, Z.; Shao, Q.; He, H.; Guo, X. From meteorological to agricultural drought: Propagation time and probabilistic linkages. J. Hydrol. Reg. Stud. 2023, 46, 101329. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Wang, X.; Hao, Z.; Singh, V.P.; Hao, F. Propagation from meteorological drought to hydrological drought under the impact of human activities: A case study in northern China. J. Hydrol. 2019, 579, 124147. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Cheng, H.; Wang, H.; Zhu, Y. Propagation from Meteorological to Hydrological Drought and Its Influencing Factors in the Huaihe River Basin. Water 2021, 13, 1985. [Google Scholar] [CrossRef]
- Seo, J.Y.; Lee, S.I. Probabilistic Evaluation of Drought Propagation Using Satellite Data and Deep Learning Model: From Precipitation to Soil Moisture and Groundwater. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 6048–6061. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, J.; Wang, X.; Cai, H.; Zhou, Z.; Sun, Y.; Shi, H. Propagation of meteorological to hydrological drought for different climate regions in China. J. Environ. Manag. 2021, 283, 111980. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Q.; Wang, L.; Lei, L.; Huang, M.; Xiang, J.; Feng, W.; Zhao, Y.; Xue, D.; Liu, C.; et al. Impact of Climate Change and Land-Use on the Propagation from Meteorological Drought to Hydrological Drought in the Eastern Qilian Mountains. Water 2019, 11, 1602. [Google Scholar] [CrossRef]
- Han, Z.; Huang, S.; Huang, Q.; Leng, G.; Liu, Y.; Bai, Q.; He, P.; Liang, H.; Shi, W. GRACE-based high-resolution propagation threshold from meteorological to groundwater drought. Agric. For. Meteorol. 2021, 307, 108476. [Google Scholar] [CrossRef]
- Dai, M.; Huang, S.; Huang, Q.; Zheng, X.; Su, X.; Leng, G.; Li, Z.; Guo, Y.; Fang, W.; Liu, Y. Propagation characteristics and mechanism from meteorological to agricultural drought in various seasons. J. Hydrol. 2022, 610, 127897. [Google Scholar] [CrossRef]
- Adeyeri, O.E.; Zhou, W.; Laux, P.; Ndehedehe, C.E.; Wang, X.; Usman, M.; Akinsanola, A.A. Multivariate Drought Monitoring, Propagation, and Projection Using Bias-Corrected General Circulation Models. Earth’s Future 2023, 11, e2022EF003303. [Google Scholar] [CrossRef]
- Bevacqua, A.G.; Chaffe, P.L.B.; Chagas, V.B.P.; AghaKouchak, A. Spatial and temporal patterns of propagation from meteorological to hydrological droughts in Brazil. J. Hydrol. 2021, 603, 126902. [Google Scholar] [CrossRef]
- Gevaert, A.I.; Veldkamp, T.I.E.; Ward, P.J. The effect of climate type on timescales of drought propagation in an ensemble of global hydrological models. Hydrol. Earth Syst. Science. 2018, 22, 4649–4665. [Google Scholar] [CrossRef]
- Inocêncio, T.d.M.; Ribeiro Neto, A.; Oertel, M.; Meza, F.J.; Scott, C.A. Linking drought propagation with episodes of climate-Induced water insecurity in Pernambuco state—Northeast Brazil. J. Arid Environ. 2021, 193, 104593. [Google Scholar] [CrossRef]
- van Langen, S.C.H.; Costa, A.C.; Neto, G.G.R.; van Oel, P.R. Effect of a reservoir network on drought propagation in a semi-arid catchment in Brazil. Hydrol. Sci. J. 2021, 66, 1567–1583. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, H.; Baiyinbaoligao; Hu, H.; Khan, M.Y.A.; Wen, J.; Chen, L.; Tian, F. Future projection of seasonal drought characteristics using CMIP6 in the Lancang-Mekong River Basin. J. Hydrol. 2022, 610, 127815. [Google Scholar] [CrossRef]
- Tang, J.; Cao, H. Drought and flood occurrences in the Lancang River Basin during the last 60 years: Their variations and teleconnections with monsoons. J. Water Clim. Change 2019, 11, 1798–1810. [Google Scholar] [CrossRef]
- Zhang, L.; Song, W.; Song, W. Assessment of Agricultural Drought Risk in the Lancang-Mekong Region, South East Asia. Int. J. Environ. Res. Public Health 2020, 17, 6153. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Qu, Y.; Ma, M.; Liu, H.; Su, Z.; Lv, J.; Peng, J.; Leng, G.; He, X.; Di, C. Satellite-Based Operational Real-Time Drought Monitoring in the Transboundary Lancang–Mekong River Basin. Remote Sens. 2020, 12, 376. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Li, Y.; Ming, W.; Long, Y.; Zhang, M. Relationship between meteorological and hydrological droughts in the upstream regions of the Lancang–Mekong River. J. Water Clim. Change 2021, 13, 421–433. [Google Scholar] [CrossRef]
- Luo, X.; Luo, X.; Ji, X.; Ming, W.; Wang, L.; Xiao, X.; Xu, J.; Liu, Y.; Li, Y. Meteorological and hydrological droughts in the Lancang-Mekong River Basin: Spatiotemporal patterns and propagation. Atmos. Res. 2023, 293, 106913. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Hassler, B.; Lauer, A. Comparison of Reanalysis and Observational Precipitation Datasets Including ERA5 and WFDE5. Atmosphere 2021, 12, 1462. [Google Scholar] [CrossRef]
- Huang, X.; Han, S.; Shi, C. Multiscale Assessments of Three Reanalysis Temperature Data Systems over China. Agriculture 2021, 11, 1292. [Google Scholar] [CrossRef]
- Xin, Y.; Yang, Y.; Chen, X.; Yue, X.; Liu, Y.; Yin, C. Evaluation of IMERG and ERA5 precipitation products over the Mongolian Plateau. Sci. Rep. 2022, 12, 21776. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, L.; Zhang, X.; Chen, X.; Mi, J.; Xie, S. Consistency Analysis and Accuracy Assessment of Three Global 30-m Land-Cover Products over the European Union using the LUCAS Dataset. Remote Sens. 2020, 12, 3479. [Google Scholar] [CrossRef]
- Jokar Arsanjani, J.; See, L.; Tayyebi, A. Assessing the suitability of GlobeLand30 for mapping land cover in Germany. Int. J. Digit. Earth 2016, 9, 873–891. [Google Scholar] [CrossRef]
- Mi, J.; Liu, L.Y.; Zhang, X.; Chen, X.D.; Gao, Y.; Xie, S. Impact of geometric misregistration in GlobeLand30 on land-cover change analysis, a case study in China. J. Appl. Remote Sens. 2022, 16, 014516. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Liu, D.; Yang, W.; Zhang, W. Accuracy Assessment of GlobeLand30 2010 Land Cover over China Based on Geographically and Categorically Stratified Validation Sample Data. Remote Sens. 2018, 10, 1213. [Google Scholar] [CrossRef]
- Zhu, L.; Jin, G.; Zhang, X.; Shi, R.; La, Y.; Li, C. Integrating global land cover products to refine GlobeLand30 forest types: A case study of conterminous United States (CONUS). Int. J. Remote Sens. 2021, 42, 2105–2130. [Google Scholar] [CrossRef]
- Higginbottom, T.P.; Symeonakis, E. Assessing Land Degradation and Desertification Using Vegetation Index Data: Current Frameworks and Future Directions. Remote Sens. 2014, 6, 9552–9575. [Google Scholar] [CrossRef]
- Fensholt, R.; Rasmussen, K.; Nielsen, T.T.; Mbow, C. Evaluation of earth observation based long term vegetation trends—Intercomparing NDVI time series trend analysis consistency of Sahel from AVHRR GIMMS, Terra MODIS and SPOT VGT data. Remote Sens. Environ. 2009, 113, 1886–1898. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Xiao, J.; Huang, K.; Lin, Y.; Ren, P.; Zu, J. Assessing Vegetation Phenology across Different Biomes in Temperate China—Comparing GIMMS and MODIS NDVI Datasets. Remote Sens. 2022, 14, 6180. [Google Scholar] [CrossRef]
- Steinemann Anne, C.; Cavalcanti Luiz, F.N. Developing Multiple Indicators and Triggers for Drought Plans. J. Water Resour. Plan. Manag. 2006, 132, 164–174. [Google Scholar] [CrossRef]
- Farahmand, A.; AghaKouchak, A. A generalized framework for deriving nonparametric standardized drought indicators. Adv. Water Resour. 2015, 76, 140–145. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef]
- Zhou, Z.; Shi, H.; Fu, Q.; Ding, Y.; Li, T.; Wang, Y.; Liu, S. Characteristics of Propagation From Meteorological Drought to Hydrological Drought in the Pearl River Basin. J. Geophys. Res. Atmos. 2021, 126, e2020JD033959. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Meng, E.; Luan, J. Reference evapotranspiration forecasting based on local meteorological and global climate information screened by partial mutual information. J. Hydrol. 2018, 561, 764–779. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Wang, H.; Leng, G.; Wang, L. Identifying drought propagation by simultaneously considering linear and nonlinear dependence in the Wei River basin of the Loess Plateau, China. J. Hydrol. 2020, 591, 125287. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophysics. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Liu, S.; Huang, S.; Xie, Y.; Leng, G.; Huang, Q.; Wang, L.; Xue, Q. Spatial-temporal changes of rainfall erosivity in the loess plateau, China: Changing patterns, causes and implications. CATENA 2018, 166, 279–289. [Google Scholar] [CrossRef]
- Peng, J.; Luo, X.; Liu, F.; Zhang, Z. Analysing the influences of ENSO and PDO on water discharge from the Yangtze River into the sea. Hydrol. Process. 2018, 32, 1090–1103. [Google Scholar] [CrossRef]
- Li, Q.; He, P.; He, Y.; Han, X.; Zeng, T.; Lu, G.; Wang, H. Investigation to the relation between meteorological drought and hydrological drought in the upper Shaying River Basin using wavelet analysis. Atmos. Res. 2020, 234, 104743. [Google Scholar] [CrossRef]
- Li, R.; Chen, N.; Zhang, X.; Zeng, L.; Wang, X.; Tang, S.; Li, D.; Niyogi, D. Quantitative analysis of agricultural drought propagation process in the Yangtze River Basin by using cross wavelet analysis and spatial autocorrelation. Agric. For. Meteorol. 2020, 280, 107809. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Aldrich, C. Process Variable Importance Analysis by Use of Random Forests in a Shapley Regression Framework. Minerals 2020, 10, 420. [Google Scholar] [CrossRef]
- Zhang, T.; Su, X.; Zhang, G.; Wu, H.; Wang, G.; Chu, J. Evaluation of the impacts of human activities on propagation from meteorological drought to hydrological drought in the Weihe River Basin, China. Sci. Total Environ. 2022, 819, 153030. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Miao, C.; Gou, J.; Wu, J.; Jiao, W.; Song, Y.; Xu, D. Spatiotemporal characteristics of meteorological to hydrological drought propagation under natural conditions in China. Weather Clim. Extrem. 2022, 38, 100505. [Google Scholar] [CrossRef]
- Palanisamy, B.; Narasimhan, B.; Paul, S.; Srinivasan, R.; Wangpimool, W.; Lim, S.; Sayasane, R. Studying Onset and Evolution of Agricultural Drought in Mekong River Basin through Hydrologic Modeling. Water 2021, 13, 3622. [Google Scholar] [CrossRef]
- Palanisamy, B.; Narasimhan, B.; Paul, S.; Srinivasan, R.; Wangpimool, W.; Sith, R.; Sayasane, R. Development and propagation of hydrologic drought from meteorological and agricultural drought in the Mekong River Basin. Hydrol. Process. 2023, 37, e14935. [Google Scholar] [CrossRef]
- Wang, T.; Tu, X.; Singh, V.P.; Chen, X.; Lin, K.; Zhou, Z.; Tan, Y. Assessment of future socioeconomic drought based on CMIP6: Evolution, driving factors and propagation. J. Hydrol. 2023, 617, 129009. [Google Scholar] [CrossRef]
- Zhu, K.; Xu, Y.; Lu, F.; Sun, X.; Gao, M.; Han, X.; Li, D.; Jiang, M. Spatio-Temporal Evolution and Propagation of Meteoro-Hydrological Drought in Yalong River Basin. Water 2023, 15, 1025. [Google Scholar] [CrossRef]
- Scherrer, S.C.; Hirschi, M.; Spirig, C.; Maurer, F.; Kotlarski, S. Trends and drivers of recent summer drying in Switzerland. Environ. Res. Commun. 2022, 4, 025004. [Google Scholar] [CrossRef]
- Torres-Vázquez, M.Á.; Halifa-Marín, A.; Montávez, J.P.; Turco, M. High resolution monitoring and probabilistic prediction of meteorological drought in a Mediterranean environment. Weather Clim. Extrem. 2023, 40, 100558. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, R.; Li, L.; Zhang, S.; Zhang, Y.; Huang, F.; Li, J.; Liu, W. Assessment of Agricultural Drought Based on Reanalysis Soil Moisture in Southern China. Land 2022, 11, 502. [Google Scholar] [CrossRef]
- Zhang, R.; Li, L.; Zhang, Y.; Huang, F.; Li, J.; Liu, W.; Mao, T.; Xiong, Z.; Shangguan, W. Assessment of Agricultural Drought Using Soil Water Deficit Index Based on ERA5-Land Soil Moisture Data in Four Southern Provinces of China. Agriculture 2021, 11, 411. [Google Scholar] [CrossRef]
- Dergunov, A.; Yakubailik, O. Comparative analysis of data on air temperature based on current weather data sets for 2007-2019. IOP Conf. Ser. Earth Environ. Sci. 2020, 548, 032034. [Google Scholar] [CrossRef]
- Li, M.; Wu, P.; Ma, Z. A comprehensive evaluation of soil moisture and soil temperature from third-generation atmospheric and land reanalysis data sets. Int. J. Climatol. 2020, 40, 5744–5766. [Google Scholar] [CrossRef]
- Harrigan, S.; Zsoter, E.; Alfieri, L.; Prudhomme, C.; Salamon, P.; Wetterhall, F.; Barnard, C.; Cloke, H.; Pappenberger, F. GloFAS-ERA5 operational global river discharge reanalysis 1979–present. Earth Syst. Sci. Data 2020, 12, 2043–2060. [Google Scholar] [CrossRef]
- Bain, R.L.; Shaw, M.J.; Geheran, M.P.; Tavakoly, A.A.; Wahl, M.D.; Zsoter, E. Intercomparison of global ERA reanalysis products for streamflow simulations at the high-resolution continental scale. J. Hydrol. 2023, 616, 128624. [Google Scholar] [CrossRef]
- Rangecroft, S.; Van Loon, A.F.; Maureira, H.; Verbist, K.; Hannah, D.M. An observation-based method to quantify the human influence on hydrological drought: Upstream–downstream comparison. Hydrol. Sci. J. 2019, 64, 276–287. [Google Scholar] [CrossRef]
- Sam, T.T.; Khoi, D.N. The responses of river discharge and sediment load to historical land-use/land-cover change in the Mekong River Basin. Environ. Monit. Assess. 2022, 194, 700. [Google Scholar] [CrossRef]



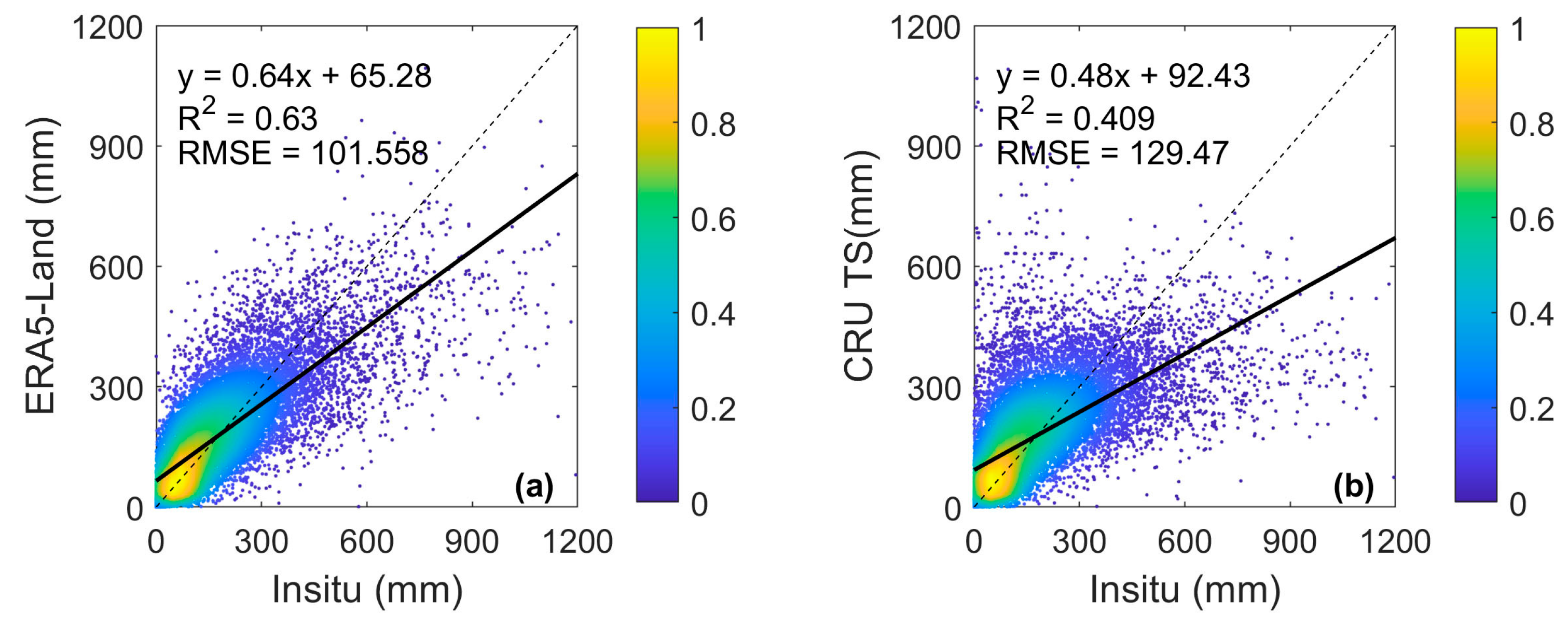
| Reference | Study Area | Propagation Type 1 | Method 2 | Result |
|---|---|---|---|---|
| [27] | China | PMAD | CA | 3.4 months |
| [28] | Heihe River Basin | PMAD | CA | Average 8 months |
| [29] | Northeast Asia | PMAD | CA | 1–3 months in summer and 5–12 months in winter |
| [24] | North China Plain | PMED | CA | 1.33 months in summer and 2.67 months in winter |
| [23] | China | PMED | CA | 2.67 months in summer and 7 months in winter |
| [25] | China | PMAD, PMED | CA | 1–2.5 months under PMAD and no delay under PMED |
| [30] | Tarim River Basin | PMHD | CA | 2–21 months |
| [31] | India | PMAD, PMHD | CA | 4–5 months under PMAD and 1 month shorter than that under PMHD |
| [32] | Global | PMAD, PMHD | CA | 5.7 months under PMAD and 3.5–14.47 months under PMHD |
| [33] | Longchuan River Basin | PMAD, PMHD, PHAD | CA | Approximately 2 months under three types of propagation |
| [34] | Yangtze River Basin | PMAD, PMHD | CA | Less than 2 months under PMAD and 2–6 months under PMHD |
| [35] | China | PMAD | CA | 1–2 months in summer and 2–7 months in the next spring |
| [36] | Xijiang River Basin | PMHD | RT | Less than 3 months, with the maximum being 78 days |
| [37] | Yangtze River Basin | PMAD | CA | 48 days |
| [38] | Luanhe River Basin | PMHD | CA | 1–7 months in rainy season and 7–12 months in dry season |
| [39] | Huaihe River Basin | PMHD | RT | 1–47 days |
| [40] | South Korea | PMAD, PMHD | RT | 2.83 months under PMAD and 4.34 months under PMHD |
| [41] | China | PMHD | CA | 2–4 months |
| Data Type | Spatiotemporal Resolution | Time Span | Data Source |
|---|---|---|---|
| ERA5-Land reanalysis data | 0.1° (~10 km), monthly | 1950–2021 | https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land-monthly-means?tab=overview (accessed on 4 October 2022) |
| GlobeLand30 land cover | 30 m, yearly | 2020 | httes://www.globallandcover.com (accessed on 12 July 2023) |
| GIMMS_3g NDVI | 1/12° (~8 km), 15 days | 1981–2015 | https://ecocast.arc.nasa.gov/data/pub/gimms/ (accessed on 27 July 2023) |
| SRTM DEM | 30 m | 2000 | https://earthexplorer.usgs.gov/ (accessed on 8 September 2022) |
| Sub-Region | Method | 1 Month | 2 Months | 3 Months or More |
|---|---|---|---|---|
| Sub-region I | linear | 33.02% | 66.98% | 0 |
| nonlinear | 15.41% | 84.59% | 0 | |
| Sub-region Ⅱ | linear | 39.91% | 60.09% | 0 |
| nonlinear | 15.41% | 84.59% | 0 | |
| Sub-region Ⅲ | linear | 41.39% | 58.61% | 0 |
| nonlinear | 32.96% | 67.04% | 0 | |
| Sub-region Ⅳ | linear | 83.33% | 16.67% | 0 |
| nonlinear | 50.62% | 49.38% | 0 | |
| Sub-region Ⅴ | linear | 64.07% | 34.91% | 1.02% |
| nonlinear | 49.03% | 49.77% | 1.2% | |
| Sub-region Ⅵ | linear | 71.39% | 28.61% | 0 |
| nonlinear | 66.67% | 33.33% | 0 |
| Sub-Region | Method | 1–3 Months | 4–6 Months | 7–9 Months | 10–12 Months |
|---|---|---|---|---|---|
| Sub-region Ⅰ | linear | 70.76% | 29.24% | 0 | 0 |
| nonlinear | 76.42% | 23.58% | 0 | 0 | |
| Sub-region Ⅱ | linear | 80.48% | 18.91% | 0.61% | 0 |
| nonlinear | 78.26% | 21.07% | 0.67% | 0 | |
| Sub-region Ⅲ | linear | 15.26% | 50.11% | 28.91% | 5.72% |
| nonlinear | 12.18% | 49.73% | 28.83% | 9.26% | |
| Sub-region Ⅳ | linear | 68.91% | 30.25% | 0.84% | 0 |
| nonlinear | 62.92% | 36.67% | 0.41% | 0 | |
| Sub-region Ⅴ | linear | 36.13% | 53.25% | 9.61% | 1.01 |
| nonlinear | 35.34% | 51.26% | 9.91% | 3.49% | |
| Sub-region Ⅵ | linear | 32.77% | 64.84% | 1.68% | 0.71% |
| nonlinear | 33.26% | 62.21% | 1.92% | 2.61% |
| Sub-Region | PMAD | PMHD | ||
|---|---|---|---|---|
| Linear Method | Nonlinear Method | Linear Method | Nonlinear Method | |
| Sub-region Ⅰ | 2 months | 2 months | 3 months | 3 months |
| Sub-region Ⅱ | 2 months | 2 months | 3 months | 3 months |
| Sub-region Ⅲ | 2 months | 2 months | 5 months | 5 months |
| Sub-region Ⅳ | 1 month | 1 month | 3 months | 3 months |
| Sub-region Ⅴ | 1 month | 2 months | 4 months | 4 months |
| Sub-region Ⅵ | 1 month | 1 month | 4 months | 4 months |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, G.; Chen, Y.; Mansaray, L.R.; Xu, H.; Shi, A.; Chen, Y. Propagation of Meteorological Drought to Agricultural and Hydrological Droughts in the Tropical Lancang–Mekong River Basin. Remote Sens. 2023, 15, 5678. https://doi.org/10.3390/rs15245678
Feng G, Chen Y, Mansaray LR, Xu H, Shi A, Chen Y. Propagation of Meteorological Drought to Agricultural and Hydrological Droughts in the Tropical Lancang–Mekong River Basin. Remote Sensing. 2023; 15(24):5678. https://doi.org/10.3390/rs15245678
Chicago/Turabian StyleFeng, Ganlin, Yaoliang Chen, Lamin R. Mansaray, Hongfeng Xu, Aoni Shi, and Yanling Chen. 2023. "Propagation of Meteorological Drought to Agricultural and Hydrological Droughts in the Tropical Lancang–Mekong River Basin" Remote Sensing 15, no. 24: 5678. https://doi.org/10.3390/rs15245678
APA StyleFeng, G., Chen, Y., Mansaray, L. R., Xu, H., Shi, A., & Chen, Y. (2023). Propagation of Meteorological Drought to Agricultural and Hydrological Droughts in the Tropical Lancang–Mekong River Basin. Remote Sensing, 15(24), 5678. https://doi.org/10.3390/rs15245678








