Quantitative Assessment of Factors Influencing the Spatiotemporal Variation in Carbon Dioxide Fluxes Simulated by Multi-Source Remote Sensing Data in Tropical Vegetation
Abstract
:1. Introduction
2. Materials and Methods
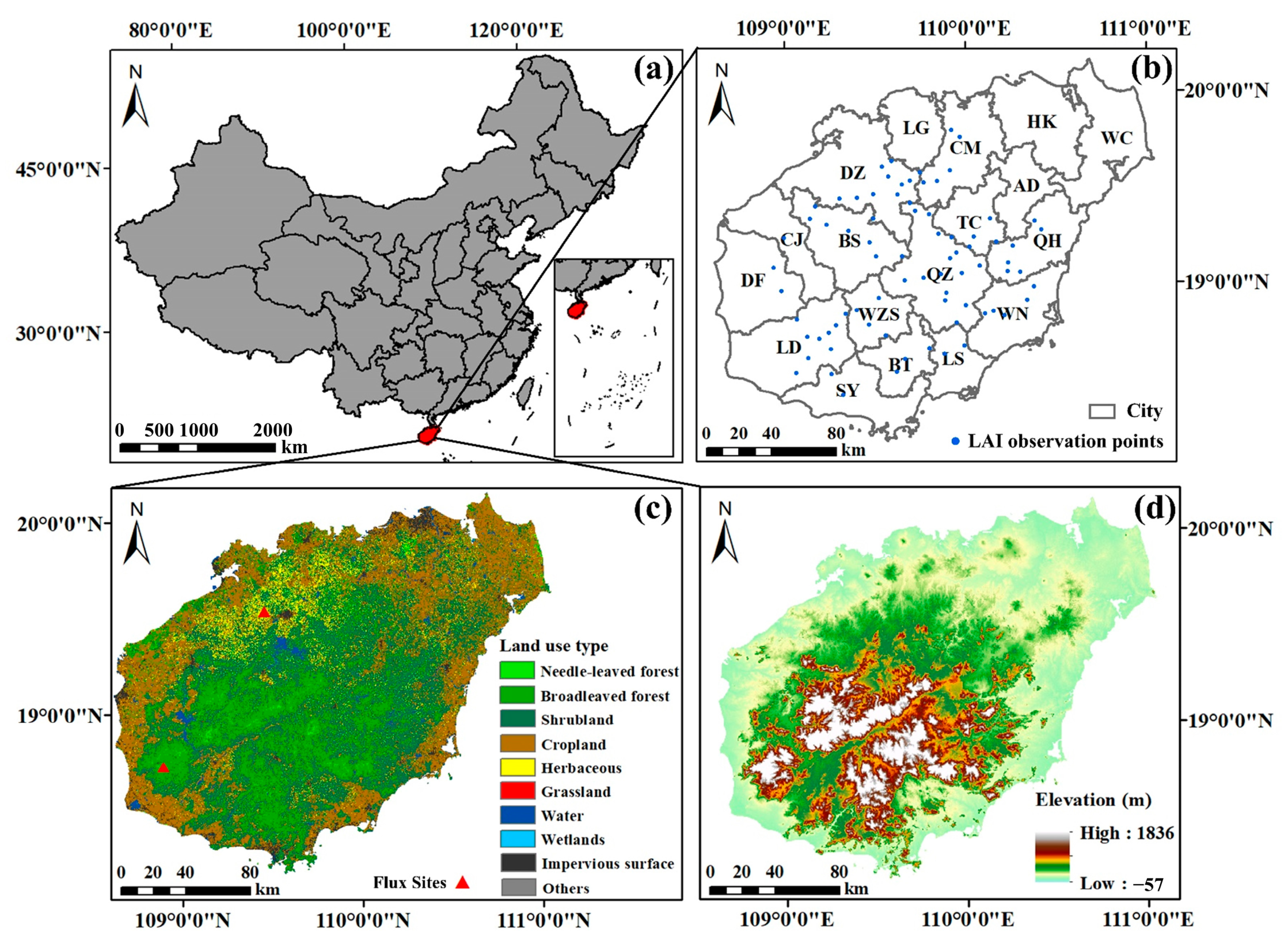
2.1. Study Area
2.2. Data and Data Pre-Processing
2.2.1. Land Use and Land Cover
2.2.2. Land Surface Water Index (LSWI) and Leaf Area Index (LAI)
2.2.3. Other Input Data of Model
- Meteorological data
- 2.
- Nitrogen data
- 3.
- Elevation Data
2.2.4. Evaluation Data
- NPP benchmark maps
- 2.
- NEE evaluation map and measured NEE from flux stations
- 3.
- LAI benchmark map and measured LAI
2.3. Methods
2.3.1. Vegetation Productivity Simulation
- NPP simulation
- 2.
- NEP simulation
2.3.2. Evaluation of Model Performance
2.3.3. Trend Analysis
2.3.4. Variation Stability Analysis
2.3.5. Limitations of NPP by Natural Factors
2.3.6. Impact of Anthropogenic Activities on NPP
3. Results
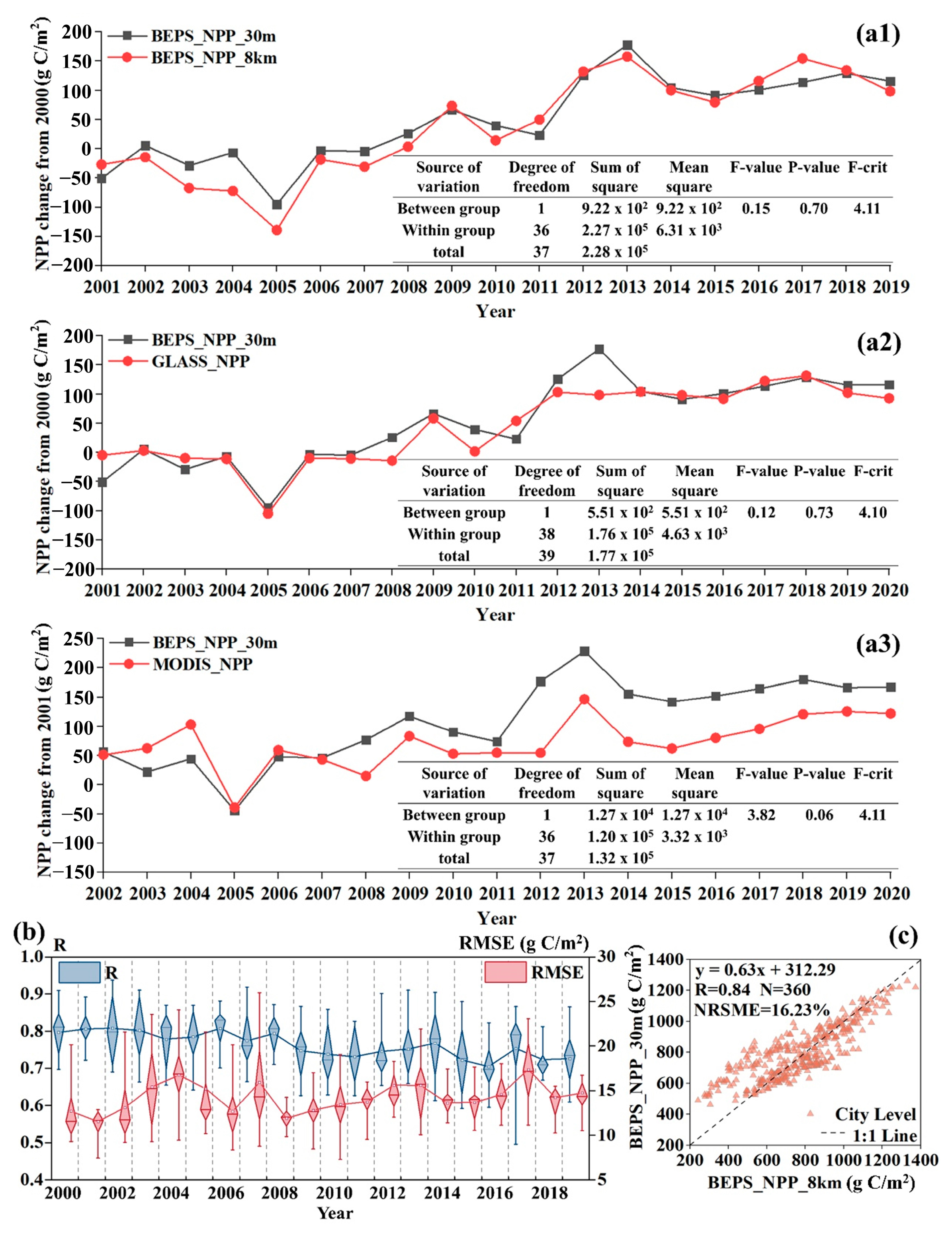
3.1. Accuracy of Carbon Dioxide Flux Simulation
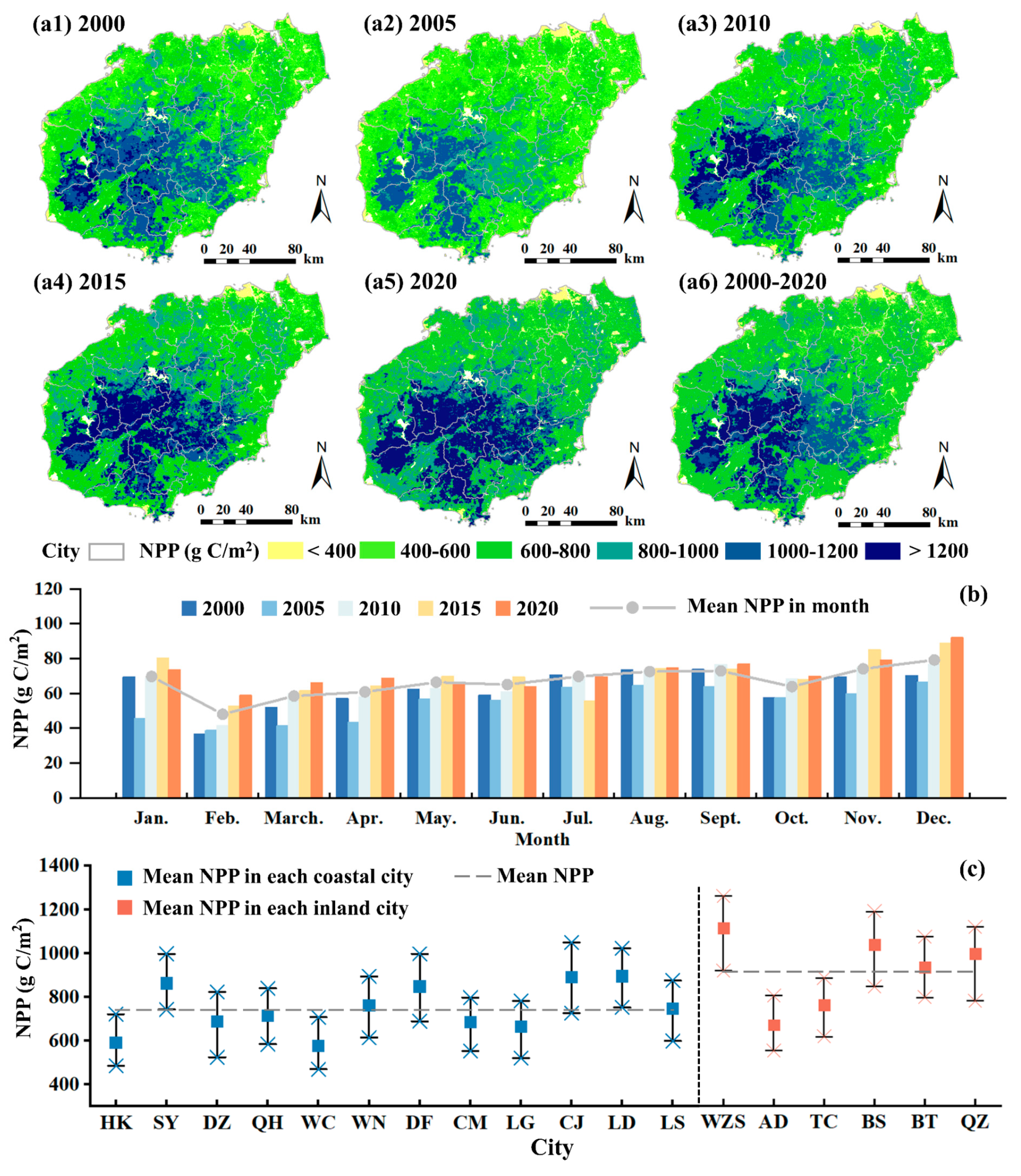
3.2. Spatiotemporal Variations in NPP
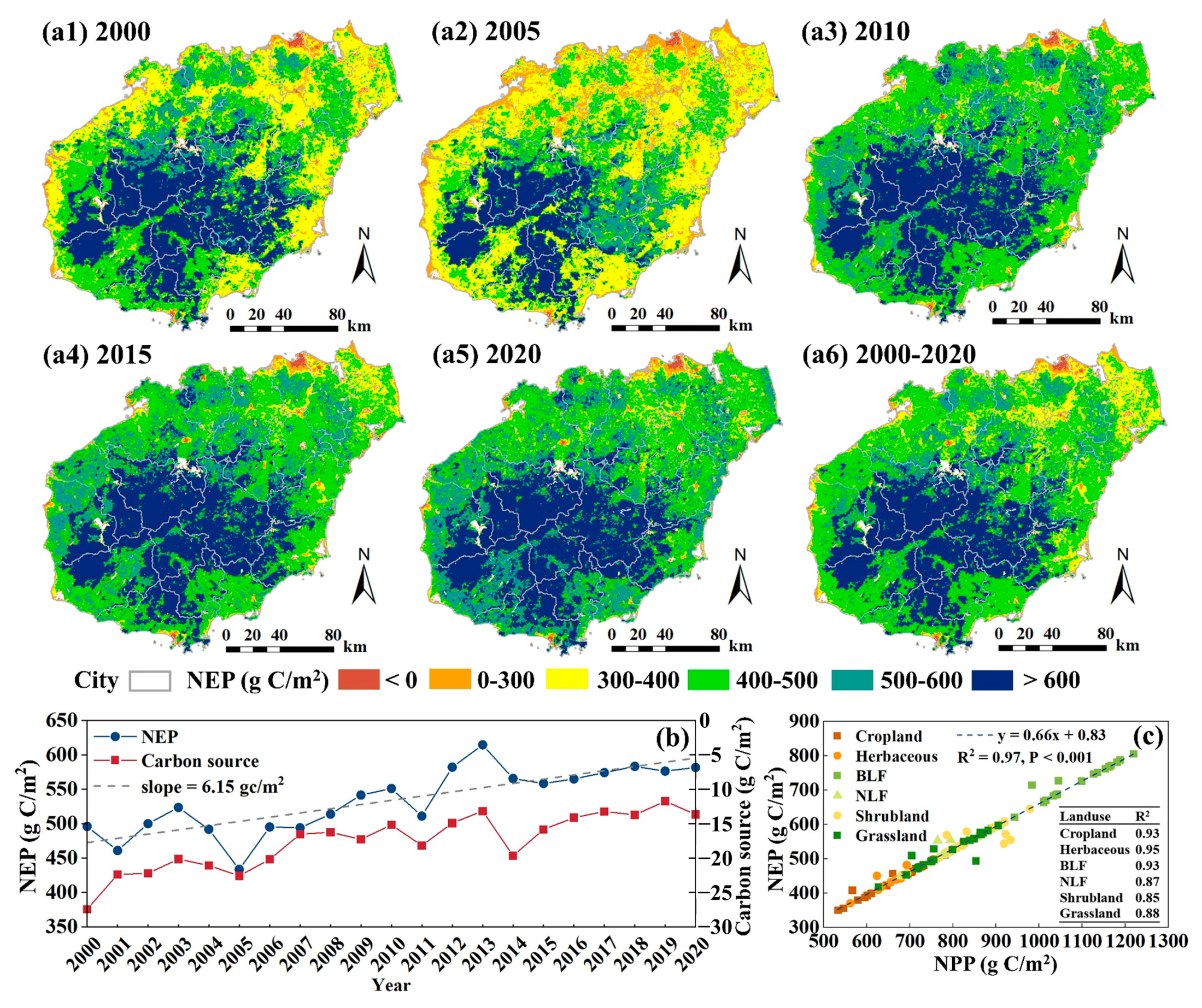
3.3. Evaluation of Carbon Sink Based on NEP
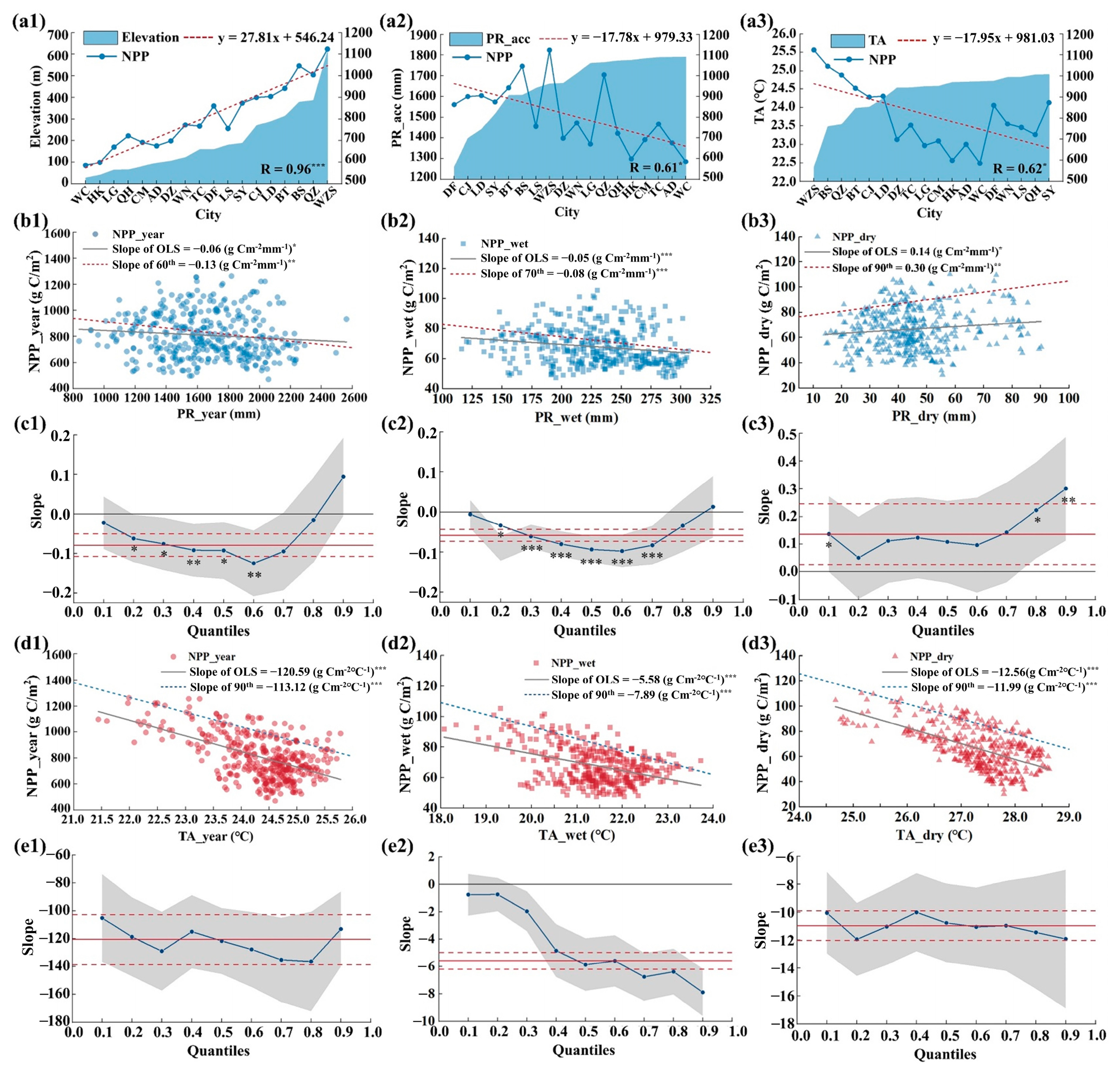
3.4. Effects of Natural Factors on NPP
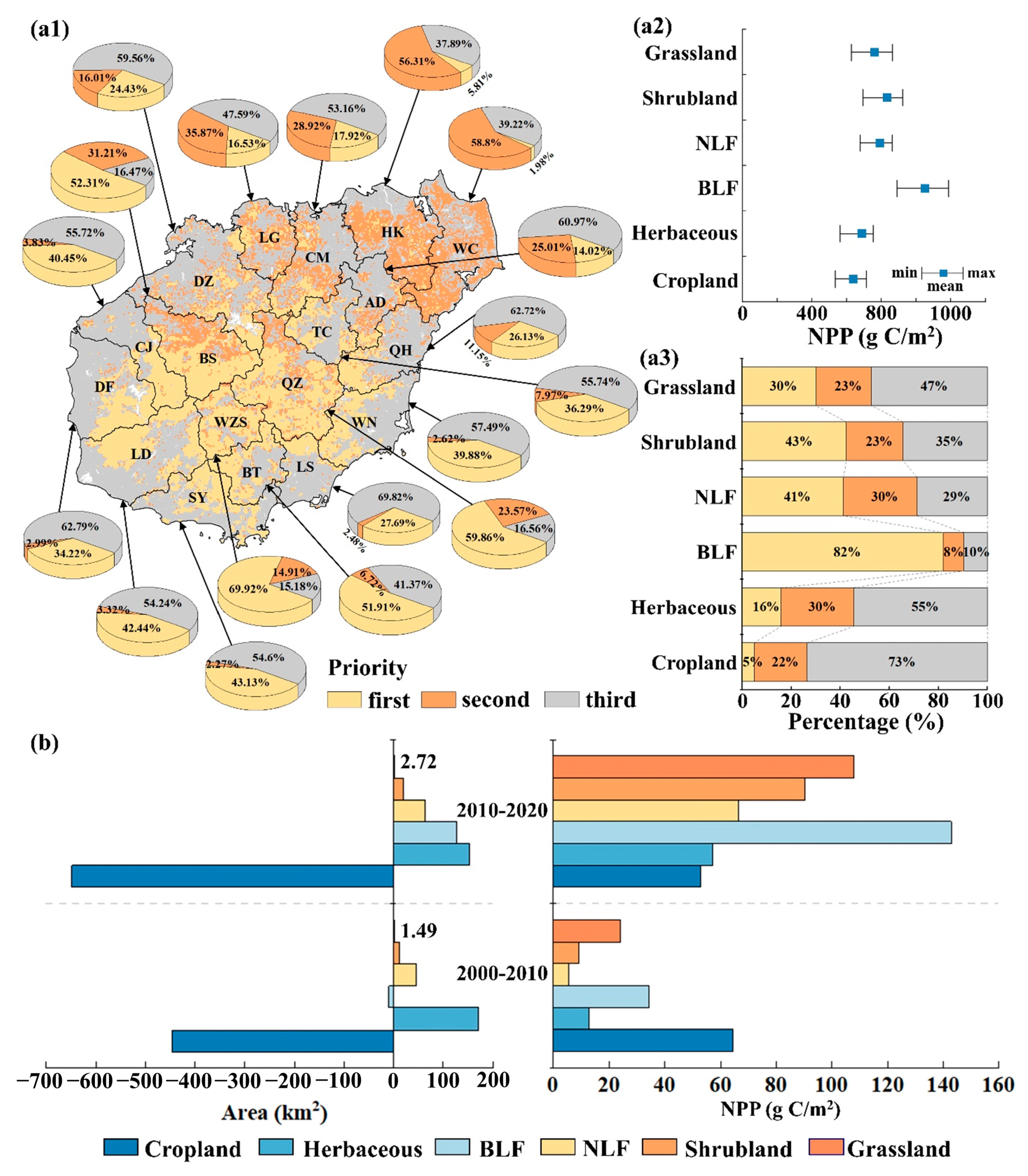
3.5. Response of NPP to Land Use Change
4. Discussion
4.1. Improvements of the Remote Sensing Methods to Estimate Carbon Dioxide Flux
4.2. Influencing Factors of Vegetation NPP
4.3. Uncertainties and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Model Structure Supplement
Appendix B. Accuracy of NPP Simulations at Pixel Scales
| Year | GLASS_NPP | MODIS_NPP | ||||
|---|---|---|---|---|---|---|
| R | RMSE (g C/m2) | NRMSE | R | RMSE (g C/m2) | NRMSE | |
| 2000 | 0.78 | 159.56 | 14.87% | |||
| 2001 | 0.83 | 146.59 | 11.63% | 0.74 | 256.03 | 17.51% |
| 2002 | 0.82 | 155.03 | 12.10% | 0.77 | 218.46 | 14.91% |
| 2003 | 0.75 | 170.87 | 13.41% | 0.80 | 184.06 | 12.67% |
| 2004 | 0.84 | 160.93 | 12.60% | 0.72 | 265.09 | 17.64% |
| 2005 | 0.73 | 177.91 | 15.13% | 0.69 | 274.53 | 19.47% |
| 2006 | 0.76 | 171.75 | 13.64% | 0.78 | 184.06 | 12.64% |
| 2007 | 0.78 | 146.51 | 11.96% | 0.75 | 182.71 | 13.10% |
| 2008 | 0.81 | 169.60 | 14.12% | 0.77 | 241.39 | 16.63% |
| 2009 | 0.80 | 157.83 | 12.56% | 0.70 | 278.40 | 19.07% |
| 2010 | 0.77 | 179.58 | 14.45% | 0.70 | 271.23 | 18.62% |
| 2011 | 0.85 | 142.21 | 11.25% | 0.74 | 200.82 | 12.97% |
| 2012 | 0.77 | 218.62 | 16.69% | 0.73 | 264.29 | 16.57% |
| 2013 | 0.84 | 139.25 | 10.90% | 0.78 | 192.43 | 11.47% |
| 2014 | 0.86 | 144.74 | 11.10% | 0.76 | 228.50 | 14.84% |
| 2015 | 0.75 | 180.59 | 13.83% | 0.70 | 279.59 | 17.71% |
| 2016 | 0.77 | 168.88 | 13.30% | 0.71 | 240.78 | 16.21% |
| 2017 | 0.82 | 176.52 | 13.83% | 0.76 | 247.27 | 16.74% |
| 2018 | 0.80 | 166.30 | 12.74% | 0.73 | 240.13 | 15.79% |
| 2019 | 0.78 | 194.50 | 15.30% | 0.74 | 252.73 | 16.51% |
| 2020 | 0.79 | 200.65 | 12.61% | 0.74 | 268.70 | 17.87% |
Appendix C. Accuracy of LAI Simulations
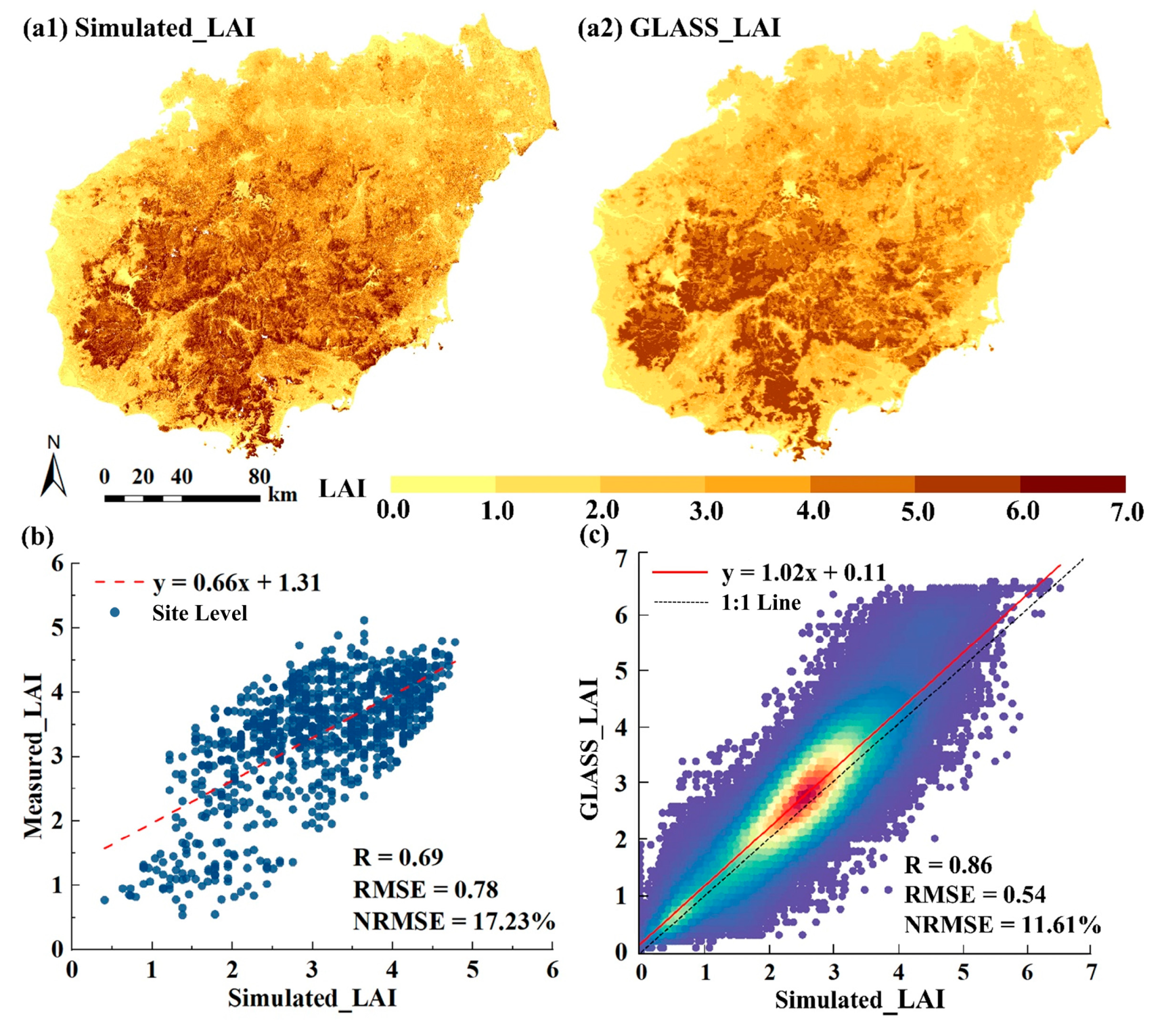
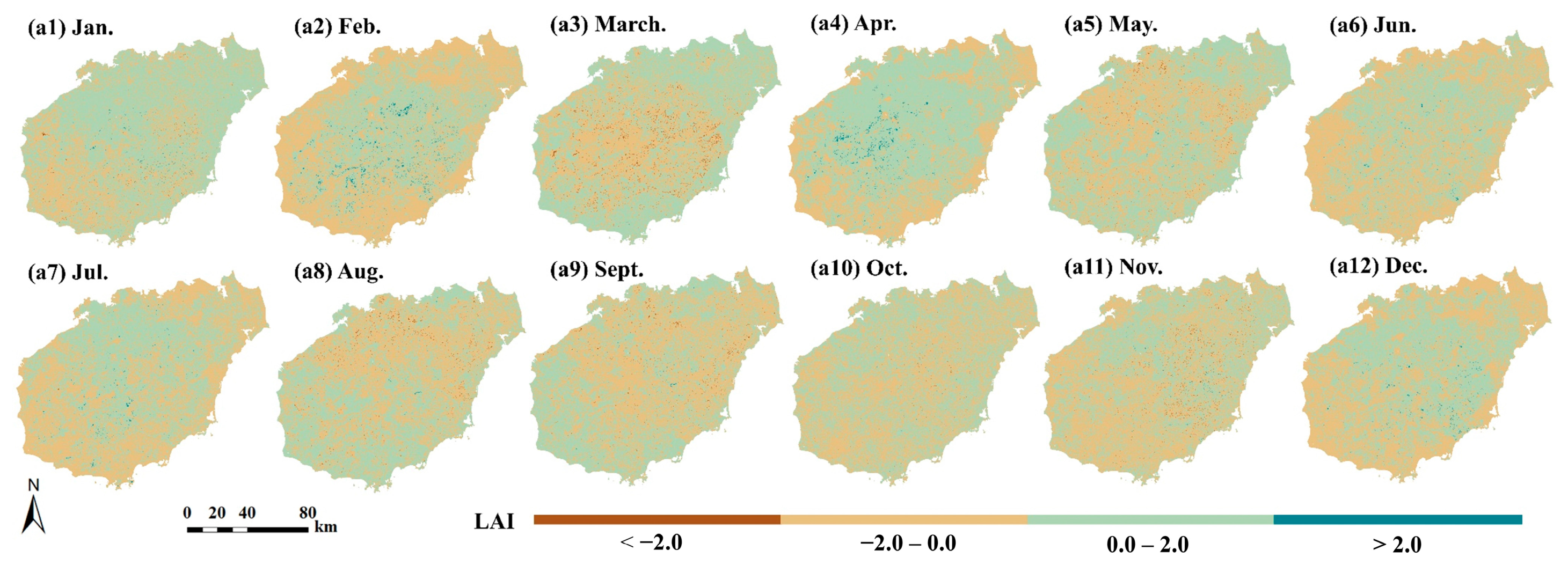
References
- Piao, S.L.; Yue, C.; Ding, J.Z.; Guo, Z.T. Perspectives on the role of terrestrial ecosystems in the ‘carbon neutrality’ strategy. Sci. China-Earth Sci. 2022, 65, 1178–1186. [Google Scholar] [CrossRef]
- Zhang, D.N.; Zhao, Y.H.; Wu, J.S. Assessment of carbon balance attribution and carbon storage potential in China’s terrestrial ecosystem. Resour. Conserv. Recycl. 2023, 189, 106748. [Google Scholar] [CrossRef]
- Cao, S.P.; Yi, H.; Zhang, L.F.; Sun, Q.; Zhang, Y.L.; Li, H.Z.; Wei, X.; Liu, Y.X. Spatiotemporal dynamics of vegetation net ecosystem productivity and its response to drought in Northwest China. GIlscience Remote Sens. 2023, 60, 2194597. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Ju, W.; Chen, J.M.; Ciais, P.; Cescatti, A.; Sardans, J.; Janssens, I.A.; Wu, M.; Berry, J.A.; et al. Recent global decline of CO2 fertilization effects on vegetation photosynthesis. Science 2020, 370, 1295–1300. [Google Scholar] [CrossRef]
- Gamage, D.; Thompson, M.; Sutherland, M.; Hirotsu, N.; Makino, A.; Seneweera, S. New insights into the cellular mechanisms of plant growth at elevated atmospheric carbon dioxide concentrations. Plant Cell Environ. 2018, 41, 1233–1246. [Google Scholar] [CrossRef] [PubMed]
- O’ishi, R.; Abe-Ouchi, A. Influence of dynamic vegetation on climate change arising from increasing CO2. Clim. Dyn. 2009, 33, 645–663. [Google Scholar] [CrossRef]
- Alo, C.A.; Wang, G.L. Potential future changes of the terrestrial ecosystem based on climate projections by eight general circulation models. J. Geophys. Res.-Biogeosci. 2008, 113, G01004. [Google Scholar] [CrossRef]
- Grace, J.; Mitchard, E.; Gloor, E. Perturbations in the carbon budget of the tropics. Glob. Chang. Biol. 2014, 20, 3238–3255. [Google Scholar] [CrossRef] [PubMed]
- Bond-Lamberty, B.; Bailey, V.L.; Chen, M.; Gough, C.M.; Vargas, R. Globally rising soil heterotrophic respiration over recent decades. Nature 2018, 560, 80–83. [Google Scholar] [CrossRef]
- Running, S.W. A Measurable Planetary Boundary for the Biosphere. Science 2012, 337, 1458–1459. [Google Scholar] [CrossRef]
- Hou, E.Q.; Ma, S.; Huang, Y.Y.; Zhou, Y.; Kim, H.S.; Lopez-Blanco, E.; Jiang, L.F.; Xia, J.Y.; Tao, F.; Williams, C.; et al. Across-model spread and shrinking in predicting peatland carbon dynamics under global change. Glob. Chang. Biol. 2023, 29, 2759–2775. [Google Scholar] [CrossRef] [PubMed]
- Hinko-Najera, N.; Isaac, P.; Beringer, J.; van Gorsel, E.; Ewenz, C.; McHugh, I.; Exbrayat, J.F.; Livesley, S.J.; Arndt, S.K. Net ecosystem carbon exchange of a dry temperate eucalypt forest. Biogeosciences 2017, 14, 3781–3800. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Guo, Q.H. Application of CASA model to the estimation of Chinese terrestrial net primary productivity. Chin. J. Plant Ecol. 2001, 25, 603–608. (In Chinese) [Google Scholar]
- Qu, S.; Wang, L.C.; Lin, A.W.; Yu, D.Q.; Yuan, M.X.; Li, C.A. Distinguishing the impacts of climate change and anthropogenic factors on vegetation dynamics in the Yangtze River Basin, China. Ecol. Indic. 2020, 108, 105724. [Google Scholar] [CrossRef]
- Cai, W.W.; Yuan, W.P.; Liang, S.L.; Liu, S.G.; Dong, W.J.; Chen, Y.; Liu, D.; Zhang, H.C. Large Differences in Terrestrial Vegetation Production Derived from Satellite-Based Light Use Efficiency Models. Remote Sens. 2014, 6, 8945–8965. [Google Scholar] [CrossRef]
- Xie, X.Y.; Li, A.N.; Tan, J.B.; Jin, H.A.; Nan, X.; Zhang, Z.J.; Bian, J.H.; Lei, G.B. Assessments of gross primary productivity estimations with satellite data-driven models using eddy covariance observation sites over the northern hemisphere. Agric. For. Meteorol. 2020, 280, 107771. [Google Scholar] [CrossRef]
- Chiesi, M.; Maselli, F.; Moriondo, M.; Fibbi, L.; Bindi, M.; Running, S.W. Application of BIOME-BGC to simulate Mediterranean forest processes. Ecol. Model. 2007, 206, 179–190. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, W.F.; Liu, B.J.; Tian, X.; Chen, S.X.; Wang, H.Y.; Mao, Y.W. Forest Carbon Flux Simulation Using Multi-Source Data and Incorporation of Remotely Sensed Model with Process-Based Model. Remote Sens. 2022, 14, 4766. [Google Scholar] [CrossRef]
- Zhang, H.K.K.; Roy, D.P.; Yan, L.; Li, Z.B.; Huang, H.Y.; Vermote, E.; Skakun, S.; Roger, J.C. Characterization of Sentinel-2A and Landsat-8 top of atmosphere, surface, and nadir BRDF adjusted reflectance and NDVI differences. Remote Sens. Environ. 2018, 215, 482–494. [Google Scholar] [CrossRef]
- Niu, Z.E.; He, H.L.; Peng, S.S.; Ren, X.L.; Zhang, L.; Gu, F.X.; Zhu, G.F.; Peng, C.H.; Li, P.; Wang, J.B.; et al. A Process-Based Model Integrating Remote Sensing Data for Evaluating Ecosystem Services. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002451. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- He, Q.N.; Ju, W.M.; Dai, S.P.; He, W.; Song, L.; Wang, S.H.; Li, X.C.A.; Mao, G.X. Drought Risk of Global Terrestrial Gross Primary Productivity Over the Last 40 Years Detected by a Remote Sensing-Driven Process Model. J. Geophys. Res.-Biogeosci. 2021, 126, e2020JG005944. [Google Scholar] [CrossRef]
- Zhao, M.S.; Running, S.W. Drought-Induced Reduction in Global Terrestrial Net Primary Production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.C.; Zhao, X.; Shi, J.K.; Huang, J.C.; Tang, J.; Zhang, R.R.; Chen, J.; Wang, Q.F.; Zeng, J.Y. The influence of temperature and precipitation on the vegetation dynamics of the tropical island of Hainan. Theor. Appl. Climatol. 2021, 143, 429–445. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.L.; Lai, C.G.; Wu, X.Q.; Zeng, Z.Y.; Chen, X.H.; Lian, Y.Q. Response of net primary production to land use and land cover change in mainland China since the late 1980s. Sci. Total Environ. 2018, 639, 237–247. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.H.; Wang, S.J.; Bai, X.Y.; Tian, Y.C.; Luo, G.J.; Wang, J.F.; Li, Q.; Chen, F.; Deng, Y.H.; Yang, Y.J.; et al. Climate change weakens the positive effect of human activities on karst vegetation productivity restoration in southern China. Ecol. Indic. 2020, 115, 106392. [Google Scholar] [CrossRef]
- Tong, X.W.; Brandt, M.; Yue, Y.M.; Horion, S.; Wang, K.L.; De Keersmaecker, W.; Tian, F.; Schurgers, G.; Xiao, X.M.; Luo, Y.Q.; et al. Increased vegetation growth and carbon stock in China karst via ecological engineering. Nat. Sustain. 2018, 1, 44–50. [Google Scholar] [CrossRef]
- Cao, F.F.; Li, J.X.; Fu, X.; Wu, G. Impacts of land conversion and management measures on net primary productivity in semi-arid grassland. Ecosyst. Health Sustain. 2020, 6, 1749010. [Google Scholar] [CrossRef]
- Wei, X.D.; Yang, J.; Luo, P.P.; Lin, L.G.; Lin, K.L.; Guan, J.M. Assessment of the variation and influencing factors of vegetation NPP and carbon sink capacity under different natural conditions. Ecol. Indic. 2022, 138, 108834. [Google Scholar] [CrossRef]
- Lin, M.Z.; Ling, Q.P.; Pei, H.Q.; Song, Y.N.; Qiu, Z.X.; Wang, C.; Liu, T.D.; Gong, W.F. Remote Sensing of Tropical Rainforest Biomass Changes in Hainan Island, China from 2003 to 2018. Remote Sens. 2021, 13, 1696. [Google Scholar] [CrossRef]
- Dong, H.W.; Li, P.; Feng, Z.M.; Yang, Y.Z.; You, Z.; Li, Q. Natural capital utilization on an international tourism island based on a three-dimensional ecological footprint model: A case study of Hainan Province, China. Ecol. Indic. 2019, 104, 479–488. [Google Scholar] [CrossRef]
- Baccini, A.; Walker, W.; Carvalho, L.; Farina, M.; Sulla-Menashe, D.; Houghton, R.A. Tropical forests are a net carbon source based on aboveground measurements of gain and loss. Science 2017, 358, 230–233. [Google Scholar] [CrossRef] [PubMed]
- Longo, M.; Keller, M.; dos-Santos, M.N.; Leitold, V.; Pinage, E.R.; Baccini, A.; Saatchi, S.; Nogueira, E.M.; Batistella, M.; Morton, D.C. Aboveground biomass variability across intact and degraded forests in the Brazilian Amazon. Glob. Biogeochem. Cycles 2016, 30, 1639–1660. [Google Scholar] [CrossRef]
- Sun, R.; Wu, Z.X.; Chen, B.Q.; Yang, C.; Qi, D.L.; Lan, G.Y.; Fraedrich, K. Effects of land-use change on eco-environmental quality in Hainan Island, China. Ecol. Indic. 2020, 109, 105777. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.Y.; Zhao, T.T.; Gao, Y.; Chen, X.D.; Mi, J. GISD30: Global 30 m impervious-surface dynamic dataset from 1985 to 2020 using time-series Landsat imagery on the Google Earth Engine platform. Earth Syst. Sci. Data 2022, 14, 1831–1856. [Google Scholar] [CrossRef]
- Bajgain, R.; Xiao, X.M.; Wagle, P.; Basara, J.; Zhou, Y.T. Sensitivity analysis of vegetation indices to drought over two tallgrass prairie sites. Isprs J. Photogramm. Remote Sens. 2015, 108, 151–160. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. S2ToolBox Level 2 products: LAI, FAPAR, FCOVER, Version 1.1. In ESA Contract nr 4000110612/14/I-BG; INRA Avignon: Paris, France, 2016; p. 52. [Google Scholar]
- Eilers, P.H.C. A perfect smoother. Anal. Chem. 2003, 75, 3631–3636. [Google Scholar] [CrossRef] [PubMed]
- Li, W.J.; Weiss, M.; Waldner, F.; Defourny, P.; Demarez, V.; Morin, D.; Hagolle, O.; Baret, F. A Generic Algorithm to Estimate LA!, FAPAR and FCOVER Variables from SPOT4 HRVIR and Landsat Sensors: Evaluation of the Consistency and Comparison with Ground Measurements. Remote Sens. 2015, 7, 15494–15516. [Google Scholar] [CrossRef]
- Wang, J.W.; Lopez-Lozano, R.; Weiss, M.; Buis, S.; Li, W.J.; Liu, S.Y.; Baret, F.; Zhang, J.H. Crop specific inversion of PROSAIL to retrieve green area index (GAI) from several decametric satellites using a Bayesian framework. Remote Sens. Environ. 2022, 278, 113085. [Google Scholar] [CrossRef]
- Djamai, N.; Fernandes, R.; Weiss, M.; McNairn, H.; Goita, K. Validation of the Sentinel Simplified Level 2 Product Prototype Processor (SL2P) for mapping cropland biophysical variables using Sentinel-2/MSI and Landsat-8/OLI data. Remote Sens. Environ. 2019, 225, 416–430. [Google Scholar] [CrossRef]
- Wolanin, A.; Camps-Valls, G.; Gomez-Chova, L.; Mateo-Garcia, G.; van der Tol, C.; Zhang, Y.G.; Guanter, L. Estimating crop primary productivity with Sentinel-2 and Landsat 8 using machine learning methods trained with radiative transfer simulations. Remote Sens. Environ. 2019, 225, 441–457. [Google Scholar] [CrossRef]
- Zheng, J.; Sun, N.X.; Yan, J.L.; Liu, C.J.; Yin, S. Decoupling between carbon source and sink induced by responses of daily stem growth to water availability in subtropical urban forests. Sci. Total Environ. 2023, 877, 162802. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.L.; Wang, Q.F.; Zhu, J.X.; Chen, Z.; He, N.P.; Yu, G.R. A spatial and temporal dataset of atmospheric inorganic nitrogen wet deposition in China (1996–2015). China Sci. Data 2019, 4, 1. [Google Scholar] [CrossRef]
- Jia, Y.L.; Wang, Q.F.; Zhu, J.X.; Chen, Z.; He, N.P.; Yu, G.R. A spatial and temporal dataset of atmospheric inorganic nitrogen dry deposition in China (2006–2015). China Sci. Data 2021, 6, 1. [Google Scholar] [CrossRef]
- Zeng, J.; Matsunaga, T.; Tan, Z.H.; Saigusa, N.; Shirai, T.; Tang, Y.; Peng, S.; Fukuda, Y. Global terrestrial carbon fluxes of 1999–2019 estimated by upscaling eddy covariance data with a random forest. Sci. Data 2020, 7, 313. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.X. Dynamics and Controls of Carbon Exchange of a Tropical Montane Rain Forest at Jianfengling, China. Ph.D. Thesis, Chinese Academy of Forestry, Beijing, China, 2010. [Google Scholar]
- Yang, S.Q.; Liu, J.Y.; Yang, C.; Lan, G.Y.; Song, B.; Wu, Z.X. A dataset of carbon and water fluxes and micrometerological elements from rubber plantations of Danzhou City, Hainan Province (2010–2018). Sci. Data Bank 2022, 7, 354–366. [Google Scholar] [CrossRef]
- He, H.; Wang, S.; Zhang, L.; Wang, J.; Ren, X.; Zhou, L.; Piao, S.; Yan, H.; Ju, W.; Gu, F.; et al. Altered trends in carbon uptake in China’s terrestrial ecosystems under the enhanced summer monsoon and warming hiatus. Natl. Sci. Rev. 2019, 6, 505–514. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Liang, S. Development of the GLASS 250-m leaf area index product (version 6) from MODIS data using the bidirectional LSTM deep learning model. Remote Sens. Environ. 2022, 273, 112985. [Google Scholar] [CrossRef]
- Dai, S.P.; Luo, H.X.; Zheng, Q.; Hu, Y.Y.; Li, H.L.; Li, M.F.; Yi, X.; Chen, B.Q. Comparison of Remote Sensing Estimation Models for Leaf Area Index of Rubber Plantation in Hainan Island. Smart Agric. 2021, 3, 45–54. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Cihlar, J.; Park, W.M. A process-based boreal ecosystem productivity simulator using remote sensing inputs. Remote Sens. Environ. 1997, 62, 158–175. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Cihlar, J.; Chen, W. Net primary productivity distribution in the BOREAS region from a process model using satellite and surface data. J. Geophys. Res. Atmos. 1999, 104, 735–754. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, J.S.; Zhang, S.; Koju, U.A.; Yao, F.M.; Igbawua, T. Using precipitation, vertical root distribution, and satellite-retrieved vegetation information to parameterize water stress in a Penman-Monteith approach to evapotranspiration modeling under Mediterranean climate. J. Adv. Model. Earth Syst. 2017, 9, 168–192. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, D.M.; Zhao, X.Y. Impact of aerosols on terrestrial gross primary productivity in North China using an improved boreal ecosystem productivity simulator with satellite-based aerosol optical depth. GIscience Remote Sens. 2020, 57, 258–270. [Google Scholar] [CrossRef]
- Lu, X.M.; Zheng, G.; Miller, C.; Alvarado, E. Combining Multi-Source Remotely Sensed Data and a Process-Based Model for Forest Aboveground Biomass Updating. Sensors 2017, 17, 2062. [Google Scholar] [CrossRef] [PubMed]
- Kang, F.F.; Li, X.J.; Du, H.Q.; Mao, F.J.; Zhou, G.M.; Xu, Y.X.; Huang, Z.H.; Ji, J.Y.; Wang, J.Y. Spatiotemporal Evolution of the Carbon Fluxes from Bamboo Forests and their Response to Climate Change Based on a BEPS Model in China. Remote Sens. 2022, 14, 366. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Caemmerer, S.V.; Berry, J.A. A Biochemical-Model of Photosynthetic CO2 Assimilation in Leaves of C-3 Species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycles 2012, 26, 1–18. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Bai, Y.; Koju, U.A.; Igbawua, T.; Chang, Q.; Zhang, D.; Yao, F. Evaluation and improvement of the daily boreal ecosystem productivity simulator in simulating gross primary productivity at 41 flux sites across Europe. Ecol. Model. 2018, 368, 205–232. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B., III. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Pei, Y.Z.; Zhou, C.P.; Ouyang, H.; Yang, W.B. A carbon budget of alpine steppe area in the Tibetan Plateau. Geogr. Res. 2010, 29, 102–110. [Google Scholar] [CrossRef]
- Xiang, H.; Zhang, J.; Mao, D.; Wang, Z.; Qiu, Z.; Yan, H. Identifying spatial similarities and mismatches between supply and demand of ecosystem services for sustainable Northeast China. Ecol. Indic. 2022, 134, 108501. [Google Scholar] [CrossRef]
- Shen, W.; Zhang, J.; Wang, K.; Zhang, Z. Identifying the spatio-temporal dynamics of regional ecological risk based on Google Earth Engine: A case study from Loess Plateau, China. Sci. Total Environ. 2023, 873, 162346. [Google Scholar] [CrossRef] [PubMed]
- Cade, B.S.; Noon, B.R.; Flather, C.H. Quantile regression reveals hidden bias and uncertainty in habitat models. Ecology 2005, 86, 786–800. [Google Scholar] [CrossRef]
- Chang, Q.; Xiao, X.; Jiao, W.; Wu, X.; Doughty, R.; Wang, J.; Du, L.; Zhou, Z.; Qin, Y. Assessing consistency of spring phenology of snow-covered forests as estimated by vegetation indices, gross primary production, and solar-induced chlorophyll fluorescence. Agric. For. Meteorol. 2019, 275, 305–316. [Google Scholar] [CrossRef]
- Wagle, P.; Xiao, X.; Torn, M.S.; Cook, D.R.; Matamala, R.; Fischer, M.L.; Jin, C.; Dong, J.W.; Biradar, C. Sensitivity of vegetation indices and gross primary production of tallgrass prairie to severe drought. Remote Sens. Environ. 2014, 152, 1–14. [Google Scholar] [CrossRef]
- Dong, G.; Chen, S.; Liu, K.; Wang, W.; Hou, H.; Gao, L.; Zhang, F.; Su, H. Spatiotemporal variation in sensitivity of urban vegetation growth and greenness to vegetation water content: Evidence from Chinese megacities. Sci. Total Environ. 2023, 905, 167090. [Google Scholar] [CrossRef] [PubMed]
- Bandaru, V.; Yaramasu, R.; Jones, C.; Izaurralde, R.C.; Reddy, A.; Sedano, F.; Daughtry, C.S.T.; Becker-Reshef, I.; Justice, C. Geo-CropSim: A Geo-spatial crop simulation modeling framework for regional scale crop yield and water use assessment. J. Photogramm. Remote Sens. 2022, 183, 34–53. [Google Scholar] [CrossRef]
- Huang, X.L.; Han, S.; Shi, C.X. Evaluation of Three Air Temperature Reanalysis Datasets in the Alpine Region of the Qinghai-Tibet Plateau. Remote Sens. 2022, 14, 4447. [Google Scholar] [CrossRef]
- Zhu, X.J.; Fan, R.X.; Chen, Z.; Wang, Q.F.; Yu, G.R. Eddy covariance-based differences in net ecosystem productivity values and spatial patterns between naturally regenerating forests and planted forests in China. Sci. Rep. 2022, 12, 20556. [Google Scholar] [CrossRef]
- Wang, W.; Chen, W.; Wang, S. Forest soil respiration and its heterotrophic and autotrophic components: Global patterns and responses to temperature and precipitation. Soil Biol. Biochem. 2010, 42, 1236–1244. [Google Scholar] [CrossRef]
- Zhang, S.R.; Bai, X.Y.; Zhao, C.W.; Tan, Q.; Luo, G.J.; Wu, L.H.; Xi, H.P.; Li, C.J.; Chen, F.; Ran, C.; et al. China’s carbon budget inventory from 1997 to 2017 and its challenges to achieving carbon neutral strategies. J. Clean. Prod. 2022, 347, 130966. [Google Scholar] [CrossRef]
- Zhu, L.; Li, W.; Ciais, P.; He, J.Y.; Cescatti, A.; Santoro, M.; Tanaka, K.; Cartus, O.; Zhao, Z.; Xu, Y.D.; et al. Comparable biophysical and biogeochemical feedbacks on warming from tropical moist forest degradation. Nat. Geosci. 2023, 16, 244–249. [Google Scholar] [CrossRef]
- Yang, Y.; Saatchi, S.S.; Xu, L.; Yu, Y.; Choi, S.; Phillips, N.; Kennedy, R.; Keller, M.; Knyazikhin, Y.; Myneni, R.B. Post-drought decline of the Amazon carbon sink. Nat. Commun. 2018, 9, 3172. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Merow, C.; Liu, Z.H.; Park, D.S.; Roehrdanz, P.R.; Maitner, B.; Newman, E.A.; Boyle, B.L.; Lien, A.; Burger, J.R.; et al. How deregulation, drought and increasing fire impact Amazonian biodiversity. Nature 2021, 597, 516–521. [Google Scholar] [CrossRef] [PubMed]
- Villen-Perez, S.; Heikkinen, J.; Salemaa, M.; Makipaa, R. Global warming will affect the maximum potential abundance of boreal plant species. Ecography 2020, 43, 801–811. [Google Scholar] [CrossRef]
- Schuur, E.A.G. Productivity and global climate revisited: The sensitivity of tropical forest growth to precipitation. Ecology 2003, 84, 1165–1170. [Google Scholar] [CrossRef]
- Baumann, M.; Gasparri, I.; Piquer-Rodrguez, M.; Pizarro, G.G.; Griffiths, P.; Hostert, P.; Kuemmerle, T. Carbon emissions from agricultural expansion and intensification in the Chaco. Glob. Chang. Biol. 2017, 23, 1902–1916. [Google Scholar] [CrossRef]
- Zhou, X.Z.; Wang, Q.F.; Zhang, R.R.; Ren, B.Y.; Wu, X.P.; Wu, Y.; Tang, J.K. A Spatiotemporal Analysis of Hainan Island’s 2010-2020 Gross Ecosystem Product Accounting. Sustainability 2022, 14, 15624. [Google Scholar] [CrossRef]
- Pei, Z.Y.; Ouyang, H.; Zhou, C.P. Carbon balance in an alpine grassland ecosystemon the Tibetan Plateau. J. Integr. Plant Biol. 2009, 51, 521–526. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, S.; Li, C.; Xiong, L.; Song, F.; Du, C.; Li, M.; Luo, Q.; Xue, Y.; Wang, S. A carbon-neutrality-capactiy index for evaluating carbon sink contributions. Environ. Sci. Ecotechnol. 2023, 15, 100237. [Google Scholar] [CrossRef]
- Xu, L.; Saatchi, S.S.; Yang, Y.; Yu, Y.; Pongratz, J.; Bloom, A.A.; Bowman, K.; Worden, J.; Liu, J.; Yin, Y.; et al. Changes in global terrestrial live biomass over the 21st century. Sci. Adv. 2021, 7, eabe9829. [Google Scholar] [CrossRef] [PubMed]
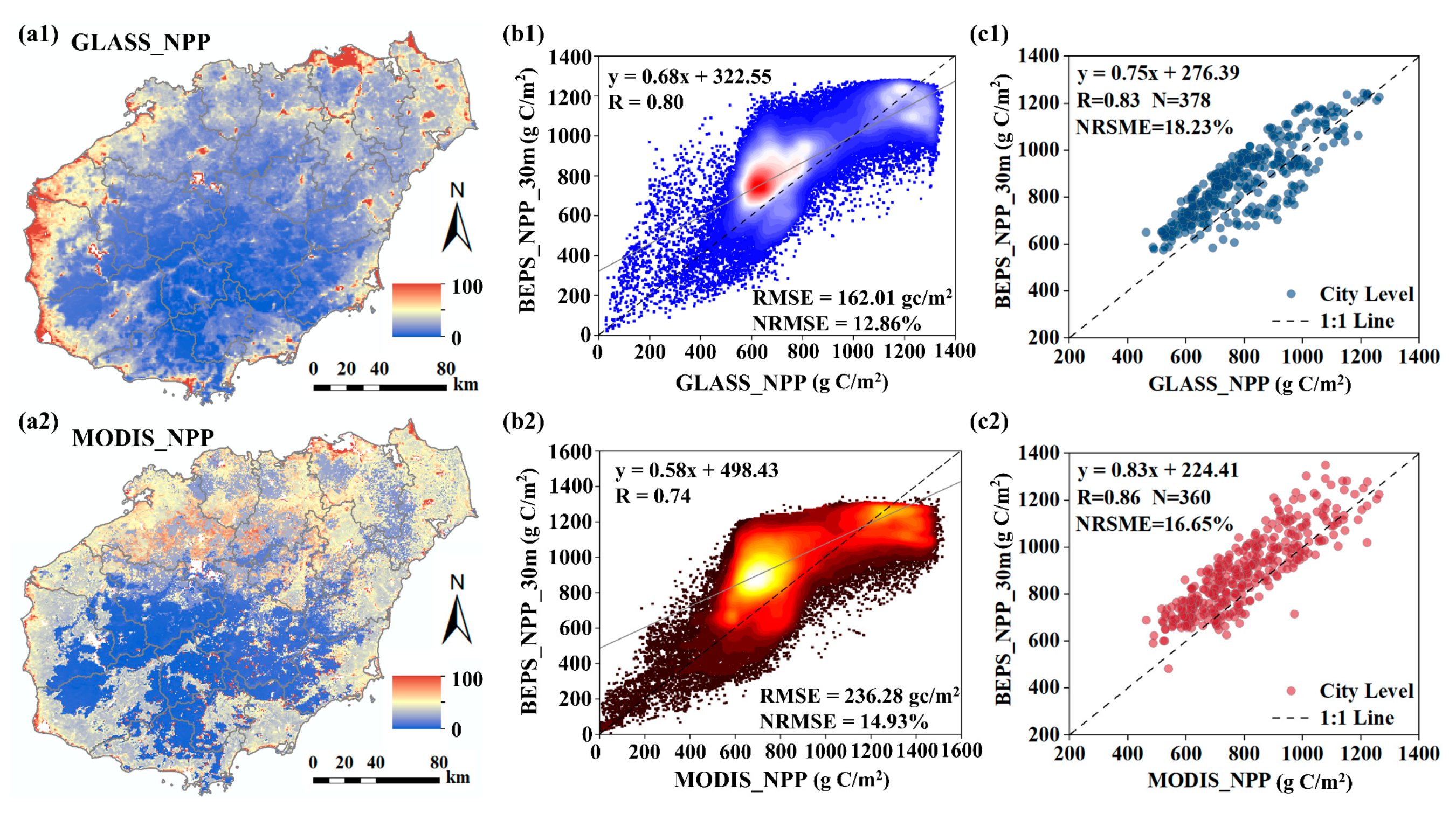
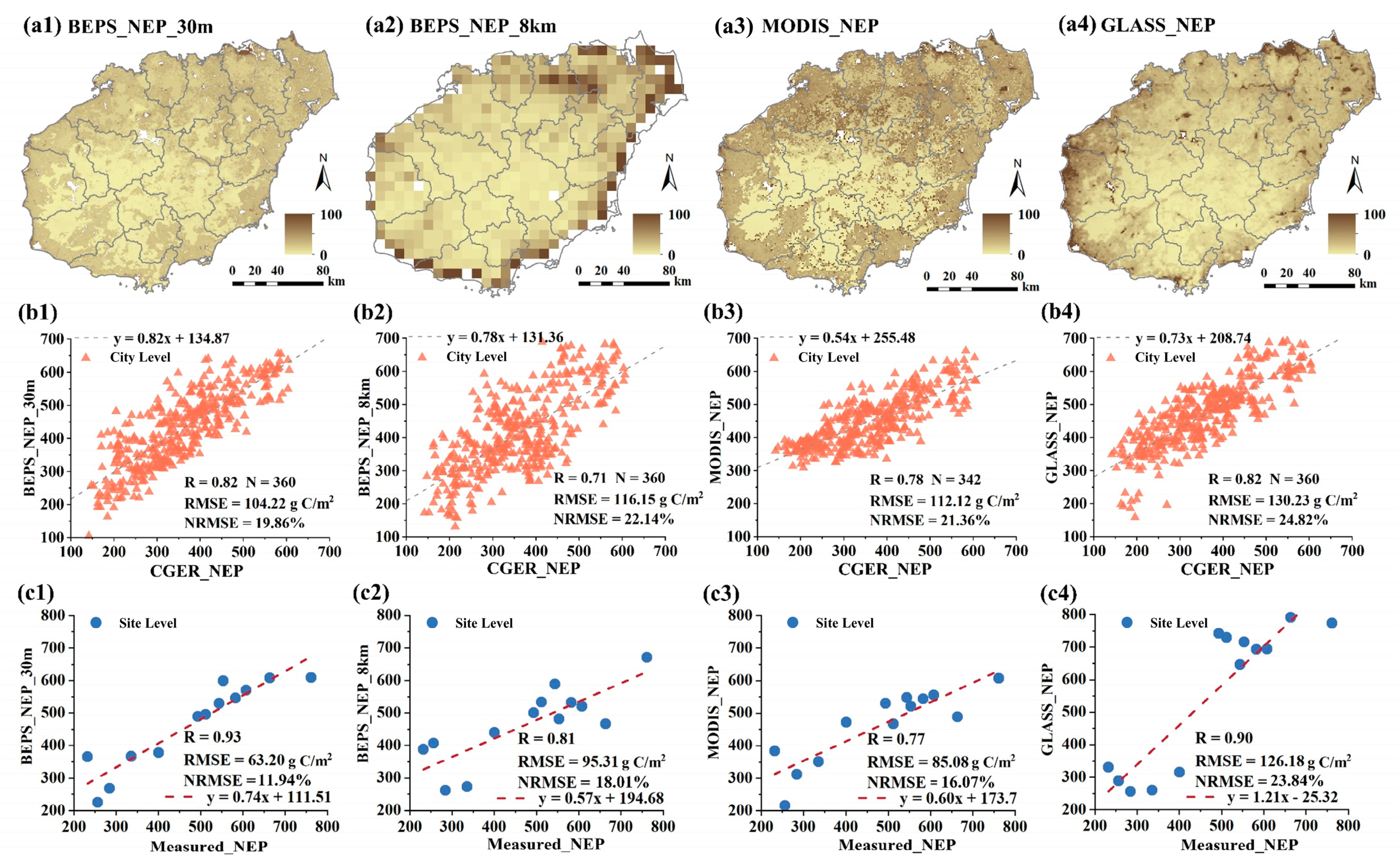

| Sensor (Revisit Period) | Time Period | Spatial Resolution (m) | Bands (μm) | Use |
|---|---|---|---|---|
| Landsat-5 TM (16 days) | 2000–2011 | 30 | Band2-Green (0.52–0.60) | LAI calculation |
| 30 | Band3-Red (0.63–0.69) | LAI calculation | ||
| 30 | Band4-NIR (0.76–0.90) | LSWI and LAI calculation | ||
| 30 | Band5-SWIR 1 (1.55–1.75) | LSWI and LAI calculation | ||
| 30 | Band7-SWIR 2 (2.08–2.35) | LAI calculation | ||
| Landsat-7 ETM+ (16 days) | 2000–2017 | 30 | Band2-Green (0.52–0.60) | LAI calculation |
| 30 | Band3-Red (0.63–0.69) | LAI calculation | ||
| 30 | Band4-NIR (0.76–0.90) | LSWI and LAI calculation | ||
| 30 | Band5-SWIR 1 (1.55–1.75) | LSWI and LAI calculation | ||
| 30 | Band7-SWIR 2 (2.08–2.35) | LAI calculation | ||
| Landsat-8 OLI (16 days) | 2013–2020 | 30 | Band3-Green (0.53–0.60) | LAI calculation |
| 30 | Band4-Red (0.63–0.68) | LAI calculation | ||
| 30 | Band5-NIR (0.85–0.89) | LSWI and LAI calculation | ||
| 30 | Band6-SWIR 1 (1.56–1.66) | LSWI and LAI calculation | ||
| 30 | Band7-SWIR 2 (2.10–2.30) | LAI calculation | ||
| Sentinel-2A MSI (10 days) | 2018–2020 | 10 | Band 3-Green (0.54–0.58) | LAI calculation |
| 10 | Band 4-Red (0.65–0.68) | LAI calculation | ||
| 20 | Band 5-Vegetation Red Edge(0.70–0.71) | LAI calculation | ||
| 20 | Band 6-Vegetation Red Edge(0.73–0.75) | LAI calculation | ||
| 20 | Band 7-Vegetation Red Edge(0.70–0.71) | LAI calculation | ||
| 20 | Band 8A-NIR (0.85–0.88) | LSWI and LAI calculation | ||
| 20 | Band 11-SWIR 1 (1.54–1.69) | LSWI and LAI calculation | ||
| 20 | Band 12-SWIR 2 (2.10–2.28) | LAI calculation |
| 2000 | Variables | 2020 | ||||||
|---|---|---|---|---|---|---|---|---|
| CL | HB | BLF | NLF | SL | GL | IS | ||
| CL | ΔArea (km2) | 30.8 | 328.1 | 63.4 | 1097.9 | 1.9 | 389.8 | |
| ΔNPP (g C/m2) | 83.2 | 150.1 | 135.5 | 108.2 | 126.5 | −76.3 | ||
| HB | ΔArea (km2) | 0.2 | 0.2 | 0.0036 | 1.4 | 0 | 0.05 | |
| ΔNPP (g C/m2) | 41.3 | 99.5 | 127.3 | 84.5 | 0 | −63.2 | ||
| BLF | ΔArea (km2) | 166.9 | 54.5 | 14.7 | 425.2 | 0.3 | 13.6 | |
| ΔNPP (g C/m2) | 64.2 | 24.6 | 59.4 | 43.8 | 54.3 | −94.3 | ||
| NLF | ΔArea (km2) | 1.1 | 0.2 | 2.1 | 0.9 | 0 | 0.1 | |
| ΔNPP (g C/m2) | 58.5 | 59.7 | 191.1 | 120.7 | 0 | −69.7 | ||
| SL | ΔArea (km2) | 701.0 | 235.8 | 462.7 | 25.9 | 0.6 | 64.5 | |
| ΔNPP (g C/m2) | 54.5 | 56.7 | 148.4 | 130.5 | 113.5 | −79.3 | ||
| CL | HB | BLF | NLF | SL | GL | IS | |
|---|---|---|---|---|---|---|---|
| Total transfer in (Tg c) | 0.569 | 0.214 | 0.662 | 0.065 | 1.124 | 0.002 | 0.227 |
| Total transfer out (Tg c) | 1.225 | 0.001 | 0.535 | 0.004 | 1.097 | 0 | 0 |
| Transfer difference (in–out) (Tg c) | −0.356 | 0.213 | 0.227 | 0.061 | 0.027 | 0.002 | 0.127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Zhang, J.; Wang, J.; Yao, F.; Zhang, S. Quantitative Assessment of Factors Influencing the Spatiotemporal Variation in Carbon Dioxide Fluxes Simulated by Multi-Source Remote Sensing Data in Tropical Vegetation. Remote Sens. 2023, 15, 5677. https://doi.org/10.3390/rs15245677
Xu R, Zhang J, Wang J, Yao F, Zhang S. Quantitative Assessment of Factors Influencing the Spatiotemporal Variation in Carbon Dioxide Fluxes Simulated by Multi-Source Remote Sensing Data in Tropical Vegetation. Remote Sensing. 2023; 15(24):5677. https://doi.org/10.3390/rs15245677
Chicago/Turabian StyleXu, Ruize, Jiahua Zhang, Jingwen Wang, Fengmei Yao, and Sha Zhang. 2023. "Quantitative Assessment of Factors Influencing the Spatiotemporal Variation in Carbon Dioxide Fluxes Simulated by Multi-Source Remote Sensing Data in Tropical Vegetation" Remote Sensing 15, no. 24: 5677. https://doi.org/10.3390/rs15245677
APA StyleXu, R., Zhang, J., Wang, J., Yao, F., & Zhang, S. (2023). Quantitative Assessment of Factors Influencing the Spatiotemporal Variation in Carbon Dioxide Fluxes Simulated by Multi-Source Remote Sensing Data in Tropical Vegetation. Remote Sensing, 15(24), 5677. https://doi.org/10.3390/rs15245677







