MSISR-STF: Spatiotemporal Fusion via Multilevel Single-Image Super-Resolution
Abstract
:1. Introduction
- 1.
- The multilevel SISR strategy can effectively solve spatiotemporal fusion with large differences in the spatial resolution.
- 2.
- IGNN uses similar blocks in the image to complete the details, which introduces more spatial information for spatiotemporal fusion.
- 3.
- MSISR-STF introduces more spatial information through constraint methods to improve the fusion accuracy.
2. Problem Definition
- 1.
- A pair of an HSLT image and HTLS image at time .
- 2.
- An HTLS image at time k.
3. MSISR-STF
- 1.
- We show the fusion framework used for the research goal, as well as its advantages.
- 2.
- For the prediction of spatial information under a large spatial resolution difference, we introduce a multilevel SISR strategy and introduce the constraint information to enhance this strategy.
- 3.
- For predicting temporal domain information, we use an unmixing-based method to solve the time-varying information.
- 4.
- We calculate the actual change, which is calculated by calculating the weight of the real change by using the amount of change in the predicted image in the temporal and spatial domains. The neighborhood pixels are used to enhance the robustness of the algorithm and fusion accuracy.
3.1. Fusion Framework
3.2. Prediction Based on the Spatial Domain
- 1.
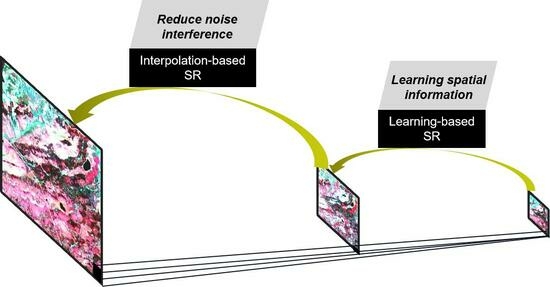
- Aiming at noise accumulation in multilevel SISR, we propose the idea of using the learning-based SISR method IGNN first and, then, the interpolation-based SISR method TPS.
- 2.
- Aiming at obtaining the insufficient spatial information of the HTLS images under large spatial resolution differences, we introduce more information and constraints to ensure information gain and information transmission.
3.2.1. Noise Accumulation: IGNN + TPS
3.2.2. Insufficient Spatial Information: Information Gain + Information Transmission
3.3. Prediction Based on the Temporal Domain
3.3.1. Endmember and Abundance
3.3.2. Change in Temporal Domain:
3.3.3. Temporal Prediction:
3.4. Final Fusion
3.4.1. Temporal and Spatial Prediction Weight: w
3.4.2. Image Fusion Using Neighborhood Information
4. Experiments and Analysis
4.1. Datasets
4.2. Quantitative Evaluating Indicators and Comparison Methods
4.3. Experimental Results
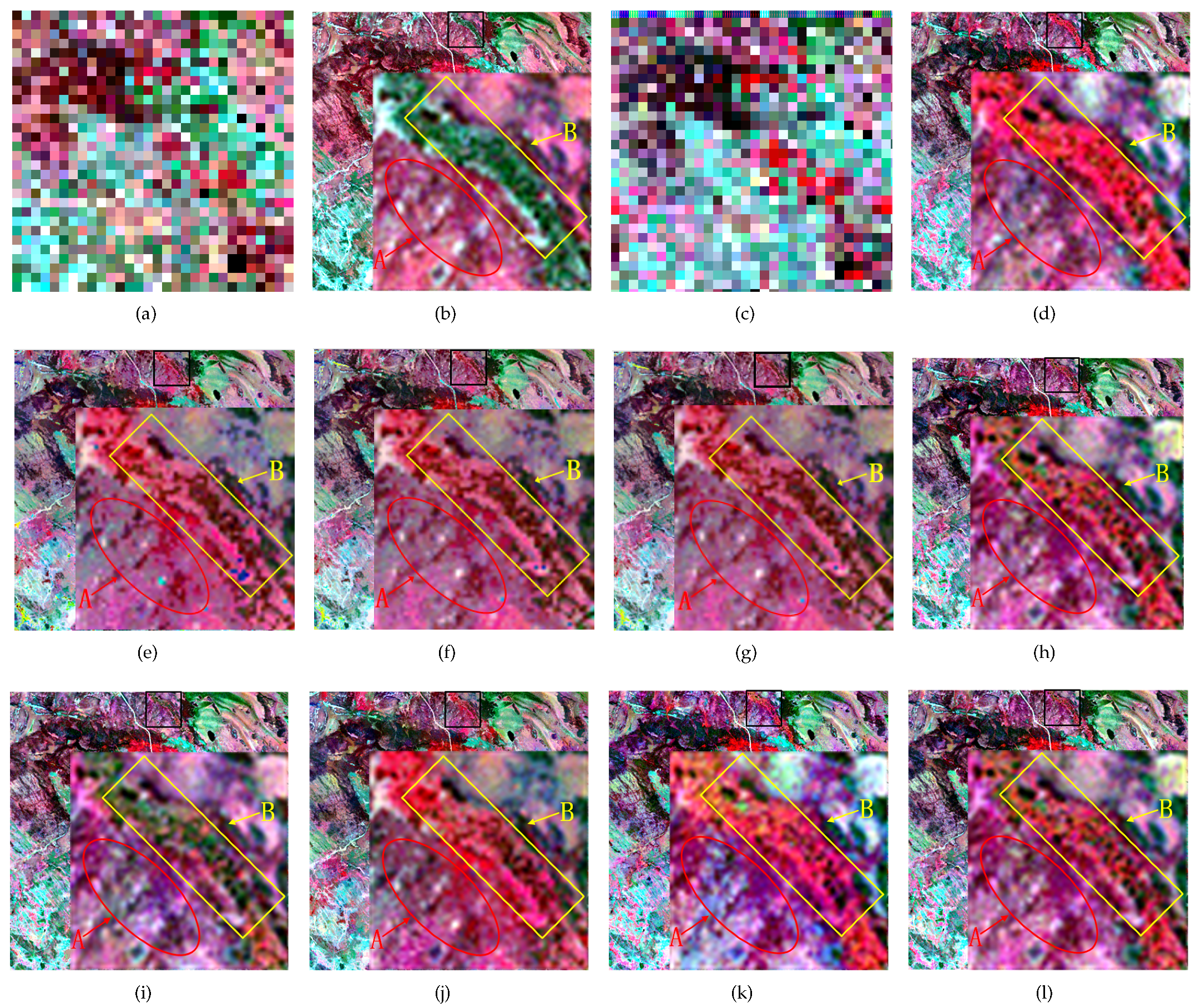
4.3.1. The First Experimental Results: Heterogeneity Changes
4.3.2. The Second Experimental Results: Land Cover Changes
4.4. Computational Costs
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Masek, J.G.; Huang, C.; Wolfe, R.; Cohen, W.; Hall, F.; Kutler, J.; Nelson, P. North American forest disturbance mapped from a decadal Landsat record. Remote Sens. Environ. 2008, 112, 2914–2926. [Google Scholar] [CrossRef]
- Brezini, S.; Deville, Y. Hyperspectral and Multispectral Image Fusion with Automated Extraction of Image-Based Endmember Bundles and Sparsity-Based Unmixing to Deal with Spectral Variability. Sensors 2023, 23, 2341. [Google Scholar] [CrossRef] [PubMed]
- Senf, C.; Leitão, P.J.; Pflugmacher, D.; van der Linden, S.; Hostert, P. Mapping land cover in complex Mediterranean landscapes using Landsat: Improved classification accuracies from integrating multi-seasonal and synthetic imagery. Remote Sens. Environ. 2015, 156, 527–536. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Howard, S.M.; Yang, L.; Larson, C.R.; Wylie, B.K.; Van Driel, N. Completion of the 1990s National Land Cover Data Set for the conterminous United States from Landsat Thematic Mapper data and ancillary data sources. Photogramm. Eng. Remote Sens. 2001, 67, 650–662. [Google Scholar]
- Dou, M.; Chen, J.; Chen, D.; Chen, X.; Deng, Z.; Zhang, X.; Xu, K.; Wang, J. Modeling and simulation for natural disaster contingency planning driven by high-resolution remote sensing images. Future Gener. Comput. Syst. 2014, 37, 367–377. [Google Scholar] [CrossRef]
- Gao, F.; Hilker, T.; Zhu, X.; Anderson, M.; Masek, J.; Wang, P.; Yang, Y. Fusing Landsat and MODIS data for vegetation monitoring. IEEE Geosci. Remote Sens. Mag. 2015, 3, 47–60. [Google Scholar] [CrossRef]
- Justice, C.; Townshend, J.; Vermote, E.; Masuoka, E.; Wolfe, R.; Saleous, N.; Roy, D.; Morisette, J. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Zhu, X.; Cai, F.; Tian, J.; Williams, T. Spatiotemporal fusion of multisource remote sensing data: Literature survey, taxonomy, principles, applications, and future directions. Remote Sens. 2018, 10, 527. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial-and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Fu, D.; Chen, B.; Wang, J.; Zhu, X.; Hilker, T. An improved image fusion approach based on enhanced spatial and temporal the adaptive reflectance fusion model. Remote Sens. 2013, 5, 6346–6360. [Google Scholar] [CrossRef]
- Wu, B.; Huang, B.; Cao, K.; Zhuo, G. Improving spatiotemporal reflectance fusion using image inpainting and steering kernel regression techniques. Int. J. Remote Sens. 2017, 38, 706–727. [Google Scholar] [CrossRef]
- Wang, Q.; Atkinson, P.M. Spatio-temporal fusion for daily Sentinel-2 images. Remote Sens. Environ. 2018, 204, 31–42. [Google Scholar] [CrossRef]
- Guo, D.; Shi, W.; Zhang, H.; Hao, M. A Flexible Object-Level Processing Strategy to Enhance the Weight Function-Based Spatiotemporal Fusion Method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Li, H.; Feng, R.; Wang, L.; Zhong, Y.; Zhang, L. Superpixel-Based Reweighted Low-Rank and Total Variation Sparse Unmixing for Hyperspectral Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 629–647. [Google Scholar] [CrossRef]
- Zhukov, B.; Oertel, D.; Lanzl, F.; Reinhäckel, G. Unmixing-based multisensor multiresolution image fusion. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1212–1226. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Clevers, J.G.; Schaepman, M.E. Unmixing-based Landsat TM and MERIS FR data fusion. IEEE Geosci. Remote Sens. Lett. 2008, 5, 453–457. [Google Scholar] [CrossRef]
- Wu, M.; Niu, Z.; Wang, C.; Wu, C.; Wang, L. Use of MODIS and Landsat time series data to generate high-resolution temporal synthetic Landsat data using a spatial and temporal reflectance fusion model. J. Appl. Remote Sens. 2012, 6, 063507. [Google Scholar]
- Zhang, W.; Li, A.; Jin, H.; Bian, J.; Zhang, Z.; Lei, G.; Qin, Z.; Huang, C. An enhanced spatial and temporal data fusion model for fusing Landsat and MODIS surface reflectance to generate high temporal Landsat-like data. Remote Sens. 2013, 5, 5346–5368. [Google Scholar] [CrossRef]
- Wu, M.; Huang, W.; Niu, Z.; Wang, C. Generating daily synthetic Landsat imagery by combining Landsat and MODIS data. Sensors 2015, 15, 24002–24025. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; Chen, J.; Tang, H.; Rao, Y.; Yang, P.; Wu, W. Land cover change detection by integrating object-based data blending model of Landsat and MODIS. Remote Sens. Environ. 2016, 184, 374–386. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, B. Unmixing-Based Spatiotemporal Image Fusion Accounting for Complex Land Cover Changes. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, W.; Meng, X.; Yang, G.; Ren, K.; Peng, J. Generalized Linear Spectral Mixing Model for Spatial–Temporal–Spectral Fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Li, A.; Bo, Y.; Zhu, Y.; Guo, P.; Bi, J.; He, Y. Blending multi-resolution satellite sea surface temperature (SST) products using Bayesian maximum entropy method. Remote Sens. Environ. 2013, 135, 52–63. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, H.; Song, H.; Wang, J.; Song, C. Unified fusion of remote-sensing imagery: Generating simultaneously high-resolution synthetic spatial–temporal–spectral earth observations. Remote Sens. Lett. 2013, 4, 561–569. [Google Scholar] [CrossRef]
- Shen, H.; Meng, X.; Zhang, L. An integrated framework for the spatio-temporal-spectral fusion of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7135–7148. [Google Scholar] [CrossRef]
- Liao, L.; Song, J.; Wang, J.; Xiao, Z.; Wang, J. Bayesian method for building frequent Landsat-like NDVI datasets by integrating MODIS and Landsat NDVI. Remote Sens. 2016, 8, 452. [Google Scholar] [CrossRef]
- Xue, J.; Leung, Y.; Fung, T. A Bayesian data fusion approach to spatio-temporal fusion of remotely sensed images. Remote Sens. 2017, 9, 1310. [Google Scholar] [CrossRef]
- Liu, P.; Wang, L.; Ranjan, R.; He, G.; Zhao, L. A Survey on Active Deep Learning: From Model Driven to Data Driven. ACM Comput. Surv. 2022, 54, 221:1–221:34. [Google Scholar] [CrossRef]
- Huang, B.; Song, H. Spatiotemporal reflectance fusion via sparse representation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Song, H.; Huang, B. Spatiotemporal satellite image fusion through one-pair image learning. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1883–1896. [Google Scholar] [CrossRef]
- Li, L.; Liu, P.; Wu, J.; Wang, L.; He, G. Spatiotemporal Remote-Sensing Image Fusion With Patch-Group Compressed Sensing. IEEE Access 2020, 8, 209199–209211. [Google Scholar] [CrossRef]
- Tao, X.; Liang, S.; Wang, D.; He, T.; Huang, C. Improving satellite estimates of the fraction of absorbed photosynthetically active radiation through data integration: Methodology and validation. IEEE Trans. Geosci. Remote Sens. 2017, 56, 2107–2118. [Google Scholar] [CrossRef]
- Wei, J.; Wang, L.; Liu, P.; Song, W. Spatiotemporal fusion of remote sensing images with structural sparsity and semi-coupled dictionary learning. Remote Sens. 2016, 9, 21. [Google Scholar] [CrossRef]
- Song, H.; Liu, Q.; Wang, G.; Hang, R.; Huang, B. Spatiotemporal satellite image fusion using deep convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
- Tan, Z.; Gao, M.; Li, X.; Jiang, L. A Flexible Reference-Insensitive Spatiotemporal Fusion Model for Remote Sensing Images Using Conditional Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Hou, S.; Sun, W.; Guo, B.; Li, X.; Zhang, J.; Xu, C.; Li, X.; Shao, Y.; Li, C. RFSDAF: A New Spatiotemporal Fusion Method Robust to Registration Errors. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, B.; Xu, Y.; Cao, K.; Guo, C.; Meng, D. Spatial and temporal image fusion via regularized spatial unmixing. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1362–1366. [Google Scholar]
- Gevaert, C.M.; García-Haro, F.J. A comparison of STARFM and an unmixing-based algorithm for Landsat and MODIS data fusion. Remote Sens. Environ. 2015, 156, 34–44. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Xie, D.; Zhang, J.; Zhu, X.; Pan, Y.; Liu, H.; Yuan, Z.; Yun, Y. An improved STARFM with help of an unmixing-based method to generate high spatial and temporal resolution remote sensing data in complex heterogeneous regions. Sensors 2016, 16, 207. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ling, F.; Foody, G.M.; Ge, Y.; Zhang, Y.; Du, Y. Generating a series of fine spatial and temporal resolution land cover maps by fusing coarse spatial resolution remotely sensed images and fine spatial resolution land cover maps. Remote Sens. Environ. 2017, 196, 293–311. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Feng, R.; Liu, P.; Han, W.; Chen, X. CycleGAN-STF: Spatiotemporal Fusion via CycleGAN-Based Image Generation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5851–5865. [Google Scholar] [CrossRef]
- Jing, W.; Lou, T.; Wang, Z.; Zou, W.; Xu, Z.; Mohaisen, L.; Li, C.; Wang, J. A Rigorously-Incremental Spatiotemporal Data Fusion Method for Fusing Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 6723–6738. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Xu, Y.; Wu, Z.; Chanussot, J.; Wei, Z. Hyperspectral Images Super-Resolution via Learning High-Order Coupled Tensor Ring Representation. IEEE Trans. Neural Netw. Learn. Syst. 2020, 11, 4747–4760. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, R.; Wang, L.; Zeng, T. Gradient Prior Dilated Convolution Network for Remote Sensing Image Super-Resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3945–3958. [Google Scholar] [CrossRef]
- Lin, Z.; Shum, H.Y. Fundamental limits of reconstruction-based superresolution algorithms under local translation. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 83–97. [Google Scholar]
- Bookstein, F.L. Principal warps: Thin-plate splines and the decomposition of deformations. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 31, 567–585. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, J.; Zuo, W.; Loy, C.C. Cross-scale internal graph neural network for image super-resolution. Adv. Neural Inf. Process. Syst. 2020, 33, 3499–3509. [Google Scholar]
- Huang, X.; Belongie, S. Arbitrary Style Transfer in Real-Time with Adaptive Instance Normalization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1510–1519. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Proceedings of the Summaries of the Third Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]





| Symbol | Definition |
|---|---|
| k | k refers to time, where , k, and represent the past time, the fusion time, and the future time in this paper, respectively. |
| i, j | The ith HTLS image pixel is denoted by i, and the jth HSLT image pixel in one HTLS image pixel is denoted by j. |
| The coordinate values of the ith HTLS image pixel. | |
| The coordinate values of the jth HSLT pixel in the HTLS pixel at location . | |
| C is the HTLS image and F is the HSLT image. | |
| The position of k refers to time. | |
| The cth class. |
| Method | RMSE | CC | SSIM | SAM | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Red | Green | NIR | All | Red | Green | NIR | All | Red | Green | NIR | All | ||
| TPS + TPS | 0.142 | 0.161 | 0.171 | 0.166 | 0.853 | 0.873 | 0.813 | 0.866 | 0.882 | 0.734 | 0.835 | 0.825 | 0.042 |
| IGNN + IGNN | 0.127 | 0.154 | 0.178 | 0.157 | 0.891 | 0.866 | 0.806 | 0.862 | 0.906 | 0.785 | 0.863 | 0.853 | 0.036 |
| TPS + IGNN | 0.143 | 0.157 | 0.132 | 0.142 | 0.923 | 0.893 | 0.843 | 0.873 | 0.915 | 0.835 | 0.853 | 0.874 | 0.033 |
| MSISR-STF | 0.071 | 0.100 | 0.090 | 0.088 | 0.968 | 0.946 | 0.940 | 0.959 | 0.954 | 0.854 | 0.913 | 0.908 | 0.023 |
| STARFM | 0.177 | 0.187 | 0.179 | 0.182 | 0.776 | 0.771 | 0.804 | 0.791 | 0.698 | 0.529 | 0.626 | 0.619 | 0.059 |
| FSDAF | 0.173 | 0.181 | 0.166 | 0.174 | 0.792 | 0.791 | 0.835 | 0.812 | 0.716 | 0.538 | 0.641 | 0.632 | 0.054 |
| CycleGAN-STF | 0.099 | 0.135 | 0.138 | 0.125 | 0.937 | 0.887 | 0.893 | 0.907 | 0.913 | 0.759 | 0.789 | 0.821 | 0.038 |
| MSISR-STF | 0.071 | 0.100 | 0.090 | 0.088 | 0.968 | 0.946 | 0.940 | 0.959 | 0.954 | 0.854 | 0.913 | 0.908 | 0.023 |
| Method | RMSE | CC | SSIM | SAM | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Red | Green | NIR | All | Red | Green | NIR | All | Red | Green | NIR | All | ||
| TPS + TPS | 0.182 | 0.170 | 0.193 | 0.184 | 0.874 | 0.857 | 0.811 | 0.873 | 0.871 | 0.727 | 0.714 | 0.738 | 0.062 |
| IGNN + IGNN | 0.173 | 0.151 | 0.175 | 0.172 | 0.881 | 0.866 | 0.832 | 0.849 | 0.906 | 0.731 | 0.715 | 0.757 | 0.058 |
| TPS + IGNN | 0.151 | 0.141 | 0.174 | 0.159 | 0.905 | 0.853 | 0.834 | 0.895 | 0.864 | 0.745 | 0.736 | 0.755 | 0.058 |
| MSISR-STF | 0.102 | 0.143 | 0.150 | 0.134 | 0.936 | 0.946 | 0.868 | 0.895 | 0.912 | 0.770 | 0.776 | 0.821 | 0.044 |
| STARFM | 0.117 | 0.149 | 0.157 | 0.142 | 0.913 | 0.867 | 0.848 | 0.876 | 0.884 | 0.755 | 0.771 | 0.805 | 0.046 |
| FSDAF | 0.095 | 0.145 | 0.157 | 0.134 | 0.927 | 0.883 | 0.851 | 0.887 | 0.906 | 0.768 | 0.768 | 0.817 | 0.050 |
| CycleGAN-STF | 0.101 | 0.147 | 0.162 | 0.139 | 0.939 | 0.881 | 0.848 | 0.890 | 0.912 | 0.775 | 0.728 | 0.815 | 0.047 |
| MSISR-STF | 0.102 | 0.143 | 0.150 | 0.134 | 0.936 | 0.946 | 0.868 | 0.895 | 0.912 | 0.770 | 0.776 | 0.821 | 0.044 |
| STARFM | FSDAF | CycleGAN-STF | MSISR-STF | |||||
|---|---|---|---|---|---|---|---|---|
| Train | Fusion | Train | Fusion | Train | Fusion | Train | Fusion | |
| Time | - | 97 | - | 150 | 9/epoch | 86 | 12/epoch | 132 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Feng, R.; Fan, J.; Han, W.; Yu, S.; Chen, J. MSISR-STF: Spatiotemporal Fusion via Multilevel Single-Image Super-Resolution. Remote Sens. 2023, 15, 5675. https://doi.org/10.3390/rs15245675
Zheng X, Feng R, Fan J, Han W, Yu S, Chen J. MSISR-STF: Spatiotemporal Fusion via Multilevel Single-Image Super-Resolution. Remote Sensing. 2023; 15(24):5675. https://doi.org/10.3390/rs15245675
Chicago/Turabian StyleZheng, Xiongwei, Ruyi Feng, Junqing Fan, Wei Han, Shengnan Yu, and Jia Chen. 2023. "MSISR-STF: Spatiotemporal Fusion via Multilevel Single-Image Super-Resolution" Remote Sensing 15, no. 24: 5675. https://doi.org/10.3390/rs15245675
APA StyleZheng, X., Feng, R., Fan, J., Han, W., Yu, S., & Chen, J. (2023). MSISR-STF: Spatiotemporal Fusion via Multilevel Single-Image Super-Resolution. Remote Sensing, 15(24), 5675. https://doi.org/10.3390/rs15245675