Weather Radar Parameter Estimation Based on Frequency Domain Processing: Technical Details and Performance Evaluation
Abstract
:1. Introduction
2. Simulation and Estimation Methods
2.1. I/Q Data Simulator
- Set the simulation length , where . The auto-correlation threshold () can be calculated as follows:
- Generate an ideal Gaussian power spectrum (; the argument denotes the spectral index) based on the given mean (i.e., ) and SD (i.e., ), as follows:which can be computed on an extended Nyquist co-interval (from to ), where denotes an integer factor, and its setting depends on the spectral threshold (). Specifically, the spectrum must be extended to cover the frequency range up to below its peak. Then, alias the extended spectrum to produce a spectrum on the desired Nyquist co-interval (from to );
- Set all values in the spectrum to zero, which is greater than below the peak of the spectrum;
- Appropriately scale the so that the signal power is equal to the desired ;
- Simulate an independent and identically distributed complex Gaussian random process with zero mean, unit variance, and length;
- Multiply by the square root of the result of Step 4 and perform the inverse discrete Fourier transform (IDFT) to transform from the frequency domain to the time domain, as follows:
- Repeat Steps 2–6 to generate (the extra “2” in the subscript is for the convenience of distinguishing it from ). can be calculated as follows:
- Return the first samples from the simulated samples;
- To add noise to the simulated signal, an independent and identically distributed Gaussian random process () is generated with zero mean, variance (), and length. Then, add it to ().
2.2. TDP
2.3. FDP
3. FDP Details
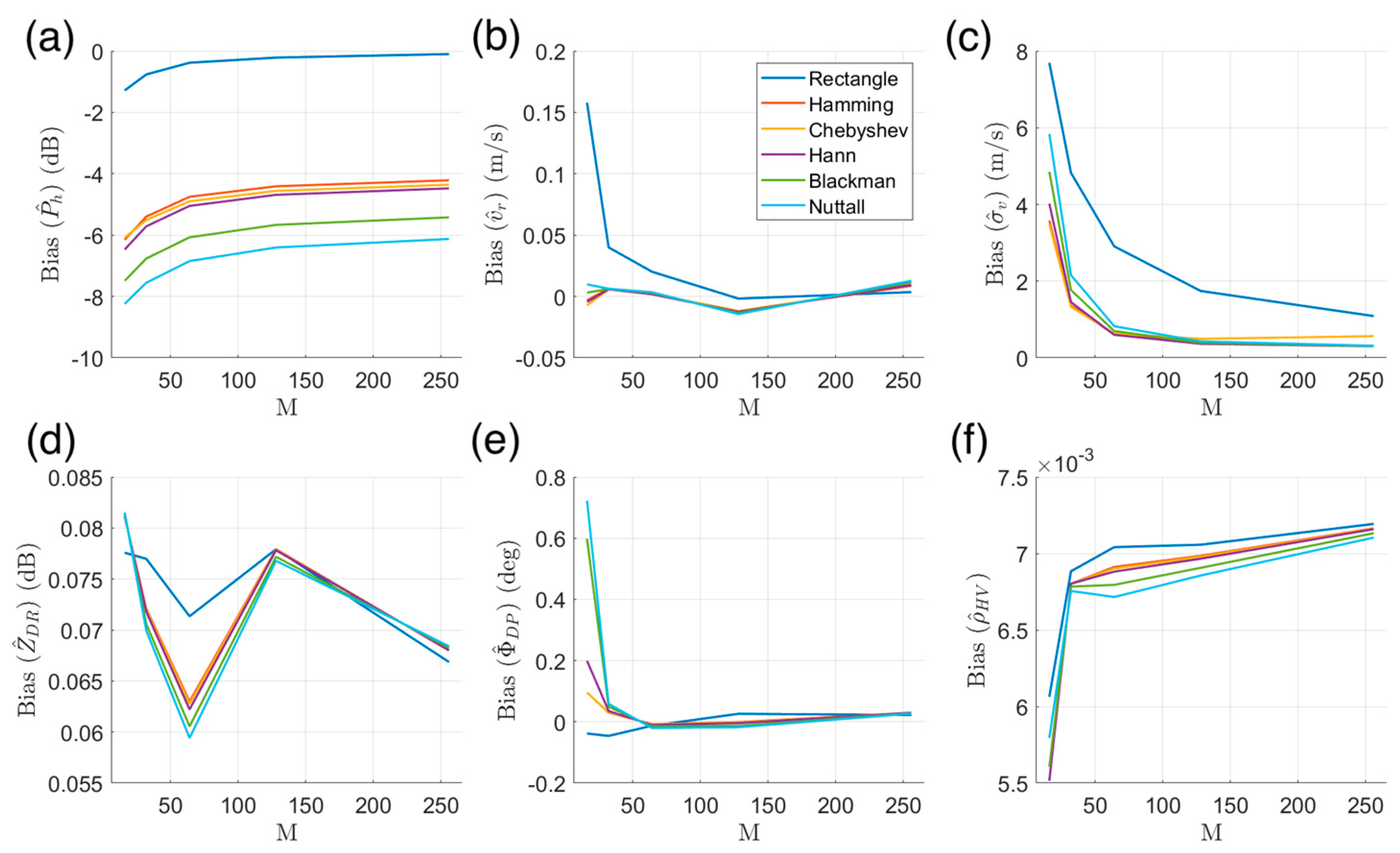
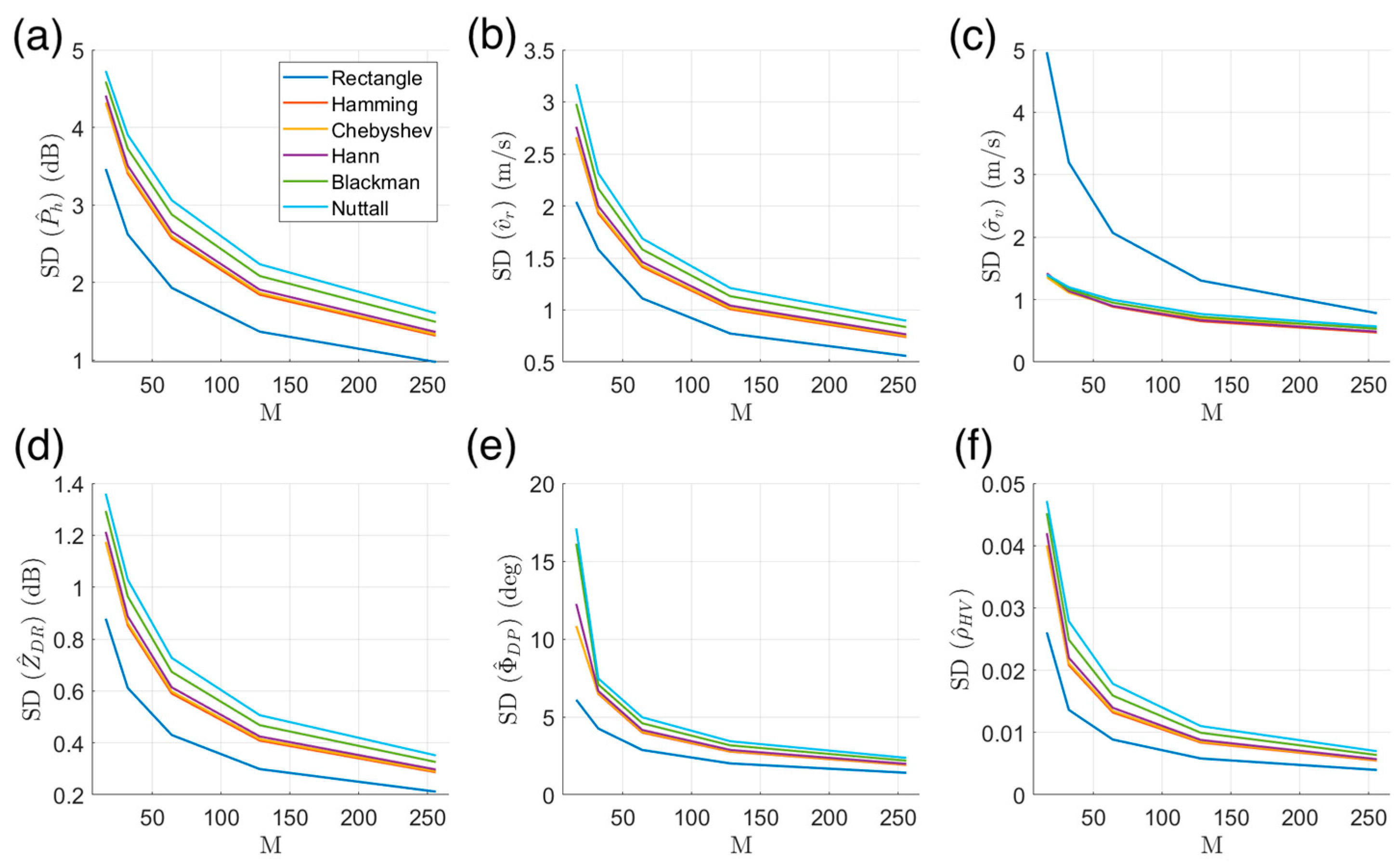
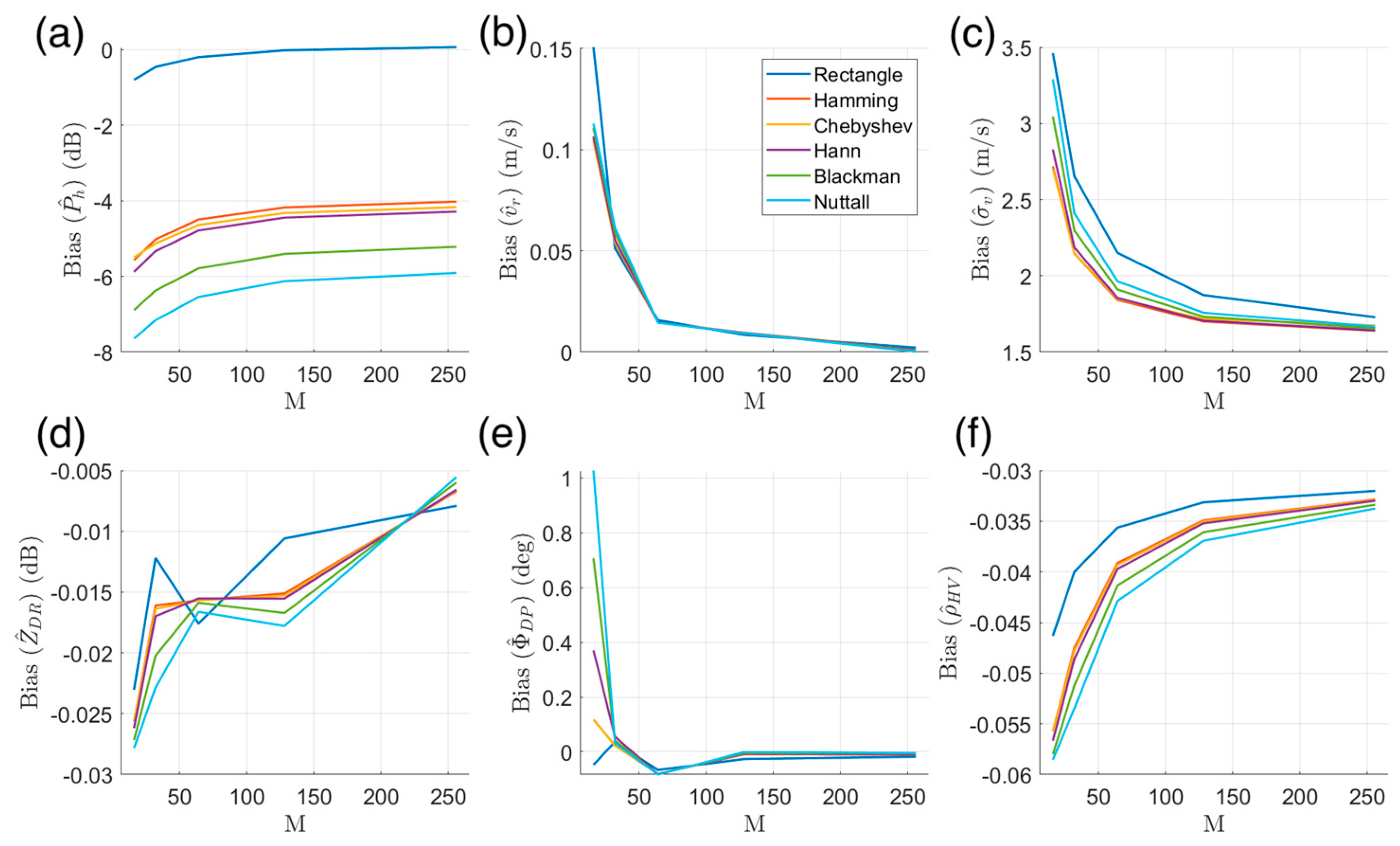
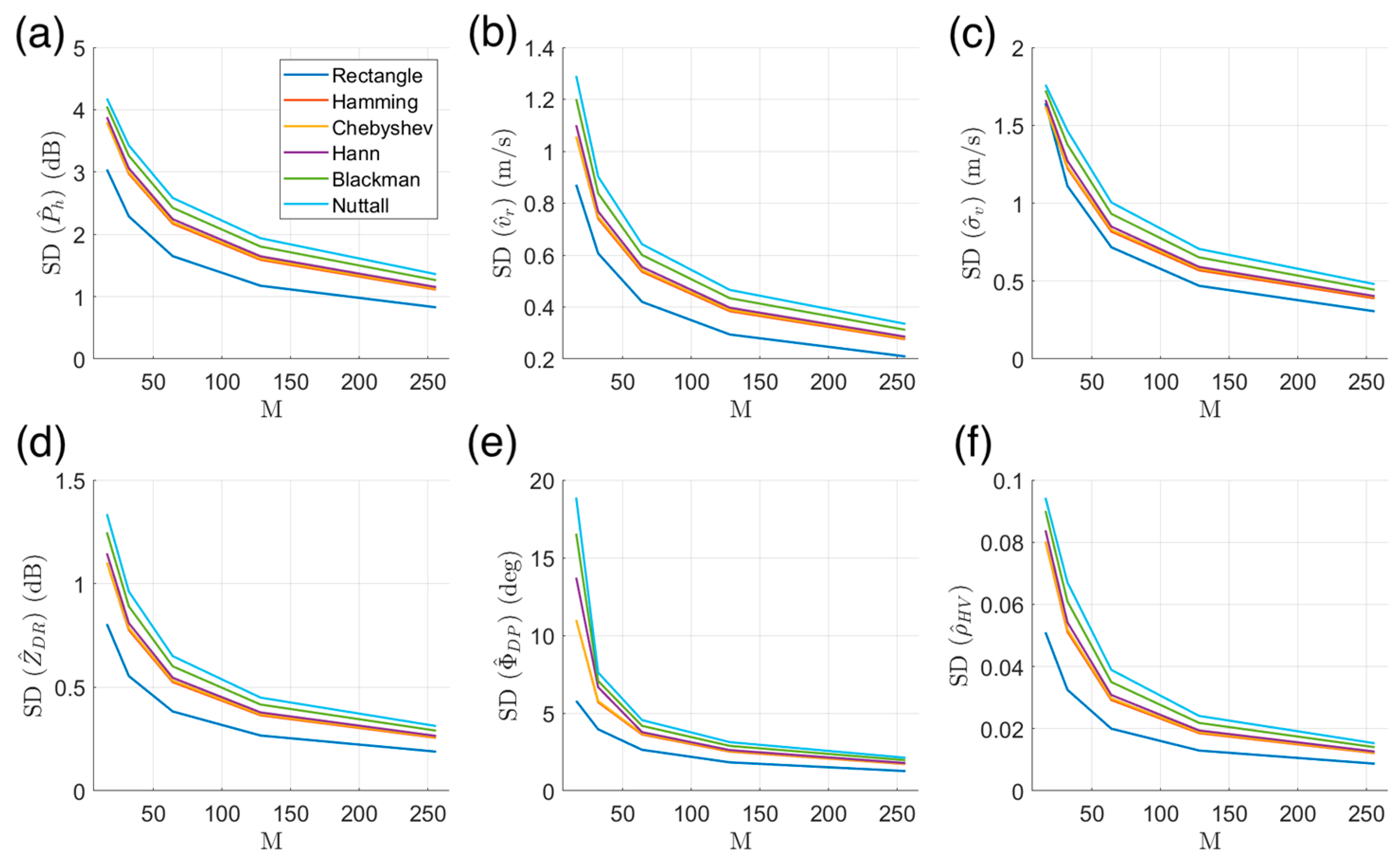
3.1. Window Function Selection
3.2. Aliasing Correction
- Find the spectral Doppler velocity with maximum power in the power spectrum (), which can be used as an approximate estimate.
- The power spectrum distribution can be rearranged by circular shifting, such that the corresponding position of is adjusted to zero. This can cause the estimation results to be immune to or minimized by spectrum aliasing.
- Perform the Doppler estimates of FDP using the equations given in Table 1.
- Add to the estimation result of in Step 3 to obtain the final estimates.
3.3. Noise Correction
4. FDP and TDP Performance Comparison
4.1. Based on Simulated I/Q Data
4.1.1. Gaussian Power Spectrum
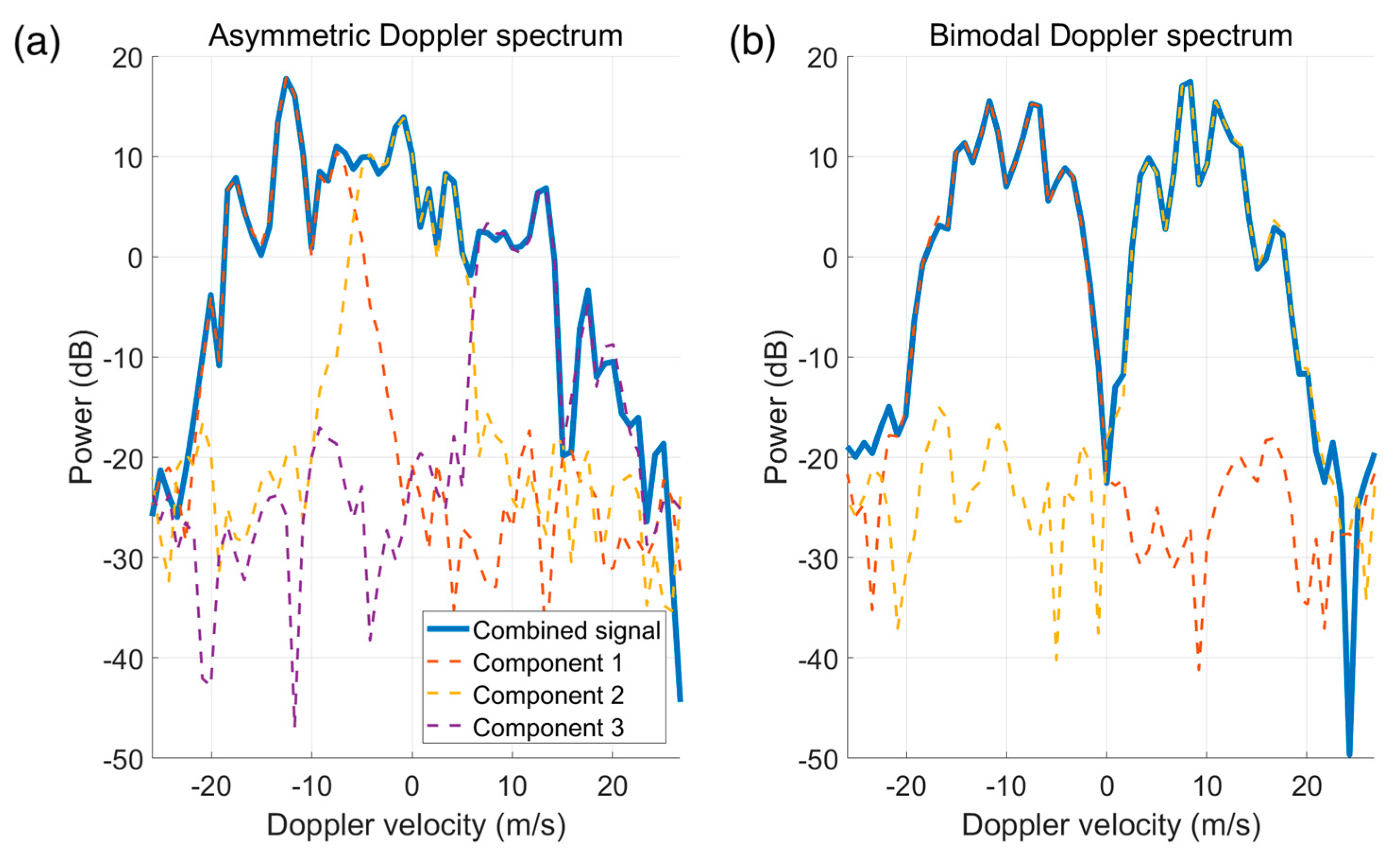
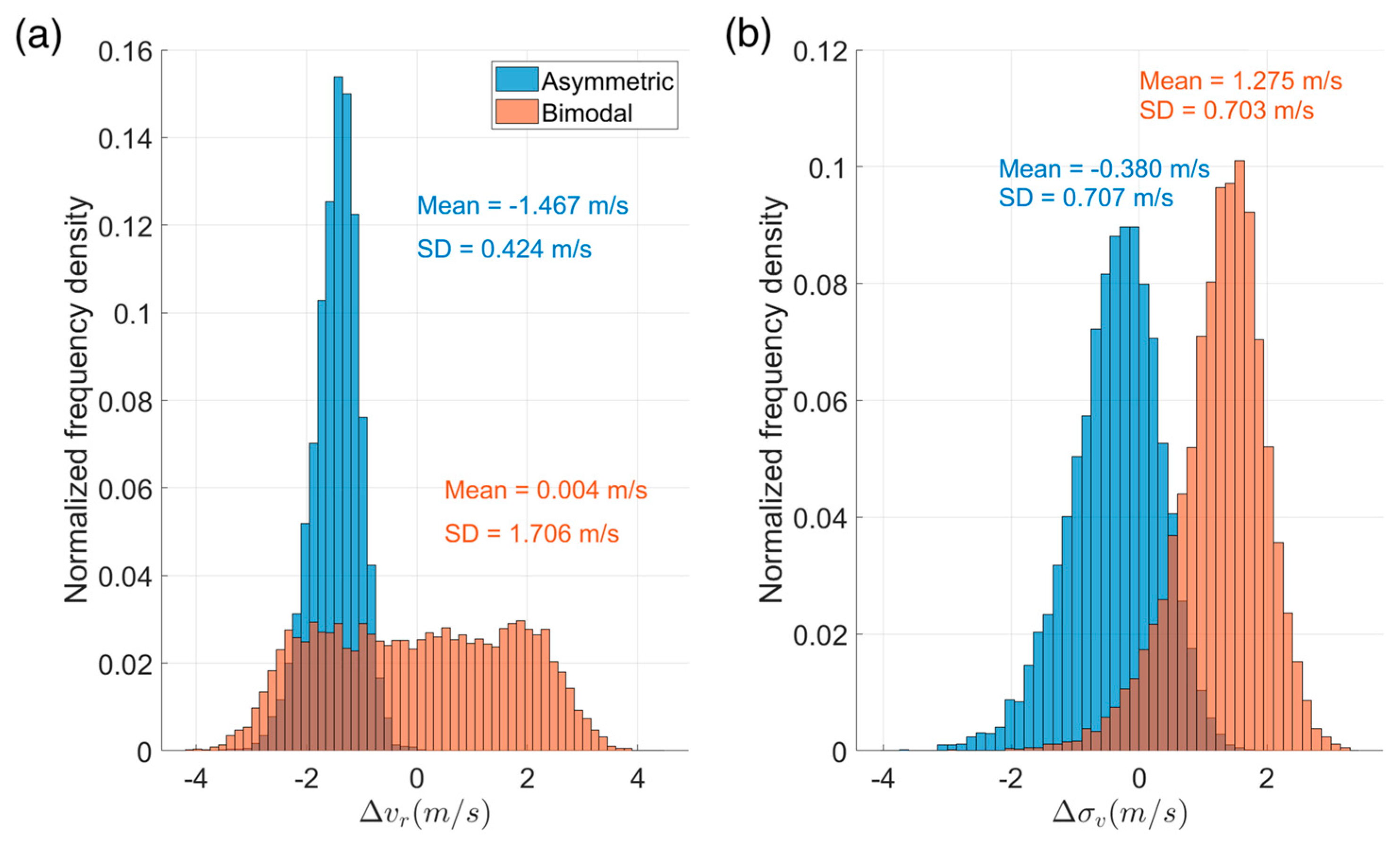
4.1.2. Non-Gaussian Power Spectrum
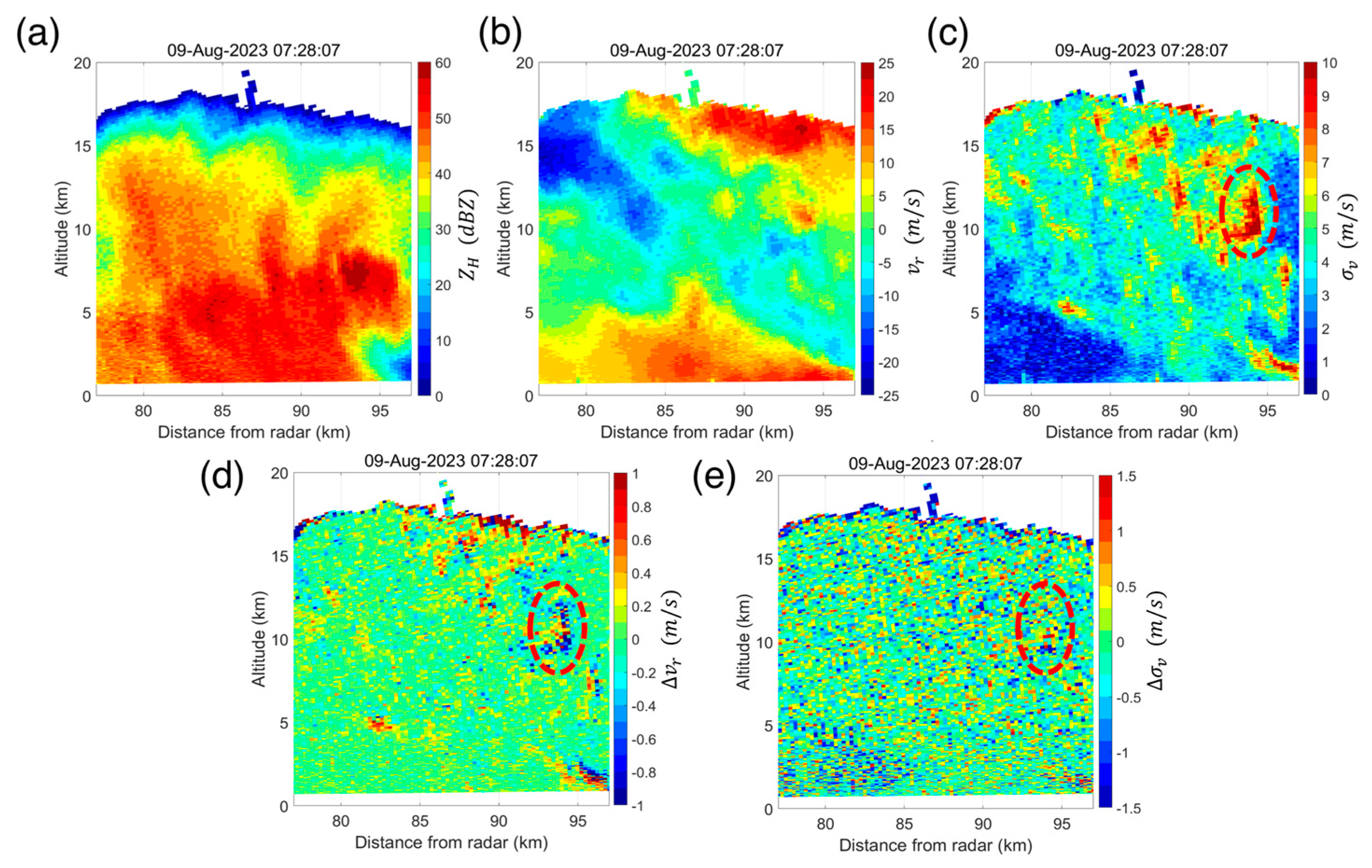
4.2. Based on Measured I/Q Data
5. Discussion
6. Conclusions
- The use of window functions (except for the rectangular window) in performing DFT was beneficial for improving the accuracy of estimates. For other radar variables, the use of window functions (except for the rectangular window) resulted in a decrease in the number of effective samples and an increase in the SD. Therefore, two types of DFT were performed in FDP, one for estimates using a window function with a low taper (the default being the Hamming window), and another for other radar variables estimates using a rectangular window;
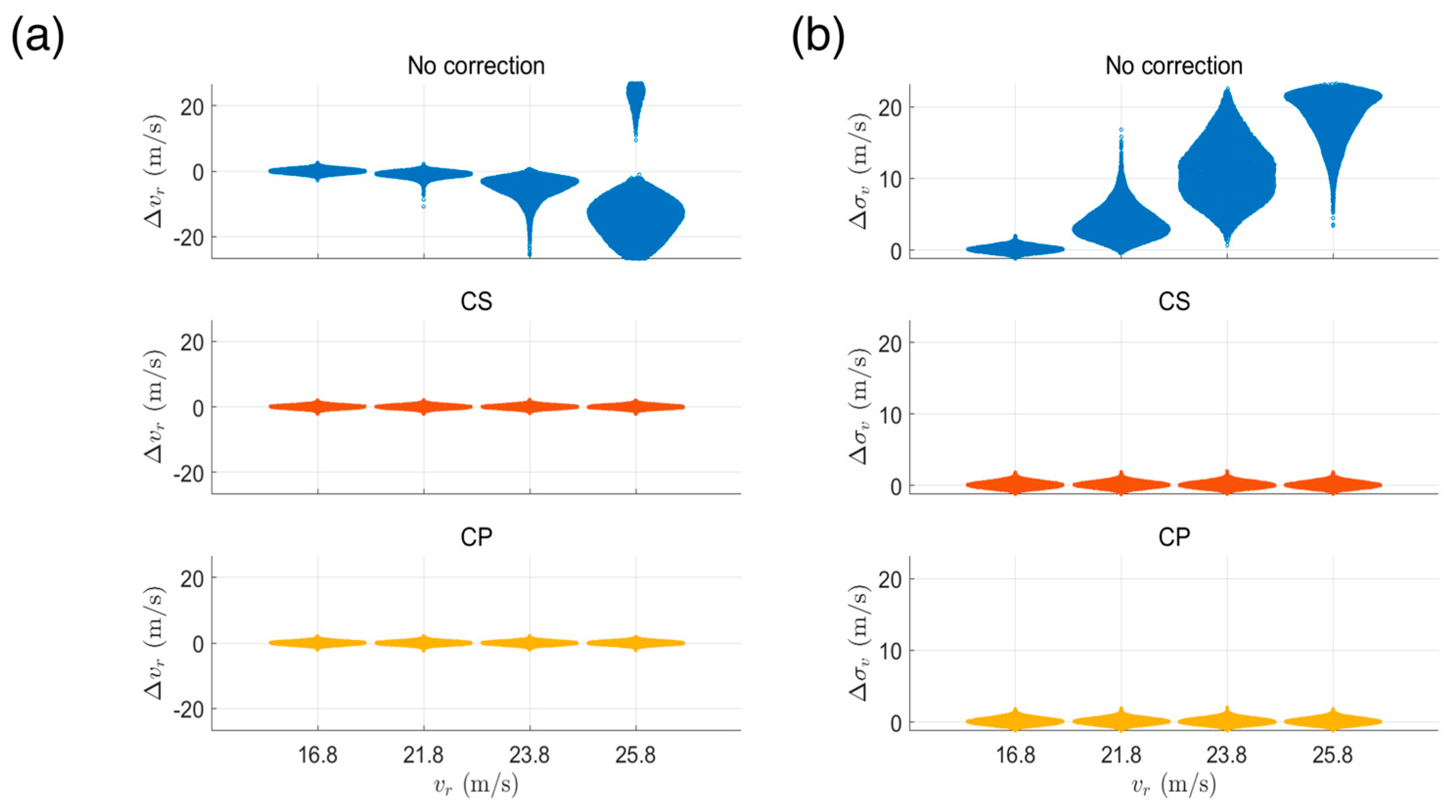
- Both aliasing correction methods described in this paper satisfactorily corrected the spectrum aliasing, such that the performance of Doppler estimates of FDP was independent of the value of , which was beneficial in improving the performance of Doppler estimates when was close to the edge of the measurement range. However, owing to advantages such as algorithm complexity, CP should be a better choice for operational applications;
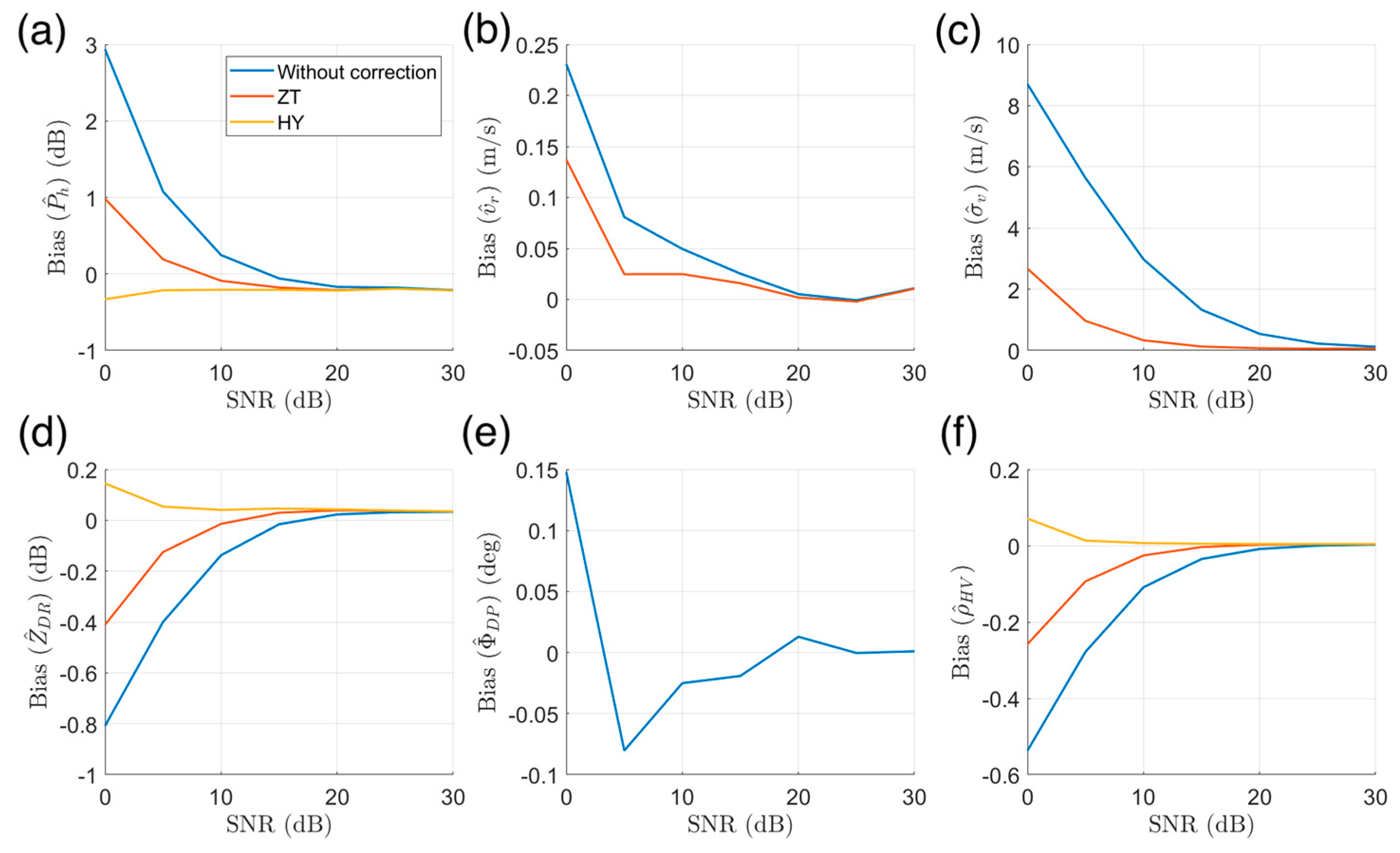
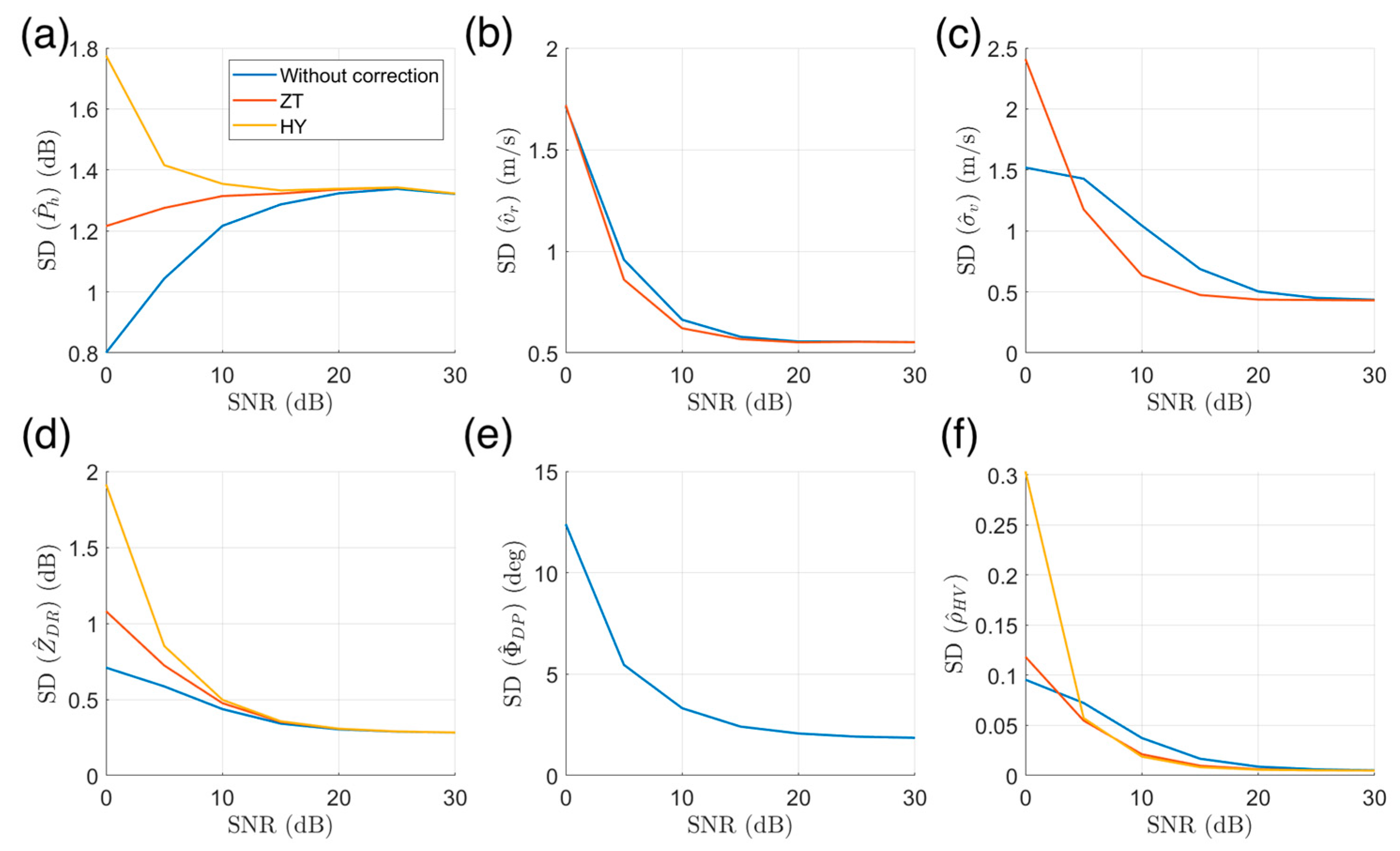
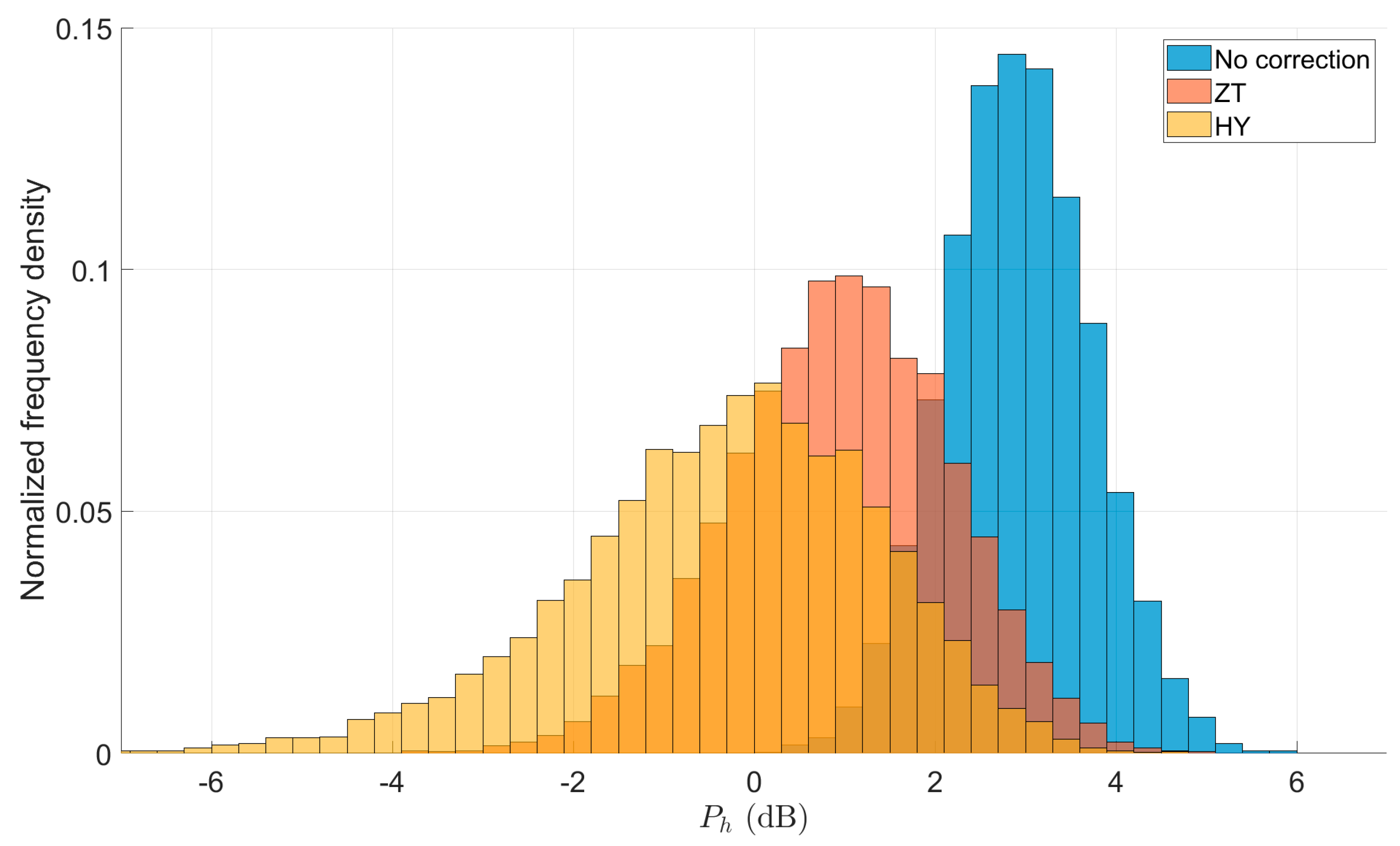
- The parameter estimation performance improved after noise correction, and the HY method introduced in this study exhibited a better performance in , , and estimates than the ZT method;
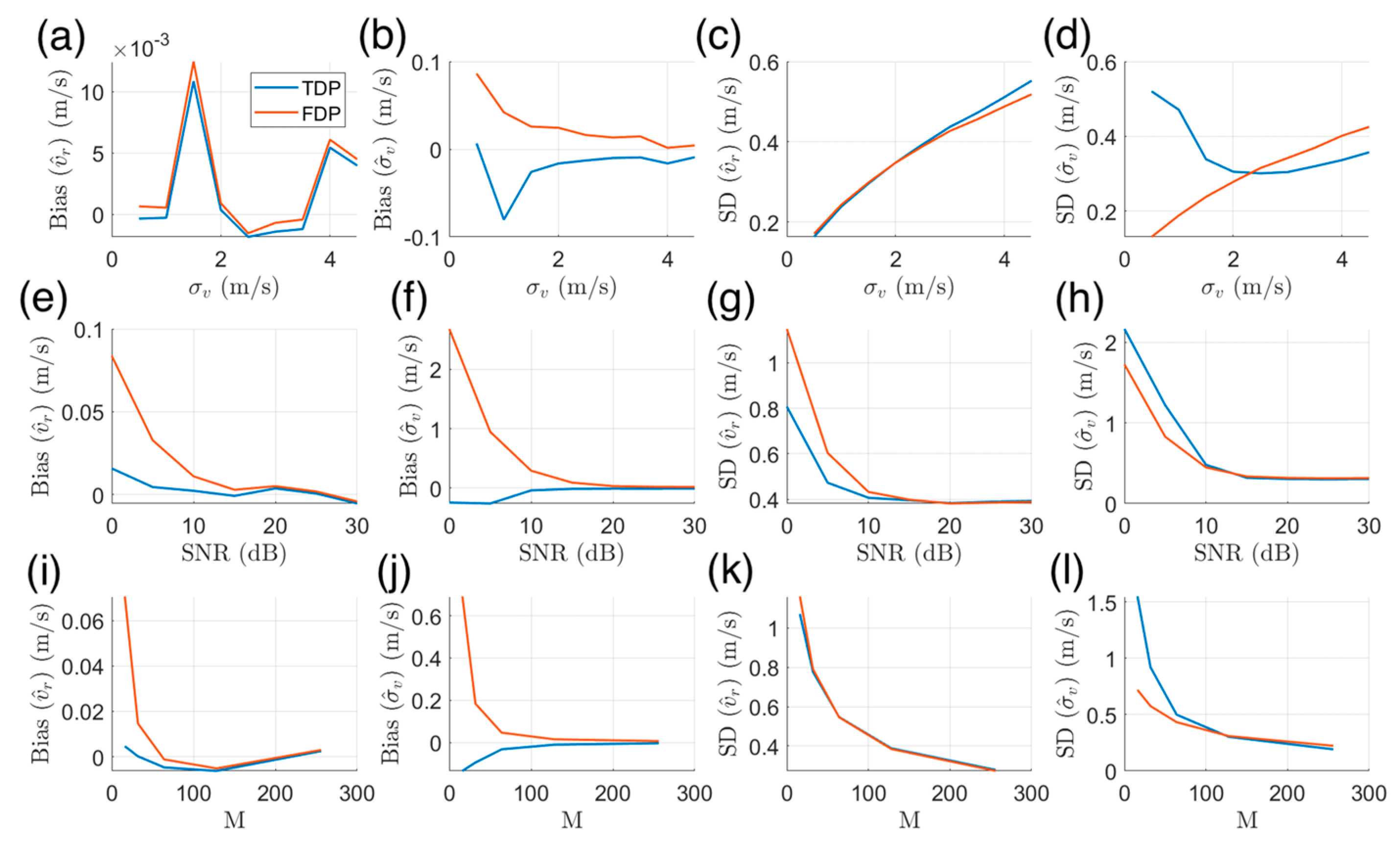
- For Gaussian power spectrum signals, FDP was more advantageous than TDP in estimates when was low, while the Doppler estimate performance of FDP exhibited a certain gap compared to that of TDP when the was low or was small;
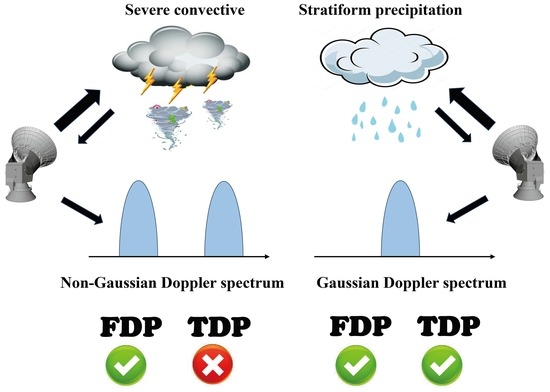
- For non-Gaussian (e.g., asymmetric or multi-peak) power spectrum signals, the Doppler estimate results of TDP were biased or fluctuated considerably if FDP was used as the benchmark, indirectly demonstrating that FDP exhibited more advantages than TDP in Doppler estimates for non-Gaussian power spectrum signals.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Tang, L.; Cocks, S.; Zhang, P.; Ryzhkov, A.; Howard, K.; Langston, C.; Kaney, B. A dual-polarization radar synthetic QPE for operations. J. Hydrometeorol. 2020, 21, 2507–2521. [Google Scholar] [CrossRef]
- Hanft, W.; Zhang, J.; Simpson, M. Dual-pol VPR corrections for improved operational radar QPE in MRMS. J. Hydrometeorol. 2023, 24, 353–371. [Google Scholar] [CrossRef]
- Yang, L.; Chen, M.; Wang, X.; Song, L.; Yang, M.; Qin, R.; Cheng, C.; Li, S. Classification of precipitation type in North China using model-based explicit fields of hydrometeors with modified thermodynamic conditions. Weather. Forecast. 2021, 36, 91–107. [Google Scholar] [CrossRef]
- Tiira, J.; Moisseev, D. Unsupervised classification of vertical profiles of dual polarization radar variables. Atmos. Meas. Tech. 2020, 13, 1227–1241. [Google Scholar] [CrossRef]
- Li, H.; Moisseev, D. Two layers of melting ice particles within a single radar bright band: Interpretation and implications. Geophys. Res. Lett. 2020, 47, e2020GL087499. [Google Scholar] [CrossRef]
- Li, H.; Moisseev, D. Melting layer attenuation at Ka-and W-bands as derived from multifrequency radar Doppler spectra observations. J. Geophys. Res. Atmos. 2019, 124, 9520–9533. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Doviak, R.J.; Zrnic, D.S. Doppler Radar and Weather Observations; Courier Corporation: North Chelmsford, MA, USA, 2006. [Google Scholar]
- Keeler, R.J.; Passarelli, R.E. Signal processing for atmospheric radars. In Radar in Meteorology: Battan Memorial and 40th Anniversary Radar Meteorology Conference, Boston, MA, USA; American Meteorological Society: Boston, MA, USA, 1990; pp. 199–229. [Google Scholar]
- Melnikov, V.M.; Zrnic, D.S. Autocorrelation and cross-correlation estimators of polarimetric variables. J. Atmos. Ocean. Technol. 2007, 24, 1337–1350. [Google Scholar] [CrossRef]
- Lei, L.; Zhang, G.; Doviak, R.J.; Palmer, R.; Cheong, B.L.; Xue, M.; Cao, Q.; Li, Y. Multilag correlation estimators for polarimetric radar measurements in the presence of noise. J. Atmos. Ocean. Technol. 2012, 29, 772–795. [Google Scholar] [CrossRef]
- Ivic, I.R. On the use of a radial-based noise power estimation technique to improve estimates of the correlation coefficient on dual-polarization weather radars. J. Atmos. Ocean. Technol. 2014, 31, 1867–1880. [Google Scholar] [CrossRef]
- Ivic, I.R.; Curtis, C.; Torres, S.M. Radial-based noise power estimation for weather radars. J. Atmos. Ocean. Technol. 2013, 30, 2737–2753. [Google Scholar] [CrossRef]
- Ivic, I.R. A technique to improve copolar correlation coefficient estimation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5776–5800. [Google Scholar] [CrossRef]
- Ivic, I.R. A simple hybrid technique to reduce bias of copolar correlation coefficient estimates. J. Atmos. Ocean. Technol. 2019, 36, 1813–1833. [Google Scholar] [CrossRef]
- Rummler, W.D. Introduction of a new estimator for velocity spectral parameters. Rep. MM-68-4141 1968, 5, 680–696. [Google Scholar]
- Janssen, L.H.; Van Der Spek, G.A. The shape of Doppler spectra from precipitation. IEEE Trans. Aerosp. Electron. Syst. 1985, 2, 208–219. [Google Scholar] [CrossRef]
- Yu, T.Y.; Wang, Y.; Shapiro, A.; Yeary, M.B.; Zrnić, D.S.; Doviak, R.J. Characterization of tornado spectral signatures using higher-order spectra. J. Atmos. Ocean. Technol. 2007, 24, 1997–2013. [Google Scholar] [CrossRef]
- Yu, T.Y.; Rondinel, R.R.; Palmer, R.D. Investigation of non-Gaussian Doppler spectra observed by weather radar in a tornadic supercell. J. Atmos. Ocean. Technol. 2009, 26, 444–461. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, T.Y.; Ryzhkov, A.V.; Kumjian, M.R. Application of spectral polarimetry to a hailstorm at low elevation angle. J. Atmos. Ocean. Technol. 2019, 36, 567–583. [Google Scholar] [CrossRef]
- Schvartzman, D.; Bruning, E.; Yu, T.Y.; Chmielewski, V.; Bodine, D.; Bluestein, H.B. Analysis of Polarimetric Spectral Densities in Severe Thunderstorms for the Identification of Lightning-Induced Signatures. 2022. Available online: https://www.researchgate.net/profile/David-Schvartzman/publication/364838455_Analysis_of_polarimetric_spectral_densities_in_severe_thunderstorms_for_the_identification_of_lightning-induced_signatures/links/635d3cb812cbac6a3e07e509/Analysis-of-polarimetric-spectral-densities-in-severe-thunderstorms-for-the-identification-of-lightning-induced-signatures.pdf (accessed on 14 September 2023).
- Vaisala. User’s Manual: RVP900 Digital Receiver and Signal Processor; Vaisala Oyj: Vantaa, Finland, 2016; p. 513. [Google Scholar]
- Siggia, A.D.; Passarelli, R.E. Gaussian model adaptive processing (GMAP) for improved ground clutter cancellation and moment calculation. In Proceedings of the ERAD, Westford, MA, USA; 2004; Volume 2, pp. 421–424. [Google Scholar]
- Torres, S.M.; Warde, D.A. Ground clutter mitigation for weather radars using the autocorrelation spectral density. J. Atmos. Ocean. Technol. 2014, 31, 2049–2066. [Google Scholar] [CrossRef]
- Zrinc, D.; Mahapatra, P. Two methods of ambiguity resolution in pulse Doppler weather radars. IEEE Trans. Aerosp. Electron. Syst. 1985, 4, 470–483. [Google Scholar]
- Sachidananda, M.; Zrnic, D.S. Systematic phase codes for resolving range overlaid signals in a Doppler weather radar. J. Atmos. Ocean. Technol. 1999, 16, 1351–1363. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, T.Y.; Yeary, M.; Shapiro, A.; Nemati, S.; Foster, M.; Andra, D.L.; Jain, M. Tornado detection using a neuro–fuzzy system to integrate shear and spectral signatures. J. Atmos. Ocean. Technol. 2008, 25, 1136–1148. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, T.Y. Novel tornado detection using an adaptive neuro-fuzzy system with S-band polarimetric weather radar. J. Atmos. Ocean. Technol. 2015, 32, 195–208. [Google Scholar] [CrossRef]
- Zrnić, D.S. Simulation of weatherlike Doppler spectra and signals. J. Appl. Meteorol. Climatol. 1975, 14, 619–620. [Google Scholar] [CrossRef]
- Curtis, C.D. Weather radar time series simulation: Improving accuracy and performance. J. Atmos. Ocean. Technol. 2018, 35, 2169–2187. [Google Scholar] [CrossRef]
- Galati, G.; Pavan, G. Computer simulation of weather radar signals. Simul. Pract. Theory 1995, 3, 17–44. [Google Scholar] [CrossRef]
- Umeyama, A.Y.; Torres, S.M.; Cheong, B.L. Bootstrap dual-polarimetric spectral density estimator. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2299–2312. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Beauchamp, R.M.; Bechini, R. Introduction to Dual Polarization Weather Radar: Fundamentals, Applications, and Networks; Cambridge University Press: Cambridge, MA, USA, 2023. [Google Scholar]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Fang, M.; Doviak, R.J.; Melnikov, V. Spectrum width measured by WSR-88D: Error sources and statistics of various weather phenomena. J. Atmos. Ocean. Technol. 2004, 21, 888–904. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Zrnic, D.S. Radar Polarimetry for Weather Observations; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Zhang, S.; Huang, X.; Min, J.; Chu, Z.; Zhuang, X.; Zhang, H. Improved fuzzy logic method to distinguish between meteorological and non-meteorological echoes using C-band polarimetric radar data. Atmos. Meas. Tech. 2020, 13, 537–551. [Google Scholar] [CrossRef]
- Zhang, G. Weather Radar Polarimetry; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Schvartzman, D.; Torres, S.M.; Warde, D. The Hybrid-Scan Estimators: Exploiting WSR-88D Split Cuts to Improve the Quality of Polarimetric-Variable Estimates. J. Atmos. Ocean. Technol. 2020, 37, 299–315. [Google Scholar] [CrossRef]


| TDP | FDP |
|---|---|
| (dB) | (m/s) | (m/s) | (dB) | (deg) | |||
|---|---|---|---|---|---|---|---|
| Sim1 | 30 | 0 | 3.5 | 2.5 | 50 | 0.98 | 16, 32, 64, 128, 256 |
| Sim2 | 15 | 1.5 | 0.5 | 0.99 | |||
| Sim3 | 30 | 1, 2, 4 | / | / | / | 64 | |
| Sim4 | 4 | 16, 32, 64 | |||||
| Sim5 | 16.8, 21.8, 23.8, 25.8 | 2.5 | 64 | ||||
| Sim6 | 0, 5, 10, 15, 20, 25, 30 | 0 | 1.5 | 50 | 0.985 | ||
| Sim7 | 30 | 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5 | / | / | / | 128 | |
| Sim8 | 0, 5, 10, 15, 20, 25, 30 | 2.5 | |||||
| Sim9 | 30 | 16, 32, 64, 128, 256 | |||||
| Sim10 | 30, 25, 20 | −12, 0, 12 | |||||
| Sim11 | 30 | −10, 10 | 64 |
| Window Function | Aliasing Correction | Noise Correction | |
|---|---|---|---|
| Sim1 | Rectangle, Hamming, Chebyshev, Hann, Blackman, Nuttall | No | No |
| Sim2 | |||
| Sim3 | Hamming | ||
| Sim4 | |||
| Sim5 | Rectangle, Hamming (only for ) | CS, CP | |
| Sim6 | CP | ZT, HY | |
| Sim7 | HY | ||
| Sim8 | |||
| Sim9 | |||
| Sim10 | |||
| Sim11 |
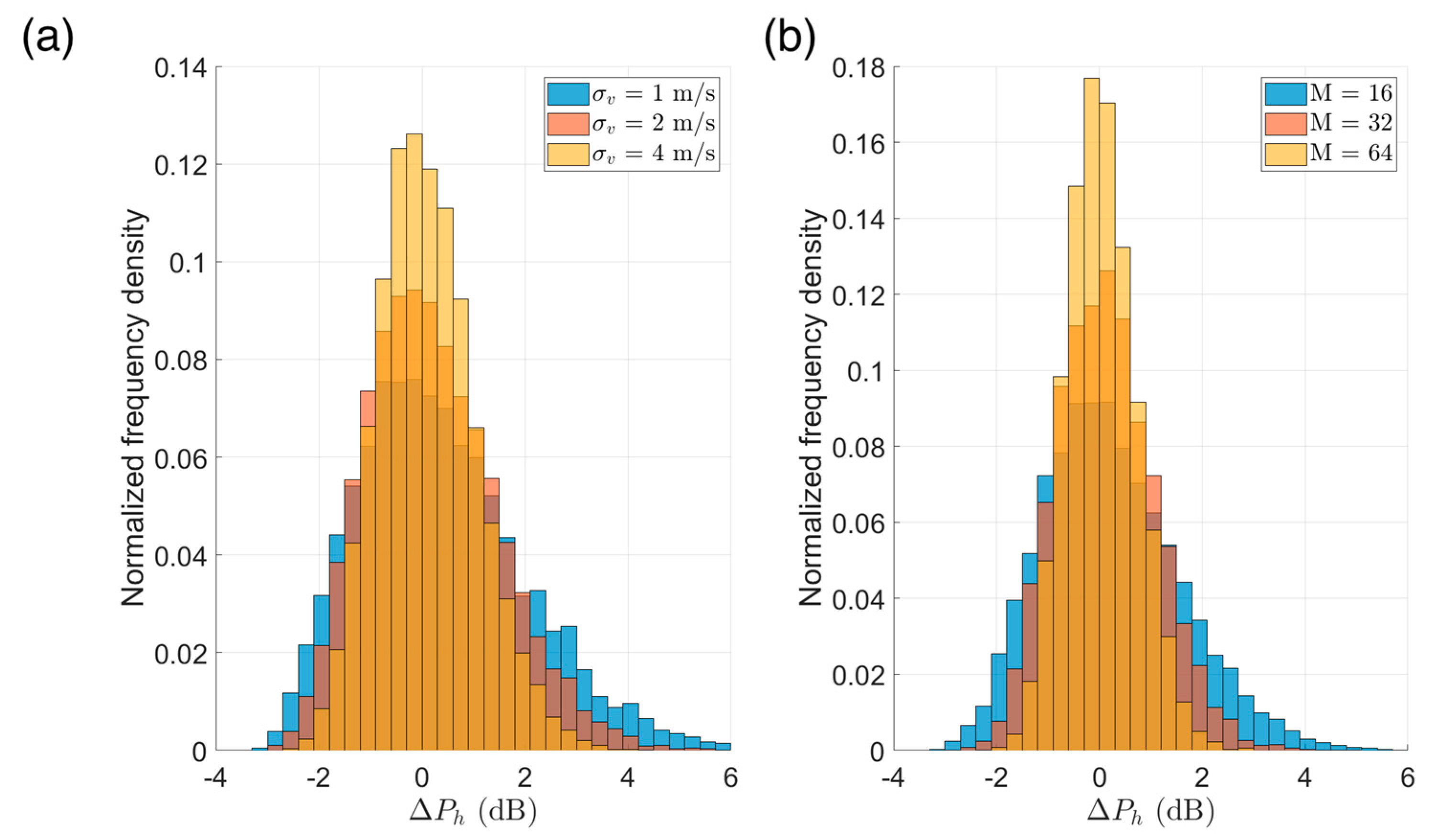
| 1 m/s | 2 m/s | 4 m/s | 16 | 32 | 64 | |
|---|---|---|---|---|---|---|
| Mean | 0.374 dB | 0.194 dB | 0.101 dB | 0.223 dB | 0.121 dB | 0.04 dB |
| SD | 1.641 dB | 1.282 dB | 0.948 dB | 1.344 dB | 0.96 dB | 0.677 dB |
| Mean | SD | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 16.8 | 21.8 | 23.8 | 25.8 | 16.8 | 21.8 | 23.8 | 25.8 | ||
| No correction | −0.025 | −1.018 | −5.263 | −11.285 | 0.708 | 1.029 | 3.448 | 11.906 | |
| 0.141 | 3.892 | 11.057 | 18.635 | 0.434 | 2.233 | 4.085 | 3.257 | ||
| CS | 0.01 | 0.002 | 0.012 | 0.005 | 0.551 | 0.555 | 0.55 | 0.549 | |
| 0.104 | 0.107 | 0.112 | 0.108 | 0.434 | 0.435 | 0.435 | 0.433 | ||
| CP | 0.006 | −0.003 | 0.008 | 0.001 | 0.561 | 0.565 | 0.56 | 0.558 | |
| 0.103 | 0.106 | 0.111 | 0.108 | 0.434 | 0.434 | 0.435 | 0.433 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Chen, Y.; Shu, Z.; Yu, H.; Wang, H.; Chen, J.; Li, L. Weather Radar Parameter Estimation Based on Frequency Domain Processing: Technical Details and Performance Evaluation. Remote Sens. 2023, 15, 5624. https://doi.org/10.3390/rs15235624
Zhang S, Chen Y, Shu Z, Yu H, Wang H, Chen J, Li L. Weather Radar Parameter Estimation Based on Frequency Domain Processing: Technical Details and Performance Evaluation. Remote Sensing. 2023; 15(23):5624. https://doi.org/10.3390/rs15235624
Chicago/Turabian StyleZhang, Shuai, Yubao Chen, Zhifeng Shu, Haifeng Yu, Hui Wang, Jianjun Chen, and Lu Li. 2023. "Weather Radar Parameter Estimation Based on Frequency Domain Processing: Technical Details and Performance Evaluation" Remote Sensing 15, no. 23: 5624. https://doi.org/10.3390/rs15235624
APA StyleZhang, S., Chen, Y., Shu, Z., Yu, H., Wang, H., Chen, J., & Li, L. (2023). Weather Radar Parameter Estimation Based on Frequency Domain Processing: Technical Details and Performance Evaluation. Remote Sensing, 15(23), 5624. https://doi.org/10.3390/rs15235624