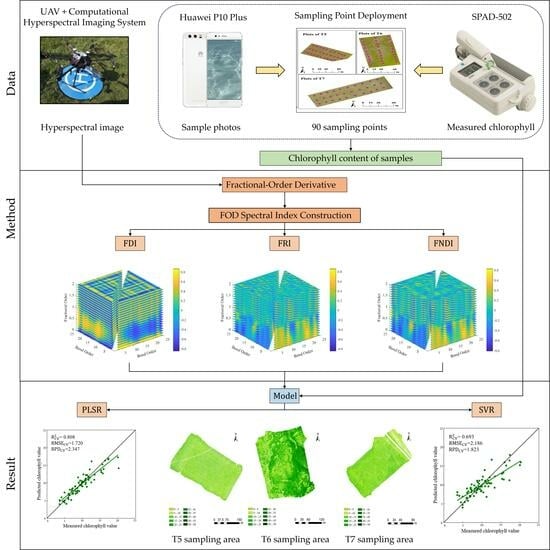
Grassland Chlorophyll Content Estimation from Drone Hyperspectral Images Combined with Fractional-Order Derivative
Abstract
1. Introduction
2. Materials and Methods
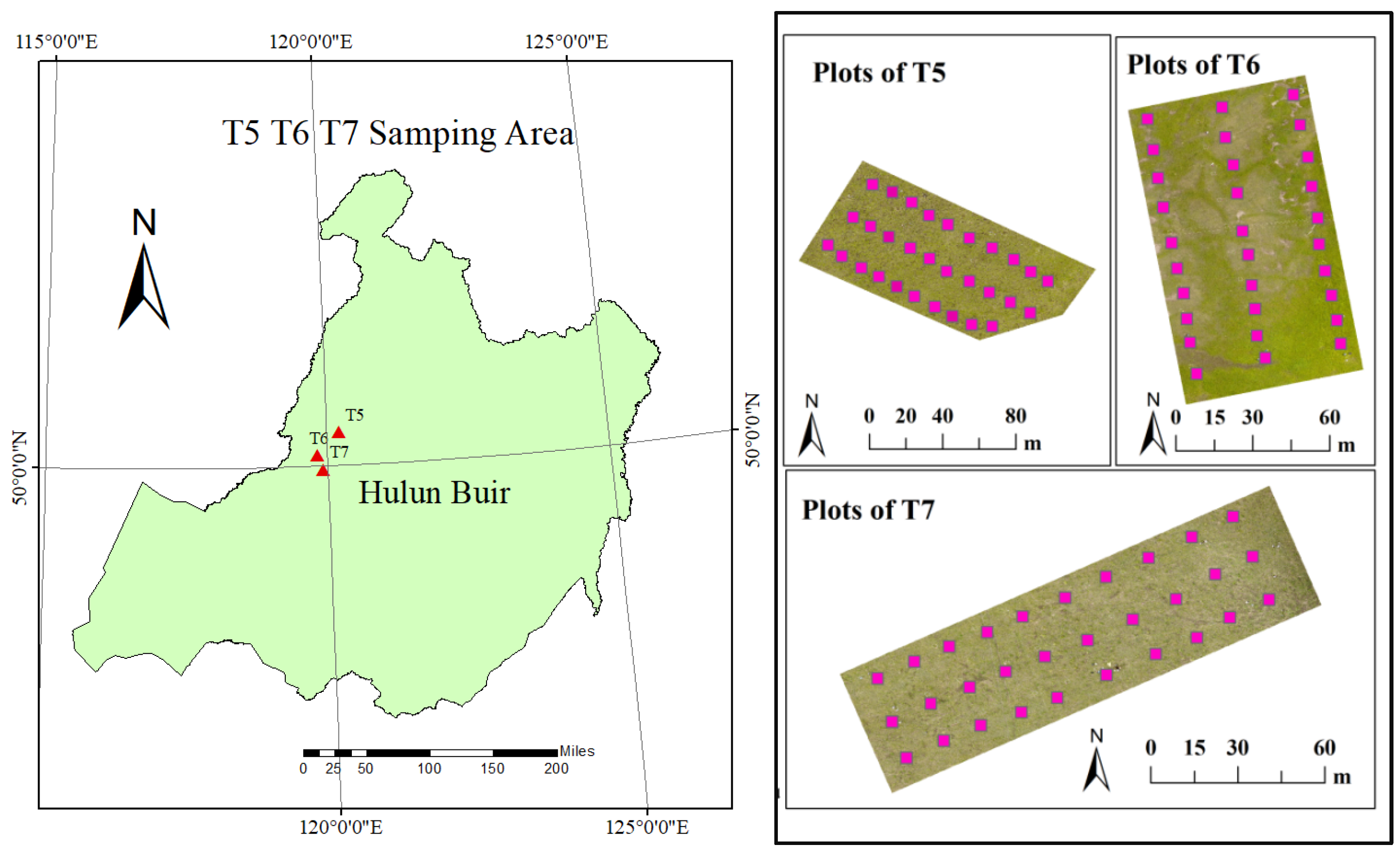
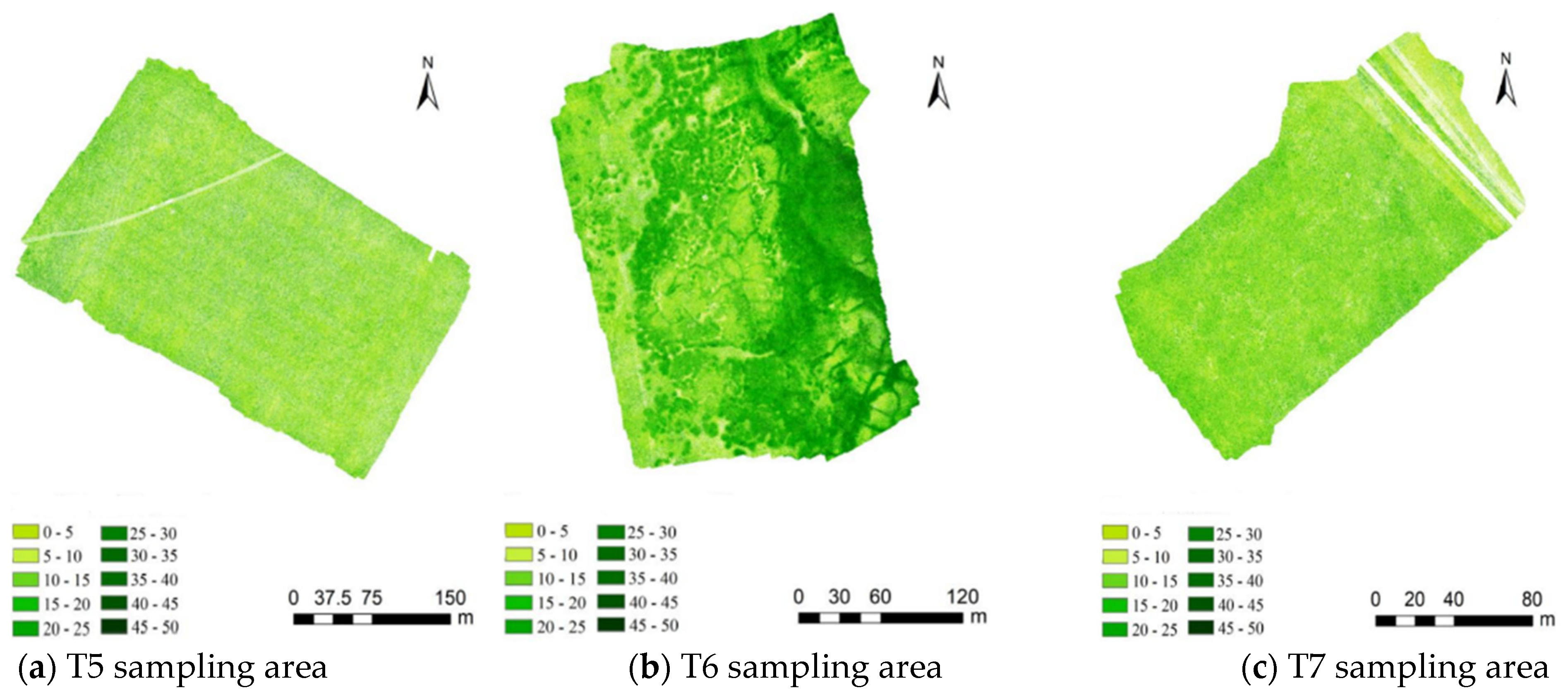
2.1. Study Area
2.2. UAV Hyperspectral Data
2.3. Calculation of Chlorophyll Content in the Sample
- -
- SPAD_cover: The estimated chlorophyll value of the sample canopy obtained through upward extrapolation of green vegetation coverage.
- -
- Cover_greengrass: The green vegetation coverage within the sample, expressed as a proportion.
- -
- SPAD_mean: The average SPAD value of the sample canopy.
- -
- SPADi: The individual SPAD-502 measurements obtained during the experiment.
- -
- n: The number of SPAD measurements taken.
- -
- S_greengrass: The number of pixels occupied by green vegetation in the image.
- -
- S_plot: The area of the sample square, which represents the size of the sampled area.
2.4. Methods
2.4.1. Fractional-Order Derivative
- -
- d: The derivative operator, which represents the mathematical operation of taking the derivative.
- -
- Γ: The Gamma function, which is a mathematical function that generalizes the factorial function to complex numbers.
- -
- λ: The corresponding wavelength for which the derivative is being calculated.
- -
- n: The difference between the upper and lower limits of the derivative. When n is 0, 1, or 2, it represents the integer-order derivative.
- -
- a: An arbitrary order that can be any real or complex number, representing the fractional order of the derivative.
- -
- f(λ): The spectral reflectance value at the wavelength λ.
2.4.2. FOD Spectral Index Construction
2.4.3. Chlorophyll Inversion Model Construction and Accuracy Verification
- (a)
- Full-band models with different fractional-order values ranging from 0 to 2. This group focuses on evaluating the modeling performance using the entire spectral range with varying fractional-order values.
- (b)
- Two-band index models using the FDI, FRI, and FNDI constructed from fractional-order spectra ranging from 0 to 2. This group investigates the effectiveness of these specific spectral indices in estimating chlorophyll content.
- (c)
- Combination models that include both the fractional-order full-band data and the optimal combinations of FDI, FRI, and FNDI indices. This group aims to assess the potential improvement in modeling accuracy by incorporating FOD and selected spectral indices together.
3. Results
3.1. Grassland Canopy Spectral Curves and Their Correlation with Chlorophyll
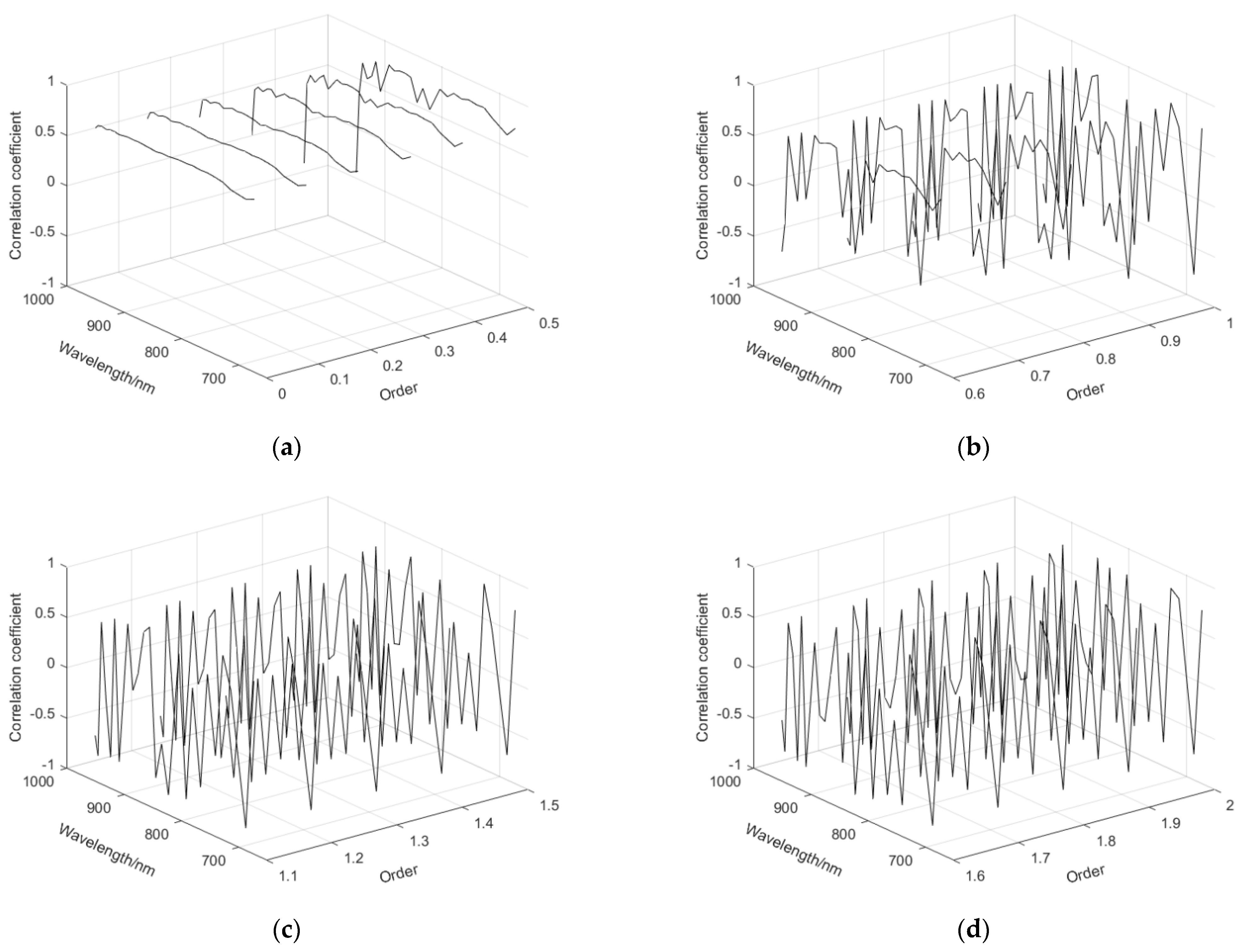
3.2. FOD Spectroscopy and Chlorophyll Correlation Analysis
3.3. Reflectance Spectral Index Preference
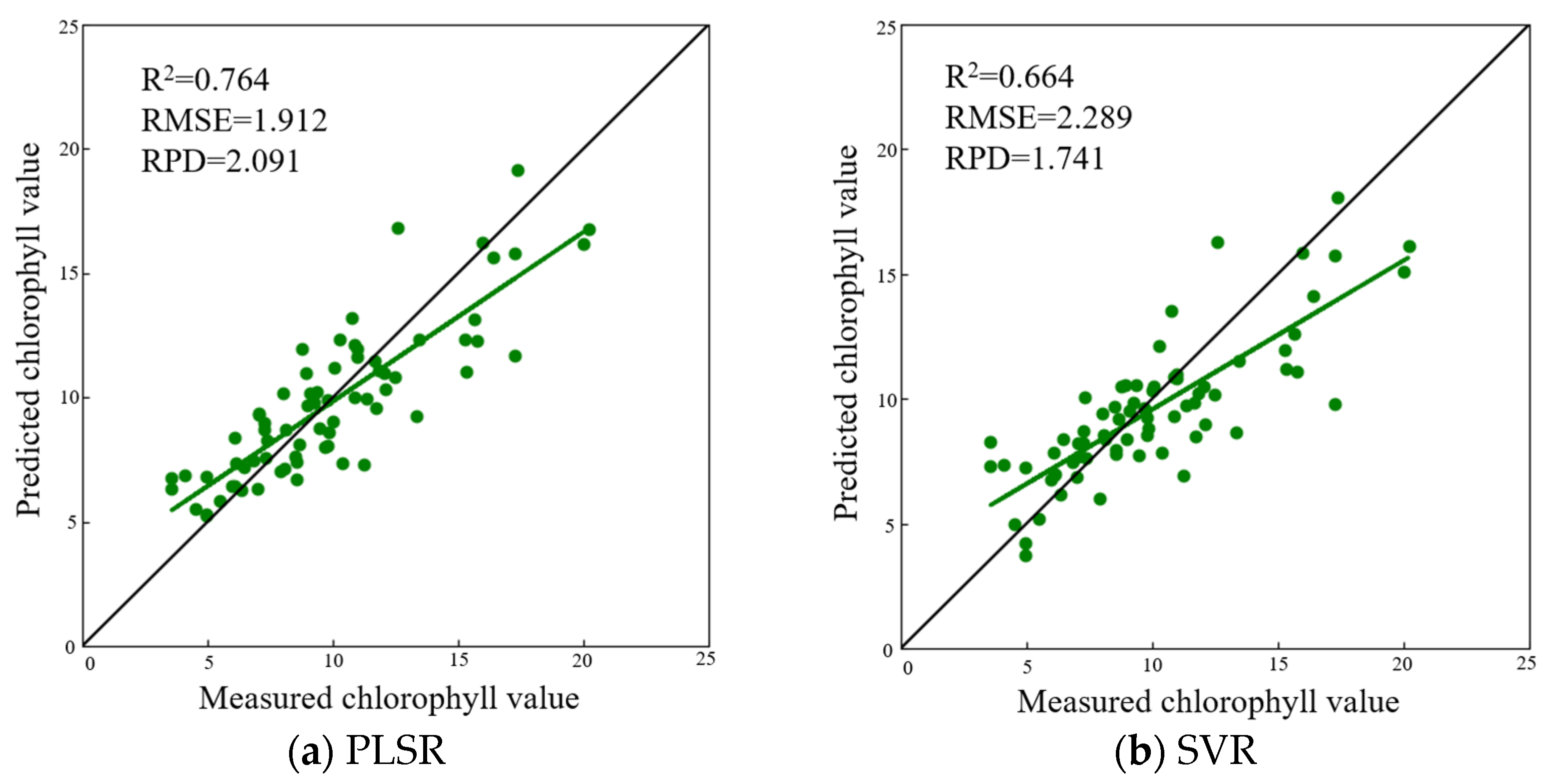
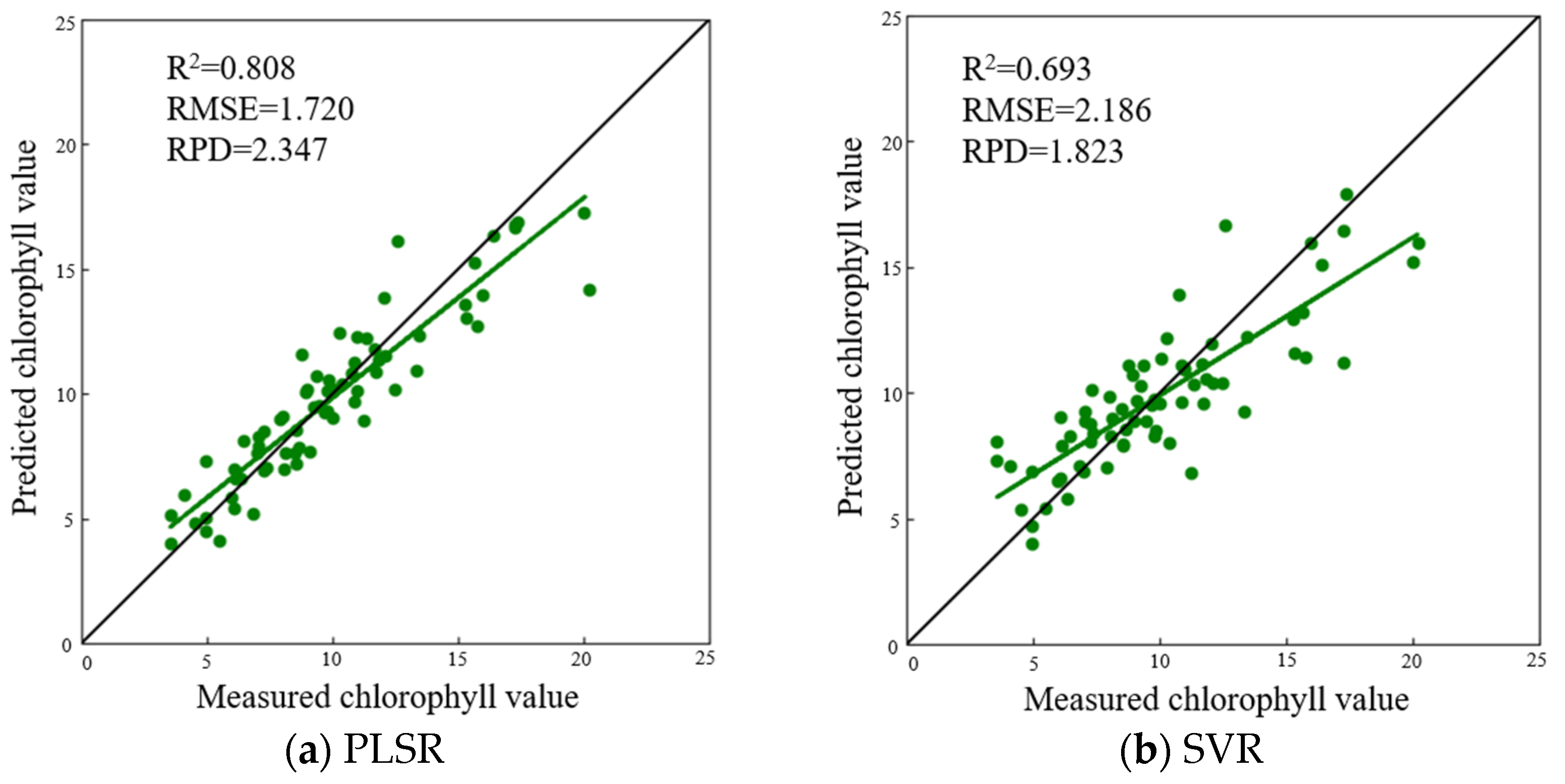
3.4. Chlorophyll Inversion Model Construction and Evaluation
- 1.
- FOD full-band spectra.
- 2.
- Preferential FOD spectral indices.
- 3.
- Spectral indices derived from the full-band spectra.
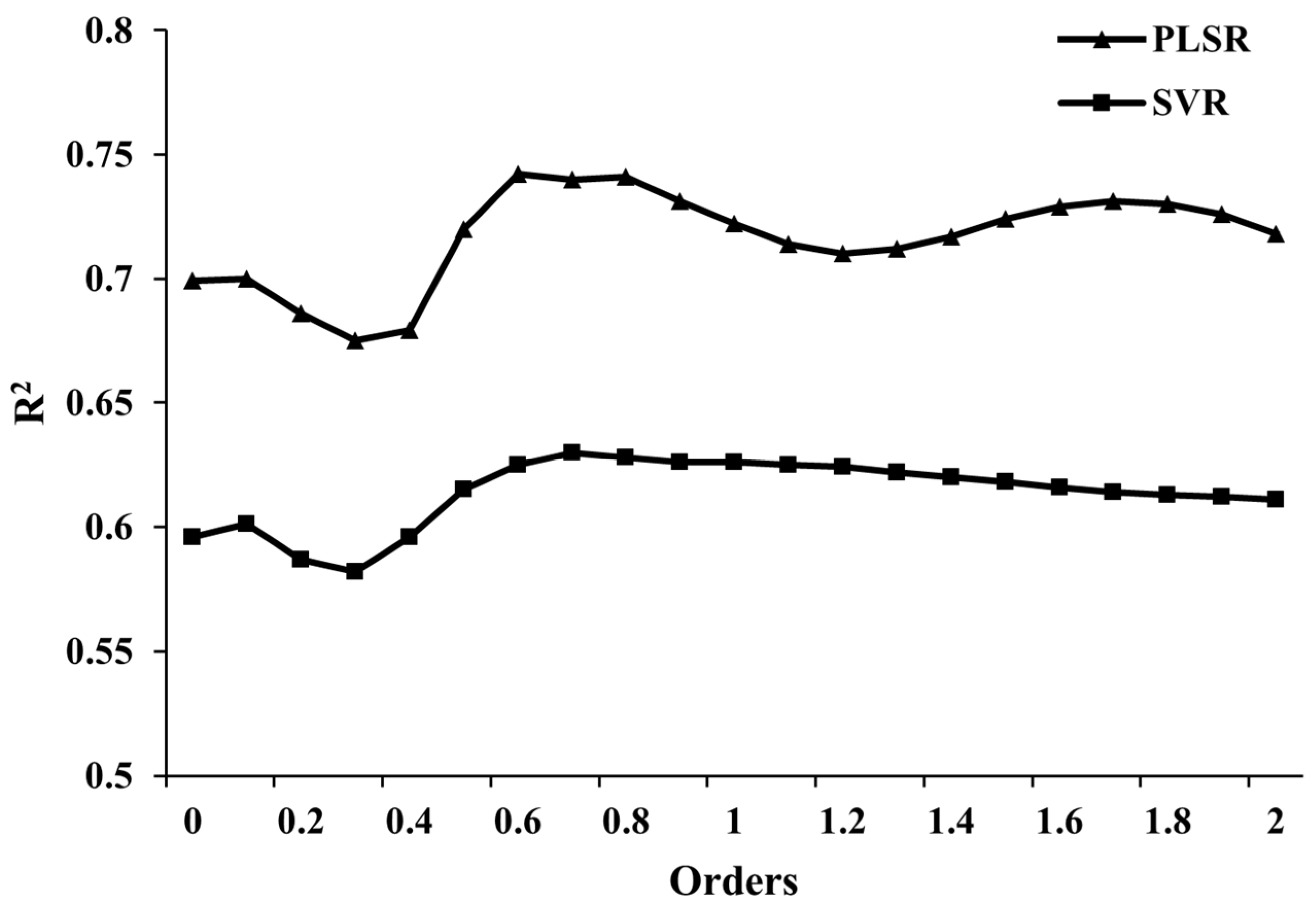
3.4.1. Full-Band FOD Spectra Model Construction
3.4.2. Chlorophyll Inversion Model Based on Two-Band FOD Spectral Indices
3.4.3. Chlorophyll Model Combining Spectral and Constructive Indices
4. Discussion
4.1. Contribution of FOD to Chlorophyll Estimation
4.2. Selected Spectral Indices
4.3. Modeling Results
4.4. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Clevers, J.G.P.W.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Gitelson, A.A. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote estimation of crop chlorophyll content using spectral indices derived from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, A. Hyperspectral remote sensing estimation of pasture crude protein content based on multi-granularity spectral feature. Trans. Chines 2019, 35, 161–169. [Google Scholar]
- Liu, H.; Zhao, Y.; Wen, Y.; Sun, H.; Li, M.; Zhang, Q. Diagnose of chlorophyll content in corn canopy leaves based on multispectral detector. J. Agromed. 2015, 46 (Suppl. S1), 228–233. [Google Scholar]
- Wen, Y.; Li, M.; Zhao, Y.; Liu, H.; Sun, H.; Chen, J. Multispectral reflectance inversion and chlorophyll content diagnose of maize at seeding stage. Trans. Chines 2015, 31, 193–199. [Google Scholar]
- Niu, L.; Sun, J.; Liu, Y.; Zhang, X. Research of estimation models of wheat chlorophyll content based on imaging hyperspectral data. J. Henan Agric. Sci. 2016, 45, 150–154. [Google Scholar]
- Zhang, J.; Xu, S.; Zhai, Q.; Zhang, Y.; Ma, X. Hyper-spectral Remote Sensing Response and Estimation Model of Leaf Chlorophy Content of Wheat under Different Soil Textures. J. Triticeae Crops 2014, 34, 642–647. [Google Scholar]
- Ma, W.; Wang, X. Progress on grassland chlorophyll content estimation by hyperspectral analysis. Prog. Geogr. 2016, 35, 25–34. [Google Scholar]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Rossini, M.; Cogliati, S.; Meroni, M.; Migliavacca, M.; Galvagno, M.; Busetto, L.; Cremonese, E.; Julitta, T.; Siniscalco, C.; Morra di Cella, U.; et al. Remote sensing-based estimation of gross primary production in a subalpine grassland. Biogeosciences 2012, 9, 2565–2584. [Google Scholar] [CrossRef]
- Wong, K.K.; He, Y. Estimating grassland chlorophyll content using remote sensing data at leaf, canopy, and landscape scales. Can. J. Remote Sens. 2014, 39, 155–166. [Google Scholar] [CrossRef]
- Reza Amiri, J.B.; Isaac, P. Narrowband spectral indices for the estimation of chlorophyl along a precipitation gradient. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Xiao, H.; Chen, X.; Yang, Z.; Li, H.; Zhu, H. Vegetation index estimation by chlorophyll content of grassland based on spectral analysis. Guang Pu Xue Yu Guang Pu Fen Xi 2014, 34, 3075–3078. [Google Scholar] [PubMed]
- Pu, R.; Gong, P. Hyperspectral Remote Sensing and Its Applications; Higher Education Publishing House: Beijing, China, 2000. [Google Scholar]
- Rukeya Sawuti, A.A.; Nijati, K.; Li, H.; Wumuti, A.; Yasenjiang, K.; Li, X. Spectral estimation of chlorophyll content in spring wheat leaves based on fractional differential. J. Triticeae Crops 2019, 6, 738–746. [Google Scholar]
- Wang, J.; Tiyip, T.; Ding, J.; Zhang, D.; Liu, W. Estimation of desert soil organic carbon content based on hyperspectral data preprocessing with fractional differential. Trans. Chines 2016, 32, 161–169. [Google Scholar]
- Tarasov, V.E. On chain rule for fractional derivatives. Commun. Nonlinear Sci. 2016, 30, 1–4. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Kung, H.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the ebinur lake wetland national nature reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Yasenjiang, K.; Yang, S.T.; Nigara, T.; Zhang, F. Hyperspectral estimation of soil electrical conductivity based on fractional order differentially optimised spectral indices. Acta Ecol. Sin. 2019, 19, 7237–7246. [Google Scholar]
- Abulaiti, Y.; Sawut, M.; Maimaitiaili, B.; Chunyue, M. A possible fractional order derivative and optimized spectral indices for assessing total nitrogen content in cotton. Comput. Electron. Agric. 2020, 171, 105275. [Google Scholar] [CrossRef]
- Jing, X.; Zeng, T.; Zou, Q.; Yan, J.; Dong, Y. Construction of remote sensing monitoring model of wheat strip rust based on fractional-order differential spectral index. Trans. Chines 2021, 17, 142–151. [Google Scholar]
- Zhao, B.; Duan, A.; Ata-Ul-Karim, S.T.; Liu, Z.; Chen, Z.; Gong, Z.; Zhang, J.; Xiao, J.; Liu, Z.; Qin, A.; et al. Exploring new spectral bands and vegetation indices for estimating nitrogen nutrition index of summer maize. Eur. J. Agron. 2018, 93, 113–125. [Google Scholar] [CrossRef]
- Feng, W.; Shen, W.; He, L.; Duan, J.; Guo, B.; Li, Y.; Wang, C.; Guo, T. Improved remote sensing detection of wheat powdery mildew using dual-green vegetation indices. Precis. Agric. 2016, 17, 608–627. [Google Scholar] [CrossRef]
- Wang, R.; Chen, Y.; Chen, L.; Peng, S.; Wang, X.; Yang, X.; Ma, L. Correlation analysis of SPAD value and chlorophyll congtent in leaves of Camellia oleifera. J. Cent. South. Univ. For. Technol. 2013, 33, 77–80. [Google Scholar]
- Li, M. Study on High-Spectral Quantitative Inversion Method of Chlorophyll Content in Natural Grassland Canopy; Capital Normal University: Beijing, China, 2021. [Google Scholar]
- Liu, Y.; Feng, H.; Sun, Q.; Yang, F.; Yang, G. Estimation of potato above-ground biomass based on fractional differential of UAV hyperspectral. J. Agric. Mach. 2020, 51, 202–211. [Google Scholar]
- Lin, S.; Xu, C. Theoretical and numerical investigation of fractional differential equations. Math. Numer. Sin. 2016, 38, 1–24. [Google Scholar]
- Tian, A.; Zhao, J.S.; Zhang, S.; Fu, C.; Xiong, H. Hyperspectral estimation of saline soil electral conductivity based on fractioanal derivative. Chines J. Eco-Agric. 2020, 28, 599–607. [Google Scholar]
- Jin, X.; Yang, G.; Xu, X.; Yang, H.; Feng, H.; Li, Z.; Shen, J.; Lan, Y.; Zhao, C. Combined multi-temporal optical and radar parameters for estimating LAI and biomass in winter wheat using HJ and Radarsar-2 data. Remote Sens. 2015, 7, 13251–13272. [Google Scholar] [CrossRef]



| Band Order | Wavelength /nm | Band Order | Wavelength /nm | Band Order | Wavelength /nm |
|---|---|---|---|---|---|
| 1 | 672.7 | 11 | 812.6 | 21 | 923.8 |
| 2 | 687.2 | 12 | 833.7 | 22 | 930.8 |
| 3 | 713.1 | 13 | 843.7 | 23 | 939.3 |
| 4 | 727.4 | 14 | 854.6 | 24 | 944.9 |
| 5 | 739.5 | 15 | 864.8 | 25 | 950.1 |
| 6 | 754.2 | 16 | 876.2 | ||
| 7 | 766.4 | 17 | 883.8 | ||
| 8 | 779.6 | 18 | 893.5 | ||
| 9 | 790.8 | 19 | 907.8 | ||
| 10 | 803.5 | 20 | 916.2 |
| Orders | Correlation | Wavelength/nm | Orders | Correlation | Wavelength/nm |
|---|---|---|---|---|---|
| 0 | 0.774 | 779.6 | 1.1 | 0.838 | 727.4 |
| 0.1 | 0.776 | 779.6 | 1.2 | 0.841 | 727.4 |
| 0.2 | 0.781 | 779.6 | 1.3 | 0.843 | 727.4 |
| 0.3 | 0.786 | 754.2 | 1.4 | 0.844 | 727.4 |
| 0.4 | 0.791 | 754.2 | 1.5 | 0.844 | 727.4 |
| 0.5 | 0.795 | 754.2 | 1.6 | 0.842 | 727.4 |
| 0.6 | 0.798 | 754.2 | 1.7 | 0.838 | 727.4 |
| 0.7 | 0.807 | 727.4 | 1.8 | 0.830 | 727.4 |
| 0.8 | 0.817 | 727.4 | 1.9 | 0.817 | 727.4 |
| 0.9 | 0.826 | 727.4 | 2.0 | 0.799 | 727.4 |
| 1.0 | 0.833 | 727.4 |
| Orders | FDI | FRI | FNDI | |||
|---|---|---|---|---|---|---|
| Correlation | Band Combination | Correlation | Band Combination | Correlation | Band Combination | |
| 0 | 0.838 | (14,8) | −0.817 | (10,14) | 0.817 | (14,10) |
| 0.1 | −0.838 | (4,3) | 0.816 | (12,10) | 0.816 | (12,10) |
| 0.2 | −0.841 | (4,3) | 0.81 | (12,10) | 0.809 | (12,10) |
| 0.3 | −0.843 | (4,3) | 0.812 | (3,4) | −0.81 | (4,3) |
| 0.4 | −0.844 | (4,3) | 0.815 | (3,4) | −0.811 | (4,3) |
| 0.5 | −0.844 | (4,3) | 0.814 | (1,10) | −0.812 | (10,1) |
| 0.6 | −0.842 | (4,3) | 0.819 | (2,10) | −0.821 | (10,2) |
| 0.7 | 0.838 | (4,3) | 0.803 | (2,10) | −0.806 | (10,2) |
| 0.8 | 0.848 | (22,4) | 0.758 | (1,4) | −0.753 | (4,1) |
| 0.9 | 0.856 | (22,4) | 0.772 | (1,4) | −0.767 | (4,1) |
| 1.0 | 0.861 | (22,4) | 0.784 | (1,4) | −0.779 | (4,1) |
| 1.1 | 0.86 | (22,4) | −0.818 | (19,4) | 0.818 | (4,2) |
| 1.2 | 0.852 | (22,4) | −0.85 | (19,4) | 0.819 | (4,2) |
| 1.3 | 0.838 | (13,4) | −0.858 | (19,4) | 0.82 | (4,2) |
| 1.4 | 0.838 | (11,4) | 0.856 | (20,4) | 0.82 | (4,2) |
| 1.5 | 0.839 | (11,4) | 0.852 | (20,4) | 0.818 | (4,2) |
| 1.6 | 0.838 | (11,4) | 0.836 | (20,4) | 0.812 | (4,2) |
| 1.7 | 0.835 | (11,4) | 0.808 | (20,4) | 0.799 | (4,2) |
| 1.8 | 0.831 | (11,4) | 0.777 | (1,4) | 0.78 | (4,2) |
| 1.9 | 0.831 | (19,4) | −0.775 | (1,11) | 0.777 | (11,1) |
| 2.0 | 0.832 | (19,4) | −0.773 | (1,11) | 0.776 | (11,1) |
| Order | PLSR | SVR | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | RPD | R2 | RMSE | RPD | |
| 0 | 0.699 | 2.165 | 1.847 | 0.596 | 2.529 | 1.58 |
| 0.1 | 0.7 | 2.164 | 1.842 | 0.601 | 2.515 | 1.588 |
| 0.2 | 0.686 | 2.218 | 1.796 | 0.587 | 2.559 | 1.561 |
| 0.3 | 0.675 | 2.257 | 1.765 | 0.582 | 2.571 | 1.552 |
| 0.4 | 0.679 | 2.246 | 1.769 | 0.596 | 2.524 | 1.579 |
| 0.5 | 0.72 | 2.089 | 1.907 | 0.615 | 2.464 | 1.615 |
| 0.6 | 0.742 | 2.001 | 1.994 | 0.625 | 2.435 | 1.626 |
| 0.7 | 0.74 | 2.023 | 1.966 | 0.63 | 2.418 | 1.648 |
| 0.8 | 0.741 | 2.009 | 1.983 | 0.628 | 2.425 | 1.645 |
| 0.9 | 0.731 | 2.05 | 1.943 | 0.626 | 2.434 | 1.641 |
| 1.0 | 0.722 | 2.084 | 1.912 | 0.626 | 2.435 | 1.641 |
| 1.1 | 0.714 | 2.11 | 1.889 | 0.625 | 2.437 | 1.639 |
| 1.2 | 0.71 | 2.124 | 1.878 | 0.624 | 2.441 | 1.636 |
| 1.3 | 0.712 | 2.118 | 1.883 | 0.622 | 2.447 | 1.632 |
| 1.4 | 0.717 | 2.098 | 1.9 | 0.62 | 2.454 | 1.627 |
| 1.5 | 0.724 | 2.075 | 1.92 | 0.618 | 2.46 | 1.623 |
| 1.6 | 0.729 | 2.057 | 1.936 | 0.616 | 2.466 | 1.618 |
| 1.7 | 0.731 | 2.049 | 1.944 | 0.614 | 2.471 | 1.615 |
| 1.8 | 0.73 | 2.052 | 1.942 | 0.613 | 2.474 | 1.613 |
| 1.9 | 0.726 | 2.067 | 1.928 | 0.612 | 2.478 | 1.611 |
| 2.0 | 0.718 | 2.094 | 1.905 | 0.611 | 2.481 | 1.609 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Yin, S.; Wang, J.; He, N.; Chai, S.; Pang, H. Grassland Chlorophyll Content Estimation from Drone Hyperspectral Images Combined with Fractional-Order Derivative. Remote Sens. 2023, 15, 5623. https://doi.org/10.3390/rs15235623
Zhang A, Yin S, Wang J, He N, Chai S, Pang H. Grassland Chlorophyll Content Estimation from Drone Hyperspectral Images Combined with Fractional-Order Derivative. Remote Sensing. 2023; 15(23):5623. https://doi.org/10.3390/rs15235623
Chicago/Turabian StyleZhang, Aiwu, Shengnan Yin, Juan Wang, Nianpeng He, Shatuo Chai, and Haiyang Pang. 2023. "Grassland Chlorophyll Content Estimation from Drone Hyperspectral Images Combined with Fractional-Order Derivative" Remote Sensing 15, no. 23: 5623. https://doi.org/10.3390/rs15235623
APA StyleZhang, A., Yin, S., Wang, J., He, N., Chai, S., & Pang, H. (2023). Grassland Chlorophyll Content Estimation from Drone Hyperspectral Images Combined with Fractional-Order Derivative. Remote Sensing, 15(23), 5623. https://doi.org/10.3390/rs15235623