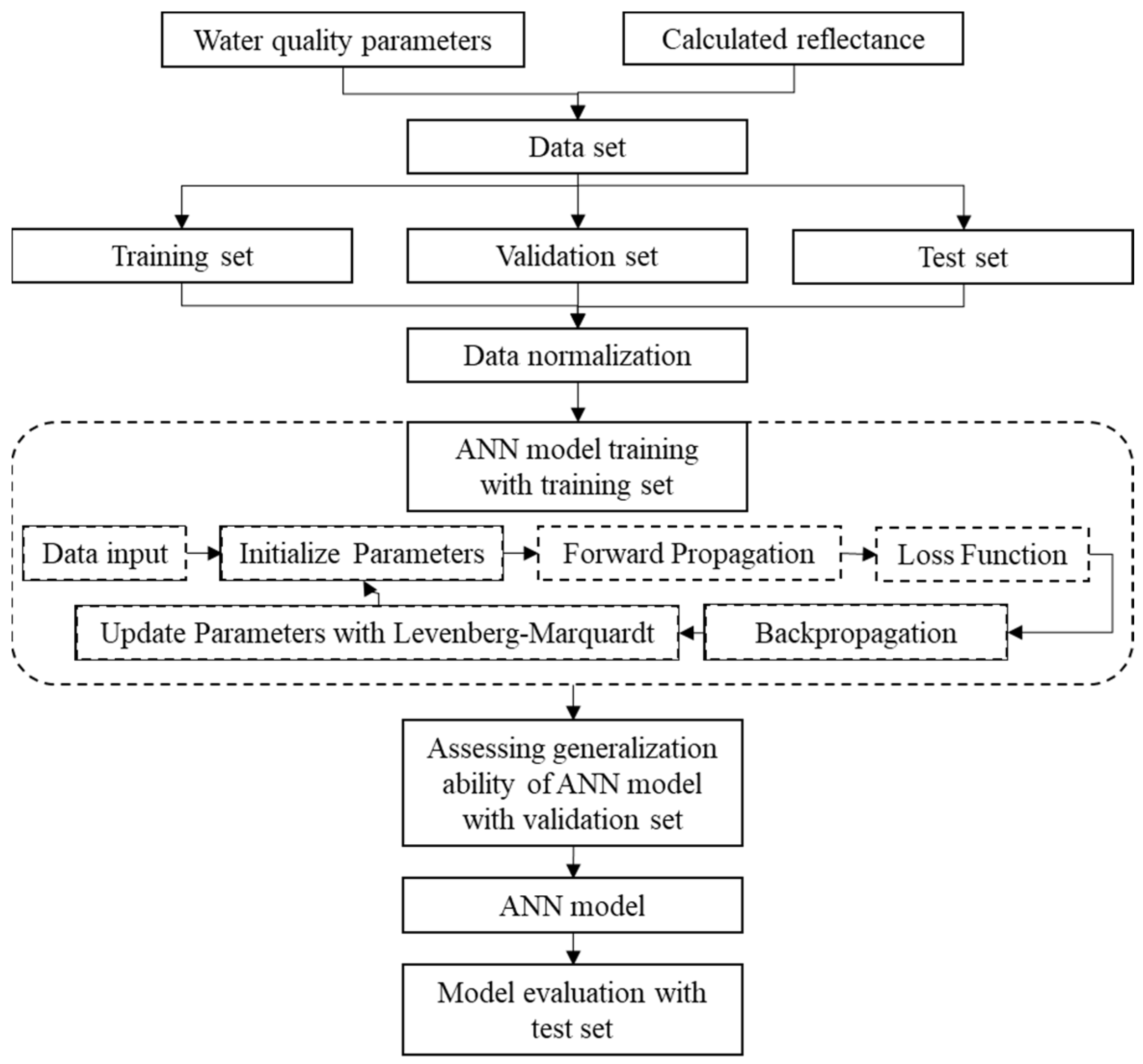
In this section, we introduce the methodology employed in this paper, which includes data matching, data processing, determination of characteristic spectral bands, regression modeling, and model evaluation. The water quality parameters and hyperspectral data do not possess a direct one-to-one correspondence; the data matching method is to establish a consistent correspondence between water quality data collected at the same geographical location and time and the corresponding satellite hyperspectral data. Preprocessing of the water quality parameters and hyperspectral satellite data is necessary to normalize the distribution of the water quality parameters and ensure the hyperspectral data are processed within the spectral range of interest specific to this paper. The determination of characteristic spectral bands represents a crucial innovation in this research, allowing for efficient selection of relevant bands for different water quality parameters through correlation analysis with a regression model. Various regression modeling methods are presented in this section to evaluate and compare their performance in modeling, and to determine the optimal approach for regression modeling between the water quality parameters and calculated reflectance. Model evaluation is necessary to clearly elaborate the specific parameters used to compare different regression models and to specify the calculation formulas for these comparison metrics.
3.1. Data Matching of Water Quality Parameters and Hyperspectral Satellite Data
The data matching method integrates geometric and temporal information to establish correspondence between water quality parameters and hyperspectral satellite data, enabling the spectral characteristics from the satellite data to represent the water quality parameters.
This paper realizes the heterogeneous data matching of water quality monitoring data and ZY1-02D satellite hyperspectral data of the same NSWAMS based on the location and time, whose principle is shown in
Figure 5. Twenty scenes of hyperspectral data with the highest utilization rate were selected as the research data of this paper.
The specific methods are shown in
Figure 6, as follows:
(1) Data extraction for a range of locations and times. On the Natural Resources Satellite Remote Sensing Cloud Service Platform, the time condition is “December 2020–August 2022”, the geographical conditions are Suzhou, Shanghai, Jiaxing, Huzhou, and Wuxi, the satellite sampling conditions are the AHSI sensor of ZY1-02D and 0 cloud amount; a total of 61 scenes were found, of which 8 scenes had low-altitude cloud phenomenon, so 53 scenes were available for selection. Water quality monitoring data were obtained from each NSWAMS in Suzhou, Shanghai, Jiaxing, Huzhou, and Wuxi from December 2020 to August 2022 from the National Surface Water Automatic Monitoring Real-Time Data Release System. Each datum includes the name, time, water quality classification, temperature, pH, DO, CODMn, NH3-N, TP, TN, EC, and TUB of the NSWAMS, together with latitude and longitude;
(2) Determination if each NSWAMS is within the satellite data. For the ith scene of the hyperspectral satellite data shi, the sampling date and time is ti, the four vertices are ai, bi, ci and di, whose latitudes and longitudes are (lonai, latai), (lonbi, latbi), (lonci, latci), and (londi, latdi). Assuming that the water quality parameter set rwqi was collected at the same sampling time ti, and that the number of water quality parameters records in this set is ni, the latitude and longitude of the NSWAMS ei,j corresponding to the jth water quality parameter record rwqi,j is (lonei,j, latei,j), where . The area method is used to determine if this NSWAMS is within the satellite hyperspectral data of this scene. The area of the parallelogram formed by ai, bi, ci, and di is si, and ei,j forms four triangles with each side of the quadrangle area, whose areas are si,j,1, si,j,2, si,j,3, and si,j,4, respectively. If si is less than the sum of the four areas noted, then it proves that the NSWAMS is within the scene data, and these water quality parameter records are collected in the selected set swqi. Otherwise, if it is higher, it is outside the hyperspectral satellite data of this scene. If the NSWAMS is determined to be within the geographic location of the ith satellite data according to the method described above, then the water quality parameter records within the satellite data are collected into the dataset swqi.
(3) Selection of satellite data with the top 20 water quality parameter records. The number of water quality parameter records in this dataset is calculated, which is the number of NSWAMS in this satellite scene numi. The number of NSWAMS in each scene of satellite data is calculated using on the method described above, and the numbers of water quality parameter records of all scenes are sorted. The 20 scenes of satellite data with the highest number of NSWAMS are taken for analysis, which are the 20 scenes of satellite hyperspectral data with the highest effective information density;
(4) Extraction of spectral value curve corresponding to each water quality parameter sample. According to the geographic information for the NSWAMSs collected from each scene, ENVI 5.3 software is used to extract the entire spectral value curve for the water body at the corresponding position in the hyperspectral satellite image, the spectral mean of scale 1 is taken as the spectral value [
20].
All of the water quality parameter records and the spectral curves for the water body with the same position and time are collected. Using these methods, 188 records of water quality parameters at different times and locations and their corresponding satellite hyperspectral data in time and space were obtained, realizing the matching of 20 scenes of satellite hyperspectral data with the highest effective information density together with their water quality parameters.
3.3. Determination of Characteristic Spectral Bands for Water Quality Parameters Based on the Correlation between Reflectance of Different Bands
From the perspective of water quality parameter measurement, the effective utilization of hyperspectral data leads to selection of the characteristic spectral band combinations for different water quality parameters. By using multiple characteristic bands, accurate inversion of each water quality parameter can be achieved, which can ensure the accuracy of water quality parameter measurement and the simplicity of spectral bands, remove redundant data, improve spectral data processing speed, and achieve efficient utilization of spectral data.
This paper proposes a method to determine the optimal characteristic bands based on the reflectance correlation of different bands, which is shown in
Figure 10. For the given band set, the number of bands contained in the band set is
nbs. The steps of the approach follow.
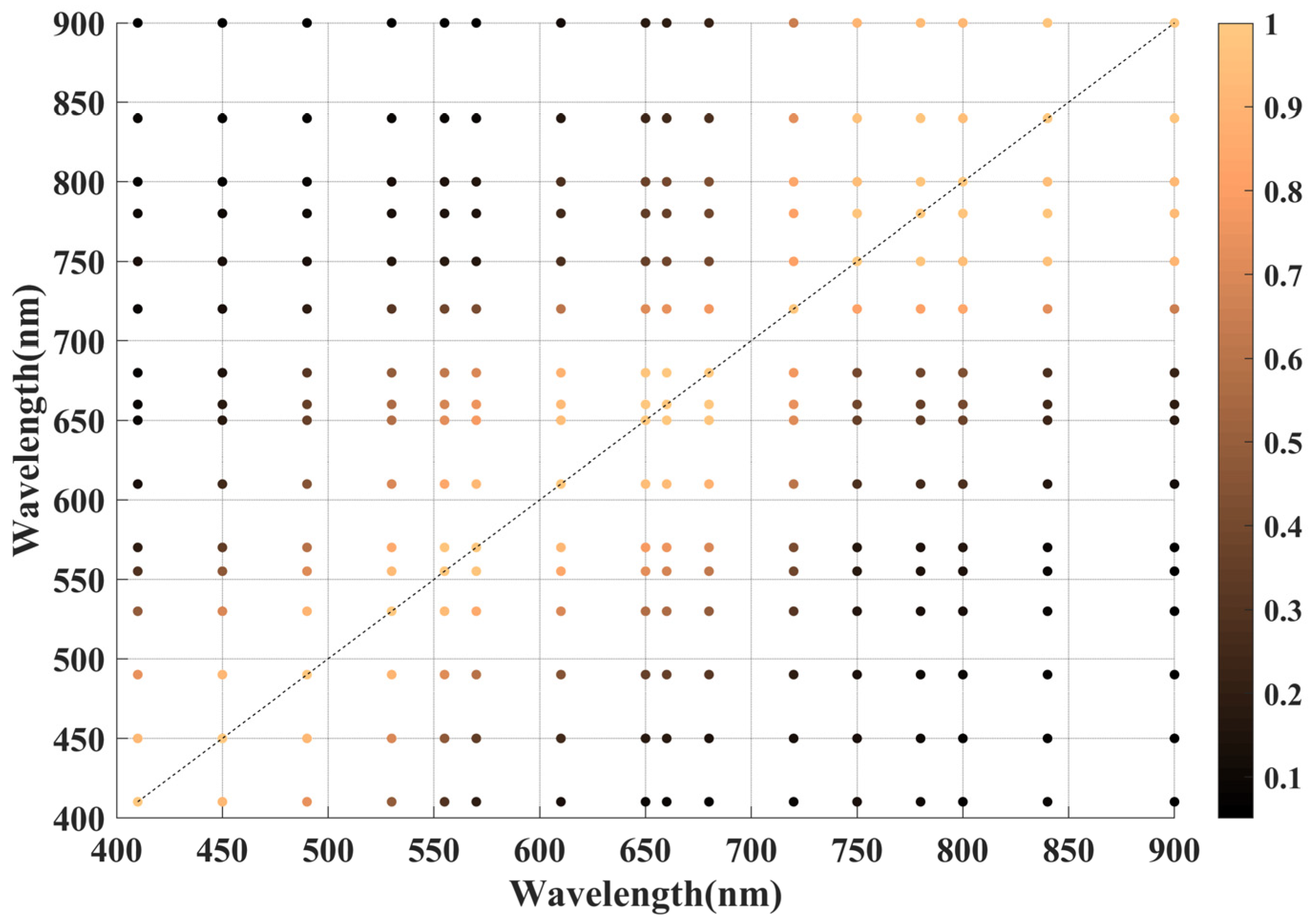
(1) Determination of a high correlation two-band set. The determination coefficient
[
26] between the reflectance data corresponding to each two-band combination in a given band set was calculated by Equation (1).
where
n is the number of the reflectance data samples,
represents the reflectance data corresponding to band A, and
represents the reflectance data corresponding to band B.
The two bands with the determination coefficient
greater than 0.9 were considered to have the same effect in the same characteristic spectral band combination. Therefore, they cannot appear simultaneously in a characteristic spectral band combination containing two or more bands [
34]. The dataset of the two-band combinations with
higher than 0.9 is expressed as
S.
The maximum number of spectral bands nbmax contained in a spectral band combination and the number of different spectral band combinations with different numbers of bands could also be determined so that the spectral band combination cannot contain the two highly correlated bands.
(2) Calculated reflectance of the spectral band combination without high correlation between two bands. For the
cith spectral band wavelength combination
, consisting of the
ith,
jth, …, and
zth bands wavelength,
represents arbitrary wavelength combination of two bands from
. If
does not belong to the dataset
S, then the reflectance data corresponding to the wavelengths in the spectral band combinations
can be used to calculate the combination reflectance
with Equation (2).
The definition and restriction conditions of the notations are listed in
Table 6.
(3) Characteristic spectral bands determination. The combination reflectance corresponding to the spectral band combinations containing one to nbmax bands that meet the requirements were traversed to build the regression models with the selected method for inversion with different water quality parameters. The models with the best performance are used to determine the different characteristic spectral band combinations and the number of bands included in the combinations for different water quality parameters. Using the same method mentioned above, other band sets Par, Mic, DJ3, DJ4, MS600, and AQ600 were fitted, and the characteristic spectral band combination for each water quality parameter was selected. The band set that can achieve optimal results was determined by comparing the performance of different band combination models. The characteristic spectral bands of each water quality parameter were summarized within the optimal band set.
(4) Optimal spectral bands selection. By ensuring accurate monitoring of the required water quality parameters while satisfying the overall band quantity requirement, the optimal spectral bands were selected based on the specific monitoring requirements for water quality parameters and the total number of bands that was needed. This approach aimed to achieve precise remote sensing measurements of water quality parameters within the specified number of bands.
3.4. Regression Modeling with the Empirical Method
Considering that empirical models are usually one-band, two-band, and three-band models, this paper adopts a one-, two-, and three-band reflectance index to establish the inversion model for water quality parameters [
35]. The reference two-band indexes are to calculate the band ratio (
BR) [
36] and the differential spectral index (
NDSI) [
37] of the reflectance of the two bands. The three-band reference indexes are to calculate the three-band index (
TBI) [
38], the enhanced three-band index (
ETBI) [
39], and the baseline height index (
BH) [
40].
The calculation equation for the single band reflectance data value is expressed as Equation (3).
The equations for the calculated reflectance of the two-band combination are expressed as Equations (4) and (5).
The equations for the calculated reflectance of the three-band combination are expressed as Equations (6)–(8).
In this study, the relationship between these different variables and water quality parameters was established using linear least squares regression fitting. In each regression analysis conducted in this section, the water quality parameter of interest was considered as the response variable, such as DO, CODMn, NH3-N, TP, TN, TUB, and EC. The corresponding variables, including , , , , , and , calculated by Equations (3)–(8), were included as covariates. There was a one-to-one correspondence between the response variable and the respective covariate in each regression analysis.