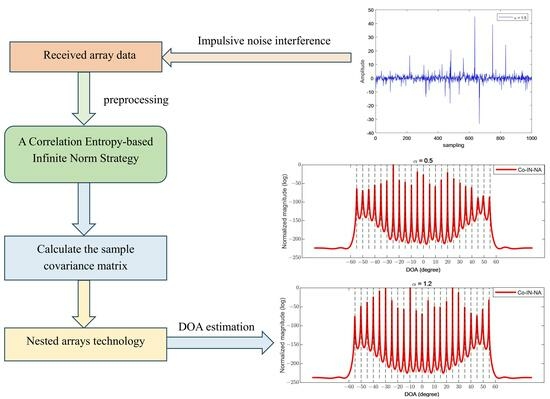
Direction of Arrival Estimation with Nested Arrays in Presence of Impulsive Noise: A Correlation Entropy-Based Infinite Norm Strategy
Abstract
:1. Introduction
- We propose a data-adaptive zero-memory exponential infinity norm strategy based on correlation entropy to suppress the impulsive noise outliers without the prior information of impulsive noise.
- We analyze the pseudocovariance matrix of the processed signal data and prove its boundedness.
- We extend the proposed Co-IN method to the nested array scenario [34].
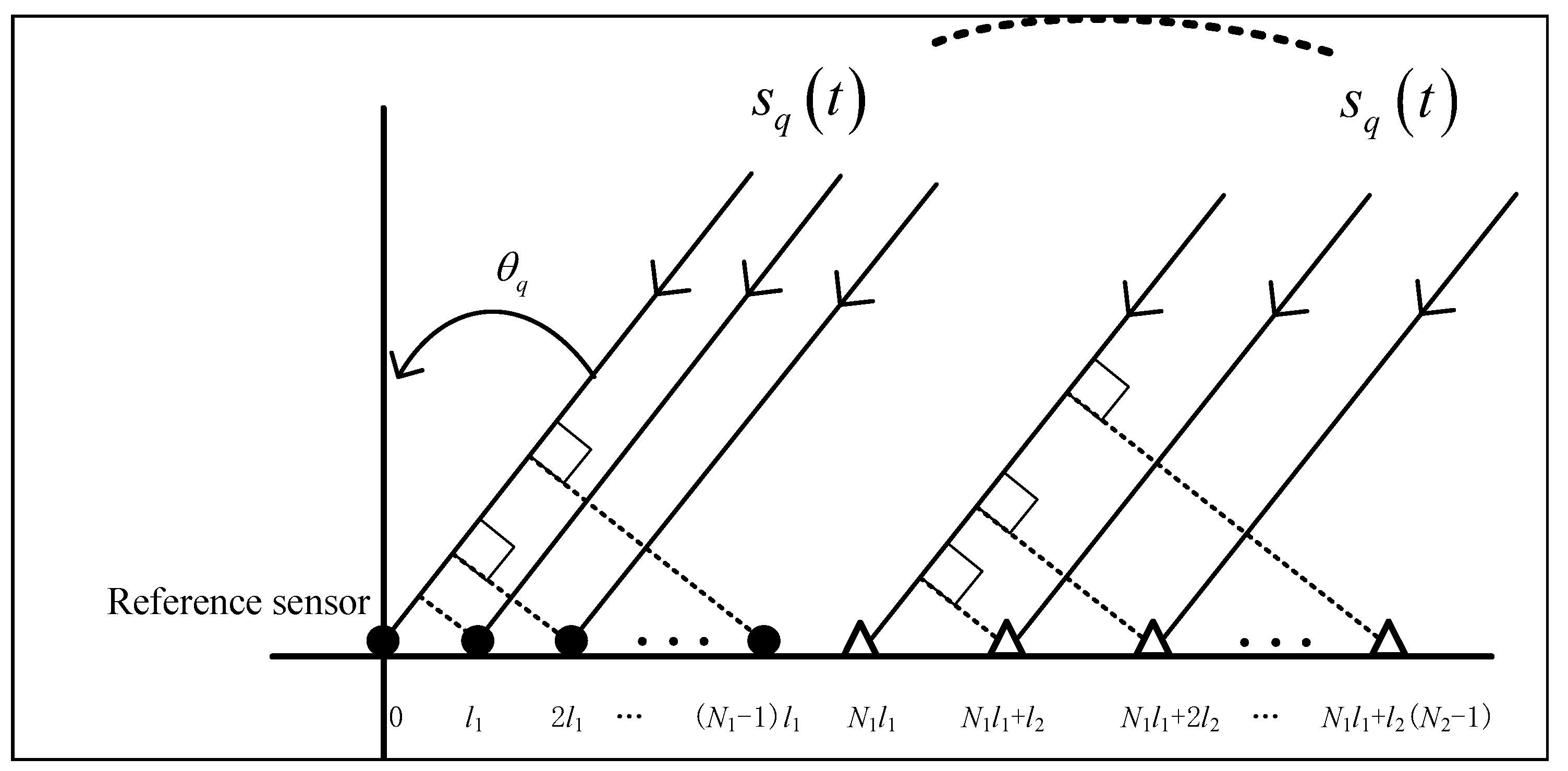
2. Signal Models with a Nested Array Structure
3. Proposed Method
3.1. Correlation Entropy-Based Infinite Norm (Co-IN) Strategy
3.2. Statistical Analysis of the Co-IN Strategy
3.3. Algorithm Flow of Co-IN Strategy
| Algorithm 1: Proposed Co-IN method. |
Input: , ; fordo |
 end |
1: Construct the pseudo-covariance matrix and obtain the new covariance matrix according to Equations (13) and (24), respectively. 2: Perform an EVD operation on to obtain the signal subspace spanned by the eigenvectors corresponding to the first Q eigenvalues. 3: Decompose to and , as follows 4: Construct a new signal matrix , and calculate ; 5: Perform EVD on to obtain the matrix of eigenvectors , which is decomposed to , and . 6: Calculate ; 7: Perform EVD on to obtain the eigenvalue ; 8: Estimate the DOAs: . Output: The estimated DOAs . |
4. Simulation Results
4.1. Complexity Analysis
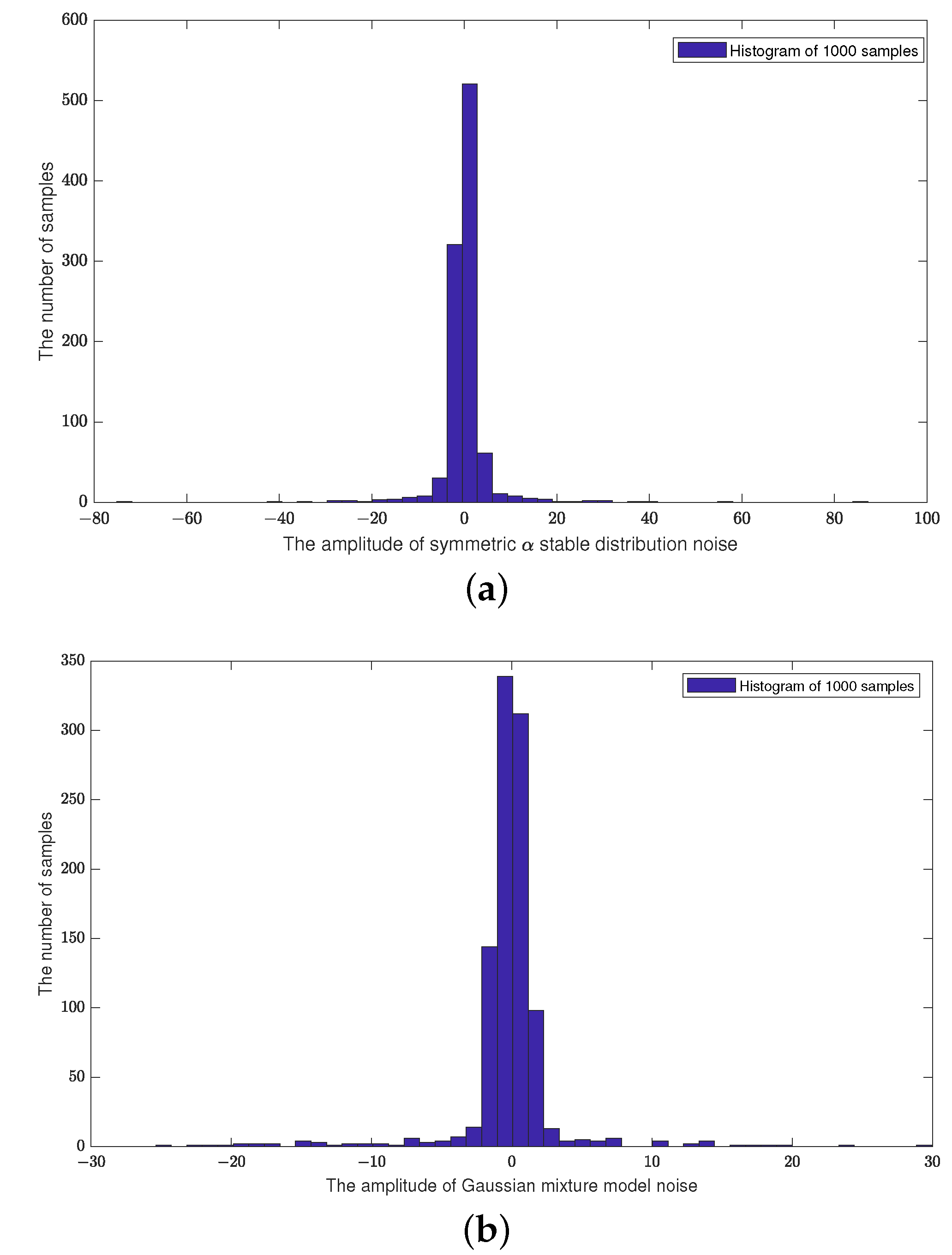
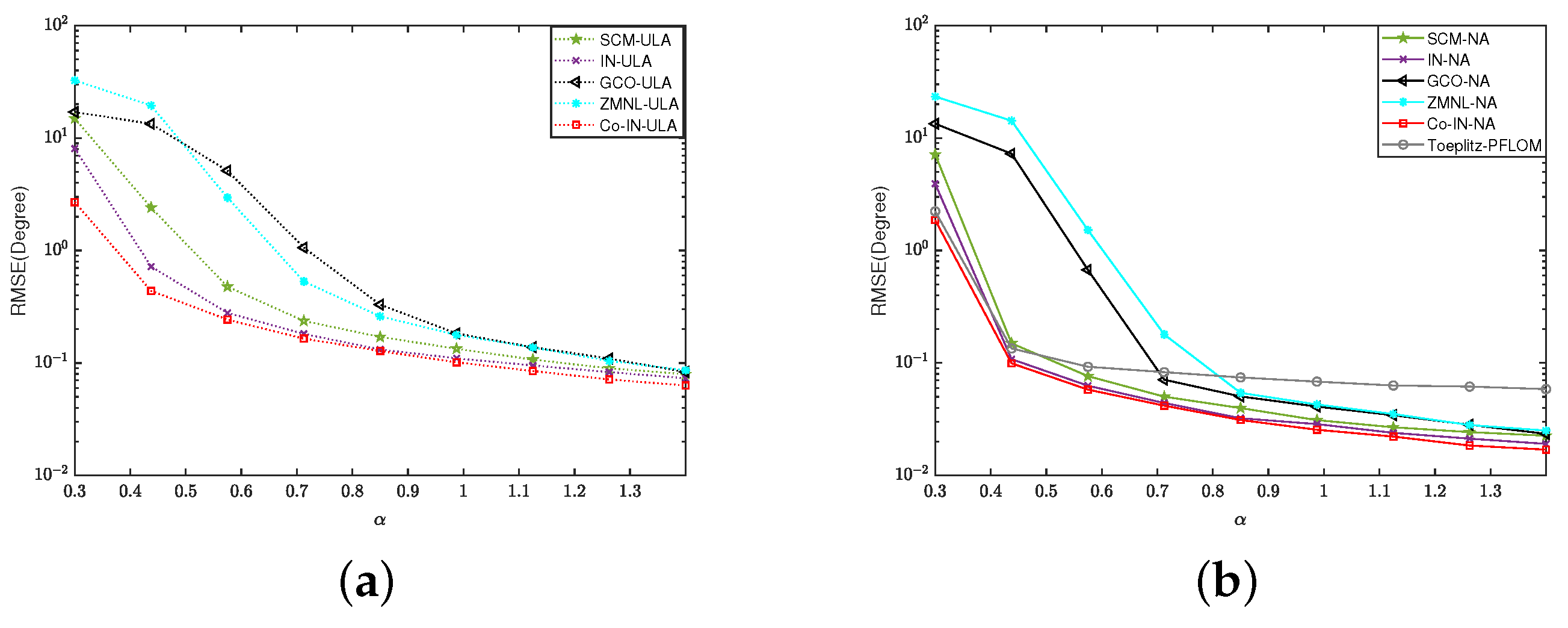
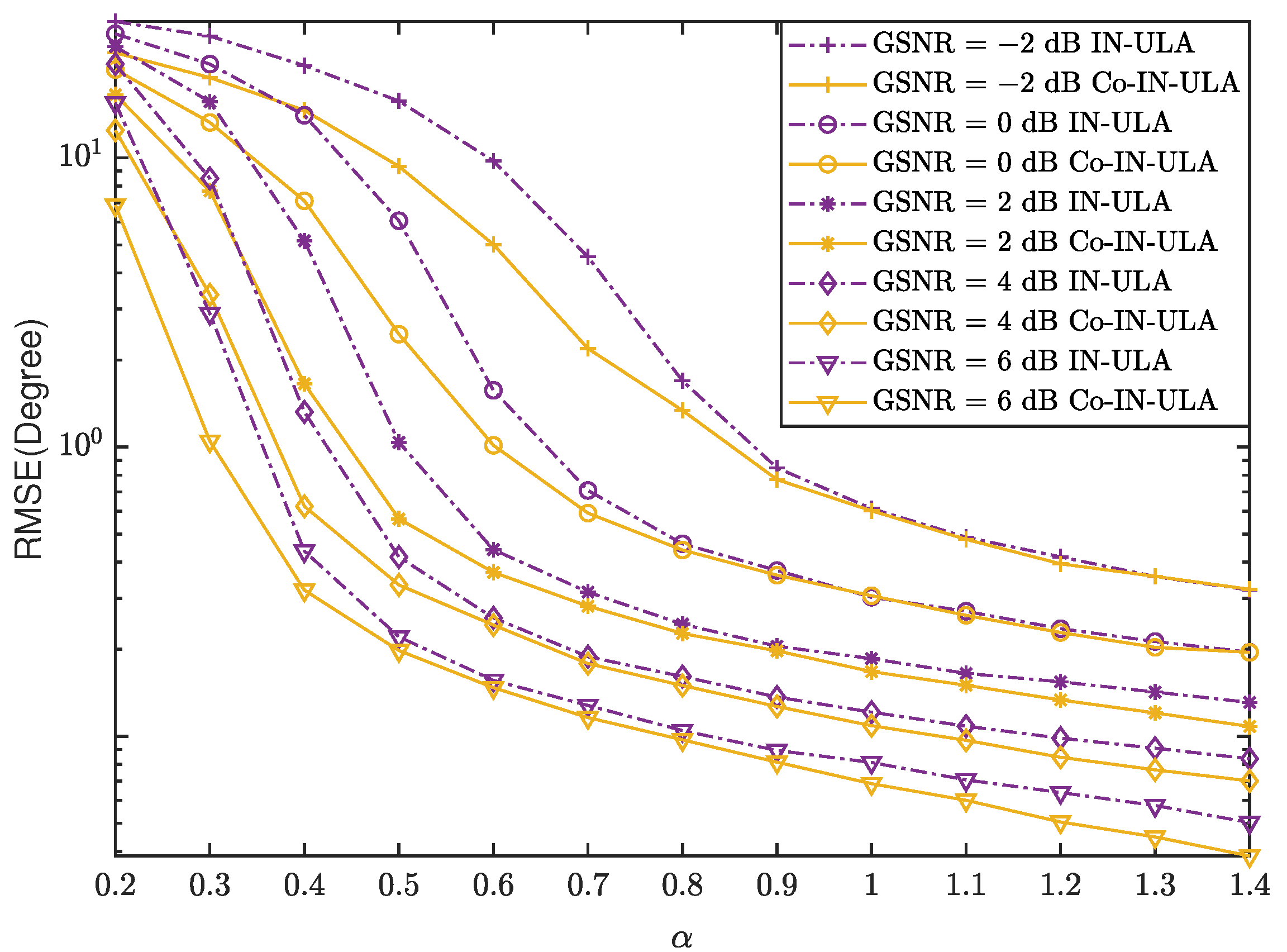
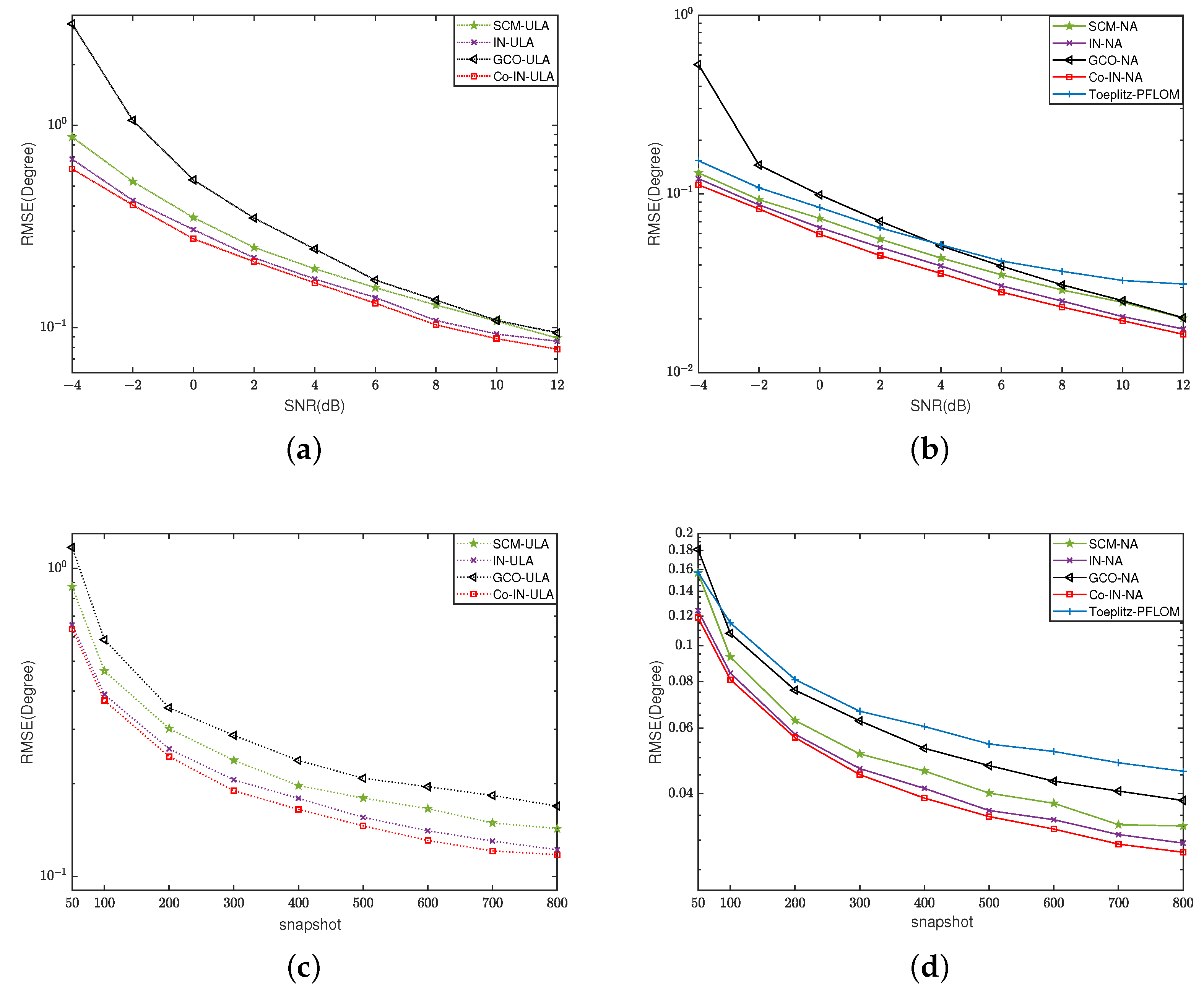
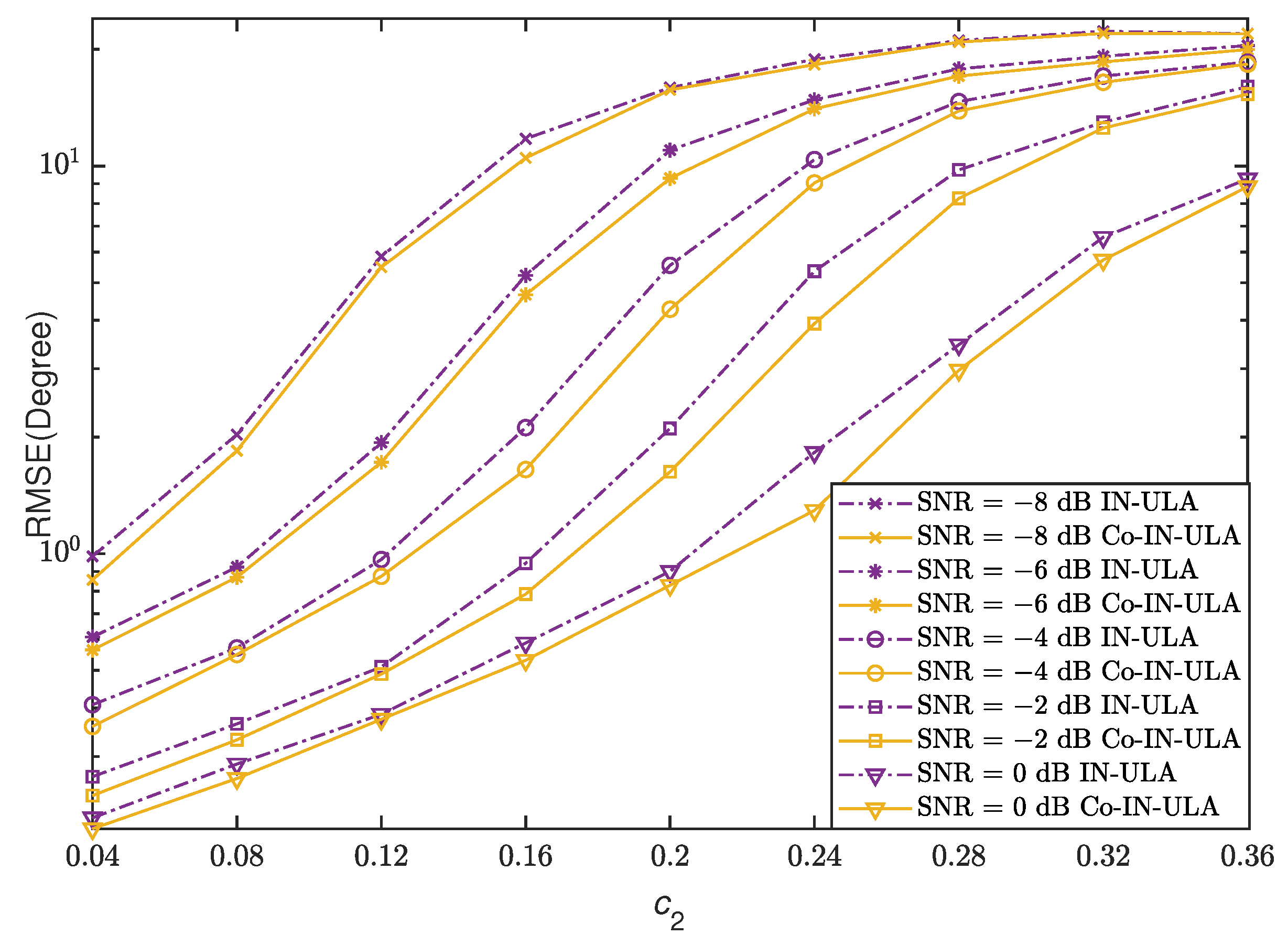
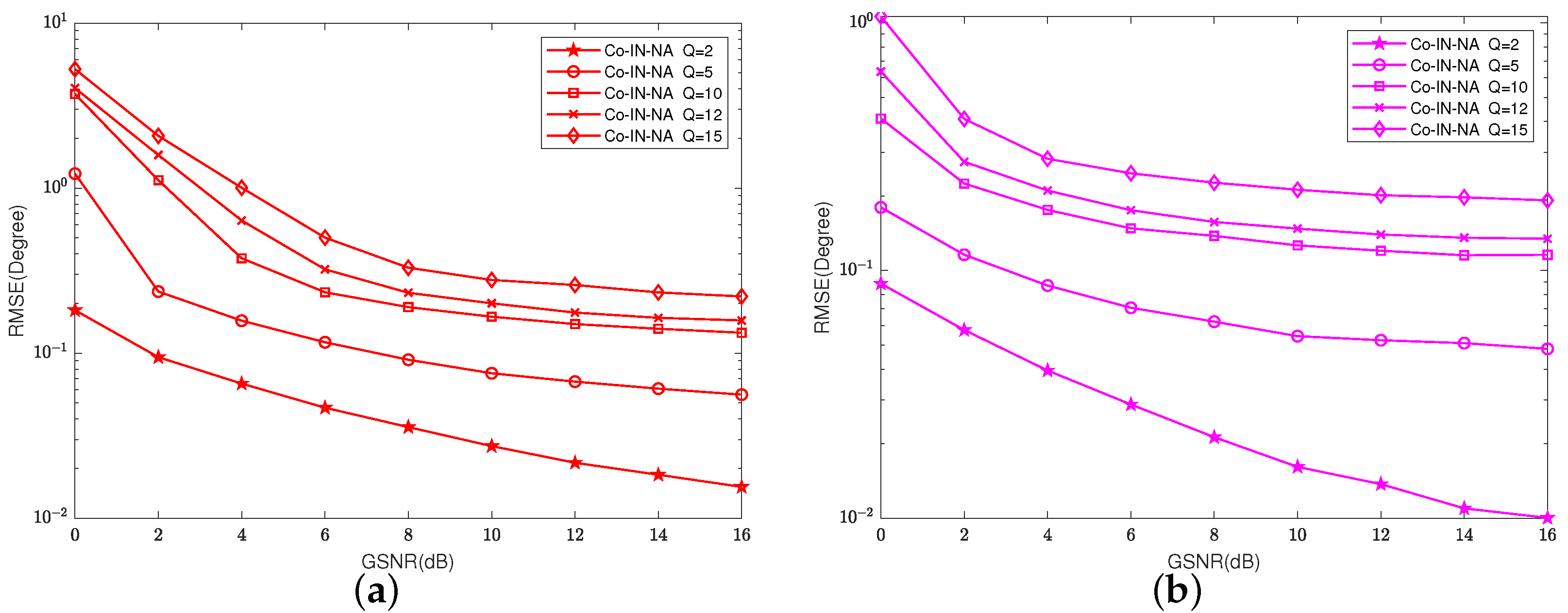
4.2. Impulsive Noise
4.3. Gaussian Mixture Heavy-Tailed Noise
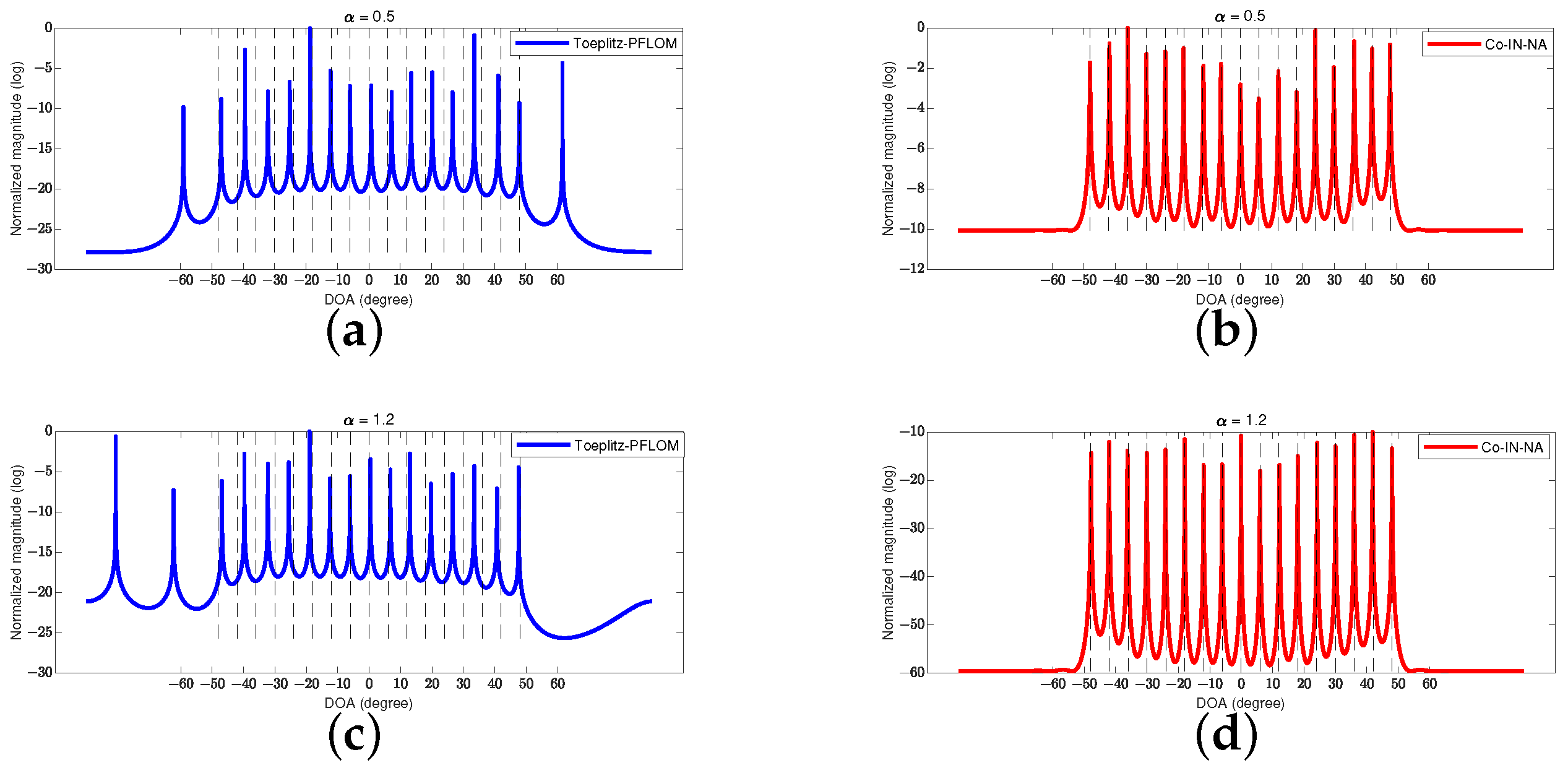
4.4. Underdetermined DOA Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Zhang, J.; Chu, P.; Liao, B. DOA estimation in impulsive noise based on FISTA algorithm. Remote Sens. 2023, 15, 565. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Yang, Q. DOA estimation of multiple coherent targets using weight vector orthogonal decomposition in TDM-MIMO HF-radar. Remote Sens. 2023, 15, 4073. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT—Estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Kozick, R.J.; Sadler, B.M. Maximum-likelihood array processing in non-Gaussian noise with Gaussian mixtures. IEEE Trans. Signal Process. 2000, 48, 3520–3535. [Google Scholar]
- Mirza, H.A.; Aslam, L.; Raja, M.A.Z.; Chaudhary, N.I.; Qureshi, I.M.; Malik, A.N. A new computing paradigm for off-grid direction of arrival estimation using compressive sensing. Wirel. Commun. Mob. Comput. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Mirza, H.A.; Raja, M.A.Z.; Chaudhary, N.I.; Qureshi, I.M.; Malik, A.N. A robust multi sample compressive sensing technique for DOA estimation using sparse antenna array. IEEE Access 2020, 8, 140848–140861. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, Z.W.; Khong, A.W.H.; Liu, H. An iterative implementation-based approach for joint source localization and association under multipath propagation environments. IEEE Trans. Signal Process. 2023, 71, 121–135. [Google Scholar] [CrossRef]
- Zamani, H.; Zayyani, H.; Marvasti, F. An iterative dictionary learning-based algorithm for DOA estimation. IEEE Commun. Lett. 2016, 20, 1784–1787. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, X.G.; Liu, H.; Nguyen, A.H.T.; Khong, A.W.H. Iterative implementation method for robust target localization in a mixed interference environment. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5107813. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H. Target height measurement under complex multipath interferences without exact knowledge on the propagation environment. Remote. Sens 2022, 14, 3309. [Google Scholar] [CrossRef]
- Shao, M.; Nikias, C.L. Signal processing with fractional lower order moments: Stable processes and their applications. Proc. IEEE 1993, 81, 986–1010. [Google Scholar] [CrossRef]
- Tsakalides, P.; Nikias, C.L. The robust covariation-based MUSIC (ROC-MUSIC) algorithm for bearing estimation in impulsive noise environments. IEEE Trans. Signal Process. 1996, 44, 1623–1633. [Google Scholar] [CrossRef]
- Mahmood, A.; Chitre, M.; Armand, M.A. PSK communication with passband additive symmetric α-stable noise. IEEE Trans. Commun. 2012, 60, 2990–3000. [Google Scholar] [CrossRef]
- Liu, T.H.; Mendel, J.M. A subspace-based direction finding algorithm using fractional lower order statistics. IEEE Trans. Signal Process. 2001, 49, 1605–1613. [Google Scholar]
- Visuri, S.; Oja, H.; Koivunen, V. Subspace-based direction-of-arrival estimation using nonparametric statistics. IEEE Trans. Signal Process. 2001, 49, 2060–2073. [Google Scholar] [CrossRef]
- Belkacemi, H.; Marco, S. Robust subspace-based algorithms for joint angle/Doppler estimation in non-Gaussian clutter. Signal Process. 2007, 87, 1547–1558. [Google Scholar] [CrossRef]
- He, J.; Liu, Z.; Wong, K.T. Snapshot-instantaneous infinity normalization against heavy-tail noise. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1221–1227. [Google Scholar]
- Swami, A.; Sadler, B.M. On some detection and estimation problems in heavy-tailed noise. Signal Process. 2002, 82, 1829–1846. [Google Scholar] [CrossRef]
- Zhang, J.; Qiu, T.; Song, A.; Tang, H. A novel correntropy based DOA estimation algorithm in impulsive noise environments. Signal Process. 2014, 104, 346–357. [Google Scholar] [CrossRef]
- Tian, Q.; Qiu, T.; Li, J.; Li, R. Robust adaptive DOA estimation method in an impulsive noise environment considering coherently distributed sources. Signal Process. 2019, 165, 343–356. [Google Scholar] [CrossRef]
- Ma, F.; Bai, H.; Zhang, X.; Xu, C.; Li, Y. Generalised maximum complex correntropy-based DOA estimation in presence of impulsive noise. IET Radar Sonar Navig. 2020, 14, 793–802. [Google Scholar] [CrossRef]
- Liu, Z.M.; Huang, Z.T.; Zhou, Y.Y. Array signal processing via sparsity-inducing representation of the array covariance matrix. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1710–1724. [Google Scholar] [CrossRef]
- Dai, J.; So, H.C. Sparse Bayesian learning approach for outlier-resistant direction-of-arrival estimation. IEEE Trans. Signal Process. 2017, 66, 744–756. [Google Scholar] [CrossRef]
- Zheng, R.; Xu, X.; Ye, Z.; Dai, J. Robust sparse Bayesian learning for DOA estimation in impulsive noise environments. Signal Process. 2020, 171, 107500. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P. Super Nested Arrays: Linear Sparse Arrays With Reduced Mutual Coupling Part I: Fundamentals. IEEE Trans. Signal Process. 2016, 64, 3997–4012. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P.P. Super Nested Arrays: Linear Sparse Arrays With Reduced Mutual Coupling Part II: High-Order Extensions. IEEE Trans. Signal Process. 2016, 64, 4203–4217. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Lu, Y.; Ren, S.; Cao, S. Augmented Nested Arrays With Enhanced DOF and Reduced Mutual Coupling. IEEE Trans. Signal Process. 2017, 65, 5549–5563. [Google Scholar] [CrossRef]
- Shaalan, A.M.; Du, J.; Tu, Y.H. Dilated nested arrays with more degrees of freedom (DOFs) and less mutual coupling—part I: The fundamental geometry. IEEE Trans. Signal Process. 2022, 70, 2518–2531. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Shi, Z.; Haardt, M. Structured Nyquist correlation reconstruction for DOA estimation with sparse arrays. IEEE Trans. Signal Process. 2023, 71, 1849–1862. [Google Scholar] [CrossRef]
- Zheng, H.; Zhou, C.; Shi, Z.; Gu, Y.; Zhang, Y.D. Coarray tensor direction-of-arrival estimation. IEEE Trans. Signal Process. 2023, 71, 1128–1142. [Google Scholar] [CrossRef]
- Zhao, J.; Gui, R.; Dong, X. DOA tracking with nested arrays via an improved multisource multi-Bernoulli filtering in the presence of impulsive noise. IEEE Sens. Lett. 2022, 6, 5501504. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, W.; Zhang, X.; Zheng, W. Transformed nested array designed for DOA estimation of non-circular signals: Reduced sum-difference co-array redundancy perspective. IEEE Commun. Lett. 2020, 24, 1262–1265. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing With Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Zheng, Z.; Huang, Y.; Wang, W.Q.; So, H.C. Augmented covariance matrix reconstruction for DOA estimation using difference coarray. IEEE Trans. Signal Process. 2021, 69, 5345–5358. [Google Scholar] [CrossRef]
- Dong, X.; Sun, M.; Zhang, X.; Zhao, J. Fractional Low-Order Moments Based DOA Estimation With co-Prime Array in Presence of Impulsive Noise. IEEE Access 2021, 9, 23537–23543. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, X.; Zhao, J.; Sun, M. Non-circular sources DOA estimation for coprime array with impulsive noise: A novel augmented phased fractional low-order moment. IEEE Trans. Veh. Technol. 2022, 71, 10559–10569. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Gui, R.; Dong, X.; Sun, M.; Wang, Y. Direction of Arrival Estimation with Nested Arrays in Presence of Impulsive Noise: A Correlation Entropy-Based Infinite Norm Strategy. Remote Sens. 2023, 15, 5345. https://doi.org/10.3390/rs15225345
Zhao J, Gui R, Dong X, Sun M, Wang Y. Direction of Arrival Estimation with Nested Arrays in Presence of Impulsive Noise: A Correlation Entropy-Based Infinite Norm Strategy. Remote Sensing. 2023; 15(22):5345. https://doi.org/10.3390/rs15225345
Chicago/Turabian StyleZhao, Jun, Renzhou Gui, Xudong Dong, Meng Sun, and Yide Wang. 2023. "Direction of Arrival Estimation with Nested Arrays in Presence of Impulsive Noise: A Correlation Entropy-Based Infinite Norm Strategy" Remote Sensing 15, no. 22: 5345. https://doi.org/10.3390/rs15225345
APA StyleZhao, J., Gui, R., Dong, X., Sun, M., & Wang, Y. (2023). Direction of Arrival Estimation with Nested Arrays in Presence of Impulsive Noise: A Correlation Entropy-Based Infinite Norm Strategy. Remote Sensing, 15(22), 5345. https://doi.org/10.3390/rs15225345